1월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
많은 분들이 참여해주셨는데 그 중 정답과 좋은 풀이를 함께 보내주신 김명수님께 Horizon에서 준비한 선물을 전달드릴 예정입니다.
첫 번째 숫자를 맨 뒤로 보냈을 때 원래 수의 절반이 되는 수는 여러 가지 방 법으로 구할 수 있다. 우선 마지막 숫자를 앞으로 보내서 원래 수의 두 배가 되는 것으로 바꾸어 생각해 보면, 우선 마지막 자리가 1이면 그 앞 자리는 2가 되어야 한다. 또, 2의 앞 자리는 4가 되고, 4의 앞 자리는 8, 이런 식으로 차례로 각 자리 수를 결정할 수 있다.
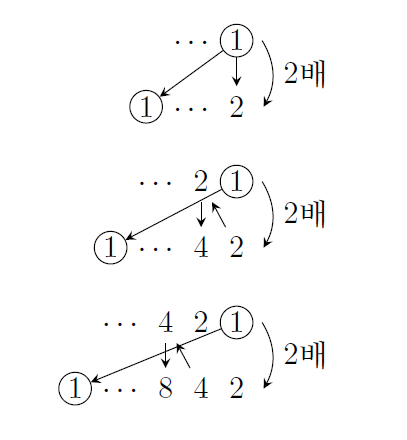
이제 마지막 네 자리수가 8421인 수를 두 배하면, 2 × 8 = 16으로부터 8의 앞 자리가 6이라는 것은 분명하다. 그러면, 다시 마지막 다섯 자리수가 68421인 수를 두 배하면, 2 × 6 = 12로부터 6의 앞 자리가 2가 되어야 하는데, 그 다음 자리인 8 을 두 배하면서 받아올린 1이 있으므로, 결국 6의 앞 자리는 2가 아닌 3이 된다.
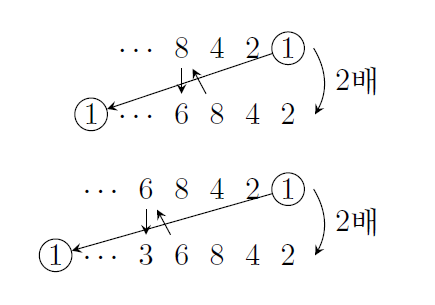
이런 식으로 각 자리 수를 두 배한 결과를 계속 적어 보면, 052631578947368421 을 두 배하여 첫 번째 자리에 1이 나타나는 105263157894736842에서 이 과정이 끝나게 된다. 그러면 우리가 찾는 수는 210526315789473684이고 이 수의 첫 번째 숫자 2를 맨 뒤로 보내면 정확하게 절반이 된다.
실은 더 간결한 풀이가 있다. 우리가 찾으려는 수를 무한히 반복하여 붙인 다음 앞에 소수점을 찍어 순환소수를 만들었다고 생각하면, 이 순환소수에 10을 곱한 결과의 소수 마디는 원래 순환마디의 첫 번째 숫자를 순환마디 맨 뒤로 보낸 것으로 생각할 수 있다.
\begin{align*}
&10 \times 0.\underline{a_1 a_2 a_3 \dots a_k} \, \underline{a_1 a_2 a_3 \dots a_k} \dots \\
&= a_1. \underline{a_2 a_3 \dots a_k a_1} \, \underline{a_2 a_3 \dots a_k a_1} \dots
\end{align*}
두 번째 순환소수의 순환마디가 첫 번째 순환소수의 순환마디의 절반이므로, 첫 번째 순환소수를 \(x\)라 하면,
\[
10x = a_1 + \frac12 x
\]
가 된다. 방정식을 풀면 \(x = \frac{2}{19}a_1\)이므로, \(a_1=1\)이면
\[
\frac{2}{19} = 0.\dot{1}0526315789473684\dot{2}
\]
로부터 열여덟 자리 수인 105263157894736842를 얻는다. 이 수의 첫 번째 숫자 1을 맨 뒤로 보내도 절반이 되기는 하지만, 이 경우는 첫 번째 숫자가 0이 되므로, \(a_2=2\)일 때를 생각하면 우리가 원하는 수 210526315789473684를 얻고 이것이 조건을 만족하는 가장 작은 수라는 사실까지 알 수 있다.