4월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
4월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 김종일님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
이번 문제는 Journal of Recreational Mathematics 1978년 10권 53호에 실린 599번 문제로 원작자는 Les Marvin이다. 유명한 마틴 가드너의 저서에도 실려 있는데, 틱택토와 관련된 문제 가운데 어려운 문제로 소개하는 정도여서, 풀이 없이 “정답은 1978년 11권 1호를 보라”라고만 적어 놓았다.
먼저 이 게임의 마지막 수를 누가 두었는지 생각해 보자. 만약 이 게임을 다시 시작하였을 때 X가 둘 차례라면 4번 자리에 X를 놓는 순간 게임은 X의 승리로 끝이 난다. 반면에 O가 둘 차례라면 비어 있는 세 자리 어디를 두어도 절대로 이길 수가 없다. 따라서 이 게임은 분명히 X가 어딘가에 두면서 무승부로 끝이 났음을 알 수 있다.
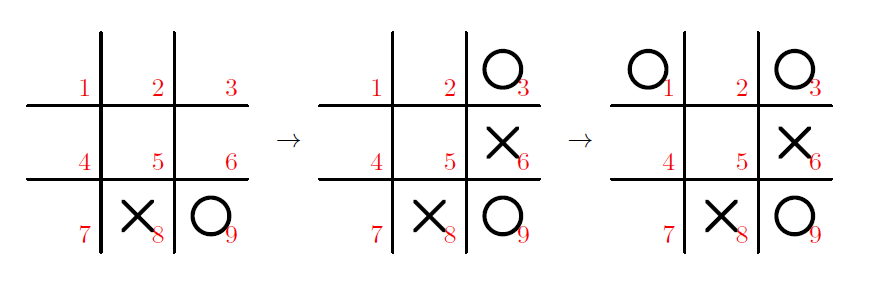
이제 X가 두었던 마지막 수가 어디인지 알아보자. X가 마지막으로 둔 수가 8번 자리였다면, 이 자리에 두기 직전 상황은 다음과 같고, 이때는 X가 4번 자리에 두어 이길 수 있다. 따라서 X가 마지막에 둔 수는 8번일 수가 없다.
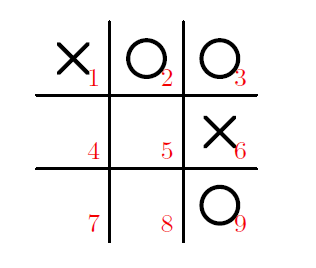
그러면 X가 마지막 수를 두기 직전 상황은 다음 두 경우 가운데 하나이다. 두 경우 모두 O 두 개가 나란히 놓여서 비어 있는 한 자리를 막는 상황이다.
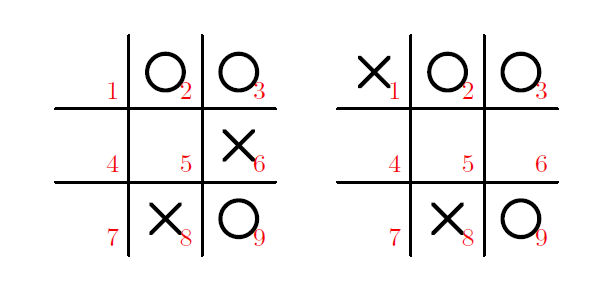
왼쪽 상황의 경우, O가 어딘가에 두어서 만들어진 것인데, 명백히 9번 자리에 두었을 리가 없다. 바로 1번 자리에 놓으면 승리하기 때문이다. 또, O가 2번 자리에 놓아서 이 상황이 만들어졌다면, 2번에 놓는 대신 1번에 놓아서 이길 수 있었다. 3번의 경우도 마찬가지. 따라서 첫 번째 상황은 O가 엉터리로 게임을 진행하지 않는 한 나타날 수가 없다. 그러므로 X의 마지막 수는 6번 자리에 놓으면서 3번과 9번의 O가 한 줄이 되지 않게 막은 것이라는 결론을 내릴 수 있다.
이제 오른쪽 상황을 O의 차례에서 생각해 보면, O가 2번 자리에 놓아서 저런 상황이 될 수는 없다. 6번 자리에 놓는 순간 이길 수 있기 때문이다. 따라서 오른쪽의 상황은 다음 두 상황에서 O가 3번 또는 9번에 놓으면서 만들어진다고 할 수 있다.
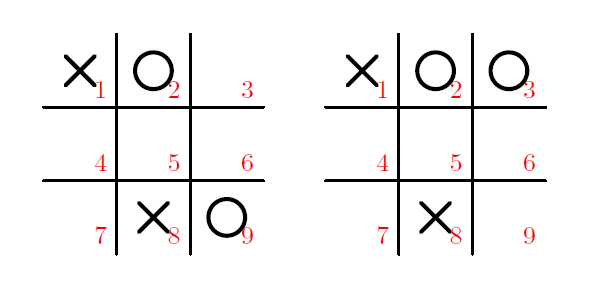
그런데 O가 첫 수를 3번이나 9번에 놓는 경우, X가 1번이나 8번에 놓는 것으로는 O가 이기는 것을 막을 수가 없다. 예를 들어, O가 첫 수를 9에 놓고, X가 다음 수를 8에 놓았다면, O3 – X6 – O1로 O가 이길 수 있다.
따라서 O는 첫 수를 2번에 두었고, X는 마지막 수를 6번에 두었음을 알 수 있다.
같은 방식으로 O와 X가 놓은 수를 조사해 보면, 이 게임이 진행된 수순은
O2 – X1 – O9 – X8 – O3 – X6
O2 – X8 – O9 – X1 – O3 – X6
O2 – X8 – O3 – X1 – O9 – X6
의 세 가지가 가능하다.
다음은 4월의 정답자로 선정된 김종일님의 해설입니다.
1) 누가 먼저 시작했는지부터 생각해보자. 만약 현재 X가 할 차레라면, 4에 놓음으로써 이길 수 있다. 따라서 지금은 O의 차례이고, O가 제일 처음에 시작했다는 것을 알 수 있다.
2) 첫번째 수에 대하여 하나씩 제거해나가는 방법을 써보자.
2-1) 첫번째 O의 수가 3이었다고 가정해보자.
2-1-1) X가 1에 놓았다면, O(9)-X(6)-O(7)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다,
2-1-2) X가 8에 놓았다면, O(9)-X(6)-O(1)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
2-1-3) X가 6에 놓았다면, O(1)-X(2)-O(7)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
따라서 O가 처음 3에 놓은 것은 아니라는 것을 알 수 있다.
2-2) 첫번째 O의 수가 9였다고 가정해보자.
2-2-1) X가 1에 놓았다면, O(3)-X(6)-O(7)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다,
2-2-2) X가 8에 놓았다면, O(3)-X(6)-O(1)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
2-2-3) X가 6에 놓았다면, O(7)-X(8)-O(1)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
따라서 O가 처음 9에 놓은 것은 아니라는 것을 알 수 있다.
그러므로 O가 처음 2에 놓았다는 것을 알 수 있다.
3) 비슷한 방식으로 X의 다음 수를 생각해보자
3-1) 만약 X가 6에 놓았다면, O(5)-X(8)-O(3)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
3-2) X가 1에 놓았다고 가정해보자,
O의 다음수가 3이었다면, X(7)-O(4)-X(9)라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
따라서 O의 다음 수는 9일 수 밖에 없고,
O(2)-X(1)-O(9)-X(6)-O(3) 의 순서로 진행되었다면, X를 4에 놓아 이길 수 있는데도 8에 놓았다는 것이 비논리적이므로,
O(2)-X(1)-O(9)-X(8)-O(3)-X(6) 의 순서가 유일한 가능성이다.
3-3) X가 8에 놓았다고 가정해보자.
3-3-1) 만약 O의 다음 수가 9였다면,
O(2)-X(8)-O(9)-X(6)의 진행은, O(1)이라는 외통수가 존재하는데 그렇게 하지 않았으므로 아니다.
따라서 O(2)-X(8)-O(9)-X(1)-O(3)-X(6)의 순서가 유일한 가능성이다
3-3-2) 만약 O의 다음 수가 3이었다면,
O(2)-X(8)-O(3)-X(1)-O(9)-X(6)의 순서로 진행되었어야 한다.
따라서 다음과 같이 3가지 가능한 순서가 있다는 것을 알 수 있다.
O(2)-X(1)-O(9)-X(8)-O(3)-X(6)
O(2)-X(8)-O(9)-X(1)-O(3)-X(6)
O(2)-X(8)-O(3)-X(1)-O(9)-X(6)
이 세가지 경우 모두 시작은 2이고 마지막은 6이다.