패턴의 과학 [1]: 패턴의 자기닮음꼴과 프랙탈 차원

1. 왜 패턴에 관심을 갖는가

자연에는 다양한 종류의 패턴이 존재한다. 작게는 나노미터 스케일에서 관측되는 단결정^{single crystal}의 격자^lattice 패턴부터 애니메이션 <니모를 찾아서>의 주인공이자 남태평양에서 서식하는 열대어 흰동가리의 줄무늬 패턴과 뭉게구름의 변화무쌍한 형태까지, 스케일을 더 확장하면 목성의 두꺼운 대기 순환이 만들어낸 지구보다 수 배나 큰 대적점 같은 소용돌이 패턴^{vortex pattern}부터 우리 은하에 분포하는 수천억 개의 별들이 이루는 나선형 팔 모양의 패턴까지, 더 나아가면 우주 마이크로파 배경^{cosmic microwave background, CMB}의 미세하지만 분명히 존재하는 열적 요동^{thermal fluctuation}의 패턴까지 우주의 거의 모든 스케일에 걸쳐 갖가지 종류의 패턴이 관측된다.

물론 패턴이 자연에만 존재하는 것은 아니다. 시시각각 변동하여 투자자들의 마음을 졸이게 만드는 주가 변동 시계열 데이터에도 패턴이 감춰져 있고 나일강의 범람 규모를 수천 년 동안 추적한 지리 관측 데이터에도 패턴이 숨어 있다. 히말라야 산맥에 위치한 고산준봉들의 높이와 면적 분포도에도 지배적인 패턴이 있고 야구 경기에서 타자를 속이기 위해 유인구를 배합하는 투수의 투구에도 패턴은 존재한다. 소셜네트워크^SNS 상에서 사람들의 의견이 형성되고 전파되는 과정에도 특정한 종류의 패턴이 발견되며 도시의 도로가 연결되는 방식을 추상화한 데이터에도 패턴이 있고 인류 문명사에 켜켜이 수 놓인 전쟁의 역사에도 반복되는 패턴이 있는 것처럼 보인다.

자연에서든 사회에서든 역사에서든 그리고 인공적인 것이든, 인간이 패턴을 인식하는 과정은 감각 기관에서 관찰 대상의 신호를 처리함으로써 시작된다. 예를 들어 전자현미경으로 관찰한 나노미터 스케일의 결정 구조는 일련의 신호처리과정을 거쳐 2차원 혹은 3차원 이미지로 인간의 시각 기관이 인지할 수 있는 스펙트럼, 즉, 가시광선 대역에서 시각화된다. 격자 같은 패턴은 질서정연하다는 특징이 있기 때문에 재료의 결정 구조를 잘 모르는 사람이 봐도 한눈에 규칙성 있는 패턴의 존재를 알아차리는 것은 어렵지 않다.

예를 들면 가청 주파수 범위에 섞여 있는 다양한 주파수의 진동하는 공기 밀도는 파동의 형태로 인간의 귀로 전달되고 달팽이관 속에서 청각 신호로 바뀌어 그것이 아름다운 하모니의 패턴인지 아니면 불규칙한 소음인지 구분된다. 필자의 장남이 다섯 살 무렵, 필자의 노트북에서 블록공중합체^{block copolymer} 박막의 미세한 자기조립 패턴^{self-assembly pattern}의 전자현미경 사진을 비교한 데이터를 보고, 열 개의 샘플 사진 중 어떤 샘플이 가장 예쁜 패턴을 가지고 있는지 (다른 말로 하면 어떤 샘플이 가장 반듯한지를) 단번에 알아맞힌 적이 있다. 이에 깜짝 놀란 필자는 어린 아이도 패턴의 규칙적인 수준을 상대적으로 비교하고 그로부터 심미적 가치도 느끼는 것을 보고 인간에게 모종의 정보 처리 회로 혹은 그에 해당하는 기능이 있는 것은 아닐까 생각한 적이 있다.

하지만 특정 신호 속에 숨어 있는 패턴의 특징을 명확하게 감지하는 것은, 설사 훈련받은 연구자라고 해도 인간의 감각 기관에만 의존하는 것만으로는 충분하지 않은 경우가 대부분이다. 예를 들어 컴퓨터의 도움 없이 거대한 데이터 속에 숨어 있는 신호의 주기성^periodicity이나 특이성을 본능적으로 알아 내기는 쉽지 않으며 신호의 구조가 복잡할수록 관찰만으로 패턴을 단번에 인식하기가 어려워진다. 그럼에도 불구하고 인간의 호기심과 미적 가치를 탐하는 본능은 주변 데이터에 내재된 패턴을 무시하기보다는 찾는 쪽을 선호하는 것으로 보인다. 애초 인간이 패턴을 인식하고 싶어하는 이유 중 하나가 예측 가능성을 높여서 주변 환경 변화에 대비하거나 정보 처리에 필요한 자원의 소모를 줄이려는 목적이라고 추정하는 심리학 혹은 인지 과학 이론도 있다.[1]

인간은 대칭 구조에서 아름다움을 느끼는 경우가 많은데 이 역시 대칭으로 대표되는 아름다움이라는 가치 속에 패턴이 갖는 정보 처리의 효율성이 내재되었기 때문이라고 생각할 수 있다. 따라서 아무리 복잡한 신호와 데이터라고 해도 어떤 패턴이 숨어 있다면 그것이 무엇인지, 얼마나 복잡한 것인지, 다른 것과 어떻게 구분이 되는지 알아내려고 하는 인간의 노력은 계속될 것이다. 불운하게도 그것이 개인의 암묵지나 경험에만 의존할 수는 없으므로 결국 패턴에 대한 이해는 과학적인 방법, 특히, 주로 수학과 물리학적 방법에 의존할 수밖에 없다.

필자의 연구 분야는 나노미터 수준에서 관측되는 갖가지 재료의 자기조립, 마이크로미터 스케일에서 관측되는 빛과 물질의 상호작용, 밀리미터나 센티미터 수준의 현상을 해석하는 계산 과학까지 비교적 넓은 스케일에 걸쳐 다양한 편이지만, 전체를 관통하는 핵심 키워드가 있다면 그중 하나는 아마도 ‘패턴’일 것이다. 나노미터 스케일의 격자나 자기조립 패턴부터 뇌파 등 생체 신호의 복잡도 계산까지 필자가 관심있는 것은 바로 데이터나 신호에 내재된 패턴의 수학적 특징을 명확히 밝혀내고 그것을 공학적으로 응용하는 일이다. 이를 다른 말로 풀어 쓰면 분석 대상인 데이터에 내재된 질서도^order 혹은 정보를 알아내는 것이고 조금 더 상세하게 이야기한다면 이를 정량적으로 측정하고 다른 신호와 구분하는 것이다.

단도직입적으로 필자가 연구하는 분야의 패턴 분석에 대한 이야기를 바로 시작하는 것도 나쁘지는 않겠으나, 그에 앞서 패턴 분석이 어떠한 방식을 거치고 있는지에 대해 살펴보는 것도 좋을 것이다. 본 글은 주로 패턴의 복잡도 분석에 초점을 맞출 것이고 1부에서는 패턴에 내재된 자기닮음꼴과 프랙탈 차원 분석, 2부에서는 패턴의 정보량을 직접적으로 측정할 수 있게 해 주는 엔트로피^entropy의 개념과 실제 측정 사례 등에 대한 내용을 살펴볼 것이다.

2. 패턴의 자기닮음꼴

자연에 존재하는 패턴 중에는 축척^scale을 달리해도 비슷한 특징이 계속 나타나는 경우가 자주 보인다. 예를 들어 산에 가면 흔히 볼 수 있는 고사리 같은 양치 식물은 적어도 세 번 정도 일부분만 계속 확대해도 원래의 이파리 배치 패턴이 그대로 유지되는 것을 볼 수 있다. 적란운 같은 구름 역시 멀리서 볼 때나 가까이에서 확대해서 볼 때나 축척을 가리면 구분할 수 없는 비슷한 뭉게구름 형태를 가지는 경우가 있으며 산의 지형적 특성 역시 관측하는 스케일에 상관 없이 서로 닮아 보이는 형태가 유지되는 경우를 자주 볼 수 있다. 이렇게 관측하는 축척에 상관 없이 특정한 모양^motif이 지속적으로 유지되는 특징을 자기닮음꼴^{자기상사성, self-similarity}이라고 한다. 자연에서 이러한 닮음꼴 유지가 자주 관측되는 것은 우연이 아니다. 고사리나 브로콜리 같은 식물을 예로 들어 보자. 자기닮음꼴만 유지된다면 유전 정보를 여러 종류로 갖출 필요 없이 간단한 유전 정보의 조합만으로도 제한된 공간에서 최대한 복잡한 형태를 만들고 나아가 다양한 기능을 갖출 수 있다. 그것이 왜 생명체에 유리한 것일까? 예상할 수 있다시피 이는 생명체가 오랜 시간 동안 살아 남고 또한 다음 세대에 무사히 유전 정보를 넘기는 과정에 더 유리하기 때문이다.

지난 6월, 영국의 과학잡지 네이처에는 두뇌가 외부의 정보를 인지하는 과정에서 가능한 단위 시간 동안 많은 시각 정보를 처리하고 외부의 노이즈에 유연하게 대처하기 위해 시각 중추의 시각 반응이 신경 자극에 대해 멱함수^{거듭제곱함수, power-law} 의존성을 보인다는 연구 논문이 게재되었다.[2] 정보 처리 과정에서 관측된 멱함수 관계는 시신경 세포들의 신경 반응에 자기닮음꼴 패턴이 있다는 것을 의미하는 것이기도 하다. 앞서 언급한 고사리의 경우 대칭의 기준이 되는 한 선분에서 양쪽으로 이파리가 몇 개 나올 것인지 정도만 유전자 속에 암호화 해 놓으면 (나중에 살펴 보겠지만 이는 L-system이라는 자기닮음꼴 생성을 코딩하는 컴퓨터 형식 문법으로 재현이 가능하다.) 별다른 어려움 없이 제한된 면적에 최대한 많은 이파리들을 채워 넣어서 단위 면적 당 광합성의 효율을 높일 수 있다.

반면 자기닮음꼴을 통해 유전 정보가 절약되는 이점이 없다면, 고사리는 주어진 면적을 복잡한 모양으로 채우기 위해 매번 분기할 때마다 서로 다른 유전 정보에 대한 참조가 반복적으로 필요할 것이고, 다음 세대로 복잡한 유전 정보를 전달하는 과정에서 오류율^{error rate}도 누적될 것이다. 결국 고사리는 유전 정보를 수백 수천 세대에 걸쳐 안정적으로 전달할 수 있을 정도로 오래 존속할 수 없었을 것이다. 물론 생명체의 유전 정보 활용만이 생명체에서 관측되는 자기닮음꼴의 근본 원인은 아니다. 다만 왜 자기닮음꼴이 생명체에 나타날 수 있는지 주요 원인 중 하나 정도로 해석하면 될 것이다.

자기닮음꼴은 비단 생명체에서만 관측되는 것은 아니다. 자기닮음꼴이 항상 동반하는 특징이 척도불변성^{scale-invariance}라는 사실을 상기하면 자기닮음꼴은 통계물리학에서 말하는 임계 현상^{critical phenomena}에서도 자주 관측된다. 예를 들어 계가 상전이를 겪을 때 계의 질서도 파라미터^{order parameter}는 상전이를 일으키는 변수(예를 들어 온도나 압력, 자기장의 세기 등)에 대해 멱함수 의존 관계를 갖는다. 상전이는 계가 열역학적으로 불안정한 상태에 있다는 것이므로 시간에 따라 계는 상태 변화를 겪는다. 예를 들어 작은 입자가 액상에 분산되어 있다가 분산 안정성을 잃어버리면 시간이 지남에 따라 입자들이 서로 뭉치게 된다. 이 현상의 동적 특징이 주로 확산^diffusion에 의해 지배를 받으면 이를 확산한계응집^{diffusion-limited aggregation, DLA}이라고 한다. [그림1]처럼 작은 클러스터가 생기는 지점을 중심으로 바깥 방향을 향해 점점 응집 구조가 확산되는 양상이 DLA의 대표적인 특징이다. 이는 나뭇가지의 가지치기, 혹은 번개의 갈라짐 형상(분기 패턴)과도 매우 닮았다. DLA를 비롯하여 나무와 번개의 패턴 등은 공통적으로 척도불변성을 보이는데, 따라서 이들은 모두 자기닮음꼴을 갖는다.

또한 지진이 발생하는 빈도와 지진의 강도 사이 혹은 산불의 빈도와 규모 사이, 인구 규모 별로 줄 세운 도시의 규모 분포 등에서도 척도불변성이 자주 관측되고, 따라서 이러한 동적 현상의 이면에도 자기닮음꼴이 숨어 있음을 알 수 있다. 바흐의 첼로 조곡 ^{cello suites}에서도 자기닮음꼴이 발견되는데[3], 바흐가 의도적으로 수학 이론을 상정하여 자기닮음꼴을 갖게끔 인위적으로 화성을 설계했을 것 같지는 않지만 복잡한 멜로디 속에 단순한 원칙이 자리잡고 있다는 것은 사뭇 흥미로운 부분이다.

자기닮음꼴을 찾는 과정에서 빈도와 형상의 크기 사이에는 멱함수 관계가 자주 관측된다. 예를 들어 앞서 언급한 고사리 이파리의 경우 길이가 반으로 줄어들면 이파리 개수는 서너 배로 늘어나는 관계, DLA 현상의 경우 입자들이 뭉치는 과정에서 관측되는 클러스터의 크기와 출현 빈도의 관계, 지진의 진도와 빈발 횟수의 관계 등 다양한 현상, 다양한 패턴에서 멱함수 의존성이 관측된다. 사실 멱함수가 척도불변성을 만들어 낼 수 있는 유일한 수학적 관계라는 사실을 알게 되면 이는 그렇게 신기한 사실이 아닐 수 있다. 척도불변성을 동반하는 자기닮음꼴은 어떤 대상의 부분을 확대해도 전체와 비슷하다는 것을 의미하고, 이를 수학적으로 표현하면 어떤 대상을 묘사하는 함수 \(f(x)\)에 대해, \(x\)를 상수 \(b\)배 만큼 변화시켰을 때 \(f(bx) = g(b)f(x)\)의 관계식을 가짐을 의미한다. 이 관계식에서 볼 수 있다시피 \(x\)가 \(bx\)로 바뀌었음에도 불구하고 그 결과물인 \(f(bx)\)에는 여전히 원래의 함수가 주는 정보인 \(f(x)\)가 포함되어 있다. 단지 비례 상수 \(g(b)\)만 추가로 생겨났을 뿐이다.

이러한 관계식을 만족하는 함수가 왜 멱함수 밖에 없는지 알아 보자. 우선 관계식 \(f(bx) = g(b)f(x)\)에서 \(x=1\)이라고 한다면, \(g(b) = \frac{f(b)}{f(1)}\)이 되므로 관계식은 \(f(bx) = \frac{f(b)f(x)}{f(1)}\)이라고 쓸 수 있다. 이제 양변을 \(b\)에 대해 미분하면 \(xf’(bx) = f’(b)\frac{f(x)}{f(1)}\)이 되는데, 이 관계식에 \(b=1\)을 대입하면 \(xf’(x) = f’(1)\frac{f(x)}{f(1)}\)이 된다. 이때 \(a= -\frac{f’(1)}{f(1)}\)이라고 정의한다면 \(\frac{f’(x)}{f(x)} = -\frac{a}{x}\)가 되고, 양변을 \(x\)에 대해 적분하면 \(\log f(x) = -a*\log (x) + \log f(1)\)이 된다. 이를 다시 쓰면 \(f(x) = f(1)x^{-a}\)의 관계가 나오는데 이 관계는 다름 아닌 멱함수, 즉, 거듭제곱함수다. 특히 \(\log f(x) = -a*\log (x) + \log f(1)\)의 관계식을 다시 쓰면 \(\log f(x) = a*\log (\frac{1}{x}) + \log f(1)\)이며, 이때, 양변을 \(\log (\frac{1}{x})\)로 나눠 주면 \(\frac{\log f(x)}{\log (\frac{1}{x})} = a + [\frac{\log f(1)}{\log (\frac{1}{x})}]\)이 되고, 여기서 \(f(1)\)는 상수로 생각할 수 있으므로 \(x\)가 점점 작아지면 \([\frac{\log f(1)}{\log (\frac{1}{x})}]\)는 무시할 수 있게 되어\[\lim_{x \to 0} \frac{\log f(x)}{\log (\frac{1}{x})} =a\]의 관계식을 얻을 수 있다.

이 관계식을 이용하면 이제 자기닮음꼴을 갖는 대상의 차원, 즉, 프랙탈 차원^{fractal dimension}을 추정할 수 있는 도구가 생긴다. ‘프랙탈^fractal’이라는 용어는 프랑스의 수학자 망델브로^{B. Mandelbrot}가 1970년대 비선형 동역학^{nonlinear dynamics}의 시간매개형 궤적에서 관측되는 혼돈계^{chaotic system}의 자기닮음꼴을 설명하기 위해 처음 창안한 단어로서, 대상의 차원이 정수가 아닌 경우, 즉, 부분적 차원^{fractional dimension}이라는 의미에서 비롯된 용어다. 우리가 사는 공간은 \(3\)차원이고 이미지는 \(2\)차원이며 선분은 \(1\)차원이라는 것은 당연해 보이는데 어떻게 \(1, 2, 3\) 같은 자연수가 아닌 차원이 존재할 수 있는 것일까? 마치 ‘\(9\)와 \(\frac{3}{4}\)번 승강장’은 해리포터 소설 속에만 존재하는 것처럼 프랙탈 차원도 가상의 세계에서나 존재하는 대상인 것일까? 다행히 프랙탈 차원은 해리포터가 마법처럼 사라졌던 승강장과는 달리 수학적으로 명확하게 정의되고 물리적 의미도 부여할 수 있는 대상이다. 그리고 그 정의는 앞서 유도했던 자기닮음꼴의 관계식으로부터 자연스럽게 유도되는 개념이기도 하다.

여기서 한 가지 유의할 부분은 프랙탈이 반드시 ‘완벽한’ 자기닮음꼴을 가져야만 한다는 것은 아니라는 것이다. 엄밀한 의미에서 완벽한 자기유사성을 갖는 프랙탈은 기하학적 프랙탈 밖에 없으며, 이는 이론적으로는 반복함수계^{iterated function systems, IFSs}를 통해서만 생성될 수 있다. 여기서 말하는 반복함수계는 이름 그대로, 어떤 기하학적 특성을 만들어내는 함수를 재귀적으로 반복 적용하는 개념을 말한다. 통계적인 유사성을 만족하는 패턴(망델브로 집합^{Mandelbrot set}이나 쥘리아 집합^{Julia set}이나 대략적인/느슨한 유사성을 갖는, 자연에서 발견되는 자기닮음꼴 패턴 등), 무작위적 프랙탈^{stochastic fractal}은 넓은 의미에서는 프랙탈로 분류되지만, 척도에 무관한 자기닮음꼴이 완벽하게 유지되는 것은 아니다. 그렇지만 본 글에서는 완벽한 자기유사성과 느슨한 자기유사성을 엄밀하게 구분하지 않고 넓은 의미에서 자기닮음꼴-프랙탈 차원의 관계를 다룰 것이다.

정수가 아닌 차원이 어떤 의미를 갖는지 알아보자. 바삭바삭한 튀김옷이 잘 입혀진 치킨 한 조각을 생각해 보자. 그리고 뜬금없는 질문을 던져 보자. 이 치킨 조각의 표면적은 얼마인가? 넓게 잡아 봐야 \(100\, cm^2\)도 안 될 것 같아 보인다. 그렇지만 사실 이 문제는 치킨이 지극히 친숙한 간식이라는 사실과는 달리 만만한 문제가 아니다. 예를 들어 누군가는 치킨의 튀김옷을 전부 떼어 내 그것의 부피를 측정하려는 시도를 할 수도 있을 것이고 누군가는 치킨을 다양한 각도에서 사진 찍어서 치킨이 차지하는 픽셀 개수의 평균을 구해 보려는 사람도 있을 것이다. 만약 치킨을 전

자현미경으로 관찰한다면 튀김옷을 이루는 튀김가루와 기름 그리고 첨가물이 만들어 낸 미세한 다공성의 거친 구조까지 관찰할 수 있을 것이고 더 자세하게 관찰하면 관찰할수록 치킨 조각의 표면적은 점점 증가할 것이다. 즉, 치킨 조각의 표면적은 어떤 스케일에서 얼마나 자세하게 관찰하느냐에 따라 달라지는 것이다. 불행히도 전자현미경으로 관찰하여 표면적이 엄청나게 넓어졌다고 해서 치킨의 양이 더 늘어나는 것은 아니다.

앞서 이미지 픽셀을 이야기했으니 이 개념을 계속 차용해 보자. 치킨의 표면적을 계산하기 위해 낮은 해상도의 픽셀 개수를 세었을 때와 높은 해상도의 픽셀의 개수를 세었을 때, 당연히 후자의 픽셀 개수가 더 많을 것이다. 앞서 살펴 본 \[\lim_{x \to 0} \frac{\log f(x)}{\log (\frac{1}{x})} =a\]의 관계에서 \(x\)를 정사각형 모양 픽셀 한 개의 한 변의 길이라고 하고 \(f(x)\)를 치킨 조각을 덮기 위한 픽셀의 수라고 한다면 만약 치킨 조각에 자기닮음꼴이 존재하는 경우 앞서 증명한 자기닮음꼴을 지배하는 멱함수의 법칙에 따라 \(\log f(x)\)와 \(\log (1/x)\)의 비율은 상수로 고정되어야 한다. 만약 평평한 형태의 치킨 부위를 찍은 이미지의 넓이가 \(A\)고 이를 한 변의 길이 \(x\)의 정사각형으로 덮기 위해서는 대략 \(f(x)\,\sim A/x^2\)개의 픽셀이 필요할 것이다. 따라서 양변에 로그를 취하면 \(a=2\)가 되고 이는 평평한 치킨 조각은 원래 주어진 유클리드 공간의 차원(\(D_{EUC}\)), 즉, 이 경우 \(D_{EUC}=2\)차원을 가진다는 뜻이 된다.

그런데 치킨 조각이 날개나 다리 같은 복잡한 부위라면 필요한 픽셀 개수가 더 늘어날 수 있고, 이 경우 \(a\)는 \(2\)보다 커질 수 있다. 이를 일반화하여 결국 특정 대상을 덮기 위한 선분 (\(1\)차원 대상일 경우), 정사각형(\(2\)차원 대상일 경우), 정육면체(\(3\)차원 대상일 경우), 하이퍼 큐브(\(4\)차원 이상인 경우) 등 각 차원에 맞는 단위 블록의 크기가 점점 작아질 때마다 블록 개수가 얼마나 더 필요한지의 로그 비율을 분석할 수 있고 이 값이 만약 상수라면 그 값을 실질적 ‘차원’이라고 정의할 수 있다. 물론 그 상수가 꼭 자연수일 필요는 없으므로 이를 일반화하여 프랙탈 차원이라고 정의할 수 있다.

예를 들어 [그림2]에 보인 칸토어 집합^{middle-third Cantor set}의 경우 자기닮음꼴을 만들어내는 과정을 반복할 때마다 중간의 \(1/3\)이 없어지므로 \(p\)번 되풀이하면 길이는 \(1/{3^p}\)이 되고 토막의 개수는 \(2^p\)개가 된다. 따라서 \(p\)가 계속 커진다면 이 패턴의 프랙탈 차원은 \(\frac{\log 2}{\log 3} = 0.631\)로 계산될 것이다. 이 숫자가 차원을 나타내는 값이라고 직관적으로 이해하기는 쉽지 않지만 원래 \(1\)차원에서 시작한 선분이 무한한 \(1/3\) 토막내기에서 살아 남아 \(0\)차원의 점보다는 정보량이 보존된 패턴으로 변모함을 고려하면 이 집합의 실질적 차원은 \(0\)과 \(1\) 사이에 있어야 할 것이고 칸토어 집합은 그 값이 \(0.631\)로 주어졌다는 것으로 이해할 수 있다.

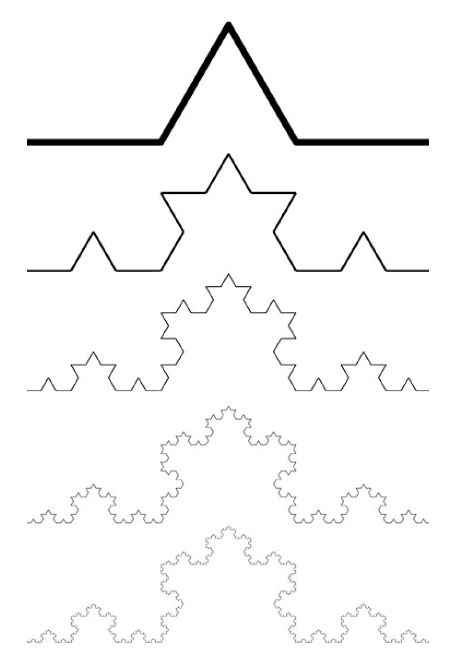
[그림3]의 코흐 눈송이^{Koch curve} 패턴의 경우 자기닮음꼴 되풀이 과정에서 선분 길이는 \(1/3\)로 줄어드는 대신 선분 개수는 \(4\)개로 늘어나므로 프랙탈 차원은 \(\frac{\log 4}{\log 3} = 1.262\)이다. 앞서 보인 칸토어 집합과는 달리 \(1\)차원 선분의 차원이 오히려 \(1\)을 초과한 것을 볼 수 있는데 이는 선분의 개수 증가 속도가 선분의 길이 감소 속도보다 빠르기 때문이다.

한 가지 유의할 부분은 모든 자기닮음꼴 도형이나 패턴의 프랙탈 차원이 항상 비^非자연수가 되는 것은 아니라는 것이다. 그 대표적인 예가 [그림4]와 같은 바로 공간충전곡선^{space-filling curves}인데 이들은 기본적으로 자기닮음꼴을 갖고 있음에도 불구하고 유클리드 차원(\(D_{EUC}\))과 동일한 프랙탈 차원, 즉, 자연수 차원을 갖는다. 예를 들어 [그림4]의 페아노 곡선^{Peano curve type 1}이나 힐버트 곡선^{Hilbert curve}의 프랙탈 차원은 \(2\)다. 참고로 힐버트 곡선류의 공간충전곡선에서 말하는 ‘곡선’은 기하학적으로 곡률을 정의할 수 있다는 의미에서의 곡선이 아닌, 연속적으로 움직이는 점들이 그리는 궤적으로 이해해야 한다.

3. 패턴의 프랙탈 차원 계산

앞서 살펴 본 것처럼 패턴의 자기닮음꼴 특성은 곧 프랙탈 차원을 계산하는 것으로부터 분석될 수 있다. 수학자 모란^{P. Moran}의 이론에 의하면 일반적으로 자기닮음꼴을 갖는 패턴은 다음 정리가 성립한다[4].\[1=\sum\limits_{k=1}^N\,{\lambda_k}^{D_S}\]위 식에서 \(N\)은 한 번 반복될 때마다 생기는 자기닮음꼴의 개수, \(\lambda_k\)는 \(k\)번째 자기닮음꼴 성분의 자기닮음비^scale, 그리고 \(D_S\)는 패턴 전체의 자기닮음꼴 차원^{similarity dimension}이다. (자기닮음꼴 차원과 프랙탈 차원을 혼동하면 곤란하다. 프랙탈은 자기닮음꼴을 가지고 있기 때문에 프랙탈 차원과 자기닮음꼴 차원이 일치하지만 자기닮음꼴 형태라고 해서 늘 프랙탈이 되는 것은 아니기 때문에 자기닮음꼴 패턴의 프랙탈 차원이라는 이야기는 성립하지 않는다.) 예를 들어 앞서 살펴 본 칸토어 집합은 \(N=2\)이고 \(\lambda_1 = \lambda_2 = \frac{1}{3}\)이므로 \(1 = 2(\frac{1}{3})^{D_S}\), 즉, \(D_S=\frac{\log 2}{\log 3} = 0.631\)이다. 이는 앞서 계산했던 프랙탈 차원과 일치하는 값이다. 이를 응용하면 [그림5]와 같은 비대칭 칸토어 집합^{asymmetric Cantor set}의 프랙탈 차원도 계산할 수 있는데 이 경우 되풀이 과정에서 왼쪽 붉은 선분은 \(0.4\)배, 오른쪽 녹색 선분은 \(0.5\)배로 축소되어 자기닮음꼴이 형성되므로 이 패턴의 프랙탈 차원은 위 관계식에서 \(1=0.4^{D_S}+0.5^{D_S}\), 즉, \(D_S=0.867\)이라는 것을 알 수 있다. 이는 대칭적 칸토어 프랙탈 패턴의 프랙탈 차원 \(0.631\)보다는 큰데, 더 촘촘한 자기닮음꼴 패턴임을 고려하면 직관적으로 이해할 수 있는 부분이다.

닮음비가 알려져 있거나 직관적으로 관찰할 수 있는 대상이 아닌 경우 프랙탈 차원을 계산하기 위해서는 앞서 설명한 단위 블록의 척도 비율에 따른 개수 증가 비율에 대한 추적이 필요하다. 인공적인 것이든, 자연에서 관찰되는 것이든, 주어진 패턴의 프랙탈 차원은 원리적으로는 일명 박스개수세기 방법^{box-counting method}으로 측정할 수 있다. 이 방법은 이름 그대로, 어떤 형태나 패턴을 단위 블럭(예를 들어, \(m=1\)차원은 단위 선분, \(m=2\)차원은 단위 정사각형, \(m=3\)차원은 단위 정육면체 (즉, 박스), \(m \geq 4\)차원은 하이퍼큐브^Hypercube)으로 조밀하게 덮고자 할 때 필요한 블럭의 개수를 세고, 그 개수와 블럭의 크기 사이의 관계를 멱함수로 가정하여 지수^power를 계산하고, 그 지수를 프랙탈 차원으로 정의하는 방식이다. 참고로 박스개수세기 방법^{box-counting method}을 확장하면 정사각형 외에도 \(2\)차원의 경우 정육각형, 정삼각형 등, \(3\)차원의 경우 정사면체, 정십이면체 등 다양한 다각형 혹은 다면체를 단위 박스로 활용할 수 있는데, 그중 가장 작은 차원을 갖는 경우를 채택하여 계산된 차원을 하우스도르프 차원^{Hausdorff dimension, \(FD_{hauss}\)}이라고도 한다.

하우스도르프 차원은 용량 차원^{capacity dimension} 혹은 콜모고로프 용량^{Kolmogorov capacity}이라고도 불린다. [그림6-1]은 앞서 살펴 본 DLA 패턴의 프랙탈 차원을 박스개수세기 방법으로 계산한 사례다. 그림의 오른쪽 그래프는 이중 로그 척도로 그린 박스크기-박스개수 관계인데, 이 그래프에서 선형성이 관측되면 박스크기-박스개수 관계에 멱함수 의존성이 있다고 말할 수 있다. 따라서, 선형성이 관측되는 경우, 그래프를 선형회귀하여 기울기를 계산하면 그 절대값이 프랙탈 차원이 된다. 그리고 선형성이 보존되는 척도까지가 실제로 자기닮음꼴이 유지되는 척도라고 할 수 있다.

DLA 같이 컴퓨터로 생성된 패턴이 아닌, 임의의 1차원 데이터나 2차원 이상의 이미지도 적절한 처리 과정을 거치면 프랙탈 차원을 계산할 수 있다. [그림6-2]처럼 주변에서 흔히 볼 수 있는 나무 사진 같은 경우, 나무의 형태만 이진화 필터^{binary filter}로 추출한 형상의 프랙탈 차원을 박스개수세기 방법으로 계산할 수 있다. 주어진 이미지의 픽셀 개수가 충분하다면 박스 크기를 변화시킬 수 있는 범위가 넓어져 더 정확한 프랙탈 차원 계산이 가능하다.

다만 한 가지 주의 깊게 고려해야 할 사실은 주어진 이미지로부터 프랙탈 차원을 계산하는 것은 이미지에서 측정하고자 하는 대상의 복잡도에 의존한다는 사실이다. 이는 원본 이미지를 이진화 이미지 혹은 회색조 이미지^{gray-scale image}로 변환하여 형태를 구분짓는 경계선(엣지^edge) 정보 등을 추출하는 필터를 어떻게 쓰느냐에 따라 프랙탈 차원이 다르게 측정될 수 있다는 것을 의미한다.

프랙탈 차원은 수학적으로 더 확장된 의미에서 정의되고 계산될 수 있다. 박스개수세기 방법은 한 단위 박스 안에 독립된 데이터가 있는지 여부만 따져서 필요한 박스의 최소 개수를 세기 때문에 박스 안에 데이터가 몇 개나 있는지 혹은 각 데이터의 중요도나 가중치를 고려할 수 있는지 여부는 고려되지 않는다. 따라서 이를 반영할 수 있는 개념이 필요한데, 정보 이론^{information theory}에서 도입한, ‘일반화된 \(q\)차 엔트로피^{Generalized entropy at order \(q\)}‘ 혹은 ‘레니 엔트로피^{Rényi entropy}‘라는 수학적 개념을 활용할 수 있다. 프랙탈 차원과 관련된 정보를 측정하는데 활용되는 레니 엔트로피에서 정의되는 일반화된 \(q\)차 프랙탈 차원은 다음과 같이 정의된다.\[D_q =\lim_{r \to 0} \frac{1}{q-1}\frac{\log \sum_{i=1}^{M(r)} p_i^q}{\log r},\,p_i=\frac{N_i}{N},\,q=0,1,2,\cdots\]위 방정식에서 \(M(r)\)은 주어진 데이터나 기하학적 패턴을 한 변의 길이가 \(r\)인 \(m\)차원(\(m\geq1\))의 단위 블럭으로 담기 위해 필요한 개수, \(p_i\)는 \(i\)번째 단위 블럭에 데이터나 패턴의 신호가 담겨 있을 확률을 의미한다. (여기서 \(N\)은 데이터에 포함된 독립된 포인트의 총 개수, \(N_i\)는 \(i\)번째 단위 블럭에 포함된 데이터 포인트의 개수를 의미한다.) 먼저 \(q=0\)인 경우\[D_0\, =\lim_{r \to 0}\frac{\log M(r)}{\log (1/r)}\]이므로 \(D_0\)는 앞서 살펴 본 박스개수세기 방법에서 얻어지는 프랙탈 차원(즉, 용량 차원^{capacity dimension} 혹은 하우스도르프 차원)과 같다. \(q\geq1\)인 경우 개별 하이퍼큐브가 담고 있는 데이터 포인트의 분율^fraction, 즉, 정보량^information이 중요해지는데 \(D_1\)은
\[D_1\, =\lim_{r \to 0}\lim_{q \to 1}\frac{1}{q-1}\frac{\log \sum_{i=1}^{M(r)} p_i^q}{\log r}\,=\lim_{r \to 0}\frac{-\sum_{i=1}^{M(r)} p_i\,\log p_i}{\log (1/r)}\]
으로 표현된다. \(D_1\)은 ‘정보 차원^{information dimension}’이라고 부르기도 하는데 이는 위 식의 분자, 즉,
\[S=-\sum_{i=1}^{M(r)} p_i\log p_i\]
가 샤논^{C. Shannon}의 정보 엔트로피^{information entropy}에 해당하는 양이기 때문이다. 카플란-요크 추측 ^{Kaplan-Yorke conjecture}에 따르면 정보 차원은 특히 동역학계의 랴푸노프 차원^{Lyapunov dimension}에 근접할 것임, 즉, 정보 차원은 동역학계의 실질적인 프랙탈 차원에 근접할 것임이 알려져 있다[5]. \(q=2\)인 경우의 레니 차원, \(D_2\)는
\[D_2=\lim_{r \to 0} \frac{\log C(r)}{\log r},\,C(r)=\sum_{i=1}^{M(r)} {p_i}^2\]

라고 표현할 수 있으며 이를 상관 차원^{correlation dimension}이라 한다. 위 식에서 \(C(r)\)은 상관합^{correlation sum}이라고 부르며 해석적으로 이를 계산할 방법이 없으므로 수치해석적 방법이 필요하다. 그 중 대표적인 방법은 Grassberger와 Procaccia가 개발한 방법으로, 샘플링한 데이터들의 체비세프 거리^{Chebyshev distance}를 계산하여 이를 이진화시키는 헤비사이드 함수^{Heaviside function}의 변수로 삼아 상관합, 나아가 상관 차원을 계산하는 방법이다[6]. 수학적 정의로부터 예상할 수 있다시피, 일반적으로 \(q\)가 커질수록 프랙탈 차원은 조금씩 감소하는 경향, 즉, \(D_0 \geq D_1 \geq D_2\)의 관계가 관측된다. 이들 레니 엔트로피 기반의 프랙탈 차원을 이용하여 \(1\)차원뿐만 아니라 자기닮음꼴을 갖는 \(2\)차원 이상의 프랙탈 패턴의 차원을 측정할 수 있다.

[그림7]은 허스트 지수^{Hurst exponent} \(H\)가 주어졌을 때 생성된 \(2\)차원 자기닮음꼴 지형인 프랙탈 브라운 운동 패턴^{2D fractional Brownian motion pattern}의 프랙탈 차원을 측정한 결과를 나타낸다. 허스트 지수는 데이터에서 샘플링한 일부 데이터의 변동 범위가 샘플 크기에 대해 멱함수 관계를 보일 때, 그 지수를 의미하는 통계 지표로서, 보통 프랙탈 브라운 운동 패턴의 복잡도를 측정하는 1차적인 지표로 활용된다. 이에 대해서는 2부에서 더 자세히 설명할 것이지만, 일반적으로 프랙탈 브라운 운동 패턴에 자기닮음꼴 특성이 있는 경우,\[FD_{hauss} = 1 + D_{EUC} – H\]의 관계를 보인다. 그림에서 볼 수 있다시피 허스트 지수로 예측되는 이론적인 프랙탈 차원, 즉 \(FD_{hauss} = 3 – H\)와 비교할 때 세 측정 지표는 이론적 예측값과 비슷한 값을 보여주고 있다. 다소 차이는 있으나 세 지표가 거의 같은 양상으로 생성된 프랙탈 지형의 차원 값을 보여 주는 것을 알 수 있다.

4. 프랙탈 패턴의 생성

패턴의 프랙탈 차원을 계산할 수 있다면 반대로 주어진 프랙탈 특성을 만족시키는 기하학적 형태, 물리적인 대상, 혹은 추상적인 데이터를 인공적으로 생성하는 것도 가능할 것이다. 먼저 수학적으로는, 복소평면 상에서 평면의 각 점이 발산하는 속도를 표현한, 시간매개형 프랙탈 패턴^{Escape-time fractals} 생성 방법이 있다. 이에 대한 유명한 사례로, 복소 공간에서 시간매개형 재귀 사상^{recursive mapping}으로 생성되는 망델브로 집합이나 쥘리아 집합이 있다. 여기서 말하는 재귀 사상이란 추상화된 함수 개념으로서, 간단하게 말해 바로 이전에 생성된 계의 산출값이 다음 단계에서 다시 계의 입력값이 되는 수학적 구조다. 19세기 후반-20세기 초반에 증명된 푸앵카레-벤딕손 정리^{Poincaré–Bendixson theorem}에 따르면, 연속 시공간 상에서는 \(3\)차원 이상의 동역학계에서만 혼돈계가 발현될 수 있다. 따라서 \(2\)차원 이하의 동역학계에서는 연속 시간 상에서의 시간매개형 프랙탈 패턴이 나타날 수 없지만[7], 이산 공간에서라면 \(1\)차원 동역학계에서도 프랙탈 패턴이 발현될 수 있다. 망델브로 집합을 예로 들어 보자. 복소수 \(c=r+is,\,r,\,s\, \in \mathbb{R}\)를 계의 파라미터로 갖는 복소 사상은\[z_{n+1}=f(z_n)={z_n}^2+c,\,z_0=0\]이라고 쓸 수 있고, 복소수 \(z_n\)를 실수부 \(x_n\)와 허수부 \(y_n\)으로 분리하면

\(\begin{align*}
x_{n+1} &= {x_n}^2-{x_n}^2+r\\
y_{n+1} &= 2x_ny_n+s
\end{align*}\)

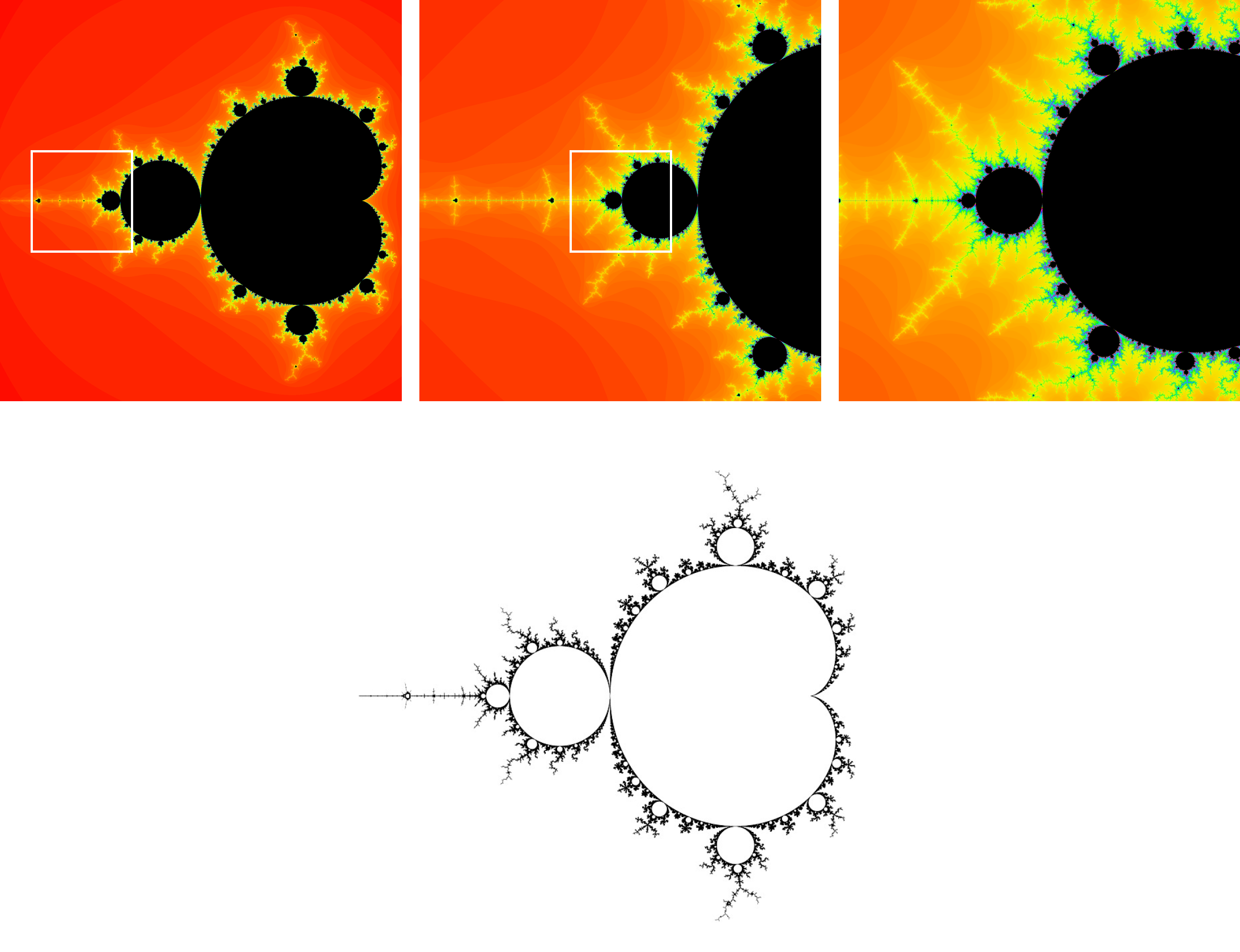
로 풀어 쓸 수 있다. 이때 주어진 복소수 파라미터 \(c\)에 대해 되풀이 순서인 \(n\)이 충분히 커질 때 \(z_n\)의 절대값이 발산하지 않는다면 \(c\)는 망델브로 집합의 원소가 된다. \(r\)을 \(x\)축, \(s\)를 \(y\)축에 배치하면 망델브로 집합의 원소 \(c\)의 분포를 복소 평면 상에 \(2\)차원 이미지로 시각화할 수 있고, 각 \(c\)에 대해 \(z_n\)이 수렴하는 속도를 색깔별로 구분하면 [그림8-1]처럼 잘 알려진 망델브로 집합의 자기닮음꼴 패턴이 관찰된다.

흥미롭게도 [그림8-1]처럼 망델브로 집합 패턴의 스케일을 네 배로 계속 확대해도 원래의 자기닮음꼴이 유지되는 척도불변성을 관찰할 수 있다.

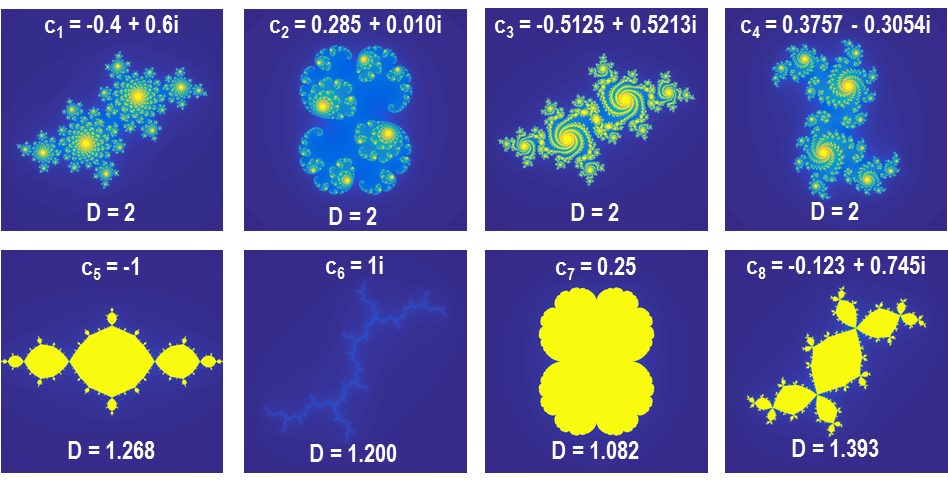
참고로 1991년 일본의 수학자 시시쿠라^{M. Shishikura}가 수치해석 방법을 사용해 망델브로 집합의 경계선([그림8-2] 참조)의 프랙탈 차원은 정확히 \(2\)인 것을 증명하였다. (사실 이 때문에, 망델브로 집합의 경계선 패턴은 비자연수의 프랙탈 차원을 가지지 않는다는 맥락에서는, 프랙탈에 속하지 않는다고 봐야 한다.)[8] 이는 망델브로 집합의 경계선도 페아노 곡선이나 힐버트 곡선 같은 공간충전곡선(평면충전곡선)에 속함을 의미하는 것이기도 하다. 만약 \(c\)가 고정되었다면 변수 \(z_n\)은 복소 공간에서 어떤 경로를 보일까? 그것은 초기값 \(z_0\)가 어떤 값인지에 따라 바뀐다. 즉, 초기값의 실수부를 \(x\)축으로 허수부를 \(y\)축으로 놓고 발산하지 않는 \(z_0\)의 분포를 복소 평면 상에서 \(2\)차원 이미지로 시각화할 수 있으며, 이를 쥘리아 집합이라고 한다. 망델브로 집합과 마찬가지로 [그림9]의 쥘리아 집합에서도 초기값이 수렴하는 속도를 표현할 수 있다. 흥미로운 부분은 \(c\)가 망델브로 집합의 원소인지 여부가 쥘리아 집합의 프랙탈 패턴 특성을 결정한다는 것이다. \(c\)가 망델브로 집합에 속할 경우 쥘리아 집합은 비교적 단순한 패턴을 보이는데 이들의 공통점은 경계선 안쪽 영역이 모두 채워져 있다는 것이고 이는 프랙탈 차원이 \(1\)과 \(2\) 사이라는 것을 의미한다. 반대로 \(c\)가 망델브로 집합에 속하지 않을 경우, 쥘리아 집합은 복잡한 패턴을 보이는데 흥미롭게도 이들의 프랙탈 차원은 망델브로 집합과 마찬가지로 모두 정확히 \(2\), 즉, 평면충전곡선에 속하게 된다.

복소 공간에서의 사상을 이용하여 망델브로 집합이나 쥘리아 집합 류의 패턴을 생성하는 것은 수학적으로는 반복함수계를 사용하여 자기닮음꼴 패턴을 생성하는 것에 해당한다. 예를 들어 [그림8-2]의 고사리를 닮은 것 같은 자기닮음꼴 패턴은
\begin{align*}
x_{n+1} &= ax_n+by_n+e\\
y_{n+1} &= cx_n+dy_n+f
\end{align*}
같이 단순한 선형 결합과 상수 연산을 활용한 반복함수계를 통해 생성할 수 있다. 물론 어떠한 파라미터 조합을 어떤 순서로 택할 것인지에 따라 패턴의 세부 정보가 달라진다. 예를 들어 [그림10]의 자기닮음꼴 패턴은 네 가지 서로 다른 파라미터 조합 \(\{a, b, c, d, e, f\}\)을 번갈아가며 적용하여 생성된 결과물이다.

반복함수계는 형식 문법^{formal grammar}을 재귀적으로 반복 적용할 수 있는 컴퓨터 코드를 사용해 만들 수도 있다. 대표적인 형식 문법은 헝가리 식물학자 린덴마이어^{A. Lindenmeyer}가 1960년대에 고안한 \(L-system\)으로서, 이는 점과 선을 잇는 방식을 문법 요소로 정리한 알고리즘이다. 식물의 성장 과정에서 보이는 가지치기 패턴에 대한 관심이 많았던 린덴마이어는 재귀 사상^{recursion mapping}을 이용하여 가능한 단순한 문법의 조합만으로 상대적으로 더 복잡한 자기닮음꼴 분기 패턴을 만들 수 있음을 보였다. \(L-system\) 같은 형식 문법은 비단 식물의 분기 패턴뿐만 아니라 다양한 자기닮음꼴 패턴을 비교적 쉽게 생성할 수 있다는 장점이 있다. 예를 들어 앞서 보았던 코흐의 눈송이^{Koch curve} 패턴은 \(F \mapsto F-F++F-F\) 같은 문법 규칙으로 [그림10]의 과정을 거쳐 생성할 수 있다. 이 규칙에서 \(F\)는 한 점에서 다른 한 점으로 정해진 길이만큼 일직선으로 이동하면서 선분을 그리라는 뜻이며, \(-\)혹은 \(+\)는 반시계 혹은 시계 방향으로 정해진 각도만큼 방향을 바꾸라는 뜻이다. 만약 각도를 \(60^\circ\)로 설정해 둔다면 (물론 각도는 임의로 설정할 수 있다) 이 규칙의 의미는 [그림10]처럼

1. 일단 짧은 선분을 그리고
2. \(60^\circ\)만큼 반시계 방향으로 방향을 튼 다음
3. 다시 짧은 선분을 그리고
4. 이번에는 \(60 + 60 = 120^\circ\)만큼 시계 방향으로 방향을 튼 다음
5. 다시 짧은 선분을 그린 후
6. 다시 \(60^\circ\)만큼 반시계 방향으로 방향을 튼 다음
7. 다시 짧은 선분을 그리라

는 뜻이다.

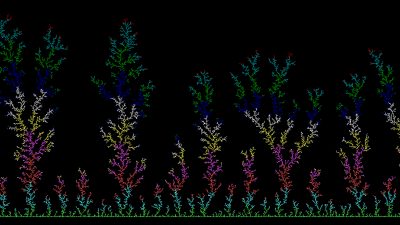
이러한 변형을 계속 반복하면 코흐 곡선이 생성됨을 알 수 있다. 문법 요소의 종류를 다양하게 만들면 훨씬 복잡한 형태의 자기닮음꼴 패턴도 생성할 수 있다. 예를 들어 [그림 11]처럼 실제 나무와 유사한 자기닮음꼴 패턴을 만들 수 있다. 이때 추가된 문법 요소인 ‘\([\)’와 ‘\(]\)’는 각각 가지치기를 ‘시작’하고 ‘종료’하라는 의미인데, 이 두 가지 문법 요소의 추가만으로도 그럴듯한 나무가지 패턴을 생성할 수 있다. 컴퓨터의 계산 및 메모리 저장 자원을 적게 소모한다는 장점이 있기 때문에 \(L-system\) 같은 형식 문법은 게임이나 영화에 활용되는 고해상도 컴퓨터 그래픽 요소로도 폭넓게 활용된다.

\(L-system\) 외에도 자기닮음꼴 패턴을 만드는 방법이 있다. 컴퓨터 그래픽에 많이 활용되는 일명 ‘마름모-정사각형 방법^{Diamond-square method}‘이라 불리는 방법인데(random midpoint displacement fractal, the cloud fractal or the plasma fractal라고도 부른다) 원리는 간단하다. 먼저 [그림12-1]에 보인 것 같이 바둑판 모양의 격자^grid를 준비한다. 그리드 평면의 한 변에는 점을 \(2^N +1\)개 배치한다. 예를 들어 [그림12-1]에는 한 변에 \(2^2+1=5\)개씩, 총 \((2^2+1)(2^2+1)=25\)개 점이 있다. 처음에는 격자의 네 코너를 씨앗으로 삼아 미리 정해둔 범위의 값 중 하나를 임의로 선택하여 배치한다.

다음 단계에서는 네 코너를 두 개의 대각선으로 잇고 두 대각선이 만나는 점을 찾은 후, 그 점에 네 코너 값의 평균과 일정한 범위 내에서 선택한 난수^{random number}를 합친 값을 대응시킨다. 이제 가운데 점의 값이 생성되었으므로 세번째 그림처럼 각 씨앗들로 둘러싸인 또 다른 씨앗을 격자 평면의 각 변의 중심 점에 대응시키고, 각 중심 점의 값은 앞의 방식과 비슷한 방식으로 생성한다. 이를 반복하면 정사각형과 마름모의 크기가 번갈아가며 축소되면서 격자 위에서 계속 생성된다.

재귀적 되풀이 과정에서 내삽된 값에 난수가 더해지는 덕분에 새로 생성된 값의 분포에도 불확실성이 가미된다. 이 때문에 [그림12-2]처럼 꽤 자연스러워 보이는 지형을 인공적으로 만들어내는 것도 가능하다. 예를 들어 이러한 알고리즘은 그럴듯해 보이는 산맥을 생성하는데 활용할 수 있는데, 이 경우 각 격자 점에 배치되는 값을 일종의 해발 고도라고 생각할 수 있을 것이다. 당연히 배치되는 값은 음수도 가능하며 (이 경우 해수면 아래라고 생각하면 된다) 높이의 변화는 허용되는 난수의 범위에 의해 결정된다. 사실 재귀적 되풀이 과정에서 사용되는 난수의 범위, 즉, 난수 분포의 표준편차를 어떻게 정할 것인지가 3차원 산맥 형태의 프랙탈 차원을 정하는 변수가 될 수 있다. 2부에서는 이러한 변수 설정이 어떻게 패턴이나 데이터의 복잡도와 연결되는지 보다 자세한 내용을 소개할 것이다.

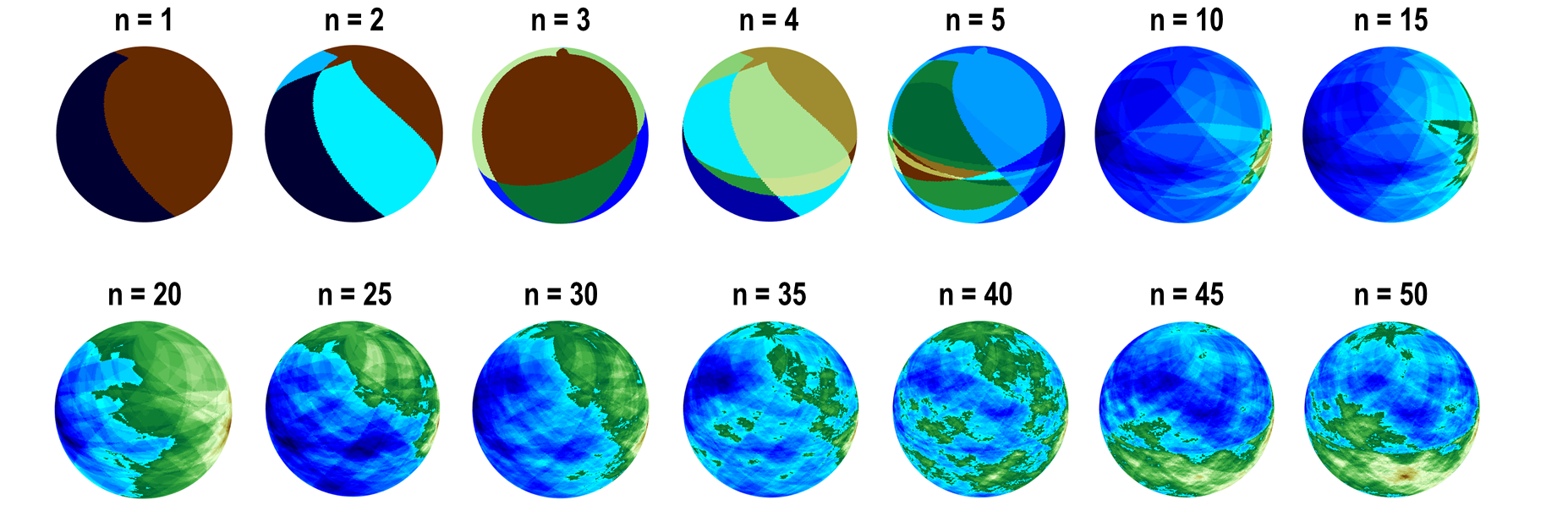
프랙탈 지형은 비단 \(2\)차원 평면에만 국한되지 않으며 \(3\)차원 구면 상에서도 구현될 수 있다. 예를 들어 격자 평면 대신 구면조화함수^{spherical harmonic function}를 반복적으로 겹치되 조화함수의 모드^mode와 변동폭을 선택하는 과정에 프랙탈 차원을 미리 설정하고 조화함수들이 겹치는 부분에 난수를 발생시켜 값을 배정하면, 되풀이 과정이 반복되면서 [그림13]처럼 가상의 행성 지형도 만들어 낼 수 있다.

인공적으로 생성된 프랙탈 지형이나 이미지를 논할 때 유의할 부분이 있다. 그것은 바로 자연의 생물체 혹은 지형에 자기닮음꼴 특성이 있어도 그것이 완벽한 의미에서의 프랙탈은 아니라는 사실이다. 수학적 의미에서의 프랙탈 패턴은 척도 변화 범위가 무한이지만 실제 자연에서는 척도의 변화가 무한일 수는 없으므로 (즉, 어느 이상 확대하면 자기닮음꼴이 사라지므로), 인공적으로 만들어내는 프랙탈 패턴과는 달리, 자연의 프랙탈 패턴은 준-자기유사적 프랙탈^{Proto-fractal}이라고 불린다. 따라서 실제 자연의 이미지는 인공적으로 생성된 프랙탈 나무나 지형의 이미지와의 유사성이 일정 범위의 척도 내에서만 존재한다고 할 수 있다.

1부에서는 자연에서 관찰되거나 인공적으로 만들어진 패턴의 자기닮음꼴과 프랙탈 특성을 분석하는 방법에 대해 소개했다. 2부에서는 일반적 맥락에서 패턴 혹은 데이터의 복잡도를 어떻게 측정할 수 있는지에 대해 엔트로피 위주로 개념을 소개하고, 실제로 어떻게 엔트로피를 활용하여 패턴과 데이터의 복잡도를 측정할 수 있는지 사례를 탐색해 볼 것이다.