좁은 수학의 세계: 계통 나무, 열대기하학, 그리고 점의 배치

수학 연구를 하면서 자주 느끼는 감정 중 하나는 수학의 세계가 매우 넓으면서 동시에 매우 좁다는 것입니다. 불규칙해 보이는 소수의 분포에서부터 우주를 비롯한 여러 공간의 모양, 복잡한 생명 현상의 원인 탐구에 이르기까지, 많은 수학자들이 이루어 놓은 수학적 결과들은 너무 방대해서 극히 일부분만을 이해하는 것도 참 어렵습니다. 하지만 한편으로는 서로 상관없어 보이는 완전히 다른 수학적 영역 사이에 뜻밖의 연결 고리가 있는 경우가 많습니다. 마치 수백 광년 떨어진 다른 행성계를 태양계와 연결하는 웜홀이 있는 것 같다고나 할까요. 수학의 세계는 단순히 끝없이 펼쳐진 공간이 아니라, 넓은 우주의 여러 부분들이 거미줄이나 뇌 속의 뉴런처럼 서로 복잡하게 얽혀 있는 모양이 아닐까 상상하곤 합니다. 이번 글에서는 앞서 말한 무수한 연결 고리 중 작은 하나를 소개해 볼까 합니다.

계통 나무

생물학의 한 분야인 계통학^{Phylogenetics}에서 계통 나무^{phylogenetic tree}는 생물의 진화 과정을 보여주기 위해 나무 모양의 그래프로 나타낸 것입니다. 아마도 많은 분들이 [그림1]과 비슷한 삽화를 과학책에서 보신 적이 있으실 것입니다. 계통 나무는 다양한 생물 종들이 하나의 조상에서 진화하여 여러 종으로 분화되었다고 할 때, 공동 조상을 나무의 뿌리에 두고 종들이 분화될 때마다 나무의 가지가 갈라져 나오는 모양을 그려 표시한 것입니다. 그래서 계통 나무를 통해 어떤 종들이 유전적으로 서로 가까운지 그리고 분화가 얼마나 오래전에 일어났는지를 알아낼 수 있습니다. 생명의 역사를 살펴볼 수 있는 것이지요.

매우 자연스러운 질문은 우리에게 여러 종의 화석 또는 살아있는 생물의 표본이 있을 때, 이 종들의 계통 나무를 어떻게 그리느냐는 것입니다. 우선 주어진 종들 중 어떤 것들이 상대적으로 가깝고 먼지를 아는 것이 도움이 될 것입니다. 예전에는 각 종들 사이의 형태적, 기능적 유사성 또는 차이점을 살펴 종 간의 거리를 결정했는데, 이제는 유전자의 구조를 파악함으로써 각각의 종을 그들의 유전자 정보로 바꾸고 이들을 비교함으로써 종 간의 거리를 잴 수 있게 되었습니다.

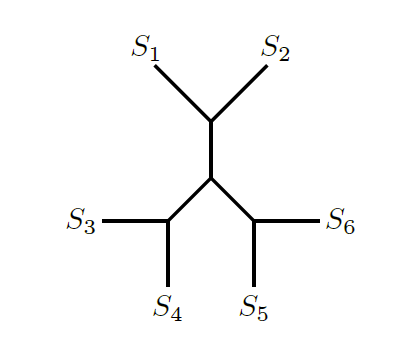
이제 종 간의 거리가 주어졌을 때 계통 나무를 그리는 문제를 해결해야 합니다. 이 계통 나무 그리기 문제를 수학 문제로 바꾸어 보도록 하겠습니다. 나무 그래프는 임의의 두 꼭짓점을 연결하는 경로가 정확히 하나 존재하는 그래프입니다. 나무 그래프는 인접한 변이 단 하나인 종단 꼭짓점들이 존재하는데 이들을 잎이라고 부르겠습니다. 우리는 각 변에 길이(=거리)가 주어진 거리 나무 그래프를 다룰 것입니다. 계통 나무는 거리 나무 그래프의 예로 이해할 수 있고 종들이 잎의 역할을 하게 됩니다. 이제 두 잎 사이의 거리는 한 잎으로부터 다른 잎으로 이동할 때 거쳐야 하는 변들의 길이의 합으로 생각할 수 있습니다. 예를 들어, [그림2]와 같은 나무 그래프를 생각하고 모든 변의 길이가 1이라고 하면, 잎 \(S_{1}\)과 잎 \(S_{2}\) 사이의 거리는 2, 잎 \(S_{1}\)과 잎 \(S_{5}\) 사이의 거리는 4가 됩니다.

우리에게 \(n\)개의 종 \(S_{1}, S_{2}, \cdots, S_{n}\)이 있고, 이 종들의 유전 정보의 차이를 이용해서 서로 다른 두 종 \(S_{i}, S_{j}\) 사이의 거리 \(d_{ij}\)를 계산할 수 있다고 합시다. 만약 이 종들이 하나의 거리 나무 그래프의 잎들이고 거리가 앞에서와 같이 변들의 길이의 합으로 주어진다면, 집합 \(\{d_{ij}\}\)가 일반적인 거리와 같이 다음의 부등식 \(d_{ij} > 0\), \(d_{ij} + d_{jk} > d_{ik}\)를 만족해야 한다는 것을 금방 확인할 수 있습니다. 앞으로 이 부등식들을 만족하는 수들의 열 \(\vec{v} = (d_{ij})\)을 거리 벡터라고 부르겠습니다. 이제 계통 나무 그리기 문제는 거리 벡터가 주어져 있을 때 나무 그래프를 복구할 수 있냐는 문제가 됩니다.

질문 1.1 (계통 나무 그리기 문제 1) 종 \(S_{1}, S_{2}, \cdots, S_{n}\) 사이의 거리 벡터 \(\vec{v} = (d_{ij})\)가 알려져 있을 때, 이 종들을 잎으로 가지고 두 잎 \(S_{i}, S_{j}\) 사이의 거리가 \(d_{ij}\)가 되는 거리 나무 그래프를 찾아라.

위의 문제를 다음과 같이 다시 번역할 수 있습니다. \(n\)개의 잎을 가지는 거리 나무 그래프들의 집합을 \(\mathcal{T}_{n}\)이라 하겠습니다. 그러면 각각의 거리 나무 그래프 \(G \in \mathcal{T}_{n}\)에 대해 잎들의 순서쌍마다 거리를 재어 \({n \choose 2} = \frac{n(n-1)}{2}\)차원 벡터를 하나 만들 수 있게 됩니다. 다시 말해 우리는 함수

\[
d : \mathcal{T}_{n} \to \mathbb{R}^{{n \choose 2}}, \quad d(G) = (d_{ij})
\]
를 얻게 됩니다. 이 함수를 이용해서 계통 나무 그리기 문제와 이 문제가 함의하는 다른 문제들을 기술할 수 있습니다.

질문 1.2 (계통 나무 그리기 문제 2) 거리 벡터 \(\vec{v} = (d_{ij}) \in \mathbb{R}^{{n \choose 2}}\)가 주어져 있을 때,

1. \(n\)개의 종 \(S_{1}, S_{2}, \cdots, S_{n}\)들을 잎으로 가지고 두 잎 \(S_{i}, S_{j}\) 사이의 거리가 \(d_{ij}\)가 되는 나무 그래프를 만들 수 있는가? 즉 함수 \(d\)의 상 \(\mathrm{im}\; d\)은 무엇이며, \(\vec{v} \in \mathrm{im}\; d\)인가?
2. 그렇다면 그런 성질을 가지는 거리 나무 그래프는 유일한가? 즉 함수 \(d\)는 일대일함수인가?
3. 잎이 매우 많을 때 거리 나무 그래프를 효율적으로 만들어내는 방법을 찾아라. 다시 말해 임의의 \(\vec{v} \in \mathrm{im}\; d\)에 대해서 \(d^{-1}(\vec{v})\)를 빨리 계산할 수 있는 알고리즘을 찾아라.¹

그런데 이 문제들은 수학의 한 분야인 조합론에서 이미 오래전에 알려져 있었던 문제입니다.

나무-거리 정리

정리를 이해하기 위해 \(n = 4\)인 경우를 살펴봅시다. 잎이 네 개인 나무 그래프는 [그림3]처럼 두 가지를 생각할 수 있습니다. 여기에서는 조금 더 복잡해 보이는 왼쪽 그래프를 살펴봅시다. 각각의 변에 길이 \(a, b, c, d, e\)를 주고, 네 잎을 \(S_{1}, S_{2}, S_{3}, S_{4}\)라고 하겠습니다. 두 잎 사이의 거리는 \(a, b, c, d, e\)에 대한 일차식으로 주어집니다. 예를 들어, \(d_{13} = a + e+ c\)가 되지요. 그러면 여섯 개의 수 \(\{d_{ij}\}\)들이 다섯 개의 수 \(a, b, c, d, e\)로 표현되어야 하기 때문에 이들은 독립변수일 수 없습니다. 보다 정확하게 \(e\ge 0\)을 이용하면,
\[
d_{13} + d_{24} = d_{14}+d_{23} \ge d_{12} + d_{34}
\]를 얻습니다. 금방 확인할 수 있는 것은 두 번째 그래프의 경우에도 위의 부등식이 성립한다는 점입니다(이 경우에는 등식이 됩니다). 이제 위의 부등식은 다음과 같이 해석할 수 있습니다.

네 점 조건 세 수 \(d_{12}+d_{34}\), \(d_{13} + d_{24}\), \(d_{14}+d_{23}\)의 최댓값이 두 번 이상 나타난다.

나무-거리 정리는 이것이 사실상 유일한 제약조건임을 알려줍니다.

정리 2.1 (나무-거리 정리 [2]) 거리 벡터 \(\vec{v} = (d_{ij})\)가 주어져 있을 때, 잎 \(S_{i}, S_{j}\) 사이의 거리가 \(d_{ij}\)가 되는 거리 나무 그래프 \(G \in \mathcal{T}_{n}\)이 존재할 필요충분조건은, 임의의 \(i, j, k, \ell\)에 대해 네 점 조건이 성립하는 것, 즉 \(d_{ij}+d_{k\ell}\), \(d_{ik} + d_{j\ell}\), \(d_{i\ell}+d_{jk}\)의 최댓값이 두 번 이상 나타나는 것이다. 이러한 성질을 만족하는 거리 나무 그래프 \(G\)는 유일하다 (따라서 함수 \(d\)는 일대일함수이다).

위 정리는 앞의 질문의 1, 2에 대한 해답을 제공합니다. 질문 3에 대해서도 이웃 연결 알고리즘^{Neighbor-Joining Algorithm}이라고 하는 방법이 잘 알려져 있습니다.

열대기하학

네 점 조건은 우리가 익숙한 방정식으로 표현할 수 있는 종류의 조건이 아닙니다. 그래서 대수 또는 해석적인 아이디어를 이용해서 다룰 수 있는 유용한 조건이 아니라고 생각하기 쉽습니다. 하지만 20세기 말에 등장한 새로운 종류의 기하학 덕분에, 우리는 네 점 조건과 나무 거리 정리를 이해할 수 있는 새로운 관점을 얻게 되었습니다. 이 새로운 기하학을 열대기하학^{tropical geometry}이라 합니다.²

중고등학교 수학 수업 시간에 우리는 도형을 다루는 기하학과 식과 수를 다루는 대수학 사이의 연관관계를 배웁니다. 예를 들어, 우리에게 다항식 \(x^{2}+y^{2}-1\)이 있으면, 좌표평면 위의 점들 중 등식 \(x^{2}+y^{2}-1 = 0\)을 만족시키는 점들의 집합 \(V(x^{2}+y^{2}-1) := \{(x, y)\in \mathbb{R}^{2}\;|\; x^{2}+y^{2}-1= 0\}\)을 생각할 수 있고, 이는 중심이 원점이고 반지름이 1인 원이 됨을 알고 있습니다. 즉 우리는 [그림4]의 첫 번째 열에 해당하는 대수학과 기하학 사이의 멋진 대응을 얻을 수 있습니다.

열대기하학에서는 두 번째 열에 해당하는 새로운 열대대수와 열대기하의 상관관계를 연구합니다. 일반적인 다항식 \(f\)에 대해서 대응하는 열대다항식 \(\mathrm{Trop}(f)\)을 다음과 같은 방법(열대화)으로 얻습니다. 지수를 제외한 모든 상수는 0으로 바꿉니다. 곱셈은 덧셈으로 바꾸고, 덧셈은 두 수의 최댓값으로 바꿉니다. 그러면 다항식 \(f(x, y) = x^{2}+y^{2}+(-1)\) \(= x\cdot x +y\cdot y + (-1)\)에 대해서 \(\mathrm{Trop}(f) = \mathrm{max}\{2x, 2y, 0\}\)이 됨을 확인할 수 있습니다.³ 뿐만 아니라 첫 번째 열의 대수/기하 대응에서처럼, 열대다항식 \(\mathrm{Trop}(f)\)가 있을 때마다 그에 해당하는 열대다항식의 해집합(열대다양체) \(\mathrm{Trop}(V(f))\)를 열대다항식 \(\mathrm{Trop}(f)\)의 최댓값이 두 번 이상 얻어지는 점들의 집합으로 정의할 수 있습니다. 위의 예에서 볼 수 있듯이 열대다양체는 더 이상 원처럼 매끈한 미분다양체가 아니지만, 조합론에서 오랜 기간 연구해 온 평평한 도형들을 붙여서 얻어지는 펼침도형^fan 구조를 가지게 됩니다.

이러한 아이디어는 다변수 다항식 여러 개에 대해서 확장할 수 있습니다. 도표 (1)과 같이 다항식의 집합 \(I\)에 대응하는 기하적 공간(대수다양체) \(X\)를 \(I\) 안의 다항식들의 공통해집합으로 정의할 수 있는데, 대수기하학은 대수다양체의 구조와 다항식의 집합 사이의 연관관계를 연구하는 수학의 분야이고, 열대기하학은 이러한 대수/기하 대응의 열대화를 연구합니다.

많은 독자분들이 계통 나무 문제와 열대기하학 사이의 관계를 눈치채셨을 거라 생각합니다. 네 점 조건에서 등장하는 낯선 ‘최댓값이 두 번 이상 나타난다’라는 표현이 열대다양체의 정의에 다시 한 번 등장하는 것입니다. 뿐만 아니라 네 점 조건에 등장하는 열대다항식 \(\mathrm{max}\{d_{12}+d_{34}, d_{13}+d_{24}, d_{14}+d_{23}\}\)은 \(d_{12}d_{34} + (-1)d_{13}d_{24} + d_{14}d_{23}\)이라는 다항식을 열대화해서 얻을 수 있습니다.⁴  이 관찰이 매우 흥미로운 이유는 변수 6개를 가지는 이 다항식은 대수기하학을 공부하는 거의 모든 사람이 알고 있는 그라스만 다양체^Grassmannian \(\mathrm{Gr}(2, 4)\)를 정의하는 다항식이기 때문입니다. 그라스만 \(\mathrm{Gr}(m, n)\)은 고정된 \(n\)차원 벡터 공간 안에 들어있는 \(m\)차원 부분 공간의 집합으로 19세기부터 가장 활발히 연구되어온 대수다양체 중 하나입니다.

열대기하학에 대한 최초의 수학 논문 중 하나에서 슈파이어^Speyer와 스텀펠스^Sturmfels는 다음의 결과를 보였습니다.

정리 3.1. [6] 거리 벡터 \(\vec{v} \in \mathbb{R}^{{n \choose 2}}\)가 \(\vec{v} \in \mathrm{im}\; d\)일 필요충분조건은 \(\vec{v} \in \mathrm{Trop}(\mathrm{Gr}(2, n))\)인 것이다.

그라스만의 정의가 부분 공간의 집합임을 생각하면 이 대응은 참으로 놀랍습니다. 벡터 공간들의 집합과 거리 나무들의 집합 사이에 이런 멋진 대응관계가 있을 거라고 누가 상상을 했을까요?

다름 벡터와 점의 배치

실용적인 관점에서 계통 나무 그리기 문제가 가지는 어려움 중 하나는, 데이터 노이즈 때문에 이웃 연결 알고리즘 등의 여러 방법으로 계산된 계통 나무가 실제 계통 나무와 비슷한지를 증명하는 것이 매우 어렵다는 점이었습니다. 그래서 거리 벡터 대신에 노이즈의 영향이 상대적으로 적은 입력 데이터를 가지고 계통 나무를 그려보자는 아이디어들이 제시되었습니다. 그중 하나가 슈파이어^Speyer와 계산생물학자인 팍터^Pachter에 의해 제안된 다름 벡터를 이용하는 것입니다.

정의 4.1. 자연수 \(m\)을 고정하고 \(G \in \mathcal{T}_{n}\)을 선택하자. 크기가 \(m\)인 \(\{1, 2, \cdots, n\}\)의 부분집합 \(I\)에 대해, \(d_{I}\)를 \(j \in I\)인 잎 \(S_{j}\)들을 포함하는 가장 작은 부분나무 \(G_{I}\)의 크기, 즉 \(G_{I}\) 위의 변들의 길이의 합으로 정의하자. 이제 \(G\)의 \(m\)-다름 벡터^{dissimilarity vector}는 \((d_{I}) \in \mathbb{R}^{{n \choose m}}\)이다. 

그리고 앞서 만났던 \(d\)의 일반화로, \(m\)-다름 함수 
\[
d_{m} : \mathcal{T}_{n} \to \mathbb{R}^{{}_{n}\choose m}, \quad d_{m}(G) = (d_{I})
\]를 생각할 수 있습니다. \(m = 2\)인 경우에는\(d_{2} = d\)인 것도 금방 확인할 수 있습니다. 팍터^Pachter와 슈파이어^Speyer는 만약 잎의 수가 \(m\)에 비해 충분히 크면 \(d_{m}\)은 일대일함수임을 증명하였습니다.[5] 즉 \(m\)-다름 벡터로부터, 거리 나무를 복구할 수 있는 것이지요. 이제 우리는 다음과 같은 질문들을 던질 수 있습니다.

질문 4.2. \(\mathrm{im}\;d_{m} \subset \mathbb{R}^{{n \choose m}}\)을 열대다양체로 해석할 수 있는가? 그렇다면 \(\mathrm{im}\;d_{m} = \mathrm{Trop}(X)\)이 되는 대수다양체 \(X\)를 찾을 수 있는가?⁵

매우 단순하게 생각해서 \(m = 2\)인 경우 \(\mathrm{im}\; d_{2} = \mathrm{im}\;d = \mathrm{Trop}(\mathrm{Gr}(2, n))\)이니까 \(\mathrm{im}\;d_{m} = \mathrm{Trop}(\mathrm{Gr}(m, n))\)이 아닐까 추측할 수 있습니다. 하지만 이 추측은 거짓임이 알려져 있고, 많은 연관 결과들이 있었음에도 불구하고 질문 4.2.는 최근까지도 해답이 알려지지 않았습니다.

개인적인 생각으로는 이 문제가 해결되는데 16년이나 걸린 이유 중 한 가지는 기존의 결과를 바탕으로 주어진 오답이 너무 매력적이었기 때문입니다. 우선 \(m\)-차이 함수 \(d_{m}\)의 정의가 너무 자연스러운 \(d_{2}\)의 일반화처럼 보였고⁶,그라스만의 깜짝 등장은 너무 흥미로워서 분명히 중요한 역할을 할 것처럼 보였거든요.

최근 [3]에서 \(m \ge 4\)이면, \(\mathrm{im}\; d_{m}\)은 열대다양체 구조를 가질 수 없다(!)는 것이 증명되었습니다. 이 부정적 결과는 \(d_{m}\)의 정의가 올바른 \(d_{2}\)의 일반화가 아닐 수 있다는 것을 알려줍니다. 올바른 일반화를 위해 먼저 우리는 다음과 같은 \(m\)-다름 벡터의 변형을 생각해야 합니다.

정의 4.3. 자연수 \(m\)과 \(G \in \mathcal{T}_{n}\)을 고정하자. 크기 \(m\)인 \(\{1, 2, \cdots, n\}\)의 부분집합 \(I\)에 대해 \(d_{I}^{wt}\)을 \(I\)의 두 잎 사이의 거리의 합, 즉
\[
d_{I}^{wt} = \sum_{i, j \in I}d_{ij}
\]로 정의하자. \(G\)의 \(m\)-가중 다름 벡터는 \((d_{I}^{wt}) \in \mathbb{R}^{{n \choose m}}\)으로 정의한다. 그리고 \(m\)-가중 다름 벡터 \(d_{m}^{wt} : \mathcal{T}_{n} \to \mathbb{R}^{{n \choose m}}\)을 \(d_{m}^{wt}(G) = (d_{I}^{wt})\)으로 정의한다.

예를 들어 \(m = 4\)라 합시다. [그림2]의 나무 그래프 \(G\)를 생각하고 각 변의 길이가 1이라 하겠습니다. \(I = \{1, 2, 3, 4\}\)이면,
\[
d_I^{wt} = d_{12} + d_{13} + d_{14} + d_{23} + d_{24} + d_{34} = 2+4+4+4+4+2=20
\]입니다. 그리고 \(J=\{1,2,3,5\}\)이면 \(d_J^{wt}=2+4+4+4+4+4=22\)입니다. 한편 쉽게 확인할 수 있는 것은 \(m = 2\)이면 \(d_{2} = d = d_{2}^{wt}\)라는 점입니다.

또한 거리 벡터가 삼각부등식을 포함한 두 종류의 부등식을 만족해야 했던 것처럼, \(m\)-가중 다름 벡터 또한 두 종류의 확인하기 쉬운 부등식들을 만족해야 함을 보일 수 있는데, 이를 다름 조건이라 하겠습니다.

이제 그라스만 \(\mathrm{Gr}(m, n)\)을 대체할 대수다양체가 필요합니다. \(\mathrm{Gr}(m, n)\)이 \(n\)차원 벡터공간의 \(m\)차원 부분 공간의 집합이기 때문에, 각각의 원소(=부분 공간)에서 \(m\)개의 벡터들을 골라서⁷ 크기가 \(m \times n\)인 행렬로 표현할 수 있습니다. 그런데 이 행렬의 각 열을 마지막 숫자로 나눈 몫을 생각하면 우리는 \((m-1)\)차원 공간의 점 \(n\)개의 배치^{configuration}를 얻을 수 있습니다.⁸

더 나아가 평면(\(m-1 = 2\)인 경우) 위의 5개의 점을 무작위적으로 고르면, 거의 대부분의 경우에 5개의 점 모두를 지나는 이차곡선이 유일하게 존재합니다. 이제 6개의 점을 무작위적으로 고르면, 거의 모든 경우에 [그림6]의 오른쪽처럼 6번째 점이 앞의 5개의 점을 지나는 이차곡선 위에 있을 때에만 이들을 지나는 이차곡선을 찾을 수 있게 되고, 이런 맥락에서 곡선 위의 점의 배치를 특별하다고 할 수 있습니다. 보다 일반적으로 차원이 \((m-1)\)인 공간 안의 \(n\)개의 점을 모두 지나는 차수 \((m-1)\)인 곡선이 존재하는 특별한 배치들의 집합을 \(V_{m, n}\)이라 부르겠습니다.⁹

이제 우리의 마지막 정리를 기술할 수 있습니다.

정리 4.4.[3] 모든 \(2 \le m \le n-2\)에 대해 \(d_{m}^{wt} : \mathcal{T}_{n} \to \mathbb{R}^{{n \choose m}}\)은 일대일 함수이다. 즉 계통 나무는 \(m\)-가중 다름 벡터로부터 복원이 유일하게 가능하다. 또한 다름 조건을 만족하는 벡터 \(\vec{v}\)에 대해 \(\vec{v} \in \mathrm{im}\; d_{m}^{wt}\)일 필요충분조건은 \(\vec{v} \in \mathrm{Trop}(V_{m, n})\)인 것이다.

한편 \(m = 2\)인 경우에는 특별히 \(\mathrm{Trop}(\mathrm{Gr}(2, n)) = \mathrm{Trop}(V_{2, n})\)임이 열대기하학이 등장하기 오래 전부터 전혀 다른 형태로 알려져 있었습니다.¹⁰ 그런 의미에서 정리 4.4.는 정리 3.1.의 일반화라고 할 수 있겠습니다.

마무리하며

앞의 정리 4.4.에 등장하는 대수다양체 \(V_{m, n}\)의 정의(곡선 위에 놓일 수 있는 점들의 배치의 집합)를 다시 한 번 곱씹어 보면 이 대응이 정말 신기하다는 것을 느낄 수 있습니다. 서로 아무 상관없어 보이는 기하학에서의 점들의 배치와 조합론에서의 거리 나무들 사이에, 열대기하학을 매개로 한 뜻밖의 관계가 존재하는 것이지요.¹¹ 독자들이 뒤로가기 버튼을 누르기 전 잠깐만 이 결과를 커피 한 잔과 함께 곱씹어 생각해 보고, ‘좁은 수학의 세계’를 느껴보실 수 있으면 좋겠습니다.