“Selected Articles in English”
Selected articles originally published in Korean are now
translated into English,
making them accessible to the readers worldwide.
Mathematics and physics are two foundational disciplines that have greatly influenced one another over the centuries. Physical mathematics — a discipline that took shape in the late twentieth century — explores the newly revealed connections between mathematics and physics. In what follows I set most technicalities aside and aim to convey the central ideas of this still-young field.
1. Mathematics: The Most Misunderstood Discipline
To explain the relationship between mathematics and physics, we must first discuss what each field is about.1In conversations with friends outside academia, I am often reminded that many people still think of mathematics as little more than memorizing formulas and plugging them in to solve problems. As a mathematician, I find that reputation grossly unfair, and I would like to take this opportunity to set the record straight — if only a little.
Returning to the question of what mathematics actually is, it turns out even mathematicians themselves do not have a single, universally accepted answer. Still, by pointing out two characteristics that distinguish mathematics from other branches of the natural and social sciences, we can begin to introduce the subject.
First, mathematics has no single, overarching end-goal. Instead, anything that can be described precisely by human intellect — no matter how far removed it may seem from the natural world or human society — can become a legitimate object of mathematical study.
Second, mathematics determines the truth of a statement deductively: starting from agreed-upon definitions and axioms, a proof derives the statement step-by-step. Since mathematics begins from a fixed set of assumptions and proceeds through purely logical reasoning, any proven theorem is, in this strict sense, absolutely true — a sharp contrast to theories in the natural or social sciences, which are validated inductively through experiment, observation, or statistics.
Putting aside the abstract description for now, let us illustrate the nature of mathematics with an example. One of the most important and famous results in all of mathematics, the Pythagorean theorem, states2 that
For a right triangle with side lengths $a,b,c$ and hypotenuse $c$, the equation $a^2+b^2=c^2$ holds.
Although many readers may regard the theorem as so familiar as to be unremarkable, it is striking — and increasingly beautiful on reflection — that a single line about an abstract object conveys a universal truth every right triangle, of any shape or size, must satisfy anywhere it is drawn.
Let us now look at the Pythagorean theorem through the eyes of a mathematician — that is, with curiosity — and pose several natural questions, together with the answers mathematicians have provided.
• A very natural question is whether we can generalize the Pythagorean theorem from right triangles to arbitrary triangles.
Given an arbitrary triangle,
can we find a relationship among its three side lengths?
To answer this precisely, mathematicians developed the theory of trigonometric functions, and the answer is provided by the law of cosines.
• Whenever mathematicians encounter a theorem, they inevitably ask, `Does the converse hold?’
If a triangle with side lengths $a, b, c$ satisfies $a^2 + b^2 = c^2$,
is it necessarily a right triangle with hypotenuse $c$?
The law of cosines again tells us that the answer is `Yes.’
• Consider the simple right triangle with $a=1$ and $b=1$. Its hypotenuse $c$ must satisfy $c^2=2$.
What is $c$ such that $c^2=2$?
This question leads to the concept of an `irrational number,’ which cannot be expressed as a ratio of integers. Together, rational and irrational numbers form the real numbers, a notion that later underpins calculus and analysis.
• Can we construct right triangles without using sides whose lengths are irrational?
Are there any triples of natural numbers $(a,b,c)$ satisfying $a^2 + b^2 = c^2$? If so, how many such triples are there?
Such triples are called `Pythagorean triples’; examples include $(3,4,5)$, $(5,12,13)$, and so on. They correspond bijectively to rational points on the unit circle, and hence infinitely many exist.
• Let us generalize further.
For natural numbers $n \ge 3$, do there exist natural number triples $(a,b,c)$ satisfying $a^n+ b^n=c^n$?
In the 17th century Pierre de Fermat scribbled that no such triples exist, a remark that grew into what we now call Fermat’s Last Theorem. For more than 350 years the problem resisted proof — until Andrew Wiles finally settled it in 1994, simultaneously confirming a pivotal case of the far-reaching Langlands program.
• Taking a more philosophical perspective, we might ask:
What, exactly, is a (right) triangle?
Once one realizes that the Pythagorean theorem is logically equivalent to Euclid’s parallel postulate, the issue becomes a challenge to that very axiom. On a sphere, for example, you can draw a triangle whose three interior angles are each $90^{\circ}$. All three sides then have equal length, so the familiar relation $a^{2}+b^{2}=c^{2}$ simply fails. In other words, the Pythagorean theorem is not a statement about triangles in general, but about triangles in Euclidean space.
Dropping Euclid’s parallel postulate leads to new geometries, called `non‑Euclidean geometry.’
• We can also view the Pythagorean theorem as a way to compute the length of the hypotenuse from the other two sides. From this perspective, the following question naturally arises.
How can we determine the length of a general curve?
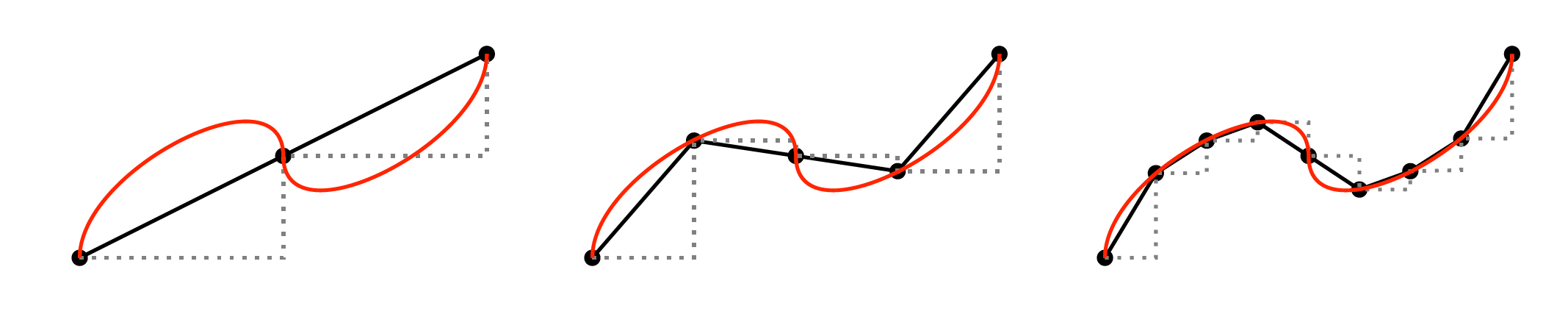
To find an answer, consider the following figure.
Picture slicing the curve into ever finer straight-line segments. In the limit the curve’s length is the sum of infinitely many segment lengths. If you treat each tiny segment as the hypotenuse of a right triangle, the Pythagorean theorem lets you express that length in terms of the segment’s horizontal and vertical displacements — an idea that, pushed to the infinitesimal scale, yields the familiar arc-length integral of calculus. Abstracting this “local Pythagoras” beyond the plane leads to the modern concept of a manifold, a space whose distances are measured by a generalized quadratic rule valid even in non-Euclidean geometries. The systematic study of such spaces is the realm of Riemannian geometry.
To sum up: mathematics often begins with a single, crisply stated fact — say, the Pythagorean theorem. Guided by curiosity, we abstract, generalize, and reason rigorously until that lone statement flowers into a host of new, universally valid truths. Each of those truths then becomes its own launching point: we ask fresh questions, pursue rigorous proofs, and extend the landscape still further. In reality there are hundreds, even thousands, of such “starting points,” every one capable of nurturing an ever-branching tree of results. What makes the subject truly astonishing is that branches grown from seemingly unrelated roots frequently converge, revealing deep and unforeseen connections. Uncovering and understanding those hidden links lies at the very heart of contemporary mathematical research.
2. Physics and Mathematical Physics: The Unreasonable Effectiveness of Mathematics in the Natural Sciences
What is physics? Physics is the science that seeks to understand the fundamental workings of our universe by studying concepts such as matter, force, energy, motion, and space-time.
Then what is the relationship between mathematics — driven by curiosity to explore abstract structures — and physics, which aims to uncover the laws governing reality?
Historically, the two fields have been deeply intertwined. From the mathematician’s perspective, physics has served as one of the richest sources of mathematical activities, alongside number theory (which studies the properties of integers) and geometry (which studies shapes and space).
From the physicist’s side, mathematics is essential as the precise language in which the laws of the universe are formulated and understood.
To make this intimate relationship more concrete, let us look at a few major physical theories and the branches of mathematics that have evolved alongside them.
• Classical Mechanics is the study of the relationship between forces and the motion of macroscopic objects. Sir Isaac Newton, independently of Gottfried Wilhelm Leibniz, developed calculus to formulate the laws of motion and universal gravitation that form the foundation of classical mechanics.
• Electromagnetism is the field that studies phenomena arising from electricity and magnetism. James Clerk Maxwell unified earlier theories of electricity and magnetism, expressing these phenomena in terms of the electric field and magnetic field, governed by just four partial differential equations— now known as Maxwell’s equations.
• The Theory of Relativity concerns the structure and behavior of space-time. Albert Einstein’s general theory of relativity described gravity as the curvature of space-time. To express this physical idea precisely, it turned out that Riemannian geometry — the subject we reached earlier from the Pythagorean theorem purely through curiosity and abstraction — and its variations were indispensable.
• Quantum Mechanics studies phenomena in the microscopic world where classical mechanics no longer applies. Physicists such as Niels Bohr, Erwin Schrödinger, Werner Heisenberg, Max Born, and Paul Dirac developed a new theoretical framework to describe the discontinuous and probabilistic nature of quantum phenomena. This framework relies heavily on the mathematical languages of linear algebra, group theory, and differential equations.
As one can see, in most cases the mathematics essential to physics had already been developed independently within mathematics itself. Physicists were then able to draw on this existing body of work to articulate their ideas with precision. That a discipline born from curiosity about abstract structures turns out to be the right language for describing the laws of the universe is nothing short of astonishing. Eugene Wigner famously emphasized this by calling it
the unreasonable effectiveness of mathematics in the natural sciences.
The interplay between mathematics and physics did not end there — in fact, each field continued to spur advances in the other. Consider first an instance where physics spurred progress in mathematics. To describe phenomena in quantum mechanics, Paul Dirac introduced a class of “generalized functions” that, at the time, had no rigorous mathematical foundation. This inspired Laurent Schwartz to develop the theory of distributions, which has since become fundamental across much of modern mathematics.
Conversely, mathematical advances have also led to breakthrough predictions in physics. Through a mathematical study of Einstein’s field equations in general relativity, the existence of black holes was predicted. Likewise, analysis of the Dirac equation, formulated within relativistic quantum mechanics, led to the theoretical prediction of antimatter. These once purely theoretical predictions were later confirmed through experiments and are now essential to our understanding of the universe.
In this way, the field that develops the mathematical methods needed to understand physical concepts and solve physical problems, and that applies mathematical theories to uncover new results in physics, is called mathematical physics.
To conclude our introduction to mathematical physics, let us now turn to its “holy grail”: quantum field theory. Quantum mechanics is a physical theory that describes particles (or waves) in the microscopic world. In contrast, classical electromagnetism treats concepts like electric and magnetic fields from a purely classical perspective. However, since particles and fields influence one another, any theory that aims to fully describe the workings of our universe must also treat fields in a quantum mechanical framework.
This leads us to quantum field theory (QFT) — a theoretical framework that successfully combines quantum mechanics with the notion of fields. QFT remains the most comprehensive and internally consistent model we have for explaining how the universe operates. Among its crowning achievements is the Standard Model, which describes, with astonishing accuracy, all known forces and elementary particles — with the sole exception of gravity.
At the heart of quantum field theory lie the correlation functions, schematically written as
\[\langle \mathcal{O}_1 , \cdots, \mathcal{O}_n \rangle = \int_{\phi\in\mathcal{F}(M)} \mathcal{O}_1(\phi ) \ldots \mathcal{O}_n(\phi ) e^{-S[\phi]} d\phi .\]
We omit a detailed explanation of the notation here. If $\mathcal{F}(M)$ is taken to be the space of real numbers, then this expression is an integral of the familiar kind from calculus. An intriguing point is that these field-space integrals are taken over an infinite-dimensional space and hence are not, in any straightforward sense, mathematically well-defined. Yet physicists have invented techniques that extract finite, predictive numbers from these expressions — and those numbers agree with nearly every experiment to astonishing precision. From a mathematician’s standpoint, it seems almost miraculous: an undefined integral somehow yields a finite result that actually corresponds to physical reality. The central challenge of mathematical physics, then, is to develop a rigorous mathematical framework needed to underlie quantum field theory.3 Success in this endeavor would not only put our most powerful physical theory on solid footing but almost certainly lead to entirely new discoveries in physics.
3. Physical Mathematics: The Unreasonable Effectiveness of Physics in the Mathematical Sciences
Toward the end of the 20th century, a new revolution transformed the relationship between mathematics and physics: ideas originally developed to describe the universe began solving problems in pure mathematics itself. This marked the beginning of a new discipline known as physical mathematics. In stark contrast to the premise of mathematical physics, one can say physical mathematics seeks
the unreasonable effectiveness of physics in the mathematical sciences
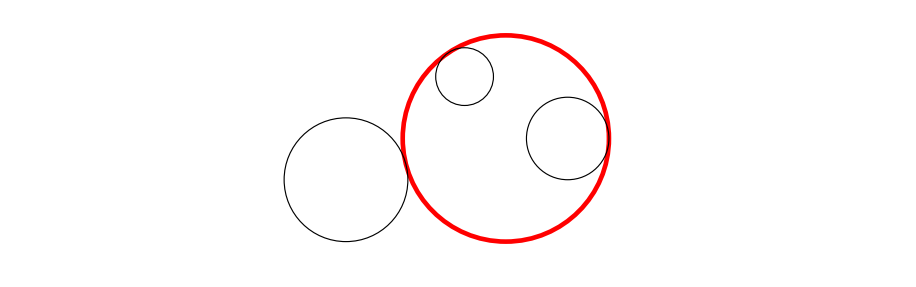
Let us illustrate this with an example. Enumerative geometry is the branch of mathematics devoted to counting the number of geometric objects satisfying specified conditions. For instance, one may ask, “How many lines pass through two distinct points in the plane?” Of course, the answer is one. A more intriguing question was posed by Apollonius of Perga around 200 BCE: “How many circles in the plane are tangent to three given circles?”
Apollonius answered that generically there are always eight such circles.
A historically important question in the field is: “for a generic quintic threefold $X$ in $\mathbf P^4$, how many rational curves of degree $d$ does $X$ contain?” Here $d$ is a positive integer, and the resulting count $n_d$ becomes dramatically harder to compute as $d$ grows.4 In fact, for $d=1$, Hermann Schubert developed what is now called Schubert calculus in 1886 to show $n_1=2875$. About a century later, in 1986, using modern algebro-geometric techniques, mathematicians proved $n_2=609250$. Then in 1991 a group of Norwegian algebraic geometers used computer-assisted methods to compute $n_3=317206375$.
There is, however, a remarkable twist. In 1991, a team of physicists announced predictions for the entire sequence of numbers $n_d$. When the two groups met at a conference and compared values, they found that their results for $n_3$ did not agree. Knowing that the physicists had relied on quantum-field-theoretic ideas and on methods not yet made rigorous, the mathematicians were certain that the physicists must have made a mistake somewhere.
Yet less than three months later the Norwegian group discovered a bug in their own computer code. After correcting it, they obtained exactly the same value of $n_3$ as the physicists. Armed with those confirmed figures, mathematicians then went on to give fully rigorous proofs by 1996, thereby establishing that every one of the physicists’ original predictions was indeed correct.5
Imagine the shock those enumerative geometers must have felt! Experts in abstraction and generalization, they found themselves outpaced by physicists in their own home turf — beaten by $\infty$ to $2$ (or, if you want to blame it on computers, $\infty$ to $3$). How could this possibly happen? Had the physicists learned some kind of black magic?
In fact, they had — its name is duality in physics. Let me now reveal the magicians’ ‘trick’ for tackling this enumerative problem:
(A) Given any Calabi–Yau threefold $X$, one can construct two related quantum field theories, which we will denote $\mathcal{T}(X,A)$ and $\mathcal{T}(X,B)$. 6 In particular, one may take $X$ to be the quintic threefold as introduced before.
(B) The enumerative problem of computing $n_d=n_d(X)$ for the quintic threefold $X$ is precisely equivalent to computing certain correlation functions in the theory $\mathcal{T}(X,A)$.
(C) For each Calabi–Yau threefold $X$, there exists a dual Calabi–Yau threefold $X^\vee $, called its mirror manifold. Then a duality asserts that, although the two theories $\mathcal{T}(X,A)$ and $\mathcal{T}(X^\vee,B)$ look very different, their correlation functions must coincide.7
(D) The correlation functions of $\mathcal{T}(X^\vee,B)$ can be computed by certain explicit integrals, which turn out to be far more tractable than the direct enumerative counts on $X$.
(E) By equating the two, one conjectures that the numbers $n_d=n_d(X)$ we seek are given by the correlation functions of $\mathcal{T}(X^\vee,B)$.
In this way, the duality framework that extracts information about a space $X$ by relating it to a different space $X^\vee$ is known as the theory of mirror symmetry. As we have seen, the physicists’ reasoning — though not mathematically rigorous — nevertheless produced correct predictions in infinitely many cases. Unsurprisingly, mathematicians became eager to uncover the “black magic” that seemed to yield mathematical truths without traditional methods. Since its emergence in 1991, mirror symmetry has reshaped multiple areas of pure mathematics and grown into a rich field in its own right.
Mirror symmetry is but one example of physical mathematics. More generally, one can view the workflow of physical mathematics as three steps:
(1) Identify a physical context for a problem originally posed in pure mathematics. (In the mirror symmetry example, steps (A) and (B).)
(2) Apply the “black-magic” of physics in that context to derive new physical results. (In the mirror symmetry example, step (C).)
(3) Translate those physical results back into mathematical form. (In the mirror symmetry example, steps (D) and (E).)
As we have seen, applying this three-step recipe in mirror symmetry led to conjectures that would have been inconceivable by purely mathematical means.
Another striking example comes from the theory of smooth four-dimensional manifolds. In geometry and topology, one of the fundamental questions is the classification problem: when are two $n$-dimensional manifolds the same, and when are they different? The classification of 1- and 2-manifolds has been known since the 19th century. For 3-manifolds, Grigori Perelman’s resolution of Thurston’s Geometrization Conjecture (and, as a special case, the Poincaré Conjecture) marked a dramatic breakthrough. One might expect the problem to become even harder in dimensions four and higher, but surprisingly, it is known that simply-connected manifolds in five or more dimensions can, in fact, be classified.
In contrast, four dimensions are considered the most difficult case: there is no analogue of the Geometrization Conjecture as in three dimensions, nor can one apply the general theory that works in dimensions five and higher. The most effective method for distinguishing manifolds is to construct and compute invariants — but for smooth 4-manifolds, even this has proven extremely difficult. In this context, Simon Donaldson introduced what are now called Donaldson invariants, using ideas from classical gauge theory. This marked the beginning of the modern study of smooth 4-manifolds. However, computing Donaldson invariants was notoriously hard, making substantial progress in the field difficult. It was at this point that the physicist Edward Witten introduced a much more effective invariant, based on the following ideas from physical mathematics.
(1) He identified the Donaldson invariants of a smooth 4-manifold $M$ with certain correlation functions in a 4-dimensional non-abelian topological quantum field theory.
(2) He then showed — using what is now called Seiberg—Witten theory — that this complicated non-abelian theory is equivalent, at low energy, to a much simpler abelian gauge theory.8
(3) By computing the correlation functions in this abelian theory, one constructs the Seiberg—Witten invariants, which carry the same distinguishing power as the Donaldson invariants but are vastly easier to work with.9
These new invariants, born of physical dualities, were inconceivable by previous mathematical methods, and they enabled a host of revolutionary results in the study of smooth 4-manifolds.
More recently, ideas from physics have similarly transformed the geometric Langlands program — an algebro-geometric incarnation of the arithmetic Langlands program — by suggesting new conjectures, constructing novel objects, uncovering hidden structures, and even proving theorems that had eluded purely mathematical approaches.
4. Conclusion
Mathematics and physics are two foundational disciplines with very different aims and methods. Mathematics pursues precise answers to questions about abstract objects, guided purely by curiosity, while physics seeks to uncover the fundamental laws governing our universe. Astonishingly, mathematics has proven to be an extraordinarily powerful language for developing physical theories — and this synergy has driven advances in both fields.
In the late twentieth century, even more remarkably, ideas originating in physics began to yield groundbreaking results within pure mathematics itself. The field dedicated to exploring these newly revealed connections between mathematics and physics is known as physical mathematics. By bringing fresh perspectives and contexts to a wide range of mathematical areas, physical mathematics has greatly enriched the direction of pure-math research — and its influence shows every sign of continuing to expand.