고대 그리스 수학을 읽는 세 가지 길: 놀라움, 보임, 그리고 아름다움 [2]

얼마 전 봉준호 감독이 칸 영화제에서 영화 <기생충>의 상영을 앞두고, 영화의 스포일러를 자제할 것을 부탁하는 편지를 쓴 것이 화제가 되었습니다. 감독은 편지에 “스토리의 크고 작은 고비마다 관객들이 때론 숨죽이고 때론 놀라며 매 순간의 생생한 감정들과 함께 영화 속으로 빠져들기를” 바란다는 마음을 담았습니다. 그와 같은 마음으로 저는 오늘 고대 그리스 수학도 서스펜스를 느끼면서 읽는 것이 가능하다고, 또 그렇게 읽는 것이 좋겠다는 말씀을 드리고 싶습니다. 불행한 사실은 우리가 고대의 수학자들이 고안해 놓은 서스펜스를 제대로 느끼지 못할 만큼 이미 수많은 스포일러에 노출되어 있다는 점입니다. 그들이 희열을 느꼈을 위대한 수학적 발견이 우리에게는 시시하게 보일 수도 있게 된 것이지요. 어쩌면 우리는 원뿔의 부피는 원기둥의 부피의 삼 분의 일이라는 사실을 너무 성급하게 학생들에게 발설해 버리는 실수를 했는지도 모르겠습니다.

그나마 한 가지 다행인 것은 고대 그리스 수학자들의 많은 저작들이 아직 한국어로 제대로 번역되어 있지 않다는 점이지요. 특별히 가장 기지 있고 위트가 넘치는 방식으로 자신의 수학을 전개했던 아르키메데스의 대다수 작품이 아직 개봉되지 않은 상태로 남아 있습니다. 그래서 오늘은 아르키메데스의 비교적 덜 알려진 정리를 중심으로 그 당시에는 놀라움으로 다가왔을 고대 그리스 수학의 몇 가지 발견을 소개하려고 합니다. 학창 시절 이후 한동안 수학에 손을 놓았던 독자분들께서는 아직 스포일러에 노출이 되지 않은 것처럼 이 정리들을 신선한 눈으로 읽으실 수 있겠으나, 여전히 수학과 친하게 지내시는 독자분들께서는 이 글을 읽는 내내 아마도 끊임없이 인테그랄을 필두로 한 적분법을 쓰고 싶은 유혹과 싸우셔야 할 것 같습니다.

먼저 고대 그리스 수학을 읽는 첫 번째 키워드로 꼽은 놀라움이라는 단어에 대해 조금 더 자세히 설명드리겠습니다. 제가 놀라움으로 번역하고 있는 헬라스어 타우마^θαῦμα라는 단어는 타우마조^{θαυμάζω}라는 동사에서 나왔습니다. 이 단어에는 “감탄하다”라는 뜻이 함께 담겨있는데, 더 구상적인 언어로 표현하자면 경탄하며 입을 벌리고 놀라는 모습이 가장 어울릴 만한 그림일 것입니다. 물론 수학이 입을 벌려 경탄할 거리들을 선사한 경우가 비단 고대 그리스 수학에서만 발견되는 것은 아닙니다. 수학사의 굵직한 줄기를 이루는 위대한 발견들은 늘 경탄의 대상이 되어 왔습니다. 그 수많은 빛나는 순간 중에서 오늘은 우리의 시계를 약 2300년 전으로 돌려 고대 그리스인들이 어떤 수학적 발견에 이런 경탄을 보였을지에 대해 생각해 보고자 합니다.

사실 무엇인가를 발견하고 경탄을 느낄 수 있다는 것이 마냥 쉬운 일만은 아닙니다. 가장 아름다운 등식이라는 오일러 등식을 \({ e }^{ i\pi }+1=0\) 보고 그 아름다움을 알아차리기 위해서는 적어도 자연로그의 밑이라든지 허수단위에 대한 기본적인 이해를 갖고 있어야 합니다. 진자의 운동공식 \(T=2\pi \sqrt { \frac { l }{ g } }\)을 보고 어떤 이는 눈물을 흘릴 정도로 아름답다고 하겠지만 어떤 사람에게는 지루한 물리공식에 불과할 수도 있겠지요. 이렇듯 자신이 가진 앎의 지평에 따라 얼마든지 사람마다 놀라움은 다르게 느껴질 수 있습니다. 누군가가 가진 지식체계의 잔잔한 수면에 어떻게 파문을 일으킬 것인가, 그것이 지적 희열을 불러일으키기 위한 최대 관건일 것입니다.

고대 그리스 수학에서는 가장 그럴듯하지 않은 사실을 내세우는 것이 놀라움의 파문을 일으키는 가장 손쉬운 방법이었습니다. 예를 들어, 그리스 수학에서 중요하게 다루어졌던 원적문제^{Quadrature of a Circle}는 여러 독자들로 하여금 많은 경탄의 순간을 경험하게 했을 것입니다. 둥그스름한 어떤 것과 반듯한 어떤 것에 대한 직관적인 이해와 경험은 보편적입니다. 그러나 그 둘의 넓이 사이에 특별한 관계가 있다는 것을 아는 것은 그다지 보편적이지 않지요. 이 역접의 관계 때문에 사람들은 놀라움을 경험하게 됩니다.

그런 사례 중 아마 가장 오래된 것은 수학자 히포크라테스^{Hippocrates, 기원전 5세기}에서 찾아볼 수 있습니다. 사실 피타고라스 이후 고대 그리스 수학의 가장 오래된 기록 중 하나가 히포크라테스가 탐구했다는 몇몇 넓이 문제들에 남아 있습니다.¹ 우리가 히포크라테스 선서로 알고 있는 의학자 히포크라테스와는 다른 사람이기 때문에 흔히 출신지를 붙여서 그 둘을 구분합니다. 오늘 우리가 살펴보는 수학자 히포크라테스는 키오스섬의 히포크라테스로, 의학자 히포크라테스는 코스섬의 히포크라테스로 부르곤 합니다. 수학자 히포크라테스가 어떻게 수학을 공부하게 됐는지에 관해서는 아래와 같은 일화가 남아있습니다.

키오스 섬의 히포크라테스는 상인이었는데 해적선을 만나 그의 모든 재산을 빼앗기게 되었다. 그는 해적들을 고소하고자 아테네로 왔다가 기소를 위해서 아테네에 오래 머무르게 되었는데, 머무는 동안 철학자들과 교제하면서 기하학을 배우며 원의 넓이를 구하는 문제까지 다룰 정도로 능숙하게 되었다. 그가 원적문제를 푼 것은 아니었고 초승달 모양의 넓이를 구하는 문제를 풀었을 뿐인데, 그 해법을 기반으로 원적문제도 풀 수 있으리라고 착각하였다. 그가 보기에는 초승달의 넓이를 구하는 것으로부터 원의 넓이를 계산하는 것도 가능하리라 믿었기 때문이다.

– 필로포누스^Philoponus, Commentary on Aristotle’s Physics A2 (185 a16)

이 이야기에 남아있는 것처럼 히포크라테스는 원의 넓이를 구하는 문제에 관심을 가졌던 것으로 널리 알려졌습니다. 고대 그리스에서 원의 넓이를 구하는 해법 중 하나로 다각형을 반복적으로 원에 내접시킨 뒤, 내접한 다각형들의 넓이의 합으로 원의 넓이를 근사시키는 방법이 논의된 적이 있습니다. 안티폰^{Antiphon, 기원전 5세기}의 해법으로 알려진 이 방법은 원 안에 먼저 정사각형을 내접시키고, 정사각형의 각 변을 밑변으로 가지면서 원주 위에 꼭짓점을 갖는 네 개의 이등변삼각형을 내접시킴으로써 정팔각형을 얻게 됩니다. 다시 또 이렇게 얻은 정팔각형으로부터 정십육각형을 얻는 방식으로, 원을 다 채울만한 정다각형을 얻을 때까지 계속 진행합니다. 하지만 이 해법에는 원의 곡선과 다각형의 직선이 포개질 때까지 무한히 반복해야 한다는 치명적인 약점이 존재합니다.

히포크라테스는 이 무한의 문제를 피하기 위해 다른 방식으로 원적문제에 접근했습니다. 원적문제를 직접 다루기에 앞서 원의 일부분과 같은 넓이를 갖는 직선으로 둘러싸인 도형을 찾으려 노력했던 것이지요. 그 일환으로 히포크라테스가 발견한 하나의 예를 살펴볼까요?

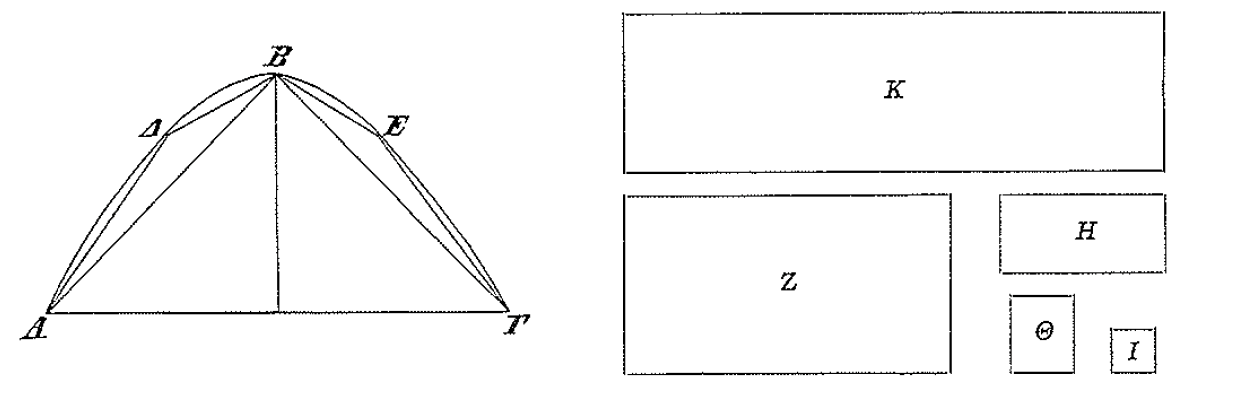
이를테면 [그림2]에서 그는 초승달 ΗΘΙ와 내부의 원 ΑΒΓΔΖΕ의 넓이의 합이 삼각형 ΗΘΙ와 정육각형 ΑΒΓΔΖΕ의 넓이의 합과 같다는 점을 발견했습니다. 여기서 그가 곡선으로 둘러싸인 도형들의 합을 직선으로 둘러싸인 도형들의 합으로 표현할 수 있었다는 점이 중요합니다. 자연스럽게 비슷한 방식으로 원도 그와 마찬가지로 같은 크기를 갖는 직선으로 둘러싸인 도형을 찾을 수 있으리라는 기대를 갖게 되었겠지요.

원적문제와 관련된 또 다른 결정적인 순간은 아르키메데스의 여러 저작에서 등장합니다. 사실 아르키메데스가 우리나라 일반 대중에게 알려진 것은 수학 외적인 내용들이 대부분입니다. 이를테면 유레카^{εὕρηκα}를 외치면서 목욕탕에서 뛰어나간 이야기, 그의 고향 시라쿠사가 로마군에 의해 함락되었을 때 여러 기계의 발명으로 맞선 이야기, 또 내 원을 망치지 말라^{noli turbare circulos meos2}고 말하면서 로마군에 의해서 죽는 순간까지도 초연히 수학을 공부했다는 이야기와 같은 극적인 이야기들이 대표적입니다. 정작 우리는 아직 그가 남긴 수학에 대해서, 또 그가 얼마나 위트 넘치는 수학자였는지에 대해서 깊게 들여다보지 못했습니다.

제가 아르키메데스의 작품에서 거듭 발견하게 되는 것은 얼핏 큰 상관이 없어 보이거나 설령 관련이 있더라도 복잡하게 표현될 것 같은 두 도형 사이에서 아주 단순한 관계를 짚어내는 힘입니다. 그가 수학의 구석구석에 심어놓은 경탄을 자아낼 만한 발견들을 마주할 때마다, 독자들도 왕관의 순금의 비율에 관한 유명한 문제에 대해서 그가 느꼈었을 수학적 희열을 경험하게 되는 것이지요.

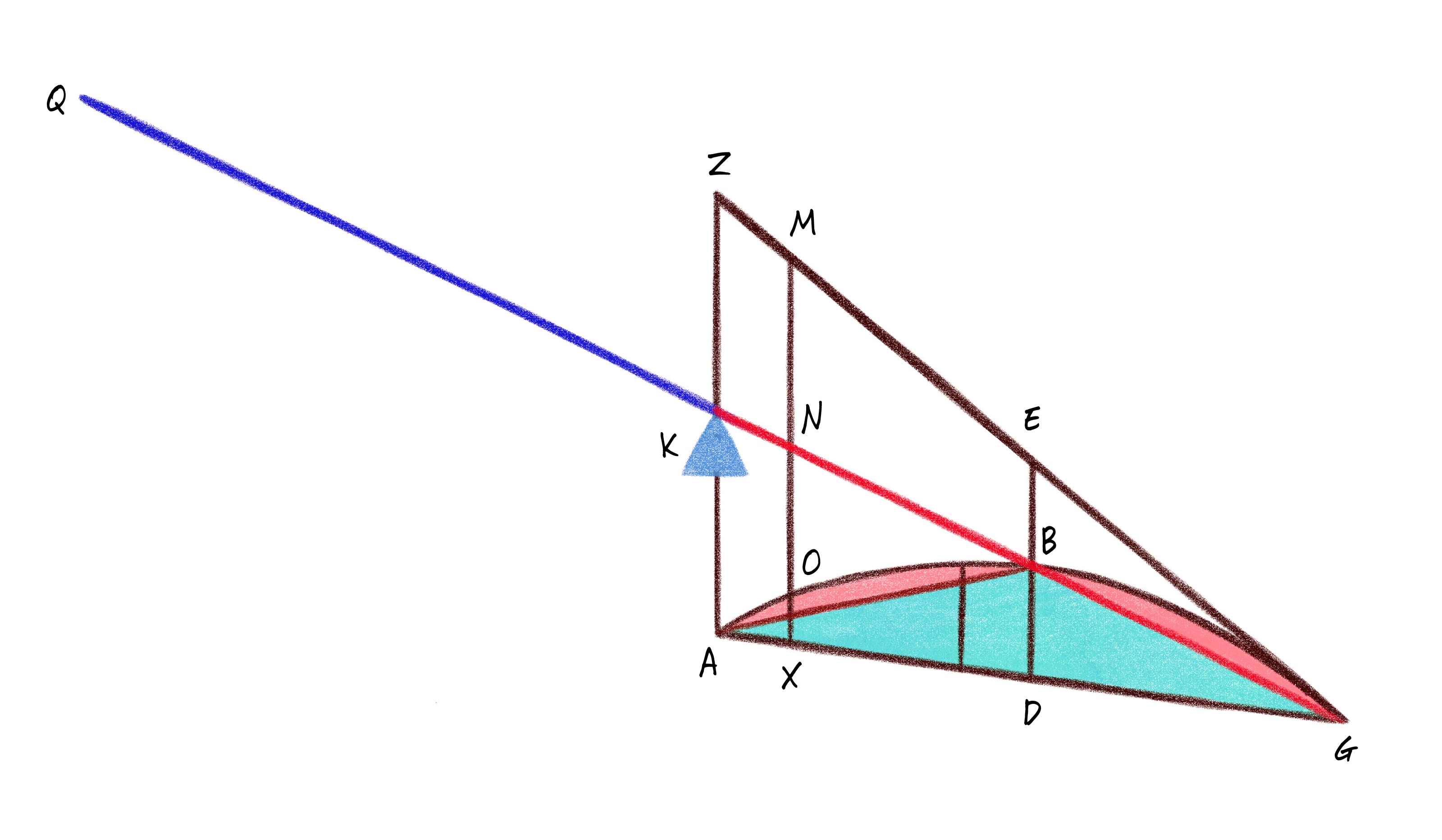
그러한 경탄의 대표적인 사례를 <나선에 관하여^{On Spirals}>라는 작품에서 발견할 수 있습니다. 아르키메데스는 나선과 원 사이의 넓이 관계에서 흥미로운 점을 발견했습니다. 이 정리는 <나선에 관하여>에 수록된 스물 네 번째 정리로 책의 절정에 해당합니다. 내용을 쉽게 이해할 수 있도록 최대한 자연스럽게 번역하는 것도 좋겠지만 원문의 맛이 살도록 가다듬지 않고 적힌 그대로 옮겨 보겠습니다.

첫 회전을 통해서 그려진 나선과 여러 선들 중에서도 회전의 시작점에 놓인 첫 선으로 둘러싸인 넓이는 첫 원의 넓이의 삼 분의 일과 같다.

첫 회전 동안에 나선이 그려진다고 하자. 그 위에 선ABΓΔEΘ이 놓이고, 점Θ를 나선의 시작점이라고 하자. 선ΘA가 회전의 시작점에 있는 여러 선들 중 첫 번째라 하고, 원AKZHI를 첫 번째 원이라 하자. 그 원의 삼 분의 일이 되는 원을 원Ϙ라 하자. 이제 앞서 언급한 넓이가 원Ϙ와 같음을 보이려 한다.

[그림3]은 아르키메데스의 그리스어 사본에 남아있는 명제의 그림을 최대한 있는 그대로 복원한 것입니다.³ 증명과정에 사용된 여러 호가 함께 그려져 있어 이해하기에 까다로울 수 있습니다. 명제의 내용을 좀 더 풀어서 설명해 보겠습니다. 잘 알려진 것처럼 아르키메데스가 말하고 있는 나선은, 오늘날 방식으로 말하자면 원점에서 어떤 반직선이 일정한 속도로 회전하는 동안 그 반직선 위에서 어떤 점이 원점에서부터 일정한 속도로 멀어지면서 얻게 되는 자취입니다. 이 운동의 첫 회전을 통해서 우리가 얻게 되는 나선과 첫선(ΘΑ)으로 둘러싸인 도형은 뚱뚱한 알파벳 b모양을 갖게 되는데 이 넓이가 첫선(ΘΑ)을 반지름으로 갖는 첫 번째 원(AKZHI)의 넓이의 삼 분의 일과 같다는 것이 정리의 내용입니다. 오른쪽에 따로 그려져 있는 원 콥파는 첫 번째 원(AKZHI)의 넓이의 삼분의 일에 해당하는 원으로 상정되어 있습니다. 일종의 측정장치처럼 별도의 원을 만들었다는 점이 흥미롭습니다.

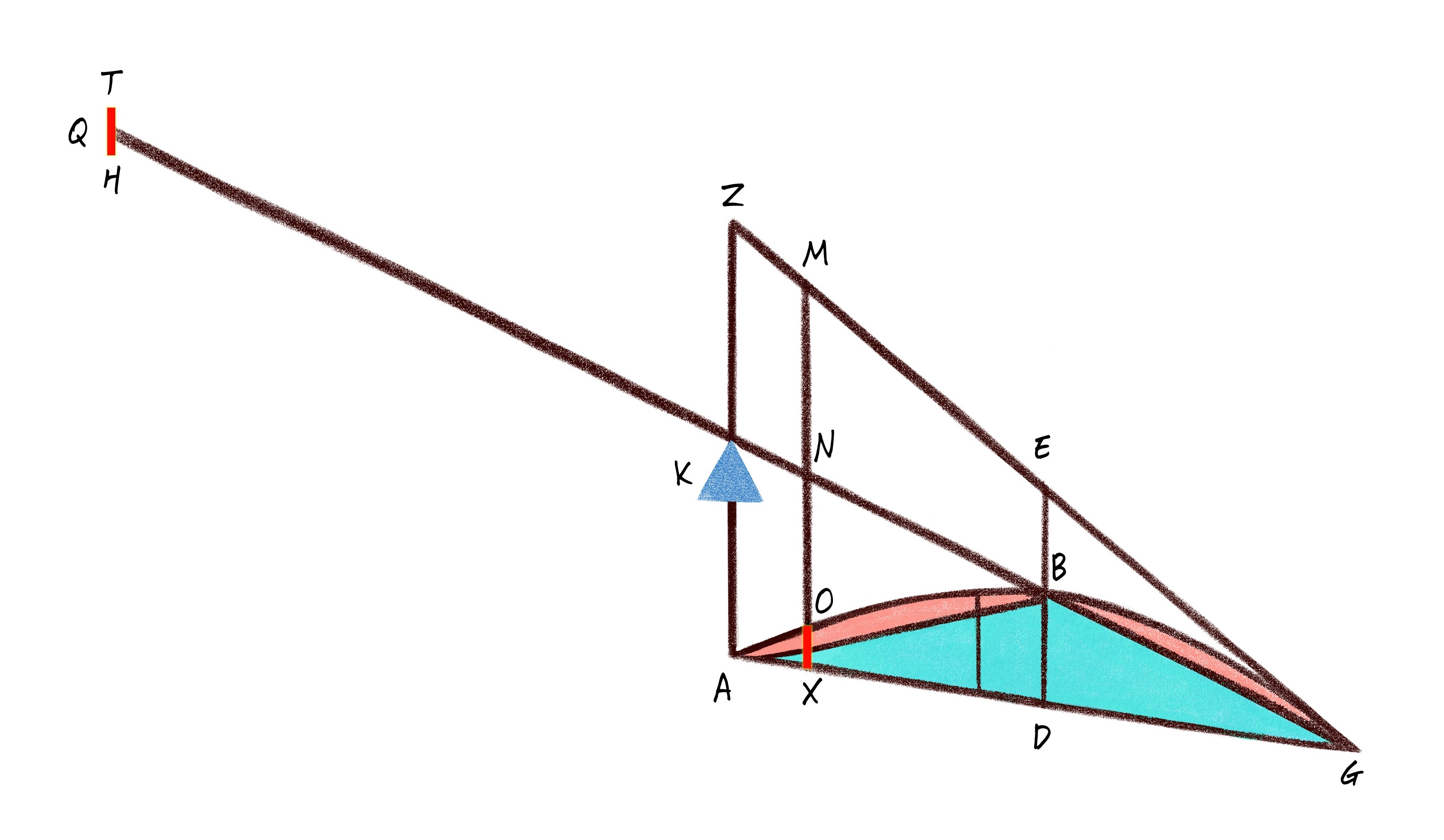
비슷한 예를 <포물선의 넓이에 관하여^{Quadratrue of Parabola}>에서도 찾을 수 있습니다. 제목이 암시하는 대로 이 책의 내용은 포물선 활꼴의 넓이를 구하는데 초점을 맞추고 있습니다. 아르키메데스는 포물선에 관한 여러 정리를 소개한 이후 스물 네 번째 정리에서 비로소 포물선 활꼴의 넓이와 그에 상응하는 삼각형의 넓이 사이의 관계를 다음과 같이 설명합니다.

직원뿔을 절단한 선(포물선을 가리킴)⁴과 직선으로 둘러싸인 모든 활꼴은 그것과 같은 밑변과 같은 높이를 갖는 삼각형보다 그 삼각형의 삼 분의 일만큼 더 크다.

직원뿔을 절단한 선과 직선으로 둘러싸인 활꼴 ΑΔΓΕΒ가 있다고 하자. 그리고 그 활꼴과 같은 밑변과 같은 높이를 갖는 삼각형 ΑΒΓ도 있다고 하자. 넓이 Κ를 삼각형 ΑΒΓ보다 그 삼각형의 삼분의 일만큼 더 크다고 하자. 이제 그 넓이 Κ가 활꼴 ΑΔΓΕΒ과 같음을 보이려 한다.

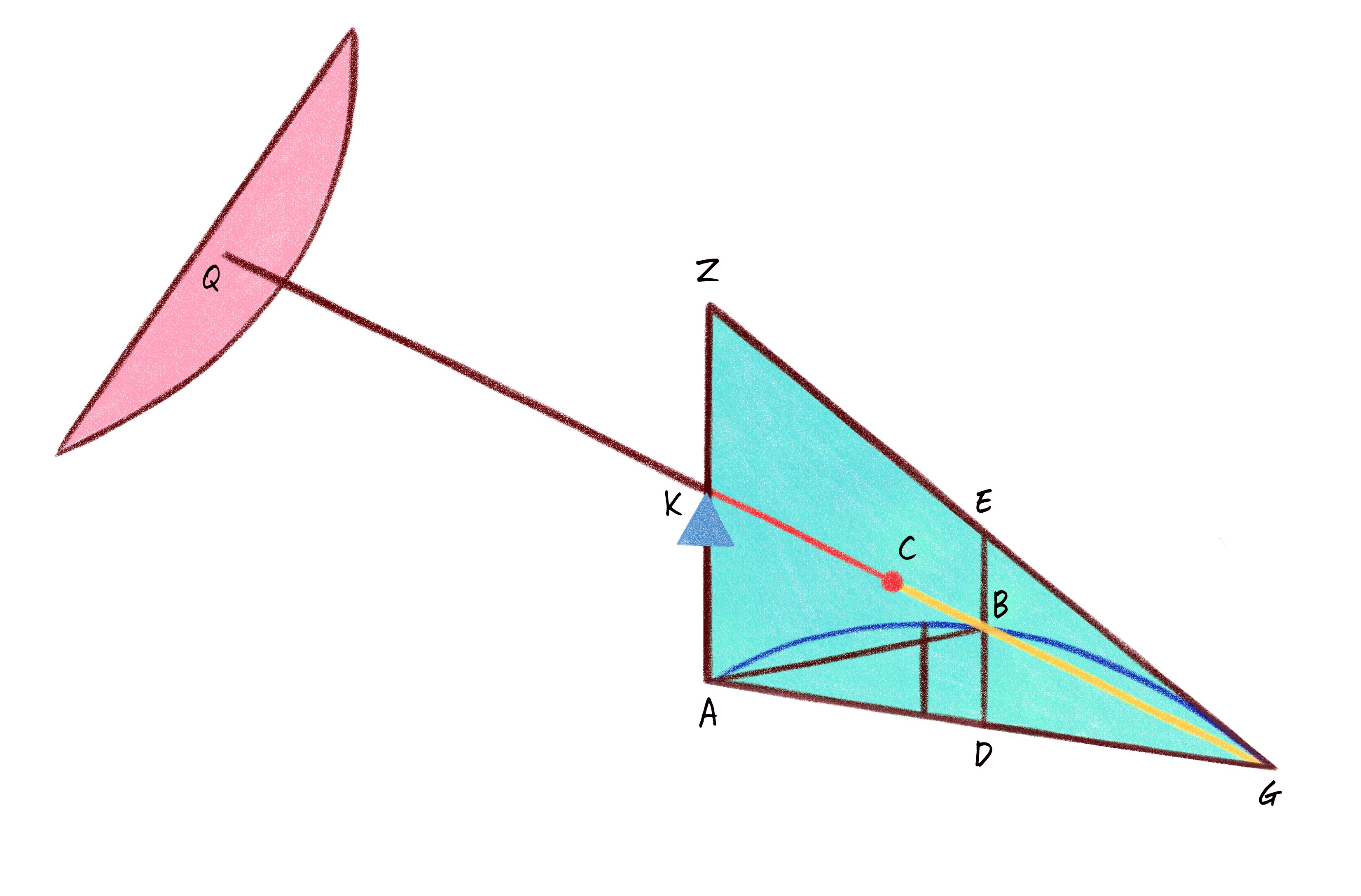
이 문제를 고등학교 시험 현장으로 가져간다면 아마 포물선의 대표적인 사례로 \(y=-{ x }^{ 2 }+1\)이 주어질 것이고, [그림4]에서 밑변 ΑΓ는 \(x\)축에 점Α는 \((-1,0)\)에, 점 Γ는 \((1,0)\)에 위치시키겠지요. 그리고는 학생들은 주저하지 않고 아래와 같이 적분을 할 가능성이 높습니다.

\(\int _{ -1 }^{ 1 }{ (-{ x }^{ 2 }+1)dx } ={ \left[ -\frac { 1 }{ 3 } { x }^{ 3 }+x \right] }_{ -1 }^{ 1 }=\frac { 4 }{ 3 }\)

포물선 활꼴ΑΔΓΕΒ의 넓이가 삼각형 ΑΒΓ의 넓이 \(1\)의 \(\frac { 4 }{ 3 }\)배만큼 크다는 것이 쉽게 얻어집니다. 여기서 우리의 접근법은 포물선 활꼴의 넓이를 \(\frac { 4 }{ 3 }\)로 수치화시키고, 삼각형의 넓이를 \(1\)로 수치화시켜서 두 수 사이의 비율을 생각하는 셈입니다. 지금 이 그리스어 사본의 그림이 묘사하고 있는 것처럼 주어진 포물선 활꼴 안에 삼각형을 얼마나 더 집어넣을 수 있을까 생각하는 학생은 거의 없겠지요. 넓이와 부피의 문제에 관한 마스터키 같은 미적분학은 우리에게 엄청난 편리를 가져다준 위대한 도구이지만 동시에 그와 함께 우리가 경탄을 느낄만한 수많은 기회를 앗아가 버렸는지도 모릅니다.

물론 그리스 수학에 등장하는 모든 수학적 명제들이 경탄할만한 것, 눈길을 끌 만한 것, 지적희열을 가져다줄 수 있는 것은 아닙니다. 어떤 명제들은 사소하고 지루할만큼 당연한 사실들을 이야기할 때도 있습니다. 그러나 그리스 수학은 이 명제들을 하나씩 쌓아 나가다가 독자들로 하여금 결국 예상하지 못했던 어떤 수학적 사실을 마주하게 만듭니다. 마치 플라톤의 많은 대화편들에서 여러 대화자가 자신감 있게 자신의 소신을 피력하다가 결국에 어떤 아포리아에 도달하게 되는 것과 비슷합니다. 그리스 수학의 연역체계는 그 자체로도 아름답지만, 어떤 한두 명제가 결국 이 연역체계의 절정을 이루기도 합니다. 그 캡스톤^capstone명제들 속에 수학자는 놀라움을 담아 두었습니다.

이쯤에서 그렇다면 수학자들은 어떻게 이런 놀라움의 거리들을 찾을 수 있었을까 하는 의문이 생겨납니다. 누군가에게 놀라움을 선사하기 위해서는 내가 먼저 그 놀라움을 경험해야 하는데, 경탄할만한 대상을 찾는다는 것이 만만한 일은 아니기 때문입니다. 이 영업비밀을 어느 수학자도 속 시원하게 밝혀 두었을 리가 없지요. 그러나 한 가지 힌트가 아르키메데스가 남긴 <방법론^Method>에 남아있습니다. 이 책에서 아르키메데스는 자신이 어떤 수학적 발견에 이르게 된 경위를 특별히 기계와 관련한 관점에서 밝혀두고 있습니다. 예를 들어 책의 첫 번째 명제에서 아르키메데스는 방금 우리가 다루었던 포물선 활꼴의 넓이가 상응하는 삼각형의 넓이보다 그 삼각형의 삼 분의 일만큼 더 크다는 사실을 어떻게 발견하게 되었는지 설명하고 있습니다.

그리스 수학에서 제가 가장 좋아하는 정리 중 하나인 <방법론>의 첫 번째 명제를 아래 자세히 옮겨보겠습니다.⁵

직선 AG와 직원뿔의 절단(포물선)으로 둘러싸인 활꼴 ABG가 있다고 하자.
직선 AG가 점D에서 이등분된다고 하고, (포물선의) 지름에 평행하도록 DBE가 그려지게 하자.
AB와 BG를 연결하자.
나는 활꼴 ABG가 삼각형 ABG보다 삼각형 자신에 1/3을 더한 만큼 더 크다고 말한다.
선 AZ가 선DBE에 평행하게 그리고, 직원뿔의 절단(포물선)에 접하는 선GZ을 그린 다음, 선 GB를 점 K까지 연장하자. 그리고 QK와 GK의 길이가 같도록 점 Q를 잡자. 여기서 GQ를 받침이 점 K에 놓인 지렛대라고 생각하자.
.^그림5 아르키메데스 <방법론> 정리 1 (재구성 그림1) / 이은수 제공, 김태균
선 ED와 평행한 임의의 선 MX를 그리자.
GBA가 포물선이고, GZ가 이 포물선의 접선인 상황에서 GD가 포물선의 종좌표^Ordinate이기 때문에, EB는 BD와 길이가 같다.
이런 이유로 (EB=BD), 또 선ZA와 선MX가 선ED와 평행하기 때문에, MN은 NX와 길이가 같고 ZK는 KA와 길이가 같다. (세 삼각형 ZGA, MGX, EGD의 닮음 때문)
MX : XO = AG : AX <포물선의 넓이에 관하여> 명제5
MX : XO = AG : AX = KG : KN = QK : KN
MN이 NX와 길이가 같기 때문에, 만일 XO와 길이가 같은 TH를 그것의 무게중심을 TQ와 QH가 같도록 점 Q에 오도록 놓는다면, MX는 TQH와 이 지렛대에서 균형을 이룰 것이다.
^그림6 아르키메데스 <방법론> 정리1 (재구성 그림2) / 이은수 제공, 김태균
QN이 TH와 MX의 무게에 반비례하도록 분할되어 있어서, QK가 KN에 대한 것과 같은 만큼 MX가 TH에 대해 비를 갖기 때문이다. 그러므로 점 K는 이 둘(MX와 TH)로 구성된 무게의 중심인 셈이다.
마찬가지로, 삼각형 GZA안에서 ED와 평행한 모든 그러한 평행선들이 포물선에 의해 잘려서 Q로 이동시켜진 선분들과 점 K가 이 무게들의 중심이 되도록 균형을 이룰 것이다.
삼각형 GZA는 삼각형 GZA안의 선들로 이루어져 있고, 활꼴 ABG는 같은 방식으로 XO처럼 활꼴안의 선들로 이루어지기 때문에, 전체적으로 삼각형 GZA는 그 자리에 머문 채로 무게중심이 Q에 놓인 포물선의 활꼴과 점 K에서 균형을 이루게 된다.
이제 선 GK가 KC의 세 배가 되도록 점 C에서 분할되게 하자. 따라서 점C는 삼각형 GZA의 무게중심이 된다. <균형에 관하여 (On the Equilibrium)> I.15
삼각형 GZA가 그 자리에 머문 채로 무게중심이 Q에 놓인 활꼴 ABG와 점K에서 균형을 이루고, 점C는 삼각형 GZA의 무게중심이기 때문에, 삼각형 GZA는 무게중심 Q에 위치한 활꼴 ABG와 QK가 CK에 대한 갖는 것만큼의 비를 갖는다.
그런데 QK는 CK의 세 배이기 때문에, 삼각형 GZA는 활꼴 ABG의 세 배가 된다.
하지만 삼각형 GZA는 삼각형 ABG의 네 배이다. 왜냐하면 ZK가 KA와 길이가 같고, AD가 DG와 길이가 같기 때문이다.
그러므로 활꼴 ABG는 삼각형 ABG보다 삼각형 자신에 1/3을 더한 만큼 더 크다.
이것이 바로 보여져야 했던 바이다 (Q.E.D.)
^그림7 아르키메데스 <방법론> 정리 1 (재구성 그림3) / 이은수 제공, 김태균

누군가는 이 천재의 기록에서 모든 선^{Omnes Lineae}의 총합으로 넓이를 구하려했던 카발리에리^{Bonaventura Cavalieri, 1598-1647}의 원리나 더 나아가 미적분의 기본적인 아이디어들을 연상할 법합니다. 그러나 우리의 눈길을 더 끄는 것은 <방법론>의 공식적인 원제목 <기계적인 정리의 방법론에 관하여>가 암시하고 있듯이, 아르키메데스가 포물선의 활꼴과 삼각형의 넓이에 관한 아름다운 사실을 지렛대를 중심으로 한 기계적인 사고를 기반으로 발견했다는 점이지요. 물론 위에서 소개한 아이디어는 기계적인 접근이지 수학적 증명이라고 부르기에는 몇 가지 문제점이 있습니다. 예를 들면, 선들에 무게를 부여한 이후에도 여전히 선들을 추상화된 수학적 대상으로 볼 수 있는가의 문제도 있고, 지렛대와 무게중심에 관한 논의들도 순수하게 수학의 범주 안에서의 증명이라고 보기에는 무리가 있어 보입니다.

더 흥미로운 것은 그가 이 포물선의 활꼴과 삼각형의 넓이에 관한 증명을 여러 번 각색하여 제시하고 있다는 점입니다. 방금 <방법론>에서 그가 보인 것이 첫 번째, <포물선의 넓이에 관하여>의 열여섯-열일곱 번째 명제에서 조금 더 추상화된 기계적 접근으로 증명한 것이 두 번째, 마지막으로 우리가 읽었던 스물네 번째 명제에서 순수한 기하학의 방식으로 증명한 것이 세 번째입니다. 아르키메데스는 왜 같은 정리를 여러 번 가다듬었을까요?

저는 그의 재작업을 보면서 그리스 수학의 증명에 대해 새롭게 생각해 볼 기회를 갖게 되었습니다. 그들이 증명을 왜 하려 했는지 그 동기와 어떻게 증명을 하려 했는지 그 방식을 더 깊게 들여다보고 싶어졌습니다. 그것이 제가 다음 글에서 자세히 말씀드릴 내용입니다. 지금 제가 가진 잠정적인 결론은 증명의 동기와 방식에 놀라움이 밀접하게 연관되어 있다는 것입니다.

한편으로 놀라움이 증명의 동기가 되는 이유는 그럴듯하지 않은 사실을 주장했던 그리스 수학자들에게 그것을 증명할 책임도 따르기 때문입니다. 흔히 이야기하는 입증책임의 원리^{Burden of Proof: Onus probandi}에 따라 어떤 주장을 펼친 이는 그 주장이 참이라는 것을 보여야 할 책임도 함께 맡아야 하는 것이지요. 놀라움이 그리스 수학의 중심에 있었던 것이 사실이라면, 그 놀라운 사실을 증명해야 하는 것은 아주 자연스러운 귀결입니다.

다른 한편으로 놀라움이 증명의 방식에도 관여하는 것은 증명이 이 놀라움을 “잘” 해소시키는 과정이어야 하기 때문입니다. 네. 여기서 저는 더 아름다운 증명과 덜 아름다운 증명을 구분하고 있습니다. 덜 아름다운 증명은 주장한 사실이 참이라는 것을 말해주기는 하는데, 어쩐지 모르게 그래 인정할 수밖에 없다는 패배감을 남기지요. 하켄과 아펠이 컴퓨터를 이용해서 4색 정리를 처음 증명했을 때 사람들이 느꼈을 법한 감정과도 같습니다. 모든 지도를 네 가지 색으로 칠할 수 있다는 이 놀라운 사실을 너무 무미건조하게 증명하였다는 아쉬움을 남긴 것이지요. 그래서 때로 수학자들은 놀라움으로 한껏 고조된 긴장감을 한순간에 김새게 만들지 않도록 각별히 신경을 씁니다. 놀라운 사실만큼이나 놀라운 사실을 증명하는 방식도 놀랍다면 더욱 좋겠다는 생각을 가지고서요.

맥락은 조금 다르지만 고대 그리스의 고전적인 작도문제들이 눈금 없는 자와 컴퍼스만으로 원하는 도형을 얻어야 한다는 제한을 둔 것에서도 저는 비슷한 동기와 방식을 읽습니다. 왜 눈금이 표시된 자나 각도를 잴 수 있는 도구로 정삼각형을 그리는 것은 허락되지 않았을까요? 왜 <원론>의 1권 첫 명제는 한 선분의 양 끝점에서 그 선분을 반지름으로 갖는 두 원을 그려서 그 교점으로부터 정삼각형을 얻어야 한다고 가르쳤을까요? 물론 측정의 부정확함을 피하고 더 완벽한 정삼각형을 얻을 수 있다는 장점도 있었겠지요. 그러나 그리스 수학에서 직선을 그을 수 있는 자와 원을 그릴 수 있는 컴퍼스라는 가장 기본적인 두 가지 도구만으로 기하학의 수많은 도형들을 만들어낼 때, 우리는 그 작도 안에서 엄청난 수학적 희열을 느낍니다. 작도가 단순히 무슨 도형을 만드는 것으로 그치는 것이 아니었던 것처럼, 증명도 단순히 어떤 사실이 참이라는 것을 보이는 것 그 이상이어야 했습니다.

흔히 우리는 고대 그리스 수학의 가장 위대한 업적을 그들의 증명, 더 정확히는 증명을 수학의 중요한 요건으로 도입했다는 점에서 찾곤 합니다. 그렇듯 그리스 수학에서 증명은 너무 중요한 위치에 놓여 있습니다. 하지만 증명이 우선은 아니었습니다. 놀라움은 증명으로 들어가는 문과도 같았습니다. 경탄할 것을 마련해 두지 않고 누군가를 설득한다는 것 자체가 성립하지 않기 때문입니다. 때로 우리는 수학에서의 증명을 일종의 프로그램적인 혹은 박제된 언술로 이해하는 경향이 있습니다. 우리가 증명을 어떤 표준화된 스타일에 따라 가르치고 배워왔기 때문이지요.⁶ 혹은 근대 과학이 시작되면서 과학자들이 자신의 실험결과에 좀 더 객관화된 효과를 부여하고자 비인칭화된 표현을 점진적으로 사용해 온 영향일지도 모릅니다.⁷ 이 습관이 우리에게 고대 그리스 수학의 증명에 관해서도 일종의 오해를 갖게 합니다. 증명에는 늘 사람의 온기가 깃들 구석이 없는 것이라는 선입견을 남기면서요.

그러나 놀라움을 주고받던 그리스인들에게 증명은 기본적으로는 여전히 사람과 사람 사이의 설득이었습니다. 놀라움을 먼저 발견한 나와, 내가 그 놀라움에 동참시키고자 하는 타자 사이의 아주 친밀한 의사소통과도 같은 것이었지요. 유희를 빼고는 고대 그리스의 수학을 말하기 어렵다고 믿는 저로서는 수학이 지루하다는 이야기를 듣는 것이 가장 안타깝습니다. 학생들이 증명에 관심을 갖지 않는다고 지적하기 전에, 과연 우리가 학생들을 이 놀라움의 자리로 초대해 왔는지 돌아볼 이유입니다.