[4월의 퍼즐] 포커 칩과 4색 문제

평면 위에 그린 어떤 지도도 네 개의 색으로 모든 나라를 구별되게 칠할 수 있다는 유명한 4색 정리는 문제가 단순한데도 컴퓨터를 써서야 겨우 풀렸다는 점에서도 유명하다. 4색 정리는 여러 방향으로 일반화가 되었다. 예를 들어 평면이나 구면이 아닌 원환면^torus 위의 지도를 구별되게 칠하려면 일곱 가지 색이 필요하다. 이 결과는 4색 정리보다 먼저 컴퓨터를 쓰지 않고 증명되었다는 점도 흥미롭다.

평면에 지도를 그리는 대신 크기가 같은 원을 나열하는 문제를 생각해 보자. 알기 쉽게 포커 게임에서 쓰이는 칩을 생각하자. 평면 위에 서로 맞닿은 칩은 서로 다른 색이 되도록 칩을 나열한다면 네 가지 색으로 충분하다. 더 적은 수의 색으로는 어떨까? 다음 그림과 같은 배치를 생각하면 적어도 세 가지 색이 필요하다는 것은 분명하다.

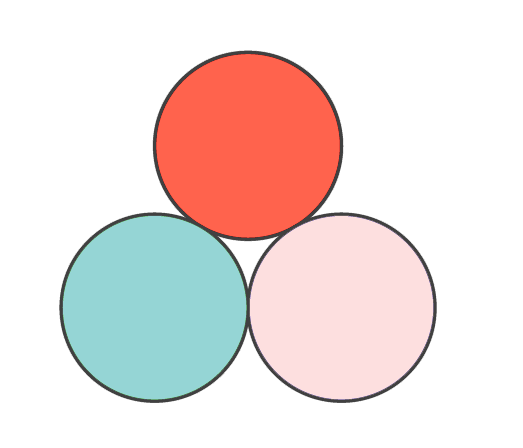그렇다면 서로 맞닿은 칩이 서로 다른 색이 되면서 반드시 네 가지 색이 필요한 배치를 만들려면 최소 몇 개의 칩이 필요할까?