매월 정답자 한 분을 선정하여 고등과학원에서 소정의 상품을 드릴 예정입니다
퍼즐 참여는 8월 27일까지 가능하며 다음달 초 해설과 함께 상품받으실 정답자가 공개됩니다
(답안과 함께 이름, 연락처를 남겨주셔야 정답자 선정 연락이 가능합니다!!)
체스판은 가로 세로 8칸씩 64개의 정사각형으로 이루어져 있으며, 한 칸씩 건너가며 교대로 색깔이 칠해져 있다. 체스판에서 변을 공유하는 정사각형을 인접한 칸이라고 하면, 체스판의 각 칸은 인접한 칸과 색깔이 반대로 칠해져 있다.
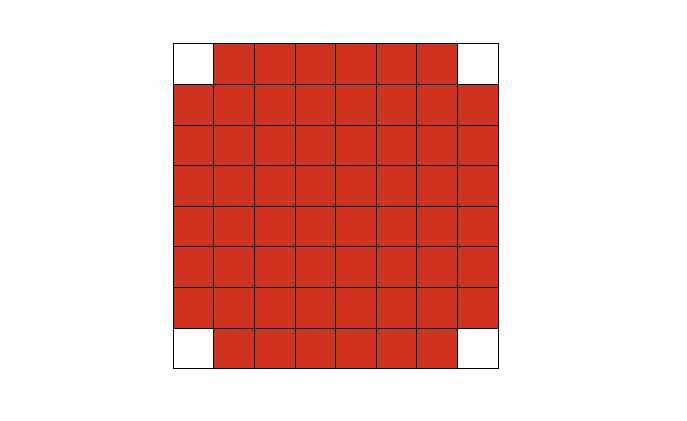
체스판의 각 칸은 최대 네 개의 칸과 인접해 있으며, 위의 그림에서 모든 흰 칸은 적어도 두 개의 붉은 칸과 인접해 있다.
이번 호 퍼즐에서는 \(8 \times 8\) 체스판을 색칠해 보자. 모두 흰 칸으로 이루어진 체스판에서 몇 개의 칸을 빨갛게 색칠하여, 모든 흰 칸이 꼭 두 개의 붉은 칸과 인접하게 만들 수 있을까? 예를 들어 다음처럼 네 귀퉁이만 남겨 놓으면 조건이 충족되므로 이런 일이 가능하다는 것은 분명하다. 그러면 최소 몇 개의 칸을 붉게 칠하면 될까?







13 댓글
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.