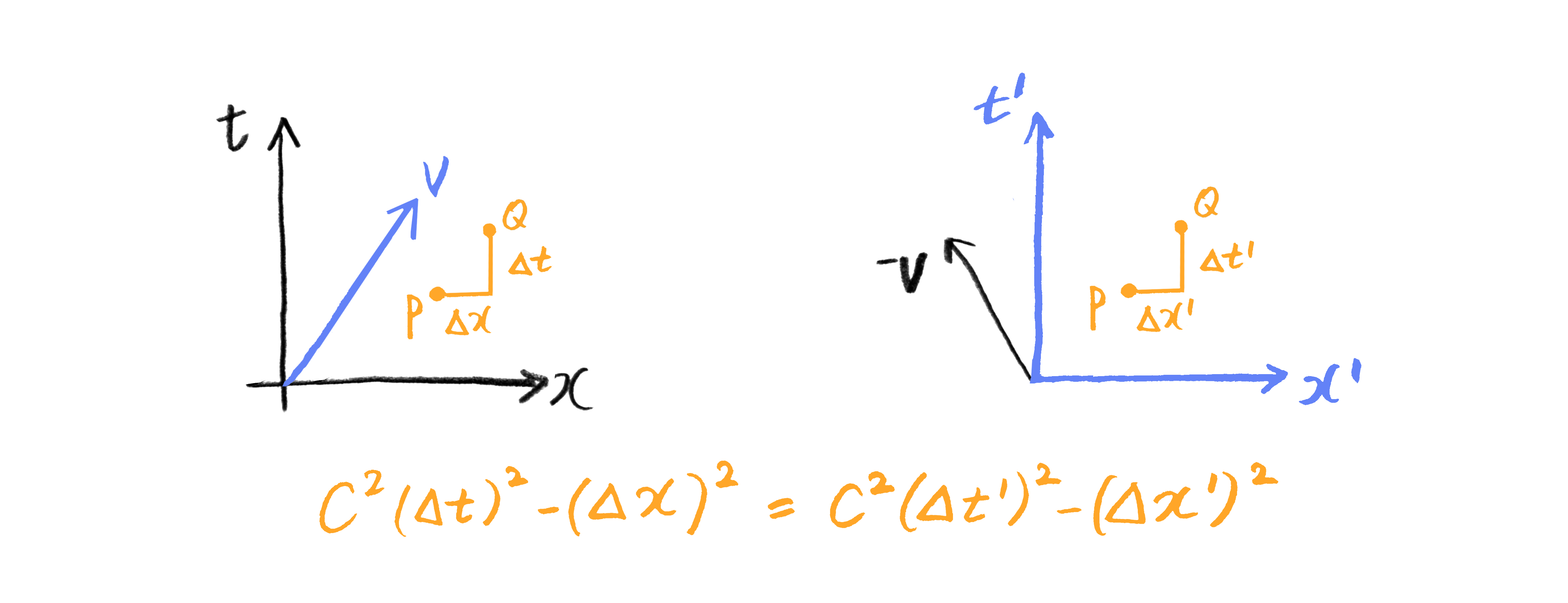블랙홀 안에서는 어떤 일이 벌어질까?: 특수 상대성 이론에서 블랙홀까지

블랙홀이란 중력이 너무나도 강한 나머지 어떤 물체나 신호도 외부로 빠져나올 수 없는 시공간의 영역을 가리킵니다. 매우 극단적인 상황이지만, 일반 상대성 이론의 놀라운 예측 중 하나는 바로 이런 블랙홀이 천체의 중력 붕괴의 산물로서 자연에 수도 없이 존재한다는 것입니다. 지난 수십 년간 얻어진 간접적 및 직접적 증거는 블랙홀의 존재를 강하게 뒷받침해주고 있으며, 블랙홀은 어느덧 현재까지 알려진 우주를 설명하는데 필수적인 개념으로 자리 잡았습니다.

그럼 블랙홀 안에서는 무슨 일이 벌어질까요? 블랙홀 내부는 원칙적으로 우리와 같은 블랙홀 외부의 존재가 직접 볼 수 없는 영역입니다. 그러나 우리는 블랙홀 내부에서도 일반 상대성 이론이 성립한다는 가정 하에, 이 질문에 이론적으로 접근해 볼 수 있습니다. 일반 상대성 이론에 따르면 블랙홀 내부에는 일반 상대성 이론이 더 이상 타당하지 않은 “특이점”이 있다고 예측됩니다. “우주 검열 가설^{cosmic censorship hypotheses}“로 통칭되는 일반 상대성 이론의 여러 가설은 바로 블랙홀과 특이점의 구조에 관한 추측입니다.

블랙홀에 관한 이러한 질문은 수학적으로 잘 정의된, 매우 중요하고 흥미로운 문제이기도 합니다. 뒤에서 더 자세히 설명하겠지만, 일반 상대성 이론의 핵심 방정식인 아인슈타인 중력장 방정식^{Einstein gravitational field equation}은 편미분방정식의 일종으로, 일반 상대성 이론의 “특이점”은 결국 아인슈타인 중력장 방정식에 대한 초기값 문제의 유일한 해를 더 이상 확장시킬 수 없는 경계로 표현될 수 있습니다. “우주 검열 가설”은 결국 이 편미분방정식의 초기값 문제의 해의 성질에 관한 추측이 됩니다.

우주 검열 가설에 관한 최근 연구를 이해하기 위한 초석을 마련해 보고자, 본 글에서는 특수 상대성 이론에서 시작해 일반 상대성 이론과 블랙홀의 개념을 설명하고자 합니다. 단, 저는 편미분방정식의 연구자로서, 일반 상대성 이론을 아인슈타인 중력장 방정식이라는 편미분방정식에 대한 초기값 문제로 보는 관점을 강조할 것입니다. 

1. 특수 상대성 이론에서 블랙홀까지

서론에서 말씀드렸듯 본 글에서는 아인슈타인의 특수 및 일반 상대성 이론과 블랙홀의 개념을 소개하도록 하겠습니다. 일반 상대성 이론을 제대로 이해하기 위해서는 학부 고학년 수준의 미분기하학과 편미분방정식이 필요하지만, 여기서는 가장 중요한 아이디어를 최대한 간단한 형태로 풀어보도록 하겠습니다. \(\ast\)로 표시된 부분은 수학적으로 좀 더 어려운 부분으로, 처음 읽는 분들은 일단 넘어가셔도 무방합니다.

1.1. 갈릴레이의 상대성 원리

이 이론의 가장 기본이 되는 상대성 원리^{principle of relativity}는 사실 우리가 모두 중학교 물리 시간에 배운 다음과 같은 명제입니다:

모든 “물리 법칙”은 모든 “등속으로 움직이는 관찰자”에 대해 동일하게 기술된다.

단, 중학교 물리 시간에 배우는 모든 “물리 법칙”은 (실제 역사적으로도 오랜 기간 그랬듯이) 뉴턴 역학^{Newtonian mechanics}이었습니다. 이렇게 뉴턴 역학에 대해 성립하는 상대성 원리는 갈릴레이 상대성 원리라고 불립니다. 여기서 “등속으로 움직이는 관찰자”는 아무런 외력이 없는 이상적인 우주 공간에 떠다니는 관찰자를 상상해야 합니다. 이런 관찰자가 재는 시간 \(t\) 및 공간 좌표 \((x, y, z)\)를 “관성계^{inertial system}”라 합니다.

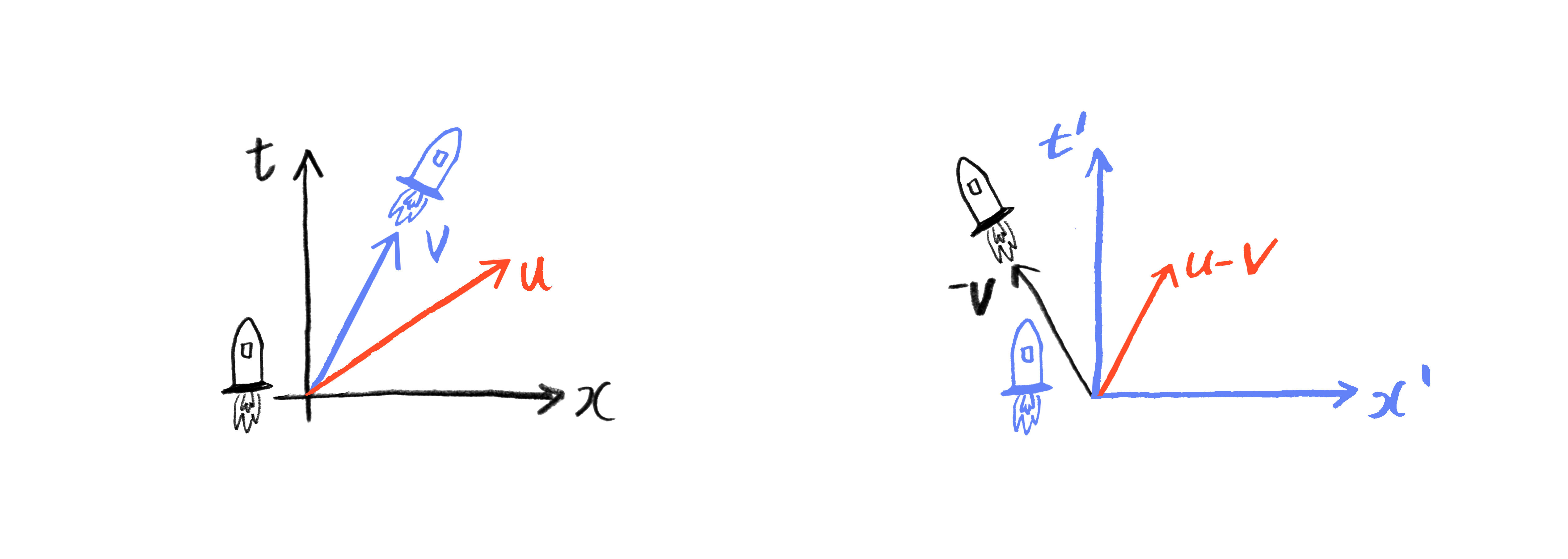
갈릴레이 상대성 원리에 따르면 한 관성계 \((t,x,y,z)\)와 이에 대해 속도 \(V = (V_x, V_y, V_z)\)로 움직이는 다른 관찰자에 의해 정의된 관성계 \((t’, x’, y’, z’)\) 사이에는 (\((t, x, y, z) = (0, 0, 0, 0)\)과 \((t’, x’, y’, z’) = (0, 0, 0, 0)\)에 해당하는 점이 같은 때) 갈릴레이 변환^{Galilean transform}이라고 불리는 다음과 같은 간단한 관계가 있습니다:

\begin{equation} \tag{1.1}
t’ = t, \quad x’ = x – V_x t, \quad y’ = y – V_y t, \quad z’ = z – V_y t.
\end{equation}

이에 따르면 관성계 \((t, x, y, z)\)에 대해 속도 \(u\)로 등속운동하는 물체는, 관성계 \((t, x, y, z)\)에 대해 속도 \(V\)로 움직이는 관성계 \((t’, x’, y’, z’)\)에서는 속도 \(u – V\)로 등속운동하는 것으로 보입니다.([그림1] 참조) 이는 우리의 일상 생활에서 (그리고 뉴턴 역학에서) 익숙한 상황입니다.

1.2. 아인슈타인의 특수 상대성 이론

그러나 19세기 말, 전자기학을 설명하는 맥스웰^Maxwell 방정식이 발견되면서 갈릴레이 상대성 이론은 문제에 직면했습니다. 맥스웰 방정식에 따르면 진공에서의 빛의 속력이 모든 관성계에서 일정하다는 명제가 유도됩니다. 그리고 마이컬슨-몰리^{Michelson & Morley}의 유명한 실험으로 인해, 갈릴레이 상대성 이론 하에서 다른 방법으로 이 현상을 설명하려는 시도들이 부정되었습니다.[6]

이러한 역사적 상황에서 나온 아인슈타인^Einstein의 특수 상대성 이론^{theory of special relativity}[1]은 다름이 아니라, 위의 상대성 원리의 “모든 물리 법칙”에 맥스웰 방정식을 포함시킨 것입니다:

(맥스웰 방정식을 포함한) 모든 물리 법칙은 모든 관성계에서 동일하게 기술된다.

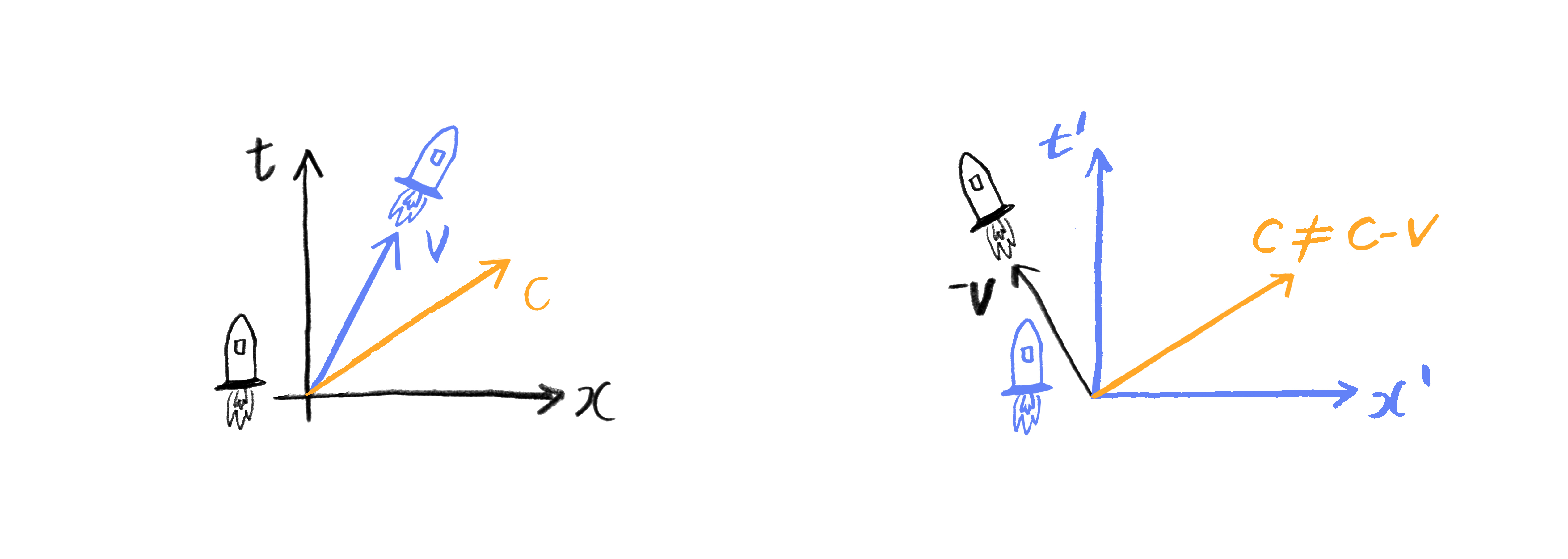
이에 따르면 한 관성계 \((t, x, y, z)\)에서 측정한 진공에서의 빛의 속력이 \(c\)라 할 때, 다른 모든 관성계 \((t’, x’, y’, z’)\)에서도 빛의 속력은 변함없이 \(c\)입니다. 이렇게 상대성 원리에 모든 관성계에서 동일한 속력(즉, 진공에서의 빛의 속력)이 있다라는 공리를 더 하면 아인슈타인의 특수 상대성 이론 (1905)에 다다르게 됩니다.

1.3. 민코프스키 시공간과 아인슈타인 특수 상대성 이론의 기하학적 기술

아인슈타인의 특수 상대성 이론은 다음과 같은 “기하학적 성질”로 정리됩니다:

명제  1.1. 서로에 대해 등속으로 움직이는 두 관성계 \((t, x, y, z)\)와 \((t’, x’, y’, z’)\)에서 관측한 두 점 \(P\), \(Q\)를 관측한 좌표값을 각각 \((t_{P},x_{P},y_{P},z_{P}), (t_{Q}, x_{Q}, y_{Q}, z_{Q})\)와 \((t’_{P},x’_{P},y’_{P},z’_{P}), (t’_{Q}, x’_{Q}, y’_{Q}, z’_{Q})\)라고 할 때, 다음과 같은 등식이 성립한다:

\(\begin{equation} \tag {1.2} c^{2} (t_{Q} – t_{P})^{2} – (x_{Q} – x_{P})^{2} – (y_{Q} – y_{P})^{2} – (z_{Q} – z_{P})^{2} \\ = c^{2} (t’_{Q} – t’_{P})^{2} – (x’_{Q} – x’_{P})^{2} – (y’_{Q} – y’_{P})^{2} – (z’_{Q} – z’_{P})^{2}.\end{equation}\)

이 명제는 상대성 원리와 모든 관성계에서 똑같이 측정되는 속력 \(c\)의 존재성, 그리고 관성계에 대한 몇 가지 “상식적인” 가정으로부터 유도될 수 있습니다. \([4, \S~1.2] \) 여기서는 이 명제의 증명 대신, 그 의의를 설명하고자 합니다.

식 \((1.2)\)에서 정의된 양을 두 점 \(P\), \(Q\) 사이의 시공간 간격^{spacetime interval}이라고 합니다. 이에 따라 명제 \(1.1\)을 다시 간단히 표현하면 시공간 간격은 관성계의 변환에 불변이라고 할 수 있습니다. 이는 마치 유클리드 기하학에서 두 점 \(p = (x_{p}, y_{p}, z_{p})\)와 \(q = (x_{q}, y_{q}, z_{q})\) 사이의 길이의 제곱

\(\begin{equation} \tag {1.3} (x_{p} – x_{q})^{2} + (y_{p} – y_{q})^{2} + (z_{p} – z_{q})^{2}\end{equation}\)

이 직교 좌표계의 변환에 불변인 것(피타고라스의 정리)과 매우 유사합니다. 이것이 바로 명제 \(1.1\)을 “기하학적”이라고 부른 이유입니다.

유클리드 기하학에서는 위의 성질을 뒤집어서, 3차원 공간과 두 점 사이의 길이의 개념에서 시작해서, 이 3차원 공간을 기술하는 모든 좌표계 \((x, y, z)\) 중 길이의 제곱이 \((1.3)\)으로 표현되는 좌표계를 직교 좌표계라고 정의해도 무방합니다. 마찬가지로 우리는 (3+1)-차원 시공간과 두 (시공간) 점 사이의 시공간 간격에서 시작하여, 이 (3+1)-차원 시공간을 기술하는 모든 좌표계 \((t, x, y, z)\) 중 시공간 간격이 \((1.2)\)처럼 표현되는 좌표계를 관성계로 정의할 수 있습니다. 이것이 바로 민코프스키 시공간의 개념입니다.

민코프스키 시공간과 시공간 간격의 개념에서 시작하면 특수 상대성 이론 전체를 유도해낼 수 있습니다. 예를 들면 속력 \(c\)의 등속으로 움직이는 시공간 궤적 위 두 점의 시공간 간격은 항상 \(0\)인데, 이로부터 모든 관성계에서의 속력 \(c\)의 불변성을 간단히 볼 수 있습니다. 특수 상대성 이론 하에서 (시공간 원점이 같은) 두 관성계 사이의 관계인 로렌츠 변환^{Lorentz transformation} 또한 시공간 간격이 \((1.2)\)의 형태로 불변인 모든 선형 변환을 구함으로써 유도할 수 있습니다. 또한 서로 다른 관성계에서의 시간과 공간 변화의 관계를 살펴보면 동시성의 상대성, 시간 팽창과 길이 수축 등 특수 상대성 이론의 다른 잘 알려진 결과도 읽어낼 수 있습니다.

1.4. \(\ast\)쌍둥이 역설, 고유 시간과 민코프스키 계량

여기서는 시공간 간격의 불변성을 사용해 (특수 상대성 이론이 적용 가능하도록 설계된) “쌍둥이 역설”이라는 예제를 다루도록 하겠습니다. 이로부터 유도해낼 고유 시간^{proper time}과 민코프스키 계량^{Minkowski metric}이라는 개념은, 밑에 있는 일반 상대성 이론의 설명을 더 깊게 이해하는 데 도움이 될 것입니다.

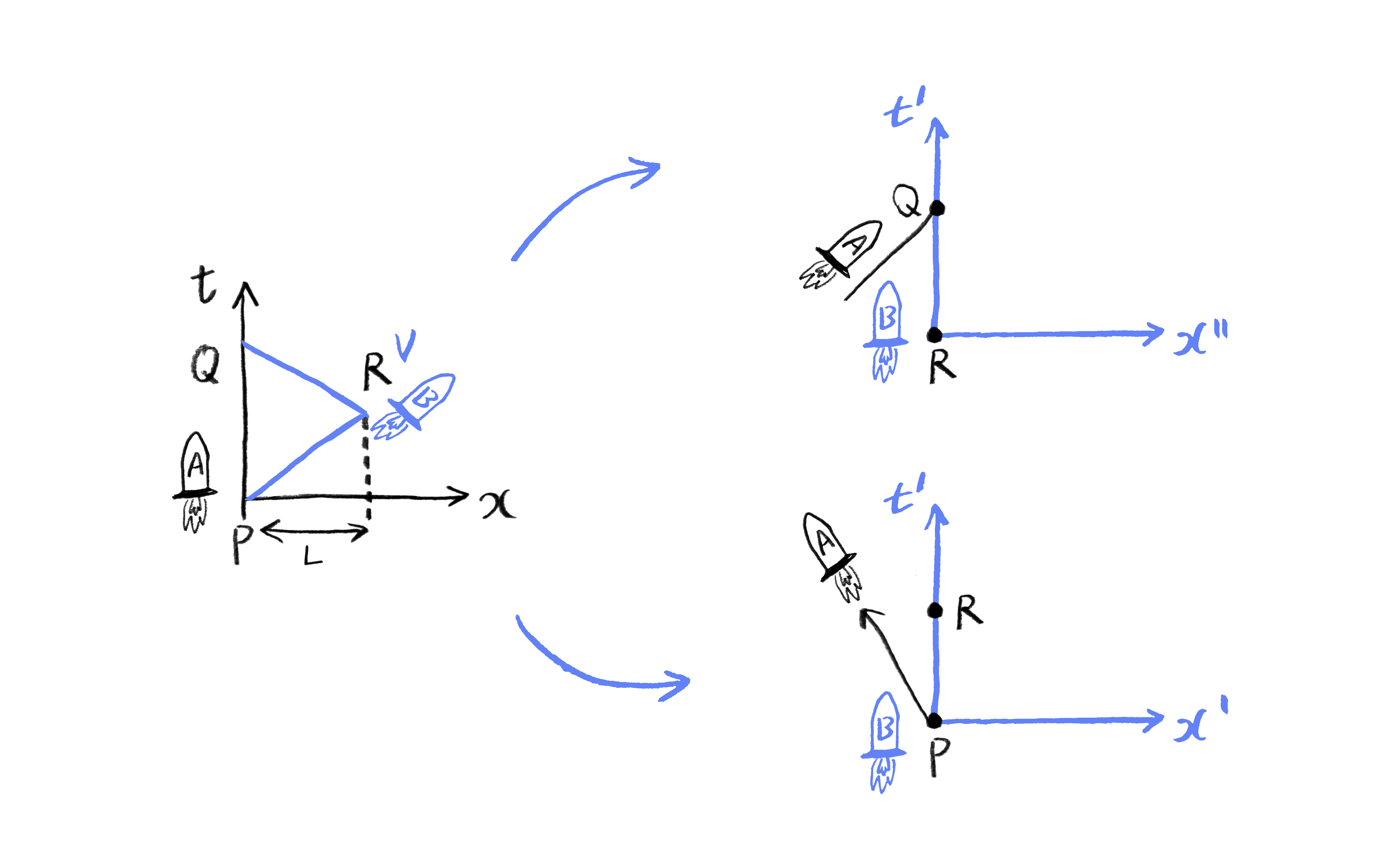
예제 1.2 쌍둥이 역설^{Twin paradox}: 같은 시간에 태어난 쌍둥이 형과 동생을 각각 우주선 \(A\), \(B\)에 태우도록 하자. 우주선 \(A\)는 등속 운동을 하고 있고, 우주선 \(B\)가 우주선 \(A\)에 대해 등속으로 거리 \(L\)만큼 날아갔다가, 다시 등속으로 돌아와 우주선 \(A\)와 다시 만났다고 하자. 이때, 두 쌍둥이 중 누가 나이가 더 적은가?

이 질문이 역설이라고 불리는 이유는 상대성 이론이라고 하면 흔히 떠올리는 “빠르게 움직이면 시간이 느리게 간다”라는 명제와 맞지 않는 것처럼 보이기 때문입니다. 형의 입장에서는 동생을 태운 우주선이 빠르게 움직이고 있으므로 동생의 시간이 더 느리게 가는 것으로 보이지만, 동생의 입장에서도 형이 빠르게 움직이니 형의 시간이 더 느리게 가는 것으로 보일 것입니다. 그럼 누구의 시간이 더 느리게 간 것일까요

이 역설의 해답은 쌍둥이의 상황이 완전 대칭적이지 않다는 사실에서 시작합니다. 쌍둥이 형제가 헤어진 시공간 점을 \(P\), 다시 만난 시공간 점을 \(Q\)라고 합시다. 그리고 우주선 \(B\)가 회항한 시공간 점을 \(R\)이라고 부르도록 합시다. 우주선 \(A\)에 탄 형의 입장에서 경과된 시간 \(\tau_{A}\)는 계속 등속운동한 우주선 \(A\)에 해당하는 관성계¹ \((t, x, y, z)\)에서 경과된 시간인 \(t_{Q} – t_{P}\)입니다. 반면 우주선 \(B\)에 탄 동생의 입장에서 경과된 시간 \(\tau_{B}\)를 계산하려면, 우주선 \(B\)의 \(P\)에서 \(R\)까지 등속운동에 해당하는 관성계 \((t’, x’, y’, z’)\)에서 경과된 시간 \(t’_{R} – t’_{P}\)과 \(R\)에서 \(Q\)까지 등속운동에 해당하는 관성계 \((t″, x″, y″, z″)\)에서 경과된 시간 \(t″_{Q} – t″_{R}\)을 더해야 할 것입니다.

여기서 중요한 아이디어는 시공간 간격의 불변성(명제 \(1.1\))을 사용해 \(t″_{Q} – t″_{R}\)와 \(t’_{R} – t’_{P}\)를 관성계 \((t, x, y, z)\)에서 측정하는 양으로 변환하는 것입니다. 관성계 \((t, x, y, z)\)에서 우주선 \(B\)가 회항하기 전 이동한 거리가 \(L\)이므로, 명제 \(1.1\)에 따라 다음과 같은 식이 성립합니다:

\(\begin{equation*}
c^{2} (t″_{Q} – t″_{R})^{2} = c^{2} (t_{Q} – t_{R})^{2} – L^{2}, \qquad
c^{2} (t’_{R} – t’_{P})^{2} = c^{2} (t_{R} – t_{P})^{2} – L^{2}.
\end{equation*}\)

우주선 \(A\)와 \(B\) 입장에서 경과된 시간은 각각 \(\tau_{A} = t_{Q} – t_{P}\)와  \(\tau_{B} = (t″_{Q} – t″_{R}) + (t’_{R} – t’_{P})\)이므로, 이를 정리하면:

\(\begin{align*}
\tau_{A}
= t_{Q} – t_{P}
= \sqrt{(t″_{Q} – t″_{R})^{2} + \frac{L^{2}}{c^{2}}}
+ \sqrt{(t’_{R} – t’_{P})^{2} + \frac{L^{2}}{c^{2}}}
> (t″_{Q} – t″_{R}) + (t’_{R} – t’_{P}) = \tau_{B},
\end{align*}\)

즉, 우주선 \(B\)를 타고 왕복한 쌍둥이가 더 나이가 적은 것을 알 수 있습니다.

이 간단한 예제의 풀이를 조금만 일반화시키면, 여러 가지 의미 있는 결과들을 도출해낼 수 있습니다. 시공간의 두 점 \(P\), \(Q\)를 잇는 궤적 \(\Gamma\)에 대해, 그 궤적의 입장에서 경과된 시간을 \(\Gamma\)의 고유시간^{proper time}이라 합니다. 예제 \(1.2\)는 결국 \(P\), \(Q\)를 잇는 직선 궤적 \(\Gamma_{A}\)와 선분 \(\overline{PR}\)과 \(\overline{RQ}\) 두 개로 이루어진 궤적 \(\Gamma_{B}\)의 고유시간을 계산하는 문제입니다.

위 예제의 접근 방식에 따르면, 점 \(P\), \(Q\)를 잇는 직선 궤적 \(\Gamma_{A}\)의 고유시간은 정확히 \(P\), \(Q\) 사이의 시공간 간격의 제곱근입니다. 이때 이 제곱근이 양수로 잘 정의되려면 시공간 간격이 양수여야 하는데, 이는 “\(\Gamma_{A}\)의 속력이 \(c\)보다 작아야 한다”는 자연스러운 제한과 동치입니다. 같은 논리로 모든 관성계는 서로에 대해 \(c\)보다 작은 속력으로 운동해야 함을 유도할 수 있습니다.

반면 두 개의 선분 \(\overline{PR}\)과 \(\overline{RQ}\)로 이루어진 궤적 \(\Gamma_{B}\)의 고유시간은 선분 \(\overline{PR}\)과 \(\overline{RQ}\)에 해당하는 고유시간의 합으로 계산합니다. 앞에서 언급한 사실을 이용하면 \(\Gamma_{B}\)의 고유시간은 점 \(P\), \(R\) 사이의 시공간 간격의 제곱근과 점 \(R\), \(Q\) 사이의 시공간 간격의 제곱근의 합을 구해 어느 관성계에서나 \(\Gamma_{B}\)의 고유시간을 간단히 계산할 수 있습니다.

같은 아이디어를 통해, 우리는 이제 유한 개의 선분으로 이루어진 궤적 \(\Gamma\)의 고유시간을 계산할 수 있습니다. 뿐만 아니라 미적분학에서 일반적인 곡선의 길이를 유한 개의 선분으로 근사하여 계산하는 과정을 따라가면 일반적인 시공간의 궤적 \(\Gamma\)의 고유시간 \(\tau\)를 유한 개의 선분으로 이루어진 궤적 \(\Gamma’\)으로 근사하여 계산할 수 있습니다.([그림5] 참조)

위와 같은 아이디어로 얻어지는 \(\Gamma\)의 고유시간 공식은 다음과 같습니다:

\begin{equation} \tag{1.4}
\tau = \int_{0}^{1} \sqrt{-\eta(\dot{\gamma}(s), \dot{\gamma}(s))} \, ds.
\end{equation}

이 때 \(\gamma(s)\) (\(s \in [0, 1]\))은 궤적 \(\Gamma\)의 매개변수화이며, \(\dot{\gamma}\)은 이를 \(s\)로 미분해 얻은 접벡터^{tangent vector}입니다. 그리고 \(\eta({\bf v}, {\bf v})\)는 민코프스키 계량^{Minkowski metric}이라고 불리며, 접벡터 \({\bf v} = ({\bf v}^{0}, {\bf v}^{1}, {\bf v}^{2}, {\bf v}^{3})\)에 대해 다음과 같이 주어지는 양입니다:

\begin{equation} \tag{1.5}
\eta({\bf v}, {\bf w}) = – c^{2} {\bf v}^{0} {\bf w}^{0} + {\bf v}^{1} {\bf w}^{1} + {\bf v}^{2} {\bf w}^{2} + {\bf v}^{3} {\bf w}^{3}.
\end{equation}

민코프스키 계량의 주요 성질은 \({\bf v} = {\bf w} = (t_{Q} – t_{P}, x_{Q} – x_{P}, y_{Q} – y_{P}, z_{Q} – z_{P})\)로 주어질 때, \(-\eta({\bf v}, {\bf w})\)는 정확히 점 \(P\), \(Q\) 사이의 시공간 간격이 된다는 것입니다.

식 \((1.4)\)에서 \(\sqrt{-\eta(\dot{\gamma}(s), \dot{\gamma}(s))}\)이 양수로 잘 정의되기 위한 조건은 전처럼 \(\Gamma\) 위의 각 점에서 순간속력이 \(c\)보다 작아야한다는 자연스러운 조건이 됩니다. 이런 조건을 만족하는 궤적을 각각 시간꼴궤적^{timelike trajectory}이라고 합니다. 정리하면 식 \((1.4)\)를 통해 임의의 (충분히 매끈한) 시간꼴궤적의 고유시간을 계산할 수 있습니다.

마지막으로 예제 \(1.2\)의 결론 부분의 계산을 일반화하면, 결국 점 \(P\), \(Q\)를 잇는 모든 시간꼴궤적 중 가장 고유시간이 긴 (즉, 나이가 많이 드는) 궤적은 등속 궤적(즉, 직선 궤적)임을 알 수 있습니다. 이는 유클리드 공간에서 두 점을 최소 길이로 잇는 방법이 직선이라는 명제와 대응되는 민코프스키 시공간의 기하학적 성질입니다.

1.5. 아인슈타인의 일반 상대성 이론

일반 상대성 이론의 시작점은 우리가 역시나 중학교 물리 시간에 배운 다음과 같은 원리입니다:

(진공에서) 모든 물체는 같은 중력가속도로 떨어진다.

뉴턴 역학에서는 이 원리를 중력이 물체의 관성 질량에 비례한다는 식으로 표현합니다. 이 방식은 잘 알려져 있다시피 여러 현상을 설명하는데 매우 유용합니다. 그러나 이 방식에는 왜 중력이 특별히 관성 질량과 관계가 있어야 하는지 명확한 이유가 없다는 단점이 있습니다.

위의 원리를 (특수) 상대성 이론과 자연스럽게 합치기 위한 아인슈타인의 놀라운 아이디어는 다음과 같았습니다:

중력은 각기 다른 질량에 비례하는 외부 힘이 아니라, 
모든 물체가 똑같이 따라가야 하는 시공간의 휘어짐이다!

이에 따르면 중력 외의 힘이 작용하지 않는 물체(자유 낙하 물체)는 시공간의 휘어짐을 따라가는 “자연스러운 궤적”을 취합니다. 중력으로 인해 사과가 지구에 떨어지는 것과 같은 현상은, 사과와 지구의 “자연스러운 궤적”이 시공간의 휘어짐으로 인해 서로 점점 가까워지는 것으로 표현됩니다. 중력이 없는 경우 “자연스러운 궤적”은 직선(즉, 등속 운동)이 되어, 특수 상대성에 해당하는 상황이 됩니다. (휘어진 시공간은 로렌츠 다양체에, 자유 낙하하는 물체의 “자연스러운 궤적”은 로렌츠 다양체 상의 시간꼴 측지선^{timelike geodesic}에, 자유 낙하하는 빛 신호는 로렌츠 다양체 상의 빛꼴 측지선^{lightlike geodesic}에 해당합니다. 이 수학적 개념들은 밑의 \(1.6\)절에서 \(1.4\)절에서 도입한 개념을 이용해 보다 조금 더 상세히 설명할 예정입니다.)

또한 아인슈타인은 중력, 즉 시공간의 휘어짐이 어떻게 시공간의 에너지·물질 분포에 따라 결정되는지 알려주는 아인슈타인 중력장 방정식(밑의 식 \((1.6)\)을 발견했습니다.[2] 이에 대해서는 \(1.7\)절에서 다시 다루도록 하겠습니다.

정리하자면 (1)시공간의 휘어짐을 통한 중력의 묘사와 (2)그 중력을 결정하는 아인슈타인 중력장 방정식, 이 두 가지가 일반 상대성 이론의 기본 개념입니다.

1.6. \(\ast\)로렌츠 다양체와 중력의 묘사

여기서는 \(1.4\)절에서 도입된 개념을 사용해 일반 상대성 이론에서 중력을 묘사하는 과정을 설명하도록 하겠습니다.

휘어진 시공간을 수학적으로 기술하기 위해서는, \((3+1)\)-차원 민코프스키 시공간의 개념을 매끈한 \((3+1)\)-차원 로렌츠 다양체^{Lorentzian manifold}의 개념으로 확장해야 합니다. 이 확장 과정은 19세기 독일의 수학자 리만^Riemann이 유클리드 공간의 개념을 리만 다양체의 개념으로 확장한 것과 매우 유사합니다.

매끈한 \((3+1)\)-차원 다양체^{smooth \((3+1)\)-dimensional manifold}란 각 점의 주변 영역을 4개의 좌표로 이루어진 좌표계로 표현할 수 있고 겹치는 영역의 좌표 변환이 항상 매끈한 수학적 대상을 뜻합니다. 로렌츠 다양체란 로렌츠 측량^{Lorentzian metric}이 존재하는 다양체로, 로렌츠 측량이란 각 점에서 적절한 좌표계 변환으로 민코프스키 측량과 (그 점에서의 거리에 대한 1차 항까지) 형태가 같아지는 텐서 \({\bf g}\)를 뜻합니다. 이를 종합하면 로렌츠 다양체는 각 점 주변에서 시공간의 휘어짐(중력)을 비관성적 좌표계 변환(즉, 가속계의 사용)을 통해 국소적으로 민코프스키 시공간과 같이 평평하게 만들 수 있다는 성질은 가지고 있는데, 이는 “중력과 가속계의 가상의 힘을 구분할 수 없다”는 아인슈타인의 등가 원리^{Einstein’s equivalence principle}라고 불리기도 합니다.

\(1.4\)절에서 우리는 민코프스키 시공간 내의 궤적에 대해 미적분의 아이디어를 사용해 민코프스키 측량을 이용한 고유시간 공식 \((1.4)\)를 유도했습니다. 비슷한 과정을 로렌츠 다양체 내의 궤적 \(\Gamma ={ \left\{ \gamma (s) \right\} }_{ s\in [0,1] }\)에 적용하면, \(\Gamma\)의 고유시간이 그 궤적 위 각 점의 로렌츠 측량 \({\bf g}\)를 사용한 다음과 같은 공식으로 주어지는 것이 적절하다는 것을 알 수 있습니다:

\begin{equation*}
\tau = \int_{0}^{1} \sqrt{-{\bf g}(\dot{\gamma}(s), \dot{\gamma}(s))} \, ds.
\end{equation*}

민코프스키 시공간에서 외력의 작용이 없는 물체의 궤적, 즉 등속 운동이 두 점을 잇는 최대 고유시간 궤적이었던 것을 생각하면, 중력 외 힘의 작용 없이 자유낙하하는 물체는 휘어진 시공간에서 매 순간 고유시간이 최대인 궤적을 따르는 것이 자연스럽습니다. 이것이 바로 위에서 “자연스러운 궤적”이라고 불렸던 것으로, 수학적으로는 로렌츠 다양체 위의 측지선^geodesic이 됩니다. 각 점에서 제곱근 \(\sqrt{-{\bf g}(\dot{\gamma}(s), \dot{\gamma}(s))}\)이 양수로 잘 정의된 측지선과 \(0\)인 측지선을 각각 시간꼴 측지선^{timelike geodesic}과 빛꼴 측지선^{lightlike geodesic}이라고 부르며, 이들은 각각 휘어진 시공간에서 자유낙하하는 물체의 궤적과 광선의 궤적을 기술합니다.

1.7. 아인슈타인 중력장 방정식

중력, 즉 시공간의 휘어짐을 결정하는 일반 상대성 이론의 핵심 방정식은 1915년 11월 발표된 아인슈타인의 중력장 방정식입니다.[2] 미분기하학의 언어를 빌리면, 아인슈타인 중력장 방정식은 단 한 줄로 다음과 같이 간결하게 표현됩니다:

\begin{equation} \tag{1.6}
\mathbf{Ric}_{\mu \nu} – \frac{1}{2} \mathbf{R} {\bf g}_{\mu \nu} = \frac{8 \pi G}{c^{4}} {\bf T}_{\mu \nu}.
\end{equation}

식 \((1.6)\)의 좌변과 우변은 각각 시공간의 기하적 성질(중력)과 물리적 성질(에너지·물질 분포)을 나타내며, 아인슈타인 중력장 방정식은 이 두 성질을 관계 짓는 역할을 합니다. 조금 더 자세하게 설명하면 방정식 좌변의 \({\bf g}_{\mu \nu}\)는 시공간의 로렌츠 측량, \(\mathbf{Ric}_{\mu \nu}\)와 \(\mathbf{R}\)은 각각 리치 곡률, 스칼라 곡률이라고 불리는 기하학적인 대상으로, 방정식 좌변 전체는 결국 시공간의 곡률을 결정하는 역할을 합니다. 방정식 우변의 \(G\)는 중력 상수, \(c\)는 진공에서 빛의 속력, \({\bf T}_{\mu \nu}\)는 에너지-운동량-스트레스 텐서로, 시공간 내 중력 외의 에너지 및 물질 분포를 나타내는 역할을 합니다. 중력 외 아무것도 없는 경우, 즉 진공 상태는 \({\bf T}_{\mu \nu} = 0\)의 조건으로 표현됩니다.

중력장과 시공간 속 물질 분포 간의 관계를 알려준다는 점에서 아인슈타인 중력장 방정식 \((1.6)\)은 뉴턴의 만유인력 법칙과 비슷합니다. 중력 포텐셜 \(\Phi\)의 관점에서 뉴턴의 만유인력은 다음과 같은 형태로 적을 수 있습니다:

\begin{equation} \tag{1.7}
-\Delta \Phi =4\pi G\rho .
\end{equation}

이때 \(\Delta ={ \partial }_{ x }^{ 2 }+{ \partial }_{ y }^{ 2 }+{ \partial }_{ z }^{ 2 }\)으로 주어지는 라플라스 편미분연산자이며, \(\rho\)는 질량 분포를 나타내는 함수입니다. 아인슈타인 중력장 방정식처럼 식 \((1.7)\) 또한 중력을 나타내는 좌변과 물질 분포를 나타내는 우변의 관계를 표현합니다.

그러나 아인슈타인 중력장 방정식과 뉴턴의 만유인력 법칙은 중요한 차이점이 있습니다. 식 \((1.6)\)은 선형 타원^elliptic 편미분방정식의 일종으로, 우변이 주어지면 동시에 중력 포텐셜 \(\Phi\)가 곧바로 결정되는 성질을 가지고 있습니다. 그러나 아인슈타인 중력장 방정식 \((1.6)\)을 통해서는 우변이 주어진 동시에 중력을 결정하는 것이 불가능합니다. (이 성질은 “동시”라는 개념 자체가 아인슈타인 상대성 이론에서 부자연스러운 것과 일맥상통합니다.)

아인슈타인 중력장 방정식 \((1.6)\)은 (로렌츠 측량 \({\bf g}\)에 대한) 비선형 쌍곡^hyperbolic 편미분방정식의 일종으로, 빛(전파)이나 소리(음파)를 기술하는 파동^wave 방정식과 비슷한 특성을 지닙니다. 식 \((1.6)\)을 통해 시공간을 결정하기 위해서는 파동 방정식을 풀듯, 우변과 함께 “시공간의 초기값”을 아는 상태에서 초기값 문제^{initial value problem}를 풀어야 합니다. 이렇듯 일반 상대성 이론에서는 중력장(즉, 시공간)이 그 속에서 운동하고 있는 물질의 분포를 통해 바로 결정되는 무대가 아니라, 함께 시간에 따라 동적으로 변화하는 주인공 중 하나가 됩니다.

1.8. 쇼케-브뤼아의 정리

일반 상대성 이론에서 중력장(즉, 시공간)을 구하는 과정은 초기값 문제를 풀어야 한다는 점에서 마치 뉴턴의 제 2법칙 \(({\bf F} = m \ddot{\bf x})\)을 통해 물체의 운동을 풀어내는 것과 비슷합니다. 뉴턴의 제 2법칙과 같은 2계 상미분방정식에 관련된 가장 근본적인 수학적 정리는 (간단히 서술하면) 다음과 같습니다:

정리 1.3 피카드-린델뢰프^{Picard-Lindelöf}: 정리2계 상미분방정식의 초기값 문제에는 주어진 초기값과 초기미분값에 대해 유일한 해가 존재한다.

이를 2계 상미분방정식의 초기값 문제의 타당성이라고 합니다. 뉴턴 제 2법칙 \({\bf F} = m \ddot{\bf x}\)의 경우 초기값과 초기미분값은 초기 위치 \({\bf x}(0)\)와 초기 속도 \(\dot{\bf x}(0)\)에 해당되어, 위의 정리는 결국 “초기 위치와 초기 속도, 힘을 알면 물체의 운동을 결정할 수 있다”는 명제가 됩니다.

아인슈타인 중력장 방정식에서 이와 대응되는 근본적인 정리는 1952년 프랑스의 수학자 쇼케-브뤼아^{Choquet-Bruhat} [3]에 의해 증명되었습니다. 쇼케-브뤼아의 정리는 간단히 이야기하면 “휘어진 시공간의 초기값과 초기미분값, 그리고 시공간 내의 에너지-운동량 텐서를 알면 시공간의 휘어짐(중력)을 결정할 수 있다”는 명제입니다. 이를 통해 일반 상대성 이론은 아인슈타인 중력장 방정식이라는 편미분방정식에 대한 초기값 문제의 해에 관한 연구라는 보다 넓은 수학적 관점에서 바라볼 수 있게 됩니다. 추후에 소개할 일반 상대성 이론의 “특이점”이라는 개념과 “우주 검열 가설”이라는 추측은 모두 이러한 관점에서 다뤄질 것입니다.

1.9. \(\ast\)쇼케-브뤼아의 정리: 조금 더 자세한 설명

흥미가 있는 독자를 위해, 쇼케-브뤼아의 중요한 정리를 가장 간단한 진공의 경우(즉, \({\bf T} = 0\))에 관해 조금 더 구체적으로 설명하겠습니다. 더 정확한 설명은 [9]의 10장을 참조하시기 바랍니다.

고전물리의 다른 미분방정식들과 비교했을 때 쇼케-브뤼아의 정리가 흥미로운 점은 아인슈타인 중력장 방정식이 휘어진 시공간 \(({\cal M}, {\bf g})\) 자체에 관한 식인 만큼 ” 초기값”과 “초기미분값”의 개념이 명확하지 않다는 점입니다. 쇼케-브뤼아는 이 개념적 문제를 아인슈타인 중력장 방정식의 초기값을 3차원 휘어진 공간(즉, 리만 다양체) \(\sum\)\(_{0}\), 초기미분값을 \(\sum\)\(_{0}\)가 휘어진 시공간 \({\cal M}\)에 매장된 형태 \(k\)(즉, 공간꼴 부분다양체 \(\sum\)\(_{0}\)의 2차 기본형식)로 기하학적으로 해석함으로써 우아하게 풀어냈습니다. 이를 통해 쇼케-브뤼아의 정리를 간단히 표현하면 다음과 같습니다:

정리 1.3 쇼케-브뤼아 정리: 충분히 매끈하고 “제한 방정식^{constraint equation}“을 만족하는 주어진 초기값(3차원 리만다양체) \(\sum\)\(_{0}\)과 초기미분값(2차 기본형식) \(k\)에 대응되는 진공 아인슈타인 중력장 방정식의 해 \(({\cal M}, {\bf g})\)는 유일하게 존재한다.

여기서 초기값과 초기미분값이 만족해야 하는 “제한 방정식”은 진공 아인슈타인 중력장 방정식의 일부로, 전자기학의 맥스웰 방정식 중 초기값이 만족해야 하는 가우스 방정식(\(\Delta \cdot {\bf E} = 4 \pi \rho\), \(\Delta \cdot {\bf B} = 0\))과 매우 유사합니다. 단, 간단한 가우스 방정식과는 달리 일반 상대성 이론의 제한 방정식은 복잡한 비선형 편미분방정식이며, 그 속에는 양수 질량 정리 [7],[10] 등 아름다운 결과들이 숨어있습니다. 일반 상대성 이론의 제한 방정식에 대한 연구는 여전히 미분기하학의 중요한 연구주제 중 하나입니다.

1.10. 고립된 천체와 블랙홀

이제 블랙홀의 개념이 일반 상대성 이론에서 어떻게 자연스럽게 나타나는지 소개하고자 합니다.

진공 아인슈타인 중력장 방정식의 해 중 (쇼케-브뤼아 정리에 따른) 초기값이 유한한 지름을 가진 영역 밖에서 평평한 민코프스키 시공간의 초기값으로 점근하는 해를 점근적으로 평평하다^{asymptotically flat}고 부릅니다. 이러한 해는 물리적으로 고립된 천체의 외부 시공간 휘어짐을 기술합니다. 이때 점근적 평평함 조건은 고립된 중력계를 고려하고 있기에 타당하고, 진공 조건이 타당한 이유는 천체 외부 영역을 고려하고 있기 때문입니다. 일반 상대성 이론에서는 시공간의 휘어짐이 곧 중력장이므로, 진공 아인슈타인 중력장 방정식의 점근적으로 평평한 해는 곧 태양이나 달과 같은 하나의 천체가 똑 떨어져 있을 때 그 외부에 생기는 중력장이라고 다시 표현될 수 있습니다.

진공 아인슈타인 중력장 방정식은 몇 가지 매우 흥미로운 명시적인, 즉 형태를 식으로 직접 쓸 수 있는 점근적으로 평평한 해를 지니고 있습니다. 아인슈타인이 식 \((1.6)\)을 발표한지 불과 한 달 만에 독일의 물리학자 슈바르츠실드^{Schwarzschild}가 발견한 해(슈바르츠실드 시공간)는 구형 대칭성을 지니고 움직이지 않는, 즉 회전하지 않는 천체 외부의 시공간을 기술합니다.[8] 그리고 1963년 뉴질랜드의 물리학자 커^Kerr에 의해 발견된 해(커 시공간)는 보다 일반적인 회전하는 천체 외부의 시공간을 기술합니다.

흥미롭게도 이 명시적인 해의 기하적 성질 속에 바로 블랙홀의 개념이 내포되어 있습니다. 슈바르츠실드와 커 시공간 모두의 경우, 천체의 크기가 그 질량과 각운동량에 비해 크면 클수록 천체 외부의 중력장은 뉴턴 역학에서 예측되는 중력장과 비슷한 성질을 가집니다. 그런데 천체의 크기가 너무 작으면, 시공간의 휘어짐이 너무 강해 어떠한 시간꼴 혹은 빛꼴 측지선으로도 천체에서 “무한히 멀리 떨어진 관찰자”와 연결될 수 없는 영역이 존재함을 직접적인 계산을 통해 유도해낼 수 있습니다.([9]의 6, 12장 참고) 여기서 “무한히 멀리 떨어진 관찰자”가 중요한 이유는, 고립된 천체의 입장에서는 저 멀리 지구에 있는 우리 인간들이 바로 이렇게 무한히 멀리 떨어진 관찰자나 다름없기 때문입니다. 천체와 무한히 멀리 떨어진 관찰자에게 그 어떠한 물체나 광선조차 쏘아보낼 수 없는 시공간 영역, 그것이 바로 블랙홀의 정의입니다.

1.11. 슈바르츠실드와 커 블랙홀, 그리고 일반적인 블랙홀

앞서 이야기했듯 슈바르츠실드와 커 블랙홀 모두 명시적인 (즉, 형태를 식으로 직접 쓸 수 있는) 해인 만큼, 그 시공간에 대한 직접적인 계산을 통해 이 블랙홀들에 대한 많은 정보를 알아낼 수 있습니다. 재미있는 예 중 하나는, 1979년 프랑스의 물리학자 뤼미네(1979)가 슈바르츠실드의 빛꼴 측지선의 계산을 통해 블랙홀 주변을 회전하며 빛을 내는 물질의 고리가 무한히 떨어진 관찰자에게 어떻게 보이는지를 나타낸 그림입니다 ([그림8-1]). 흥미롭게도 이 그림은 앞서 HORIZON 8월호에서 소개한 2019년 4월 10일 Event Horizon Telescope에서 공개한 사진([그림8-2])과 각도만 다를 뿐, 어두운 중심부 및 중력 렌즈 효과로 인한 밝은 고리 형상, 도플러 효과로 인한 양쪽의 명도 차이 등 그 기본 요소가 매우 비슷합니다!

그런데 뤼미네의 계산은 슈바르츠실드라는 특정 시공간에 대한 것일 뿐인데, 어떻게 이 특별한 해의 그림이 실제 블랙홀의 사진과 이렇게 깊은 관계가 있을까요? 조금 더 일반적으로, 슈바르츠실드와 커 시공간에서 직접적인 계산을 통해 알아낼 수 있는 여러 성질들은 일반적인 블랙홀의 구조와 성질과는 어떤 관계가 있을까요? 지금까지 특수 상대성 이론, 일반 상대성 이론, 그리고 블랙홀에 관해 살펴보았습니다. 언젠가 기회가 된다면 앞의 질문들과 함께 블랙홀에 대한 여러 흥미로운 사실과 가설들, 그리고 이에 관련된 최근 (수학적) 결과들을 소개하는 글로 다시 또 만나보기를 바라봅니다.