아인슈타인이 이해한 동시성의 규약성

두 사건이 동시에 발생했다는 것은 자연이 가진 속성이 아닙니다.
계산을 위해 사용하는 약속일 뿐이에요.

상대성이론의 유명한 쌍둥이 역설에 대해 들어 보았을 것이다. 쌍둥이 두 명 중 한 명은 지구에 남아 있고 다른 한 명은 지구를 떠나 멀리 여행하고 돌아오면, 여행하고 돌아온 쌍둥이가 지구에 남아 있던 쌍둥이보다 나이를 더 적게 먹는다는 이야기 말이다. 이것이 역설로 불리는 이유는, “모든 운동이 상대적”이라면 여행을 떠난 쌍둥이가 지구에 남은 쌍둥이에 대해 운동을 하는 것과 마찬가지로 지구에 남은 쌍둥이도 여행을 떠난 쌍둥이에 대해 운동을 하는 것일 뿐이므로, 다시 만났을 때 왜 둘의 나이 차이가 나는지를 설명할 수 없기에 그렇다. 

과학은 우리의 상식적인 세계관에 큰 도전을 던진다. 그중 한 가지는 우리가 자연의 특성을 반영한 것이라 믿으며 널리 사용하는 여러 개념이 실은 과학에 따르면 (자연에 존재하는 것을 지칭하지 않는) 허구적인 개념에 해당하는 경우다. 가령 무생물과 다르게 생물은 ‘생기’ 또는 ‘활력’을 가지고 있다는 믿음은 상식적으로 보이고 또 한 때 널리 받아들여졌다. 하지만 현대 과학은 이 개념에 대응하는 물질이나 대상이 자연에 존재하지 않는다고 본다. 또한 높은 온도의 물체는 낮은 온도의 물체에 비해 뭔가 다른 물질, 가령 ‘열소’ 같은 물질을 갖고 있는 것이 아닌가 하는 생각도 자연스러워 보인다. 하지만 물체의 온도가 높은 것은 물체를 이루는 입자들이 보다 큰 평균 에너지를 가지고 있기 때문이며, 자연에 열소라는 것은 존재하지 않는다는 것이 현대물리학의 관점이다.

그런데 우리가 일상적으로 사용하는 개념이 과연 자연의 특성을 반영하는 것인가 하는 질문이 물리학의 혁명으로 이어진 예가 있다. 바로 동시성 개념에 대한 아인슈타인의 탐구가 그렇다. 서로 다른 두 사건이 동시에 발생하는 것은 자연에 존재하는 특성으로 보는 것은 상식적이고 직관적이다. 하지만 아인슈타인은 이 동시성 개념이 자연의 특성을 반영하는 개념이 아니라고 보았다. 대신 길이나 무게의 단위처럼 무언가를 측정하기 위해 임의로 정한 정의나 약속으로 보았다.

필자가 보기에 아인슈타인이 특수상대론을 만들 때 사용한 중요한 기준 중 하나는 ‘어떤 개념이나 주장이 자연이 실제로 가진 속성을 반영한 것이라면, 그 개념에 해당하는 양의 값을 측정을 통해 정할 수 있어야 하고, 그 주장을 측정을 통해 입증할 수 있어야 한다’는 것이다. 얼핏 보기에 이 기준을 적용하는 것은 어렵지 않아 보이지만, 실제로는 복잡하다.

가령 ‘길이’를 생각해 보자. 우리는 물체가 어느 방향으로든 길이를 가지고 있다고 생각한다. 즉, 우리가 생각하는 ‘길이’ 개념에 대응하는 속성을 물체가 실제로 갖고 있다고 생각한다. 그런데 아인슈타인에 따르면, ‘길이’라는 개념이 물체가 실제로 갖는 속성을 반영한 것이라면 이 개념에 해당하는 양의 값을 측정할 수 있어야 한다. 그럼 길이를 어떻게 측정하는가? 우리가 아는 한 가지 방법은 자를 이용하는 것이다. 물체의 왼쪽 끝에 자의 영점을 대고, 물체의 오른쪽 끝에 대응하는 자의 눈금을 읽으면 그 눈금값이 물체의 길이다.

이 간단한 방법에 매우 중요한 전제가 숨어 있다. 가령 자에 대해 오른쪽으로 운동하고 있는 막대를 생각해 보자. 막대의 왼쪽 끝 A가 자의 영점을 만나는 사건이 발생하고 오른쪽 끝 B가 자의 눈금, 가령 1m라는 눈금을 만나는 사건이 발생한다고 해서, 이것만으로 막대의 길이가 1m라고 할 수 없다. 이 두 사건이 동시에 발생하지 않았다면, 가령 막대의 왼쪽 끝 A가 영점을 만나는 사건이 먼저 발생하고, 오른쪽 B가 1m 눈금을 만나는 사건이 나중에 발생했다면, 막대의 길이는 1m보다 짧다고 결론을 내려야 한다.([그림1]) 즉, 움직이는 물체의 길이를 재기 위해서는 공간적으로 떨어진 곳에서 발생하는 두 사건이 동시에 발생하는지를 먼저 판단해야 한다.

이 문제를 간단히 해결할 수 있지 않을까? 가령 막대의 운동상태를 바꿔 자에 대해 상대적으로 정지하게 만든 상태에서 길이를 재면 되는 것이 아닐까? 구체적으로 말해, 막대의 왼쪽 끝 A가 오랜 시간 변함없이 자의 영점과 계속 만나고, 막대의 오른쪽 끝 B가 오랜 시간 변함없이 자의 1m 눈금과 만나면, 동시성을 판단할 필요 없이 막대의 길이가 1m라고 결론지을 수 있지 않을까. 하지만 이 방법은 문제가 있다. 물체가 운동상태와 관계없이 길이를 가진다면, 운동상태와 관계없이 길이를 측정할 수 있어야 한다. 그리고 원래 재려고 했던 것은 막대가 자에 대해 오른쪽으로 운동하고 있을 때 길이다. 그런데 제시된 방법은 막대의 운동상태를 바꿔서 자에 대해 정지시켜 놓고 길이를 재는 것이다. 이 방법으로 얻은 측정치가 옳은 답이 되려면 운동상태가 바뀌어도 막대의 길이가 변하지 않는다는 보장이 있어야 한다.

상대성이론에 익숙하지 않은 사람은 물체가 정지해 있든 운동하든 길이가 일정한 것은 너무나 당연한 얘기라고 생각할 것이다. 하지만 아인슈타인이 특수상대론을 만들면서 제시한 기준을 생각해 보라. 아무리 직관적으로 당연해 보이는 주장이라도 측정을 통해 입증할 수 있어야만, 자연이 실제로 가진 속성을 반영한 주장이라는 기준 말이다. 이 기준에 따르면 “막대의 운동상태가 바뀌어도 길이가 변하지 않는다”는 믿음이 자연의 속성을 반영한 것이기 위해서는 운동상태가 바뀌기 전후의 막대 길이를 모두 측정한 후 두 값을 비교할 수 있어야 한다.

이 방법을 적용하기 위해서는, 자에 상대적으로 움직이고 있는 물체의 길이를 자로 직접 잴 수 있어야만 한다. 결국 자에 대해 상대적으로 운동하고 있는 물체의 길이를 자로 직접 재는 것을 피하려고 물체를 세운 뒤 재는 방법을 도입했는데, 이 방법을 적용하기 위해서는 운동하는 물체의 길이를 자로 직접 잴 수 있어야 한다는 순환의 문제가 발생한다. 따라서 이 방법으로는 자에 대해 상대적으로 움직이는 물체의 길이를 잴 수 없다. 자에 상대적으로 움직이는 물체의 길이를 재기 위해서는, 물체나 자의 운동상태를 바꾸지 말고 자로 길이를 측정을 할 수 있어야 하고, 그러기 위해서는 앞의 문단에서 말했듯이 동시성 판단이 필요한 것이다. (연습 문제1: 자를 이용하지 않고도 물체의 길이를 재는 방법이 있을까? 그 방법을 사용할 때도 동시성 판단이 필요할까?)

그렇다면 동시성은 어떻게 판단하는가? 이 문제는 1905년에 발표된 아인슈타인의 특수상대론 논문 첫 절의 주제다.[1] 여기서 말하는 동시성은 흔히 원격 동시성^{distant simultaneity}이라고 부르는 것으로 서로 공간적으로 떨어져서 발생하는 두 사건이 동시에 발생했는가의 문제다. 두 사건이 동시동소에, 즉 동시에 같은 곳에서, 발생하는지는 바로 판단할 수 있다고 가정한다.

서로 떨어져 있는 두 개의 시계 C1과 C2를 생각해 보자. C1과 C2는 크기, 모양, 제조 방식, 구성 부품 모든 것이 같아 두 시계를 같은 장소에서 같은 시각을 가리키게 만들면, 이 둘이 서로에 대해 계속 정지해 있는 한 이후에도 계속 같은 시각을 가리킨다고 할 때, 두 시계를 서로 등시적^isochronous이라고 하자. 그리고 C1과 C2는 서로 떨어져서 둘 사이의 거리는 변하지 않는 관성운동을 하고 있다고, 즉, 같은 관성운동^comoving을 하고 있다고 하자. (여기서 ‘관성운동’이라는 개념은 매우 중요한 개념이지만 논의 없이 물리적으로 유의미한 개념이라고 전제한다. 그리고 둘 사이의 거리가 변하는지 아닌지는 C1에서 1초마다 쏜 빛이 C2에서 반사되어 되돌아올 때 1초마다 되돌아오는지를 보고 판단할 수 있다.)

이 경우, 가령 시계 C1이 2시를 가리키는 사건과 시계 C2가 2시를 가리키는 사건이 동시에 발행했는지 어떻게 판단할 수 있을까? 이에 대해 아인슈타인은 표준 동기화^{standard synchrony} 또는 아인슈타인 (동시성) 기준라고 부르는 다음과 같은 기준을 제시한다. 시계 C1이 1시를 가리킬 때 C1로부터 빛이 발사되고, 이 빛이 C2에 반사되어 다시 C1로 돌아오는데, 그때 C1이 3시를 가리킨다고 하자. 아인슈타인 기준에 따르면, 빛이 C2에 반사되는 사건 a는 시계 C1이 2시를 가리키는 사건 b와, 시계 C1에 (또는 C2에) 상대적으로, 동시에 발생한다.([그림 2])

다른 말로 하면 C1로부터 C2로 이동하는 빛의 (평균)속력과 C2로부터 C1로 이동하는 빛의 속력이, 시계 C1에 상대적으로, 서로 같다는 말이다. 가령 손오공이 근두운을 타고 1시에 서울에서 출발해 직선으로 포항까지 날아간 후 방향을 바꾸어 직선으로 되돌아와 3시에 서울에 도착했다고 하자. 만약 서울에서 포항까지 이동할 때의 속력이 포항에서 서울로 되돌아올 때의 속력보다 크다면, 서울에서 포항까지 가는 데 걸리는 시간이 포항에서 서울로 되돌아오는 데 걸리는 시간보다 작을 것이므로, 손오공은 2시 이전에 포항에 도착했을 것이다. 반면 양방향 속력이 같다면, 손오공은 1시와 3시의 중간값인 2시에 포항에 도착했을 것이다. 마찬가지로 C1로부터 C2로 이동하는 빛의 속력이 C2로부터 C1로 이동할 때의 빛의 속력과 같은 경우에만, 사건a(빛이 C2에 반사되는 사건)와 사건b(C1이 1시와 3시의 중간값인 2시를 C1이 가리키는 사건)가 동시에 발생한다고 판단해야 하는 것이다. 즉, 아인슈타인 동시성 기준은 빛이 어느 방향으로 운동하든지 그 일방향 속력이 모두 같다는 가정에 근거해 있다.

이처럼 같은 관성운동을 하고 있는 서로 떨어져 있는 두 개의 시계가 동시에 같은 시각을 가리키도록 만드는 문제를 시계의 동기화 문제라고 부른다. 이 문제를 간단히 해결할 수 있으리라 생각하는 분이 많을 것이다. 가령 두 시계가 동기화되어 있는지는 보거나 들으면 바로 알 수 있지 않을까? 그렇지 않다.

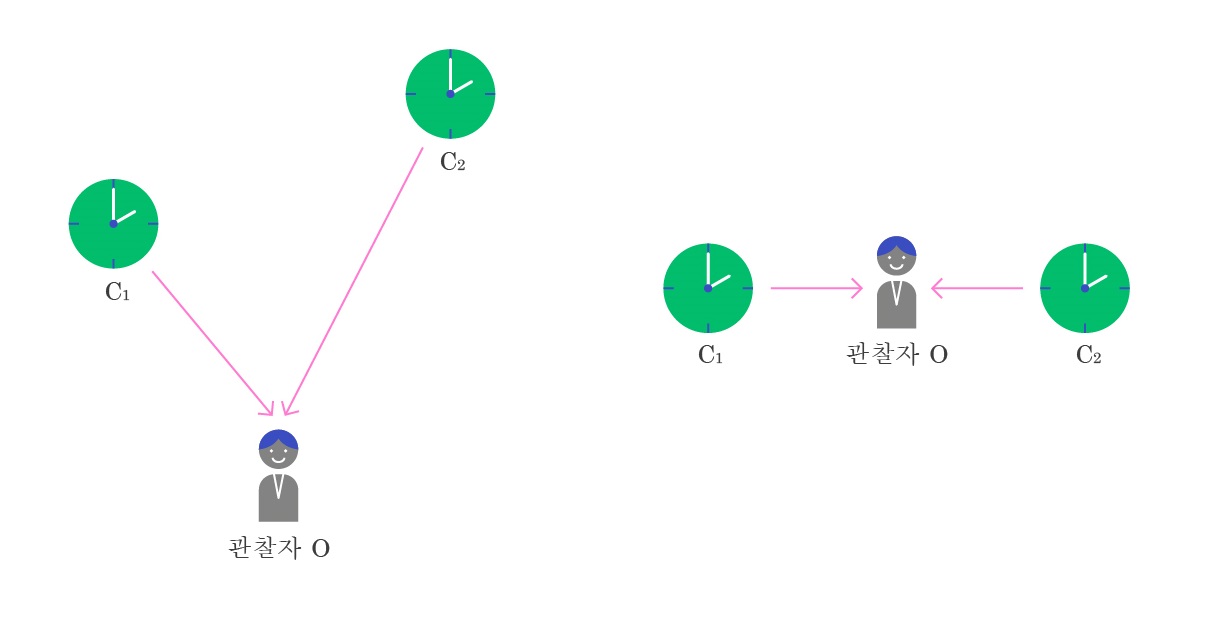
예를 들어, C1이 2시를 가리키는 모습과 C2가 2시를 가리키는 모습이 관찰자 O에게 동시에 보였다고 해서, C1이 2시를 가리키는 사건과 C2가 2시를 가리키는 사건이 동시에 발생했다고 할 수 없다.([그림3] 왼쪽) 빛의 (양방향) 속력이 유한하기 때문이다. 빛의 속력이 유한하기에, C1과 O 사이의 거리와 C2와 O 사이의 거리가 다르다면, 빛이 C1에서 출발하여 O까지 도달하는 시간이 C2에서 출발하여 O까지 오는 시간과 같다고 볼 이유가 없으므로 (빛의 속도가 무한히 크다면 이 두 시간이 모두 0으로 같을 것이지만) 두 사건이 동시에 발생했다고 판단할 수 없다.

그렇다면 C1과 O 사이의 거리와 C2와 O 사이의 거리가 같다면 어떠한가? ([그림3] 오른쪽) 이 경우, 빛이 C1로부터 O까지 이동할 때의 속력과 C2로부터 O까지 이동할 때의 속력이 같다고 해야만, 두 사건이 동시에 발생했다고 판단할 수 있다. 즉, 시각 정보를 통해 동시성을 판단하기 위해서도 역시 빛의 일방향 속력이 어떠한지에 관한 판단이 필요하다. (연습 문제2: 자를 이용하지 않고도 물체의 길이를 재는 방법이 있을까? 그 방법을 사용할 때도 동시성 판단이 필요할까?)

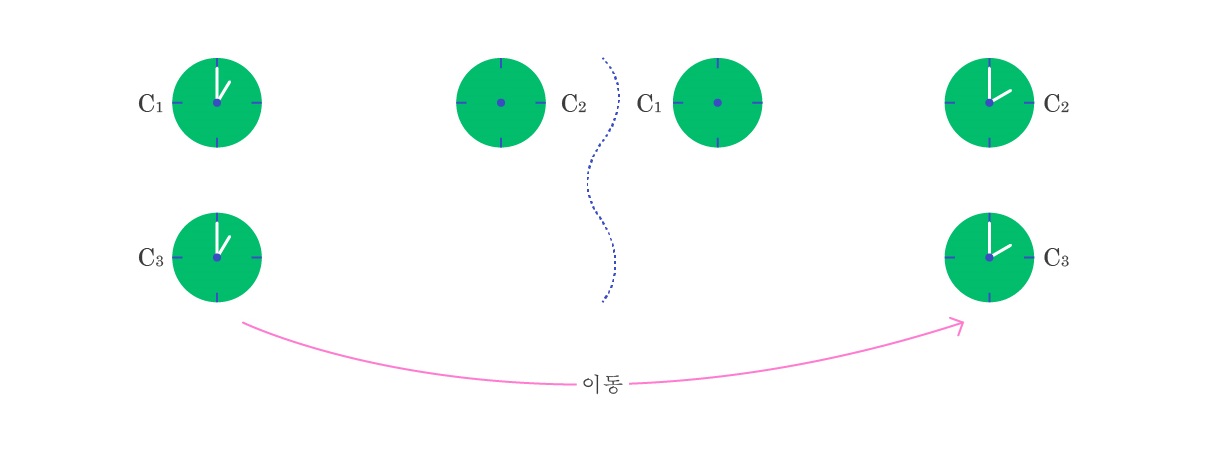
그렇다면 또 다른 시계를 사용하는 것은 어떨까? 가령 C1과 등시적인 또 다른 시계 C3이 있어서, C1이 1시를 가리키는 사건과 C3이 1시를 가리키는 사건이 (거의) 동시동소에서 발생했다고 하자. 그다음 C3을 이동 시켜 C2와 만나게 하는데, 둘이 만날 때 C3이 2시를 가리키고 있다면 C2도 2시를 가리키게 만듦으로써 C1과 C2를 동기화할 수 있지 않을까? ([그림4]) 이 방법도 통하지 않는다. 이 방법에 깔린 생각은 C1과 C3이 등시적이므로, C1이 1시를 가리키는 사건과 C3이 1시를 가리키는 사건이 동시동소에서 발생하게 한 후 C3를 이동 시키면, 이후 임의의 시간 t에 대해서 C1이 t를 가리키는 사건과 C3이 t를 가리키는 사건이 동시에 발생할 것이라는 생각이다.

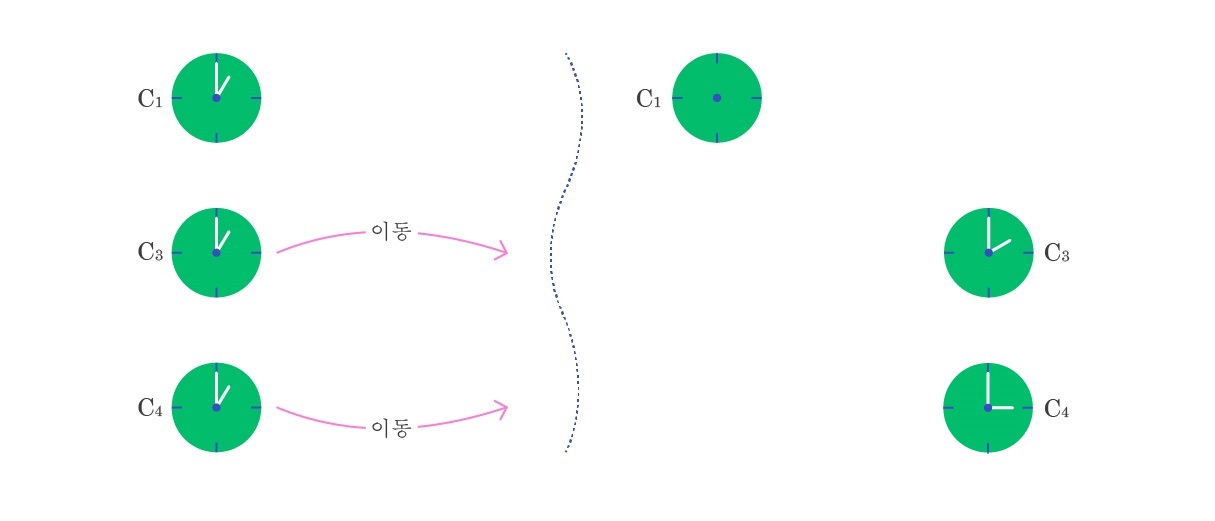
하지만 C3이 C1에 대해 움직이기 시작하면 더 이상 둘 사이의 등시성이 성립하지 않는다. 가령 쌍둥이 역설에서와 마찬가지로 C3이 C1에 대해 움직인 다음 다시 C1로 돌아오게 만들면, C1과 C3이 서로 만날 때에는 둘이 다른 시각을 가리키는 것을 실험적으로 확인할 수 있다. 또한 또 다른 시계 C4를 이용하여, C1, C3, C4가 모두 동시동소에서 1시를 가리키게 한 후, C3과 C4를 경로를 달리하여 이동 시켜 다시 만나게 하면, 둘이 같은 시각을 가리키지 않는 것이 일반적이다. ([그림5]) 따라서 또 다른 시계를 사용하는 방법으로는 시계를 동기화시킬 수 없다. (일반상대론을 실험적으로 검증한 것으로 유명한 스탠리 에딩턴과, 노벨 물리학상을 받은 퍼시 브리지만은 C3를 점점 더 느리게 이동 시켜 C1과 C2를 동기화하는 방식을 제안했는데, 필자는 이 방법 역시 아인슈타인 동시성 기준과 마찬가지로 빛의 일방향 속력에 대한 가정을 전제한 방법이라고 생각한다.)

드디어 가장 중요한 얘기다. 아인슈타인 동시성 기준은 빛의 일방향 속력이 어느 방향으로 운동하든지 같다는 가정에 근거하고 있다고 했다. 그렇다면 빛의 일방향 속력은 어떻게 측정하는가? 한 위치에서 다른 위치로 이동하는 대상의 속력은 두 위치 사이의 거리를 걸린 시간으로 나눈 값으로 정의된다. 그런데 빛이 한 위치에서 다른 위치로 이동하는 시간을 재기 위해서는 동기화된 두 개의 시계가 필요하다.

가령 빛이 C1을 출발할 때 C1이 1시를 가리키고, C2에 도착했을 때 C2가 2시를 가리키고 있었다면, C1과 C2가 동기화되어 있을 경우에만 빛이 C1로부터 C2까지 이동하는 데 걸린 시간이 1시간이라고 판단할 수 있는 것이다. 여기서 다시 순환의 문제가 발생한다. 아인슈타인의 동시성 기준을 적용하려면 빛의 일방향 속력이 모두 같다고 가정해야 하는데, 빛의 일방향 속력을 재려면 동기화된 두 개의 시계가 필요한 문제 말이다. 만약 이 순환의 문제를 깰 수 없다면, 아인슈타인 동시성 개념은 이에 해당하는 양의 값을 측정을 통해 잴 수 있는 것이 아니므로, 자연이 실제로 가진 속성을 반영한 것이 아니게 된다.

1905년 논문에서 아인슈타인은 동시성은 측정을 통해 정할 수 있는 것이 아니고 편의를 위해 임의로 설정하는 정의^definition라 했다. 따라서 빛의 일방향 속력 역시 자연이 가진 속성을 반영한 것이 아닌 편의를 위해 설정한 정의가 된다. 스탠리 에딩턴도 아인슈타인의 동시성 기준과 일방향 속력에 관한 주장 모두 관찰 가능한 사실에 관한 주장이나 빛이나 시계의 속성에 관한 주장이 아닌 허구적인 시간분할을 세계에 부여하는 규칙일 뿐이라고 했다.[2] 또한 앞에서 말했듯이 자에 상대적으로 움직이는 물체의 길이를 재기 위해서는 동시성 기준이 필요한데, 동시성이 자연의 속성이 아니게 되면 움직이는 물체의 길이 역시 마찬가지로 자연의 속성이 아니게 된다. 즉 정지해 있는 물체의 길이는 자연의 속성이지만 움직이는 물체의 길이는 자연이 가진 속성이 아니게 된다.

여기서 많은 분들이 빛의 속력은 방향과 관계없이 일정하다는 주장이 수많은 실험을 통해 이미 입증된 것이 아닌가 하고 의아해할 것이다. 하지만 실험을 통해 빛의 속력을 잰 것들은 아인슈타인 기준을 적용해 동기화된 시계들을 사용하거나, 아니면 일방향 속력이 아닌 양방향 속력(혹은 왕복 속력)을 잰 것이다.[3] 

가령 피조^Fizeau의 유명한 광속 측정 실험을 생각해 보자. 톱니 사이를 통과한 빛이 거울에 반사된 뒤 다음 톱니 사이를 통과하는 빛의 왕복 속력을 재는 것이 피조의 방법이다. (연습문제 3: 그렇다면 목성의 달의 모습을 이용해 빛의 속력을 측정한 뢰머의 방법은 어떠한가?) 빛의 일방향 속력을 재기 위해서는 동기화된 두 개의 시계가 필요하지만 양방향 속력은 시계 하나만으로도 잴 수 있다. 가령 길이가 d인 막대의 왼쪽 끝 A에 위치한 시계 C가 시각 t1을 가리킬 때 빛을 발사시킨 뒤, 이 빛이 오른쪽 끝 B에 반사되어 다시 A로 되돌아올 때 시계 C가 t2를 가리켰다면, 빛이 A와 B 사이를 왕복할 때의 평균 속력을 D/2(t2-t1)로 구할 수 있다. 따라서 아인슈타인의 기준에 따르면 빛의 양방향 속력은 자연이 가진 속성을 반영한 것이다. 하지만 일방향 속력은 그렇지 않다는 것이 아인슈타인의 생각이었고 필자도 이 생각이 옳다고 믿는다.

하지만 빛의 일방향 속력이 방향에 따라 다를 수 있다고 믿는 것은 공간의 등방성에 어긋나지 않을까? 즉 공간이 방향에 따라 아무런 차이가 없이 대칭적인데, 어떻게 빛의 일방향속력이 방향에 따라 다를 수 있을까? 이런 의문은 아인슈타인의 주장을 오해한 결과다. 아인슈타인은 빛의 일방향 속력이 어떤 값을 가질 텐데 무슨 값을 갖는지를 측정을 통해 알아낼 방법이 없으니, 그 값을 임의로 정하자고 한 게 아니다.

아인슈타인의 기준에 의하면 빛은 일방향 속력이라는 속성 자체를 갖고 있지 않다. 그 값을 모르는 것이 아니라 아예 그 값이라는 게 자연에 존재하지 않는다. 자연에 존재하지 않으니 대칭성이나 등방성에 영향을 받을 수도 없다. 가령 미터를 길이의 단위로 잡는 것은 하나의 약속으로 길이에 관한 자연의 속성을 반영하지 않는다. 미터를 길이의 단위로 잡는 것이 야드를 단위로 잡는 것에 비해 자연의 속성을 더 잘 반영하는 것이 아니다. 그리하여 동쪽 방향의 거리를 나타낼 때는 미터법을 사용하고 서쪽 방향의 거리를 나타낼 때는 야드법을 쓴다고 해서 (불편하겠지만) 자연의 대칭성에 어긋나는 것도 아니다. 마찬가지로 한쪽 방향의 빛의 속력과 다른 쪽 방향의 빛의 속력을 다르게 정한다 해서 대칭성과 등방성에 어긋나는 것이 아니다.

빛이 양방향 속력은 갖지만 일방향 속력을 갖지 않는다는 주장이 매우 이상하게 들릴 것이다. 하지만 이는 서로 떨어져 발생하는 많은 사건들 사이에 시간적 선후 혹시 동시 관계가 관찰자에 독립적으로도 상대적으로도 존재하지 않는다는 점의 귀결일 뿐이다. 그리고 이 주장에 따라 일관되게, 그리고 모든 관찰 결과와 일치하는 방식으로 세계를 기술할 수 있다. 가령 모든 관성운동 하는 관찰자에 대해 빛의 일방향 속력이 빛의 양방향 속력과 같다고 (즉 모든 일 방향 속력 값이 같다고) 정의하면, 다음과 같은 잘 알려진 로런츠 변환식을 얻게 된다.

\begin{equation}
\tag{1}
x’= \gamma (x- \beta t) \qquad x= \gamma (x’+ \beta t’)\\
t’= \gamma (t- \beta x) \qquad t= \gamma (t’+ \beta x’)
\end{equation}
위 식이 낯선 분들도 식이 매우 대칭적인 형태를 띄고 있다는 것은 알 수 있을 것이다. 이는 빛의 일방향 속력의 값이 방향과 관계없이 모두 같다는 정의한 결과다. 그리고 이로부터 동시성의 상대성(즉 어느 두 사건이 동시에 일어났는가의 판단이 관찰자마다 달라진다는 성질, 이 논문에서 다루는 동시성의 규약성과는 전혀 다른 개념), 길이수축, 시간지연 등의 효과가 보통 알려진 방식대로 도출된다.

다른 정의를 채택해서 자연을 기술할 수도 있다. 가령 한쪽 방향으로 진행하는 빛의 속력을 무한대로 설정하고 반대 방향의 속력은 c(빛의 양방향속력)의 절반으로 잡아 현상들을 기술할 수 있다. 또한 어느 특정한 관성관찰자를 골라 특권관찰자로 정하고, 특권관찰자에게 상대적으로 아인슈타인의 동시성 기준을 사용해 사건들의 시간 선후 혹은 동시성 관계를 정하게 한 후, 이렇게 정한 관계를 모든 다른 관성관찰자들이 그대로 가져와 저마다의 일방향 속력을 정할 수가 있다. 이 경우 변환식은 다음과 같은 모양의 갖게 된다.

\begin{equation}
\tag{2}
x’= \gamma (x- \beta t) \qquad x= \frac{1}{\gamma} (x’+ \gamma ^{2} \beta t’)\\
t’=\frac{1}{\gamma} t \qquad  \qquad  \qquad \qquad \qquad t= \gamma t’
\end{equation}

이 변환식을 보통 탠거리니^Tangherlini 변환식이라고 부른다. 탠거리니 변환식을 사용할 경우, 특권관찰자에게만 방향과 관계없이 빛의 일방향 속력이 일정하고, 특권관찰자에 대해 상대적으로 운동하고 있는 관성관찰자들은 방향에 따라 다른 일방향 속력 값을 부여받는다. 그리고 이 변환식을 사용하면, 주어진 두 사건 사이의 동시 혹은 선후 관계를 모든 관찰자들이 동일하게 판단하게 되어 동시성은 상대적인 것이 아니라 절대적인 것이 된다. 그리고 모든 방향으로 무한히 열려있는 민코프스키 공간에서 발생하는 사건들에 대해 로런츠 변환식과 탠거리니 변환식은 동일한 예측을 제공한다.

(지금까지 설명한 동시성의 규약성은 물리학자들에게도 잘 알려진 주장이 아니고 교과서에도 거의 등장하지 않는 내용이어서 여러 의문을 가지신 분이 많을 것이다. 가령, 탠거리니 변환식을 사용하면 물리법칙이 관찰자에 따라 다른 형태를 띄게 되는데, 이것이 소위 특수상대론의 핵심 원리인 상대성원리를 위배하게 되는 것이 아닌가 하는 의문을 갖는 이가 있을 것이다. 또한 상대성이론에 익숙하신 분들은 소위 로런츠 불변성^{Lorentz invariance}을 실재성의 기준(가령 어떤 물리량의 값이나 식이 관찰자마다 다르면 자연에 실재하는 속성을 반영한 것이 아니지만 모든 관성 관찰자에 대해 동일하면 이는 자연의 속성을 반영한 것으로 판단하는 기준)으로 생각하는 분들도 많을 것인데, 탠거리니 변환식을 사용하면 흔히들 자연의 법칙을 표현한다고 생각되는 식들이 관찰자마다 형태를 달리해 나타난다.

더 나아가 상대성이론을 군론 등을 통해 고차원적으로 이해하시는 분들은, 군론에서는 몇 가지 근본적인 가정으로부터 로런츠 변환식을 유도할 수 있기에 탠거리니 변환식은 이런 근본적인 가정을 위배하는 잘못된 것이 아닌가 생각하실 수도 있다. 또 인과성과 관련된 근본적 가정을 통해 로런츠 변환식을 유도하는 지만^{Erik Christopher Zeeman} 등의 연구 결과에 익숙하신 분들도 그런 생각을 하실 것이다.

이런 의문들에 대한 짧은 답은, 상대성원리를 “모든 관성 관찰자에게 물리 법칙은 같은 형태를 지닌다”가 아니라 “모든 관성 관찰자에게 물리 법칙은 같다”라고 이해해야 한다는 것이다. 즉 탠거리니 변환식을 사용하면 물리법칙을 표현하는 식의 모양은 달라지지만 그렇다고 해서 물리법칙이 달라지는 것이 아니다. 동쪽 방향의 거리를 나타낼 때는 미터법을 사용하고 서쪽 방향의 거리를 나타낼 때는 야드법을 써서 뉴턴의 운동법칙을 표현하면 괴상한 모양의 식이 나오겠지만, 그렇다고 해서 물리법칙이 달라지는 것은 아니다. 그리고 로런츠 불변성의 개념도 식의 형태의 불변성이 아니라 식의 내용의 불변성으로 이해해야 한다. 그리고 군론이나 지만의 유도에 사용되는 가정들은 일견 빛의 일방향 속력과 무관한 매우 근본적인 가정인 것처럼 보이지만, 일방향속력이 양방향속력과 같다는 가정을 함축하고 있다고 필자는 생각한다.)

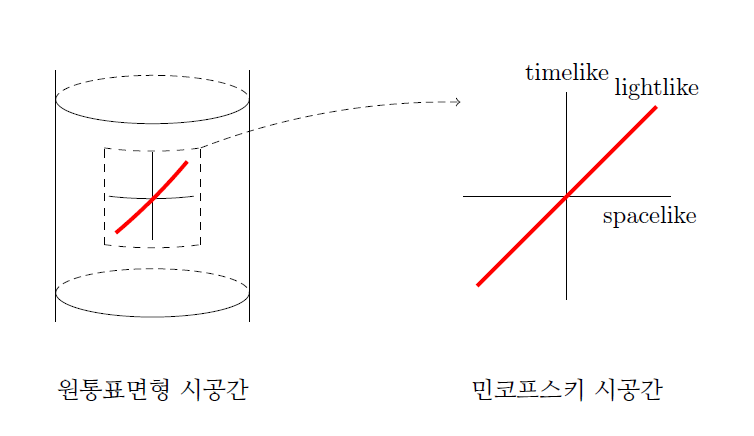
민코프스키 시공간에서 탠거리니 변환식을 사용하는 것은 불편하겠지만, 그렇지 않은 시공간도 있다. 서두에서 말한 원통표면형 시공간이 그렇다. 가령 2차원 민코프스키 시공간의 (공간적으로는 유한하지만 시간적으로 무한한) 조각을 떼어내 (공간 방향으로) 둥글게 말면, 원통표면형 시공간이 만들어진다. 이 시공간은 국소적으로는 2차원 민코프스키 시공간과 동일하여, 국소적인 실험과 관찰을 통해서는 2차원 민코프스키 시공간과 구별할 수 없다.([그림6])

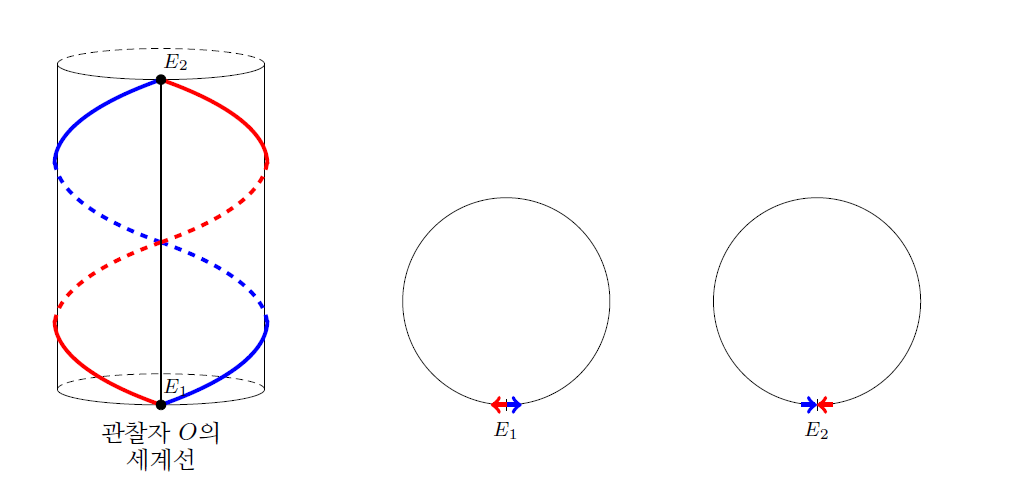
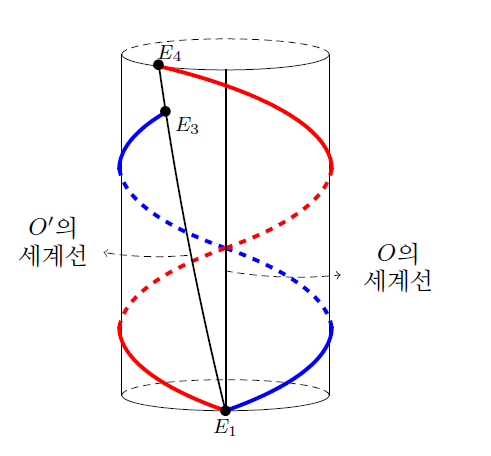
하지만 광역적으로는 다른데, 민코프스키 시공간에서는 모든 관성운동이 동등한 데에 비해, 원통표면형 시공간에는 특별한 관성운동이 존재한다. 원통표면형 시공간에서 각각 다르게 관성운동하고 있는 관찰자들이 저마다 반대방향으로 동시동소에 붉은 빛과 푸른 빛을 발사한다고 하자. 두 빛이 동시에 돌아오는 관성 관찰자 O가 존재할 것이다 .([그림7]) 이제 O에 대해 상대적으로 관성운동하고 있는 관찰자 O’를 생각해 보자. O가 반대 방향으로 두 빛을 발사하는 것과 동시동소에 O’도 두 빛을 발사한다고 하자. 그런데 빛이 경로는 발사체의 운동 상태에 의존하지 않는다. 따라서 O’에서 발사된 두 빛은 O에서 발사된 두 빛과 똑같이 운동할 것이다.([그림8])

그런데 O’은 O에 대해서 상대적으로 운동하므로 이 두 빛은 O’에게 동시에 도착하지 않게 된다. 따라서 내가 어떤 관성 운동을 하고 있느냐에 따라 양방향으로 빛을 보내는 실험의 결과가 달라지기에, 이렇게 닫힌 공간에서는 상대성원리가 성립하지 않게 된다.[4] 원통표면형 시공간처럼 닫힌 공간들은 상대성원리가 성립하지 않는 하지만 상대론이론이 적용되는 시공간인 것이다. 그리하여 원통형 공간에서 쌍둥이들이 다시 만났을 때, 둘이 모두 관성운동을 함에도 불구하고, 양쪽 방향으로 두 빛을 쏘았을 때 동시에 돌아오는 특권운동을 하는 쌍둥이가 그렇지 않은 쌍둥이보다 나이를 더 먹게 되는 것이다. 이 점을 탠거리니 변환식을 이용하면 로런츠 변환식을 사용할 때 발생하는 여러 문제점을 피하면서 간단하게 보일 수 있다.[5]