양자 컴퓨터의 기원

요즘 실리콘 밸리에서는 양자 컴퓨터가 상당한 화두다. 지난 10월, 존 마티니스^{John Martinis}가 이끄는 구글의 양자 컴퓨터 연구팀은 자신들이 만든 양자 컴퓨터를 이용해서 기존의 슈퍼 컴퓨터로는 10,000년 이상이 걸릴 계산을 했다고 주장했다. (이에 대한 이야기는 마지막 글에서 적을 예정이다.) 이 때문인지, 필자는 최근 소프트웨어 개발자 친구들로부터 양자 컴퓨터에 대한 질문을 많이 받기 시작했다. 10여 년 전만 해도 필자가 어떤 연구를 하는지 설명하는데 많은 애로 사항이 있었는데, 이제 대부분의 사람들에게 양자 컴퓨터는 한 번쯤 들어본 단어 정도는 되는 것 같다. 그렇다면 양자 컴퓨터는 인류에 어떤 영향을 미칠 수 있을까? 또 그런 변화는 언제부터 나타나기 시작할까? 그리고 지난 10여 년 동안 양자 컴퓨터에 대한 관심이 급격하게 올라간 이유는 무엇일까? 앞으로 이어지는 연재를 통해서 이에 대한 필자의 생각을 적어 보려고 한다. 첫 번째 글에서는 양자 컴퓨터라는 분야가 어떻게 시작되었는지, 또 양자 컴퓨터는 어떤 면에서 기존 컴퓨터와 다른지 이야기해보려고 한다.

21세기 정보화 사회에서 컴퓨터는 더 이상 일상생활과 분리시킬 수 없는 존재가 되어버렸다. 우리가 매일 같이 사용하는 컴퓨터는 물론이거니와, 핸드폰, 스마트 시계, 그리고 태블릿에 이르기까지 컴퓨터만큼 우리 일상생활에 밀접한 영향을 미치는 장치는 찾기 쉽지 않다. 하지만 100여 년 전으로만 거슬러 올라가도 컴퓨터라는 개념은 대부분의 사람들에게 꽤나 생소한 개념이었다. 예를 들어 1800년대의 찰스 배비지^{Charles Babbage}와 아다 러브레이스^{Ada Lovelace}가 개발한 difference engine이라는 기계에 대해서 살펴보자.([그림1]) 생긴 것 자체가 우리가 아는 컴퓨터와는 많이 다르다.

생긴 것뿐만이 아니다. 이 기계가 할 수 있는 연산 기능 자체도 우리가 알고 있는 컴퓨터에 비해 굉장히 제한적이다. 이 기계가 할 수 있는 일은 다항식의 계산인데, 예를 들자면 \(f(x)=3x^2+2x+5\)라는 함수가 주어졌을 때 \(f(0), f(1), \cdots , f(5)\) 같은 값들을 계산하는 것이다. 좀 더 최근으로 와서 1900년대 중반에 나온 세계 최초의 컴퓨터 에니악^ENIAC을 보아도([그림2]), 현재 우리가 알고 있는 컴퓨터의 모습과는 많은 차이가 있다. 에니악의 기본 연산을 담당하는 장치는 진공관이었고, 현재 컴퓨터는 대부분의 연산이 집적회로상에서 이루어진다. 이렇게 컴퓨터의 물리적인 부품과 기본 연산 기능만을 놓고 보면 과거의 컴퓨터와 현재의 컴퓨터는 많은 차이가 있어 보인다.

1. (고전) 컴퓨터들은 ‘동일’하다

그렇다면 에니악의 연산 방식과 독자들이 현재 가지고 있는 노트북의 연산 방식을 비교해 보면 어떤 게 더 우월할까? 대부분의 독자들은 노트북이 더 뛰어나다고 답변할 것으로 예상된다. 하지만 컴퓨터를 이론적으로 연구하는 과학자들에게 물어보면 두 개의 연산 방식에는 큰 차이가 없다는 답변을 듣게 될 가능성이 크다. 언뜻 들어보면 잘 이해가 가지 않을 수도 있다. 에니악은 초당 10만여 개의 기본 연산을 할 수 있고 대부분의 노트북들은 초당 10억여 개의 기본 연산을 할 수 있다. 대략 만 배의 차이가 있는데 왜 연산 방식에는 큰 차이가 없다는 결론을 내리게 되는 걸까?

이를 이해하기 위해서는 컴퓨터를 구성하고 있는 하드웨어와 그 안에서 연산이 이루어지는 소프트웨어적인 측면을 분리해서 생각해야 한다. 이렇게 소프트웨어적인 부분만을 놓고 보면 에니악과 노트북은 비슷한 면이 많다. 때문에 정도의 차이가 있을 수는 있어도, 에니악이 쉽게 해결할 수 있는 문제는 기본적으로 노트북도 쉽게 해결할 수 있고, 마찬가지로 노트북이 쉽게 해결할 수 있는 문제는 에니악도 쉽게 해결할 수 있다. 에니악이 해결하기 힘든 문제는 노트북으로도 해결하기 힘들고, 노트북으로 해결하기 힘든 문제는 에니악으로도 해결하기 힘들다.

컴퓨터 과학자들에게 문제가 쉽거나 어렵다는 개념은 우리가 일상 생활에서 생각하는 쉬움 혹은 어려움이라는 개념과는 다른 의미를 지닌다. 일단 쉬운 문제의 예를 들어 보겠다. 우리가 모두 알고 있는 덧셈을 생각해 보자. 덧셈을 하기 위해서는 얼마나 많은 연산을 해야 할까? \(235\)와 \(573\)을 더하는 연산을 생각해 보자. 초등학교 때 배웠던 것처럼 우리는 다음과 같은 방식으로 계산을 할 수 있다. 우선 \(5+3 = 8\)이므로 마지막 자릿수는 \(8\)이 된다. \(3+7 = 10\)이므로 둘째 자릿수는 \(0\)이 되고 \(1\)은 다음 자릿수에 더해줘야 한다. 이제 두 숫자의 첫째 자릿수(\(2\)와 \(5\))와 이전 자릿수에서 올라온 \(1\)을 더해주면 \(8=(2+5+1)\)이 첫째 자릿수가 된다.

여기서 우리는 덧셈을 하기 위해서 총 세 번의 ‘기본 연산’을 했다는 사실을 알 수 있다. 여기서 말하는 기본 연산은 \(0\)과 \(10\) 사이의 숫자 두 개를 더한 후 이 결과의 마지막 자릿수를 기록하고 결과가 \(10\)을 넘으면 \(1\)을 다음 자릿수에 더해주는 연산이다. 만약에 총 자릿수가 \(n\)개이면, 이런 기본 연산은 \(n\)번을 통해서 결과를 도출할 수가 있을 것이다. 이젠 조금 더 복잡한 문제를 생각해 보자. 자릿수가 \(n\)개인 자연수 두 개를 곱하는 연산을 생각해 보자. 우리가 \(0\)과 \(10\) 사이의 숫자 두 개를 더하거나 곱하는 기본 연산을 할 수 있다고 가정해 보자. 예를 들어서 이번에는 \(235\)와 \(573\)을 곱하는 연산을 생각해 보자. 초등학교 때 배웠던 것처럼 우리는 다음과 같은 방식으로 계산을 할 수 있다.

\begin{equation*}
\begin{aligned}
235 \times 3 &= 705 \\
235 \times 70 &= 16450 \\
235 \times 500 &= 117500
\end{aligned}
\end{equation*}

위에 나와 있는 각각의 곱셈을 하는 데는 총 \(3\)번의 기본 연산으로 충분하고, 최대 자릿수가 \(6\)인 숫자 \(3\)개를 더해서 우리는 답을 구할 수 있다. 만약 자릿수가 \(n\)개인 자연수 두 개를 곱한다고 가정하면 총 \(n\)개의 곱셈을 하게 되는데, 각각의 곱셈은 \(n\)번의 기본 연산을 통해 계산할 수 있다. 따라서 이들을 구하는데 총 \(n^2\)번의 기본 연산이 필요하게 된다. 이제 우리가 구한 \(n\)개의 계산 결과를 더해야 하는데, 최대 자릿수는 \(2n\)이므로 \(2n^2\)번의 추가적인 기본 연산으로 덧셈 결과를 계산할 수 있다. 때문에 최대한 \(3n^2\)의 기본 연산을 통해서 답을 구할 수가 있다. 덧셈이나 곱셈처럼 \(n\)이 커짐에 따라 문제를 풀기 위해 필요한 기본 연산의 숫자가 다항식처럼 증가하는 문제를 컴퓨터 과학자들은 ‘쉬운 문제’라고 한다.

이와 반대로 필요한 기본 연산의 숫자가 그 어떠한 다항식보다도 빠르게 증가하는 문제들을 ‘어려운 문제’라고 한다. 어려운 문제의 예로는 소인수 분해가 있다. 예를 들어서 우리에게 어떤 자연수가 주어졌다고 하자. 소인수 분해는 이 자연수를 소수들의 곱으로 분해하는 것이 목표이다. 만약에 주어진 숫자가 작은 숫자, 예를 들어 \(21\)이라고 하면, 비교적 쉽게 소인수 분해를 할 수 있다. 하지만 만약 주어진 숫자가 커진다면 어떻게 이 문제를 풀 수 있을까? 예를 들어서 다음과 같은 자연수가 주어졌다고 하자.¹

\begin{equation*}
\begin{aligned}
&129895396741246553668360505100358528009034248654597911903\\&2419788920529412656720656434689083151546312549961835740547\\&3739459716268218354855529177740708735566475171028057188040\\&6531327239043488184077558685850291966602576247279397700973\\&8940666999399511612742609680406936426170508943678960162131\\&61648156293388870043
\end{aligned}
\end{equation*}

현재 알려진 방법 중 가장 빠른 연산 방식으로는 자릿수가 \(n\)개인 기본 숫자를 분해하는데 필요한 연산량이 \(n^{\frac{1}{3}}\)에 대해 지수함수적으로 증가한다.[1] 여기서 지수함수적으로 증가하는 함수의 예로는 \(f(n)=2^n\)을 들 수 있겠다. 중요한 점은 \(n\)이 커질수록 함수값의 자릿수가 달라질 정도로 빨리 증가한다는 점이다. 예를 들어 \(n=4\)를 집어넣으면 \(f(n)=16\)이지만, \(n=100\)만 되어도 \(f(n)\)은 \(10^{30}\)을 넘어선다. 우리는 이제 \(n\)에 다양한 범위의 숫자를 집어 넣어보면 소인수 분해가 곱셈에 비해서 얼마나 많은 연산을 해야 하는지 정성적으로 분석해 볼 수가 있다.

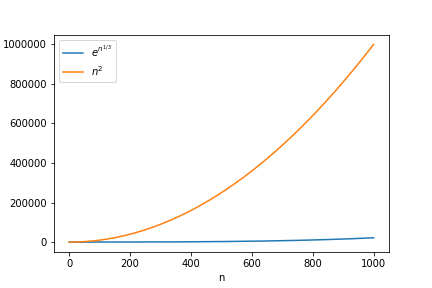
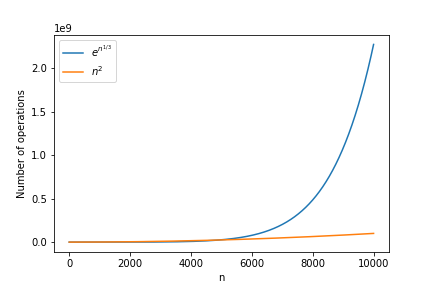
앞에서도 말했듯이 곱셈은 \(n\)이 커짐에 따라 필요한 연산의 숫자가 \(n^2\)에 비례해서 증가하는 반면에, 현재 알려진 가장 빠른 소인수 분해 알고리즘은 \(n^{\frac{1}{3}}\)에 대해 지수함수적으로 증가한다. 일단 \(n\)이 \(1\)부터 \(1000\)인 범위를 대입해 보았다.([그림3-1]) 여기서 \(x\)축은 \(n\)이고 \(y\)축은 필요한 연산량을 대략적으로 나타낸다. 아직은 \(n^2\)에 비례해서 증가하는 함수가 연산량이 훨씬 많다. 이제 \(n\)의 범위를 \(5000\)으로 늘려보겠다.([그림3-2]) 이제 \(n=4700\)인 부근에서 두 개의 연산량이 교차하기 시작한다. 이제 \(n\)의 범위를 \(10000\)으로 늘려보면, \(n\)이 \(1000\) 미만이었을 때와는 완전히 반대의 양상을 보인다.([그림3-3])

위의 예를 통해서 우리는 어려운 문제와 쉬운 문제의 차이를 다음과 같이 이해할 수 있다. 문제의 쉽고 어려움은 문제를 풀기 위해서 필요한 절대적인 계산량으로 정해지는 것이 아니라, 문제가 어려워질수록 필요한 연산량이 얼마나 빠르게 증가하느냐에 따라 정해진다. 만약 필요한 연산의 숫자가 문제의 크기(\(n\))에 대해 다항식처럼 증가하게 되면 그런 문제는 ‘쉽다’고 한다. 반대로 필요한 연산의 숫자가 지수함수적으로 증가하게 되면 그런 문제는 ‘어렵다’고 한다.

이런 면에서 봤을 때, 에니악과 노트북의 연산 방식에 큰 차이가 없다고 하는 이유는 ‘쉬운 문제’와 ‘어려운 문제’의 개념이 에니악에게나 노트북에게나 동일하게 적용되기 때문이다. 더 나아가 에니악과 노트북뿐만이 아니라 어떠한 형태의 컴퓨터를 사용하더라도 쉬운 일과 복잡한 일이라는 개념 자체는 컴퓨터의 형태와 무관하다. 슈퍼 컴퓨터를 사용한다고 해도 노트북과 비교해서 같은 시간 안에 단지 더 많은 계산을 할 수 있다는 차이가 있을 뿐이지 문제를 풀기 위한 절대적인 연산량 자체가 현격하게 줄어드는 것은 아니다. 문제를 푸는데 필요한 기본 연산의 숫자가 다항식처럼 증가하는 문제는 모든 형태의 컴퓨터에서 ‘쉽게’ 풀 수 있고, 기본 연산의 숫자가 지수함수적으로 증가하는 문제는 그 어떤 형태의 컴퓨터에서도 필요한 연산량이 지수함수적으로 증가한다.

양자 컴퓨터가 기존의 컴퓨터들과 다른 이유는 기존 컴퓨터로는 연산량이 지수함수적으로 증가하는 특정한 문제를 양자 컴퓨터의 새로운 연산 방법을 이용하면 연산량이 다항식처럼 증가하는 경우가 있기 때문이다. 즉, 기존의 컴퓨터들에게는 ‘어려운’ 특정한 문제를 양자 컴퓨터를 이용해서 ‘쉽게’ 풀 수 있는 경우들이 있다. 이런 면에서 봤을 때 양자 컴퓨터는 기존의 컴퓨터와는 패러다임 자체가 완전히 다른 컴퓨터라고 할 수 있겠다.

2. 양자 컴퓨터라는 가능성

기존 컴퓨터의 연산 방식은 고전 물리학 법칙에서 벗어나지 않는다. 하지만 20세기 물리학자들은 자연 원리가 고전 역학이 아닌 양자 역학으로 설명된다는 사실을 이미 알고 있었다. 이런 양자 역학적인 효과를 사용하는 컴퓨터는 기존 컴퓨터와 어떤 점이 다를까? 기존 컴퓨터에게 쉬운 문제들은 양자 컴퓨터에게도 쉬울까? 그리고 양자 컴퓨터에게 쉬운 문제들은 과연 기존 컴퓨터에게도 쉬울까?

우선 첫 번째 질문부터 생각해 보자. 모든 논리적인 연산은 NAND라는 기본 연산들로 나타낼 수 있다. NAND는 두 개의 비트(0 혹은 1)를 받아서 하나의 비트를 되돌리는 함수이다. 그 연산의 결과는 다음과 같다.

\begin{equation*}
\begin{aligned}
\text{NAND}(0, 0) &= 1 \\
\text{NAND}(0, 1) &= 1 \\
\text{NAND}(1, 0) &= 1 \\
\text{NAND}(1, 1) &= 0 \\
\end{aligned}
\end{equation*}

모든 논리 연산은 NAND를 통해서 이루어질 수 있기 때문에, 양자 컴퓨터로 NAND 연산을 쉽게 할 수 있으면 기존 컴퓨터에게 쉬운 문제는 양자 컴퓨터에게도 쉽다는 결론을 내릴 수 있다. 이게 실제로 가능할까? 정확히 NAND는 아니지만 양자 컴퓨터에서는 실제로 토폴리 게이트^{Toffoli gate}로 알려져 있는 다음과 같은 연산을 할 수 있다.

\begin{equation*}
xyz \to xy(\text{XOR}(z, \text{AND}(x, y)))
\end{equation*}

여기서 \(x, y, z\)는 \(0\) 혹은 \(1\)이고 AND는 NAND의 연산 결과에서 \(1\)과 \(0\)을 바꾸는 함수이다. 마지막으로 XOR는 다음과 같은 기본 연산이다.

\begin{equation*}
\begin{aligned}
\text{XOR}(0, 0) &= 0 \\
\text{XOR}(0, 1) &= 1 \\
\text{XOR}(1, 0) &= 1 \\
\text{XOR}(1, 1) &= 0 \\
\end{aligned}
\end{equation*}

좀 복잡해 보일 수도 있겠지만, 가능한 \(x,y,z\)의 경우의 수는 총 \(8\)가지뿐이므로, 손쉽게 이 함수가 어떤 일을 하는지 적어 볼 수 있다.

\begin{equation*}
\begin{aligned}
000 \to 000 \\
010 \to 010 \\
100 \to 100 \\
110 \to 111 \\
001 \to 001 \\
011 \to 011 \\
101 \to 101 \\
111 \to 110 \\
\end{aligned}
\end{equation*}

마지막 절반 부분을 보면 정확히 우리가 원하는 NAND 게이트의 결과를 얻을 수 있다는 사실을 알 수 있다. 이를 통해서 기존 컴퓨터가 할 수 있는 모든 일은 양자컴퓨터로도 할 수 있다는 결론을 얻을 수 있다. NAND의 중간 연산 과정을 저장할 수만 있다면, 기존 컴퓨터에게 쉬운 연산들은 양자 컴퓨터로도 쉽게 할 수 있다. 모든 NAND 게이트들을 토폴리 게이트로 바꾸기면 하면 되기 때문이다.

그렇다면 반대는 어떨까? 양자 컴퓨터에게는 기존 컴퓨터에 존재하지 않는, 양자 역학적인 효과를 이용하는 기능들이 추가로 존재한다. 이런 추가적인 기능들을 이용하면 기존 컴퓨터들에게 어려운 연산들을 쉽게 계산할 수 있을까? 그리고 실제로 어려운 연산들을 해낼 수 있다면, 그러한 연산들은 실생활에 어떻게 유용하게 쓰일 수 있을까?

3. 양자 컴퓨터는 어떻게 다른가?

양자 컴퓨터를 유용한 곳에 쓸 가능성에 대해 가장 처음 질문을 던진 사람은 20세기의 가장 위대한 물리학자 중 한 명인 리처드 파인만^{Richard Feynman}이다. 1982년에 쓴 논문 “컴퓨터를 이용한 물리 시뮬레이션^{Simulating Physics with Computers}“[2]을 통해 파인만은 다음과 같은 사실을 서술한다. 그 당시에도 사람들은 이미 다양한 물리적 계산을 위해 컴퓨터를 사용하곤 했었는데, 이러한 물리적 계산을 위해 필요한 컴퓨터의 연산량은 실로 엄청난 양이었다. 1980년대 이후 컴퓨터의 성능에 많은 발전이 있어왔지만, 이러한 계산을 위해 필요한 연산량 자체가 많다는 사실은 크게 변하지 않았다. 파인만은 특히나 양자역학 적인 효과를 연구하는데 필요한 연산량이 지나치게 많이 필요하다는 사실에 대해 말한다. 이는 누구에게나 알려진 사실이기는 했으나, 파인만은 역시 유명한 천재답게 발상을 뒤집는 생각을 한다. 만약 양자역학 적인 효과를 직접적으로 계산하기 힘들다면, 직접 비슷한 양자역학적인 효과를 내는 또 다른 양자역학적인 시스템을 만들면 되지 않을까?

파인만의 논문은 양자 컴퓨터가 유용하게 쓰일 수도 있다는 가능성을 제시했지만, 양자 컴퓨터가 왜 고전 컴퓨터보다 더 빠른 연산을 할 수 있는지, 또 어떤 유용한 계산을 양자 컴퓨터를 이용해서 할 수 있는지를 이해하기 위해서는 또 10여 년의 시간이 필요했다. 1992년에 데이비드 도이치^{David Deustch}라는 물리학자는 리처드 조사^{Richard Jozsa}라는 수학자와 함께 양자 컴퓨터에서는 손쉽게 풀 수 있고 고전적인 컴퓨터로는 지수함수적으로 많은 시간이 걸리는 문제를 발견한다. 양자컴퓨터를 이용해 이 문제를 서 푸는 방법은 도이치-조사 알고리즘^{Deutsch-Jozsa Algorithm}이라고 알려져 있다. 이번 글의 남은 부분에서 도이지-조사 알고리즘에 대해서 이야기해보고자 한다.

도이치-조사 알고리즘은 다음과 같은 문제를 푸는 것이 목표이다. 두 개의 값을(0 혹은 1) 가지는 어떤 함수 \(f(x)\)를 생각해 보자. 여기서 \(x\)는 \(n\)개의 비트이다. 중요한 가정은 이 함수가 다음과 같은 두 가지 경우 중 하나라는 가정이다.

1. \(f(x)\)가 상수인 경우

예) 변수 \(x\)가 두 개의 비트라고 가정해 보자. \(f(x)\)가 상수인 함수의 예로는 다음과 같은 함수를 들 수 있다: \(f(00)=f(01)=f(10)=f(11)=0.\) 상수의 값은 중요하지 않다. 즉 \(f(00)=f(01)=f(10)=f(11)=1\)인 경우도 가능하다.

2. \(x\)에 대해서는 \(f(x)=0\)이고 나머지 절반은 \(f(x)=1\)이다.²

도이치-조사 알고리즘이 풀려고 하는 문제는 위의 조건을 만족하는 \(f(x)\)가 주어졌을 때 첫 번째 혹은 두 번째 경우에 해당되는지를 알아내는 것이다. 고전 컴퓨터를 이용해서 이 문제를 확실히 풀기 위해서는 일일이 모든 \(x\)를 대입해 보아야 하기 때문에 최악의 경우 \(f(x)\)를 \(2^{n-1}+1\)번 연산해야 한다. 운이 나쁘면 가능한 모든 \(x\) 중 절반 이상을 확인해 보지 않는 이상 첫 번째와 두 번째 경우를 100% 구분할 수 없기 때문이다. 그에 반해 양자 컴퓨터를 이용하면 \(f(x)\)를 단 한 번만 계산해도 어느 경우에 해당되는지 100%의 확률로 알아낼 수 있다! 이것이 바로 도이치-조사 알고리즘이 놀라운 이유이다.

도이치-조사의 알고리즘을 설명하기 위해서는 우선 \(f(x)\)를 계산한다는 개념을 명확히 할 필요가 있다. 앞에서 우리는 이미 모든 고전적인 논리연산은 NAND로 할 수 있다는 사실에 대해서 이야기했다. 더불어, 양자 컴퓨터에서는 NAND를 토폴리 게이트로 바꾸어서 정확히 똑같은 연산을 할 수 있다는 사실에 대해서도 이야기했다. 이를 이용해서 연산의 결과 \(f(x)\)를 다음과 같이 저장할 수 있다.

\begin{equation*}
(x,0) \to (x,f(x))
\end{equation*}

다시 한번 강조하지만 이러한 연산을 하는데 필요한 기본 연산(NAND/토폴리 게이트)의 숫자는 양자 컴퓨터와 고전 컴퓨터가 동일하다.³

위에 제시한 문제의 해답을 얻기 위해서 필요한 시간을 계산해 보자. 기존 컴퓨터를 이용하면, 두 가지 경우 중 어떤 경우인지 알기 위해서 일일이 다른 \(x\)를 대입해 보면서 \(f(x)\)를 계산해 볼 수가 있다. 운이 나쁘면 정확히 \(2^{n-1}\)개의 \(x\)를 대입했을 경우 계속해서 한가지 결과만을 얻게 될 수도 있다. 그렇기 때문에 만약에 \(N\)개의 가능한 \(x\)가 있다면 최악의 경우 \(f(x)\)를 \(N/2+1\)번 계산해 봐야 할 수도 있다. 만약에 \(x\)의 길이가 \(500\)이라고 하면 \(f(x)\)를 \(2^{499}\)번 이상 계산해야 한다. 만약에 우주에서 가장 빠른 컴퓨터를 만들어서 기본 연산을 하는데 1플랑크 시간만큼이 걸린다고 가정해보자.⁴  이는 인간이 상상할 수 있는 가장 작은 단위의 시간이다. 그렇게 짧은 시간 안에 기본 연산을 할 수 있다고 가정해도 \(2^{100}\)초 이상의 시간이 걸린다. 이는 우주의 나이보다도 긴 시간이다.

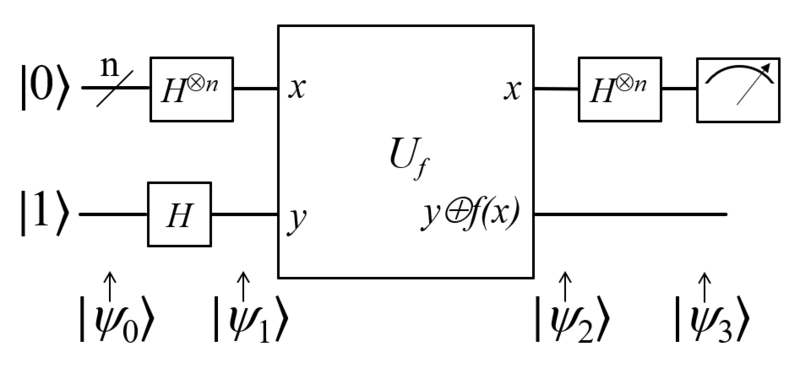
그에 반해서 도이치-조사 알고리즘을 이용하면 \(f(x)\)를 정확히 한 번만 사용해서 답을 알아낼 수가 있다.([그림5]) 이 방식으로 왜 정확한 해답을 얻을 수 있는지에 대해 간단한 예를 들어서 설명해보도록 하겠다. 이에 앞서, 우선 확실히 해야 할 것은 양자 컴퓨터에서는 0이나 1뿐만 아니라 더 다양한 상태가 존재할 수 있다는 점이다. 예를들어서 2비트로 이루어진 고전 컴퓨터는 총 4가지의 상태가 \((00, 01, 10, 11)\) 존재하는데, 양자 컴퓨터에서는 이 모든 상태들이 동시에 존재할 수 있다. 가장 일반적인 상태는 \(\alpha_{00}|00\rangle + \alpha_{10}|10\rangle + \alpha_{01}|01\rangle + \alpha_{11}|11\rangle\)로 나타내지는데, 여기서 \(\alpha_{00}, \alpha_{10}, \alpha_{01}, \alpha_{11}\) 각각의 상태가 어떠한 비율로 존재하는지를 나타내는 복소수들이다. 이런 상태의 양자 컴퓨터를 측정하게 되면 4가지 상태 중 하나로 상태가 붕괴하게 되는데, 각각의 상태를 측정하게 될 확률은 \(|\alpha_{00}|^2, |\alpha_{01}|^2, |\alpha_{10}|^2, |\alpha_{11}|^2\)이 된다. 이렇게 양자 컴퓨터는 고전 컴퓨터보다 더 다양한 상태를 구현할 수 있다. 이 때문에 컴퓨터를 구성하는 기본 단위를 다르게 부를 필요가 있다. 우리는 이를 큐빗^qubit이라고 부른다.

도이치-조사 알고리즘은 총 4개의 단계로 나눌 수 있고, 각각의 단계는 [그림5]에 있는 \(|\psi_0\rangle, |\psi_1\rangle, |\psi_2\rangle, |\psi_3\rangle\)로 나타나진다. 일단 첫 번째 단계(\(|\psi_0\rangle\))에서는 \(0\ldots 01\)인 상태로 시작한다. 두 번째 단계에서는 해다마드 게이트(\(H\))라는 연산을 한다. 이 연산 과정은 양자 컴퓨터에만 존재하는 연산이고, 때문에 준비된 \(0\)과 \(1\)들은 양자 컴퓨터 내에 존재하는 상태들이어야 한다. 이 과정을 거쳐서 양자 컴퓨터는 다양한 상태들의 중첩상태가 된다. 예를 들어서 \(n=1\)인 경우를 생각해 보자. 우리는 \(01\)이라는 상태에서 시작해서 두 번째 과정을 거치면 다음과 같은 상태에 도달한다:

\begin{equation}
(|00\rangle + |10\rangle – |01\rangle – |11\rangle)/2.
\end{equation}

세 번째 과정에서는 첫 번째 큐빗에 대해서 함수값 \(f(x)\)를 구한 다음에 두 번째 큐빗에 더해준다. 마지막으로 첫 번째 큐빗에 해다마드 연산을 가해준 다음에 측정한다. 이 두 가지 과정을 거치면 양자 컴퓨터는 다음과 같은 상태에 도달하게 된다.

1. \(f(x)\)가 상수인 경우: \((|00\rangle – |01\rangle)/\sqrt{2}\)
2. \(f(x)\)가 상수가 아닌 경우: \((|10\rangle – |11\rangle)/\sqrt{2}\)

때문에 첫 번째 큐빗을 측정해서 \(0\)이 나오게 되면 \(f(x)\)가 상수이고 \(1\)이 나오면 \(f(x)\)가 상수가 아님을 알 수가 있다. 좀더 일반적으로 \(n\)개의 큐빗이 있는 경우에는 \(f(x)\)가 상수일 경우 \(0\ldots 0\)을 측정하게 되고 그렇지 않은 경우에는 \(0\ldots 0\)을 측정하지 않게 된다. (예: \(111, 101, 001\))

그렇다면 도이치-조사 알고리즘은 기존의 알고리즘에 비해서 얼마나 빠를까? 이를 이해하기 위해서 [그림5]에 있는 연산을 하는데 물리적으로 필요한 시간에 대해서 생각해 보자. 일단 처음에 있는 해다마드 게이트는 양자 컴퓨터에서만 존재하는 새로운 종류의 기본 연산이다. \(U_f\)는 \(xy \to x(\text{XOR}(y, f(x)))\)에 해당되는 계산을 한다. 만약 연산의 결과로 \(0\ldots 0\)이 나온다면 \(f(x)\)는 상수이고 그렇지 않으면 \(f(x)\)는 정확히 절반의 \(x\)에 대해서 \(0\)이라는 결론을 내릴 수 있다. 이 계산을 하는데 쓰인 연산들은 다음과 같이 정리할 수 있다.

1. \(2n+1\)개의 \(H\)
2. 한 번의 \(U_f\)

여기서 각각의 해다마드 게이트는 양자 컴퓨터에서만 사용할 수 있는 간단한 기본 연산 중 하나이다. 양자 컴퓨터에서 해다마드 게이트에 해당되는 연산을 하는 데 필요한 시간은 한 번의 NAND를 계산하는데 필요한 시간과 크게 다르지 않다. (사실, 현재 나와 있는 대부분의 양자 컴퓨터에서는 해다마드 게이트를 토폴리 게이트보다 빠르게 처리할 수 있다.) \(U_f\)에서 사용해야 하는 기본 연산의 숫자는 \(f(x)\)를 계산하는데 필요한 NAND의 숫자와 크게 다르지 않다. 그 이유는 모든 NAND 게이트를 토폴리 게이트로 바꾸어서 정확히 동일한 연산을 할 수 있기 때문이다. 그래서 양자 컴퓨터에서 이 문제를 해결하기 위해 필요한 기본 연산의 숫자는 \(n\)에 대해서 선형적으로 증가하게 된다. 그에 반해 기존의 컴퓨터로는 이 문제를 해결하기 위한 기본 연산의 숫자가 대략 \(n\)에 대해서 지수적으로 증가하게 된다. 즉 이 문제는 기존 컴퓨터에게는 어렵지만 양자 컴퓨터에게는 쉬운 문제이다.

도이치-조사 알고리즘을 통해서 우리가 알아낼 수 있는 것은 양자 컴퓨터가 특정한 문제에 대해서는 고전 컴퓨터보다 훨씬 빠르게 답을 알아낼 수 있다는 사실이다. 그런데 여기서 중요한 점은 양자 컴퓨터가 기존 컴퓨터보다 10배, 100배, 아니면 1000배 이상 빠르다는 것이 아니다. 양자 컴퓨터와 고전 컴퓨터의 차이를 보려면, 몇 배의 속도 차이가 나는지가 아니라, 문제가 커짐에 따라서 답을 알아내는 데 필요한 시간이 얼마나 빠르게 증가하는지를 비교해 보아야 한다.

예를 들어, 도이치-조사 알고리즘에서는 \(n\)이 문제가 얼마나 어려운지를 나타내는 척도이다. 양자 컴퓨터의 경우는 \(n\)이 커져도 필요한 \(f(x)\)의 연산 숫자가 단 한 번에 불과하지만, 고전 컴퓨터의 경우에는 \(n\)이 커지면서 필요한 \(f(x)\)의 연산 숫자가 \(n\)에 대해서 지수함수적으로 증가한다. 각각의 경우 양자 컴퓨터와 고전 컴퓨터에서 연산을 하는 데 필요한 시간은 다음과 같이 근사할 수 있다. 편의상 양자 컴퓨터에서 기본 연산을 하는 데 최대한 \(t_q\)만큼의 시간이 걸린다고 가정해보자. [그림5]에서 나오는 기본 연산의 숫자는 \(H\)가 \(2n+1\)개이다. 만약 \(f(x)\)를 계산하기 위해 필요한 NAND의 숫자를 \(n_f\)라고 정의한다면 \(U_f\)를 계산하는 데는 대략 \(n_f\)개의 기본 연산이 필요하다. 그래서 양자 컴퓨터를 사용하면 최대한 \((n+n_f)t_q\)의 시간 안에 답을 구해낼 수 있다. 고전 컴퓨터에서 기본 연산을 하는 데 \(t_c\)만큼의 시간이 걸린다고 가정해보자. 이 경우 답을 알아내기 위해서는 \(f(x)\)를 \(2^n+1\)번 계산해야 하므로, 총 연산 시간은 \(n_f(2^n+1)\)이 된다. 정리하자면 다음과 같다.

1. 양자 컴퓨터: \((n+n_f) \times t_q\)
2. 고전 컴퓨터: \(n_f \times (2^n+1) t_c\)

다시 한 번 말하자면, 여기서 \(t_q\)는 양자 컴퓨터에서 기본 연산을 하는 데 드는 시간이고 \(t_c\)는 고전 컴퓨터에서 기본 연산을 하는 데 드는 시간이다. 또한 \(n_f\)는 \(f(x)\)를 계산하기 위해서 필요한 NAND의 숫자이다. 편의상 \(n_f\)가 \(n\)보다 훨씬 크다고 가정해 보자. 그러면 연산 시간의 비율은 대략 \(t_c/t_q \times 2^n\) 정도가 된다. 양자 컴퓨터에서 기본연산을 하기 위해 필요한 시간이 기존 컴퓨터보다 천배 느리다고 가정해도, \(n\)이 \(10\) 이상만 되면 양자 컴퓨터가 더 빠르다는 것을 알 수 있다.

이를 통해서 알 수 있는 점은, 양자 컴퓨터는 기존 컴퓨터와 연산을 하는 개념이 완전히 다르다는 점이다. 이 때문에 기본 연산을 하는 데 양자 컴퓨터가 고전 컴퓨터보다 더 오랜 시간이 걸린다고 하더라도, 복잡한 문제들에 대해서는 양자 컴퓨터가 속도적 우위를 점할 수도 있다는 점을 독자들이 꼭 기억해 주었으면 좋겠다. 물론 도이치-조사 알고리즘이 푸는 문제를 굉장히 작위적인 문제라고 생각할 수도 있다. 실생활에서 \(f(x)\)가 어떠한 함수인지도 모른 상태에서 상수이거나 0과 1의 비율이 1:1 인지 보장을 줄 수 있는 경우는 그다지 많지 않기 때문이다. 양자 컴퓨터를 이용해서 유용한 일을 하기 위해서는 양자 컴퓨터가 어떠한 수학적인 문제를 더 빠르게 풀 수 있는지 알아내고, 그러한 수학적인 문제를 풀어서 해결할 수 있는 현실적인 문제들을 찾아내야 한다. 다음 글에서는 사람들이 어떻게 그러한 문제들을 찾아냈는지, 또 그러한 문제를 양자 컴퓨터를 이용해서 빠르게 풀 수 있는 원리가 무엇인지에 대해서 설명하고자 한다.

4. 마치며

이번 연재를 통해서 필자는 양자 컴퓨터가 어떤 배경에서 태어났는지, 또 양자 컴퓨터가 기존 컴퓨터들과 비교해서 어떤 면에서 다른지에 대해 설명했다. 다시 한 번 강조하자면 양자 컴퓨터와 기존 컴퓨터의 차이는 절대적인 속도의 차이가 아니다. 연산 문제가 어려운지 혹은 쉬운지 결정하는데 중요한 접근 방법 중 하나는 문제가 커질수록  필요한 연산량이 얼마나 빠르게 증가하느냐이다. 특히나 필요 연산량이 지수함수적으로 증가하면 우린 그런 문제를 ‘어렵다’고 한다. 양자 컴퓨터는 기존 컴퓨터의 기본 연산 기능뿐만 아니라 양자역학적인 효과를 이용하는 추가 기능을 갖고 있는데, 이 추 기능을 통해 기존 컴퓨터에게는 ‘어려운’ 문제들을 쉽게 풀어낼 수 있다. 그런 면에서 양자 컴퓨터는 기존에 우리가 알고 있는 컴퓨터와는 완전히 다른 형태의 컴퓨터라고 생각하는 것이 맞다.