양자 오류 보정

지난 연재에서 말했듯이 양자 컴퓨터를 이용하면 암호 해독, 물질 시뮬레이션, 최적화 같은 중요한 문제들을 기존 컴퓨터보다 훨씬 적은 연산량으로 해결할 수 있다. 하지만 연산량이 기존 컴퓨터보다 적다고 해도 절대적인 연산량 자체가 작은 것은 아니다. 예를 들어서 쇼어의 소인수 분해 알고리즘을[1] 사용하기 위해서는 최소한 수십억 번의 기본 연산을 해야 한다. 이러한 연산 과정에서 오류가 발생하지 않게 하기 위해서는 연산 한 번을 할 때마다 오류가 날 확률이 수십억 분의 1보다 작아야 할 것이다.

하지만 현재 존재하는 양자 컴퓨터들은 대략 백번 내지 천 번 정도의 연산을 하면 한 개 정도의 오류가 발생한다. 쇼어의 소인수 분해 알고리즘을 돌리기에는 터무니없이 높은 오류율이다. 뿐만 아니라, 오류율을 수십억 분의 1 정도로 낮아지게 할 만한 기술은 물론이고, 아직 그러한 기술 발전이 어떻게 이루어질지에 대한 확실한 청사진마저 존재하지 않는다. 그렇다면 소인수 분해같은 대규모의 연산은 언제 가능할지 기약할 수 없는 꿈과 같은 이야기일까?

결론부터 말하면 그렇지 않다. 기본 연산의 오류율을 특정 수준 이하로만 낮출 수 있으면, 컴퓨터를 더 대규모로 만듦으로써 전체 연산의 오류율을 사실상 \(0\)에 가깝게 만들 수 있기 때문이다. 이러한 일을 가능하게 만드는 연구 분야가 바로 양자 오류 보정이라는 분야이다. 이 때문에 양자 오류 보정은 수많은 양자 알고리즘을 이용한 어플리케이션을 현실화할 수 있는 중요한 이론적인 초석 중의 하나이다.

이번 글에서는 양자 역학적인 오류 보정이 어떠한 원리로 이루어지는지 간단히 이야기해보고자 한다.

1. 오류 보정

양자 오류 보정이라는 분야를 이해하기 위해서는 우선 기존 정보 이론에서 사용하는 오류 보정 방법에 대해 간단히 살펴보는 것이 좋겠다. 현재 대부분의 컴퓨터는 오류가 날 확률이 극히 미미하지만, 과거의 컴퓨터들은 그렇지 못했다. 오류가 자주 발생하는 컴퓨터는 오류를 수정하지 않으면 사용 용도가 굉장히 제한적일 수밖에 없다. 예를 들어 독자들의 컴퓨터에서 기본 연산의 오류율이 0.1%라고 가정해 보자. 이러한 컴퓨터를 사용하면, 대략 1000번의 기본 연산을 할 때마다 오류가 발생하게 된다. 대부분의 컴퓨터는 초당 수억 개의 연산을 하는데, 이러한 확률로 오류가 나면 컴퓨터가 제대로 돌아가는 일은 거의 없을 것이다. 이러한 문제를 어떻게 해결할 수 있을까?

이에 대해서는 사실 쉬운 해결책이 있다. 같은 정보를 여러 번 반복해서 저장하는 것이다. 예를 들면, \(0\)과 \(1\)에 해당되는 정보를 \(000\)과 \(111\)로 세 번씩 중복해서 저장한다고 생각해 보자. 이러한 방식으로 저장하면 설령 세 개의 비트 중 하나가 오류를 일으켜도 (즉 \(0\)이 \(1\)로 바뀌거나 그 반대 상황이 일어나도) 나머지 두 비트의 손상되지 않은 정보를 이용해 정보를 쉽게 원상복구할 수 있다. 세 개의 비트에 저장되어 있는 정보를 이용해서 다수결 투표를 한 다음에 모든 비트를 다수결의 결과로 통일하면 다시 원래의 상태가 복구되기 때문이다. 예를 들어 \(000\)이었던 정보가 \(001\)로 손상되었다 하더라도 다수결 원칙을 적용해서 다시 \(000\)으로 되돌릴 수 있다.

이를 통해서 오류율이 어떻게 낮추어질 수 있는지 알아보자. 만약 각각의 비트가 독립적인 확률 \(p\)로 바뀌게 된다면, 이 과정에서 오류가 발생할 확률은 

\begin{equation}
p_{\text{오류}}=3p^2(1-p) + p^3
\quad \cdots \quad (1)
\end{equation}이 된다. 위에서 \(p^3\)은 세 개의 비트가 모두 오류를 일으킬 확률, 그 앞의 \(3p^2 (1-p)\)는 두 개만 오류를 일으킬 확률이다. 오류가 하나의 비트에서만 발생했을 경우 다수결을 통해서 오류를 고칠 수 있지만, 두 개 이상 발생하면 고칠 수 없다. 예를 들어서 \(p\)가 \(10^{-3}\)이라고 가정하면 오류가 날 확률은 약 \(p_{\text{오류}}=3\times 10^{-6}\)으로 매우 작음을 알 수 있다.

이처럼 같은 정보를 중복해서 저장하기 위해서는 더 많은 저장 용량이 필요하다. 하지만 추가적으로 필요한 저장 용량은 연산량에 비해서 굉장히 느리게 증가한다. 특정 연산을 하는데 총 백만 개의 기본 연산이 필요하다고 가정해 보자. 여기서 기본 연산은 AND, NOT, XOR같은 간단한 연산을 말한다. 전체 연산 과정에서 오류가 날 확률을 충분히 작게 하려면 기본 연산의 오류율을 백만분의 일보다 훨씬 작게 만들어야 한다. 예를 들어서, 각각의 기본 연산의 오류 발생 확률을 \(10^{-10}\) 수준으로 낮추면 연산 과정에서 오류가 발생할 확률은 대략 \(10^{-4}\) 정도가 된다. 위에서처럼 하나의 비트를 \(n\)개의 비트에 반복해서 저장하면 기본 연산의 오류율을 대략 \((2p)^{n/2}\) 수준으로 줄일 수 있다. 때문에 \(p_{\text{오류}}\)가 \(10^{-3}\)이라고 가정하면 \(n=8\)로도 우리가 원하는 연산 오류율을 달성할 수 있음을 알 수 있다. 저장 용량을 8배로 늘리기만 하면 오류율을 천만 배 이상 낮출 수 있는 것이다.

이처럼 고전적인 연산에서 오류가 발생할 확률을 줄이는 데에는 쉬운 해결책이 있다. 같은 정보를 반복해서 저장한 다음에 연산할 때마다 불일치하는 정보들이 있는지를 살펴보는 것이다. 그러한 정보들이 포착되면 다수결을 통해서 높은 확률로 쉽게 오류를 고칠 수 있다.

2. 양자 오류 보정

양자 컴퓨터에서도 연산할 때 오류가 발생할 확률을 줄일 수 있다. 하지만 고전 컴퓨터에서 사용하는 방식을 양자 컴퓨터에 적용하는 데에는 몇 가지 문제점들이 있다. 이제부터 필자는 이 문제점들에 대해서 간단히 이야기해 보고 사람들이 어떻게 이 문제를 해결했는지 말해보고자 한다.

첫 번째 문제점은 양자역학적인 상태를 복사할 수 없다는 점이다. 고전 컴퓨터에서는 아주 손쉽게 연산 중간 과정을 복사할 수 있다. 연산을 잠시 멈추고 중간 과정을 하드 디스크 같은 다른 저장 매체에 복사하기만 하면 되기 때문이다. 하지만 양자 역학적으로는 상태를 복사하는 것이 불가능하다. 왜 그런지 예를 들어서 생각해 보자. 큐빗 하나가 있다고 가정해 보자. 일반적으로 이 큐빗의 상태는 파동함수처럼 여러 가지 상태가 중첩된 상태로 존재할 수 있다.
\begin{equation}
|\psi\rangle = \alpha|0 \rangle + \beta |1\rangle.
\quad \cdots \quad (2)
\end{equation}여기서 \(|0\rangle\)과 \(|1\rangle\)은 두 개의 다른 상태를 의미하고 \(\alpha\)와 \(\beta\)는 \(|\alpha|^2 + |\beta|^2=1\)을 만족하는 복소수이다. 만약 연산의 중간 과정에 이 큐빗의 상태를 다른 큐빗으로 복사하고 싶다고 가정해 보자. 다른 큐빗의 상태를 \(|\phi\rangle\)이라고 나타내 보면, 우리는 복사하는 과정을 다음과 같이 나타낼 수 있다.
\begin{equation}
|\psi\rangle |\phi\rangle \to |\psi\rangle |\psi\rangle
\quad \cdots \quad (3)
\end{equation}

여기서 왼쪽은 \(\alpha\)와 \(\beta\)에 대해서 선형적인 조합으로 표현할 수 있지만 오른쪽은 \(\alpha\)와 \(\beta\)에 대해서 비선형적인 조합으로 나타난다. 양자 역학의 기본 공리상 이러한 비선형적인 변환은 일어날 수 없다. 그렇기 때문에 일반적인 상태를 복사하는 것은 양자역학적으로 불가능하다.¹

두 번째 문제는, 양자 상태를 측정하면 붕괴하게 된다는 것이다. 예를 들어서, 큐빗이 다음과 같은 일반적인 상태에 있다고 가정해 보자:
\begin{equation}
|\psi\rangle = \alpha|0\rangle + \beta |1\rangle.
\quad \cdots \quad (4)
\end{equation}이러한 상태에서 큐빗의 상태를 측정하면 확률 \(|\alpha|^2\)로 \(|0\rangle\) 상태로 붕괴되거나 확률 \(|\beta|^2\)로 \(|1\rangle\) 상태로 붕괴된다. 중요한 점은, 다시 원래의 상태인 \(|\psi\rangle\)로 돌아갈 수 없다는 점이다. 따라서 연산 도중에 상태 측정을 하면 중간 연산 과정을 잃어버리게 된다.

이러한 문제들 때문에 1994년에 쇼어의 소인수 분해 알고리즘이 발표되었을 때[1]² 많은 물리학자들이 회의적인 반응을 보였다. 앞에서도 말했듯이 이러한 알고리즘을 구현하기 위해서는 수십억 개에 달하는 연산이 필요한데, 지금까지 살펴본 문제들 때문에 도저히 오류 보정을 할 수 없다는 주장이었다.

이러한 비판에도 불구하고 쇼어는 양자 컴퓨터에서 오류를 보정할 수 있는 방법에 대한 깊은 연구를 시작했다. 비록 쇼어는 물리학자는 아니지만, 학부 때 배웠던 양자 역학에 대한 기본 개념을 또렷이 기억하고 있었다고 한다. 그리고 그에게는 당시 대부분의 물리학자들이 등한시했던 정보 이론과 오류 보정 코드에 대한 깊은 이해가 있었다. 이러한 독특한 배경지식들을 바탕으로 쇼어는 1995년에 마침내 양자 역학적으로 오류 보정이 가능하다는 사실을 발견했다.[3] 이는 실로 엄청난 사건이었다. 양자 역학적인 오류 보정이 가능하다는 것은, 양자 컴퓨터를 만드는 것이 불가능하지 않다는 것을 의미했기 때문이다.

2.1 오류 감지

그렇다면 쇼어는 도대체 어떻게 앞에서 말한 문제점들을 피해서 오류 보정을 할 수 있었을까? 쇼어가 발견한 중요한 사실 중 하나는 양자 역학적인 상태를 완전히 붕괴시키지 않으면서도 오류의 발생 여부를 확인할 수 있다는 사실이다. 예를 들어서, 두 개의 큐빗이 있으면, 두 큐빗의 상태를 완전히 측정하지 않으면서도 둘이 같은 비트를 가지고 있는지 혹은 다른 비트를 가지고 있는지 알 수 있다는 사실이다.

독자들이 얼핏 듣기에는 이상하다고 생각할 수도 있을 것이다. 두 개의 비트가 똑같은지 알려면 두 개의 비트를 모두 측정해야만 할 것처럼 생각하기 쉽기 때문이다. 그럴듯한 생각이지만 이는 사실이 아니다. 양자 역학적으로는 두 개의 비트를 측정하지 않고서도 두 개의 비트가 동일한지 혹은 동일하지 않은지 알아낼 수 있다. 이 과정을 이해하기 위해 중요한 것은 CNOT라는 연산이다. 큐빗 1로부터 큐빗 2로 CNOT을 적용하게 되면 다음과 같은 연산 결과를 얻게 된다.

\begin{equation}
\begin{aligned}
|0\rangle_1|0\rangle_2 &\to |0\rangle_1 |0\rangle_2 \\
|0\rangle_1|1\rangle_2 &\to |0\rangle_1 |1\rangle_2 \\
|1\rangle_1|0\rangle_2 &\to |1\rangle_1 |1\rangle_2 \\
|1\rangle_1|1\rangle_2 &\to |1\rangle_1 |0\rangle_2
\end{aligned}
\quad \cdots \quad (5)
\end{equation}이는 첫 번째 큐빗이 \(0\)인 상태에 있으면 아무것도 하지 않고 첫 번째 큐빗이 \(1\)인 상태에 있으면 두 번째 큐빗의 상태를 바꾸는 연산이다. 중요한 점은, 이러한 연산을 두 개의 큐빗을 측정하지 않고서도 할 수 있다는 점이다.

CNOT 연산을 이용해서 우리는 다음과 같은 방식으로 두 개의 비트를 측정하지 않고서도 둘이 같은지, 혹은 다른지를 확인해 볼 수 있다. 두 개의 비트가 다음과 같은 임의의 상태에 있다고 생각해 보자.
\begin{equation}
|\psi\rangle_{2} = \alpha_{00} |00\rangle + \alpha_{01}|01\rangle + \alpha_{10} |10\rangle + \alpha_{11} |11\rangle.
\quad \cdots \quad (6)
\end{equation}여기서 \(\alpha_{00}, \alpha_{01}, \alpha_{10}, \alpha_{11}\)은 \(|\alpha_{00}|^2 + |\alpha_{01}|^2 + |\alpha_{10}|^2 + |\alpha_{11}|^2=1\)을 만족하는 복소수들이다. 이제 우리는 새로운 큐빗(3번 큐빗이라고 하자) 하나를 추가해서 이 큐빗이 앞에서 말한 두 개의 큐빗과 다음과 같은 연산을 하게 만들 것이다.
\begin{equation}
\begin{aligned}
|\psi\rangle_{12}|0\rangle_3 &= \alpha_{00} |00\rangle_{12}|0\rangle_3 + \alpha_{01}|01\rangle_{12}|0\rangle_3 + \alpha_{10} |10\rangle_{12}|0\rangle_3 + \alpha_{11} |11\rangle_{12}|0\rangle_3 \\
&\to \alpha_{00} |00\rangle_{12}|0\rangle_3 + \alpha_{01}|01\rangle_{12}|0\rangle_3 + \alpha_{10} |10\rangle_{12}|1\rangle_3 + \alpha_{11} |11\rangle_{12}|1\rangle_3 \\
&\to \alpha_{00} |00\rangle_{12}|0\rangle_3 + \alpha_{01}|01\rangle_{12}|1\rangle_3 + \alpha_{10} |10\rangle_{12}|1\rangle_3 + \alpha_{11} |11\rangle_{12}|0\rangle_3 \\
&= (\alpha_{00}|00\rangle_{12} + \alpha_{11}|11\rangle_{12})|0\rangle_3 + (\alpha_{01}|01\rangle_{12} + \alpha_{10}|10\rangle_{12})|1\rangle_3
\end{aligned}
\quad \cdots \quad (7)
\end{equation}여기서 아래첨자에 있는 \(1,2\)와 \(3\)은 세 개의 큐빗의 상태를 지칭한다. 첫 번째 과정에서는 큐빗 \(1\)로부터 큐빗 \(3\)에게 CNOT을 적용했고 두 번째 과정에서는 큐빗 \(2\)로부터 큐빗 \(3\)에게 CNOT을 적용했다.

이제 큐빗 \(3\)의 상태를 측정하면 어떻게 되는지 알아보자. 만약 \(0\)을 측정하게 되면 우리는 측정을 하지 않은 나머지 두 개의 큐빗이 다음과 같은 상태에 있음을 저절로 알게 된다.
\begin{equation}
\alpha_{00}|00\rangle_{12} + \alpha_{11}|11\rangle_{12}
\quad \cdots \quad (8)
\end{equation}그에 반해 \(1\)을 측정하게 되면 우리는 나머지 두 개 큐빗에 대해 다음과 같은 상태를 얻게 된다.
\begin{equation}
\alpha_{01}|01\rangle_{12} + \alpha_{10}|10\rangle_{12}
\quad \cdots \quad (9)
\end{equation}즉, 3번 큐빗에서 \(0\)을 측정하면 큐빗 \(1\)과 \(2\)가 같은 비트값을 가지고 있다는 사실을 알 수 있다. 마찬가지로 \(1\)이라는 측정 결과를 얻게 되면 나머지 두 개의 큐빗이 서로 다른 비트값을 가질 수밖에 없다는 사실을 알 수 있다. 이 과정에서 우리는 큐빗 \(1\)과 \(2\)의 상태를 직접 측정하지는 않았다. 때문에, 우리는 큐빗들의 상태를 직접 측정하지 않고도 둘이 같은 비트값을 가지고 있는지 확인할 수 있다.

2.2 오류 보정

이처럼 CNOT 같은 기본 연산을 이용하면 양자 역학적인 상태를 완전히 붕괴시키지 않고서도 오류가 발생했는지 감지할 수가 있다. 물론, 오류를 감지하면 이를 고쳐야 하는 것이 마땅하다. 앞에서 말한 접근 방식을 이용하면 오류 또한 쉽게 고칠 수 있다.

고전적인 오류 보정에서 말했던 예를 다시 살펴 보자. 우리는 이제 큐빗 하나에 해당하는 정보를 큐빗 세 개에 저장하려고 한다. 이전에 \(000\)을 \(0\)이라는 상태로 보고 \(111\)을 \(1\)이라는 상태로 보았던 것처럼 우리는 \(|000\rangle\)을 \(|0\rangle\)이라는 상태로 보고 \(|111\rangle\)을 \(|1\rangle\)이라는 상태로 보려고 한다. 이 둘을 구분하기 위해서 세 개의 큐빗들을 물리적 큐빗이라고 하고 \(|000\rangle\)과 \(|111\rangle\)에 해당되는 정보를 논리적 큐빗에 저장된 정보라고 보통 이야기한다.

논리적인 큐빗의 가장 일반적인 상태는 다음과 같다.
\begin{equation}
|\bar{\psi}\rangle = \alpha|000\rangle + \beta|111\rangle
\quad \cdots \quad (10)
\end{equation}이전처럼 \(\alpha\)와 \(\beta\)는 \(|\alpha|^2 + |\beta|^2=1\)을 만족하는 복소수들이다. 이 상태에 오류가 발생했을 때 어떻게 고칠 수 있는지 이제부터 알아보도록 하겠다.

오류를 어떻게 고칠 수 있는지 이해하려면 앞에서 말한 고전적인 오류 보정 방식을 약간 수정할 필요가 있다. 앞에서 말한 방법은 모든 비트를 측정한 후 다수결을 이용해서 오류 보정을 하는 방식이었다. 하지만 조금만 생각해 보면 반드시 정확한 비트의 값을 알 필요는 없음을 알 수 있다. 각각의 비트값을 알아내는 대신에 다음과 같은 질문에 대한 답을 알고 있다고 가정해보자.

• 첫 번째 비트는 두 번째 비트와 같은가?
• 두 번째 비트는 세 번째 비트와 같은가?

이 질문에 대한 답은 총 4가지인데, 각각의 경우에 다음과 같은 방식으로 오류를 보정할 수 있다.

• 예, 예: 모든 비트가 같으므로 보정을 할 필요가 없다.
• 예, 아니오: 세 번째 비트만 다르므로, 세 번째 비트의 값만 바꾸면 된다.
• 아니오, 예: 첫 번째 비트만 다르므로, 첫 번째 비트의 값만 바꾸면 된다.
• 아니오, 아니오: 두 번째 비트만 다르므로, 두 번째 비트의 값만 바꾸면 된다.

이러한 방식으로 오류 보정을 한 결과는 앞에서 말한 오류 보정의 결과와 정확하게 똑같다. 즉, 오류 보정을 하기 위해서 우리는 각각의 비트의 값을 정확히 알 필요는 없다. 중요한 것은 단지 비트들이 서로 다른지 혹은 같은지에 관한 정보이다.

2.3 위상 오류 보정

지금까지 우리는 양자역학적인 상태의 비트 값이 바뀌는 오류가 발생해도 이 오류를 수정할 수 있는 방법이 있다는 사실을 발견했다. 하지만 양자 컴퓨터에서는 또 다른 종류의 오류가 발생할 수 있다. 이는 바로 위상 오류이다. 예를 하나 들어보자. 어떠한 큐빗이 다음과 같은 양자 상태에 있다고 가정해 보자.
\begin{equation}
|+\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}}
\quad \cdots \quad (11)
\end{equation}여기서 위상 오류는 \(|0\rangle\)을 \(|0\rangle\)으로, 그리고 \(|1\rangle\)을 \(-|1\rangle\)으로 바꾸는 오류를 말한다. 위상 오류가 중요한 이유는 이러한 위상 오류를 통해서 본래의 상태가 다른 상태로 바뀔 수 있기 때문이다. 위에서 말한 상태의 경우, 위상 오류가 생기면 다음과 같은 상태로 바뀌게 된다.
\begin{equation}
|-\rangle = \frac{|0\rangle – |1\rangle}{\sqrt{2}}
\quad \cdots \quad (12)
\end{equation}여기서 \(|+\rangle\)은 \(|-\rangle\)와는 완전히 다른 상태이다. 둘 사이의 양자역학적 겹침 정도를 계산해 보면 정확히 \(0\)이 되기 때문이다.

놀랍게도, 이러한 위상 오류 또한 직접 큐빗의 상태를 측정하지 않고서도 감지해낼 수 있다. 그 원리를 이해하기 위해서는 \(|0\rangle\)과 \(|1\rangle\)상태 대신에 \(|+\rangle\)과 \(|-\rangle\)상태를 이용해서 생각하는 것이 편하다. 이전과 비슷하게 큐빗 1로부터 큐빗 2로 CNOT연산을 한다고 생각해 보자. 이전과의 차이점은 두 개의 큐빗이 \(|+\rangle\)이나 \(|-\rangle\) 상태에 있다는 점이다. 우리는 다음과 같은 점을 쉽게 확인해 볼 수 있다.
\begin{equation}
\begin{aligned}
|+\rangle_1 |+\rangle_{2} &\to |+\rangle_1|+\rangle_2 \\
|-\rangle_1 |+\rangle_2 &\to |-\rangle_1 |+\rangle_2 \\
|+\rangle_1|-\rangle_2 &\to |-\rangle_1|-\rangle_2 \\
|-\rangle_1 |-\rangle_2 &\to |+\rangle_1|-\rangle_2
\end{aligned}
\quad \cdots \quad (13)
\end{equation}즉 두 번째 상태가 \(|+\rangle\)이면 아무 일도 벌어지지 않고, 두 번째 상태가 \(|-\rangle\)이면 첫 번째 큐빗의 \(|+\rangle\)와 \(|-\rangle\) 상태를 뒤바꾼다.

이러한 원리를 이용해서 이전과 마찬가지로 위상 오류가 발생했는지 확인해 볼 수 있다. 예를 들어서 두 개짜리 큐빗이 가질 수 있는 가장 일반적인 상태를 생각해 보자.
\begin{equation}
\alpha_{++}|++\rangle + \alpha_{+-}|+-\rangle + \alpha_{-+}|-+\rangle + \alpha_{–}|–\rangle
\quad \cdots \quad (14)
\end{equation}여기서 \(|+\rangle\)상태로 시작하는 세 번째 큐빗을 가지고 온 다음에 위에서 말한 방식을 이용해서 두 큐빗이 같은 \(|+\rangle\)나 \(|-\rangle\) 상태에 있는지, 혹은 다른 상태에 있는지 큐빗들을 직접 측정하지 않고서도 확인해볼 수가 있다.

이 사실을 이용해서 비트 오류를 수정했던 것처럼 위상 오류를 수정하는 것도 가능하다. 이를 위해서는 다음과 같은 상태의 논리적인 큐빗을 이용하면 된다.
\begin{equation}
|\bar{\psi}\rangle = \alpha|+++\rangle + \beta|—\rangle.
\quad \cdots \quad (15)
\end{equation}이전처럼 \(\alpha\)와 \(\beta\)는 \(|\alpha|^2 + |\beta|^2=1\)을 만족하는 복소수들이다. 오류 수정 방법은 이전과 매우 비슷하다. 직접 상태를 측정하는 대신에 첫 번째와 두 번째 큐빗, 그리고 두 번째와 세 번째 큐빗이 같은 \(\{|+\rangle, |-\rangle\}\) 상태에 있는지를 확인해보면 된다. 확인 후 결과에 따라서 위상을 바꾸어 주면 다시 원래의 상태로 돌아올 수 있다.

2.4 양자 오류 보정 코드

앞에서 필자가 말한 두 가지 예는 각각 비트가 바뀌는 오류와 위상적인 오류를 보정할 수 있는 양자 오류 보정 코드로 볼 수 있다. 하지만 필자가 소개한 코드들은 단점이 있다. 바로 두 가지 종류의 오류를 모두 수정할 수는 없다는 점이다. 자연적으로 발생하는 오류는 대부분 이 두 가지 오류의 조합으로 나타낼 수 있기 때문에, 자연적으로 발생하는 오류들을 보정하기 위해서는 두 종류 모두를 고칠 수 있는 방법이 필요하다.

쇼어의 중요한 발견 중 하나는 일반적인 오류와 위상적인 오류를 모두 수정할 수 있는 양자 오류 보정 코드를 발견했다는 점이다.[3] 이러한 코드가 존재할 수 있다는 사실은 양자 컴퓨터라는 아이디어가 현실화 될 수 있다는 것을 보여준 중요한 계기 중 하나였다.

하지만 이러한 코드가 존재할 수 있다는 사실만으로 양자 컴퓨터를 만들 수 있는 것은 아니다. 오류가 발생했는지 확인하기 위해 사용하는 연산들에서조차 오류가 발생할 수가 있기 때문이다. 이러한 어려움들을 어떻게 해결할 수 있을까? 이 문제에 대한 해답은 결함 감내 시스템^{fault-tolerant system}이라는 개념을 통해서 이해할 수 있다.

3. 결함 감내 시스템

쇼어의 발견 덕분에 사람들은 이론적으로는 양자 컴퓨터에서 오류가 일어날 확률을 줄일 수 있다는 사실을 알게 되었다. 하지만 앞에서 말했듯이 아직 해결해야 할 한 가지 문제가 있다. 바로 오류의 존재 여부를 체크하는 과정에서조차 오류가 날 수 있다는 사실이다. 만약 오류가 발생했는데도, 확인 과정에서 문제가 생겨서 이를 발견하지 못한다면 어떻게 될까?

사실 1900년대 중반에 사람들은 이미 정확히 똑같은 질문을 고전적인 컴퓨터에 던졌다. 사람들이 발견한 사실은 고전 컴퓨터에서 오류가 발생할 수 있고 오류를 체크하는 과정에서 문제가 생긴다고 해도 연산에서 발생하는 오류율은 여전히 쉽게 줄일 수 있다는 사실이다. 기본적인 아이디어 자체는 굉장히 간단하다. 오류가 발생했는지 확인하는 과정을 여러 번 반복하는 것이다. 이를 통해서 오류가 발생했는지 확인하는 과정에서 발생하는 오류율을 줄일 수가 있다. 이 과정에서 발생하는 오류율이 충분히 낮아지면, 다시 원래대로 컴퓨터 자체에서 발생하는 오류에만 신경 쓰면 된다.

양자 컴퓨터에서도 사람들은 비슷한 아이디어를 이용해서 비슷한 결과를 도출해 냈다. 이는 바로 결함 감내 시스템이라는 결과이다.[4] 즉, 오류가 발생하고 오류를 검사하는 과정에서도 오류가 발생한다고 해도 연산에서 생기는 오류를 많이 줄일 수 있다. 이러한 양자 역학적인 결함 감내 시스템이 존재할 수 있다는 사실은 양자 컴퓨터를 실제로 만들 수 있다는 큰 희망을 주었다.

이후 많은 사람들이 양자역학적인 결함 감내 시스템에 대해 연구를 했다. 다양한 결함 감내 시스템들을 비교해볼 때 중요한 개념 중 하나는 결함 감내 임계치라는 개념이다. 만약 오류율이 이 임계치보다 낮으면 결함 감내 시스템을 더 크게 만들어서 연산 오류 확률을 한없이 작아지게 만들 수 있다. 하지만 임계치를 넘어버리면 오류를 고치는 것보다 새로 발생하는 확률이 더 높아져서 더 이상 결함을 감내할 수 없게 된다. 

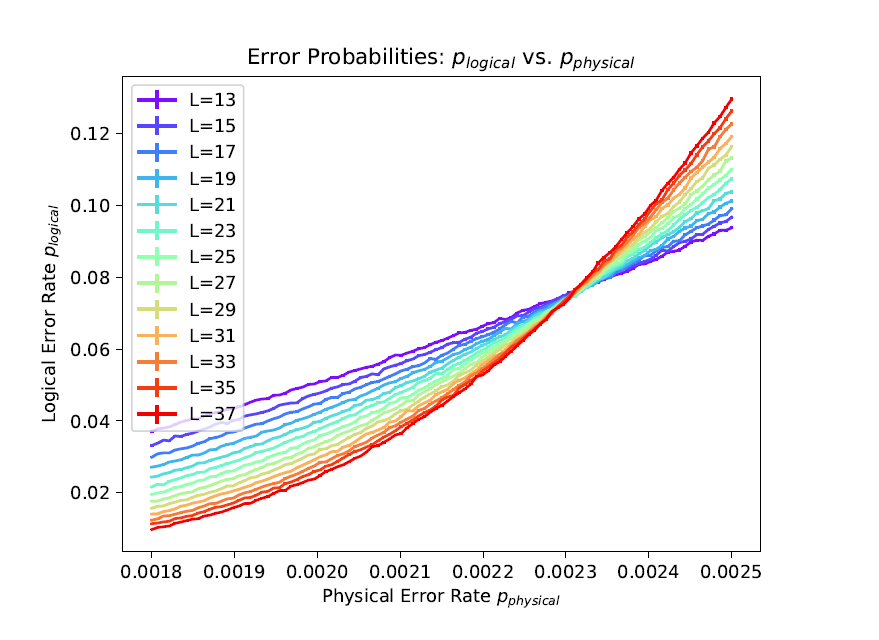
[그림1]을 살펴보자. 그림에서 \(x\)축은 물리적으로 발생하는 오류율을 의미하고 \(y\)축은 오류 보정을 한 후의 오류율을 의미한다. 그리고 여러 가지 색으로 표현되어 있는 \(L\)은 결함 감내 시스템의 크기를 의미한다. 여기서 중요한 점은 물리적인 오류율이 \(0.0023\)보다 낮으면 시스템의 크기가 커질수록 오류율이 계속해서 낮아지게 된다는 점이다.³ 이 때문에, 물리적인 오류율을 이 수치보다 낮게 만들 수 있으면, 시스템의 크기를 크게 만들어서 연산 오류율을 원하는 만큼 낮출 수 있다.⁴

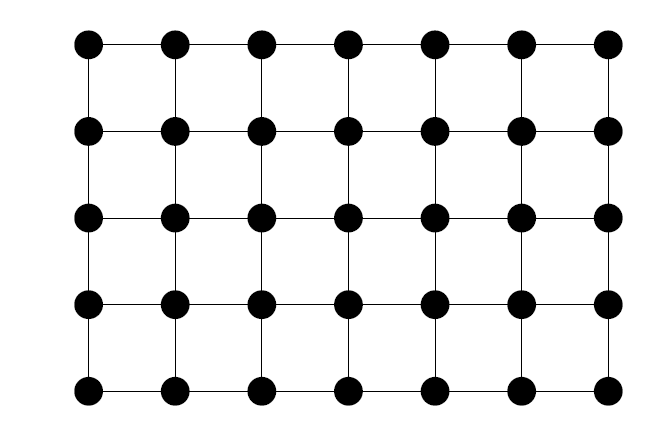
현재 사람들이 유망하게 보고 있는 결함 감내 시스템은 약 \(0.7\%\) 정도의 임계치를 가지고 있다.[6] 이 시스템은 비교적 높은 임계치를 가지고 있을 뿐만 아니라⁵, 기술적으로 보았을 때 실제로 만들 수 있는 가능성이 보인다는 점이 장점이다. 이 방식을 이용하면 [그림2]에 보이는 것처럼 2차원 평면에 큐빗들을 늘어 놓아서 이웃 간에 상호작용만을 이용해서 양자 컴퓨터를 만들 수 있기 때문이다.

실제로 최근 구글은 [그림2]와 비슷한 형태로 50여 개의 큐빗을 나열했고 이웃 간의 상호작용을 이용한 연산의 오류율이 \(0.3\%\) 정도에 해당한다는 것을 보였다. 만약 이러한 연산뿐만 아니라 다른 모든 기본 연산의 오류율도 비슷한 수준이라면, 이러한 시스템의 크기를 늘려서 오류율을 굉장히 작게 낮출 수 있을 것이다. 안타깝게도 아직 일부 연산 과정에서 생기는 오류율은 이보다 훨씬 크다. 좀 더 정확히 말하면 상태 측정에서 생기는 오류율이 \(1\sim 3\%\) 정도에 다다른다. 예를 들면 상태가 \(|0\rangle\)일 때 \(|1\rangle\)이라고 잘못 기록될 확률이 \(1\sim 3\%\) 정도 된다고 생각하면 된다. 이렇게 측정에서 생기는 높은 오류율은 대규모의 양자 컴퓨터를 만들기 위해서 반드시 넘어야 할 숙제 중 하나이다.

4. 오류 보정 오버헤드

결함 감내 시스템을 이용하면 오류율을 줄일 수 있지만, 대신에 오류 보정을 위해 더 많은 큐빗이 필요해진다. 오류 보정 오버헤드는 필요한 큐빗의 숫자와 저장 가능한 정보의 양의 비율을 말한다. 예를 들어서 100개의 큐빗을 이용해서 30개의 큐빗에 해당되는 양 만큼의 정보를 저장할 수 있다고 가정해 보자. 이 경우에 오버헤드는 \(100/30 \approx 3.33\)이 된다.

그렇다면 쇼어의 알고리즘처럼 대규모의 양자 연산을 하기 위해서는 어느 정도의 오버헤드가 필요할까? 간단해 보이는 질문이지만, 사실 복잡한 문제이다. 이 문제에 대한 답은 기본 연산 오류율과 필요로 하는 연산 오류율, 그리고 결함 감내 시스템의 특징에 따라 바뀌기 때문이다. 하지만 [그림2]에 그려져 있는 결함 감내 시스템의 경우, 다음과 같은 근사적인 공식이 알려져 있다.[6]
\begin{equation}
\text{Overhead} = c\log^2 (p/p_L),
\quad \cdots \quad (16)
\end{equation}여기서 \(c\)는 \(1\)내지 \(10\) 정도 범위 있는 상수이고 \(p\)는 물리적인 오류율, \(p_L\)은 필요로 하는 연산 오류율이다. 여기에 숫자를 집어넣어 보면 대략 수백내지 \(1000\)에 달하는 오버헤드가 발생함을 알 수 있다.

이 식을 이용하면 대규모의 소인수 분해 알고리즘을 돌리기 위해서는 대략 1000개가 넘는 논리적인 큐빗이 필요한데 이를 위해서는 수백만 개의 물리적인 큐빗이 필요함을 알 수 있다. 현재 나와 있는 양자 컴퓨터는 대략 50여 개의 큐빗이 있는 것을 생각하면 실로 엄청난 숫자이다. 이처럼 대규모의 양자 컴퓨터를 만들기 위해서는 굉장히 많은 숫자의 큐빗을 낮은 오류율로 작동시킬 수 있어야 한다.

마치며

이번 글에서 우리는 왜 양자 컴퓨터가 단지 이론적으로만 존재하는 추상적인 분야가 아니라 현실적으로 이루어질 가능성이 높은 분야인지에 대해서 이야기했다. 이것이 가능한 이유는 양자 오류 보정이라는 중요한 결과 때문이다. 이를 이용해서 오류율이 충분히 낮아지기만 하면 우리는 대규모의 결함 감내 시스템을 만들어서 양자 컴퓨터에서 생기는 오류율을 획기적으로 줄일 수 있다. 이는 양자 컴퓨터를 만드는 데 있는 어려움이 단지 기술적인 문제이지 과학적인 문제가 아니라는 뜻이기도 하다.

하지만 앞으로도 할 일은 많다. 기술적으로 보았을 때 일단 수만 내지 수십만, 수백만 개의 큐빗을 양산해 내고 조종할 수 있는 기술이 필요하다. 이렇게 대규모의 큐빗을 컨트롤 하는 일은 아직 그 누구도 해보지 못한 일이기 때문에 과학적으로나 공학적으로나 아직도 많은 투자와 노력이 필요하다. 뿐만 아니라, 이와 동시에 기본 연산의 오류율을 계속해서 낮출 필요가 있다. 이론적인 측면에서 보았을 때에는 앞에서 말한 오버헤드의 숫자를 줄이기 위한 노력이 필요할 것이다.

하지만 지금까지 계속되었던 양자 컴퓨터의 발전이 계속된다면, 어느 순간부터는 분명 이러한 대규모의 결함 감내 시스템을 만들어 낼 수 있는 때가 올 것이다. 그 순간이 오면 이전 연재에서 말했던 수많은 알고리즘들을 이용할 수 있게 될 것이고, 그러한 알고리즘을 사용해서 할 수 있는 새로운 어플리케이션의 숫자는 실로 헤아리기 어려울 것으로 생각된다.