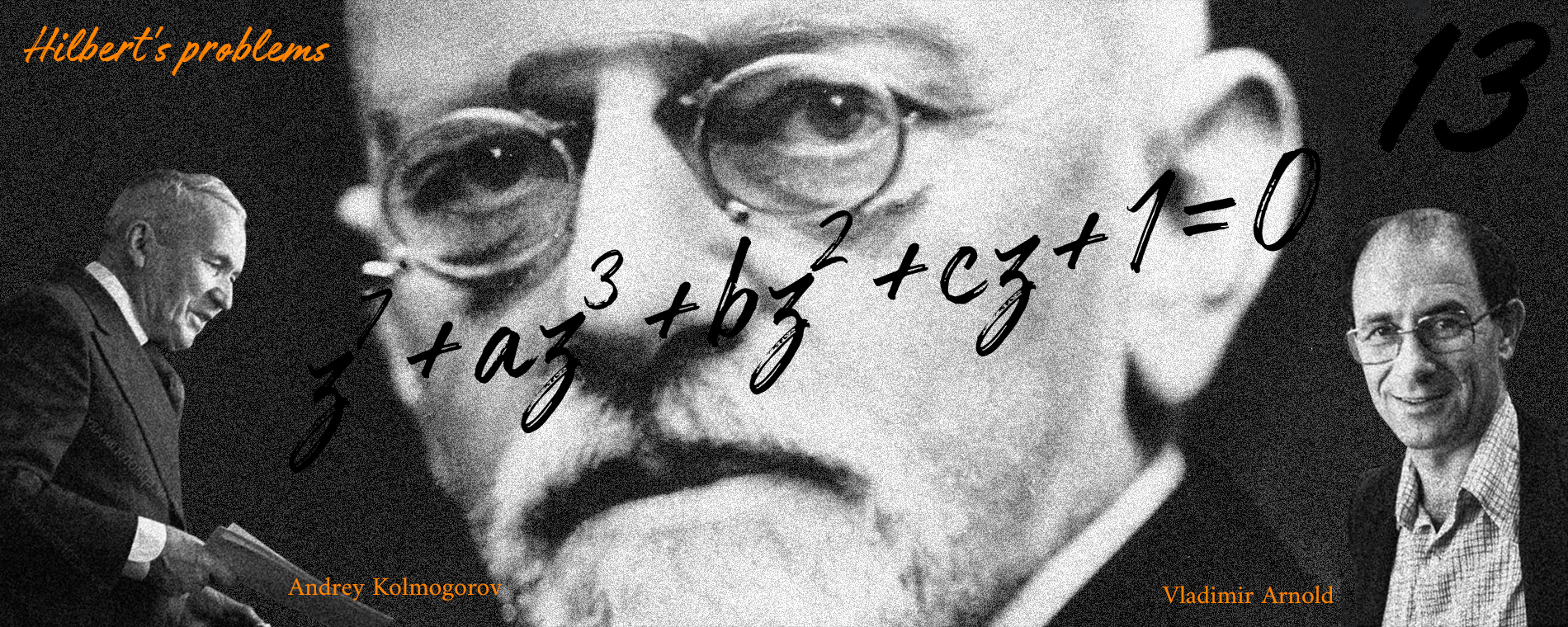방정식의 근을 찾는 것은 수학에서 가장 오래된 문제인 동시에 여전히 핵심적인 문제이다. 우리는 새로 이사한 집에서 40인치 텔레비전을 벽에 걸기 전에 가로세로 길이를 알아내기 위해, 무심코 마시던 칵테일의 알코올 도수를 알아내기 위해 방정식을 푼다. 알림을 확인하기 위해 스마트폰의 안면인식 기능을 사용할 때마다, 군것질거리를 주문하러 앱에 로그인할 때마다 부지런한 중앙처리장치는 방정식을 풀고 있다. 현대문명은 방정식을 풀지 않고서는 한순간도 존재할 수 없다.
이전글 “불멸의 힐버트 [1]: 좋은 문제는 한 번 풀리지 않는다“에서 예고한 대로 이 시리즈에서는 힐버트의 문제들1을 알아보고 그 역사성과 현재성을 확인하고자 한다. 첫 번째 순서로 방정식에 관한 문제를 꼽은 것은 그 중요성을 고려했을 때 당연한 것이다. 힐버트의 13번째 문제는 \(n\)차 1변수 다항식
\begin{equation} \tag{식1}
x ^{n} +a _{1} x ^{n-1} +a _{2} x ^{n-2} + \cdots +a _{n-1} x+a _{n} =0
\end{equation}의 풀이법에 관한 것이다. 여기서 계수들은 복소수라고 하자. 물론 복소수가 불편하면 실수라고 해도 된다. 하지만 실근이라 하더라도 근을 구하는 과정에서는 복소수가 반드시 사용되므로 애초부터 다 복소수라고 해두면 마음이 편하다. 이제부터는 종이와 연필을 준비하여 손으로 계산해 가며 읽으면 독자의 즐거움이 13배 이상 늘어날 것이다.
2차 방정식, 즉 \(x ^{2} +a _{1} x+a _{2} =0\) 부터 풀어보자. \(x=y-a _{1} /2\)라고 두면 (식1)은 2항 방정식
\[y ^{2} -t=0, \qquad t=a _{1}^{2} /4-a _{2}\]이므로 해는
\[x= \pm \sqrt {t} -a _{1} /2= \pm \sqrt {a _{1}^{2} /4-a _{2}} -a _{1} /2\]로 주어진다. 모든 2차 방정식은 이렇게 풀 수 있다.
여기까지는 중학생들도 아는 내용이다. 이제 \(n=3\)인 경우 \(x ^{3} +a _{1} x ^{2} +a _{2} x+a _{3} =0\)을 풀어보자. 3차부터는 다양한 해법이 있지만 모든 차수의 경우로 일반화할 수 있는 방법을 생각해보자. 먼저 2차의 경우와 유사하게 \(x=y-a _{1} /3\)라 두면 2차항이 없는
\begin{equation} \tag{식2}
y ^{3} +ay+b=0
\end{equation}의 꼴인 3차 방정식을 얻는다. 이 방정식을 풀 수 있으면 그 근들에서 \(a _{1} /3\)을 빼 원래 방정식의 근을 얻는다. 이제 1683년 발견된 치른하우스Tschirnhaus 변환이라는 것을 해볼 텐데 잘 보면 전혀 어렵지 않으니 한 번에 배워보자. (식2)의 세 근을 \(y _{1} , y _{2}, y _{3}\)이라 하면
\[y ^{3} +ay+b=(y-y _{1} )(y-y _{2} )(y-y _{3} )\]를 전개하고 양변을 비교하여
\[y _{1} +y _{2} +y _{3} =0, \quad y _{1} y _{2} +y _{2} y _{3} +y _{3} y _{1} =a, \quad y _{1} y _{2} y _{3} =-b\]임을 얻는다. 이제
\begin{equation} \tag{식3}
z _{1} =y _{1}^{2} +py _{1} +q, \quad z _{2} =y _{2}^{2} +py _{2} +q, \quad z _{3} =y _{3}^{2} +py _{3} +q
\end{equation}라고 두면
\[z _{1} +z _{2} +z _{3} =-2a+3q,\quad z _{1} z _{2} +z _{2} z _{3} +z _{3} z _{1} =ap ^{2} +3bp+3q ^{2} -4aq+a ^{2}\]이 된다. \(a, b\)는 주어진 상수이므로 방정식
\[-2a+3q=0, \qquad ap ^{2} +3bp+(3q ^{2} -4aq+a ^{2} )=0\]을 풀어 근 \(p,q\)를 구하자. 이 \(p,q\)에 대해, \(z _{1} z _{2} z _{3}\)는 \(a, b\)로부터 구할 수 있는데 구체적인 표현은 누구나 계산할 수 있으나 복잡하므로 이를 그저 \(t\)라고 두자. 근과 계수의 관계로부터 \(z _{1}, z _{2}, z _{3}\)을 세 근으로 갖는 3차 방정식은 2항 방정식
\[z ^{3} -t=0\]가 되어 세 근 \(z _{1}, z _{2}, z _{3}\)은 \(t\)의 세제곱근들임을 알 수 있다. 이제 (식3)에 이를 대입하고 2차 방정식을 풀어 \(y _{1} , y _{2}, y _{3}\)를 찾을 수 있다. 다시 이들에서 \(a _{1} /3\)을 빼면 원래 3차 방정식의 해가 된다.
같은 방법으로 \(n\ge4\)이면 치른하우스 변환들을 통해 (식1)은
\begin{equation} \tag{식4}
z ^{n} +b _{4} z ^{n-4} +b _{5} z ^{n-5} + \cdots +b _{n} =0
\end{equation}꼴로 바꿀 수 있다. 따라서 (식4)와 \(n-1\)차 이하의 방정식을 풀 수 있으면 임의의 \(n\)차 방정식을 다 풀 수 있음을 확인할 수 있다. 특히 \(n=4\)일 때, 3차 이하의 방정식과 2항 방정식
\[z ^{4} -t=0\]을 풀 수 있으면 모든 4차 방정식을 풀 수 있다. 따라서 사칙 연산과 거듭제곱근 \(\sqrt[m]{\phantom{x}}\) 들을 통해 4차 이하의 방정식을 모두 풀 수 있다. 이제 이런 질문을 던져보자.
질문: 임의의 \(n\)차 방정식 (식1)의 계수들 \(a _{1} ,a _{2} , \cdots ,a _{n}\)으로부터 사칙 연산과 거듭제곱근 \(\sqrt[m]{\phantom{x}}\)들만을 써서 (식1)의 근을 구할 수 있겠는가?
위에서 \(n\le4\)이면 이 질문의 답이 ‘예’임을 확인했다. 1824년 아벨은 5차 이상의 방정식에 대해서는 이 질문에 대한 답이 ‘아니오’임을 증명했고, 1832년 갈로와는 정확히 어떤 방정식이 이와 같은 방식으로 풀 수 있는지 없는지 밝혔다. 예를 들어, 실근을 3개만 갖고 유리수 위에서 더 이상 인수분해가 되지 않는 5차 방정식 \(2x ^{5} -5x ^{4} +5=0\)은 계수들로부터 사칙 연산과 거듭제곱근들만을 통해서는 근을 구할 수 없다.
이것이 끝인가? 좋은 문제는 한번 풀리지 않는다. 하나의 답은 다른 질문들을 낳고 이들에 답하는 과정에서 또 다른 질문을 낳고, 이 문제를 답하는 과정에서 원래 문제를 새로운 관점에서 볼 수 있게 되어 질문을 심화시키고 일반화시키는 선순환 과정을 만들어내는 것이 좋은 문제의 특징이다. 가장 먼저 떠오르는 질문: 왜 거듭제곱근만 사용하는가?
먼저 떠오르는 대답은 2항 방정식 \(x ^{m} -t=0\)의 근 \(\sqrt[m]{t}\)은 뉴턴의 방법으로 근사값을 쉽게 구할 수 있다는 것이다. 하지만 뉴턴의 방법으로 근사해를 구할 수 있는 다항식은 2항 방정식 말고도 많다. 예를 들어 \(x ^{5} +x-t=0\)꼴의 방정식도 그렇다. 이를 브링Bring 방정식이라고 부르는데 그 해인 브링 근호Bring radical \(B(t)\)은 테일러 전개
\begin{equation} \tag{식5}
x(t)=B(t):= \sum_{k\ge0}\binom{5k}{k} \frac{(-1) ^k t ^{4k+1} }{4k+1}
\end{equation}까지 알고 있으므로 근사값을 구하기에 좋다. 위에서 소개한 치른하우스 변환을 통해, 임의의 5차 방정식은
\begin{equation} \tag{식6}
z ^{5} +az+b=0
\end{equation}꼴로 바꿀 수 있고 따라서 이 방정식의 근과 사칙 연산, 거듭제곱근들만 있다면 모든 5차 방정식을 풀 수 있음을 안다. 다시 변환 \(z= \sqrt [4]{a} u\)을 작용하면 (식6)은 브링 방정식 \(u ^{5} +u-t=0\)이 되어 (식5)를 사용해 풀 수 있다. 따라서 사칙 연산, 거듭제곱근 \(\sqrt[m]{\phantom{x}}\)에다 브링 근호 \(B(t)\)까지 사용할 수 있다면 임의의 5차 방정식을 풀 수 있다. 거듭제곱근 \(t\mapsto\sqrt[m]{\phantom{x}}\)과 브링 근호 \(t\mapsto B(t)\), 둘 다 1변수 함수이므로 임의의 5차 방정식은 사칙 연산과, 1변수 함수들만을 써서 풀 수 있다.
이제는 6차 방정식을 생각해 보자. 1836년 해밀턴William Hamilton, 1805-1865은 위에서 소개한 치른하우스 변환을 통해 임의의 6차 방정식과 7차 방정식은 각각
\begin{equation} \tag{식7}
z ^{6} +az ^{2} +bz+1=0, \qquad z ^{7} +az ^{3} +bz ^{2} +cz+1=0
\end{equation}꼴로 쓸 수 있음을 보였다. 미적분학 시간에 배우는 음함수 정리에 의해 이 방정식의 (중근이 아닌) 근들은 각각 해석적 함수 \(z=H _{6} (a,b), z=H _{7} (a,b,c)\)로 주어진다. 특히 이렇게 다항식의 근으로 주어지는 해석적 함수를 대수적 함수라고 부르자. 따라서 임의의 6차 방정식은 사칙 연산, 거듭제곱근 함수들 \(t\mapsto\sqrt[m]{\phantom{x}}\)과 1변수 대수적 함수 \(B(t)\), 2변수 대수적 함수 \(H _{6} (a,b)\)만을 사용하여 풀 수 있다. 같은 이유로 임의의 7차 방정식은 사칙 연산, 거듭제곱근 함수들 \(t\mapsto\sqrt[m]{\phantom{x}}\)과 각각 1, 2, 3변수 대수적 함수 \(B(t)\), \(H _{6} (a,b)\), \(H _{7} (a,b,c)\)만을 사용하여 풀 수 있다. 여기서 힐버트가 1900년 세계수학자대회에서 행한 기념비적 연설을 통해 제시한 23개의 문제 중 13번째 문제와 1927년 후속논문에서 제시한 추측들이 나온다.
힐버트의 6차 방정식 추측(1927): 임의의 6차 방정식을 사칙 연산과 1변수 대수적 함수들만으로 푸는 해법(알고리즘)은 존재하지 않는다.
힐버트의 13번째 문제(1900): 임의의 7차 방정식을 사칙 연산과 1변수 또는 2변수 대수적 함수들만으로 푸는 해법은 존재하지 않는다.
힐버트의 8차 방정식 추측(1927): 임의의 8차 방정식을 사칙 연산과, 1변수 또는 2변수 또는 3변수 대수적 함수들만으로 푸는 해법은 존재하지 않는다.
이 세 문제 모두 현재까지 완전히 미해결이다. 사칙 연산과 \(r\)개 이하 변수의 대수적 함수들만으로 일반적인 \(n\)차 방정식 (식1)의 근을 찾을 수 있는, 가장 작은 자연수 \(r\)을 분해 차수resolvent degree \(RD(n)\)라고 부른다. 위에서 우리가 확인한 해법으로부터 \(2\le n \le 5\)이면 \(RD(n)=1\)이고, \(RD(6)\le2, RD(7)\le3\)임을 알 수 있다. 힐버트의 세 추측을 분해 차수로 표현하면
\[RD(6)=2,\quad RD(7)=3, \quad RD(8)=4\]
라고 쓸 수 있다. \(n\)이 커질 때 \(RD(n)\)이 무한대로 발산하는지도 많은 사람들이 궁금해한다. 치른하우스 변환을 쓰거나 기하학적인 방법으로 \(RD(n)\)의 상한값을 주는 여러 방법이 있으나 어느 누구도 자명하지 않은 하한값을 찾지 못했다. 이 추측들이 중요한 이유는 자체로 흥미롭기도 하면서, 기하학과 수론에서 제기되는 자연스러운 문제들을 해결하게 해준다는 점에 있다. 예를 들어 3차 다항식에 의해 정의되는 3차 곡면에는 27개의 직선이 존재하는 것이 알려져 있는데 구체적으로 이들을 찾는 알고리즘을 힐버트의 6차 방정식 추측 \(RD(6)=2\)을 통해 얻을 수 있다. 20세기 후반 발달한 대수기하학과 모듈라 함수modular function의 이론을 통해, 힐버트의 추측들과 동등한 다른 명제들은 많이 발견되었으나2 아무도 힐버트의 추측 자체는 해결하지 못하고 있다.
힐버트가 1900년 23개의 문제를 제시할 당시, 13번째 문제를 해결하는 방법으로 다음과 방법을 제안했다. 앞에서 임의의 7차 방정식은 사칙 연산, 거듭제곱근 함수들 \(t\mapsto\sqrt[m]{\phantom{x}}\)과 대수적 함수 \(B(t)\), \(H _{6} (a,b)\), \(H _{7} (a,b,c)\)만을 써서 풀 수 있다고 했으므로, 힐버트의 13번 문제는 3변수 대수적 함수 \(H _{7} (a,b,c)\)를 1변수 또는 2변수 대수적 함수들의 합성으로 표현할 수 있는지 물어보는 것이 된다. 힐버트는 이것이 불가능하다고 믿었는데 심지어 더 너그럽게 대수적 함수뿐만 아니라 연속함수들을 사용해도 안 될 것이라고 생각했다.
놀랍게도 1957년 모스크바의 수학자 콜모고로프Andrey Kolmogorov, 1903-1987와 아르놀트Vladimir Arnold, 1937-2010는 임의의 다변수 연속함수를 1변수 또는 2변수 연속함수들의 합성으로 쓸 수 있음을 증명하였다. 하지만 \(H _{7} (a,b,c)\)를 1변수 또는 2변수 대수적 함수들의 합성으로 쓸 수 있는지는 아직까지도 알려져 있지 않으므로 힐버트의 13번째 문제가 해결된 것은 아니다.
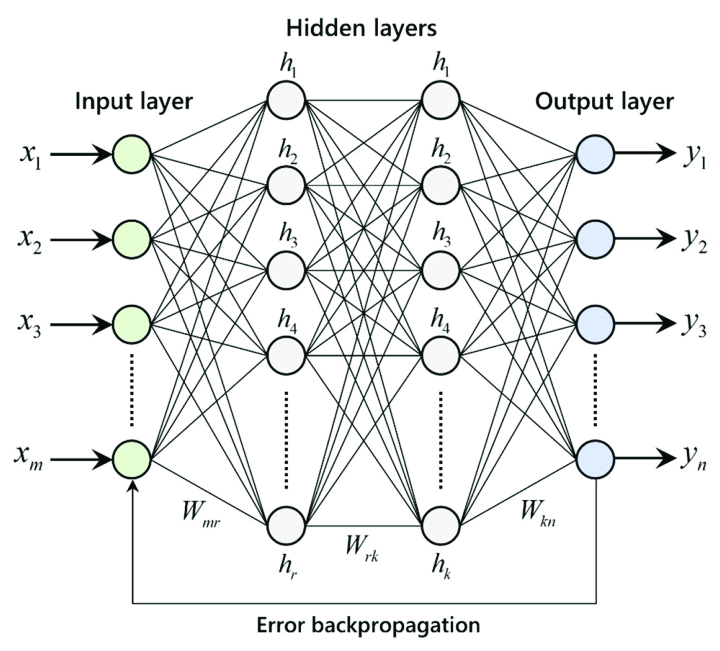
콜모고로프와 아르놀트의 결과는 간단한 함수들을 합성하고 사칙 연산을 작용하는 것을 반복하여 엄청나게 큰 함수 공간을 건설할 수 있음을 보여주는 충격적인 사실이다. 최근 딥러닝을 통한 인공지능 기술이 큰 성공을 거두고 있는데 그 근간을 이루는 사실은 선형 함수(사칙 연산)와 간단한 비선형함수 하나(활성화 함수, 예를 들어 ReLU나 Sigmoid)를 합성하는 것을 반복하여 얻는 신경망 모델이 모든 연속함수들을 얼마든지 가깝게 근사시킬 수 있다는 정리이다.3 힐버트의 13번째 문제의 잔향은 수학을 넘어 첨단의 인공지능에 이르기까지 진한 베이스음으로 울리고 있다.