룬샷loon shots은 “제안자를 나사 빠진 사람으로 취급하며 다들 무시하고 홀대하는 프로젝트, 그러나 전쟁, 의학, 비즈니스의 판을 바꾼 아이디어”1를 말한다. 정말 혁신적인 아이디어는 의심받고 거부당하기 쉽다. “적어도 세 번은 죽었다가 살아나야” 인정을 받지만 결국엔 커다란 변화를 이끌어 내는 아이디어나 프로젝트가 바로 룬샷이다. 평화롭고 질서 있는 수학의 세계에는 안 어울리는 표현처럼 들리지만, 이제 살펴볼 슈베르트Schubert 계산법처럼 학계에 받아들여지는 데 200년이 걸리고 그 과정을 통해 위상수학, 대수기하학, 물리학을 넘어 인류사의 가장 빛나는 성취들을 엮어낸 기념비적인 룬샷도 있다.
주어진 1변수 \(n\)차 방정식은 (중근을 감안하여 세면) \(n\)개의 (복소수) 근을 갖는다. 정확한 근들을 구할 수는 없지만 근의 개수는 말할 수 있다. 왜 그런가? 대수학의 기본 정리는 1변수 \(n\)차 다항식 \(f(x)\)의 근이 복소수 집합에서 반드시 존재함을 보장한다. 이제 근 하나를 \(\alpha\)라고 하면 주어진 다항식은 \(f(x) = (x-\alpha)g(x)\) 꼴로 쓰여야 하는데 \(g(x)\)는 차수가 하나 낮으므로 수학적 귀납법에 의해 이미 \(n-1\)개의 근을 갖는다고 말할 수 있다. 여기에 \(\alpha\)를 보태면 \(n\)차 다항식 \(f(x)\)는 \(n\)개의 근을 가짐을 알 수 있다. 이와 같이 정확히 해를 찾을 수는 없더라도 그 개수는 알아낼 수 있는 경우가 많이 있다.
질문1. 평면상에 주어진 일반적인 \(m\)차 곡선과 \(n\)차 곡선은 몇 개의 점에서 만나는가?
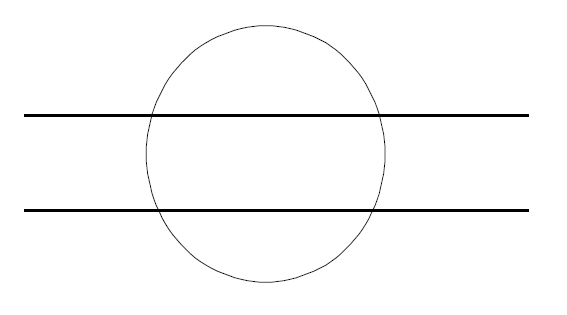
여기서 \(m\)차 곡선이란 \(m\)차 다항식에 의해 주어진 곡선을 말한다. 예를 들어 원은 2차 다항식 \(x^2+y^2-1\)을 0으로 만드는 점들의 집합이므로 2차 곡선이다. 타원이나 포물선, 쌍곡선도 모두 2차 곡선이다. \(y^2 = x(x^2-1)\), \(x^4+y^4=7\)을 만족하는 점들의 집합은 각각 3차와 4차 곡선이다. 뉴턴이 1687년 출판한 “자연철학의 수학적 원리”에 적었듯이 질문1의 답은 \(mn\)이다. 예를 들어 타원 2개가 만나는 것을 생각해보자.
\(\epsilon x^{ 2 }+y^{ 2 }=1\quad (\epsilon \to 0)\\ x^{ 2 }+y^{ 2 }=4\)
타원 중 하나는 그대로 두고 나머지 하나의 방정식의 계수들을 아주 조금 바꾸면 어떻게 되겠는가? 타원은 아주 조금만 움직일 것이고 두 타원의 교점들도 아주 조금 움직이되 그 개수는 변하지 않을 것이다. 교점들이 연속적으로 변하되 교점의 개수가 불변이도록, 아주 조금씩 타원의 방정식의 계수들을 계속 움직여서 원래의 2차 다항식이 1차 다항식 둘의 곱으로 인수분해 되도록 할 수 있다.
이제 다른 타원의 방정식도 연속적으로 변화시켜 1차식의 곱으로 분해되게 하자.
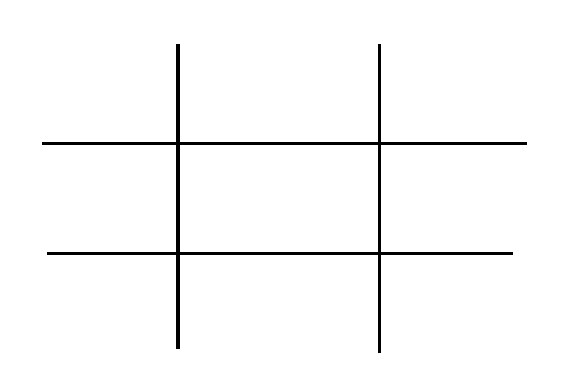결국 2개의 직선과 2개의 직선이 만나는 상황이 되고 그 과정에서 만나는 점의 수는 바뀌지 않는다. 같은 방법으로 \(m\)차 곡선과 \(n\)차 곡선은 연속적으로 변화시켜 \(m\)개의 직선과 \(n\)개의 직선으로 바꿀 수 있고 그 과정에서 만나는 점의 수는 불변이도록 할 수 있다. (일단 믿자.) 물론 \(m\)개의 직선과 \(n\)개의 직선은 \(mn\)개의 점에서 만나므로 질문1의 답은 \(mn\)이 된다.
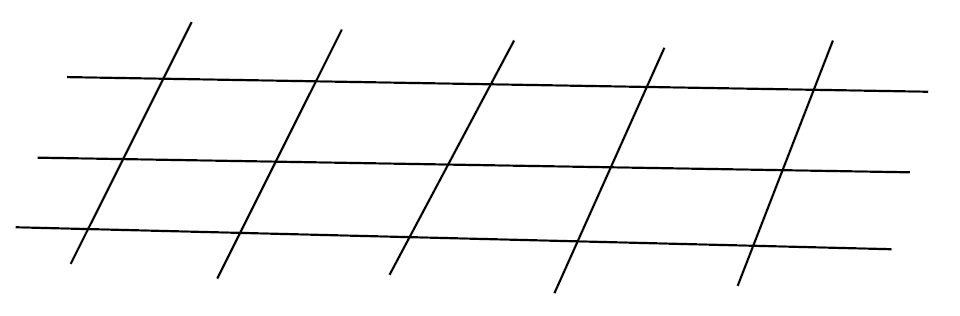
1823년 퐁슬레Jean-Victor Poncelet가 연속성 원리principle of continuity라고 부른 이 방법을 엄밀히 정당화하려면 사실 상당한 노력이 필요한데, 1930년대에 와서야 여기에 필요한 수학적 장치들이 완비되었다.
공간에서의 기하학적인 문제도 생각해보자.
질문2. 3차원 공간에 4개의 직선이 주어졌다. 4개의 직선과 모두 만나는 직선은 몇 개인가?
물론 4개의 직선 \(\ell_1,\ell_2,\ell_3,\ell_4\)가 모두 동일 평면에 놓여있는 경우처럼 주어진 4개의 직선과 만나는 직선이 무한히 많은 특수한 경우는 배제하고, 유한개의 직선만 4개의 직선과 모두 만나는 상황을 생각하는 것이다. 4개의 직선들과 모두 만나는 직선이 몇 개 있는 것을 머릿속에 상상해 보자. 이제 4개의 직선들을 연속적으로 조금씩 움직여 보자. 4개의 직선과 모두 만나는 직선도 함께 연속적으로 움직인다. 즉 이들의 수는 변하지 않는다. (연속성 원리: 일단 믿음으로 받아들이자.) \(\ell_1\)이 \(\ell_2\)와 만나고 \(\ell_3\)가 \(\ell_4\)와 만날 때까지 계속 움직이자.
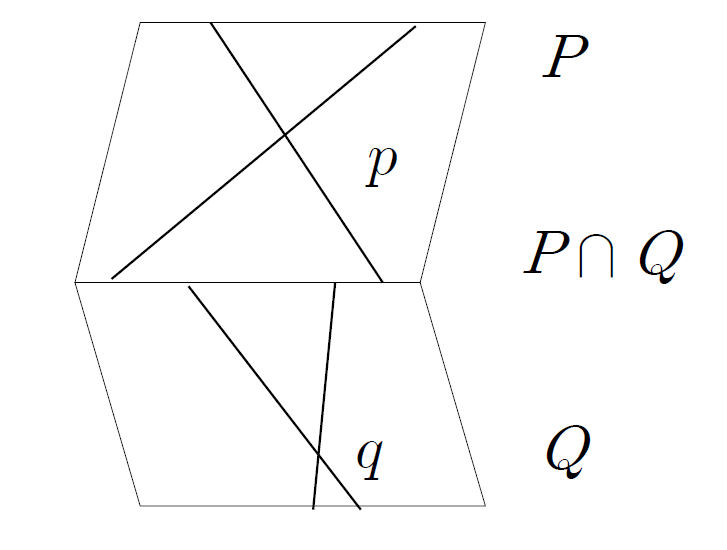
이제 \(\ell_1\)과 \(\ell_2\)를 포함하는 평면을 \(P\), \(\ell_3\)와 \(\ell_4\)를 포함하는 평면을 \(Q\), \(\ell_1 \cap \ell_2 = p\), \(\ell_3 \cap \ell_4 = q\)라고 두면, \(\ell_1,\ell_2,\ell_3,\ell_4\)와 모두 만나는 직선은 \(p,q\)를 잇는 직선 \(\overline{pq}\)와 두 평면의 교집합 \(P\cap Q\)뿐으로, 정확히 2개임을 알 수 있다.
위와 같은 퐁슬레Poncelet의 연속성 원리는 엄밀한 수학적 토대가 부족하였으므로 많은 공격을 받았다. 1848년 슈타이너Jakob Steiner는 아폴로니우스의 문제(평면상의 3개의 원이 주어졌을 때 이들과 모두 접하는 원은 몇 개인가?2)를 확장하여 다음과 같은 질문을 던졌다.
질문3. 평면상의 2차 곡선 중에서 주어진 5개의 2차 곡선과 모두 접하는 것은 몇 개인가?
왜 4개도 아니고 6개도 아닌, 5개의 2차 곡선인가? 4개의 2차 곡선과 모두 접하는 2차 곡선은 무한히 많고 일반적인 6개의 2차 곡선과 모두 접하는 2차 곡선은 없기 때문이다. 그 이유는 2차 곡선들의 집합이 5차원이고 접하는 조건 하나마다 차원을 하나씩만 떨어뜨리기 때문이다. 1864년 샬Michel Chasles은 올바른 답인 3264를 제시하였는데 그 계산이 매우 흥미롭다.
19세기 중반 수학자들은 새로운 대수적 구조의 발견에 커다란 매력을 느꼈다. 예를 들어 불George Boole은 논리적인 추론 과정을 and, or, not 등을 기본 단위로 하는 대수algebra 3로 표현할 수 있음을 발견하였다. 모든 수학의 흥미로운 발견들이 그렇듯이 순수한 학문적 호기심에서 출발한 불Boole의 대수는 뜻하지 않은 부산물을 낳았는데, 불Boole 대수를 트랜지스터를 통해 전기회로로 구현한 것이 현대적인 컴퓨터이며 이를 통해 3차와 4차 산업혁명이 촉발된 것은 주지의 사실이다. 샬Chasles은 이러한 대수적 구조 발견의 시대를 살고 있었다. 그는 기하학적 조건 또는 이를 만족하는 부분집합들의 대수를 생각했는데 이들의 합집합은 덧셈, 교집합은 곱셈, 연속적으로 변화시켜 얻는 것들에는 같은 기호를 대응시켜 대수적 연산으로 질문3의 답을 구하고자 하였다. 그 풀이를 살펴보자.
2차 다항식이 인수분해가 되면 1차 다항식의 곱이므로 대응되는 2차 곡선은 2개의 직선의 합집합이다. 먼저 연속성 원리를 믿고 사용하여 5개의 2차 곡선이 각각 직선의 쌍 \(\ell_i\cup\ell_i’\) (\(i=1,2,\cdots,5\), \(\ell_i\cap\ell_i’=p_i\))인 경우만 생각하면 된다. 2차 곡선 중 주어진 한 직선에 접하는 것들의 집합을 기호 \(\mu\), 한 점을 지나는 것들의 집합을 기호 \(\nu\)라고 쓰자. \(\ell_i\cup\ell_i’\)에 접한다는 것은 \(\ell_i\)에 접하든지 \(\ell_i’\)에 접하든지 \(p_i\)를 지나든지, 셋 중 하나를 만족시킨다는 뜻이다. 샬Chasles은 이를 기호로 \(2\mu+2\nu\)라고 썼다. 5개의 2차 곡선에 대해 접해야 하므로 교집합을 생각해야 하고 기호로는
\((2 \mu +2 \nu ) ^{5} =32( \mu ^{5} +5 \mu ^{4} \nu +10 \mu ^{3} \nu ^{2} +10 \mu ^{2} \nu ^{3} +5 \mu \nu ^{4} + \nu ^{5} )\)
라고 썼다. 그다음 각각의 항을 직관과 경험에 의해 계산하여
\(\mu ^{5} = \nu ^{5} =1, \quad \mu ^{4} \nu = \mu \nu ^{4} =2,\quad \mu ^{3} \nu ^{2} = \mu ^{2} \nu ^{3} =4\)
임을 찾았다. 예를 들어 \(\nu ^{5}\)은 일반적으로 주어진 5개의 점을 모두 지나는 2차 곡선의 수로서 1이고, \(\mu \nu ^{4}\)는 주어진 4개의 점을 지나며 1개의 직선에 접하는 2차 곡선의 수로서 2이다. 이로부터 질문3의 답
\((2 \mu +2 \nu ) ^{5} =32(1+5\cdot 2+10\cdot 4+10\cdot 4+5\cdot 2+1)=32 \times 102=3264\)
를 얻었다. 지금은 명확한 의미가 있는 엄밀한 계산이지만, 당시로써는 이러한 신비로운 계산은 수학적 근거가 부족한 것이었기 때문에 당대의 맹렬한 비난을 피할 수 없었다. 하지만 그 마력은 거부하기 어려웠는데, 다른 방법으로 접근도 못 하는 문제들에 대해 신비로운 계산법이 착착 답을 주었기 때문이었다. 현대에서는 아마도 양자장 이론의 경로적분이 이와 같은 경우가 아닌가 싶다. 왜 작동하는지 아무도 수학적으로 설명하지는 못 하지만 답은 착착 내놓는데 그 유혹을 어찌 이겨낸단 말인가? 하지만 기다리시라. 몇백 년이 걸릴지라도 결국 수학자들은 올바른 답을 찾아낼 것이다. 수학의 위대한 역사와 전통이 이를 웅변하고 있으니.
샬Chasles의 신비로운 풀이의 마법에 빠져버린 슈베르트Hermann Schubert는 이 방법을 다양한 상황으로 확대하고 또 효율적인 계산법도 정립하였다. 슈베르트Schubert의 방법을 쓰면 예를 들어 3차 곡면(3차식에 의해 정의되는 곡면)은 반드시 27개의 직선을 포함한다든지, 2차 곡면 중에서 주어진 9개의 2차 곡면에 모두 접하는 것은 666,841,048개 있다든지 하는 식의 계산을 할 수 있다. 슈베르트Schubert는 맨손으로 계산하여, 3차원 공간에 포함된 3차 유리 곡선twisted cubic curves 중에서 주어진 12개의 2차 곡면에 접하는 것은 정확히
\(5,819,539,783,680\)
개 있음을 얻었고(이 결과로 1875년 덴마크 왕립 아카데미로부터 금메달을 수상했다), 이는 100여 년이 지난 1980년대 말에 와서야 엄밀한 수학으로 확인되었다. 힐버트의 15번째 문제는 바로 이러한 슈베르트Schubert의 마법을 과학의 영역으로 끌어올리려는 것이다.
힐버트의 15번째 문제4 슈베르트Schubert가 연속성 원리에 기반하여 얻은 기하학적 수들을 엄밀히 입증하고 그의 계산법의 유효성과 한계를 확립하라.
연속성 원리는 푸앵카레Henri Poincare와 렙셰츠Solomon Lefschetz가 위상수학을 창안하는 동기를 부여했고5, 판데르바르던Bartel van der Waerden은 결국 1930년경 샬Chasles과 슈베르트Schubert의 기호들을 렙셰츠Lefschetz의 호몰로지 류homology classes로 해석하고 이들에 관한 엄밀한 이론을 발전시킴으로써 수학적 정당성을 확보했다. 이후 에레스만Charles Ehresmann과 호지W.V.D. Hodge는 (그라스만 다양체Grassmannian의 코호몰로지 환의 구조를 밝혀) 슈베르트Schubert의 효율적인 계산법을 정밀한 과학의 품에 안겼다.
여기서 끝인가? 좋은 문제는 한 번 풀리지 않는다. 1940년대 이래 대수기하학의 엄밀한 토대가 베유Andre Weil, 초우Wei-Liang Chow, 자리스키Oscar Zariski, 세르Jean-Pierre Serre, 그로텐디크Alexander Grothendieck 등에 의해 확립되었고 대수적인 호몰로지 이론이 발견되었다. 이를 바탕으로 1978년 풀턴William Fulton과 맥퍼슨Robert MacPherson이 위상수학을 추방하고 완전히 대수적으로 샬Chasles과 슈베르트Schubert의 계산법을 정립하였다. 19세기 후반의 룬샷인 슈베르트Schubert 계산법이 20세기 말에 와서 화려하게 수학의 본류로 자리 잡게 된 것이며 그 과정에서 발달한 모듈라이 이론과 교차 이론은 현대 수학의 가장 위대한 성취 중의 하나로 손꼽힌다.
위상수학적으로 해결했으면 됐지, 왜 대수기하학적인 이론이 필요했을까 궁금하지 않은가? 그 답은 1990년대부터 30년을 이어오는 초끈이론과 대수기하학의 환상적인 교류를 보면 알 수 있다. 대수기하학의 장점 중의 하나는 특이점을 잘 다룬다는 데 있다. 초끈 이론에서 필요로 하는 모듈라이 공간들은 대부분 극도로 복잡한 특이점을 지니는데 대수기하학적 방법이 아니면 접근할 도리가 없다. 풀턴Fulton과 맥퍼슨MacPherson의 교차이론은 가상교차이론으로 업그레이드 됐고 그 과정을 통해 다시 대수기하학 내에서 이전에는 꿈도 못 꾸던 문제들이 잇달아 해결되었다.6 최근에는 K-이론, 코보디즘, 모티빅 코호몰로지, 유도 범주 등의 상황으로 계속 업그레이드 되는 중이며 맹렬한 연구가 이루어지고 있다.
힐버트의 15번째 문제의 시제는 여전히 현재진행형이다.
