2020년 아벨상 수상자 그레고리 마굴리스

On the work of Gregory Margulis

2020년 그레고리 마굴리스^{Gregory Margulis} 예일대 교수는 힐렐 퍼르스텐버그^{Hillel Furstenberg} 히브리대 명예교수와 함께 확률론과 동역학의 새로운 응용, 특히 군론, 정수론과 조합론에의 응용을 개척한 공로로 아벨상을 공동 수상하였습니다. 본 글에서는 마굴리스의 아벨상 수상을 기념하며 마굴리스의 수학적 업적에 대해 음미해보고자 합니다.

오펜하임 추측 

변수 \(x,y,z\)에 대한 방정식

\(Q(x,y, z)=x^2 + y^2 -z^2=0\)

을 생각해 봅시다. (\(Q\)와 같이 모든 단항들이 2차인 다항식을 우리는 이차형식이라 부르겠습니다.) 이 방정식은 \((0,0,0\)) 외의 정수 벡터 해를 가질까요?

중학교에서 배우듯이 정수 길이의 선분으로 이루어진 직각삼각형의 세 변의 길이 \((3,4,5)\), \((5,12,13)\) 등 피타고라스 공식을 만족하는 정수 벡터는 위의 이차 형식의 해가 되고, 피타고리안 트리플^{Pythagorean triple}이라 불리는 이러한 해는 무한히 많습니다. 그러면 이제 또 다른 이차형식

\(Q(x,y,z)=x^2 + y^2 – \sqrt{2}z^2\)

에 대해서는 어떨까요? 이 이차형식도 \((0,0,0)\) 외의 정수 벡터해를 가질까요? 물론 아닙니다. 그럼 해가 없으니 0에 한없이 가까운 \(Q(x,y,z)\) 값을 갖는 정수 벡터 \((x,y,z)\)를 찾을 수 있을까라는 질문을 할 수 있겠죠.

오펜하임^Oppenhiem이 무려 1920년대에 내놓은 이 추측은 50여 년이 지난 후에야 그레고리 마굴리스^{Gregory Margulis}에 의해 증명되었습니다. 마굴리스는 변수가 3개 이상인 임의의 부정부호 무리형식 \(Q\)(유리 형식의 상수배가 아닌 형식이면서 양의 값과 음의 값을 모두 갖는 이차형식)에 대해 정수 벡터들 \((x,y,z)\)에 대한 이차형식의 값 \(Q(x,y,z)\)을 모으면 실수 집합에서 조밀하다는 것을 보였습니다. 즉 어떤 실수 \(a\)와 오차 \(\epsilon>0\)이 주어져도, 그보다 오차가 작은, 즉 \(|Q(x,y,z)-a|<\epsilon\)인 정수벡터 \((x,y,z)\)가 존재함을 보였죠.¹ 

마굴리스는 이러한 이차 형식을 하나씩 개별적으로 생각하는 대신 이차형식들을 모두 모아놓은 집합을 어떤 공간으로 생각하였습니다. 각각의 이차형식은 이 공간에서 하나의 점이 되고, 이 점이 어떤 흐름^flow에 의해 따라가는 궤도를 살펴보고 위의 오펜하임 추측을 증명하였습니다. 이렇게 주어진 공간에서 궤도의 성질에 대해 연구하는 분야를 동역학이라 하고, 그 공간이 특별히 균질 공간^{homogeneous spaces}일 때는 균질 동역학^{homogeneous dynamics}이라 하죠. 이제 이러한 균질 동역학에 대해 알아볼까요?

군의 작용과 동역학

전통적으로 동역학이나 에르고딕 이론에서는 공간 \(X\)의 한 점 \(x\)를 잡고, 주어진 부피 보존 함수(사상) \(T : X \to X\)에 의한 점의 궤도 \(\{ x, T(x), T\circ T(x), \cdots \}\)에 관한 성질들을 연구해 왔습니다. 그중 가장 기본적인 성질은 에르고딕성^ergodicity으로, 거의 모든 점에 대해 한 점의 궤도가 공간을 점점 가득 채우게 된다는 성질입니다. (즉 공간을 가득 채우지 않는 궤도를 가지는 점들이 있을 수는 있으나, 그러한 점들을 모아봤자 부피 \(m\)이 0이라는 것입니다.)² 다음 식과 같이 시간 평균이 공간 평균으로 수렴한다고 표현하기도 하죠.

\(\frac{1}{N} \sum_{k=0}^{N-1} f(T^k x) \to \int f dm.\)

에르고딕성보다 더 강한 성질로는 섞임이 있습니다. 거의 모든 점의 각각의 궤도가 점점 고르게 분포하게 되면 섞임^mixing이라고 합니다. 식으로 표현하면 모든 잴 수 있는 집합 \(A,B\)에 대하여 \(n\)이 무한대로 갈 때,

\(m(A \cap T^{-n}B) \longrightarrow m(A) m(B)\)

인 성질로, 고른 분포, 혹은 점근적 독립성^{asymptotic independence} 으로도 이해할 수 있지요.³ 

이제 위의 \(T\)와 같은 부피 보존 사상 하나의 궤도를 생각하는 대신, 여러 사상들의 집합 \(G\)에 대한 궤도를 생각합니다. 만약 \(G\)가 함수의 합성에 대해 군^group을 이루고 그 군의 합성이 사상과 잘 어울리면⁴ 군 \(G\)가 공간 \(X\)에 작용한다고 합니다. 전통적으로 보아온 사상 하나 혹은 흐름^flow 5에 대한 연구는 군이 각각 정수집합 \(\mathbb{Z}\), 실수집합 \(\mathbb{R}\)인 경우입니다.

정수론의 문제를 대칭공간의 문제로

마굴리스가 글의 초반에 언급한 오펜하임 추측을 해결하기 위해 이용한 군은 무엇이었을까요? 바로 부피를 보존할 뿐 아니라 이차형식을 보존하는 행렬들의 모임이었습니다. 가령 \(Q_0=x^2+ y^2 – z^2\)라면, \(xy\)-평면 위의 회전은 \(Q_0\)를 보존하지요. 그러면 이 군은 어떤 공간에 작용하는 것일까요? 여기서 공간은 앞에서 언급했던 이차형식들의 집합과 깊은 연관이 있어야겠죠. 그런데 부호가 \((2,1)\)인 모든 이차 형식 \(Q\)는 \(Q_0\)에 어떤 행렬을 합성해준 것과 같습니다. 만약 변수가 3개인 이차형식이라면 \(Q(x,y,z) = \lambda Q_0((g(x,y,z)^t)^t)\)인 행렬식이 1인 \(3 \times 3\) 행렬 \(g \in SL_3(\mathbb{R})\)와 상수 \(\lambda\)가 존재합니다.

한편 우리는 \(Q(\mathbb{Z}^3)\) 집합 전체에 관심이 있으므로 \(SO(Q_0) g SL_3(\mathbb{Z})\)를 생각해도 무방하겠지요. 즉 \(Q(\mathbb{Z}^3) =\)\( Q(SO(Q_0) g SL_3(\mathbb{Z})\mathbb{Z}^3)\)라는 사실을 쓸 수 있습니다. 따라서 우리는 \(SO(Q_0) g SL_3(\mathbb{Z})\)를 \(g SL_3(\mathbb{Z})\)라는 “점”의 \(H=SO(Q_0)\) 궤도로 생각할 수 있고, 이때 공간은 바로 \(X=SL_3(\mathbb{R})/SL_3(\mathbb{Z})\)가 됩니다.

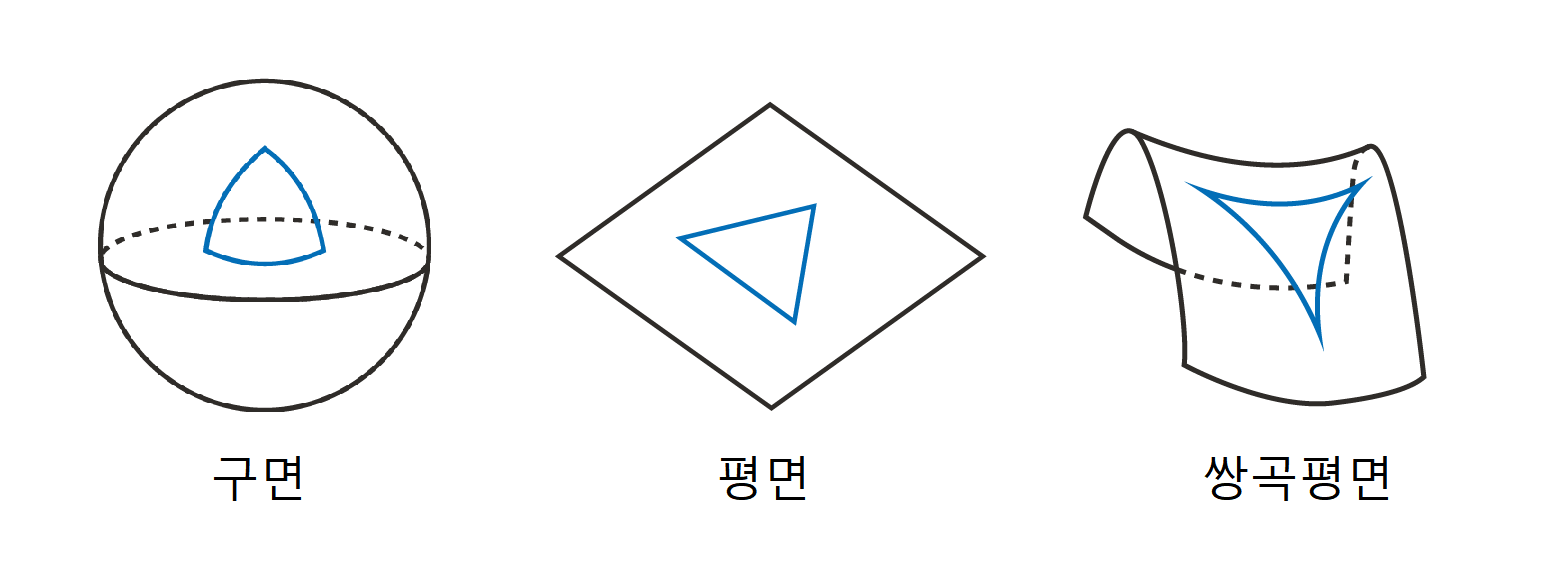
자, 그러면 이제 공간 \(X=SL_3(\mathbb{R})/SL_3(\mathbb{Z)}\), 더 일반적으로 \(SL_n(\mathbb{R})/SL_n(\mathbb{Z)}\)은 어떻게 생긴 공간일까요? 이 공간은 쌍곡곡면인 모듈라 공간^{modular surface} \(\mathbb{H}^2/SL_2(\mathbb{Z})\)과 놀랍도록 비슷하게 생겼습니다. 쌍곡평면은 곡률이 \(-1\)인 평면으로, 곡률이 \(0\)인 유클리드 평면, 곡률이 \(1\)인 구면과 함께 곡률이 음, 영, 양인 곡면들의 기본적인 모델 중 하나입니다.

쌍곡평면에서는 주어진 직선에 평행하고 한 점을 지나는 직선이 유일하다는 유클리드의 평행선 공리가 성립하지 않지요. 그리고 서로 만나지 않는 직선들⁶이 기하급수적으로 멀어지거나 가까워집니다. 위에서 “놀랍도록” 비슷하다는 표현을 썼지만, 사실 쌍곡평면에 작용하는 군을 하나 알면 자연스러워 보일 수도 있습니다.

쌍곡평면 \(\mathbb{H}^2\)에는 \(SL_2(\mathbb{R})\), 즉 행렬식이 1인 \(2\times 2\) 행렬들이 거의 추이적^transitive으로 작용을 하죠. 더 나아가 쌍곡평면 위의 단위 접벡터들의 모임에는 단순 추이적으로 작용합니다.⁷ 따라서 쌍곡평면의 단위접벡터를 모아놓은 공간인 단위 접다발^{unit tangent bundle}은 \(SL_2(\mathbb{R})\)과 동일시할 수 있죠. 이제 \(X=\)\(SL_3(\mathbb{R})/SL_3(\mathbb{Z})\)는 \(SL_2(\mathbb{R})/SL_2(\mathbb{Z})\)와 유사할 테니 모듈라 곡면과 유사하다는 것도 자연스러워 보이지요?

한편 \(X = SL_n(\mathbb{R})/SL_n( \mathbb{Z})\)를 \(\mathbb{R}^n\)의 격자들⁸의 “모듈라이”공간 moduli space of unimodular lattices로 볼 수도 있는데, 이러한 “공간을 모아놓은, 공간들의 집합”으로서의 공간에 대한 해석은 정수론의 문제들을 국소 대칭공간의 문제로 변환하는데 유용한 관점입니다. 이러한 관점을 이용하여 마굴리스는 스프린축 추측을 비롯하여 디오판틴 근사의 다양한 문제들을 해결했습니다.

리군의 격자부분군

위에서 본 \(SL(3,\mathbb{R})\)의 부분 집합 \(SL(3,\mathbb{Z})\)와 같이 이산적이면서 그 몫공간이 유한한 부피를 갖는 부분군을 격자부분군이라고 합니다. \(SL(3,\mathbb{Z})\)와 같이 \(SL(3,\mathbb{R})\)에서 계수를 정수만을 취함으로써 얻어지는 격자부분군을 특별히 산술군^{arithmetic group}이라고 합니다. 보렐^Borel과 하리슈-찬드라^{Harish-Chandra}는 산술 이론으로 이러한 산술군인 격자부분군을 건설하였었죠.

마굴리스는 거의 모든 일반적인 리군의 모든 격자부분군이 산술군이라는 것, 즉 대략적으로 말하자면 위와 같은 “정수점” 부분군이라는 셀버그의 추측^{Selberg’s conjecture}을 증명했습니다.⁹ 이를 마굴리스의 산술성 정리^{Margulis’ arithmeticity theorem}라 부릅니다.

1978년도에 마굴리스는 이러한 격자부분군의 구조를 정규부분군 정리^{Normal subgroup theorem}로 밝혀냈는데, 이 증명에서 그는 놀랍게도 랜덤보행^{random walk}, 오슬래대츠 정리^{Oseledets theorem}, 아미너블^amenability, 퍼스턴베르그 경계^{Furstenburg boundary} 등 확률론의 많은 개념들과 카즈단^Kazhdan의 property (T)를 이용하였습니다. 마굴리스는 또한 이와 같은 격자부분군의 표현^{representation}이 배경의 리군^{ambient Lie group}으로 확장될 수 있다는 초강성 정리를 보여 반단순 리군의 격자부분군에 대한 이론에서 혁명을 가져다주었습니다.

쌍곡 공간에서의 동역학

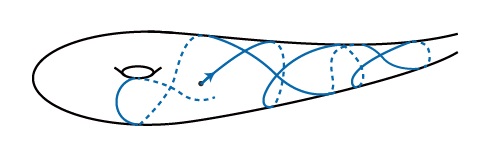
1970년 박사 학위 논문에서, 마굴리스는 음의 곡률을 가지는 옹골찬 리만 다양체에 대해 “보웬-마굴리스 측도”를 건설하였습니다. 마굴리스는 측도에 대한 측지선 흐름^{geodesic flow}의 섞임 성질^{mixing property}를 이용하여, 소수 정리의 기하학 버전인 “주어진 길이보다 같거나 작은 닫힌 측지선의 개수에 대한 점근적 공식을 증명하였습니다.

그전까지는 이러한 측지선의 개수와 관련된 유일한 결과는 셀버그의 대각합 공식 ^{Selberg’s trace formula} 뿐이었는데, 이 공식은 국소적 균질 공간에서만 성립하죠.

그 후로, 마굴리스의 혼합 성질 방법론을 이용하여 다양한 종류의 고른 분포 문제가 해결되었습니다. 예를 들어 위에서 살펴본 오펜하임 추측과 관련하여 마굴리스는 에스킨^Eskin, 모제스^Mozes와 함께 이차형식을 보존하는 부분군 안에 들어있는 대각행렬의 흐름^{diagonal flow}의 섞임 성질을 이용하여 보다 정교한 질문인 이차형식의 값이 \(a,b\) 사이이고 크기가 \(T\) 이하인 정수 벡터의 갯수 \(N_{[a,b]}(Q,T)\)를 구하였습니다. 이차형식이 5차 이상이면(4차인 경우에는 이차형식의 디오판틴 성질이 예외적이지 않으면) \(T\)가 무한대로 감에 따라

\(N_{a,b}(Q,T) \longrightarrow (b-a) c_Q T^{n-2}\)

가 되지요.

그래프 이론

그래프 이론에서 마굴리스의 창의성은 1973년에 카즈단 (T) 성질^{Kazhdan property (T)}을 이용하여 최초로 구체적인 익스팬더 그래프^{family of expanders}의 예를 건설하는 데에서도 나타났습니다. 익스팬더 그래프는 매우 높은 연결성을 가지는 그래프들의 모임입니다. 핀스커^{Mark Pinsker}에 의해 창안되었던 이 개념은 통신시스템 네트워크 연구에서 가져온 것이며 이제는 컴퓨터 과학과 오류 수정 코드에서 기본적인 도구로 이용되고 있습니다. 1988년에 마굴리스는 최적의 익스팬더류를 건설하였고, 루보츠키, 사낙, 필립스에 의해 독립적으로 건설된 이 그래프군은 라마누잔 그래프로 불립니다.

마굴리스의 생애와 수학적 결과들

마굴리스는 1946년 모스크바에서 태어났습니다. 16살에 국제 수학올림피아드 은상을 수상하고, 24살에 모스크바 대학에서 시나이(2014년 아벨상 수상자)의 지도하에 박사학위를 받는 등 마굴리스의 수학적 재능은 일찍부터 눈에 띄었습니다.

20대 초반에 쓴 학위 논문에서 마굴리스가 건설한 보웬-마굴리스 측도는 쌍곡공간의 새로운 기하적인 성질을 알려주었습니다. 그의 이러한 방법론은 후에 수많은 수학자들에게 영감을 주었고, 매우 활발한 연구 분야와 새로운 질문들을 불러 일으켰습니다.

마굴리스는 20대부터 소련 최고의 젊은 수학자로 유명했지만, 당시 소련의 반유대주의 정책으로 인해 대학에서 일자리를 찾지 못하고 정보 전송 문제 연구소^{Institute for problems in information transmission}에서 일했습니다. 그러나 그 와중에도 마굴리스는 위에서 기술한 (연구소에서 접한 문제인 정보 전송과 관련된) 익스팬드 그래프를 건설하였고, 이는 후에 마굴리스의 가장 대표적인 업적 중 하나이자 다른 분야에 지대한 영향을 준 업적이 되었습니다.

1978년, 겨우 32세의 나이에 그는 산술 정리^{Arithmeticity theory}와 초강성 정리^{Superrigidity theorem}로 필즈 메달을 받았습니다. 초강성 정리의 증명은 매우 강력한 방법론으로 에르고딕 이론의 새로운 응용을 보여주었는데, 이러한 방법론은 훗날 다양한 분야에 지대한 영향을 끼쳤습니다. 티츠^{Jacques Tits}(2008년 아벨상 수상자)는 마굴리스가 필즈 메달을 수상했을 때 “마굴리스는 전혀 손에 닿지 않을 것만 같은 문제들을 해결하여 해당 분야의 전문가들을 여러 번 놀라게 하였다”고 하였습니다.

그러나 그는 반유대주의로 소련 당국이 비자를 거부하여 헬싱키로 여행할 수 없었습니다. 마굴리스는 1980년대가 되어서야 드디어 스위스, 프랑스와 미국의 대학들을 방문하게 되었고, 1991년에 예일대학교에 정착하였습니다. 하버드대, 프린스턴대 등 많은 대학에서 그를 초빙하려 했으나, 마굴리스는 강성정리^{rigidity theorem}를 증명한 모스토우^Mostow가 있는 예일대를 선택하였다는 전설이 있습니다.

그 후 2005년 마굴리스는 “대수학에 대한 기념비적인 공헌, 특히 반-단순 리군의 격자 이론^{theory of lattices of semisimple Lie groups}과 이의 놀라운 적용, 특히 에르고딕 이론, 표현론, 정수론, 조합론 및 측도론에의 적용”에 대한 공로로 울프상^{Wolf prize}을 수상했습니다. 마굴리스는 수학자들이 전혀 예상하지 못했던 분야와 방법론으로 기하학과 정수론의 오래된 문제들을 해결하였습니다.

2008년 Pure and Appplied Mathematics Quaterly에 실린 마굴리스의 업적 리스트는 50페이지가 넘습니다. 마굴리스의 연구 분야는 특정짓기 어려울 정도로 많은 분야와 관련이 있습니다. 마굴리스의 영향력은 그의 결과들과 원래의 연구 분야를 크게 뛰어넘습니다.

글을 마치며

마굴리스는 수학 분야에서 가장 명성이 높은 세 개의 상인 필즈 메달, 울프상, 그리고 아벨상을 모두 수상한 단 5명의 수학자 중 한 명입니다. 위에서 살펴보았듯이 대칭공간, 더 일반적으로 양이 아닌 곡률을 갖는 리만 공간에 작용하는 군의 동역학적 성질을 규명하여 오펜하임 추측, 디오판틴 근사 등 정수론의 오랜 난제들을 해결하였고, 표현론을 이용하여 조합론 혹은 컴퓨터 과학의 오랜 난제인 익스팬더 그래프^{Expander graphs}를 만들기도 하였습니다.

마굴리스는 “균질 동역학”이라는 새로운 분야를 만들었습니다. 최근 필즈 메달 수상자들(린덴스트라우스, 에스킨, 미르자카니, 그리고 벤카테슈)을 비롯한 많은 젊은 수학자들이 마굴리스의 이러한 균질 동역학의 아이디어들을 토대로 연구를 해오고 있습니다.

몇 년 전 마굴리스는 은퇴를 하며 연구에 몰입할 수 있어 기뻐하였다고 합니다. 여전히 열정적으로 연구하는 모습을 앞으로도 오래오래 볼 수 있기를 바라며 글을 마칩니다.

^후기 마굴리스의 아벨상 수상을 기념하여 박사 지도교수님이신 마굴리스의 수학적 업적에 대해 풀어쓸 기회를 주신 HORIZON 편집부에 감사드립니다. 대학교에 입학하여 처음으로 배울 때는 상관없어 보였던 수많은 분야들이 연결되어 있는 신비롭고 경이로운 수학의 세계가 많은 분들께 조금이라도 전달 되었기를 바랍니다.