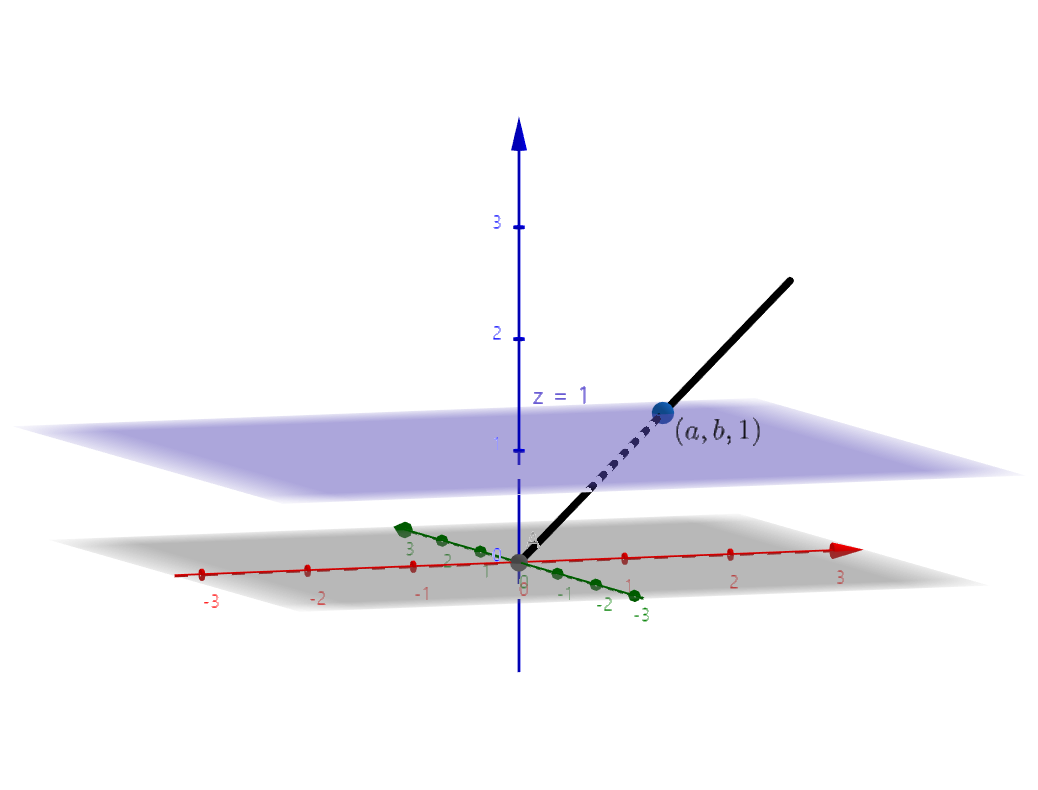
르네상스 시대 유명 화가들이 수학자들이었던 것은 원근법을 통해 사실적인 묘사가 가능하기 때문이었다. 실제로 원근법을 체계적으로 완성한 것은 17세기의 수학자 데자그르Girard Desargues, 1591-1661였으며 그 기반은 사영기하학에 있었다. 원근법에서 캔버스의 한 점은 눈과 그 점을 잇는 직선과 동일시된다. 이제 캔버스를 확장하여 무한한 평면이 놓여 있다고 하자. 눈을 지나는 직선 중 캔버스와 평행한 것을 빼면 모두 캔버스의 점들과 일대일 대응이 된다.
눈을 좌표공간의 원점이라고 하고 캔버스가 평면 \(z=1\)이라고 하자. 좌표평면의 점 \((x,y)\)는 세 번째 좌표를 무시하여 캔버스 상의 점 \((x,y,1)\)과 동일시 할 수 있고, 이는 다시 원점과 이 점을 잇는 직선 \([x,y,1]\)과 동일시 할 수 있다. 따라서 좌표평면 \(\mathbb{R}^2\)는 좌표공간 \(\mathbb{R}^3\)에서 원점을 지나는 직선들의 집합 \(\mathbb{R}\mathbb{P}^2\)의 부분집합으로 생각할 수 있는데, 이를 사영평면projective plane이라고 부른다.
원점이 아닌 점 \((x,y,z)\)와 원점을 잇는 직선을 \([x,y,z]\)라고 쓰면 임의의 0이 아닌 실수 \(t\)에 대해 \([x,y,z]=[tx,ty,tz]\)임을 알 수 있다. 사영평면 \(\mathbb{R}\mathbb{P}^2\)에서 좌표평면 \(\mathbb{R}^2\)의 여집합을 생각하면 \(xy\)-평면상의 원점을 지나는 직선들의 집합 \(\mathbb{R}\mathbb{P}^1\)인데 이를 무한대 직선line at infinity라고 부른다. 즉 \(\mathbb{R}\mathbb{P}^2=\mathbb{R}^2 \sqcup \mathbb{R}\mathbb{P}^1\)이다. 사영평면에서는 두 직선이 항상 한 점에서 만나는데, 예를 들어 좌표평면에서 두 직선이 평행하고 기울기가 \(m\)이라면 두 직선의 교점은 무한대 직선의 한 점 \([1,m,0]\)이다. 흥미롭게도 좌표평면 \(\mathbb{R}^2\)에 포함되는 원판 \(D\)를 하나 잘라내면 \(\mathbb{R}\mathbb{P}^2- D\)는 뫼비우스의 띠가 된다. 힐버트의 16번째 문제는 사영평면 속의 곡선에 관한 질문이므로 이를 이해하려면 사영평면과 익숙해져야 한다.
좌표평면 \(\mathbb{R}^2=\{(x,y)|x,y\)는 실수\(\}\)에서 \(d\)차식 \(f(x,y)=0\)을 만족하는 점들의 집합이 유한집합이 아니면 \(d\)차 곡선이라고 부른다. 1차 곡선은 1차 다항식 \(ax+by+c=0\)을 만족하는 점들의 집합이고 이것이 직선임은 누구나 알고 있다. 2차 곡선은 어떠한가? 이 글에서 우리는 항상 매끈한 곡선만 생각한다. 매끈하다는 것은 곡선의 각 점에서 접선이 유일하게 존재한다는 뜻이다. 예를 들어 3차 곡선 \(y^2 = x^2(x-1)\)의 경우 원점에서 접선이 2개 있으므로 매끈하지 않다. 직선, 타원, 포물선, 쌍곡선 등은 매끈하다.1 \(x,y\)에 관한 2차식
\(ax^2+bxy+cy^2+dx+ey+f = 0, \quad (a,b,c,d,e,f \in \mathbb{R})\)
이 정의하는 2차 곡선은 \(b^2-4ac\)가 양수이면 쌍곡선, 음수이면 타원, 0이면 포물선이 됨을 확인할 수 있는데 2차 곡선이 이들뿐임은 2200년 전 아폴로니우스도 알고 있던 사실이다.
타원, 포물선, 쌍곡선이 무척 달라 보이지만 이들을 사영평면에 넣고 보면 모두 타원처럼 생겼다. 포물선 \(y^2=4px\)의 양 끝은 무한대 직선의 동일한 점 \([1,0,0]\)으로 접근하고, 쌍곡선 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)의 두 점근선은 무한대 직선의 두 점 \([\pm a,b,0]\)에 대응된다. 이 점들을 포함 시키고 나면 사영평면에서 타원, 포물선, 쌍곡선 모두 고리oval, circuit, loop의 모양임을 알 수 있다. 이것은 우연이 아니고 사영평면 상의 매끈한 곡선은 항상 유한개의 고리의 합집합으로 주어진다.2 바로 이 때문에 사영평면에서 모양을 생각하는 것이 유리하다.
3차 곡선은 어떠한가? 곡선 \(y^2 = x(x^2\pm1)\)의 개형을 그려보면 \(+\)의 경우 1개의 고리, \(-\)인 경우 서로 각각의 바깥에 놓인 2개의 고리 모양임을 알 수 있다. 3개 이상의 고리를 갖는 3차 곡선은 존재할 수 없는데 다음의 정리 때문이다.
하르나크Harnack의 정리 (1876): 평면상의 \(d\)차 곡선은 최대
\(\frac{(d-1)(d-2)}{2} +1=:M\)
개의 고리로 이루어져 있다.
만약 \(M+1\)개의 고리를 포함한다면 고리마다 점들을 적절히 골라서 이들과 모두 만나는 \((d-2)\)차 곡선을 찾을 수 있고, \(d\)차 곡선과 \((d-2)\)차 곡선의 교점의 수가 \(d(d-2)\)를 초과할 수 없다는 사실로부터 모순을 이끌어낼 수 있다. \(d=3\)이면 고리의 수가 2개 이하이다.
4차 곡선의 차례이다. 하르나크Harnack의 정리로부터 고리의 수는 최대 4개이다. 고리의 수가 1일 때는 명백하다. 하지만 고리의 수가 2개일 때는 아래 그림과 같은 2가지 가능성이 있다.

즉 각자의 외부에 놓인 두 고리의 경우와 한 고리가 다른 고리의 내부에 들어가는 경우이다. 후자의 경우 고리가 둥지를 이룬다nested고 한다. 4차 곡선이 둥지를 포함하면 고리의 수는 정확히 2개이다. 만약 3번째 고리가 있다면 이 고리의 한점과 둥지 안쪽 고리의 내부의 한점을 잇는 직선을 생각하면 주어진 4차 곡선과 5개 이상의 점에서 만나는데, 이는 1차 곡선과 4차 곡선은 최대 4개의 점에서만 만난다는 사실에 모순이다. 따라서 고리가 3개 또는 4개일 경우 둥지를 포함할 수 없고 고리들의 모양은 아래와 같다.
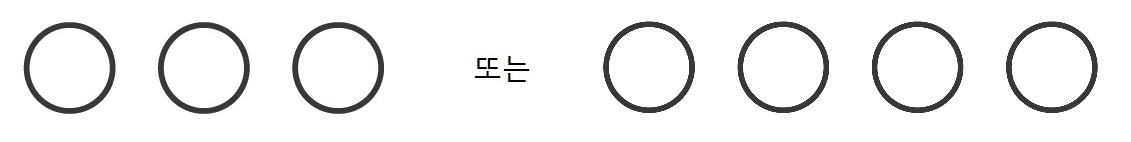
종합하면 4차 곡선의 경우 고리의 모양은 총 5가지 가능성이 있고 이들 각각의 모양을 갖는 4차 곡선은 금방 찾을 수 있다. 예를 들어 고리 2개의 경우, 서로 만나지 않는 타원의 방정식 2개를 곱하면 된다. 고리 4개의 경우 4개의 점에서 만나는 2개의 타원들의 방정식들을 곱하고 계수들을 살짝 바꿔 매끈하게 만들어주면 얻을 수 있다. 힐버트의 16번째 문제는 이런 식으로 곡선의 모양을 알아내라는 것이다.
힐버트의 16번째 문제3: \(d\)차 곡선의 모양을 분류하라. 특히 최다의 고리를 갖는 경우, 고리들의 상대적 위치를 분류하라. 또 곡면의 경우 하르나크Harnack의 정리처럼 최대 몇 개의 연결된 성분을 갖는지 알아내라. \(x,y\) 성분이 모두 다항식으로 주어진 벡터장이 있을 때 적분 곡선integral curve 중에서 고리가 되는 것의 최대 개수를 알아내라.
특별히 6차 곡선의 경우가 예로서 제시되었다. 힐버트는 6차 곡선의 경우 최다의 고리를 갖는 경우, 즉 11개의 고리를 갖는 경우, 가능한 모양이
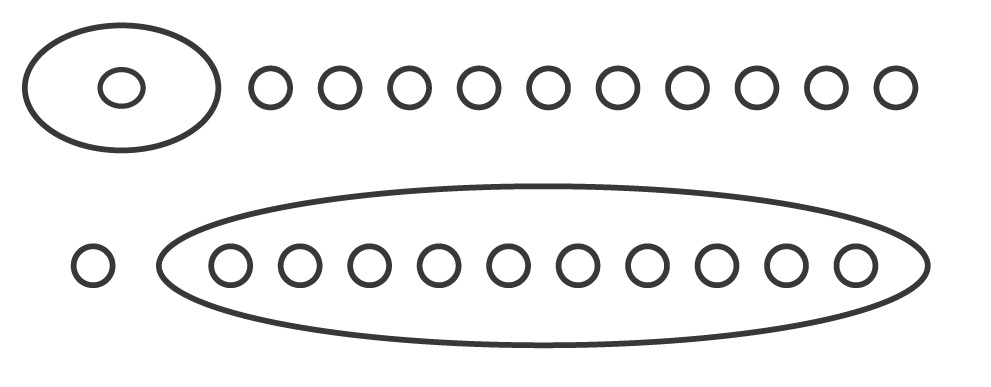
이 둘뿐이라고 확신했다. 굿코프Dmitrii Andreevich Gudkov,1918–1992는 1954년 박사학위 논문에서 힐버트의 이 주장을 증명하였(다고 생각하였)으나 출판준비 과정에서 오류를 발견하였고, 무려 15년에 걸쳐 검토한 끝에 힐버트의 주장이 사실이 아님을 발견하였다. 하나의 모양

이 더 가능하고 그 외에는 없음을 1969년에 증명하였다. 좋은 문제는 한 번 풀리지 않는다. 이 결과는 1970년대 아르놀트Vladimir Arnold, 1937-2010, 카라모프Viatcheslav M. Kharlamov,1950-, 로클린Vladimir Abramovich Rokhlin, 1919-1984 등에 의해 확장되었는데 결정적 아이디어는 실수 근들의 집합을 복소수 근들의 집합과 비교하는 것이다. 실수 계수 다항식 \(f(x,y)\)는 실수 근들의 집합
\(X _{\mathbb{R}} = \{ (x,y) \in \mathbb{R}^{2} \,:\, f(x,y)=0 \}\)
과 복소수 근들의 집합
\(X= \{ (z,w) \in \mathbb{C} ^{2} \,:\, f(z,w)=0 \}\)
을 정의하는데, \(X _{\mathbb{R}}\)은 켤레 복소수를 취하는 함수 \(\tau:(z,w)\mapsto(\bar z, \bar w)\)가 항등함수로 작용하는 \(X\)의 부분집합이다. 즉 \(X _{\mathbb{R}}\)이 \(\tau\)의 고정 점들의 집합인데 위상수학에는 이러한 고정 점들의 집합의 호몰로지 군을 \(X\)의 호몰로지 군과 \(\tau\)의 작용을 통해 분석하는 도구들이 개발되어 있다. 이들을 사용하여, 차수 \(d=2k\)가 짝수이고 고리의 수가 최대인 경우, 자신을 내부에 포함하는 다른 고리들의 수가 짝수인 고리의 수 \(P\)와 홀수인 고리의 수 \(N\)사이에
\(P-N \equiv k^2 \quad (\textrm{mod } 8)\)
임이 로클린Rokhlin에 의해 증명되었다. 특별히 \(d=6\)인 경우에 적용하면 \(P-N\)을 8로 나눈 나머지가 1이고 \(P+N=11\)이므로 \((P,N)\)이 가능한 경우는 \((6,5),(2,9),(10,1)\)의 3가지뿐임을 확인할 수 있다. 이를 통해 위의 3가지 모양만 가능함을 확인할 수 있다.
1970년대이래 꾸준히 이 방법들을 발전시켜 고리의 수가 최대인 7차와 8차 곡선의 모양은 완전히 분류가 끝났다. 또한 4차 이하의 곡면들도 완전히 분류되었다. 왜 실수 위에서 정의된 곡선 \(X _{\mathbb{R}}\)를 복소수 위에서 정의된 리만 곡면 \(X\)와 비교하는가? 그 이유는 \(X\)는 차수 \(d\)에 의해 완전히 결정되고 그 모양은 구멍의 개수가
\(g= \frac{(d-1)(d-2)} {2}\)
인 곡면
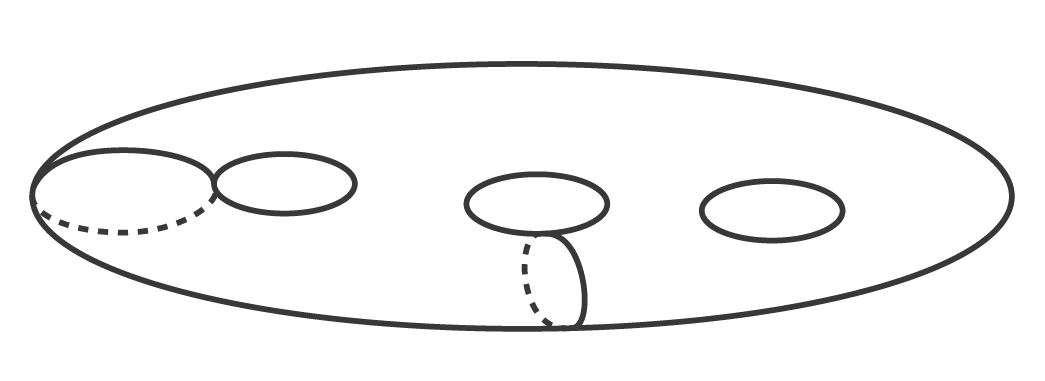
인데 이 곡면에 대해서는 너무도 많은 것을 우리가 알고 있기 때문이다. 복소수로 가면 실수일 때보다 모든 것들이 훨씬 질서 정연해지고 일관된 법칙을 찾기가 수월해진다. 그 때문에 대부분의 대수기하학자들은 복소수 위에서의 기하학이나 더 일반적으로 대수적으로 닫힌 체 위에서의 기하학만 연구한다. 실수 위에서의 기하학은 길들일 방법을 찾지 못한 야생동물과 같다. 뉴턴도 말년에 실수 위에서 3차 곡선을 100여 개가 넘는 경우들로 분류하다 길을 잃지 않았던가?
힐버트의 16번째 문제는 수학자들이 질서 있고 안전한 복소수 기하의 세계에서 뛰어내려, 거친 자연이 살아있는 실수 기하의 세계도 탐험해 보라는 제안이다. 실수 상의 대수적 곡선에 대해서도 모르는 것들 투성이지만 16번째 문제의 마지막에 제시된 벡터장의 적분 곡선에 대해서는 더욱 알려진 바가 없다. 수학의 세계에는 끝이 없다.