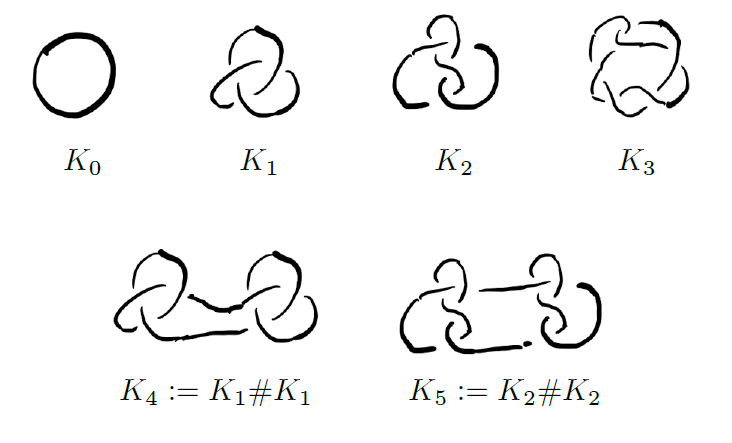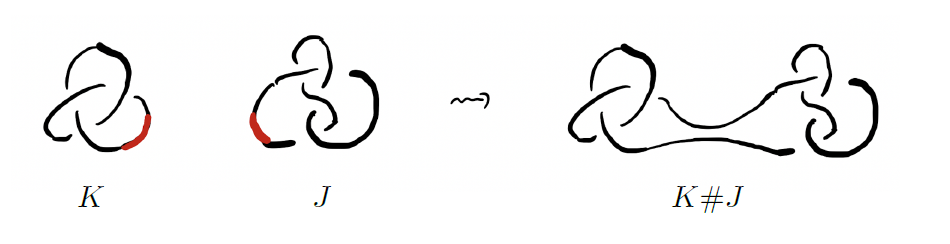매듭이론과 저차원 다양체 [1]: 단면 매듭이란 무엇인가?

이번 연재 “매듭이론과 저차원 다양체”에서는 단면 매듭^{slice knot}이라고 불리는 매우 특별한 성질을 만족하는 매듭들에 관한 이야기를 하고자 합니다. 매듭이론은 3차원과 4차원 다양체의 연구와 매우 밀접한 관계가 있습니다. 매듭의 개념을 약간 확장하면 고리라는 기학학적 개념을 생각할 수 있습니다. 60년대에 리코리쉬^{W. B. R. Lickorish}[4]와 월리스^{Andrew H. Wallace}[6]는 모든 닫힌 3차원 다양체는 고리의 덴 수술^{Dehn surgery}을 통해 얻을 수 있다는 것을 증명하였습니다. 더 나아가 단면 매듭의 개념을 이용하여 매듭들을 분류(이를 매듭 동계성이라고 부르며 뒤에서 더욱 자세히 다루도록 하겠습니다) 할 수 있는데, 이를 통해 4차원 다양체와 매듭이론과의 더 깊은 관계를 찾을 수 있습니다. 이 글에서는 특히 매듭이론과 4차원 다양체와의 연관성에 더 집중하였습니다.

3차원 4차원 다양체 연구의 발전에 힘입어 현재는 매듭에 관한 여러 가지 흥미로운 사실들이 알려져 있습니다. 또한 반대로 매듭을 이용해 3차원 4차원 다양체의 새로운 현상을 발견하기도 합니다. 가령 매듭을 이용하여 이국적 4차원 유클리디언 \(\mathbb{R}^4\)(4차원 유클리디언 \(\mathbb{R}^4\)와 위상 동형이지만 미분 동형이 아닌 매끄러운 다양체)를 만들어 낼 수도 있으며 아직 해결되지는 않았지만 매끄러운 범주^{smooth category}에서의 4차원 푸앵카레 가설을 공략하는데도 사용되기도 합니다. 4차원 다양체를 연구하는 데 매듭이 유용한 이유는 여러 가지가 있지만, 그중 한 가지는 4차원 공간은 시각적으로 상상하기 어려운 반면 4차원 공간을 작은 조각으로 분리하면 나오는 3차원 공간과 그 속의 매듭들은 상대적으로 시각화하기가 더 편리하다는 점 때문입니다.

이번 글을 포함하여 앞으로 두 번의 연재를 더 계획하고 있습니다. 이번에는 60년대 최초로 모든 매듭은 단면 매듭이 아니라는 사실을 보인 폭스^{Ralph H. Fox}와 밀너^{John W. Milnor}의 이야기, 두 번째 연재에서는 매듭 동계성을 체계적으로 연구하기 위하여 어떤 식으로 군구조를 사용하였으며 그 군구조에 대하여 어떤 사실들을 알고 있는지, 마지막으로 세 번째 연재에서는 매듭을 통해 4차원 다양체를 어떤 식으로 연구할 수 있는지에 대하여 소개하고자 합니다.

매듭과 단면 매듭^{knots and slice knots}

매듭에 관한 이야기를 하기에 앞서서 우선 \(n\)차원 공과 \(n\)차원 구에 관하여 간략하게 이야기하겠습니다. \(n\)차원 공 \(B^n\)은 \(n\)차원 공간의 유클리드 공간 \(\mathbb{R}^n\)에서 부등식

\begin{equation}
\tag{2.1}
x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}\leq 1
\end{equation}
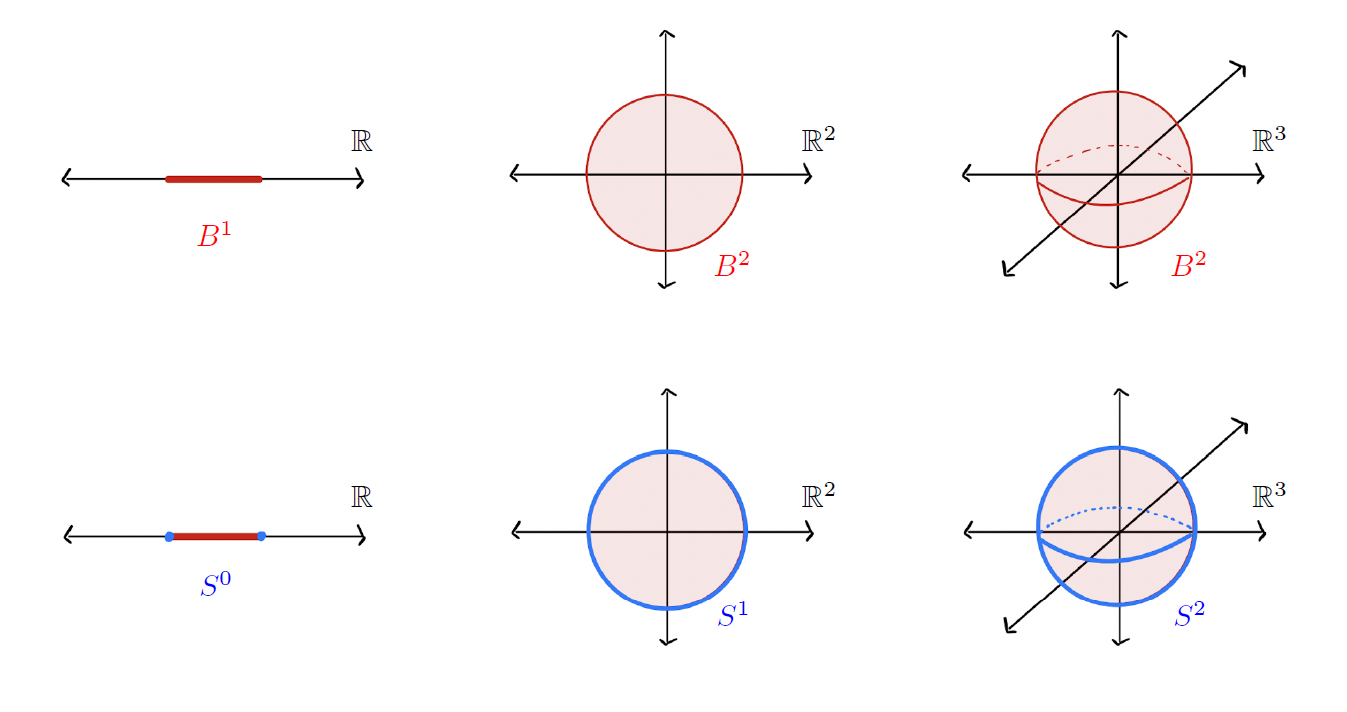
을 만족시키는 점들 \((x_1, \ldots, x_n)\)의 집합입니다. 이 개념은 수식으로 생각하면 조금 어려울 수 있으나 [그림1]에서 보이는 것과 같이 1, 2, 3차원의 공은 우리가 이미 잘 이해하고 있는 공간들이며 이를 자연스럽게 고차원으로 확장한 것이라 생각하면 됩니다.

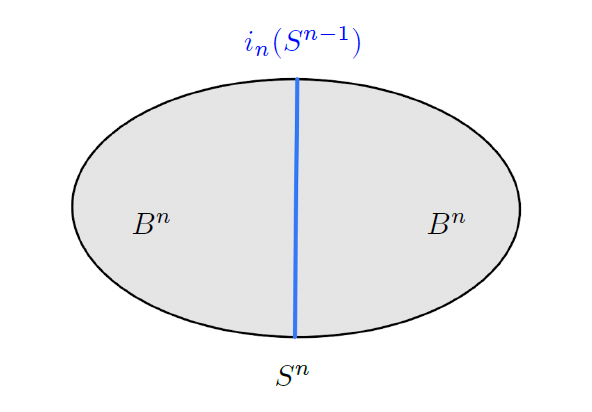
두 개의 \(n\)차원 공이 있으면 그들의 경계를 [그림2]와 같이 붙여서 \(n\)차원 구 \(S^n\)을 만들 수 있습니다.

수식으로 구체적으로 정의하자면, \(n\)차원의 구 \(S^n\)은 유클리드 공간 \(\mathbb{R}^{n+1}\)에서 등식

\( x_{1}^{2}+x_{2}^{2}+\cdots +x_{n+1}^{2} =1\)

을 만족시키는 점들 \((x_1, \ldots, x_{n+1})\)의 집합입니다. 고차원 공의 경우처럼 0, 1, 2차원의 구는 우리에게 이미 익숙하고 편하게 생각할 수 있는 공간들입니다. 그리고 고차원 구는 이 개념을 자연스럽게 확장시킨 것입니다.

여기서 한 가지 주목할 점은 \(B^{n}\)의 경계(즉 부등식 (2.1)에서 등식을 만족하는 점들)는 \(S^{n-1}\)이며 \(S^n\)은 두 개의 \(B^{n}\)을 경계를 따라 붙여서 만들어졌다는 사실입니다. 그렇기 때문에 [그림3]과 같이 \(S^n\)안에 \(S^{n-1}\)이 자연스럽게 매장되어 있다는 사실을 알 수 있습니다. 우리는 이 매장을 자명한 매장이라고 부르며 기호로는 \(i_n: S^{n-1} \hookrightarrow S^n\)을 사용하겠습니다.

매듭이란 1차원 구 \(S^1\)을 3차원 구 \(S^3\)에 매장한 것을 말합니다. 직관적으로는 긴 끈을 꼬아 묶은 후에 이 끈의 양 끝을 붙인 것이라고 생각하면 됩니다. [그림4]처럼 매듭들은 매우 복잡해질 수 있습니다.

[그림4]를 보면 마지막 두 개의 매듭은 다른 매듭들과는 조금 다른 형태를 지니고 있습니다. [그림5]와 같이 두 개의 매듭 \(K\)와 \(J\)가 있을 때 각 매듭에서 작은 변들을 떼어내고 남은 부분을 연결하면 새로운 매듭 \(K\#J\)를 만들 수 있습니다. 이 연산을 매듭의 연결합^{connected sum}이라고 부릅니다. 이 연결합은 매듭들을 체계적으로 연구하는 데 매우 중요한 역할을 합니다. 이에 대해서는 다음 글에서 더욱 자세히 알아보도록 하겠습니다.

^그림5 매듭들의 연결합 / 박정환

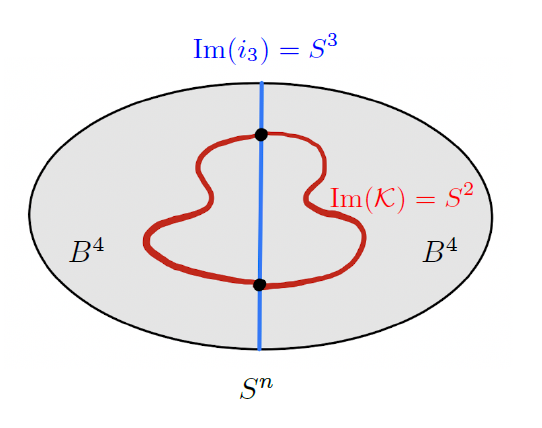
이 글에서는 자세히 다루지는 않겠지만 일반적으로는 고차원 매듭, 즉 \(n\)차원 구 \(S^n\)의 \((n+2)\)차원 구 \(S^{n+2}\)로의 매장을 생각할 수 있습니다. 20년대에 아틴^{Emil Artin}은 어떤 특별한 방법으로 만들어진 2차원 매듭들(spun knots라고 불립니다)을 생각하였습니다.[2] 그중의 하나를 \(\mathcal{K}: S^{2} \hookrightarrow S^4\)라고 부르겠습니다. 이 매듭들은 여러 가지의 특별한 성질을 만족하는데 그중 특히 우리가 주목할 성질은 이 매듭과 4차원 구 \(S^4\)안에 자명하게 매장되어 있는 3차원 구 \(i(S^3)\)가 만나는 점들이 다시 1차원 구가 된다는 사실입니다. 즉 수식으로는

\( Im(\mathcal{K}) \cap Im(i_3) = S^1\)

이며 이를 통하여 우리는 2차원 매듭 \(\mathcal{K}: S^{2} \hookrightarrow S^4\)를 이용하여 새로운 1차원 매듭

\(\mathcal{K}|_{\mathcal{K}^{-1}(Im(i_3) )}: S^1 \hookrightarrow S^3 \)

을 얻게 됩니다. 수식으로는 조금 복잡합니다만 [그림6]으로 위의 문단의 주요 내용을 요약할 수 있습니다.

^그림6 아틴의 매듭에서 1차원 매듭 얻기 / 박정환

아틴의 2차원 매듭들뿐만 아니라 많은 2차원 매듭들이 자명하게 매장되어 있는 3차원 구 \(i(S^3)\)와 1차원 구로 만나게 되는데 위와 같은 방법을 이용하여 3차원 구에 있는 많은 매듭들을 만들 수 있습니다. 이렇게 얻어진 매듭을 우리는 단면 매듭^{slice knot}이라고 부릅니다.(단면 매듭은 2차원 매듭의 한 단면으로 얻어진다고도 생각할 수 있으며 그리하여 붙여진 명칭이 “단면 매듭”입니다.)

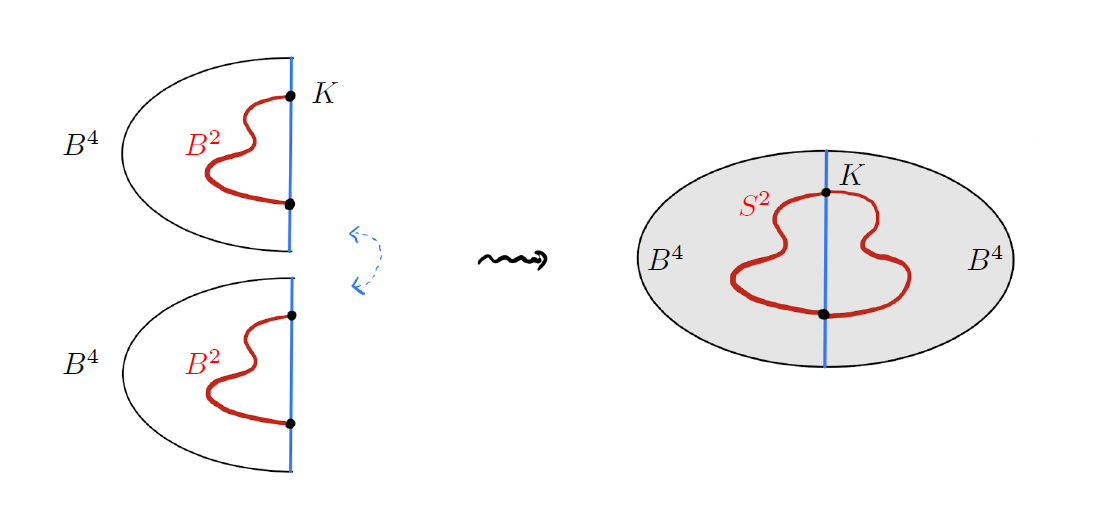
여기서 한 가지 주목해야 할 점은 단면 매듭을 정의하기 위해서는 [그림6]의 모든 부분이 필요하지는 않다는 점입니다. [그림6]에서 왼쪽 부분인 4차원 공 \(B^4\)만 살펴본다면 그 공의 경계인 3차원 구에 있는 매듭을 볼 수 있으며 이 매듭은 4차원 공 \(B^4\)매장된 2차원 공 \(B^2\)의 경계로 생각될 수 있습니다. 하지만 [그림7]에서 볼 수 있듯이 매듭 \(K\)가 4차원 공 \(B^4\)안에 매장된 2차원 공 \(B^2\)의 경계로 만들어질 수 있다면 이 \(B^4\)와 \(B^2\)를 복제한 후 경계를 따라서 붙여서 매듭 \(K\)를 2차원 매듭의 한 단면으로 생각할 수 있습니다. 즉, 이 두 조건은 동치 조건입니다. 그래서 때로는 단면 매듭을 정의할 때 4차원 공 \(B^4\)안에 매장된 2차원 공 \(B^2\)의 경계인 매듭으로 정의하기도 합니다.

이때 한 가지 조심해야 할 부분이 있습니다. 2차원 공의 4차원 공으로 매장에 어떠한 조건도 붙이지 않는다면 모든 매듭은 4차원 공안에 매장된 2차원 공의 경계가 됩니다. 이를 방지하기 위하여 2차원 공의 매장에 매끄러운^smooth 매장 혹은 국소 평탄한^{locally flat} 매장의 조건을 추가합니다. 두 조건은 미묘하게 다른데, 두 조건의 다름으로 인해 4차원 다양체에서만 발생하는 특이한 현상에 대해서는 세 번째 연재에서 더 자세히 다루도록 하겠습니다.

여기서 자연스럽게 물어볼 수 있는 질문은 어떤 매듭이 단면 매듭인지입니다. [그림4]로 돌아가면 \(K_0, K_3, K_5\)들은 단면 매듭들이지만, 나머지 매듭들은 그렇지 않습니다. 매듭이론의 한 분야인 매듭 동계성^{knot concordance}을 연구하는 분야는 궁극적으로 매듭 중 어떤 매듭이 단면 매듭인지 아닌지를 연구하는 학문입니다.

단면 매듭이 아닌 매듭^{not all knots are slice}

폭스와 밀너는 60년대에 특이점을 허용하는 2차원 다양체의 4차원 다양체로의 매장을 연구하였습니다.[3] 그들은 이 매장의 특이점을 제거하는 문제와 특이점 근처에서 자연스럽게 생기는 매듭이 단면 매듭인지 아닌지에 관한 문제가 매우 밀접하게 관련이 있다는 사실을 알게 되었습니다.

여기서 특이점과 관련된 매듭은 다음과 같이 얻을 수 있습니다. 4차원 공간 안의 특이점에서의 닫힌 근방의 경계는 3차원 구가되며, 3차원 구와 2차원 다양체가 만나는 점이 1차원 구가 됩니다. 1차원 구의 3차원 구로의 매장이 특이점에서 자연스럽게 나오는 매듭입니다.

폭스와 밀너는 단면 매듭이 아닌 매듭을 발견하게 됩니다. 놀랍게도 그들이 사용한 매듭의 불변량^{knot invariant}은 20년대에 알렉산더^{James W. Alexander}가 만든 알렉산더 다항식이었습니다.[1] 이 다항식은 매듭 여공간의 덮개공간에서 정보를 추출하여 만들어진 다항식입니다. 그들은 어떤 매듭 \(K\)가 단면 매듭일 경우 그것의 알렉산더 다항식 \(\Delta_K(t)\)가 다음과 같은 특별한 성질을 만족해야 한다는 사실을 증명하였습니다.

정리 3.1 ([4], Theorem 2). 매듭 \(K\)가 단면 매듭이고 \(\Delta_K(t)\)가 \(K\)의 알렉산더 다항식이면, 어떤 다항식 \(f(t) \in \mathbb{Z}[t]\)와 어떤 정수 \(n\)이 있어서

\(\Delta_K(t) = \pm t^n\cdot f(t)\cdot f(t^{-1})\)

을 만족한다. 특히, \(|\Delta_K(-1)|\)은 제곱수이다.

매듭의 알렉산더 다항식은 계산이 용의하기 때문에 정리 3.1은 매우 유용하게 사용됩니다.

위의 계산에서 볼 수 있듯이 단면 매듭으로 알려져 있는 매듭들을 제외한 \(K_1, K_2, K_4\) 중 두 개의 매듭들은 단면 매듭이 아님을 알 수 있습니다. 이처럼 폭스-밀너의 정리만으로는 모든 매듭들에 대하여 단면 매듭인지 아닌지에 대한 답을 알 수는 없습니다. 특히, \(K_4\)와 \(K_5\)처럼 하나의 매듭 \(K\)로 시작하여, 매듭 두 개를 연결합한 매듭 \(K \# K\)에 대해서는 폭스-밀너의 정리가 도움이 되지 않습니다. \(K_4\)가 단면 매듭이 아니라는 사실은 무라수기^{Kunio Murasugi}가 증명을 하였습니다.[5]

더 나아가 무라수기는 세잎 매듭을 아무리 여러 번 연결합을 하더라도 단면 매듭이 되지 않는다는 사실을 보였습니다. 8자 매듭은 두 번 연결합을 하면 단면 매듭이 되는 점과는 매우 대조적입니다. (이 이유에 대해서는 다음 글에서 이야기 하도록 하겠습니다.) 여기서 자연스럽게 할 수 있는 질문은 “서로 다른 두 매듭에 대하여 연결합을 할 경우 어떻게 되는가” 입니다. 이를 체계적으로 연구하기 위하여 폭스와 밀너는 매듭들에 군구조^{group structure}를 소개하였고, 현재는 군구조에 대하여 많은 사실을 알고 있습니다. 다음 글에서는 군구조에 대하여 더 자세히 알아보고자 합니다.