매듭이론과 저차원 다양체 [2]: 매듭의 동계군

이전 글 “매듭이론과 저차원 다양체 [1]: 단면 매듭이란 무엇인가?”에서는 단면 매듭에 대해 알아보았습니다. 이번 글에서는 동계성^concordance이라 불리는 매듭 간의 동치관계를 정의하고, 모든 매듭의 동치류 집합에 연산을 추가하여 만들어지는 매듭 동계군^{knot concordance group}에 대하여 이야기하고자 합니다. 동계군의 개념은 60년대에 폭스^{Ralph H. Fox}와 밀너^{John W. Milnor}가[9] 소개하였으며 우리는 이를 통해 매듭을 보다 더 체계적으로 이해할 수 있게 되었습니다. 이후 동계군에 대한 다양한 연구가 진행되어 현재는 이 군의 구조에 대하여 많은 것들이 알려졌습니다. 이번 글에서는 이에 관해 간단히 소개하도록 하겠습니다.

동계군

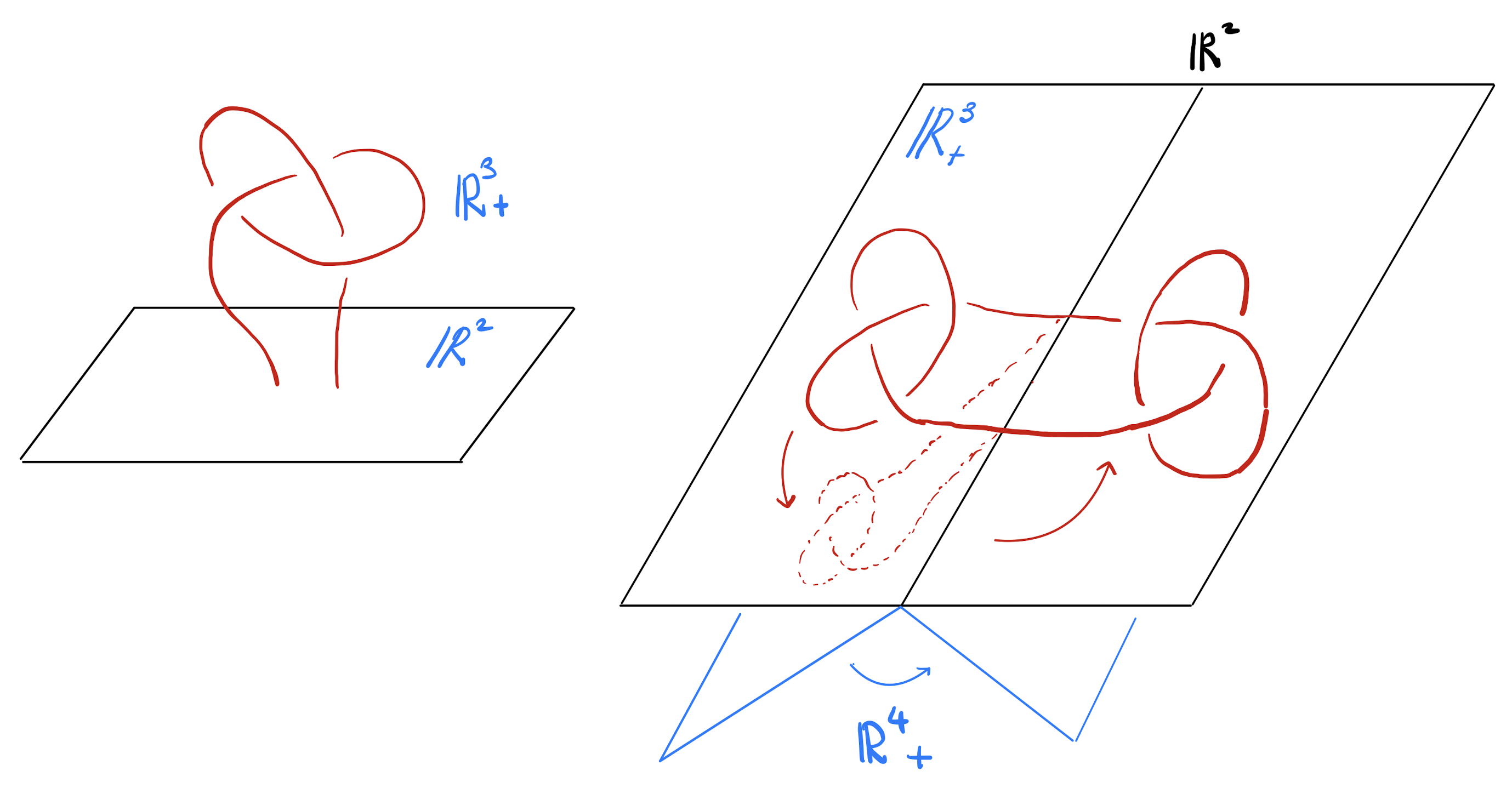
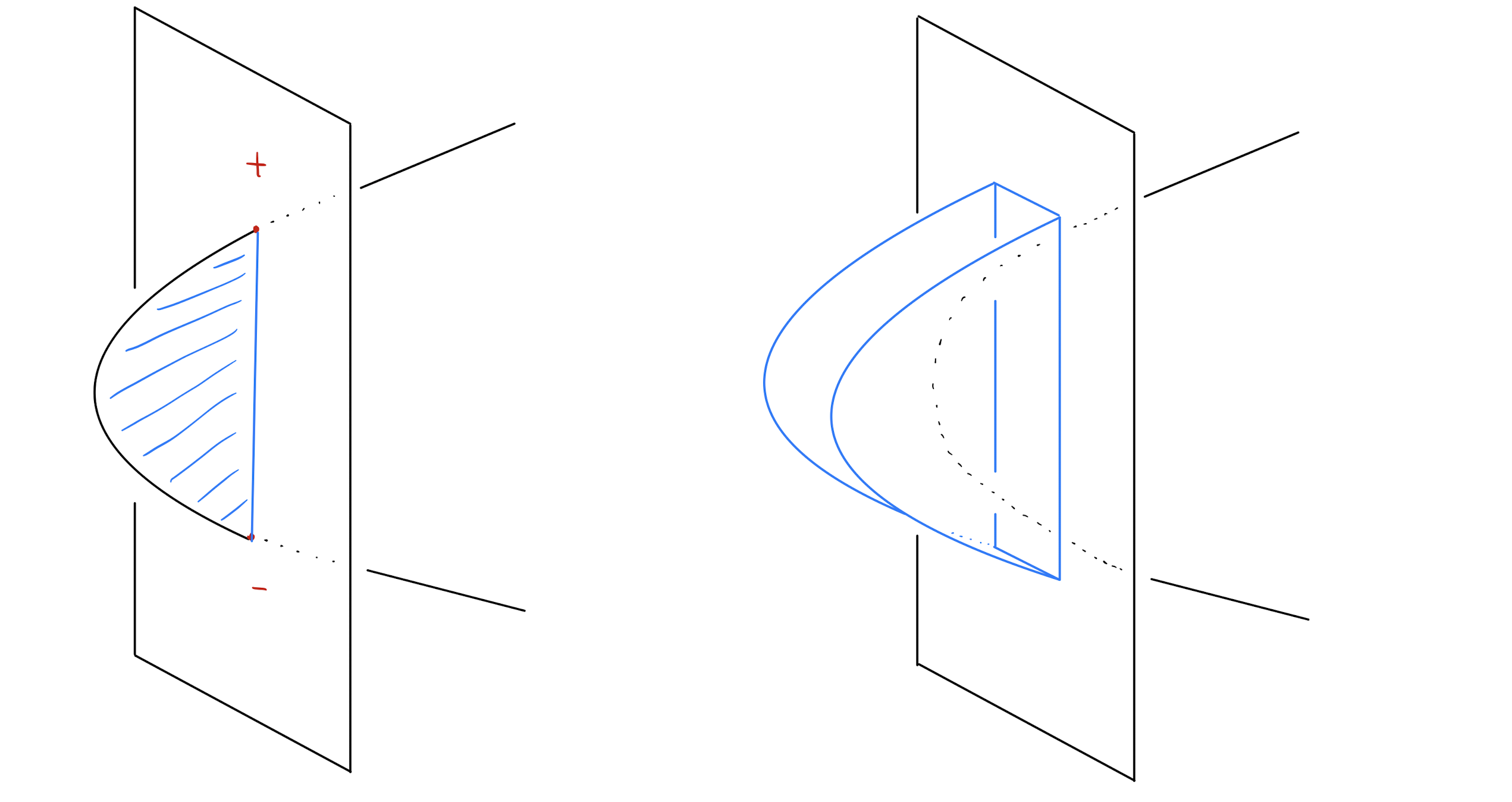
우선, 단면 매듭을 만드는 방법을 한가지 소개하겠습니다. 만약 \(K: S^1 \hookrightarrow S^3\)가 주어진 매듭이라고 하면 \(-K\)는 \(K\)를 거울에 비추었을 때 얻어지는 매듭이라고 하겠습니다. (더 정확히는 거울상의 방향을 바꾸어야 하지만 편의상 방향성은 고려하지 않겠습니다.) 두 매듭의 연결합인 \(K\# -K\)는 항상 단면 매듭이 됩니다.그 이유는 [그림1]에서 볼 수 있습니다. \(\mathbb{R}^2:=\{(x_1,x_2,0,0)\}\)를 축으로 \(\mathbb{R}^3_+:=\{(x_1,x_2,x_3,0)\mid x_3 \geq 0\}\)를 180도 회전하여 얻어진 \(\mathbb{R}^4_+\)에서 \(K\)의 궤적은 매끄럽게 매장된 \(B^2\)가 되는데, 이때 \(K\#-K\)가 이 \(B^2\)의 경계가 되기 때문입니다. 만약 180도에서 멈추지 않고 360도 회전을 한다면 2차원 매듭 \(S^2 \hookrightarrow S^4\)를 얻을 수 있는데 이는 이전 글 “매듭이론과 저차원 다양체 [1]: 단면 매듭이란 무엇인가?”에서 언급한 아틴^{Emil Artin}의 2차원 매듭^{spun knot} 입니다.[1]

매듭 \(K, J: S^1 \hookrightarrow S^3\)가 있을 때 만약 \(K\# -J\)가 단면 매듭이면 우리는 \(K\)와 \(J\)가 서로 동계^concordant라고 부릅니다. 위에서 보았듯이 모든 매듭 \(K\)에 대하여 \(K\# -K\)는 단면 매듭이기 때문에 \(K\)는 스스로와 동계이며(반사관계), 동계성이 대칭관계와 추이관계가 된다는 사실 또한 쉽게 확인할 수 있습니다. 그래서 동계성은 동치관계입니다. 앞으로 매듭 \(K\)의 동치류는 \([K]\)로 표시하겠습니다. 즉,

$$[K]:=\{K’ \mid K’\#-K\text{가 단면 매듭}\}.$$
더 나아가 모든 매듭들의 동치류를 모아놓은 집합에 연산을 연결합으로 정의하겠습니다. 즉,

$$[K]+[J]:=[K\#J].$$
그러면 이 집합은 가환군이 된다는 사실을 쉽게 확인할 수 있으며 우리는 이 가환군을 매듭 동계군^{knot concordance group}이라고 부르며, 이를 \(\mathit{C}\) 로 표기하겠습니다. 가장 간단한 매듭인 풀린 매듭의 동치류가 \(\mathit{C}\) 의 항등원이 되며 이 동치류는 모든 단면 매듭들을 모아 놓은 집합입니다.

그러므로 이전 글 “매듭이론과 저차원 다양체 [1]: 단면 매듭이란 무엇인가?”에서 보았던 모든 매듭이 단면 매듭이 아니라는 폭스와 밀너의 정리는 \(\mathit{C}\) 가 자명군이 아니라는 사실을 말해 줍니다. 또한 무라수기^{Kunio Murasugi}가[13] 증명한 세잎 매듭을 아무리 여러 번 연결합을 하더라도 단면 매듭이 되지 않는다는 사실은 \(\mathit{C}\) 에서 세잎 매듭의 동치류가 무한차수를 가지고 있다는 사실을 알려줍니다. 즉, \(\mathit{C}\) 는 \(\mathbb{Z}\)를 부분군으로 가지고 있는 것입니다.

그렇다면 \(\mathit{C}\) 에는 유한 차수를 가지는 원소가 있을까요? [그림2]에서 나오는 8자 매듭을 \(J\)라고 부르겠습니다. [그림2]에서 볼 수 있듯이 \(J\)는 그의 거울상 \(-J\)와 같습니다. 조금 더 정확하게 이야기하자면 [그림2]에서 보여주는 것은 8자 매듭이 그의 거울상의 방향을 바꾼 매듭과 같아진다는 사실입니다. 이럴 때 우리는 \(J\)는 negative amphichiral인 매듭이라고 이야기합니다. 이전 글 “매듭이론과 저차원 다양체 [1]: 단면 매듭이란 무엇인가?”에서 확인하였듯 \(J\)는 단면 매듭이 아닙니다. 그래서 \([J]\)는 \(\mathit{C}\) 에서 항등원이 아닌 원소가 되는 반면

$$[J]+[J] = [J \# J] = [J\# -J] = [\text{풀린 매듭}] \in \mathit{C}.$$
\([J]\)의 차수가 2라는 사실은 \(\mathit{C}\) 가 \(\mathbb{Z} / 2\mathbb{Z}\)도 부분군으로 가지고 있다는 것을 말해줍니다. 8자 매듭 외에도 단면 매듭이 아니면서 negative amphichiral인 매듭들이 많이 있습니다. 이를 통하여 차수가 2인 원소들은 \(\mathit{C}\) 에서 많이 찾을 수 있지만, 2가 아닌 유한 차수를 가지는 원소는 아직 발견되지 않았습니다. 또한 차수가 2인 모든 원소가 negative amphichiral한 매듭의 동치류인지도 알려지지 않았습니다.

대수적 동계군

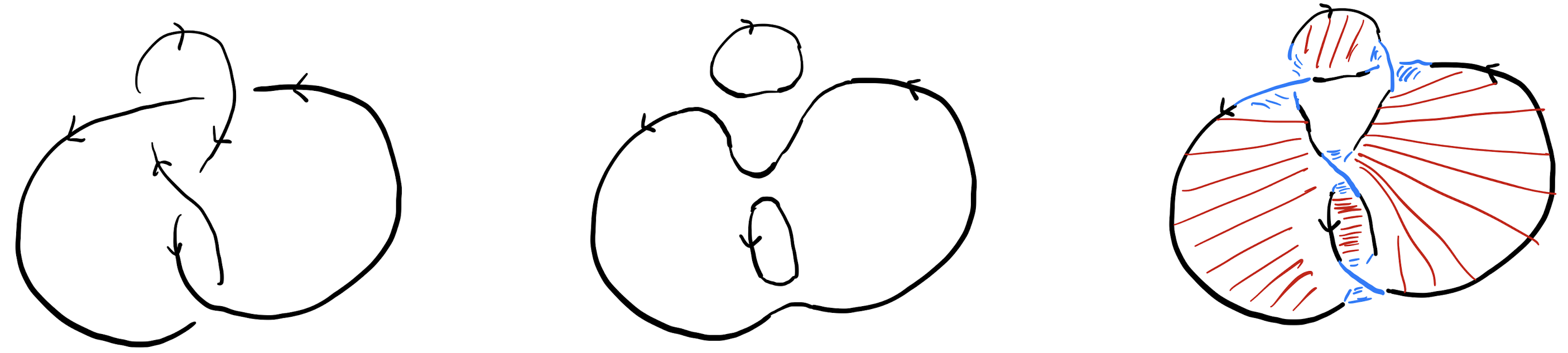
르빈^{Jerome Levine}은[11,12] 동계군 \(\mathit{C}\) 를 대수적인 방법을 통하여 체계적으로 연구하기 시작하였습니다. 모든 매듭은 \(S^3\)에 매끄럽게 매장되어 있는 어떤 2차원 다양체의 경계가 됩니다. 이 다양체는 사이퍼트 곡면^{Seifert surface}이라 불리며, [그림3]에 설명되어 있듯이 사이퍼트 알고리즘이라는 과정을 통하여 구체적으로 만들 수 있습니다.

어떤 사이퍼트 곡면이 주어졌을 때 그 곡면 위에 있는 새로운 매듭들은 기존의 매듭을 이해하는 데 많은 도움을 줍니다. 사이퍼트는[14] 사이퍼트 곡면 위의 매듭들이 얼마나 서로 엉켜있는지를 대수적(이 값은 연환수라고 불립니다)으로 측정하고 모든 대수적인 정보를 하나의 행렬로 모았습니다. 이 행렬을 사이퍼트 행렬이라고 합니다. ([그림4 참조])

위에서 우리는 모든 매듭을 모아놓은 집합에 단면 매듭의 개념을 사용해서 동치류를 정의했습니다. 더 나아가 이를 통하여 동계군 \(\mathit{C}\) 를 정의하였습니다. 비슷한 방법으로 모든 사이퍼트 행렬을 모아놓고 대수적 단면 매듭^{algebraically slice knot}이라는 개념을 통하여 대수적 동계성^{algebraic concordance}이라 불리는 동치류와, 대수적 동계군^{algebraic knot concordance group} \(\mathit{AC}\) 를 정의할 수 있습니다.

구체적으로 정의를 하지는 않겠지만 어떤 매듭이 대수적 단면 매듭인 것은 그 매듭의 사이퍼트 곡면 위에 충분히 많은 매듭들이 있어서 서로 대수적으로는 엉켜있지 않은 상태라고 생각하면 됩니다. 그리고 모든 단면 매듭은 대수적 단면 매듭이기 때문에 자연스러운 전사 준동형 사상^{surjective homomorphism} \(\phi \colon \mathit{C} \twoheadrightarrow \mathit{AC}\) 가 있습니다.

르빈은 \(\mathit{AC}\) 가 \(\mathbb{Z}^\infty \oplus (\mathbb{Z}/2\mathbb{Z})^\infty \oplus (\mathbb{Z}/4\mathbb{Z})^\infty\)와 동형이라는 사실을 보였습니다. 이는 \(\mathit{C}\) 가 최소한 \(\mathbb{Z}^\infty \oplus (\mathbb{Z}/2\mathbb{Z})^\infty \oplus (\mathbb{Z}/4\mathbb{Z})^\infty\)만큼의 복잡한 구조를 가지고 있다고 해석할 수 있습니다. 더 놀라운 사실은 고차원 동계군에서 일어납니다. 양의 정수 \(n\)에 대해 \(2n-1\)차원 매듭 \(S^{2n-1} \hookrightarrow S^{2n+1}\)을 모두 모은 것에 \(\mathit{C}\) 를 정의했던 방법을 그대로 사용하면 \(2n-1\)차원 동계군 \(\mathit{C}_{2n-1}\)을 정의할 수 있습니다. (여기서 \(\mathit{C}_{1}\)은 \(\mathit{C}\) 와 같습니다.) 그리고 르빈은, 고차원에서는 동계군에서 대수적 동계군으로의 전사 준동형 사상이 사실은 동형 사상이라는 것을 보였습니다. 즉, 만약 \(n>1\)이면

$$\phi_{2n-1} \colon \mathit{C}_{2n-1} \xrightarrow{\sim} \mathit{AC} \cong \mathbb{Z}^\infty \oplus (\mathbb{Z}/2\mathbb{Z})^\infty \oplus (\mathbb{Z}/4\mathbb{Z})^\infty.$$
그리하여 고차원 매듭들의 동계성은 각 매듭들의 대수적 정보만으로 결정이 된다는 것입니다.

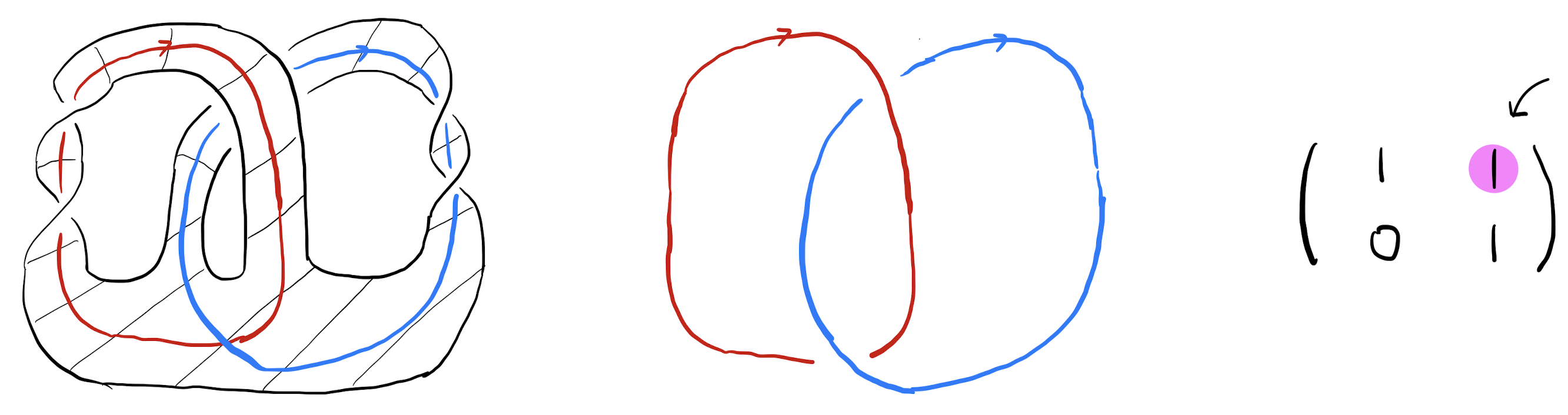
이 증명의 핵심은 다음과 같습니다. 어떤 매듭이 대수적 단면 매듭일 때 그 매듭의 사이퍼트 곡면 위에는 대수적으로 엉켜있지 않은 매듭들이 있는데 이들은 \(B^{2n+2}\)에서 각각 서로 만나지 않는 매끄럽게 매장된 \(B^{n+1}\)의 경계가 됩니다. 이 매끄럽게 매장된 \(B^{n+1}\)들과 기존의 사이퍼트 곡면을 사용하면(ambient surgery라고 불립니다) 처음 시작한 매듭이 단면 매듭이라는 사실을 증명할 수 있습니다. 위 증명이 가능한 것은 고차원에서는 대수적으로 엉켜있지 않은 매듭들이 각각 서로 만나지 않게 매끄럽게 매장된 \(B^{n+1}\)의 경계가 되기 때문입니다. 반면 4차원에서는 (\(n=1\)) 대수적인 정보를 기하학적으로 바꾸어 줄 수 있는 Whitney trick을[15] ([그림5] 참고) 사용할 수 없기 때문에, 안타깝게도 위의 증명을 적용할 수 없습니다.

르빈 이후의 동계군

70년대에 캐손^{Andrew Casson}과 고든^{Cameron Gordon}은[2,3] 1차원 동계군은 고차원의 동계군처럼 대수적인 방법만으로는 완전히 이해할 수 없다는 사실을 보였습니다. 조금 더 구체적으로 그들은 전사 준동형 사상 \(\phi \colon \mathit{C} \twoheadrightarrow \mathit{AC}\)이 단사 준동형 사상이 아니라는 사실을 보였습니다. 즉, 대수적 단면 매듭이지만 단면 매듭은 아닌 매듭의 존재를 증명한 것입니다.

더 나아가 코크란^{Tim Cochran}, 오르^{Kent Orr}, 타이크너^{Peter Teichner}는[8] \(\mathit{C}\) 에 훨씬 더 복잡한 구조가 있다는 사실을 \(\mathit{C}\) 의 여과^filtration를 통해 보였습니다. 동계군 \(\mathit{C}\) 에 다양한 여과를 줄 수 있는데, 그중 하나는 grope 여과라고 불리며 다음과 같이 표시합니다.

$$\cdots \subseteq \mathit{G}_{n.5} \subseteq \mathit{G}_{n} \subseteq \cdots \subseteq \mathit{G}_{3} \subseteq \mathit{G}_{2.5} \subseteq \mathit{G}_{2} \subseteq \mathit{G}_{1.5}\subseteq \mathit{C}.$$

이 여과는 매듭의 사이퍼트 곡면 위 매듭들이 \(B^2\) 대신 다양한 2차원 공간의 경계가 되는 것을 허용하여 얻어지는 여과입니다. 이 여과는 매듭이 기하학적으로 단면 매듭과 얼마나 가까운지를 grope이라는 공간을([그림6] 참조) 통하여 근접하려는 아이디어에서 나왔다고 생각하면 되겠습니다.

뿐만 아니라 다양한 방법으로 \(\mathit{C}\) 의 구조를 이해하려는 노력이 있습니다. 최근에는 \(\mathit{C}\) 에 거리 함수를 정의하여 연구를[4,7] 하기도 하며 또한 \(\mathit{C}\) 의 프랙털 구조가 있는지 혹은 으뜸 분해^{primary decomposition}가 있는지에 대한 연구도[5,6,10] 진행 중입니다.

이번 글에서는 매듭을 체계적으로 연구하기 위하여 단면 매듭의 개념을 사용하여 정의된 매듭의 동계군에 대하여 알아보았습니다. 정의로부터 이미 매듭 동계군과 4차원 다양체의 연구가 매우 밀접한 관계가 있음을 짐작할 수 있습니다. 다음 글에서는 이 연관성에 대해 구체적으로 알아보고자 합니다.