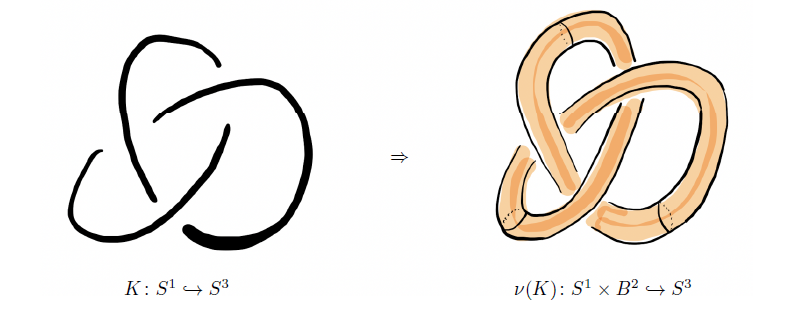매듭이론과 저차원 다양체 [3]: 매듭과 4차원 다양체

이번 글은 “매듭이론과 저차원 다양체”라는 제목으로 준비한 연재의 마지막 글입니다. 지난 두 번의 글에서는 단면 매듭과 매듭의 동계군에 대하여 알아보았습니다. 이번에는 위의 개념들이 어떤 식으로 4차원 다양체 연구에 이용되는지 알아보려고 합니다. 4차원에서는 다른 차원에서 일어나지 않는 신기한 현상들이 많이 발견됩니다. 예를 들어 \(n\neq 4\)이면 이국적 유클리디언 \(\mathbb{R}^n\)은 존재하지 않는 반면에 4차원에서는 셀 수 없이 많은 이국적 유클리디언 \(\mathbb{R}^4\)가 존재합니다. 이번 글에서는 매듭을 사용하여 이국적 유클리디언 \(\mathbb{R}^4\)를 만들어 보려고 합니다. 또한 저차원 위상수학에서 매끄러운 범주의 4차원 푸앵카레 추측은 아직 해결되지 않은 중요한 문제입니다. 이를 공략하기 위하여 매듭이 다양하게 활용되고 있습니다. 한 예로 최근 마놀레스쿠^{Ciprian Manolescu}와 피크릴로^{Lisa Piccirillo}가 발표한 논문을 소개하겠습니다.

매듭과 이국적 유클리디언 \(\mathbb{R}^4\)

어떤 4차원 다양체 \(X\)가 주어졌을때 이국적 \(X\)^{exotic \(X\)}란 \(X\)와 위상 동형이지만 미분 동형이 아닌 매끄러운 다양체를 뜻합니다. 그러므로 만약 이국적 \(X\)가 존재한다면, 위상적 4차원 다양체 \(X\)에 두 개 이상의 매끄러움 구조가 존재합니다. 이번 연재에서는 위상 동형과 미분 동형을 모두 이야기하려 합니다. 두 다양체가 위상 동형이라는 표시는 \(=_{\text{위상}}\)으로 하고 미분 동형일 때는 \(=\)으로 표시하도록 하겠습니다.

이번 섹션의 목표는 매듭을 이용하여 이국적 유클리디언 \(\mathbb{R}^4\)를 만드는 것입니다. 이를 위해서 우리는 매우 특별한 성질을 가진 매듭이 필요합니다. 우리는 지난 글에서 단면 매듭을 \(B^4\)안에 매끄럽게 매장된^{smoothly embedded} \(B^2\)의 경계로 얻어지는 매듭이라 정의하였습니다. 정의를 약간 변형하면 위상적 단면 매듭을 정의할 수 있습니다. 매듭이 만약 \(B^4\)안에 국소 평탄하게 매장된^{locally flat embedded} \(B^2\)의 경계가 된다면 이를 위상적 단면 매듭^{topologically slice knot}이라고 부릅니다.

여기서 국소 평탄한 매장은 다음과 같이 정의됩니다. 어떤 \(n\)차원 다양체 \(N\)이 \(m\)차원 다양체 \(M\)에 매장되어있고, 만약 \(N\)의 모든 점에서 근방 \(U\)를 잡아 \((U, U\cap N)\)이 \((\mathbb{R}^m,\mathbb{R}^n)\)과 위상동형이 된다면 \(N\)이 \(M\)안으로 국소 평탄하게 매장되어 있다고 합니다. 매끄러운 매장은 국소 평탄한 매장이므로 단면 매듭은 위상적 단면 매듭이 됩니다. 하지만 모든 위상적 단면 매듭이 다 단면 매듭은 아닙니다.

지난 글에서 폭스^{Ralph H. Fox}와 밀너^{John W. Milnor}가 단면 매듭이 아닌 매듭이 존재한다는 사실을 보이기 위하여 알렉산더 다항식이라고 불리는 매듭 불변량을 사용했다는 사실을 보았습니다. 프리드만^{Michael H. Freedman}은 80년대에 다음과 같은 놀라운 사실을 증명하였습니다.

정리2.1[9,10] 알렉산더 다항식이 1인 매듭은 위상적 단면 매듭이다.

위의 정리와 도널드슨^{Simon Donaldson}의 대각화 정리[6, Theorem 1]를 사용하여 악불룻^{Selman Akbulut}과 곰프^{Robert Gompf}는 독립적으로 위상적 단면 매듭이지만 단면 매듭은 아닌 매듭이 존재한다는 사실을 증명하였습니다. 현재까지도 위의 성질을 만족하는 매듭들에 대한 연구가 활발하게 진행되고 있습니다. 조금 더 구체적으로는 동계군 \(\mathcal{C}\)안에서 위상적 단면 매듭으로 이루어진 부분군을 생각할 수 있는데 이의 구조와 관련해 활발한 연구[3,4,5,7, 13, 14, ,16, 18]가 이루어지고 있습니다.

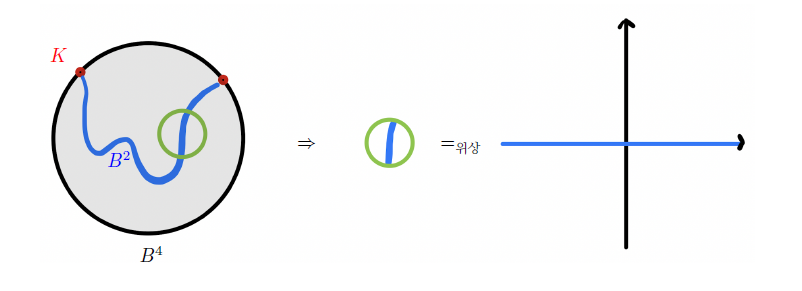
어떤 매듭이 주어졌을 때, 매듭의 자취를 정의하도록 하겠습니다. 이는 4차원 다양체이며 이국적 유클리디언 \(\mathbb{R}^4\)를 만드는 데 중요한 역할을 합니다. 우선 4차원 공 \(B^4\)를 생각하고 이 경계 \(\partial B^4 = S^3\)에서의 매듭 \(K\)를 생각하겠습니다. 매듭은 1차원 구 \(S^1\)에서 3차원 구 \(S^3\)로의 매장이지만 이를 확장하여 [그림2]와 같이 \(S^1 \times B^2\)에서 \(S^3\)로의 매장으로 생각 할 수 있습니다. (이를 위해서는 \(K \colon S^1 \hookrightarrow S^3\) 매장이 매끄러운 매장이라는 가정이면 충분합니다.) 직관적으로는 주어진 매듭을 더 굵게 만드는 과정이라고 생각하시면 되겠습니다. 그리고 이 매장을

\(\nu(K) \colon S^1 \times B^2 \hookrightarrow S^3\)

라고 부르도록 하겠습니다.

우리는 \(B^4\)에 (2-handle 이라고 불리는) \(B^2 \times B^2\)를 붙이려고 합니다. 우선 \(B^2 \times B^2\)의 경계 \(\partial(B^2 \times B^2)\)가 [그림3]과 같이 두 개의 조각

\(\partial(B^2 \times B^2)=\left(\partial(B^2) \times B^2\right) \cup \left( B^2 \times \partial(B^2)\right) = \left(S^1 \times B^2\right) \cup \left(B^2 \times S^1\right)\)

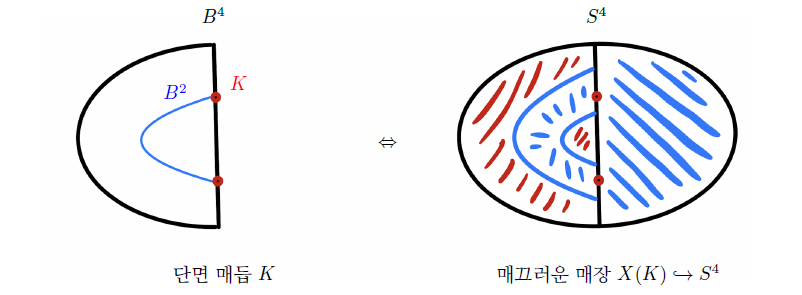
으로 나누어집니다. 이것의 첫 번째 조각 \(S^1 \times B^2\)를 \(\nu(K) \colon S^1 \times B^2 \hookrightarrow S^3\)에 따라서 \(B^4\)에 붙여 만들어지는 4차원 다양체를 매듭 \(K\)의 자취^{knot trace} \(X(K)\)라고 합니다.([그림4] 참고)

실은 여기에서 \(S^1 \times B^2\)를 \(\nu(K) \colon S^1 \times B^2 \hookrightarrow S^3 \)에 따라서 \(B^4\)에 붙이는 방법이 무한히 많이 있습니다. 이 중에서 우리가 고려하는 것은 0-framed 자취입니다. 매듭의 자취는 매듭의 동계성을 이해하는 데 매우 중요한 역할을 합니다. 그 이유는 다음의 정리 때문입니다.([그림5] 참고)

정리 2.2 매듭 \(K\)가 단면 매듭인 것과 \(X(K)\)가 매끄럽게 \(\mathbb{R}^4\)에 매장되는 것은 동치이며 매듭 \(K\)가 위상적 단면 매듭인 것과 \(X(K)\)가 국소 평탄하게 \(\mathbb{R}^4\)에 매장되는 것 또한 동치이다.

이국적 유클리디언 \(\mathbb{R}^4\)를 위해 마지막으로 필요한 정리는 콤팩트가 아닌 4차원 다양체에는 항상 매끄러움 구조가 있다는 사실입니다.

정리 2.3 [8] 모든 콤팩트가 아닌 연결 4차원 다양체는 매끄러운 다양체이다.

드디어 우리는 이국적 유클리디언 \(\mathbb{R}^4\)를 만들 준비를 마쳤습니다. 우선 위상적 단면 매듭이지만 단면 매듭이 아닌 매듭 \(J\)를 고정하겠습니다. 정리2.2에 의하면 \(J\)의 자취 \(X(J)\)는 국소 평탄하게 \(\mathbb{R}^4\)에 매장이 됩니다. 따라서

\(\mathbb{R}^4 =_{\text{위상}} X(J) \cup \mathbb{R}^4 \smallsetminus X(J)\)

로 표현됩니다. 위의 공간은 당연히 \(\mathbb{R}^4\)와 위상 동형입니다. 여기서 \(\mathbb{R}^4 \smallsetminus X(J)\)는 콤팩트가 아닌 연결 4차원 다양체이기 때문에 정리 2.3에 의해서 어떤 매끄러움 구조를 가지고 있다는 사실을 알 수 있습니다. 또한 \(X(J)\)도 매끄러움 구조를 가지고 있고 모든 3차원 다양체에는 단 하나의 매끄러움 구조를 가진다는 사실이 알려져 있습니다.[2, 12, 17] 따라서 이를 종합해보면 \(X(J) \cup \mathbb{R}^4 \smallsetminus X(J)\)에 어떠한 매끄러움 구조를 줄 수 있으며 이 매끄러움 구조를 가진 다양체에 \(X(J)\)가 매끄럽게 매장이 된다는 결론에 이르게 됩니다.

하지만 \(J\)는 단면 매듭이 아니기 때문에 정리2.2를 이용하여 \(X(J) \cup \mathbb{R}^4 \smallsetminus X(J)\)는 \(\mathbb{R}^4\)와 미분 동형이 아니라는 사실을 알 수 있습니다. 즉, \(X(J) \cup \mathbb{R}^4 \smallsetminus X(J)\)는 이국적 유클리디언 \(\mathbb{R}^4\)라는 결론을 내릴 수 있습니다. 여기서 한 가지 주목할 사실은 이 증명에서 정리 2.3이 사용되기 때문에 같은 방법으로는 이국적인 콤팩트한 4차원 다양체는 만들 수가 없습니다. 콤팩트한 이국적 4차원 다양체에 대해서는 아래에서 더욱 자세히 알아보도록 하겠습니다.

위에서는 하나의 이국적 유클리디언 \(\mathbb{R}^4\)를 만들었지만 현재 우리는 비가산적으로 무한 개의 이국적 유클리디언 \(\mathbb{R}^4\)가 존재한다는 사실을 알고 있습니다. 이는 앞서 언급하였던 도널드슨의 대각화 정리를 확장한 타우부스^{Clifford Taubes}의 정리를 통해 80년대에 증명되었습니다.[11, 19]

매듭과 4차원 푸앵카레 추측

이국적인 콤팩트한 4차원 다양체에 대한 연구도 활발하게 진행되고 있습니다. (이에 대하여 [1] 서론에 잘 정리되어 있습니다.) 콤팩트하지 않은 4차원 다양체는 셀 수 없이 많은 매끄러움 구조를 가질 수 있는 반면, 콤팩트한 4차원 다양체는 최대 가산적으로 무한개의 매끄러움 구조만 가질 수 있습니다. 그리고 \(n\neq 4\)이면 콤팩트한 \(n\)차원 다양체는 유한한 매끄러움 구조를 가지지만 많은 콤팩트한 4차원 다양체가 무한히 많은 매끄러움 구조를 가지고 있다는 사실이 알려져 있습니다.

아직까지 이러한 현상은 위상적으로 복잡한 콤팩트한 4차원 다양체에서만 발견되고 있습니다. 이는 위상적인 복잡성이 커짐에 따라 저차원 위상수학에서 개발된 다양한 기술들을 사용하기 용이해서입니다. 위상적으로 간단한 콤팩트한 4차원 다양체에 대하여 유한한 혹은 유일한 매끄러움 구조를 가질 것이라는 사실을 뒷받침해주는 증거는 발견되지 않았으며, 아직 유한개의 매끄러움 구조를 가진 콤팩트한 4차원 다양체가 존재하는지에 대해서도 전혀 알려지지 않았습니다. 이 중 가장 널리 알려진 문제는 매끄러운 범주의 4차원 푸앵카레 추측^{Poincaré conjecture}입니다.

추측 3.1 (4차원 매끄러운 푸앵카레 추측) 4차원 구 \(S^4\)에는 단 하나의 매끄러움 구조가 있다.

많은 수학자들이 매듭을 이용하여 이 문제를 풀려고 노력하였습니다. 이 중 최근 마놀레스쿠^{Ciprian Manolescu}와 피크릴로^{Lisa Piccirillo}가 발표한 논문을 간략하게 소개하고자 합니다.

우선 용어 하나와 정리 하나가 필요합니다. 위에서 매듭 \(K\)가 주어졌을 때 \(K\)의 자취 \(X(K)\)로 정의하였습니다. 이 4차원 다양체는 경계를 가지고 있으며 이 경계를 매듭 \(K\)의 덴 수술^{Dehn surgery}로 얻어진 3차원 다양체라고 부르고 \(Y(K):=\partial X(K)\)로 표시하겠습니다. 조금 더 정확히는 \(K\)에 0-framed 덴 수술로 얻어진 3차원 다양체입니다. 또한, 위에서 언급하였던 정리 2.2에서 \(\mathbb{R}^4\)를 \(S^4\)로 대체 할 수 있습니다. 이는 매듭의 자취가 \(\mathbb{R}^4\)에 매장되는 것과 \(S^4\)에 매장되는 것이 동치이기 때문입니다. 즉, 우리는 다음의 정리가 사실임을 알 수 있습니다. ([그림5] 참고)

정리 3.2 매듭 \(K\)가 단면 매듭인 것과 \(X(K)\)가 매끄럽게 \(S^4\)에 매장되는 것은 동치이다.

두 개의 매듭 \(K\)와 \(J\)가 있고 \(Y(K)\)와 \(Y(J)\)가 같은 3차원 다양체라고 가정하겠습니다. 더 나아가 \(K\)는 단면 매듭이고 \(J\)는 단면 매듭이 아니라고 가정하겠습니다. 만약 우리가 \(X(K)\)와 \(X(J)\)가 같은 4차원 다양체라고 가정했다면 정리 3.2에 의하여 \(K\)가 단면 매듭이라는 사실과 \(J\)가 단면 매듭이라는 사실이 동치가 됩니다. 하지만 우리는 이들의 경계만 같다고 가정을 하기에 충분히 \(K\)는 단면 매듭이고 \(J\)는 단면 매듭이 아닌 예가 있을 수 있습니다.

이와 같은 성질을 만족하는 매듭들과 4차원 매끄러운 푸앵카레 추측은 어떻게 연결이 되어있을까요? 매듭 \(K\)가 단면 매듭이기 때문에 정리 3.2에 의하여 \(K\)의 자취 \(X(K)\)가 \(S^4\)에 매끄럽게 매장이 되고

\(S^4 = X(K) \cup S^4 \smallsetminus X(K)\)

로 쓸 수 있습니다. 더 나아가 \(Y(K)\)와 \(Y(J)\)가 같다는 사실을 이용하여 \(S^4 \smallsetminus X(K)\)와 \(X(J)\)를 붙여 새로운 다양체

\(X(K,J):= X(J) \cup S^4 \smallsetminus X(K)\)

를 고려하도록 하겠습니다. 자세히 언급하지는 않겠지만 프리드만의 4차원 위상적 푸앵카레 추측의 해결은 \(X(K,J)\)가 \(S^4\)와 위상 동형이라는 사실을 알려줍니다. 하지만 \(X(K,J)\)에 \(X(J)\)가 매끄럽게 매장되어 있으므로 정리 3.2에 의하여 \(X(K,J)\)는 \(S^4\)와 미분 동형이 아니라는 사실을 알 수 있습니다. 즉, 이는 \(S^4\)에 적어도 두 개의 매끄러움 구조가 있다는 것을 이야기하고 4차원 매끄러운 푸앵카레 추측이 틀렸다는 사실을 말합니다.

궁극적으로 우리는 \(Y(K)\)와 \(Y(J)\)가 같으며 \(K\)는 단면 매듭이고 \(J\)는 단면 매듭이 아닌 매듭 \(K\)와 \(J\)를 찾는다면 추측 3.1을 해결할 수 있습니다. 마놀레스쿠와 피크릴로는 최근 발표한 논문에서 흥미로운 21쌍의 매듭 \(\{(K_i, J_i)\}_{1\leq i \leq 21}\)를 발표 하였습니다. 각 \((K_i,J_i)\)는 위의 성질을 모두 만족하지만 단 \(\{K_i\}_{1\leq i \leq 21}\)들이 단면 매듭인지 아닌지에 대한 사실만 알려지지 않았습니다. 즉, 이 21개의 매듭 \(\{K_i\}_{1\leq i \leq 21}\) 중에 단 하나라도 단면 매듭이라면 4차원 매끄러운 푸앵카레 추측이 해결된다는 논문을 발표한 것입니다.

다만 안타깝게도 논문이 발표된 후에 21개의 매듭이 모두 단면 매듭이 아니라는 사실이 알려졌습니다. 하지만 이 논문은 푸앵카레 추측을 매듭이론을 통해서 체계적으로 해결하려 했다는 것에 의미가 있습니다. 앞으로도 많은 수학자들이 매듭을 통하여 푸앵카레 추측뿐만 아니라 4차원 다양체와 관련된 다양한 문제에 도전하고 해결할 것이라고 기대합니다.

세 번의 연재 동안 단면 매듭이라는 개념, 이를 통해서 정의되는 매듭의 동계군, 그리고 매듭이 4차원 다양체 연구에 어떤 식으로 활용이 되는지에 대하여 알아보았습니다. 이번 글에서 언급한 문제뿐만 아니라 많은 저차원 위상수학의 문제들과 매듭이론은 깊은 연관이 있습니다. 세 번의 연재가 독자들에게 유익한 연재였기를 바랍니다.