퍼셉트론: 인공지능의 시작

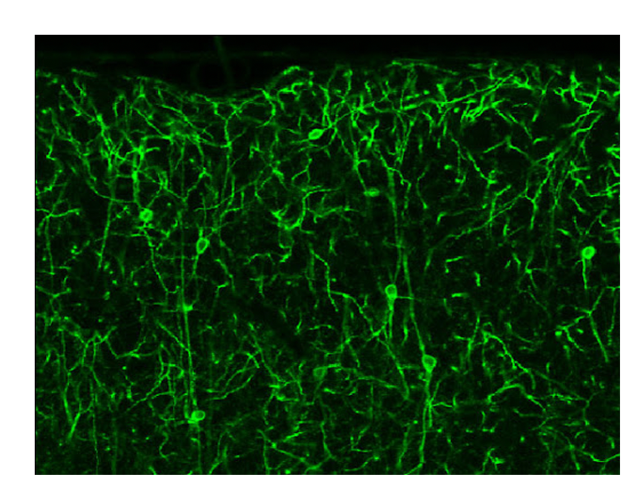
우리 뇌는 어떻게 학습할까? 뇌의 연결망을 훔쳐본 과학자는 이 궁금증을 풀었을까? 인간의 뇌에는 밤하늘의 은하를 이루는 1천억 개의 별만큼이나 많은 뉴런^Neuron들이 있다고 한다. 뉴런들의 연결망을 애써 살펴보아도 복잡하게 연결되었다는 것 말고는 다른 정보를 얻기가 힘들어 보인다.([그림1]) 이 복잡한 연결망이 어떻게 세상을 인지하고 학습하면서 우리 각자의 정체성을 형성하는 것일까?

앞으로 “머신러닝과 데이터사이언스” 연재 4회를 통해 자연지능에서 영감을 받은 인공지능 모형인 머신러닝에 대해서 소개하려고 한다. 이번 글에서는 머신러닝의 기본단위가 되는 퍼셉트론을 소개하고, 퍼셉트론을 쌓아서 구성한 다층 신경망의 학습 알고리즘을 설명하려고 한다. 이어지는 연재를 통해서는 볼츠만머신으로 대표되는 생성모형의 개념을 소개하고, 블랙박스로 치부되는 신경망의 학습원리를 정보이론을 통해서 살펴볼 예정이다. 마지막 연재에서는 데이터에서 정보를 추출하는데 중요한 개념이 되는 정보기하학을 다루려고 한다.

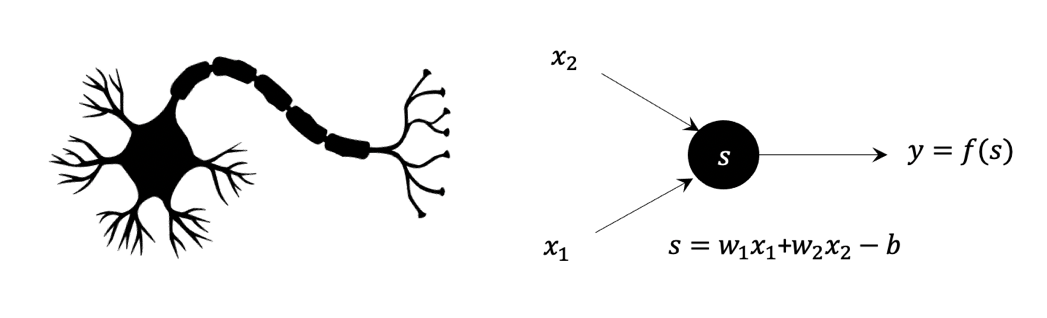
심리학을 전공한 신경생물학자 프랭크 로젠블랫^{Frank Rosenblatt}이 주목한 것은 뉴런들의 연결이었다.([그림2]) 개별 뉴런들의 역할은 자신의 위층에 연결된 뉴런들에게 받은 신호를 아래층에 연결된 뉴런들에게 넘겨주는 것이다. 복잡한 연결망의 본질을 꿰뚫은 통찰이라 하겠다. 복잡한 연결망이 과학자의 눈에는 단순한 회로로 보인다는 사실이 재미있지 않은가? 1958년 로젠블랫은 뉴런 연결망의 최소 단위를 퍼셉트론^Perceptron으로 정의하고 이들의 연결로 인지과정을 이해할 수 있을 것으로 기대했다. 일렉트론^Electron, 포지트론^Positron 등이 물질을 구성하는 기본입자인 것처럼 퍼셉트론은 인지^Perception의 기본요소이다.

수식을 써서 퍼셉트론의 동작을 좀 더 자세히 살펴보자.([그림3]) 두 개의 입력 신호 \((x_1, x_2)\)가 있는 경우를 생각하자.

\(y = f(w_1 x_1 + w_2 x_2 – b)\)

퍼셉트론은 입력신호에 가중치를 가지고 더해서 \(w_1 x_1 + w_2 x_2\)가 어떤 역치 \(b\)보다 크면 활성화된 출력 \(y=1\)을 넘겨주고, 그렇지 않으면 비활성화된 출력 \(y=0\)을 넘겨준다. 이를 결정하는 함수 \(f(s)\)를 활성화함수^{activation function}라고 부른다. 가장 유명한 활성화함수 \(f(s)=1/(1+\exp(-s))\)이다.

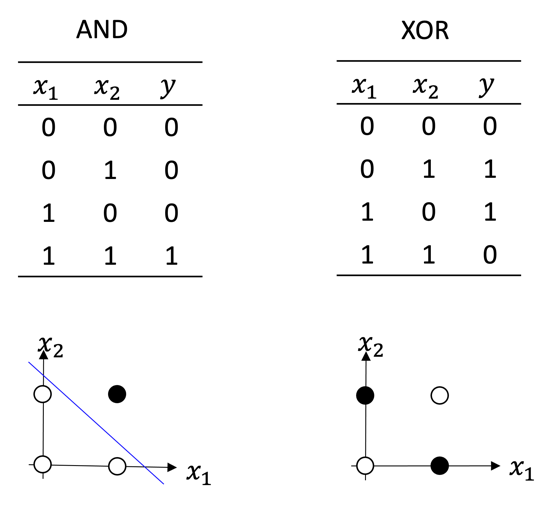
퍼셉트론으로 처음 수행한 작업은 논리연산이다. 퍼셉트론으로 논리곱 \(y=x_1 \land x_2\)을 표현할 수 있을까? 가령 입력이 \((x_1, x_2) = (0, 0)\)인 경우 퍼셉트론은 \(y=0\)라는 출력을 주어야 한다. 이 작업은 적당한 매개변수 \((w_1, w_2, b)\)을 선택함으로써 성공적으로 수행할 수 있다. 이렇게 매개변수를 최적화하는 작업을 학습^learning이라고 부른다. 마찬가지로 퍼셉트론은 논리합 \(y=x_1 \lor x_2\)도 표현할 수 있다. 퍼셉트론으로 논리연산을 표현할 수 있으면 이들의 조합으로 구성된 회로는 보편적인 컴퓨터^Computer가 될 수 있다. 뉴런의 연결에서 영감을 받아서 개발한 퍼셉트론으로 논리연산을 구현하고 컴퓨터를 만들 수 있다는 사실은 당시 과학자들을 매우 흥분시켰을 것이다.

하지만 1969년 MIT 인공지능 연구소의 마빈 민스키^{Marvin Minsky}와 페퍼트 세이모어^{Papert Seymour}는 이 들뜸에 찬물을 끼얹었다.([그림4])[1] 인공지능을 단순한 자동화 기계로 보지 않고 인간을 닮은 기계로 상상했던 민스키와 세이모어의 입장에서는 당연한 반응이었다. “글쎄, 퍼셉트론은 간단한 배타적 논리합도 표현할 수 없어!” 배타적 논리합^XOR은 입력 \((x_1, x_2)\) 가운데 한 개가 참일 때만 출력이 참이 되는 논리연산이다. 논리곱/합과는 다르게 어떤 매개변수 \((w_1, w_2, b)\)값을 선택하더라도 퍼셉트론으로 배타적 논리합은 구현할 수 없다. 이는 입력 \((x_1, x_2)\) 좌표 위에 출력 \(y\)를 점의 색깔로 표현해 보면 쉽게 알 수 있다. \(y=0\)은 흰 점으로 \(y=1\)은 검은 점으로 표시해보자.([그림5])

입력의 가중합과 역치의 차이가 \(w_1 x_1 + w_2 x_2 – b = 0\)이 되는 직선을 생각해보자. 퍼셉트론은 이 직선을 경계로 위와 아래 공간을 검은 점과 흰 점의 세상으로 나눌 수 있다. 즉 퍼셉트론의 역할을 2차원 공간을 나누는 1차원 직선으로 해석할 수 있다. 입력이 2차원 이상인 \(n\)차원 초공간^hyper-space에서 퍼셉트론은 \((n-1)\)차원 초평면^hyper-plane에 해당한다. 이 기하학적 해석에 따르면 [그림5]의 배타적 논리합은 퍼셉트론 한 개로 검은 점과 흰 점의 세상을 나눌 수 없음이 자명하다. 이 문제로 드러난 퍼셉트론의 한계는 머신러닝의 첫 번째 어둠의 시기를 촉발했다.

사실 퍼셉트론 여러 개를 영리하게 구성하면 배타적 논리합을 구현할 수 있다. 재미나게도 이 해결법은 민스키와 세이모어가 제시한 것이다. 배타적 논리합 문제에서 직선 2개를 이용하면 검은 점과 흰 점의 세상을 일단 구분할 수 있다.([그림6]) 이 직선을 수식으로 표현하면 다음과 같다.

\(s_1 = w_{11} x_1 + w_{12} x_2 – b_1 = 0,\)
\(s_2 = w_{21} x_1 + w_{22} x_2 – b_2 = 0.\)

여기서 입력 \((x_1, x_2)\)의 좌표변환 \(z_1 = f(s_1)\)과 \(z_2 = f(s_2)\)를 생각해 보자. 변환된 좌표계 \((z_1, z_2)\)에서는 검은 점과 흰 점을 비로소 한 개의 직선으로 나눌 수 있다. 이를 신경망의 신호흐름으로 해석해보자. 입력 신호 \((x_1, x_2)\)가 숨은층^{hidden layer}의 숨은 뉴런의 활성화상태 \((z_1, z_2)\)로 변환되고 이는 최종적으로 출력 신호 \(y\)로 변환된다. 즉 입력과 출력층만으로 구성된 신경망에서는 표현할 수 없었던 배타적 논리합을 숨은층을 넣음으로써 표현할 수 있게 되었다.

이 결론을 일반화한 것이 보편적 어림정리^{Universal Approximation Theorem}정리이다. 충분히 많은 뉴런들로 구성된 숨은층을 가진 신경망은 임의의 입력 \(x\)와 출력 \(y\)사이의 함수관계 \(y = f(x)\)를 표현할 수 있다는 이 정리는 1989년 조지 시벤코^{George Cybenko}가 증명했다.[2]

보편적 어림정리는 임의의 입력 \(x\)와 출력 \(y\) 사이의 관계를 표현할 수 있는 신경망이 반드시 존재함을 보장한다. 하지만 그런 신경망을 구성하기 위해서 필요한 최소한의 숨은 뉴런의 개수 그리고 신경망의 매개변수 값들을 구체적으로 알려주지는 않는다.

숨은층이 한 개 있는 신경망의 정보처리과정을 다시 생각해보자. 입력 \(x\)가 숨은층에서 \(z = f(W_1 x – b_1)\)로 변환되고 이는 출력 \(y = f(W_2 z – b_2)\)로 최종 변환된다. 다차원의 입·출력을 가진 일반적인 문제의 경우 \(x, y, z\)는 벡터가 되고 신경망의 연결세기^weight \(W\)는 행렬, 역치^bias \(b\)는 벡터가 된다. 위 식에서 입력층^{input layer}과 숨은층 사이의 연결세기와 역치는 \(W_1\)과 \(b_1\)로 나타냈고, 숨은층과 출력층^{output layer} 사이의 연결세기와 역치는 \(W_2\)과 \(b_2\)로 나타냈다. 우리는 주어진 문제를 풀 수 있는 매개변수 \((W_1, b_1, W_2, b_2)\)의 최적값을 모른다. 배타적 논리합과 같이 간단한 문제는 2차원 좌표 위의 기하학적 모습을 토대로 매개변수 값을 쉽게 정할 수 있지만, 다차원의 입력과 출력 사이의 관계를 다루는 일반적인 문제에서는 간단하지가 않다. 이 문제는 오차역전파^{error backpropagation} 알고리즘에 의해 해결되었다.

이제 머신러닝의 엔진이라고 할 수 있는 오차역전파 알고리즘을 한번 유도해보자. 편의상 \(b_1 = b_2 = 0\)인 경우를 생각해보자. 이 경우 주어진 입력 \(x\)에 대한 출력은 \(y=f(W_2 f(W_1 x))\)가 된다. 만약 매개변수 \((W_1, W_2)\)가 엉터리이면 신경망의 출력 \(y\)는 원하는 출력 \(y_{\text{true}}\)와 다를 것이다. 이제부터 우리가 할 일은 매개변수를 잘 조정해서 \(y\)와 \(y_{\text{true}}\)사이의 거리를 줄여나가는 것이다. 그 오차^Loss를 다음과 같이 정의해보자.

\(L(W_1, W_2)= || y(W_1, W_2) – y_{\text{true}} ||^2\)

여기서 거듭제곱은 가능한 한 가지 선택이고 다른 방식으로 오차를 정의할 수도 있다. 이제 매개변수 \((W_1, W_2)\) 좌표 위에서 정의되는 오차함수 \(L(W_1, W_2)\)의 경관^Landscape을 상상해보자. 오차가 최소가 되는 \((W_1, W_2)\)의 지점을 찾는 방법은 마치 산맥과 같은 오차함수의 경관에서 하산을 하면 된다. 가장 효율적인 하산은 오차함수 기울기의 반대방향으로 곧장 내려가는 것이다. 경사하강법^{Gradient Descent Method}으로 불리는 이 방법에 따라 매개변수를 다음처럼 갱신한다.

\(W_2 \leftarrow W_2 – \alpha \frac{\partial L(W_1, W_2)}{\partial W_2},\)
\(W_1 \leftarrow W_1 – \alpha \frac{\partial L(W_1, W_2)}{\partial W_1}.\)

여기서 \(\alpha\)는 학습률이라고 불리는 초매개변수로 학습속도를 결정한다. 기울기 \(\partial L / \partial W_2\)와 \(\partial L / \partial W_1\)을 미분의 체인법칙^{chain rule}을 이용해서 계산하면 다음과 같다.¹

\(\frac{\partial L}{\partial W_2}=\frac{\partial L}{\partial y} \frac{\partial y}{\partial s_2} \frac{\partial s_2}{\partial W_2} = (y-y_{\text{true}}) f’(s_2) z= \delta _{1}f'(s_2)z,\) 

\(\frac{\partial L}{\partial W_1}=\frac{\partial L}{\partial y} \frac{\partial y}{\partial s_2} \frac{\partial s_2}{\partial z} \frac{\partial z}{\partial s_1} \frac{\partial s_1}{\partial W_1} = \delta_1 f’(s_2) W_2 f’(s_1) x = \delta_2 f’(s_1) x.\)

여기서 숨은층의 신호합은 \(s_1 = W_1 x\) 출력층의 신호합은 \(s_2 = W_2 z\)로 썼다. 그리고 출력층의 오차를 \(\delta_1 = y – y_{\text{true}}\)로 정의했고, 이 출력층 오차 \(\delta_1\)가 가중치 \(W_2\)를 가지고 숨은층으로 전파된 오차를 \(\delta_2 = \delta_1 f’(s_2) W_2\)으로 정의했다. 이 알고리즘이 “오차역전파”로 불리는 이유가 여기에 있다. 여기서 미분연산을 한 \(f(s)\)의 기울기를 \(f’(s) = \partial f / \partial s\)로 줄여서 표현한다.

미분과 체인법칙이라는 수학지식만 있으면 누구나 유도할 수 있는 이 기념비적인 알고리즘은 1986년 데이비드 러멜하트^{David Rumelhart}, 제프리 힌튼^{Geoffrey Hinton}, 로날드 윌리엄스^{Ronald Willams}에 의해 네이처^Nature지에 실렸다.[3] 두 번째 저자인 힌튼은 심리학과 컴퓨터공학을 전공한 과학자로 현재 머신러닝의 대부로 불리는 분이다.([그림7]) 머신러닝 분야에서 대부분의 굵직한 돌파구들이 힌튼 연구실에서 나왔다. 우리는 이제 보편적 어림정리에 따라 어떤 입력 \(x\)와 출력 \(y\)가 주어져도 둘 사이의 관계를 표현할 수 있는 신경망이 존재함을 알았고, 오차역전파 알고리즘을 사용해서 해당 신경망의 최적화된 매개변수 \((W_1, W_2)\)을 결정할 수 있게 되었다.

^그림7 제프리 힌튼 영상

보편적 어림정리와 오차역전파 알고리즘은 머신러닝을 부활시키는 듯했다. 하지만 역설적이게도 이 성공적인 정리와 알고리즘은 더 큰 성공을 가로막는 장애물이 된다. 숨은층 하나면 충분하다는 시벤코의 보편적 어림정리는 두 개 이상의 숨은층을 상상하는 사람들의 의지를 꺾기에 충분했다. 몇 년 전 한국을 방문했던 시벤코가 농담삼아 했던 얘기가 재미있다. 보편적 어림정리 때문에 딥러닝의 출현이 늦춰졌다고 사람들이 자신을 책망한다고 했다.

그리고 위 오차역전파 알고리즘을 자세히 살펴보면 숨은층이 늘어나면 오차 기울기에서 활성화함수의 기울기 \(f’(s)\)가 계속 곱해짐을 볼 수 있다. \(f(s) = 1/(1+\exp(-s))\)을 활성화함수로 사용할 경우 \(f’(s)\)는 0과 1사이의 작은 실수값을 가지게 되고 이 작은 수를 거듭해서 곱하면 오차 기울기가 매우 작아지게 된다. 이렇게 되면 입력층에 가까운 숨은층의 매개변수는 갱신이 거의 안된다. 이 문제가 다수의 숨은층을 가지는 신경망의 학습인 딥러닝의 출현을 10년 이상 늦추게 된다. 현재는 딥러닝이 여러 분야에서 놀라운 성능을 보여주고 있는데, 이는 ReLU^{Rectified Linear Unit}라고 하는 새로운 활성화함수의 도입, GPU^{Graphics Processing Unit}를 포함하는 컴퓨터 계산 능력의 비약적 발전, 그리고 학습에 필요한 빅데이터의 등장으로 가능하게 되었다.

이제 몇 가지 생략했던 부분을 짚어보고 꼼꼼한 독자들이 던질 수 있는 질문을 살펴보자. \(x\)와 \(y\)사이의 관계를 학습하기 위해서는 데이터가 필요하다. \(N\)개의 입·출력 데이터 짝 \(\{ x(t), y_{\text{true}}(t) \}_{t=1}^N\)가 있다고 하자. 이 경우 전체 데이터의 학습오차는 다음처럼 정의할 수 있다.

\(L_N(W_1, W_2) = \sum_{t=1}^N [y(t) – y_{\text{true}}(t) ]^2\)

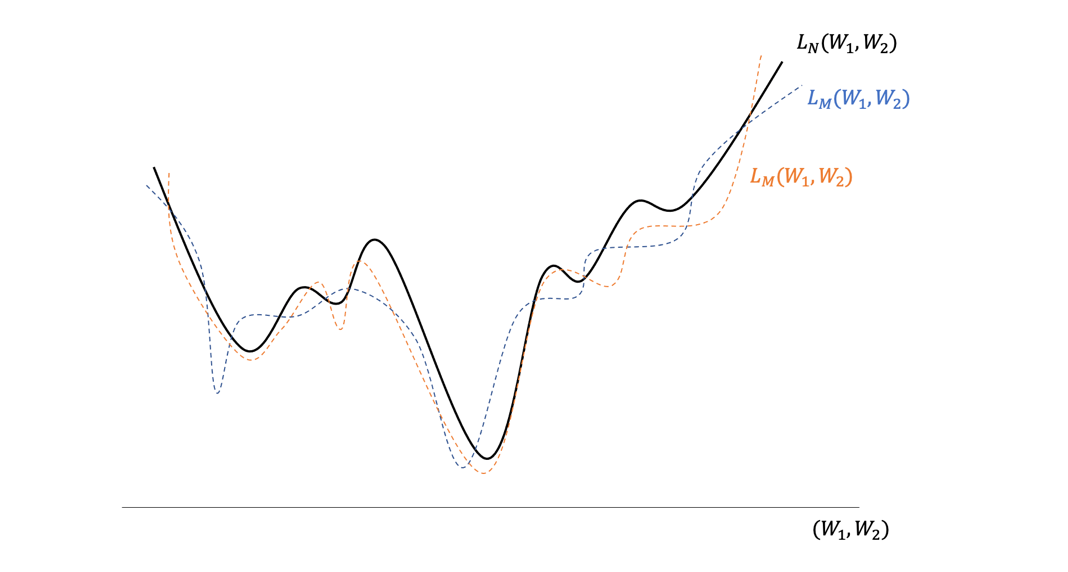
여기서 이런 질문을 할 수 있겠다. 오차함수 \(L_N (W_1, W_2)\)의 경관에서 최소점이 과연 하나만 존재할까? 산맥의 모습에서 상상할 수 있듯이 낮은 골짜기들이 여기저기 존재할 것이다. 이 골짜기들 가운데 제일 깊은 골짜기를 어떻게 찾을 수 있을까? 경사하강법을 사용하면 출발 위치에 따라서 하산 위치가 정해질 것이고 이렇게 하산하면 제일 깊은 골짜기를 찾지 못하게 된다. 이 문제를 해결한 것이 확률적 경사하강법^{Stochastic Gradient Descent Method}이다. 전체 데이터를 사용하는 대신에 \(M(<N)\)개의 묶음 데이터를 무작위로 선택해서 \(L_M (W_1, W_2)\)을 정의하고 이 오차함수의 기울기를 따라 매개변수를 갱신한다. 그리고 다시 \(M\)개의 묶음 데이터를 무작위로 선택해서 매개변수를 갱신하는 과정을 반복하게 된다. 이렇게 하면 학습과정 중에 오차함수의 경관이 조금씩 바뀌게 되면서 지역적인 최소점에 갇히는 것은 막으면서 진정한 최소점에 도달할 수 있게 된다.([그림8])

여기서 전체 데이터에 대한 오차함수 \(L_N (W_1, W_2)\)의 경관은 절대적인가 하면 그게 그렇지가 않다. 이는 우리가 가진 유한한 데이터 \(N\)개에서 얻은 경관일 뿐이다. 이를 학습해서 얻은 최적의 매개변수 \((W_1, W_2)\)가 새로운 데이터 \(x\)와 \(y\)의 관계도 일반적으로 잘 설명해줄 것이라는 보장이 없다. 이를 일반화 문제라고 한다. 매개변수가 매우 많은 신경망을 이용하는 딥러닝은 신기하게도 일반화를 잘한다는 사실이 알려져 있는데 그 이유는 아직 명쾌하게 밝혀지지 않았다.

이번 글에서 다룬 머신러닝은 입력과 출력이 짝으로 주어진 데이터를 학습하는 분류모형이었다. 다음 글에서는 입력과 출력의 구별이 없는 일반적인 데이터를 학습하는 모형인, 생성모형의 개념을 소개하겠다.