볼츠만 머신: 생성모형의 원리

기억^Memory은 어떻게 형성되는 것일까? 우리의 뇌는 어떻게 경험을 기록하고, 어떻게 저장된 기억을 꺼낼까? 이 질문은 물리학자 존 홉필드^{John Hopfield}에게도 흥미로운 질문이었던 모양이다. 홉필드는 1982년 기억의 원리로 홉필드 네트워크를 제안했다.[1] 이번 글에서는 이 아이디어를 통해서 머신러닝의 생성모형에 대해서 살펴보자.

우리는 이전 글 “퍼셉트론: 인공지능의 시작”에서 퍼셉트론을 통해서 분류모형을 공부했다. 분류모형은 입력 \(x\)와 출력 \(y\) 사이의 관계 \(y=f(x)\)를 신경망으로 구현하는 것이고, 생성모형은 데이터 \(x\)의 분포 \(P(x)\)를 신경망으로 구현하는 것이다. 머신러닝의 유명한 예제인 개와 고양이의 이미지 데이터를 바탕으로 두 모형의 목적을 구별해 보자. 분류모형은 개/고양이 이미지 \(x\)에 대한 라벨 \(y_{\text{true}}=0/1\)을 분류하는 학습이다. 반면 생성모형은 동물 이미지 \(x\)들이 가진 특징을 추출해서 데이터에 있는 동물들과 닮은 이미지 \(x\)를 생성하는 학습이다. 분류모형의 목적은 모형이 예측하는 \(y=f(x)\)와 데이터의 라벨 \(y_{\text{true}}\)을 가깝게 만드는 것이고, 생성모형의 목적은 주어진 이미지 \(x\)에 대한 데이터의 분포 \(P_0(x)\)와 모형의 분포 \(P(x)\)를 가깝게 만드는 것이다.

^그림1 존 홉필드 유튜브 영상 “Collective Properties of Neuronal Networks”

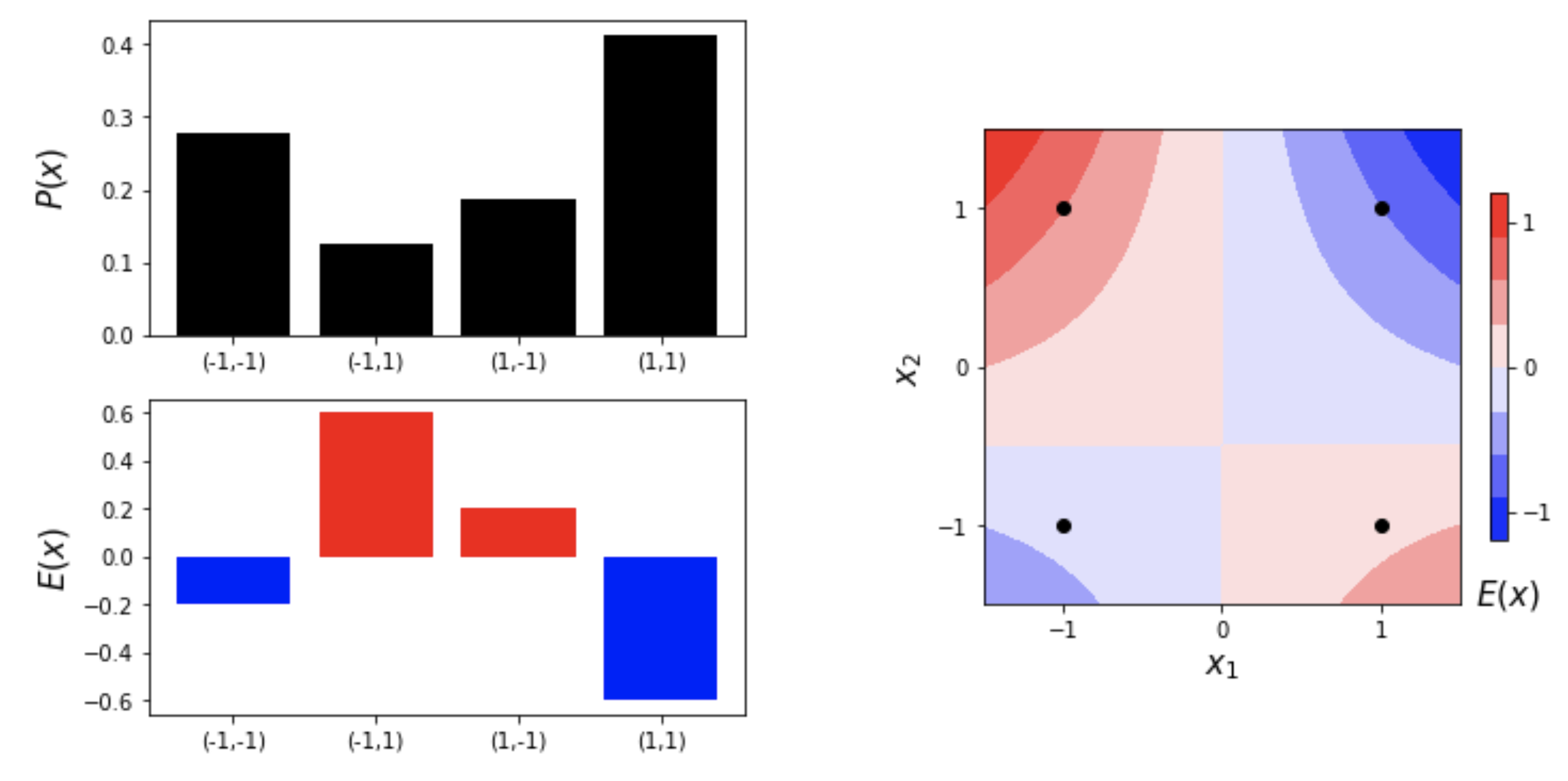
2차원 패턴 \(x=(x_1, x_2) \in \{ (-1,-1), (-1, 1), (1,-1), (1,1)\}\)가 \(\{3, 1, 2, 4\}\)번씩 관찰되었다고 해보자. 각 패턴의 확률을 \(P_0(x)\)로 정의하자. 가령, \(P_0(1,1)=0.4\)가 된다. 이 관찰을 기억하기 위해서 패턴과 빈도수를 통째로 저장할 수 있겠다. 그런데 데이터를 가만히 살펴보면, \(x_1\)과 \(x_2\)의 부호가 같은 패턴이, 그리고 \(x_1 =1\)인 패턴들이 조금 더 많이 관찰되는 것을 알 수 있다. 이런 규칙을 눈치챈 독자라면 “모형”을 이용해서 데이터를 영리하게 저장할 수 있을 것이다. 에너지 기반의 모형에 경험이 많았던 물리학자 홉필드는 패턴의 “에너지”를 다음과 같이 설계하였다.

\begin{equation}
\tag {1}
E(x) = -W x_1 x_2 – b_1 x_1 -b_2 x_2
\end{equation}
그리고 에너지가 낮은 패턴은 더 자주 관찰되는 볼츠만 분포를 가정한다.¹

\begin{equation}
\tag {2}
P(x) = \frac{\exp{[-E(x)]}}{Z}
\end{equation}

여기서 \(Z=\sum_{x} \exp [-E(x)]\)는 모든 패턴에 대해서 확률 \(P(x)\)의 합이 1이 되게 만들어 주는 상수이다. 이렇게 확률을 정의하면 모든 패턴에 대한 확률 값이 자동으로 양수가 된다. 이 에너지 모형의 매개변수 \((W, b_1, b_2)\) 값을 잘 정하면 모형의 확률 \(P(x)\)가 데이터의 확률 \(P_0(x)\)와 비슷해질 것이다. 홉필드는 좋은 매개변수 값을 금세 알아차렸던 모양이다.

\begin{eqnarray}
\tag {3}
b_1 &=& \sum_{x} x_1 P_0(x) \\
\tag {4}
b_2 &=& \sum_{x} x_2 P_0(x) \\
\tag {5}
W &=& \sum_{x} x_1 x_2 P_0(x)
\end{eqnarray}

즉, 데이터에서 \(x_1\)과 \(x_2\)의 편향이 \(b_1\)과 \(b_2\)과 일치하고, \(x_1\)과 \(x_2\)의 상관관계가 \(W\)와 일치할수록 \(E(x)\) 값은 낮아지고 패턴의 확률 \(P(x)\)은 커진다. 홉필드는 패턴의 기억이 에너지가 낮은 동역학적 끌개^Attractor에 저장된다고 생각했다.

홉필드 네트워크에서 좋은 \(W\)값이 정해지는 원리는 뇌과학에서 밝혀진 헤비안^hebbian 규칙과 닮은 구석이 있다. \(x_i\)를 \(i\)번째 뉴런의 발화정도로 해석해 보자. “Fire together, wire together”로 요약되는 헤비안 규칙은 동시에 발화하는 뉴런들의 시냅스 연결은 강화되고, 그렇지 않은 뉴런들의 연결은 퇴화한다는 것이다.[2]

이렇게 모형을 이용해서 데이터를 저장하게 되면 세 가지 이로움이 생긴다. 첫째, 데이터의 패턴과 빈도수를 통째로 저장하는 것보다 세 개의 숫자 \((W, b_1, b_2)\)을 저장하는 것이 훨씬 수월하다.² 둘째, 관찰된 데이터에는 없었던 패턴의 관찰확률을 유추할 수 있다. 가령 \(x = (0.5, 0.5)\)라는 패턴은 관찰된 적이 없지만, 확률모형은 \(P(0.5, 0.5)\)³ 값을 예측해준다. 셋째, 이 확률모형을 이용해서 상대적으로 확률이 높은 패턴을 추출할 수 있다. 이것이 바로 생성모형의 원리가 된다.

홉필드가 사용한 매개변수를 쓰면 모형의 확률 \(P(x)\)와 데이터의 확률 \(P_0(x)\)가 가깝게 된다. 이제부터 우리는 두 확률분포를 더 가깝게 만들어 보려고 한다. 이 알고리즘은 1985년 데이비드 애클리^{David Ackley}, 제프리 힌튼^{Jeoffrey Hinton}, 테렌스 세즈노프스키^{Terrence Sejnowski}에 의해서 제안되었다.[3] 이들이 사용한 에너지 모형은 홉필드 네트워크와 동일하고, 확률은 여전히 볼츠만 분포를 따른다. 아마도 이 알고리즘이 볼츠만머신으로 불리는 이유가 여기에 있으리라. 이듬해 1986년 오차역전파 알고리즘을 발표하는 제프리 힌튼이 볼츠만머신에도 관심을 가졌던 사실이 흥미롭다. 컴퓨터 공학자이자 심리학자였던 힌튼은 끊임없이 인간의 뇌가 학습하는 원리를 알고 싶었을 것이다.

힌튼은 공학적 규칙인 오차역전파 알고리즘보다는 뇌과학의 헤비안 규칙과 닮은 볼츠만머신에 더 많은 관심을 가졌을 것 같다. 이제부터 이들이 모형의 분포 \(P(x)\)와 데이터의 분포 \(P_0(x)\) 사이의 거리를 어떻게 정의했는지 살펴보자.

\begin{equation}
\tag {6}
D_{KL}(P_0||P) = \sum_{x} P_0(x) \log \frac{P_0(x)}{P(x)}
\end{equation}
두 확률분포 사이의 거리를 정의하는 수많은 방식 가운데 쿨백-라이블러 거리^{Kullback-Leibler divergence}를 선택한 것은 탁월한 결정이었다. 이는 두 분포 사이의 상대적 정보 또는 상대적 엔트로피로도 불리는 측정량으로 정보이론에 뿌리를 두고 있다.[5]

수학적으로 \(D_{KL}(P_0||P)\)는 \(P(x)\)에 대한 오목함수이고 \(P(x)=P_0(x)\)에서만 \(D_{KL}(P_0||P_0)=0\)이 된다. 따라서 임의의 \(P(x) \neq P_0(x)\)에 대해서 \(D_{KL}(P_0||P) > 0\)는 항상 양수가 된다.

이제부터 우리가 할 일은 볼츠만머신의 매개변수인 \((W, b_1, b_2)\)를 잘 조정해서 \(E(x)\)를 바꾸고, 이는 \(P(x)\)에 영향을 주고, 궁극적으로 \(P_0(x)\)와의 거리인 \(D_{KL}(P_0||P)\)를 줄이는 최적화 문제를 푸는 것이다. 경사하강법을 써서 수치적으로 접근을 하면 다음과 같다. \(W\)를 최적화하는 것을 중심으로 서술을 해보겠다.⁴

\begin{equation}
\tag {7}
W \leftarrow W – \alpha \frac{\partial D_{KL}}{\partial W}
\end{equation}
여기서 기울기를 살펴보자.

\begin{eqnarray}
\tag {8}
-\frac{\partial D_{KL}}{\partial W} &=& \frac{\partial}{\partial W}\bigg[ \sum_{x} P_0(x) \log P(x) – P_0(x) \log P_0(x) \bigg] \\
\tag {9}
&=& \frac{\partial}{\partial W}\bigg[ \sum_{x} P_0(x) \big(-E(x) – \log Z \big) \bigg] \\
\tag {10}
&=& \sum_{x} x_1 x_2 P_0(x) – \frac{\partial \log Z}{\partial W} \\
\tag {11}
&=& \sum_{x} x_1 x_2 P_0(x) – \sum_{x} x_1 x_2 P(x)
\end{eqnarray}
해당 기울기는 \(x_1\)과 \(x_2\)의 상관관계를 데이터의 분포 \(P_0(x)\)에서 구한 기대값과 모형의 분포 \(P(x)\)에서 구한 기대값의 차이가 된다. 위 경사하강법을 통해서 \((W, b_1, b_2)\)를 업데이트하면 \(D(P_0||P)\)가 줄어들면서 모형의 분포 \(P(x)\)가 데이터의 분포 \(P_0(x)\)에 점점 가까워지게 된다. 

볼츠만 분포를 정의하고, 쿨백-라이블러 거리를 써서 설계한 볼츠만머신은 대단히 멋진 알고리즘이다. 그런데 치명적인 문제가 한 가지 있다. 데이터 \(x=(x_1, x_2, \cdots, x_d)\)의 차원 \(d\)가 큰 경우 \(\sum_x\)으로 합해야 할 패턴의 가짓수가 너무 많아서 위 식을 통해 기울기를 계산하는 것이 실질적으로 불가능해진다. \(d=20\)인 경우만 생각해도 전체 패턴의 가짓수가 대충 백만 개 정도 된다. 이렇게 엄청난 합을 계산해야지 매개변수를 겨우 한 번 갱신할 수 있다. 따라서 볼츠만머신은 차원이 큰 문제에서는 매우 비효율적인 알고리즘이 되고 만다.

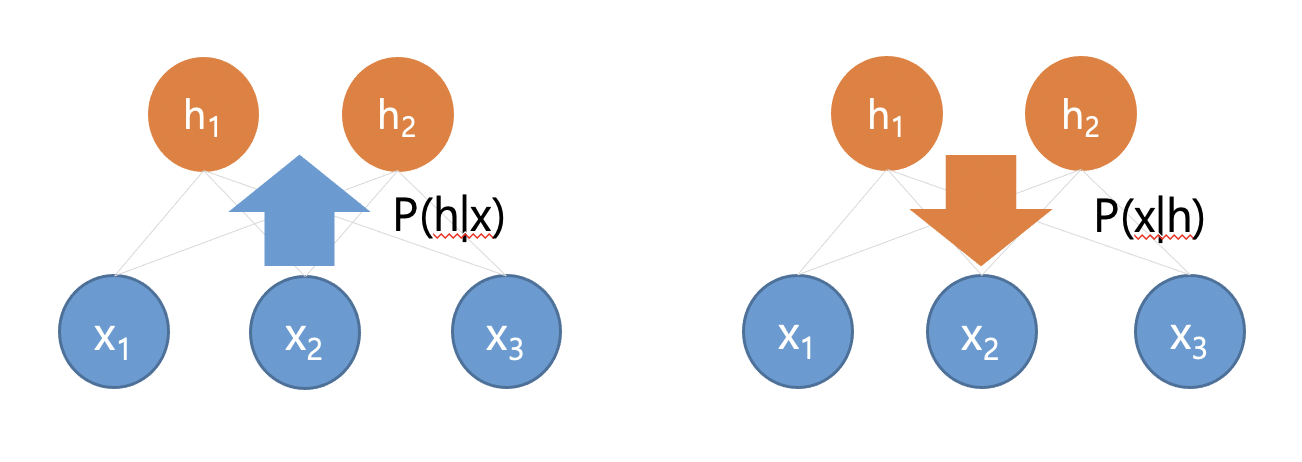
이듬해 1986년 전산 언어학자인 폴 스몰렌스키^{Paul Smolensky}는 데이터 \(x\)를 표현하는 다른 그래프^Graph 구조를 제안한다.[4] 그가 제안한 제한된 볼츠만머신^{Restricted Boltzmann Machine, RBM}은 데이터를 표현하는 변수 \(x\)와 더불어 이진값을 가지는 숨은 변수 \(h\)를 포함하고 있다.([그림 6]) 볼츠만머신은 모든 \(x_i\)들이 서로 연결된 구조이다. 하지만 제한된 볼츠만머신에서는 \(x_i\)들끼리는 연결이 없고, \(h_j\)들끼리도 연결이 없다. 오직 \(x_i\)와 \(h_j\) 사이의 연결만 허락된 구조이다. 즉, 볼츠만머신에서는 관찰된 패턴의 부분 \(x_i\)들이 서로 직접적으로 관계를 맺고 있는데, 제한된 볼츠만머신에서는 이들 사이의 관계가 숨은 내부적 표현 \(h_j\)들을 통해서 간접적으로 맺어진다.

제한된 볼츠만머신에서 패턴 \((x,h)\)의 에너지는 다음과 같이 정의된다.

\begin{equation}
\tag {12}
E(x,h) = – \sum_{i,j}W_{ij} x_i h_j – \sum_i a_i x_i -\sum_j b_j h_j
\end{equation}
그리고 패턴 \((x,h)\)에 해당하는 확률은 역시 볼츠만 분포를 따르는 \(P(x,h) = \exp[-E(x,h)]/Z\)로 정의가 된다. 그러면 제한된 볼츠만머신의 확률 \(P(x,h)\)는 데이터의 확률 \(P_0(x)\)와 어떻게 비교할까? 데이터의 분포에는 숨은 변수 \(h\)에 대한 정보가 없다. 이 문제는 \(P(x)=\sum_{h} P(x,h)\)를 통해 변수 \(h\)를 하찮게 만듦^{marginalization}으로써 가능하게 된다. 비로소 우리는 쿨백-라이블러 거리 \(D_{KL}(P_0||P)\)를 다시 정의할 수 있고, 경사하강법을 통해서 제한된 볼츠만머신의 매개변수인 \((W_{ij}, a_i, b_j)\)를 업데이트할 수 있게 된다. 가령, \(W_{ij}\)의 업데이트를 결정하는 기울기를 계산해보면 다음과 같다.

\begin{equation}
\tag {13}
-\frac{\partial D_{KL}}{\partial W_{ij}} = \sum_{x,h} x_i h_j P(h|x)P_0(x) – \sum_{x,h} x_i h_j P(x,h)
\end{equation}

눈썰미가 있는 독자는 이 기울기가 볼츠만머신에서와 같이 데이터의 분포와 모형의 분포에서 정의된 \(x_i\)와 \(h_j\)의 상관관계의 차이라는 것을 알아차렸을 것 같다. 여기서 기울기를 계산하려면 여전히 \(\sum_{x,h}\)라는 많은 가짓수의 합을 계산해야 한다. 이것이 볼츠만머신과 제한된 볼츠만머신이 실제 문제에 사용되는 것을 10년 이상 늦추는 원인이었다. 아마도 수많은 시행착오가 있었으리라. 이 문제는 결국 힌튼이 개발한 CD^{Contrastive Divergence} 알고리즘에 의해서 멋지게 해결이 된다.[6]

CD 알고리즘이 적용될 수 있는 모형은 제한된 볼츠만머신이다. 이 머신의 핵심은 \(x_i\)들끼리 그리고 \(h_j\)들끼리 연결없이 독립이라는 것이다. 이 사실은 \(h\)에 대한 조건부 확률을 \(h_j\)들 각각에 대한 조건부 확률의 곱으로 \(P(h|x) = \prod_j P(h_j|x)\)처럼 쪼개서^Factorizable 쓸 수 있게 해준다. 여기서 \(P(h_j|x)\)는 데이터 \(x\)가 주어졌을 때, \(h_j = 0\)이 될지 \(h_j = 1\)이 될지를 결정하는 확률이다. 제한된 볼츠만머신의 에너지와 확률의 규칙을 이용해서 계산을 조금 하면 이 조건부 확률을 계산할 수 있다.

\begin{equation}
\tag {14}
P(h_j=1|x) = \frac{1}{1+\exp(-s_j)} = f(s_j)
\end{equation}
이 식에서 \(s_j = \sum_i W_{ij}x_i + b_j\)는 데이터 \(x\)가 일종의 순전파를 통해서 \(h_j\)에 도착한 신호로 해석할 수 있다. 제한된 볼츠만머신에서는 숨은 노드 \(h_j\)의 값이 확률적으로 \(0\) 또는 \(1\)이 된다. 이 경우 \(h_j\)의 기대값은 \(\mathbb{E}[h_j] = 0 \cdot P(h_j=0|x) + 1 \cdot P(h_j=1|x)\)으로 이 값은 \(f(s_j)\)이다. 제한된 볼츠만머신에서 \(x\)가 순전파된 기대값 \(\mathbb{E}[h_j]\)은 사실 지난 연재에서 보았던 퍼셉트론에서 숨은 뉴런의 활성함수 \(f(s_j)\)와 일치한다.

제한된 볼츠만머신에서 \(x\)와 \(h\)의 대칭적인 구조는 역전파에 해당하는 조건부 확률 \(P(x_i|h)\)도 정의할 수 있게 해준다.([그림 7]) 우리는 순전파 확률 \(P(h_j|x)\)와 역전파 확률 \(P(x_i|h)\)을 이용해서 표본추출^Sampling을 할 수 있다. 이렇게 순전파와 역전파를 통해서 얻은 표본 \(x\)와 \(h\)는 에너지 \(E(x,h)\)를 낮출 수 있는 서로의 짝꿍을 선호한다. 

자, 데이터에서 첫 번째 표본을 하나 선택해서 \(x(1)\)라고 하자. 그리고 순전파를 통해서 \(h_j(1)\)들을 하나씩 얻고 이들로 이루어진 \(h(1)=(h_1(1), h_2(1), \cdots)\)을 결정한다. 이번에는 \(h(1)\)을 역전파시켜서 \(x(1)\)을 새로 결정한다. 여기서 우리는 위 첨자를 써서 \(x(1)\)를 데이터에서 선택한 원래 표본 \(x^{0}(1)\)와 생성한 새 표본 \(x^{1}(1)\)으로 구별하자. 순전파와 역전파를 \(n\)번 반복하면 우리는 \(x^{0}(1) \rightarrow h^{0}(1) \rightarrow x^{1}(1) \rightarrow h^{1}(1) \rightarrow \cdots \rightarrow x^{n}(1) \rightarrow h^{n}(1)\)을 얻게 된다. 우리는 두 번째, 세 번째, …, \(M\) 번째 데이터 표본에서 이 과정을 반복한다. CD 알고리즘의 핵심 아이디어는 \(x_i\)와 \(h_j\)의 상관관계를 이 표본추출을 통해서 어림할 수 있다는 것이다. 즉, \(\sum_{x,h}\)라는 무지하게 많은 가짓수의 합을 계산하는 대신 \(M\)개의 표본에서 얻은 통계량을 이용하는 전략이다.

\begin{eqnarray}
\tag {15}
\sum_{x,h} x_i h_j P(h|x)P_0(x) \approx \frac{1}{M} \sum_{m=1}^M x_i^{0}(m) h_j^{0}(m) \\
\tag {16}
\sum_{x,h} x_i h_j P(x,h) \approx \frac{1}{M} \sum_{m=1}^M x_i^{n}(m) h_j^{n}(m)
\end{eqnarray}

첫 번째 식에서 데이터의 분포 \(P(h|x)P_0(x)\)를 따르는 표본은 데이터 표본 \(x^0_i\)과 짝을 이루는 \(h^0_j\)로 이루어진 (\(x^0_i, h^0_j\))으로 어림할 수 있고, 두 번째 식에서 모형의 분포 \(P(x,h)\)를 따르는 표본은 순전파와 역전파를 \(n\)번 반복했을 때의 짝꿍 (\(x^n_i, h^n_j\))으로 어림할 수 있다.⁵ 이를 CD\(_n\) 알고리즘이라고 부른다. 놀라운 것은 \(n=1\)에 해당하는 CD\(_1\)으로도 꽤 좋은 어림이 된다는 것이다. 비로소 차원이 큰 문제에서도 제한된 볼츠만머신을 학습할 수 있게 되었다.

이제 이 머신을 이용해서 생성을 한번 시도해 보자. CelebA라는 유명 연예인 사진을 모아 둔 데이터가 있다. 각 사진은 크기가 \(32 \times 32\) 픽셀이고 RGB 컬러를 가졌으므로 이를 표현하는 \(x\)의 차원은 \(d = 32 \times 32 \times 3\)이 된다. 아래 인물 사진들은 제한된 볼츠만머신을 응용한 머신으로 CelebA 데이터를 학습해서 생성한 사진들이다.[8]([그림 8])

이들은 세상에 존재하지 않는 인물들로, 제한된 볼츠만머신에서 확률 \(P(x,h)\)가 높은 표본 \(x\)들을 추출해서 얻은 것이다.

이번 글에서는 에너지 기반의 모형인 볼츠만머신을 중심으로 생성모형의 원리에 대해 소개했다. 최근에는 변분추론^{variational inference}에 기반한 변분오토인코더^{Variational Autoencoder, VAE},[9] 분류모형을 기발하게 응용한 적대적생성망^{Generative Adversarial Network, GAN}[10]이 개발되어서 여러 분야에서 생성모형들이 활발하게 응용되고 있다.

다음 글에서는 흔히들 블랙박스로 취급하는 신경망의 학습과정을, 정보의 전달과 압축으로 해석하는 정보이론^{Information theory}의 관점에서 살펴보려고 한다.