아침에 알록달록한 색깔의 작은 고무줄로 아이의 머리를 묶어주다 보니, 문득 요즘 아이들도 고무줄놀이를 하는지 궁금해지더군요. 고무줄놀이는 두 명이 긴 고무줄을 팽팽히 당겨 낮은 위치에 고정하면, 다른 친구들이 노래에 맞추어 고무줄은 밟고 넘으며 다양한 동작을 취하는 놀이입니다. 당연한 이야기지만, 팽팽히 당겨진 고무줄은 직선이 되고 당겨진 고무줄을 다리로 건드리면 진동하면서 직선으로 돌아옵니다. 단순한 관찰이지만, 이와 비슷한 현상을 다양체에서 구현하고자 리차드 해밀턴Richard S. Hamilton교수님은 1982년[7]에 리찌 흐름Ricci flow을 만들었고, 20년 후[10] 그리고리 페렐만Grigori Perelman교수님은 리찌 흐름을 이용하여 3차원 푸앵카레 추측Poincare conjecture이 참임을 증명합니다.
아무래도 1차원인 고무줄로 3차원 다양체를 이해하기 힘드니, 2차원의 예로 고무풍선을 생각해보겠습니다. 풍선을 팽팽해지도록 바람을 불어서 묶으면 달걀모양이 됩니다. 이 상태의 풍선을 손으로 눌렀다가 떼면, 원래의 형태로 돌아옵니다. 왜 이런 일이 벌어질까요? 늘어난 풍선은 고무의 탄성에 의해 원래 모양으로 돌아가려고 하는 장력이 발생합니다. 장력은 풍선 내부에 갇힌 공기를 압축시켜서 내부의 기압을 올립니다. 이로 인한 내부와 외부의 기압 차이는 풍선을 밀어내려는 압력을 발생시킵니다. 압력과 장력의 합력은 풍선을 움직이게 하고, 풍선의 운동은 마찰을 일으키므로 역학적 에너지가 감소합니다. 결국에 운동 에너지를 모두 잃고 압축된 공기와 늘어난 풍선에 저장된 퍼텐셜 에너지(위치 에너지)가 최소가 되면, 풍선은 운동을 멈추고 달걀모양으로 고정됩니다. 이와 같은 원리로 비눗방울이 둥근 구의 모양이 되는 것도 설명할 수 있습니다.
재미있는 점은 고무줄과 비눗방울이 가장 작은 퍼텐셜 에너지를 가지기 위해서는 직선이나 둥근 구와 같이 단순한 형태를 가져야 한다는 것입니다. 그렇다면 자연의 법칙을 따라 움직이는 풍선과 같이, 주어진 곡면이 스스로 연속적으로 움직여서 점점 에너지를 잃고 최소 퍼텐셜 에너지를 가지는 형태로 수렴하도록 만들 수 있을까요? 이것이 가능하다면 최소 에너지를 가지는 최종 형태는 단순한 모양일 것으로 기대할 수 있으니, 최초에 주어진 곡면의 위상을 알 수 있지 않을까요?
이와 같은 질문에 답을 하기 위해, 곡면이나 미분다양체의 움직임을 연구하는 학문을 기하학적 흐름geometric flow이라고 부릅니다. 기하학적 흐름을 연구하기 위해서는 먼저 어떤 방식으로 스스로 흐르게 할지 고민해보아야 합니다. 위에 언급한 고무줄이나 풍선은 파동방정식을 따라 움직이지만, 사실 마찰이 역학 에너지를 감소시키는 것이 가장 중요합니다. 따라서 흐름을 연구하는 기하학적 해석학자들은 가장 단순하고 효과적으로 에너지를 감소시키기 위해서 파동방정식이 아닌 열방정식을 기하학적 흐름에 도입했습니다.
열이 시간에 따라 전도될 때, 온도 함수가 만족하는 다음의 편미분방정식을 만족하고, 이 방정식을 열방정식이라고 부릅니다.
\(\partial_t u(x,t) = \partial_x^2 u(x,t).\)
또한 함수의 변화량을 측정하는 아래의 적분값을 디리클레 에너지Dirichlet Energy라고 정의합니다.
\(E(t):=\int_0^L \frac{1}{2}\big|\partial_x u(x,t)\big|^2 dx.\)
그리고 열방정식이 온도 함수를 어떻게 변화시키는지 예상하기 위해, 온도조절기구를 이용하여 금속 막대기의 양쪽 끝점의 온도를 \(0\)도로 고정시켰다고 가정합니다.([그림1])
\(u(0,t)=u(L,t)=0.\)
이 조건은 끝점에서의 온도 변화가 없음을 뜻하기 때문에 \(\partial_tu(0,t)=\partial_tu(L,t)=0\)임을 알 수 있습니다. 이제 부분적분을 이용하여 다음과 같이 열방정식이 에너지를 단조감소시키는 것을 알 수 있습니다.
\(\frac{d}{dt} E(t)= \int_0^L (\partial_x u) (\partial_x \partial_t u) dx=(\partial_x u) ( \partial_t u)\bigg|^L_0 -\int_0^L (\partial_x^2 u) (\partial_t u) dx=- \int_0^L |\partial_x^2 u|^2 dx\leq 0.\)
결국 시간이 무한히 흐르면 초기 온도 분포와 관계없이 디리클레 에너지가 \(0\)이 되어1 온도 함수의 도함수가 \(0\)이 됩니다. 즉, 양쪽 끝점을 비롯한 막대 위의 모든 점에서의 온도가 \(0\)도가 됩니다. 이와 비슷하게 냉난방기구가 없는 단열된 방안의 온도는 시간이 흐름에 따라 균일하게 맞추어집니다.
이처럼 열방정식은 단순한 구조를 가지며, 시간이 흐름에 따라 퍼텐셜 에너지의 일종인 디리클레 에너지를 효과적으로 감소시킵니다. 그렇다면 곡선에 열방정식을 적용하면 어떻게 될까요? 가장 단순하고 자연스러운 열방정식은, 움직이는 곡선의 위치 벡터position vector \(\mathbf{x}:S^1\times [0,T)\to \mathbb{R}^2\)에2 대한 아래의 편미분방정식입니다.
\(\frac{\partial}{\partial t} \mathbf{x}(\theta,t)=\frac{1}{\|\partial_\theta\mathbf{x}(\theta,t)\| }\frac{\partial}{\partial \theta}\left(\frac{\partial_\theta \mathbf{x}(\theta,t)}{\|\partial_\theta\mathbf{x}(\theta,t)\|}\right).\)
여기서 호의 길이 매개변수arc length parameter \(s\)를 이용하면 다음과 같이 단순하게 다시 적을 수 있습니다.
\(\partial_t \mathbf{x} = \partial_s^2 \mathbf{x}.\)
이 방정식을 만족하며 움직이는 곡선의 흐름을 줄어드는 곡선 흐름curve shortening flow이라고 부릅니다.([그림2])
그런데 이 흐름은 자신의 이름이 말해주듯이 곡선의 길이가 \(0\)이 될 때까지 줄입니다. 마치 열방정식이 함수의 디리클레 에너지가 없어질 때까지 감소시키는 것과 같습니다. 이 현상을 고정된 형태로 수렴하는 풍선의 경우와 비교해보겠습니다. 줄어드는 곡선 흐름의 우변에 있는 위치 벡터의 2계 미분은 고무줄 혹은 풍선에 걸려있는 장력과 같습니다. 하지만 풍선의 경우 증가한 내부 기압으로 인한 기압 차이가 외부로 향하는 압력을 발생시키지만, 줄어드는 곡선 흐름은 압력을 고려하지 않습니다. 따라서 길이를 줄이려는 힘만 있어서 곡선이 없어질 때까지 줄어들기만 합니다. 추가로 풍선은 장력과 압력의 합력이 가속도로 치환되는 것에 비하여, 위의 흐름은 우변의 2계 미분 값을 좌변과 같이 속도로 치환합니다.
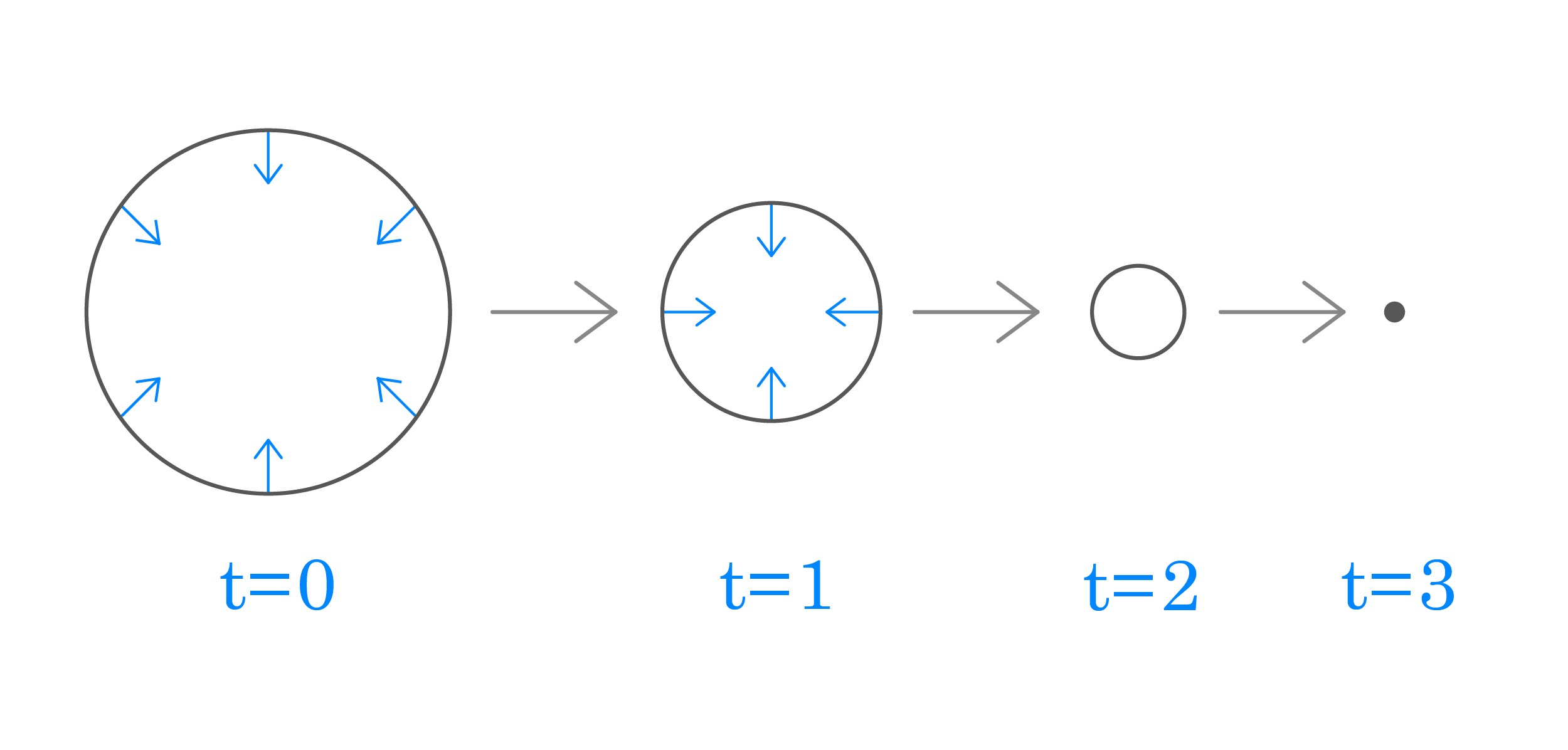
한 가지 간단한 예로, 둥근 원의 흐름을 생각해보겠습니다. 위치 벡터의 2계 미분 값의 크기는 곡률과 같고, 원은 모든 점에서 같은 크기의 곡률을 가집니다. 따라서 줄어드는 곡선 흐름은 원을 모든 점에서 같은 속도를 가지고 줄어들게 하여, 둥근 원의 모양을 유지한 채 크기만 줄어들게 합니다. 결국에 이 흐름은 둥근 원을 점으로 수렴시킵니다.([그림3])
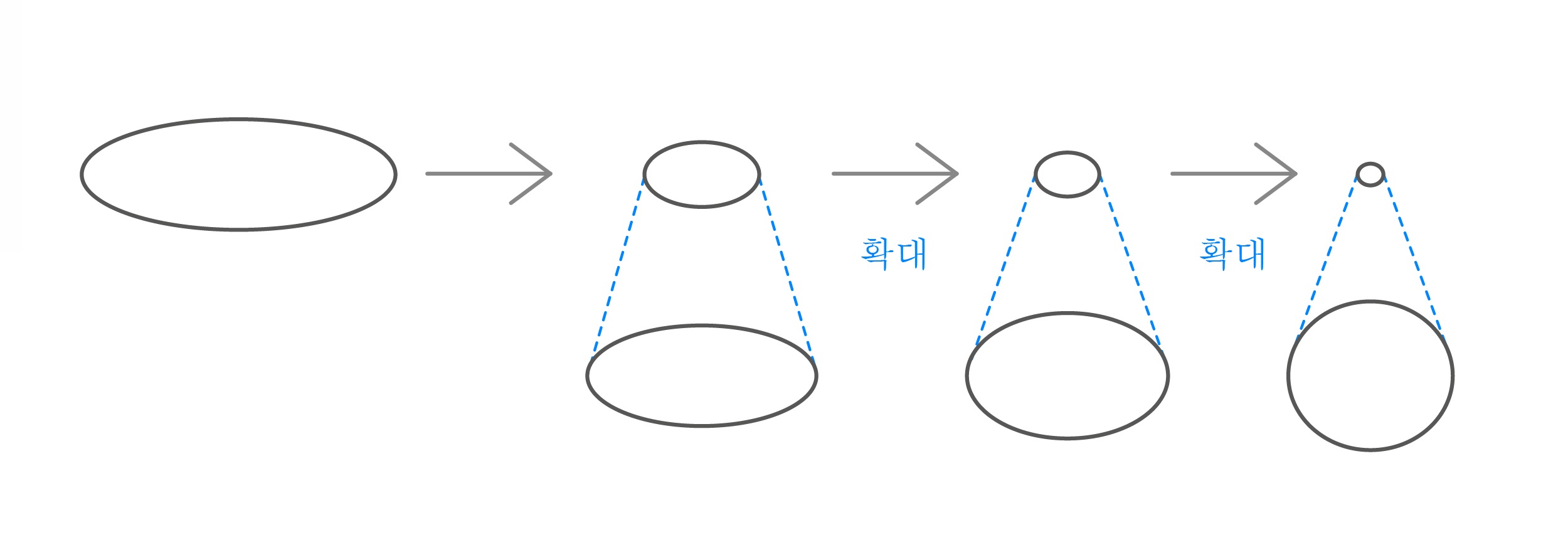
조금 더 복잡한 예를 들면, 1986년[5] 마이클 게이지Michael Gage교수님은 해밀턴 교수님과 함께 평면 위의 볼록한 폐곡선의 흐름은 볼록성을 유지하며 한 점으로 수렴하며, 줄어들고 있는 볼록 폐곡선을 일정한 크기를 가지도록 확대해 ㅇ보면 둥근 원으로 수렴한다는 것을 증명했습니다.([그림4])
이런 현상을 짧게 설명하기 위해 둥근 점으로 수렴한다고 하겠습니다. 이후, 1987년[6] 매튜 그레이슨Matthew Grayson 교수님은 평면 위의 임의의 폐곡선은 그 흐름을 따라 볼록한 폐곡선이 됨을 증명하였습니다.([그림5]) 즉, 줄어드는 곡선 흐름은 임의의 폐곡선은 둥근 원으로 부드럽게 변화시킵니다.
이러한 일이 고차원에서도 벌어질 수 있을까요? 예를 들면, 단순-연결되고simply-connected 닫혔으며closed 3차원에 매몰된embedded 곡면을 연속적으로 변화시켜서 둥근 구로 만들 수 있을까요? 놀랍게도 제임스 알렉산더James W. Alexander II교수님이 1924년[1] 발견하신 뿔달린 구Alexander’s horned sphere는 단순-연결된 닫히고 매몰된 곡면이지만 꼬여있어서knotted, 둥근 구로 연속적으로 변화시킬 수 없습니다. 하지만 알렉산더 교수님의 뿔달린 구는 미분 불가능한 곡면이고, 위에 언급한 곡면에 조건들에 부드럽다는smooth 조건을 추가하면 둥근 구로 부드럽게 변화시킬 수 있습니다. 비슷하게 5차원 이상에 매몰된 단순-연결되고 닫힌 부드러운 초곡면은 둥근 구로 변화시킬 수 있습니다. 하지만 4차원에서도 같은 일이 벌어지는지는 아직 모릅니다. 이 4차원에 매몰된 부드러운 단순-연결된 닫힌 3차원 곡면을 둥근 3차원 구로 부드럽게 변화시킬 수 있는지 묻는 질문은 부드러운 4차원 쇤플리스 문제smooth 4-dimensional Schoenflies problem라고 부릅니다. 이 문제는 그 자체로서도 흥미로운 질문이지만, 아직 미해결제인 부드러운 (일반화된) 4차원 푸앵카레 추측과 유사한 문제로서, 기하학적 흐름의 주요 연구주제로 남아있습니다.
고차원의 곡면은 상대성 이론, 아핀 기하학affine geometry, 등주 부등식isoperimetric inequality 등 다양한 목적에 따라 적합한 흐름들을 연구하고 있습니다. 하지만 쇤플리스 문제는 주로 아래의 편미분방정식을 만족시키는 평균 곡률 흐름mean curvature flow를 이용하여 연구를 진행하고 있습니다.
\(\partial_t \mathbf{x} = \Delta_g \mathbf{x}.\)
위의 방정식의 우변은 위치 벡터에 라플라스-벨트라미 연산자Laplace-Beltrami operator를 적용한 값으로서, 모든 방향의 곡률 벡터의 합인 평균 곡률 벡터를 의미합니다. 평균 곡률 흐름은 1978년[3] 케니스 브라케Kenneth A. Brakke교수님이 도입하였고, 1984년[8] 게르하르트 후이스켄Gerhard Huisken교수님께서 평균 곡률 흐름이 볼록한 닫힌 곡면을 둥근 점으로 수렴시킨다는 것을 증명하였습니다. 이 결과는 해밀턴 교수님이 1982년[7]에 증명한 양의 곡률을 가지는 닫힌 3차원 미분다양체의 측량metric이 리찌 흐름을 통하여 둥근 점으로 수렴한다는 연구 결과와 유사한 결과입니다.
80년대에 등장한 기하학적 흐름의 초기 결과인 볼록한 곡면의 둥근 점으로의 수렴성에 관한 증명은 퍼텐셜 에너지를 사용하지 않고, 최대값 원리maximum principle를 사용합니다. 이 증명은 초기부터 곡률이 양의 값을 가지는 조건이 매우 중요해서, 일반적인 곡면으로 결과를 확장할 수 없었습니다. 초기에 알려진 단조감소하는 퍼텐셜 에너지는 곡면의 넓이밖에 없었는데, 곡면이 점으로 수렴하면 당연히 넓이가 0으로 수렴하므로 곡면이 둥근 점으로 수렴하는지 찌그러진 점으로 수렴하는지 알 수 없었습니다.
그러던 중, 1990년[9] 후이스켄 교수님께서 평균 곡률 흐름 \(M_t\subset \mathbb{R}^{n+1}\)에3 따라 주어진 임의의 시공간점 \(X_0=(\mathbf{x}_0,t_0)\in \mathbb{R}^{n+1}\times \mathbb{R}\)을 기준으로 하는 열핵heat kernel을 밀도density로
\(\rho_{X_0}(\mathbf{x},t)=\frac{1}{(4\pi(t_0-t))^{\frac{n}{2}}}\exp\left(-\frac{\|\mathbf{x}_0-\mathbf{x}\|^2}{4(t_0-t)}\right)\)
가지는 수정된 곡면의 넓이가 단조감소한다는 놀라운 발견을 했습니다.4,5
\(\frac{d}{dt}\int_{M_t} \rho_{X_0}(\mathbf{x},t)d\mathcal{H}^n(\mathbf{x},t) =-\int_{M_t}\left|\Delta_g \mathbf{x}+\frac{(\mathbf{x}-\mathbf{x}_0)^\perp}{2(t-t_0)} \right|^2\rho_{X_0}(\mathbf{x},t) d\mathcal{H}^n(\mathbf{x},t) \leq 0.
\)
열핵의 밀도는 기준 시간에 가까워짐에 따라 기준점 근처로 몰리기 때문에, 수렴하는 점과 시간을 기준 시간과 점으로 잡으면 줄어드는 둥근 구는 어떤 양의 상수를 수정된 넓이로 가집니다. 또한 줄어드는 볼록한 곡면은 점점 둥글어지면서 수정된 넓이가 둥근 구의 수정된 넓이로 단조 감소합니다. 2002년[10] 페렐만 교수님은 리찌 흐름도 수정된 넓이와 유사한 퍼텐션 에너지를 단조감소시킨다는 것을 발견하였고, 이는 3차원 푸앵카레 추측 증명에 매우 중요하게 사용되었습니다. 토비아스 콜딩Tobias H. Colding 교수님과 윌리엄 미니코찌William P. Minicozzi II 교수님은 수정된 넓이를 기준점에 의존하지 않고 사용하기 위해 주어진 \(n\)차원 곡면 \(M\)의 엔트로피Entorpy를 다음과 같이 수정된 넓이의 최대값으로 정의했습니다.[4]
\(\text{Ent}(M)=\sup_{X_0\in \mathbb{R}^{n+1}\times \mathbb{R}_+}\int_M \rho_{X_0}(\mathbf{x},0)d\mathcal{H}^n(\mathbf{x})=\sup_{\mathbf{y}\in \mathbb{R}^{n+1},\lambda>0}\int_M (4\pi \lambda)^{-\frac{n}{2}} e^{-\frac{|\mathbf{x}-\mathbf{y}|^2}{4\lambda}}d\mathcal{H}^n(\mathbf{x}).\)
후이스켄 교수님이 발견한 수정된 넓이의 단조감소성에 의해 평균 곡률 흐름 $M_t\)의 엔트로피 \(\text{Ent}(M_t)\)가 단조감소함을 알 수 있고, 이 엔트로피는 평균 곡률 흐름의 가장 중요한 퍼텐셜 에너지로 널리 사용되고 있습니다.
콜딩-미니코찌 교수님의 엔트로피는 곡면의 닮음 변환homothetic transform에 대한 불변량으로서, 줄어드는 둥근 구나 둥근 원통과 같이 자신의 모양을 유지하며 줄어드는 자가동형self-similar 흐름은 엔트로피값이 변하지 않습니다.엔트로피는 열핵 밀도의 기준점을 구나 원통의 중심점으로 잡아야만 흐름에 따라 변하지 않은 수정된 넓이에 비해서, 기준점을 고려하지 않아도 되기 때문에 다루기 편리합니다. 또한 닫힌 곡면의 흐름이 점으로 사라질 때, 점으로 사라지는 순간의 곡면을 마음껏 확대하여도 엔트로피가 변하지 않기 때문에, 확대된 곡면의 모습 관찰에 엔트로피를 유용하게 사용할 수 있습니다.
이제 처음 우리가 이야기했던 가설로 돌아가 보겠습니다. 과연 단힌 곡면의 평균 곡률 흐름은 가장 작은 엔트로피를 가지는 닫힌 곡면으로 수렴할까요? 그리고 가장 작은 엔트로피를 가지는 닫힌 곡면은 무엇일까요?
먼저 두 번째 질문에 대해서는 최근에 명확한 답이 나왔습니다. 2016년[2] 제이콥 번스타인Jacob Bernstein 교수님과 루 왕Lu Wang 교수님은 7차원 이하의 공간에 매몰된 닫힌 초곡면 중에 가장 작은 엔트로피를 가지는 곡면은 둥근 구임을 증명하였습니다. 그리고 2020년[11] 조나단 주Jonathan J. Zhu 박사님이 같은 결과가 모든 차원에서 성립함을 증명하였습니다.
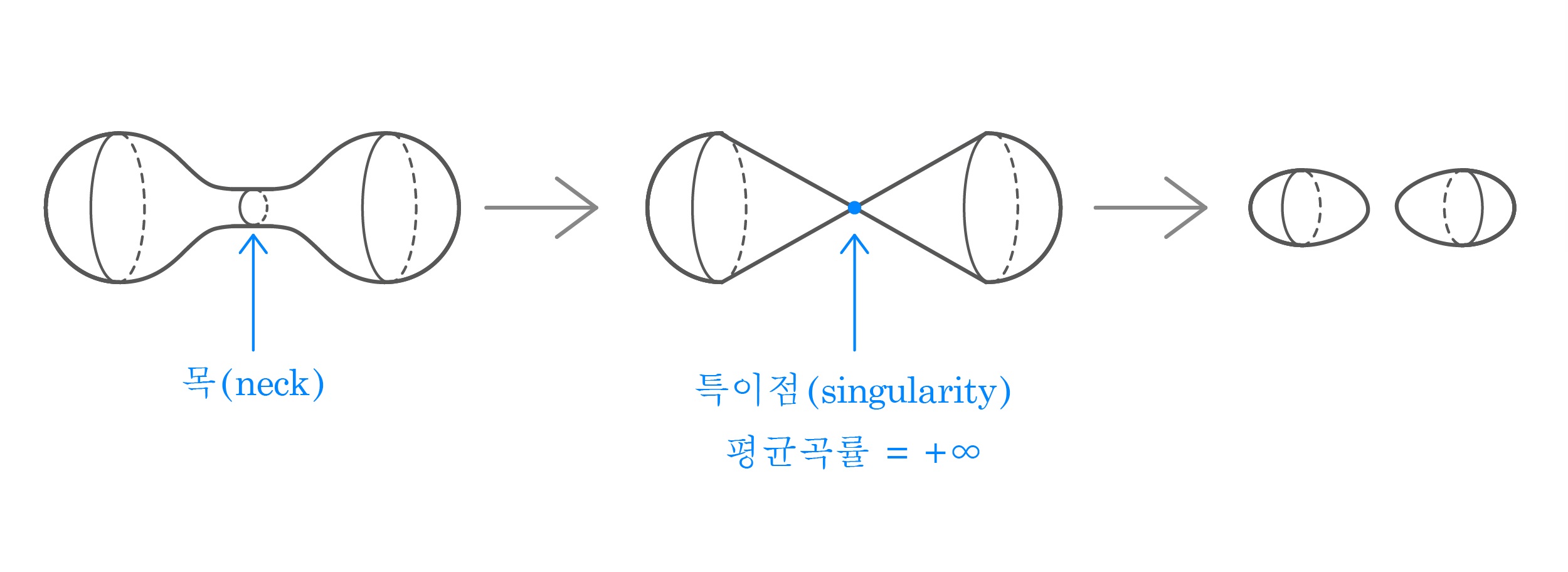
하지만 첫 번째 질문은 여러 가지 반례가 있습니다. 아주 간단한 예로서, 도넛 모양의 곡면을 평균 곡률 흐름으로 움직이면 곡면은 절대로 부드럽게 둥근 구로 수렴할 수 없습니다.([그림6]) 그렇다면 주어진 곡면이 도넛과 달리 단순-연결되었다면 부드럽게 둥근 구로 수렴할 수 있을까요? 이것 역시 아령 모양의 곡면이 반례가 됩니다. 가운데 목neck이 아주 좁은 아령은 목에서 가장 큰 평균 곡률을 가지기 때문에, 가장 빠른 속도로 줄어듭니다. 결국 목만 먼저 점으로 수렴하여, 그림과 같이 곡률이 무한대로 발산하는 특이점이 발생하고, 두 개의 곡면으로 찢어집니다.([그림7])
이런 현상은 3차원 리찌 흐름에서도 발생합니다. 아령 모양의 3차원 다양체는 가운데 목에서만 특이점이 발생하여 둥근 구로 수렴하기 전에 리찌 흐름이 멈춥니다. 다음 연재분에서는 이런 문제를 일으키는 특이점에 대해서 이야기하고, 어떻게 하면 특이점을 넘어서 둥근 구로 흐르게 할 수 있는지 생각해보겠습니다.
연재글
곡면의 열방정식 [2]: 위상 변화와 흐름의 운명
곡면의 열방정식 [3] : 불량 흐름을 개선하는 일방통행
곡면의 열방정식 [4]: 손가락 위에서 돌아가는 농구공
참고문헌
- J. Alexander. An Example of a Simply Connected Surface Bounding a Region which is not Simply Connected. Proc. Natl. Acad. Sci. U.S.A.. 10(1): 8–10, 1924.
- J. Bernstein and L. Wang. A sharp lower bound for the entropy of closed hypersurfaces up to dimension six. Inventiones mathematicae, 206(3): 601-627, 2016.
- K. Brakke. The motion of a surface by its mean curvature. volume 20 of Mathematical Notes. Princeton University Press, 1978.
- T. Colding and W. Minicozzi. Generic mean curvature flow I; generic singularities. Annals of Mathematics, 175(2):755–833, 2012.
- M. Gage and R. Hamilton. The heat equation shrinking convex plane curves. Journal of Differential Geometry, 23(1): 69-96, 1986.
- M. Grayson. The heat equation shrinks embedded plane curves to round points. Journal of Differential Geometry, 26(2): 285-314, 1987.
- R. Hamilton. Three-manifolds with positive Ricci curvature. Journal of Differential Geometry, 17(2): 255-306, 1982.
- G. Huisken. Flow by mean curvature of convex surfaces into spheres. Journal of Differential Geometry, 20(1): 237-266, 1984.
- G. Huisken. Asymptotic-behavior for singularities of the mean-curvature flow. Journal of Differential Geometry, 31(1): 285-299, 1990.
- G. Perelman. The entropy formula for the Ricci flow and its geometric applications. arXiv math/0211159, 2002.
- J. Zhu. On the entropy of closed hypersurfaces and singular self-shrinkers. Journal of Differential Geometry, 114(3): 551-593, 2020.