곡면의 열방정식 [2]: 위상 변화와 흐름의 운명

특이점의 모습은 이미 결정되어 있다

10여년 전 여름 녹음이 우거진 교정을 거닐다 선생님께서 문득 질문을 던졌습니다. “나뭇잎의 잎맥은 양분을 수송하기 적합한 형태로 형성되는데, 그 형태는 주변 환경에 맞추어 형성된 것일 수도, 유전 정보에 의해 결정된 것일 수도 있지. 이러한 현상을 미분 방정식을 활용하여 확인할 수 있겠니?” 그리고는 연구실로 돌아가 잎맥의 형태에 따른 양분의 수송에 필요한 거리를 범함수로 사용하여 방정식을 설계하셨던 것 같습니다. 물론 학부생이었던 저는 그 질문을 연구로 이어갈 능력이 없었고, 기억의 저편에 묻어 두었습니다.

이전 글 “곡면의 열방정식 [1]: 에너지가 줄어들면 단순해진다”에서 줄어드는 곡선 흐름은 닫힌 곡선을 둥근 점으로 수렴시킨다고 이야기했습니다. 초기에 주어진 곡선을 주어진 환경에, 흐름을 유전 정보에 빗대어 생각해보면, 이 흐름은 주어진 환경과 관계없이 닫힌 곡선으로 탄생함과 동시에 어떤 식으로 소멸할지 운명이 정해져 있다고 볼 수 있습니다. 이것은 곡선의 곡률이 만족하는 방정식을 보면 이해할 수 있습니다.

\begin{equation*}
\tfrac{\partial}{\partial \tau} \kappa=\tfrac{\partial^2}{\partial s^2} \kappa+\kappa^3.
\end{equation*}
흐름에 따라 곡선이 줄어들면 곡률 \(\kappa\)가 증가하고, 위의 방정식은 우변의 \(\kappa^3\)에 의해 지배됩니다. 따라서 초기에 어떤 정보를 주든 유한한 크기의 영향밖에 미치지 못하기 때문에, 소멸하는 순간 무한대로 발산하는 곡률이 미치는 어마어마한 크기의 영향력이 곡선을 둥글게 만들어버립니다. 이처럼 곡률이 무한대로 발산하는 시공간 점을 특이점^singularity이라고 부르는데, 평균 곡률 흐름 역시 특이점에서의 움직임은 방정식에 내재한 성질에 따라 주로 결정되며, 초기 곡면의 모습에는 매우 제한적인 영향을 받습니다.

이 현상을 수학적으로 조금 더 자세히 알아보겠습니다. 시간이 \(T\)로 접근함에 따라 원점으로 둥글게 수렴하는 볼록하고 닫힌 줄어드는 곡선 흐름 \(\Gamma_t\)를 관찰하겠습니다. 먼저 무한대로 발산하는 곡률을 제어하기 위해 확대한 흐름 \(\tilde{\Gamma}_t=:(T-t)^{-\frac{1}{2}}\Gamma_t\)를 생각합니다. 곡선을 확대하면 휘는 정도가 완만해지므로 곡률도 줄어듭니다. 실제로 확대한 흐름의 곡률이 일정한 상한과 하한을 가지는 것이[5] 증명되어 있습니다. 하지만 우리는 시간은 늘어뜨리지 않은 채 공간만 확대하였기에, 위의 확대된 흐름의 위치 벡터 \(\tilde{\gamma}\)가 만족하는 방정식

\begin{equation*}
\tfrac{\partial}{\partial t}\tilde{\gamma}=(T-t)^{-1}\tfrac{\partial^2}{\partial s^2}\tilde{\gamma}+\tfrac12 (T-t)^{-1}\tilde{\gamma}
\end{equation*}
은 일반적인 미분방정식 이론을 적용할 수 없습니다.¹ 따라서 새로운 시간 매개 변수 \(\tau=-\log(T-t)\)를 도입하여 조정된 줄어드는 곡률 흐름^{rescaled curve shortening flow} \(\bar \Gamma_\tau=:\tilde{\Gamma}_t\)을 정의하면, 조정된 위치 벡터 \(\bar \gamma\)는 아래의 깔끔한 방정식을 만족합니다.

\begin{equation*}
\tfrac{\partial}{\partial \tau}\bar{\gamma}= \tfrac{\partial^2}{\partial s^2}\bar{\gamma}+\tfrac12\bar{\gamma}
\end{equation*}

여기서 주목해야 할 점은 시간 \(t\)가 특이 시간^{singular time} \(T\)에 접근할수록, 새로운 시간 매개 변수 \(\tau\)가 무한대로 발산한다는 것입니다. 이는 곡률의 영향력을 유한한 크기로 제한하기 위해 시공간을 확장시키면서, 특이 시간이 무한히 멀어진 것으로 이해할 수 있습니다. 결국 초기에 어떤 곡선에서 시작하더라도, 적합한 시간 매개 변수의 입장에서 보았을 때 아득히 먼 시간이 흘러야 특이 시간이 찾아오므로, 초기 곡선의 모양이 특이점의 모양에 영향이 미치기 힘든 것으로 볼 수 있습니다.

이제 \((x_0,t_0)\in \mathbb{R}^{n+1}\times [0,+\infty)\)에서 특이점을 발현하는 평균 곡률 흐름 \(M_t\)를 위의 시간 매개 변수 \(\tau=-\log(t_0-t)\)를 이용하여 조정된 평균 곡률 흐름^{rescaled mean curvature flow} \(\bar M_\tau=:(t_0-t)^{-\frac{1}{2}}(M_t-x_0)\)를 생각해보겠습니다. 먼저 매개 변수 \(\tau\)는 위와 같이 무한 시간까지 존재합니다. 그리고 후이스켄 교수님의 단조 감소 공식[6]은 아래와 같이 다시 적을 수 있습니다.

\begin{equation}
\tag{*}
\frac{d}{d\tau}\int_{\bar M_{\tau}} e^{-\frac{|\mathbf{x}|^2}{4}}d\mathcal{H}^n(\mathbf{x},\tau) =-\int_{\bar M_{\tau}}\left|\Delta_g \mathbf{x}+\tfrac12 \mathbf{x} \right|^2 e^{-\frac{|\mathbf{x}|^2}{4}} d\mathcal{H}^n(\mathbf{x},\tau) \leq 0.
\end{equation}
그런데 수정된 넓이 \(\int_{\bar M_\tau} e^{-\frac{|\mathbf{x}|^2}{4}}\)는 항상 양수이므로, \(\tau\)가 무한대로 발산하면서 우변은 \(0\)으로 수렴해야합니다.² 따라서 조정된 흐름은 위치 벡터가 방정식 \(\Delta_g \mathbf{x}+\tfrac12 \mathbf{x}=0\)을 만족하는 곡면으로 수렴합니다.³ 이때, 이 방정식을 만족하는 곡면은 모두 자가수축자^{self-shrinker}라고 부릅니다. 왜냐하면 임의의 자가수축자 \(\mathcal{N}\)의 모양을 유지하며 크기만 줄이는 흐름 \(N_t=(1-t)^{\frac{1}{2}}\mathcal{N}\)은 그 자체로 평균 곡률 흐름이기 때문입니다. 결국 평균 곡률 흐름 역시 특이점에서의 모습은 자가수축자 중 하나로 결정됩니다.

위상 변화는 특이점을 만들고, 특이점은 위상 변화를 부른다

둥근 구와 같은 자가수축자는 한 점으로 수렴하며 특이점을 발생시키는데, 특이점을 지나면 사라지므로 위상이 변화한다고 볼 수 있습니다. 하지만 일반적으로 특이점을 지난다고 흐름이 사라지는 것은 아닙니다.

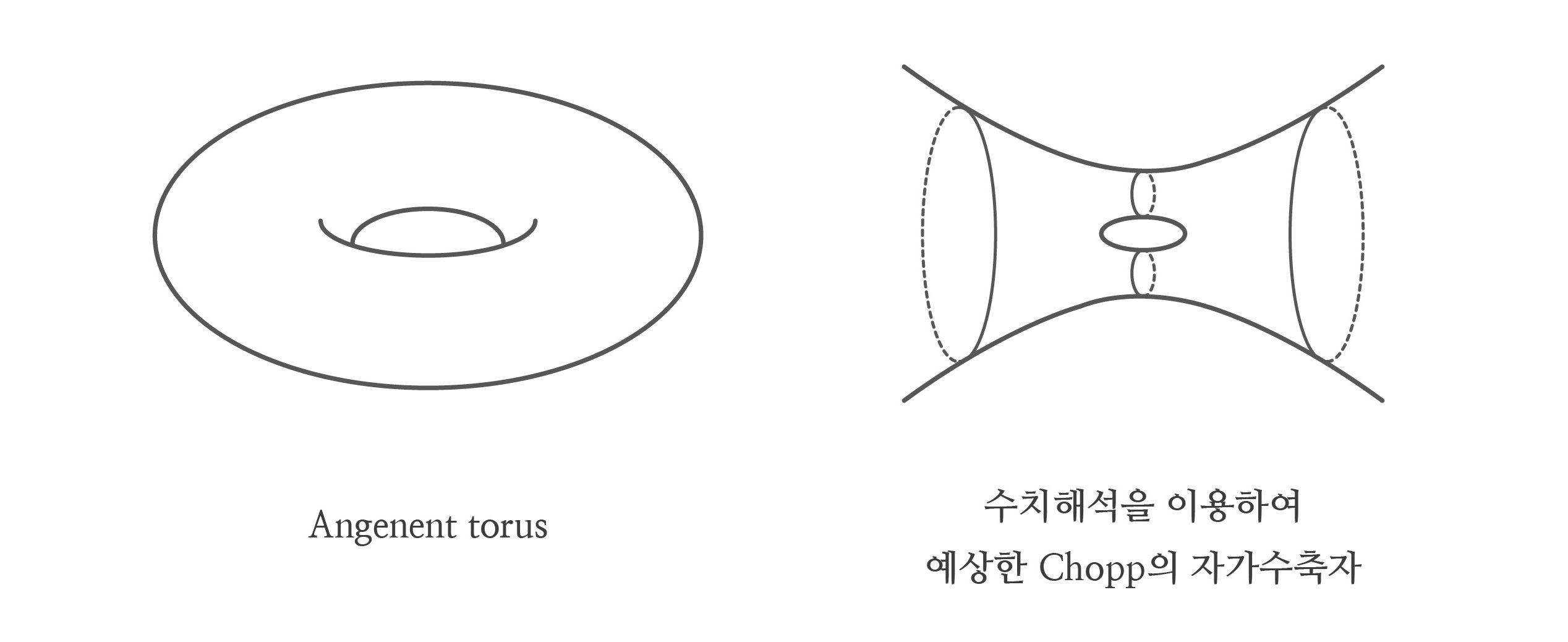
예를 들어 이전 글 “곡면의 열방정식 [1]: 에너지가 줄어들면 단순해진다”에서 이야기한 아령 모양 곡면의 경우, 손잡이 중앙이 무게 추 부분보다 빠르게 줄어들어서 하나의 특이점이 발생합니다. 그 후 특이점을 중심으로 두 개로 갈라진 흐름은 각자 둥근 점으로 수렴합니다. 이처럼 흐름은 특이점을 지나 사라지거나 갈라지며, 4차원 이상에서는 구멍이 뚫리기도 합니다.⁴ 이렇게 곡면이 소멸하거나, 갈라지거나, 구멍이 뚫리는 등 위상이 변화한다면 변화의 순간 곡률이 발산해야 하므로 특이점이 발생합니다.

한편, 흐름은 특이점에서 반드시 위상이 변화합니다. 특이점에서 관찰되는 자가수착자가 닫혀 있다면 흐름도 닫힌^closed 5 자가수축자처럼 한 점에서 소멸될 것입니다. 자가수축자가 무한히 큰 경우는 위의 아령 모양 곡면의 경우를 관찰하면 이해할 수 있습니다.

[그림1]과 같이 아령의 경우 손잡이 중앙을 중심으로 조정된 흐름이 무한히 긴 둥근 원통으로 수렴합니다. 재미있는 점은 무게 추 부분은 원점으로부터 무한히 멀어져서 극한 곡면의 모습에서 발견할 수 없습니다. 즉, 특이점에서 발견되는 자가수축자가 무한히 크다면, 특이 시간에 특이점이 흐름의 다른 부분과 연결되어 있다는 것을 의미합니다. 그리고 특이점에서 아령의 손잡이처럼 흐름의 일부가 한 점에서 유착된 후 잘려 나갑니다.⁶

따라서 특이점의 모양을 모두 분류한다면 흐름에 의해 곡면의 위상이 어떻게 변화하는지 알 수 있을 것입니다. 하지만 안타깝게도 응우옌^{Phu X. Nguyen}교수님께서 자가수축자가 무한히 많다는 것을 증명하였고[9], 이를 근거로 임의의 특이점을 지나는 흐름을 통하여 위상 변화를 관찰하는 것은 아마도 불가능할 것으로 보입니다.

위상 수학을 위한 기하학적 흐름의 목표

이제 위상 변화 관찰을 위해 기하학적 흐름을 연구하는 학자들이 해결하고자 하는 문제들을 소개하겠습니다. 아래의 문제 중 첫 번째 문제와 세 번째 문제에 대해서는 다른 글에서 자세히 설명하겠습니다.

첫 번째 문제는 불안정 특이점 회피 이론의 정립입니다. 차후에 다시 이야기하겠지만 어떤 흐름이 특이점을 갖지만, 그 흐름의 초기 곡면과 매우 유사한 곡면에서 시작한 흐름이 원래의 특이점과 같은 모양의 특이점을 갖지 않는다면, 이를 불안정 특이점이라고 부릅니다. 이 이론의 궁극적인 목표는 임의의 곡면이 주어졌을 때, 이와 매우 유사한 어떤 곡면에서 시작한 흐름이 둥근 구와 둥근 원통만을 특이점의 모양으로 가질 수 있음을 보이는 것입니다. 이렇게 초기 곡면과 유사한 곡면에서 시작하는 흐름을 일반적인 평균 곡률 흐름^{generic mean curvature flow}이라고 부릅니다. 선택된 곡면은 주어진 곡면과 같은 위상을 가지므로 일반적인 흐름으로 위상을 연구하는 데 무리가 없습니다. 3차원 회피 이론은 작년에 큰 발전이 있었고[1,2], 이론이 4차원으로 가능성이 높아 보입니다.

리찌 흐름의 경우 페렐만 교수님께서 임의의 닫힌 3차원 다양체에서 시작한 리찌 흐름은 둥근 구와 둥근 원통만을 특이점의 모양으로 가진다는 것을 증명하여[10] 푸앵카레 추측을 증명하셨습니다. 하지만 4차원 리찌 흐름의 경우에는 평균 곡률 흐름과 같이 자가수축자가 무한히 많기 때문에 불안정 특이점 회피 이론이 필요할 것으로 보입니다.

두 번째는 일반적인 특이점 고립 이론의 정립입니다. 우리가 위에서 살펴본 예제들은 모두 특이점이 고립되어 있습니다. 하지만 무한히 많은 특이점이 발생하여 특이점이 고립되지 않을 수 있습니다. 예를 들어 얇은 반지 모양에서 시작한 흐름은 두께가 점점 얇아져서 원으로 수렴합니다. 

이 흐름을 결혼 반지^{marriage ring}라고 부르는데, 결혼 반지는 특이 시간에 관찰되는 원 위의 모든 점이 특이점입니다. 그리고 각각의 특이점에서 조정된 흐름은 모두 둥근 원통으로 수렴합니다. 이 예제의 경우는 특이점이 연속적으로 발생하여 동시에 사라져버리지만, 셀 수 있는 무한 개의 특이점이 발생한다면 흐름이 무한 개로 나누어져 위상을 분석하기 매우 힘들어집니다. 따라서 주어진 곡면에서 시작한 흐름 대신 유한개의 특이점만을 가지는 일반적인 흐름을 찾는 것이 목표입니다.⁷ 

세 번째 특이점을 지나는 흐름이 잘 존재^well-posed할 수 있는지 확인해야 합니다. 흐름은 미분 방정식의 해인데 특이점에서 곡률이 발산해서 미분이 불가능해집니다. 즉, 특이점을 지나는 흐름이 존재한다면 이는 미분 불가능한 미분 방정식의 해가 됩니다. 이런 흐름을 약한^weak 흐름이라고 부르며, 적어도 둥근 원통 형의 특이점 근처에서 잘 존재할 수 있는지 증명해야 합니다. 이 문제는 3차원에서 해결되었고[3], 4차원의 경우 \(S^1 \times \mathbb{R}^2\) 모양의 특이점은 해결되었지만[4], \(S^2 \times \mathbb{R}^1\) 모양의 특이점은 아직 미해결로 남아있습니다.

마지막으로 한 겹 가설^{multiplicity one conjecture}의 증명입니다. 위에서 부등식\((*)\)을 이용하여 특이점을 기준으로 조정된 흐름은 자가수축자로 수렴함을 확인했습니다. 하지만 조정된 흐름이 여러 겹의 자가수축자로 수렴할 위험이 있습니다. 

[그림4]처럼 두 장의 둥근 구가 가느다란 목^neck들로 연결되어 있고, 특이 시간에 가까워질수록 두 장의 구면이 한 장의 구면으로 수렴하며, 목들은 점으로 수렴한다고 가정하겠습니다. 이때, 목에서는 \(\Delta_g \mathbf{x}+\tfrac12 \mathbf{x}\)의 값이 \(0\)이 아니지만, 목이 점으로 수렴하므로 목 위의 적분값은 \(0\)으로 수렴해서, 부등식 \((*)\)의 우변은 \(0\)으로 수렴할 수 있습니다. 닫힌 흐름의 경우 이런 가능성은 없다는 것이 한 겹 가설입니다. 한 겹 가설은 3차원의 경우 유의미한 발전이 있었습니다.[7,8] 리찌 흐름의 경우 닫힌 흐름은 반드시 한 겹의 특이점을 가진다는 것을 모든 차원에서 페렐만 교수님께서 증명하였습니다.[10]

연재글
곡면의 열방정식 [1]: 에너지가 줄어들면 단순해진다
곡면의 열방정식 [3] : 불량 흐름을 개선하는 일방통행
곡면의 열방정식 [4]: 손가락 위에서 돌아가는 농구공