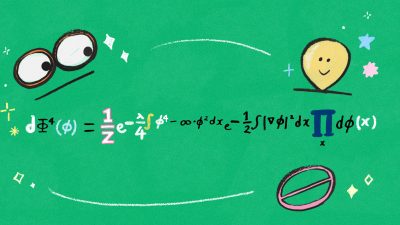To infinity and beyond.
– Buzz Lightyear
무한infinity이라는 개념이 있다. 무한은 플라톤Plato의 이데아idea, 예를 들어서 “완전한 원”과 같이 불완전한 현실을 추상화하는 수학적인 개념인가, 아니면 정말로 우주에 존재하는 물리적인 실체인가?
이 질문의 답을 얻기 위해서, 무엇보다 먼저 우주가 무한한지 유한한지 생각해 보자. 우주 안에 담긴 물질의 총량은 우주보다 클 수 없다. 따라서 만약 우주 자체가 유한하다면 우주 안에 정말로 무한인 것은 존재할 수 없을 것이다.
우주는 무한할까, 유한할까?
조금 생뚱맞게 들릴지 모르지만 이 질문은 다음 질문과 깊게 연결되어 있다.
밤 하늘은 왜 어두울까?
처음 들으면 놀랄 수도 있지만, 우주가 무한하고 영원히 변함없이 존재해 왔다면 밤 하늘은 어두울 수 없다. 아니, 밤 하늘은 단순히 어둡지 않은 정도가 아니라 태양의 표면과 같이 매우 밝고 뜨거워야 한다.
왜 그럴까?
지구에서 하늘을 가로질러서 우주의 어느 특정 방향으로 직선을 그어 나간다고 하자. 우주가 무한하다면 이 직선은 언젠가 반드시 어느 별의 표면에 닿게 된다. 이런 식으로 우주의 임의의 방향으로 직선을 그으면 결국은 모두 어느 별의 표면에 닿게 된다. 그렇다면 하늘은 모든 방향으로 별의 표면만큼 밝아야 한다.
조금 더 수학적으로 생각해 보면, 별이 멀수록 빛의 세기는 거리의 제곱에 반비례해서 약해진다. 하지만 무수히 많은 별들이 무한한 우주에 균질하게 퍼져 있다면, 거리가 멀어질수록 정확하게 거리의 제곱에 비례하는 만큼 더 많은 별이 촘촘히 하늘을 채우게 될 것이다. 따라서 지구에 도달하는 별빛의 총량은 그대로 유지되게 된다. 결국, 하늘은 낮이든지 밤이든지 결코 어두울 수 없다.
이와 같이 밤 하늘은 원칙적으로 어두울 수 없는데 실제로는 어둡다는 사실을 “올버스의 역설Olbers’ paradox”라고 부른다. 이 역설의 이름은 19세기 독일 아마추어 천문학자인 하인리히 올버스Heinrich Olbers에 기인한다. 하지만 이 역설은 사실 16세기 영국 천문학자인 토마스 딕스Thomas Digges에 의해서 처음 발견된 것으로 알려져 있다. 올버스가 유명해지게 된 것은 그가 제안한 해결책 때문이었다.
올버스의 해결책은 별빛이 지구에 도달하기 전에 지구와 별 사이에 존재하는 먼지 구름이나 가스층에 의해서 흡수되어서 사라진다는 것이다. 언뜻 들으면 매우 합리적인 이 해결책은 불행하게도 역설을 해결해 주지 않는다. 왜냐하면 먼지 구름이나 가스층이 무한히 많은 별들로부터 오는 별빛을 영원히 흡수해 왔다면 그들 자체도 결국은 별의 온도만큼 뜨거워져서 별과 같이 빛을 내는 발광 성운이 될 것이기 때문이다.
올버스의 역설의 진정한 해결책은 앞서 언급한 “우주가 무한하고 영원히 변함없이 존재해 왔다”는 가정을 부정함으로써 얻을 수 있다. 다시 말해서, 우주는 (1) 무한하지 않거나 (2) 영원히 변함없이 존재해 온 것이 아니면 된다.
우선, 첫 번째 해결책에 따라서 우주가 유한하다고 하자. 그렇다면 당연히 그 안에 담긴 별의 개수는 유한할 것이고, 별과 별 사이에는 분명히 어두운 공간이 존재하게 될 것이다. 이 경우에 올버스의 역설은 아주 쉽게 해결된다.
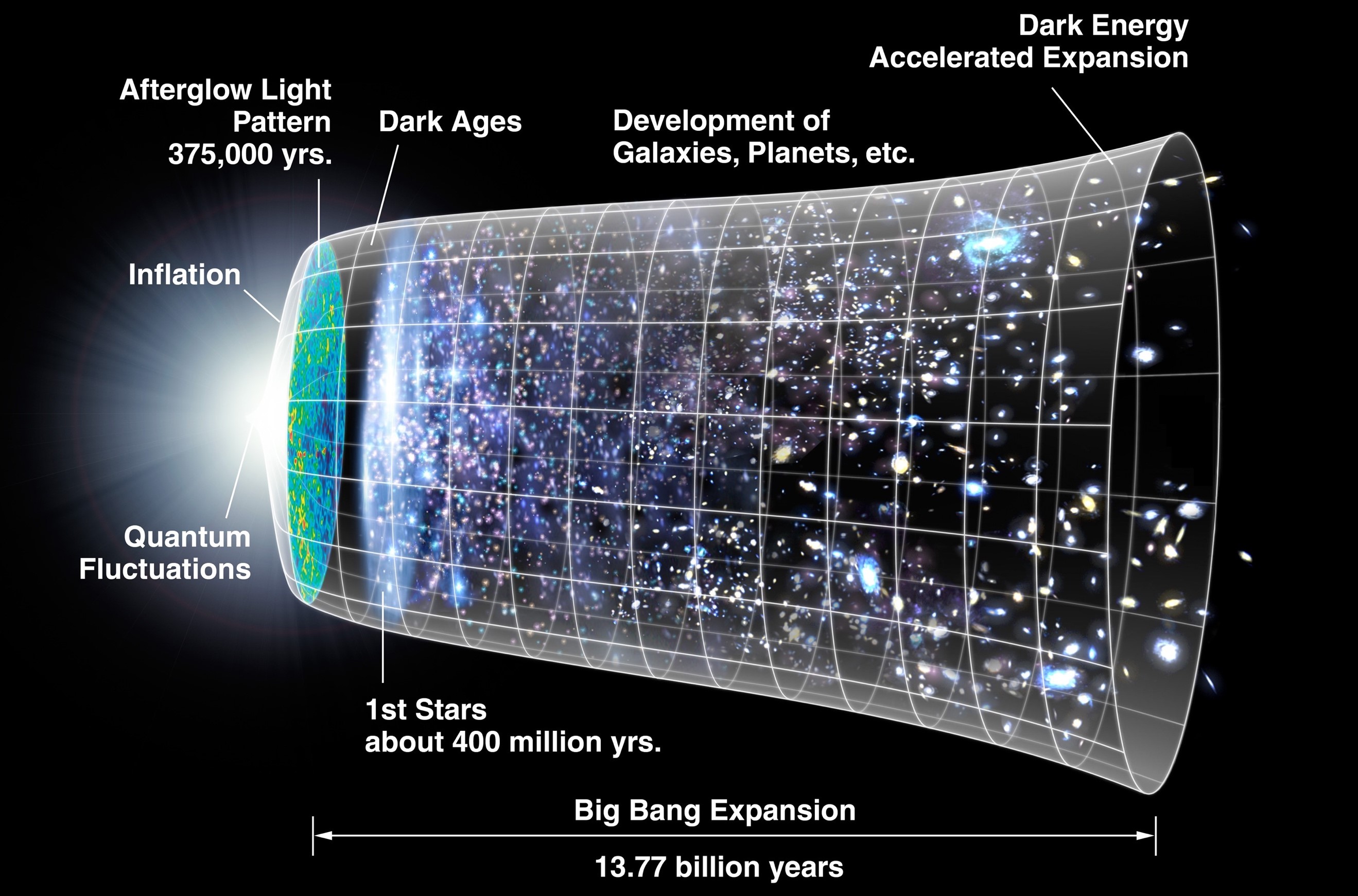
다음, 두 번째 해결책에 따라서 우주가 영원히 변함없이 존재해 온 것이 아니라고 하자. 이 경우에 우주는 어느 순간 태어났으며 유한한 나이를 지닌다. 곰곰이 잘 생각해 보면 우리는 우주가 탄생한 이후 현재 지구에 도달한 별빛만을 관찰할 수 있다. 다시 말해서, 우리는 우리에게 별빛이 도달하는 범위 안에 있는 우주만을 실제로 관찰할 수 있다. 이 범위는 대강 우주의 나이 곱하기 빛의 속도이다. (상대성 이론에 따르면 빛의 속도는 유한하며 상수이다.) 결국, 우주 자체는 혹시 급격할 폭발로 인해서 무한하게 발산할 수 있었을지 모르지만 우리가 실제로 관찰할 수 있는 우주는 유한할 수 밖에 없다. 이것은 다름 아니라 빅뱅 이론Big Bang theory이다.
빅뱅 이론에 따르면 우리 우주는 대략 138억 년 전 아주 뜨겁고 밀도가 매우 높은 작은 점으로부터 폭발하면서 태어났다. 이후 우주는 급격히 팽창하면서 식게 되었는데 그 과정에서 우리가 아는 모든 원자와 그것들이 뭉쳐진 천체들이 만들어지게 된다.
그런데 우주의 초기 팽창 속도는 굉장히 빨랐다고 한다. 놀랍게도 그 팽창 속도는 심지어 빛의 속도보다도 더 빨리 빨랐다고 한다. 처음 들으면 매우 이상하게 들릴 수 있지만, 우주의 팽창은 공간 자체의 팽창이기 때문에 빛의 속도보다 빠르게 진행될 수 있다. 결과적으로 우주 자체는 빛이 우주의 나이 동안에 나아갈 수 있는 거리 이상으로 더 멀리 팽창할 수 있게 된다. 참고로 이렇게 우주가 급격하게 팽창했다는 이론을 국문으로 급팽창 이론, 영문으로 인플레이션 이론inflation theory이라고 한다.
정리하면, 우리가 실제로 관찰할 수 있는 우주는 유한하다. 다만, 우주 전체의 크기는 우리가 실제로 관찰할 수 없기 때문에 정확하게 알 수 없다.
참고로 빅뱅 이론은 1927년 벨기에 가톨릭 대학교의 조르주 르메트르Georges Lemaître라는 물리학자 겸 신부에 의해서 처음 주창되었다. 하지만 재미있게도 그보다 한참 먼저 빅뱅 이론을 주장한 사람이 있었다. 그 사람은 바로 시인이자 <검은 고양이The Black Cat>로 유명한 소설가인 에드가 알랜 포Edgar Allan Poe이다.
포는 1848년 <유레카Eureka: A Prose Poem>라는 논픽션 작품을 하나 발표한다. 이 작품에서 포는 놀랍게도 빅뱅 이론의 기본적인 아이디어를 제기했을 뿐만 아니라, 그것으로 올버스의 역설을 해결할 수 있음을 보인다. 다음은 포가 제시한 올버스의 역설의 해결책이다.
“만약 별들이 끊임없이 존재한다면, 하늘의 배경은 마치 은하처럼 균질하게 밝을 것이다. 이것은 왜냐하면 하늘의 모든 점에 항상 별이 존재할 것이기 때문이다. 이러한 상황에서 망원경을 통해서 발견되는 우주의 어두운 빈 공간을 이해할 수 있는 유일한 방법은 아직 빛이 우리에게 도달하지 않을 정도로 우주의 보이지 않는 배경이 거대하다고 가정하는 것이다”
“Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy – since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.”
다시 한번 정리하면, 우리는 실제로 우주가 무한한지 유한한지 알지 못한다.
만족스럽지 않다. 하지만 어쩌겠는가? 우리는 우리의 무지를 받아들이는 수밖에 없다. 적어도 현재로서는. 앞으로 인류가 우주의 크기를 파악할 수 있는 방법을 발견할 수 있기를 진심으로 바라본다.
자, 이제 시선을 달리 해 보자.
우주 전체와 같이 굉장히 큰 스케일은 그렇다 치고, 우리는 작은 스케일을 제대로 이해하고 있는가?
제논의 역설
원칙적으로 우리는 공간을 잘게 쪼갬으로써 점점 더 작은 스케일의 공간으로 들어갈 수 있다.
그렇다면 공간은 무한히 잘게 쪼개질 수 있는가?
오랫동안 사람들은 그럴 수 없다고 믿었다. 왜냐하면 공간이 무한히 잘게 쪼개진다면 역설이 발생한다고 믿었기 때문이다.
역설의 내용은 다음과 같다.
만약 공간이 무한히 잘게 쪼개진다면, 그 공간 속에서 운동하는 물체는 그렇게 무한히 잘게 쪼개진 공간의 무수히 많은 구간들을 모두 훑고 지나가야 한다. 언뜻 생각해 보면 이것은 불가능하다. 무수히 많은 구간들을 모두 훑고 지나려면 무한히 긴 시간이 필요하기 때문이다.
과연 정말 그럴까?
사실 이것은 유명한 제논의 역설Zeno’s paradoxes이다. 여러 제논의 역설 중에서 가장 유명한 버전은 “아킬레스와 거북이의 역설Paradox of Achilles and the tortoise”이다. 아킬레스와 거북이의 역설을 통해서 제논의 역설을 자세히 분석해 보자.
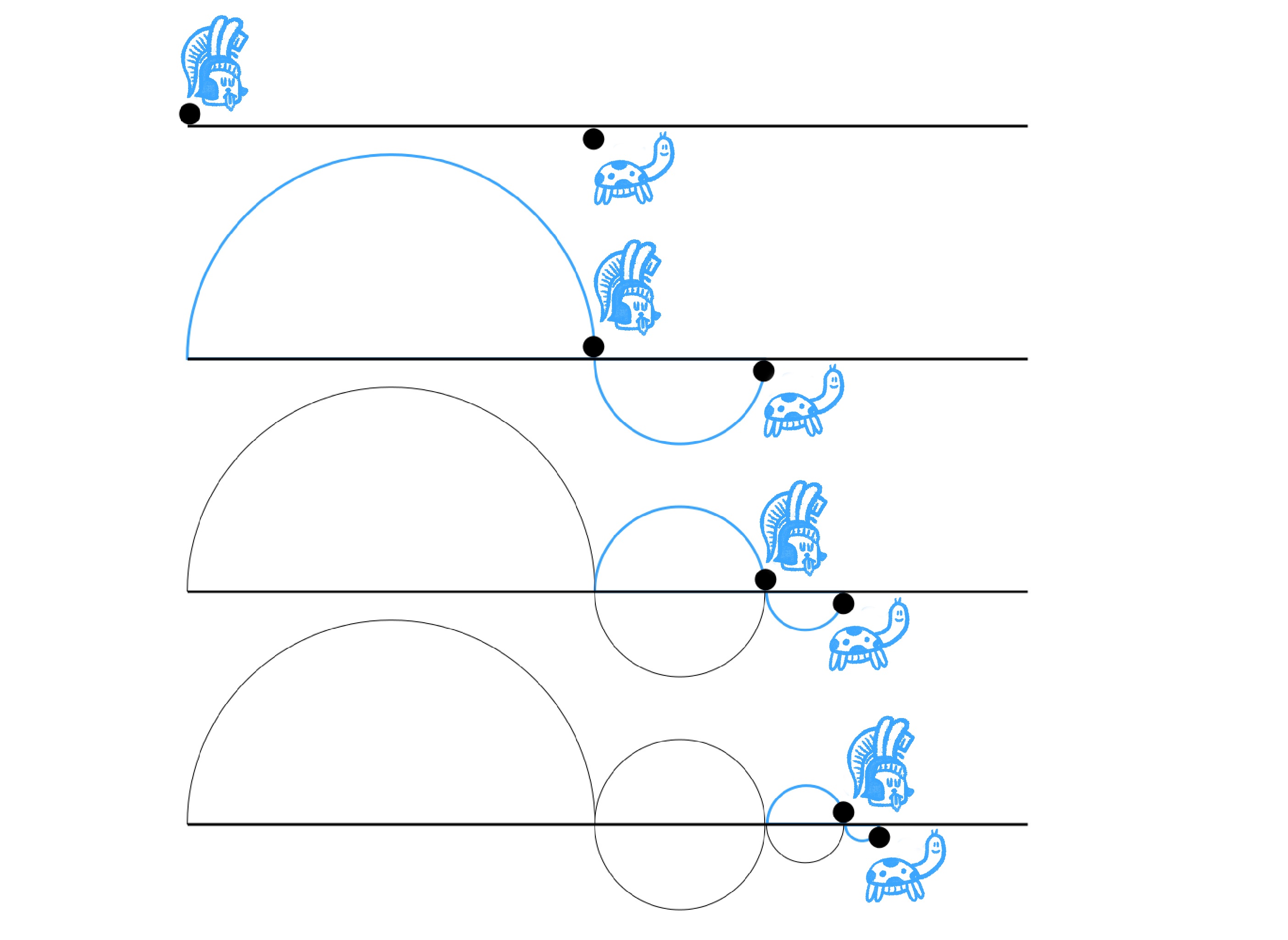
아킬레스와 거북이가 달리기 경주를 한다고 하자. 아킬레스는 거북이보다 훨씬 빠르다. 느린 거북이의 핸디캡을 감안하기 위해서 거북이는 아킬레스보다 100미터 앞에서 출발하기로 한다. 자, ‘탕’ 소리와 함께 경주가 시작되자 아킬레스는 거북이가 출발한 자리까지 빨리 도달한다. 하지만 그사이에 거북이는 조금이라도 앞으로 나아간다. 이제 다시 아킬레스는 거북이가 그렇게 조금이라도 앞으로 나아간 장소까지 도달한다. 하지만 그 짧은 사이에 거북이는 여전히 조금이라도 앞으로 나아간다. 이렇게 아무리 아킬레스가 거북이를 따라잡으려고 하더라도 거북이는 조금이라도 앞서 나아가 있게 된다. 결국 아킬레스는 절대로 거북이를 따라잡지 못한다.
이것은 물론 역설이다. 아킬레스는 당연히 거북이를 따라잡을 수 있다.
제논이 생각하기에 이러한 역설이 생기는 이유는 처음 가정이 잘못되어 있기 때문이었다. 다시 말해서, 공간은 무한히 잘게 쪼개질 수 없으며, 공간에는 모종의 최소 길이 단위가 존재한다. 따라서 아킬레스가 최소 길이 단위를 뛰어넘는 마지막 순간, 그는 거북이를 앞지를 수 있다. 제논은 그렇게 역설을 해결할 수 있다고 믿었다.
제논의 해결책은 매우 놀랍다. 물체의 운동, 그 자체가 공간에 최소 길이 단위가 존재한다는 사실을 증명하기 때문이다. 이것은 매우 놀라운 통찰이지만 유일한 해결책은 아니다. 당시 제논은 무한을 다룰 수 있는 수학이 부족했다.
제논의 역설을 해결하기 위해서는 무한히 이어지는 수열sequence을 더하는 방법을 알아야 한다.
제논의 역설을 수학적인 문제로 바꾸면 다음과 같다.
편의상, 아킬레스는 거북이보다 100배의 속도로 빨리 달릴 수 있다고 하자. 우선, 거북이는 아킬레스보다 100m 앞에서 출발한다. 따라서 아킬레스는 처음 단계에서 100m를 따라잡아야 한다. 그사이 거북이는 1m 앞으로 나아갈 수 있다. 이제 아킬레스는 두 번째 단계에서 1m를 따라잡아야 한다. 그사이 거북이는 1/100m 앞으로 나아갈 수 있다. 이제 아킬레스는 세 번째 단계에서 1/100m를 따라잡아야 한다. 그사이 거북이는 1/10,000m 앞으로 나아갈 수 있다. 이러한 과정은 무한히 이어진다.
결론적으로 아킬레스가 따라잡아야 하는 거리를 나열하면 다음과 같다.
$$100,\;\; 1,\;\; \frac{1}{100},\;\; \frac{1}{10000},\;\; \frac{1}{1000000},\;\; \cdots$$
이 수들을 다 더하면 아킬레스가 거북이를 최종적으로 따라잡을 때까지 필요한 총 거리가 나온다. 이 수열의 합은 무한할까, 유한할까?
현대에 살고 있는 우리는 이 수열의 합이 유한하다는 사실을 잘 알고 있다. 위와 같은 수열을 등비 수열geometric sequence이라고 부른다.
약간의 기호를 도입해서 등비 수열을 일반화해 보자. 첫 단계에서 아킬레스가 거북이를 따라잡기 위해서 필요한 거리를 \(a\)라고 하고, 아킬레스의 속도와 거북이의 속도 사이의 비율을 \(r\)이라고 하자. 그렇다면 우리에게 필요한 등비수열은 다음과 같이 주어진다.
$$a,\;\; ar,\;\; ar^2,\;\; ar^3,\;\; \cdots$$
이제 위 등비수열의 합을 주는 공식을 유도해 보자.
우선 등비수열의 합을 \(S\)라고 표현해 보자.
$$S=a+ar+ar^2+ar^3+\cdots$$
위 공식의 양변에 \(r\)을 곱해 보자.
$$rS=ar+ar^2+ar^3+ar^4\cdots$$
이제 앞선 두 공식을 좌변은 좌변끼리, 우변은 우변끼리 빼 보자.
$$(1-r)S=a$$
결국 등비수열의 합은 다음과 같은 간단한 공식으로 주어진다.
$$S=\frac{a}{1-r}$$
따라서 \(r\)이 1보다 작으면 등비수열의 합은 유한하게 된다. (퀴즈: \(r\)이 1보다 커지면 어떻게 되는가?)
앞선 숫자들을 대입해 보면 아킬레스는 거북이를 다음과 같은 거리 만에 따라잡을 수 있다.
$$S =\frac{100}{1-1/100} =\frac{10000}{99} \simeq 101.01$$
다시 말해서, 아킬레스는 거북이를 무한이 아닌 불과 101m 만에 따라잡을 수 있다.
정리해 보자.
제논의 역설은 실제로 역설이 아니다. 공간은 무한히 잘게 쪼개지더라도 역설이 발생하지 않는다. 적어도 제논의 역설에 관해서는 최소 길이 단위가 존재할 필요가 없다.
하지만 재미있게도 이야기가 그렇게 단순하게 끝나지 않는다.
현대 물리학의 가장 큰 난제 중 하나는 중력을 양자화시키는 것이다. 여기서 이 문제에 대해서, 특히 이 문제가 왜 그토록 풀기 어려운 난제인지 자세하게 설명할 수는 없다. 하지만 최대한 간단하게 설명하면 다음과 같다.
일반 상대성 이론general theory of relativity에 따르면 중력은 시공간이 휘어진 정도, 즉 시공간의 곡률에 의해서 결정된다. 중력이 양자화된다는 것은 시공간의 곡률이 양자역학적으로 요동친다는 의미이다. 문제는 시공간의 곡률이 작은 스케일에서 양자역학적으로 너무 강하게 요동친다는 사실이다. 이러한 강한 양자요동을 다 더하면 무한으로 발산한다. 우리가 아는 한, 작은 스케일에서 발생하는 이러한 강한 양자요동을 제대로 다룰 수 있는 방법은 현재 알려져 있지 않다.
그런데 잠깐, 혹시 공간에 최소 길이 단위가 있어서 그 이하로는 양자요동이 생기지 않으면 되지 않을까?
제논의 해결책과 매우 닮은 이 해결책은 실제로 양자 중력 문제를 해결하기 위해서 제안된 여러 이론에서 공유되는 핵심적인 아이디어이다.
예를 들어서, 루프 양자 중력 이론loop quantum gravity theory에서 시공간은 문자 그대로 띄엄띄엄 이산화된 덩어리discrete block로 나누어져 있으며, 이러한 덩어리의 크기가 공간의 최소 길이 단위를 준다. 반면에 끈 이론string theory에서 모든 물질의 기본 단위는 입자가 아니라 끈이라는 모종의 진동 모드vibration mode이다. 이러한 끈은 진동하기 위해서 어느 정도 유한한 공간을 차지해야만 하며, 이러한 공간의 크기가 공간의 최소 길이 단위를 준다. 여기서 자세하게 설명할 수는 없지만 루프 양자 중력 이론과 끈 이론 외에 다른 양자 중력 이론에서도 최소 길이 단위의 존재는 매우 중요한 역할을 한다.
재미있다. 재미있게도 공간의 최소 길이 단위에 대한 2,000년 전의 아이디어는 아직도 강한 생명력을 지니고 있다.
오묘하다. 오묘하게도 무한히 큰 스케일에 관한 올버스의 역설과 무한히 작은 스케일에 관한 제논의 역설은 깊게 연결되어 있다. 구체적으로, 두 역설은 모두 상대성 이론과 깊게 연결되어 있다.
정확히 왜 그런지는 모르겠지만 인류는 우주의 숨겨진 비밀에 다가가면 갈수록 온갖 종류의 무한을 맞닥뜨리게 된다. 어찌 보면 이것은 마치 판도라Pandora가 판도라의 상자를 여는 순간 온갖 종류의 재앙이 세상 밖으로 튀어나오는 것과 비슷하다. 이 비유에 따르면 상대성 이론은 판도라의 상자 안에 마지막까지 남아 있는 “희망”이다. 긍정적으로 보면, 인류는 상대성 이론이라는 희망을 가지고 무한이라는 재앙을 극복할 수 있다.
그런데 희망은 애초에 왜 판도라의 상자 안에 담겨 있었던 것일까? 다시 말해서, 판도라의 상자 안에 담겨 있었던 다른 모든 것들이 재앙이었다면, 왜 희망만은 예외였던 것일까?
이와 관련해서 희망도 사실은 재앙이라는 해석이 있다. 간단하게 말해서, 희망은 재앙을 극복할 수 있게도 하지만, 때때로 “헛된 희망”이 됨으로써 그 자체로 재앙이 될 수 있다. 상대성 이론도 비슷하다. 상대성 이론은 무한을 극복하게 할 수 있게도 하지만, 때때로 그 자체로 무한을 발생시킬 수 있다.
대표적인 예로, 상대성 이론과 양자역학이 통합되면 다음과 같은 수열이 발생할 수 있다.
$$S=1+2+3+4+\cdots$$
이 수열의 합은 무엇인가?
답은 당연히 무한이다. 아니, 제정신을 가진 사람이라면 당연히 무한이라고 답해야 한다. 그런데 이 수열의 합이 무한이 아니라 \(-1/12\)라고 주장하는 사람들이 있다. 이 사람들은 도대체 제정신인가?
참고로 앞선 수열은 소위 카시미르 효과Casimir effect라는 상대론적 양자역학relativistic quantum mechanics 문제에서 발생한다. 놀랍게도 실제로 실험적으로 검증된 이 효과의 핵심은 앞선 수열의 합이 정말 \(-1/12\)이라는 사실에 의존한다. 물론 앞선 수열의 합이 \(-1/12\)이라는 사실은 특정한 문맥에서 이해되어야 한다. 앞선 수열의 합을 수학적으로 엄밀하게 정의된, 특정한 문맥에서 구하는 방법을 라마누잔 합Ramanujan summation이라고 부른다.
도대체 말도 안 되는 이 사실을 이해하기 위해서 우리는 상대성 이론과 양자역학을 통합해야 한다. 다만, 앞서 말했듯이, 중력을 기술하는 일반 상대성 이론은 아직까지 양자역학과 제대로 통합되지 않았다. 여기서 우리는 특수 상대성 이론special theory of relativity과 양자역학의 통합에 집중할 것이다.
그러기 위해서 특수 상대성 이론에 대해서 자세하게 알아보자.
특수 상대성 이론
19세기 물리학에는 두 개의 큰 축이 있었다. 뉴턴의 운동 법칙으로 표현되는 고전역학과 맥스웰의 방정식으로 표현되는 전자기학이 바로 그것이다.
뉴턴의 운동 법칙은 제2 법칙인 \({\bf F}=m{\bf a}\)로 가장 유명하지만 곰곰이 잘 생각해 보면 가장 근본적인 법칙은 역시 관성 좌표계inertial frame of reference라는 개념을 정립한 제1법칙이다.
약간 동어반복적인 느낌이 들 수도 있지만 관성 좌표계란 뉴턴의 제2 법칙이 성립되는 좌표계로 정의된다. 거꾸로 말하면 관성 좌표계가 아닌 좌표계, 즉 비관성 좌표계에서는 뉴턴의 운동 법칙이 성립하지 않는다.
그렇다면 관성 좌표계는 구체적으로 어떻게 정의되는 것일까?
애초에 관성 좌표계가 하나 있다고 가정하자. 이 관성 좌표계에 상대적으로 등속도로 움직이는 좌표계는 모두 관성 좌표계이다.
조금 더 구체적으로 생각해 보자. 관성 좌표계 중의 하나인 \(S^\prime\)이 다른 관성 좌표계인 \(S\)에 비해서 상대적으로 \(v\)라는 속도를 가지고 \(x\) 축 방향으로 움직이고 있다고 하자. 이 두 좌표계 사이에서 \(x\) 좌표의 변환은 다음과 같을 것이다.
$$x^\prime=x-vt$$
그리고 당연한 말 같지만 이 두 좌표계 사이에서 \(y, z\) 좌표는 동일할 것이다.
$$y^\prime=y,\;\; z^\prime=z$$
그런데 두 좌표계 사이에서 시간은 어떻게 변환될까? 이 질문을 처음 들으면 이 무슨 의미 없는 질문인가라고 생각할지도 모르겠다. 당연히 시간은 관찰자가 움직이건 말건 동일하게 흘러야 되는 것이 아닌가?
$$t^\prime=t$$
시간이 동일하게 흐른다는, 언뜻 들으면 너무나 당연한 이 가정에 기반한 좌표 변환을 갈릴레이 변환Galilean transformation이라고 부른다.
뉴턴의 운동 법칙은 갈릴레이 변환과 천생 연분이다.
우선, 가속도는 위치 변수를 시간에 대해서 두 번 미분하는 것이다. 따라서 관성 좌표계 \(S^\prime\)과 \(S\)에서 \(x\) 축 방향으로의 가속도 \(a^\prime\)과 \(a\)는 서로 완벽하게 동일하다.
$$a^\prime=\frac{d^2}{d t^{\prime 2}}x^\prime=\frac{d^2}{d t^2} (x-vt)= \frac{d^2}{d t^2}x =a$$
다른 방향으로의 가속도는 물론 동일하다.
한편, 뉴턴 시대까지 알려진 바에 따르면 중력을 포함한 모든 힘은 상호작용하는 두 입자 사이의 상대적인 거리에만 의존한다. 상대적인 거리는 갈릴레이 변환에 대해서 불변이다. 따라서 모든 힘도 갈릴레오 변환에 대해서 불변이다. 결론적으로 뉴턴의 제2 운동 법칙 \({\bf F}=m{\bf a}\)는 갈릴레오 변환에 대해서 불변이다.
그런데 이러한 “불변성”은 단순히 뉴턴의 운동 법칙에만 적용되는 것이 아니다. 사실 이것은 특수 상대성 이론의 가장 핵심적인 원칙이기도 하다. 이 원칙을 한 문장으로 정리하면 다음과 같다.
“등속도로 움직이는 관찰자는 자신이 움직이고 있는지, 혹은 정지해 있는지를 물리적으로 구분할 방법이 없다.”
문제는 이 원칙이 갈릴레이 변환이라는 틀 안에서 맥스웰의 방정식과 충돌한다는 사실이다.
맥스웰의 방정식에 따르면 빛의 속도는 상수이다. 다시 말해서, 빛의 속도는 좌표계의 속도에 상관없이 불변이어야 한다.
여기서 문제가 발생한다. 가속도는 갈릴레이 변환에 대해서 불변이지만 속도는 그렇지 않기 때문이다. 따라서 갈릴레오 변환이 맞다면 빛과 나란한 방향으로 빠르게 움직이는 좌표계에서 빛의 속도는 느리게 관찰되어야 한다. 즉, 주어진 관찰자는 자신이 움직이고 있는 것을 확인하기 위해서 빛의 속도를 측정하면 된다.
그런데 앞서 말했듯이 그럴 수 없다. 빛의 속도는 상수이다.
뉴턴의 운동 법칙이 틀린 것인가, 아니면 맥스웰의 방정식이 틀린 것인가?
아인슈타인은 뉴턴의 운동 법칙이 틀려야 한다고 생각했다. 아인슈타인은 빛의 속도가 어느 관성 좌표계에서 보더라도 불변이어야 한다고 믿었다. 이 믿음의 결과가 바로 특수 상대성 이론이다.
간단하게 말해서, 특수 상대성 이론의 핵심은 시간과 공간의 좌표가 서로 섞인다는 것이다. 즉, 서로 상대적으로 움직이는 좌표계 사이를 연결하는 변환은 갈릴레이 변환이 아니라 시간과 공간의 좌표가 서로 섞이는 새로운 종류의 좌표 변환이다.
이 새로운 좌표 변환을 찾기 위해서 사고 실험thought experiment을 하나 생각해 보자. 구체적으로, 빛이 원점에서 사방으로 퍼져 나가고 있다고 하자. 이 빛의 진행을 어떤 주어진 관성 좌표계인 \(S\)에서 기술하는 방정식은 다음과 같다.
$$x^2+y^2+z^2-c^2 t^2=0$$
이제 이 빛을 \(S\)에 비해서 \(x\) 축 방향으로 등속도로 움직이는 다른 관성 좌표계 \(S^\prime\)에서 바라본다고 하자. 빛의 속도가 불변이라면 \(S^\prime\)에서도 빛의 진행은 정확히 같은 방정식에 의해서 기술될 것이다.
$$x^{\prime 2}+y^{\prime 2}+z^{\prime 2}-c^2 t^{\prime 2}=0$$
당연한 말 같지만, 위 두 식에서 \(x^\prime, y^\prime, z^\prime, t^\prime\)은 \(S^\prime\)에서의 좌표 변수이고, \(x, y, z, t\)는 \(S\)에서의 좌표 변수이다.
갈릴레이 변환을 적용하면 위 두 방정식을 동시에 만족할 수 없다. 왜냐하면 다음의 등식을 만족하지 않기 때문이다.
$$x^{\prime 2}+y^{\prime 2}+z^{\prime 2}-c^2 t^{\prime 2}= x^2+y^2+z^2-c^2 t^2$$
그렇다면 어떤 좌표 변환을 써야지 위 등식을 만족시킬 수 있을까?
새로운 좌표 변환을 찾기 위해서 진행 방향에 수직인 좌표 변수에는 여전히 아무런 변화가 없다고 가정하자. 즉, \(y^\prime=y\)이고 \(z^\prime=z\)라고 하자. 그러면 새로운 좌표 변환이 만족해야 할 등식은 다음과 같이 간단하게 정리된다.
$$x^{\prime 2}-c^2 t^{\prime 2}= x^2-c^2 t^2$$
이것이 아인슈타인이 찾고자 한, 새로운 좌표 변환이 만족해야 하는 등식이다.
이제 위 방정식을 살짝 정리하면 다음과 같이 바꿀 수 있다.
$$(x^\prime-ct^\prime)(x^\prime+ct^\prime)=(x-ct)(x+ct)$$
위 방정식을 만족시키는 방법은 일반적으로 무수히 많을 것이다. 하지만 가급적이면 가장 간단한 방법을 생각해 보자. 구체적으로, 변수들 사이에 다음과 같은 선형 관계식이 만족한다고 가정해 보자.
$$x^\prime-ct^\prime=\alpha(x-ct)$$
$$x^\prime+ct^\prime=\frac{1}{\alpha}(x+ct)$$
여기서 \(\alpha\)는 적절한 비례 상수이다. 우리가 해야 할 일은 이제 \(\alpha\)를 정하는 것이다.
그러기 위해서 위 두 방정식을 좌변은 좌변끼리, 우변은 우변끼리 더하거나 빼면 다음과 같이 정리할 수 있다.
$$x^\prime=\gamma x -\beta c t$$
$$ct^\prime=\gamma c t -\beta x$$
여기서 \(\gamma\)와 \(\beta\)는 다음과 같다.
$$\gamma=\frac{1}{2}\left(\alpha+\frac{1}{\alpha}\right)$$
$$\beta=\frac{1}{2}\left(\alpha-\frac{1}{\alpha}\right)$$
이제 \(\alpha\)를 결정하기 위해서 \(x^\prime\)이 관성 좌표계 \(S^\prime\)의 원점, 즉 \(x^\prime=0\)이라고 하자. 그리고 원래 관성 좌표계 \(S\)의 입장에서 볼 때 \(S^\prime\)의 원점은 등속도 \(x/t=v\)로 움직이고 있다고 하자. 이 조건으로부터 \(\alpha\)가 결정될 수 있다. 즉, 약간의 대수 작업을 거치면 다음과 같은 결론을 얻을 수 있다.
$$x^\prime=\gamma(x-vt)$$
$$ct^\prime=\gamma\left(ct-\frac{v}{c}x\right)$$
여기서 \(\gamma\)는 \(v\)의 함수로 다음과 같이 주어진다.
$$\gamma=\frac{1}{\sqrt{1-(v/c)^2}}$$
이 변환이 바로 우리가 원한 새로운 좌표 변환이다. 이 좌표 변환의 이름은 로런츠 변환Lorentz transformation이다.
로런츠 변환은 우리의 직관에 반하는 여러 결과를 초래한다. 그중 하나는 움직이는 시계의 시간이 천천히 흐른다는 것이다. 바로 그 유명한 시간 팽창time dilation이다.
시간 팽창은 로런츠 변환의 시간 좌표의 변환 부분을 고려하면 유도할 수 있다.
구체적으로, 시계가 정지해 있는 좌표계를 \(S\)라고 하고, 이 시계에 대해서 상대적으로 속도 \(v\)를 가지고 움직이는 좌표계를 \(S^\prime\)라고 하자.
이제 \(S\)에서 고정된 시계가 측정하는 어떤 두 사건 사이의 시간 차이를 \(\Delta t\)라고 하자. 우리가 알고 싶은 것은 \(S^\prime\)에서 측정하는 시간 차이 \(\Delta t^\prime\)이다.
$$c\Delta t^\prime=\gamma\left(c\Delta t-\frac{v}{c} \Delta x\right)$$
여기서 시계의 위치가 고정된다는 것은 \(\Delta x=0\)을 의미한다.
$$\Delta t^\prime=\gamma\Delta t$$
여기서 \(\gamma\)의 정의를 살펴보면 \(\gamma\)는 항상 1보다 크다. 따라서 움직이는 시계의 시간은 정지했을 때에 비교해서 느리게 흐른다.
시간 팽창은 우리의 직관에 반한다. 시간의 흐름이 상대적으로 변한 것이다. 우리는 빛의 속도가 불변이라는 조건을 만족시키기 위해서 절대적인 시간의 흐름을 포기해야 한다.
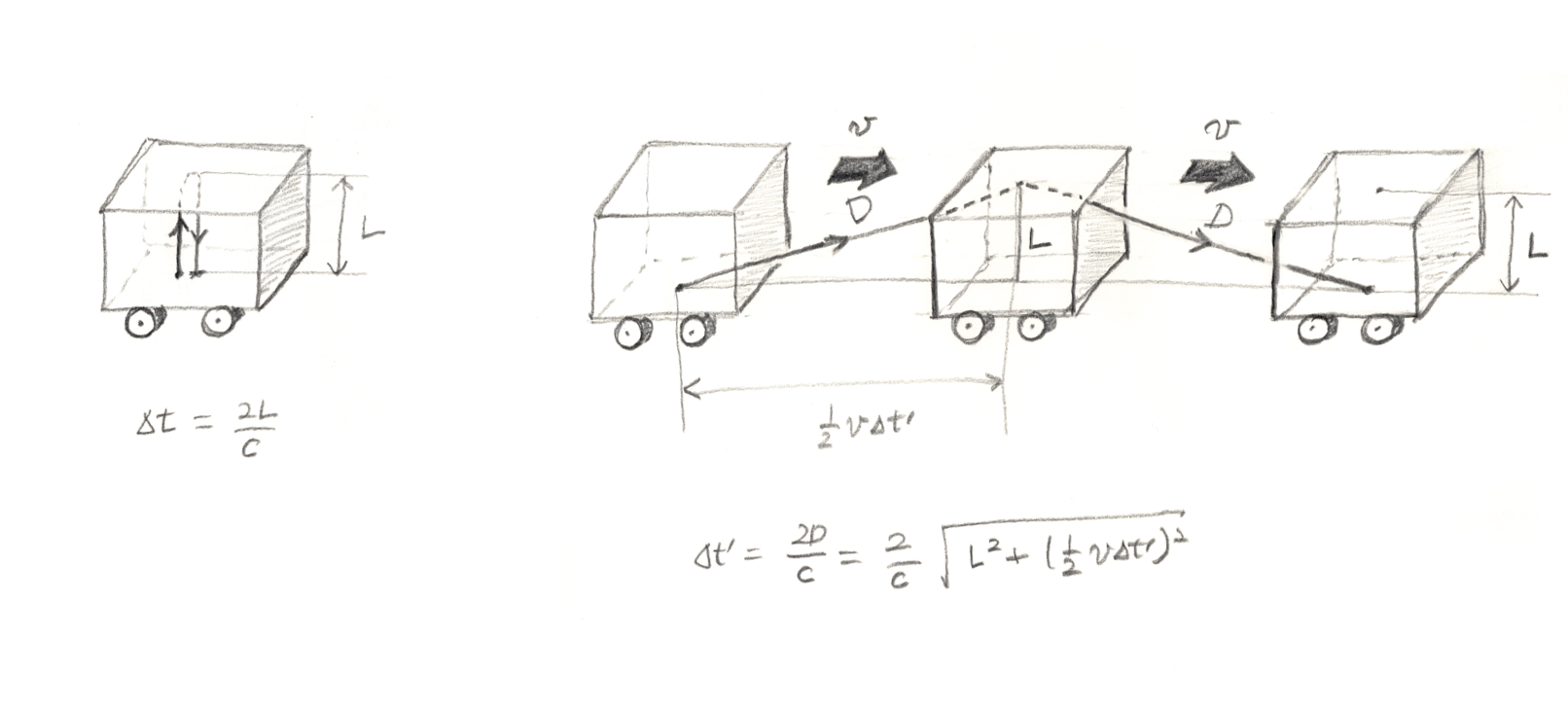
시간 팽창을 조금 더 직관적으로 이해하기 위해서 다시 한번 사고 실험을 해 보자. 구체적으로, 등속도로 움직이고 있는 어떤 기차 안에서 시간을 재는 실험을 하나 한다고 하자. 이해를 돕기 위해서 [그림6]을 참조하라.
구체적으로, 기차 안에 있는 어떤 관찰자가 바닥에서 발사된 빛이 천정에 있는 거울에 반사되어 돌아오는 시간을 측정하고 있다고 상상해 보자. 천정의 높이를 \(L\)이라고 할 때 이 시간은 다음과 같이 주어진다.
$$\Delta t=\frac{2L}{c}$$
이제 기차 밖에 있는 다른 관찰자가 이 측정 과정을 보고 있다고 하자. 이 관찰자가 보기에 빛이 돌아오는 데 걸리는 시간은 다음과 같다.
$$\Delta t^\prime=\frac{2D}{c}=\frac{2}{c}\sqrt{L^2+\left(\frac{1}{2}v\Delta t^\prime\right)^2}$$
여기서 핵심적인 가정은 빛의 속도가 여전히 \(c\)라는 사실이다. 위 공식을 잘 정리하면 우리는 다음과 같은 결론에 이를 수 있다.
$$\Delta t^\prime=\frac{2L/c}{\sqrt{1-(v/c)^2}}=\gamma \Delta t$$
위 공식은 로런츠 변환을 이용해서 얻은 시간 팽창 공식과 정확히 같다.
질량-에너지 등가
가장 유명한 물리 공식은 무엇일까?
필자가 생각하기에 둘 중의 하나이다. 바로 \({\bf F}=m{\bf a}\)이거나 \(E=mc^2\)이다.
뉴턴의 제2 운동 법칙인 \({\bf F}=m{\bf a}\)는 물론 중요하다. 물리학이라는 학문을 출발시킨 시조라고 할까? 하지만 아무래도 \({\bf F}=m{\bf a}\)가 아인슈타인의 후광이 드리워진 \(E=mc^2\)을 따라가기는 쉽지 않을 것이다.
소위 질량-에너지 등가mass-energy equivalence 법칙이라고 불리는 \(E=mc^2\)는 질량과 에너지가 근본적으로 같다고 말해 준다.
질량-에너지 등가 법칙은 어떻게 얻어지는 것일까?
질량-에너지 등가 법칙은 속도를 상대성 이론의 원리에 맞게 잘 정의하는 것으로부터 시작한다. 속도를 상대론적으로 잘 정의하기 위해서는 시간의 흐름에 대해서 다시 생각해 보아야 한다. 앞서 설명했듯이 시간의 흐름은 좌표계의 속도에 따라 바뀐다. 결국 우리는 시간의 흐름을 적절하게 잘 정의할 필요가 있다.
상대론적으로 적절한 시간이란 무엇인가?
상대론적으로 적절한 시간은 운동하는 물체와 같은 속도로 나란히 움직이는 시계로 측정하는 시간이다. 이 시간의 이름은 고유 시간proper time이다. 재미있게도 고유 시간의 영어 명칭은 문자 그대로 적절한 시간이다!
구체적으로, 운동하는 물체와 같은 속도로 나란히 움직이는 관성계에서 관찰하는 시간을 고유 시간 \(\delta \tau\)라고 하고, 정지해 있는 관성계에 측정하는 시간을 \(\delta \tau\)라고 하자. 이 두 시간 사이의 관계는 앞서 구한 시간 팽창 공식에 의해서 주어진다.
$$\delta \tau=\frac{\delta t}{\gamma}$$
이제 고유 시간을 기준으로 속도를 재정의하도록 하자. 즉, 상대론적으로 잘 정의된 속도란 위치의 변화를 고유 시간으로 나눈 것이다.
$${\bf u}=\left(
\frac{dx}{d\tau}, \frac{dy}{d\tau}, \frac{dz}{d\tau}
\right)
=\gamma\left(
\frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt}
\right)
=\gamma {\bf v}$$
여기서 \({\bf u}\)는 “고유 속도”이고 \({\bf v}\)는 주어진 관찰자가 바라보는 보통 속도이다.
이 즈음에서 상대성 이론을 위해서 중요한 일반화를 하나 하자. 상대성 이론에 따르면 시간과 공간은 서로 섞인다. 따라서 시간과 공간 좌표를 통합해서 4개의 성분을 동시에 아우르는 시공간 좌표를 정의하는 것이 편리하다.
$$x^\mu=(ct,x,y,z)$$
비슷하게 고유 속도도 다음과 같이 4차원 시공간으로 확장할 수 있다.
$$u^\mu=\left(\frac{cdt}{d\tau},\frac{dx}{d\tau}, \frac{dy}{d\tau}, \frac{dz}{d\tau}\right)
=\gamma\left( c, \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \right)
=\gamma(c,{\bf v})$$
이렇게 4차원 시공간으로 확장된 속도는 영문으로 “four velocity,” 국문으로 “4차원 속도”라고 불린다.
이제 4차원 속도에 질량을 곱하면 4차원 시공간에 정의된 4차원 운동량을 정의할 수 있다.
$$p^\mu=mu^\mu=\gamma m (c,{\bf v})$$
정리하면, 시간과 공간은 통합되어 시공간이 되고, 이를 바탕으로 4차원 운동량이 정의된다.
여기서 질문이 하나 생긴다. 4차원 운동량의 공간 성분은 운동량이다. 그런데 4차원 운동량의 시간 성분은 무엇을 의미하는가?
아인슈타인은 물론이거니와 대부분의 물리학자들은 이 시간 성분이 에너지와 관련된 어떤 물리량이 아닐까라고 곧바로 추측할 수 있다. 그렇게 할 수 있는 이유는 시간과 에너지가 근본적으로 연결되기 때문이다. 조금 더 구체적으로 그 이유는 다음과 같다.
에너지는 보존된다. 에너지는 왜 보존되는 것일까? 에너지가 보존되는 근본적인 이유는 우리 우주에 시간 대칭성이 있기 때문이다. 이것은 마치 운동량 보존 법칙이 공간의 병진 대칭성에 기인하는 것과 비슷하다. 이러한 관계를 일반적으로 뇌터의 정리Noether’s theorem라고 부른다. 결국, 운동량이 공간 좌표의 고유 시간에 따른 변화라면 에너지는 시간 좌표의 고유 시간에 따른 변화이어야 한다.
이러한 근거에 기반해서 4차원 운동량의 시간 성분을 에너지라고 추측해 보자.
$$E/c=\gamma mc$$
(참고: 에너지를 광속으로 나눈 이유는 물리 단위의 차원을 맞추기 위함이다.) 위 추측은 여러모로 꽤 그럴싸하다. 왜냐하면 속도가 광속에 비해서 충분히 느릴 때 위 추측은 우리에게 익숙한 운동 에너지의 공식을 근사적으로 주기 때문이다.
$$E=\gamma mc^2=\frac{mc^2}{\sqrt{1-(v/c)^2}}=mc^2+\frac{1}{2}mv^2+\cdots$$
자, 이제 위 추측을 받아들여서 상대론적 에너지는 \(E=\gamma mc^2\)이고 상대론적 운동량은 \({\bf p}=\gamma m{\bf v}\)라고 정의해 보자.
이렇게 정의된 상대론적 에너지와 운동량 사이에는 다음과 같은 재미있는 관계식이 성립한다.
$$E^2-({\bf p}c)^2=(mc^2)^2$$
위 공식은 상대론적 에너지-운동량 관계식이라고 불린다. 일반 대중에게 익숙한 질량-에너지 등가 공식은 위 공식에서 운동량이 0이 되면 얻어진다.
$$E=mc^2$$
(퀴즈: 엄밀하게 말해서, 질량-에너지 등가 공식은 \(E=\pm mc^2\)이라는 결과를 준다. 그렇다면 음의 부호는 어떻게 되는가?)
자, 이제 우리는 아인슈타인의 질량-에너지 등가 공식과 상대론적 에너지-운동량 관계식을 유도했다. 어쩐지 많이 똑똑해진 것 같은 기분이 들지 않는가?
상대론적 슈뢰딩거 방정식
지금까지 설명한 특수 상대성 이론은 양자역학과 어떻게 통합되는 것일까?
사실 특수 상대성 이론이 정립되는 시기는 양자역학보다 조금 앞선다. 특히 슈뢰딩거가 슈뢰딩거 방정식을 통해서 양자역학의 체계를 정립하던 시기에 특수 상대성 이론은 이미 확고하게 자리를 잡은 상태였다. 특히 특수 상대성 이론은 당대 가장 최신 이론으로 각광을 받고 있었기 때문에 모든 젊고 야망 있는 물리학자들이 관심을 가지고 있었다. 물론 슈뢰딩거도 그러한 물리학자들 중의 하나였다.
자연스럽게 슈뢰딩거는 새롭게 정립되어야 하는 양자역학의 기본 방정식이 특수 상대성 이론의 원리에 의해서 구축되어야 한다고 생각했다. 구체적으로, 슈뢰딩거는 파동 방정식이 특수 상대성 이론에 기반한 질량-에너지 등가 공식으로부터 나와야 한다고 생각했다. 참고로 지금까지 우리에게 익숙한 슈뢰딩거 방정식은 비상대론적 파동 방정식이다.
특수 상대성 이론에 부합하는 파동 방정식을 유도하기 위해서 “믿기 힘든 양자 [3]: 파동 방정식”에서 슈뢰딩거 방정식이 어떻게 유도되었는지 기억을 되살려보자.
기본적으로 슈뢰딩거 방정식의 유도는 에너지와 운동량의 관계식에서 출발한다.
$$E=\frac{{\bf p}^2}{2m}$$
여기서 운동량을 공간에 대한 미분 연산자, 즉 \({\bf p} \rightarrow -i\hbar\nabla\)로 치환하고, 에너지를 시간에 대한 미분 연산자, 즉 \(E \rightarrow i\hbar\partial/\partial t\)로 치환한 후에 파동 함수에 작용하면 슈뢰딩거 방정식이 얻어진다.
$$i\hbar\frac{\partial}{\partial t}\psi=\frac{1}{2m}(-i\hbar\nabla)^2 \psi$$
물론 위 방정식은 퍼텐셜 에너지가 전혀 없는 상황을 기술하는 슈뢰딩거 방정식이다. 다행히 퍼텐셜 에너지가 있는 상황을 기술하는 슈뢰딩거 방정식은 위 방정식을 조금만 바꾸면 된다.
구체적으로 “믿기 힘든 양자 [4]: 게이지 대칭성”에서 배우기를, 게이지 대칭성의 원리에 따르면 운동량은 벡터 퍼텐셜과, 에너지는 스칼라 퍼텐셜과 항상 짝이 되어 같이 나타나야 한다. 다시 말해서, 스칼라와 벡터 퍼텐셜은 각각 다음과 같이 에너지와 운동량을 바꾼다.
$$E \rightarrow E-e\phi$$
$${\bf p} \rightarrow {\bf p}-\frac{e}{c}{\bf A}$$
참고로 스칼라와 벡터 퍼텐셜이 위와 같은 형태로 에너지와 운동량을 바꾸는 것을 전문적으로 최소 결합minimal coupling이라고 부른다.
이렇게 바뀐 에너지와 운동량을 다시 한번 각각 시간과 공간에 대한 미분 연산자로 치환하면 우리는 원하는 슈뢰딩거 방정식을 얻을 수 있다.
$$\left( i\hbar\frac{\partial}{\partial t} -e\phi \right)\psi=
\frac{1}{2m}\left( -i\hbar\nabla-\frac{e}{c}{\bf A} \right)^2 \psi$$
약간 더 정리하면 위 슈뢰딩거 방정식은 다음과 같은 형태로 쓰일 수 있다.
$$i\hbar\frac{\partial}{\partial t}\psi=
\left[\frac{1}{2m}\left( -i\hbar\nabla-\frac{e}{c}{\bf A} \right)^2 +e\phi\right] \psi$$
이것이 바로 우리에게 익숙한 슈뢰딩거 방정식의 최종적인 형태이다.
상대론적 슈뢰딩거 방정식은 위와 비슷한 방법을 상대론적 에너지-운동량 관계식에 적용하면 얻어질 수 있다.
우선, 상대론적 에너지-운동량 관계식을 다시 써 보자.
$$E^2=(mc^2)^2+({\bf p}c)^2$$
이제 앞서 설명한 방법을 그대로 따라 하면 다음과 같은 상대론적 슈뢰딩거 방정식을 얻을 수 있다.
$$\left(i\hbar\frac{\partial}{\partial t} -e\phi \right)^2\psi=
\left[ (mc^2)^2 +c^2\left( -i\hbar\nabla-\frac{e}{c}{\bf A} \right)^2 \right] \psi$$
참고로 위 파동 방정식의 이름은 클라인-고든 방정식Klein-Gordon equation이다.
여기서 질문 하나. 클라인-고든 방정식은 올바른 상대론적 슈뢰딩거 방정식인가?
재미있게도, 클라인-고든 방정식은 맞기도 하고 틀리기도 하다. 무슨 말인가?
클라인-고든 방정식을 만족하는 입자는 분명히 존재한다. 이런 의미에서 클라인-고든 방정식은 맞다. 하지만 우리가 현재 가장 큰 관심을 가지고 있는 전자는 클라인-고든 방정식을 만족하지 않는다. 전자는 폴 디랙Paul Dirac이 발견한 디랙 방정식Dirac equation을 만족한다. 이런 의미에서 클라인-고든 방정식은 틀리다.
아, 이상하다. 입자의 성질에 따라서 다른 종류의 상대론적 슈뢰딩거 방정식이 필요하다는 의미인가?
결론부터 말하면 그렇다.
그렇다면 입자의 어떤 성질이 상대론적 슈뢰딩거 방정식을 결정하는 것일까?
답은 바로 입자의 내부 자유도internal degree of freedom인 스핀spin이다.
물론 디랙이 디랙 방정식을 고안할 때는 이 사실을 완전히 이해하지 못했다. 디랙은 우선 그저 상대론적 에너지-운동량 관계식과 양자역학을 통합하고 싶었다.
앞선 “믿기 힘든 양자 [3]: 파동 방정식”에서 배웠듯이 클라인-고든 방정식은 근본적으로 큰 문제를 하나 가지고 있었다. 그 문제는 바로 확률이 양수로 제대로 정의되지 않는다는 것이었다. 기억해 보면 이것은 클라인-고든 방정식이 시간에 대해서 2차 미분 방정식이라는 사실에 기인했다. 따라서 디랙은 시간에 대해서 1차 미분 방정식을 고안하고 싶었다.
어떻게 하면 2차 미분 방정식을 1차 미분 방정식으로 만들 수 있을까?
처음 들으면 미친 생각 같지만, 혹시 2차 미분 방정식에 모조의 제곱근을 씌우면 되지 않을까?
이 미친 생각을 구체적으로 설명하기 위해서 상대론적 에너지-운동량 관계식을 아래와 같이 다시 한번 써 보자.
$$E^2-({\bf p}c)^2=(mc^2)^2$$
이전과 같이 에너지를 시간에 대한 미분 연산자로, 운동량을 공간에 대한 미분 연산자로 바꾸어 보자.
$$\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}=\left( \frac{mc}{\hbar} \right)^2$$
위에서는 편의상 스칼라와 벡터 퍼텐셜을 쓰지 않았다.
이제 위 공식의 좌변을 다음과 같이 쓸 수 있다고 상상해 보자.
$$\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}=
\left(
A\frac{\partial}{\partial x}+B\frac{\partial}{\partial y}
+C\frac{\partial}{\partial z}+D\frac{i}{c}\frac{\partial}{\partial t}
\right)
\left(
A\frac{\partial}{\partial x}+B\frac{\partial}{\partial y}
+C\frac{\partial}{\partial z}+D\frac{i}{c}\frac{\partial}{\partial t}
\right)$$
만약 그럴 수 있다면, 아래와 같이 2차 미분 연산자의 제곱근에 해당하는 1차 미분 연산자를 정의할 수 있다.
$$\sqrt{\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}}=
A\frac{\partial}{\partial x}+B\frac{\partial}{\partial y}
+C\frac{\partial}{\partial z}+D\frac{i}{c}\frac{\partial}{\partial t}$$
이제 이 1차 미분 연산자를 이용해서 새로운 상대론적 슈뢰딩거 방정식을 만들면 다음과 같다.
$$\left(A\frac{\partial}{\partial x}+B\frac{\partial}{\partial y}
+C\frac{\partial}{\partial z}+D\frac{i}{c}\frac{\partial}{\partial t} \right) \psi=
\frac{mc}{\hbar} \psi$$
기본적으로 이것이 바로 디랙 방정식이다.
자, 그렇다면 \(A, B, C, D\)는 무엇인가?
우선, \(A, B, C, D\)는 단순한 숫자가 아니다. \(A, B, C, D\)는 행렬이 되어야 한다. 왜냐하면 \(A, B, C, D\)는 다음과 같은 연산 법칙을 만족해야 하기 때문이다.
$$A^2=B^2=C^2=D^2=1$$
$$AB+BA=AC+CA=AD+DA=0$$
$$BC+CB=BD+DB=0$$
$$CD+DC=0$$
위 연산 법칙에 따르면 \(A, B, C, D\)의 제곱은 모두 1이며, 그것들 중에서 임의의 두 개를 골라서 곱한 값은 곱하는 순서에 따라서 그 결과가 달라진다. 구체적으로, \(AB\)와 \(BA\)는 정확히 반대의 부호를 가지며, 따라서 둘을 더하면 서로를 상쇄하게 된다.
자, 이제 문제는 위 연산 법칙을 만족하는 4개의 행렬 \(A, B, C, D\)를 찾는 것으로 귀착된다.
결론부터 말하면, \(A, B, C, D\)는 다음과 같은 4개의 4차원 정사각행렬square matrix로 나타낼 수 있게 된다.
$$A=i\gamma^1,\;\; B=i\gamma^2,\;\; C=i\gamma^3,\;\; D=\gamma^0$$
위에서 소위 감마 행렬gamma matrix은 아래와 같이 주어진다.
$$\gamma^0=\left(
\begin{array}{cc}
I_2 & 0 \\
0 & -I_2
\end{array}
\right),\;\;
\gamma^1=\left(
\begin{array}{cc}
0 & \sigma_x \\
-\sigma_x & 0
\end{array}
\right),\;\;
\gamma^2=\left(
\begin{array}{cc}
0 & \sigma_y \\
-\sigma_y & 0
\end{array}
\right),\;\;
\gamma^3=\left(
\begin{array}{cc}
0 & \sigma_z \\
-\sigma_z & 0
\end{array}
\right)$$
단위 행렬unit matrix과 파울리 행렬Pauli matrix을 구체적으로 쓰면 다음과 같다.
$$I_2=\left(
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}
\right),\;\;
\sigma_x=\left(
\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}
\right),\;\;
\sigma_y=\left(
\begin{array}{cc}
0 & -i \\
i & 0
\end{array}
\right),\;\;
\sigma_z=\left(
\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}
\right)$$
입자 물리학particle physics에서 디랙 방정식은 보통 감마 행렬을 이용해서 표현된다. 다음은 디랙 방정식을 위한 보통의 표현식이다.
$$(i\hbar\gamma^\mu \partial_\mu-mc)\psi=0$$
위에서 \(\mu=0, 1, 2, 3\)이고, 간략화된 미분 연산자 \(\partial_\mu\)는 다음과 같이 정의된다.
$$\partial_0=\frac{1}{c}\frac{\partial}{\partial t},\;\;
\partial_1=\frac{\partial}{\partial x},\;\;
\partial_2=\frac{\partial}{\partial y},\;\;
\partial_3=\frac{\partial}{\partial z}$$
참고로, 위 디랙 방정식의 표현식에서는 위 첨자와 아래 첨자가 반복되면 해당 첨자가 가질 수 있는 모든 경우에 대해서 항의 값을 전부 더한다는 아인슈타인 표기법Einstein notation이 사용되었다. 즉, \(\gamma^\mu \partial_\mu\)는 다음을 의미한다.
$$\gamma^\mu \partial_\mu
=\gamma^0\partial_0
+\gamma^1\partial_1
+\gamma^2\partial_2
+\gamma^3\partial_3$$
여기서 주목할 사실은 디랙 방정식이 행렬의 형태로 주어지는 미분 방정식이라는 것이다. 따라서 파동 함수는 단순한 하나의 함수가 아니라 4개의 성분으로 이루어진 4차원 벡터 함수가 된다.
$$\psi=\left(
\begin{array}{c}
\psi_1\\
\psi_2\\
\psi_3\\
\psi_4
\end{array}
\right)$$
이 4차원 벡터 함수의 물리적인 의미에 대해서는 이어지는 섹션에서 자세하게 이야기할 예정이다.
그전에 스칼라와 벡터 퍼텐셜이 존재하는 일반적인 상황을 기술하는 디랙 방정식을 구해 보자.
일반적인 디랙 방정식은 슈뢰딩거 방정식이나 클라인-고든 방정식의 경우와 동일하게 “최소 결합” 방법을 적용하면 얻을 수 있다.
$$\left[ \gamma^\mu\left( i\hbar\partial_\mu-\frac{e}{c}A_\mu \right) -mc \right]\psi=0$$
위에서 4차원 퍼텐셜 \(A_\mu\)은 다음과 같이 정의된다.
$$A_\mu=(A_0, A_1, A_2, A_3)=(\phi,-A_x,-A_y,-A_z)$$
이것으로 드디어 디랙 방정식의 유도가 완전히 끝났다.
자, 이제 앞서 언급했던 문제가 해결된다. 다시 말해서, 디랙 방정식의 확률은 양수로 제대로 정의된다.
우선, 확률 밀도probability density \(\rho\)와 확률 흐름probability current \({\bf J}=(J_x,J_y,J_z)\)를 상대성 이론의 원리에 맞추어 소위 4차원 흐름four-current의 형태로 쓰면 다음과 같다.
$$J^\mu=(J_0,J_1,J_2,J_3)=(c\rho,J_x,J_y,J_z)$$
여기서 4차원 흐름은 연속 방정식continuity equation을 만족해야 한다.
$$\partial_\mu J^\mu =0$$
구체적으로, 약간의 계산을 해 보면 디랙 방정식은 연속 방정식을 만족하는 다음과 같은 4차원 흐름을 준다.
$$J^\mu=\psi^\dagger\gamma^0\gamma^\mu\psi$$
여기서 \(\psi^\dagger\)는 \(\psi\)의 에르미트 켤레Hermitian conjugate를 나타낸다. 간단하게 말해서, 에르미트 켤레란 전치transpose된 복소수 켤레를 의미한다.
$$\psi^\dagger=(\psi_1^*,\psi_2^*,\psi_3^*,\psi_4^*)$$
위 공식에 따르면, 확률 밀도는 비상대론적인 슈뢰딩거 방정식에서와 완전히 동일한 형태를 지닌다.
$$c\rho=\psi^\dagger\gamma^0\gamma^0\psi=\psi^\dagger\psi=\sum_{i=1}^4 |\psi_i|^2$$
위에서 \((\gamma^0)^2=1\)이라는 감마 행렬의 성질을 썼다.
이제 확률은 명백하게 양수로 주어진다.
스핀의 운명적 출현
디랙 방정식을 만족하는 파동 함수는 4개의 성분을 지니는 4차원 벡터 함수이다. 다시 말해서, 디랙 방정식을 만족하는 파동 함수는 시공간의 각 점에서 4개의 성분을 필요로 한다.
이 4개의 성분은 무엇을 의미하는 것일까?
간단하게 말하면, 4개의 성분은 모종의 내부 자유도이다.
앞선 “믿기 힘든 양자 [7]: 두 상태 이야기”에서 배운 바에 따르면 전자는 스핀이라는 내부 자유도를 지닌다. 특히, 전자의 스핀은 1/2이다. 따라서 전자는 스핀 업과 다운이라는 두 상태 중의 하나로 기술된다. 수학적으로 보면, 이것은 전자의 스핀 상태가 2차원 벡터로 표현될 수 있다는 것을 의미한다. 그렇다면 디랙 방정식을 만족하는 파동 함수가 가지는 4개의 성분 중에서 적어도 2개는 스핀과 관계된 어떤 것으로 이해될 수 있지 않을까?
이 추정을 확인하기 위해서 파동 함수를 다음과 같이 써 보자.
$$\psi=\left(
\begin{array}{c}
\psi_+ \\
\psi_-
\end{array}
\right)$$
여기서 \(\psi_+\)와 \(\psi_-\)는 각각 4개의 성분의 앞 2개와 뒤 2개를 하나로 묶은 2차원 벡터 파동 함수이다.
이제 디랙 방정식은 다음과 같이 2차원 벡터 파동 함수가 만족하는 미분 방정식의 형태로 다시 쓸 수 있다.
$$\left(
\begin{array}{cc}
mc^2-E+e\phi & c\boldsymbol{\sigma}\cdot\left( {\bf p}-\frac{e}{c}{\bf A} \right) \\
-c\boldsymbol{\sigma}\cdot\left( {\bf p}-\frac{e}{c}{\bf A} \right) & mc^2+E-e\phi
\end{array}
\right)
\left(
\begin{array}{c}
\psi_+ \\
\psi_-
\end{array}
\right)
=\left(
\begin{array}{c}
0 \\
0
\end{array}
\right)$$
여기서는 편의상 시간과 공간에 대한 미분 연산자를 에너지(\(E=i\hbar\partial/\partial t\))와 운동량(\({\bf p}=-i\hbar\nabla\))으로 다시 표시했다.
위에서 행렬로 쓰인 디랙 방정식을 아래와 같이 풀어 써 보자.
$$(E-e\phi)\psi_+ -c\boldsymbol{\sigma}\cdot\left( {\bf p}-\frac{e}{c}{\bf A} \right)\psi_-=mc^2\psi_+$$
$$-(E-e\phi)\psi_- +c\boldsymbol{\sigma}\cdot\left( {\bf p}-\frac{e}{c}{\bf A} \right)\psi_+=mc^2\psi_-$$
이 단계에서 우리가 하고 싶은 일은 디랙 방정식에 모종의 근사를 취해서 슈뢰딩거 방정식을 얻는 것이다. 여기서 모종의 근사란 비상대론적인 극한을 취하는 것이다.
구체적으로, 전자가 빛의 속도에 비해서 충분히 느리게 움직인다면, 그것의 에너지는 대략 정지 에너지rest energy인 \(mc^2\)에 퍼텐셜 에너지 \(e\phi\)가 더해진 양으로 근사할 수 있을 것이다.
$$E-e\phi \approx mc^2$$
위 조건을 앞선 두 번째 방정식에 집어넣으면 다음과 같은 결론에 이를 수 있다.
$$\psi_-=\frac{1}{2mc}\boldsymbol{\sigma}\cdot\left( {\bf p}-\frac{e}{c}{\bf A} \right) \psi_+$$
이제 다시 위 공식을 앞선 첫 번째 방정식에 집어넣으면 아래와 같다.
$$(E-mc^2)\psi_+=\left(
\frac{1}{2m}\left[ \boldsymbol{\sigma}\cdot\left({\bf p}-\frac{e}{c}{\bf A} \right) \right]^2+e\phi
\right)\psi_+$$
위 공식은 거의 기본적으로 슈뢰딩거 방정식이다. 여기에 마지막 한 가지 작업만 더 해 주면 우리에게 익숙한 형태의 슈뢰딩거 방정식으로 만들 수 있다.
구체적으로 파울리 행렬의 성질을 쓰면 위 공식은 다음과 같이 정리될 수 있다.
$$(E-mc^2)\psi_+=\left(
\frac{1}{2m}\left({\bf p}-\frac{e}{c}{\bf A} \right)^2
-\frac{e\hbar}{2mc}\boldsymbol{\sigma}\cdot(\nabla\times{\bf A})
+e\phi\right)\psi_+$$
위 공식은 우변의 두 번째 항을 제외하면 완벽하게 슈뢰딩거 방정식과 같다. 이 새로운 항은 소위 제이만 효과 Zeeman effect를 기술하는 항이다. 참고로, 슈뢰딩거 방정식의 에너지는 상대론적 에너지에서 정지 에너지인 \(mc^2\)를 뺀 양으로 정의된다.
제이만 효과란 전자의 스펙트럼이 자기장 하에서 두 개로 갈라지는 효과이다. 이 효과는 스핀이 자기장과 결합하면 발생할 수 있다. 간단하게 말해서, 제이만 효과는 스핀이 자기장과 나란한 방향으로 향할 때와 반대 방향으로 향할 때 에너지가 달라지는 효과이다.
제이만 효과는 앞선 우변의 두 번째 항에 의해서 기술될 수 있다. 즉, 우변의 두 번째 항은 벡터 퍼텐셜의 컬 미분이라는 사실을 이용하면 다음과 같이 다시 쓸 수 있다.
$$H_{\rm Zeeman}=g \mu_B {\bf S}\cdot{\bf B}$$
여기서 \(\mu_B=|e|\hbar/2mc\)는 보어 마그네톤Bohr magneton이라는 불리는 상수이고, \({\bf S}=\hbar\boldsymbol{\sigma}/2\)는 전자의 스핀 연산자이고, \({\bf B}=\nabla\times{\bf A}\)는 자기장이다. 처음 보면 왜 굳이 새로운 기호를 정의해서 표시할까 싶지만 \(g=2\)는 전자의 자기 회전 비율gyromagnetic ratio, 혹은 g-인자g-factor라고 불리는 양이다.
잠깐, 놀랍지 않은가?
디랙 방정식에 의한 상대성 이론과 양자역학의 통합은 스핀이 존재해야만 하는 이유를 말해 준다. 스핀의 출현은 운명적이었다.
게다가 디랙 방정식에 따르면 순수하게 이론적인 추론만으로 전자의 자기 회전 비율이 (거의) 정확히 2라는 사실이 도출된다. 사실 엄밀하게 말해서 전자의 자기 회전 비율은 다음과 같이 주어진다.
$$g=2\left( 1+\frac{\alpha}{2\pi}+\cdots \right)$$
여기서 \(\alpha=e^2/\hbar c\)는 미세 구조 상수fine structure constant라고 불린다.
미세 구조 상수에 비례하는 보정 항은 양자전기역학quantum electrodynamics , QED이라고 불리는 양자장론quantum field theory에 의해서 엄밀하게 계산될 수 있으며, 실제 실험 결과와 매우 높은 정확도로 맞는다는 것이 알려졌다. 참고로 현재 알려진 이론과 실험 결과는 다음과 같다.
$$\frac{g-2}{2}=0.001\;159\;652\;181\;643(764)\;\;\;\;\; {\rm (Theory)}$$
$$\frac{g-2}{2}=0.001\;159\;652\;180\;73(28)\;\;\;\;\; {\rm (Experiment)}$$
이렇게 정확하게 예측된 전자의 자기 회전 비율은 양자전기역학의 대표적인 성공 사례로 손꼽힌다. 역사적인 문맥에서 보면, 디랙 방정식으로 시작된 상대성 이론과 양자역학의 통합은 양자장론이라는 형태로 완성되게 된다.
이어지는 섹션에서 조금 더 자세히 설명하겠지만, 양자장론이란 간단하게 말해서 위치/운동량과 같은 입자의 동역학적 성질뿐만 아니라 입자의 존재 자체가 요동치는 상황을 기술하는 양자 이론이다.
입자의 존재 자체가 요동치다니, 도대체 무슨 말인가?
디랙 바다: 진공은 비어있지 않다
디랙 방정식에 따르면 스핀은 존재해야 한다.
자, 그렇다면 디랙 방정식을 만족하는 파동 함수의 나머지 2개의 성분의 의미는 무엇인가?
그 의미를 깨닫기 위해서 디랙 방정식을 아무런 근사 없이 정식으로 풀어 보자. 일반적인 경우를 풀기는 어려우니 아무런 퍼텐셜이 없는 자유 전자의 경우에 대해서 풀어 보자.
자유 전자를 기술하는 디랙 방정식은 다음과 같다.
$$E\psi_+ -c\boldsymbol{\sigma}\cdot{\bf p}\psi_-=mc^2\psi_+$$
$$-E\psi_- +c\boldsymbol{\sigma}\cdot{\bf p}\psi_+=mc^2\psi_-$$
여기서 에너지와 운동량은 연산자가 아니라 보통의 숫자로 치환될 수 있다. 왜냐하면 자유 전자의 파동 함수는 다음과 같은 “가장 순수한 형태의 파동”인 평면파plane wave로 기술될 수 있기 때문이다.
$$\psi=\left(
\begin{array}{c}
\chi_+ \\
\chi_-
\end{array}
\right)
e^{\frac{i}{\hbar}({\bf p}\cdot{\bf x}-Et)}$$
여기서 \(\chi_+\)와 \(\chi_-\)는 시공간 좌표에 의존하지 않는 순수한 스핀 상태를 기술하는 파동 함수, 즉 스피너spinor이다.
이제 위 두 공식은 아래와 같이 다시 정리될 수 있다.
$$\chi_+=\frac{c\boldsymbol{\sigma}\cdot{\bf p}}{E-mc^2} \chi_-$$
$$\chi_-=\frac{c\boldsymbol{\sigma}\cdot{\bf p}}{E+mc^2} \chi_+$$
위 두 공식은 하나의 조건으로 귀착된다.
$$\chi_\pm=\frac{c^2(\boldsymbol{\sigma}\cdot{\bf p})^2}{E^2-(mc^2)^2} \chi_\pm$$
위 조건을 만족하기 위해서는 다음의 조건을 만족해야 한다.
$$\frac{c^2(\boldsymbol{\sigma}\cdot{\bf p})^2}{E^2-(mc^2)^2} =1$$
파울리 행렬의 성질을 쓰면 위 조건은 결국 단순한 상대론적 에너지-운동량 관계식으로 귀착된다.
$$E^2=(mc^2)^2+c^2(\boldsymbol{\sigma}\cdot{\bf p})^2
=(mc^2)^2+({\bf p}c)^2$$
당연한 말 같지만, 위 공식에 따르면 에너지는 양수 혹은 음수가 될 수 있다.
$$E=\pm\sqrt{(mc^2)^2+({\bf p}c)^2}$$
자, 여기서 철학적인 문제가 발생한다.
에너지가 음수가 될 수 있다면, 특히 위 공식이 말해주는 것처럼 음수로 무한히 커질 수 있다면, 그 무수히 많은 음의 에너지 준위들은 다 어떻게 채워지는 것일까?
무릇 진공이란 아무것도 존재하지 않는 상태이다.
자, 이제 진공에 전자가 하나씩 생기면 어떤 상황이 벌어질까 생각해 보자. 전자는 에너지가 낮은 상태에서 높은 상태로 에너지 준위를 하나씩 차곡차곡 채워 올라가게 될 것이다. 그런데 처음부터 무수히 많은 음의 에너지 준위가 존재한다면 이러한 에너지 준위들을 모두 다 어떻게 채워지는 것일까?
사실 이 문제에는 매우 간단한 해결책이 있다. 진공은 사실 비어있는 것이 아니라, 애초부터 음의 에너지 준위들이 모두 꽉 채워진 상태인 것이다. 이것이 바로 디랙 바다Dirac sea이다.
단순한 말장난처럼 들리지만, 이 해결책은 매우 놀라운 예측을 하게 된다.
만약 디랙 바다 속에 있던 전자 하나가 에너지를 받아서 양의 에너지 준위로 올라갈 수 있다면, 디랙 바다 속에는 원래 있던 전자 대신에 빈 공간, 즉 정공hole이 하나 만들어지게 될 것이다. 이 정공은 음의 전하를 지니던 전자가 없어진 자리이므로 유효적으로 양의 전하를 지닌 모종의 입자처럼 행동할 것이라고 예측할 수 있다.
(혹시 눈치챘는지 모르겠지만, 디랙 바다는 앞선 “믿기 힘든 양자 [11]: 양자 물질 상태”에서 언급한 페르미 바다Fermi sea와 많이 닮아 있다.)
디랙은 처음 이 새로운 입자가 양성자라고 생각했으나, 이내 다른 물리학자들은 그럴 수 없다는 사실을 깨닫게 된다. 정공은 전자와 전기 전하는 반대이지만 다른 모든 면에서는 동일해야 하기 때문이다.
이 새로운 입자는 바로 반입자antiparticle, 혹은 반물질antimatter이다. 구체적으로, 전자의 반입자는 양전자positron이다.
다시 한번, 놀랍지 않은가?
앞서 언급하기를, 디랙 방정식에 의한 상대성 이론과 양자역학의 통합은 스핀이 존재해야만 하는 이유를 말해 준다고 했다. 스핀의 출현은 운명적이라고 했다. 그런데 디랙 방정식은 그보다 한 걸음 더 나아간다. 디랙 방정식에 따르면 순수하게 이론적인 추론만으로 반물질이 존재한다는 사실이 도출되는 것이다.
좋다.
그런데 반물질이 도입되는 순간, 어찌 보면 입자의 개수라는 것이 무의미해진다. 디랙 바다 속에서 언제든지 입자를 하나 떼어서 양의 에너지로 올릴 수 있기 때문이다. 이것은 진공으로부터 언제든지 반입자와 입자를 쌍으로 생성할 수 있다는 것을 의미한다. 즉, 입자가 존재한다는 사실조차 이제는 양자역학적으로 요동치는 것이다.
사실 엄밀하게 말해서 이 문제는 디랙 방정식 이전부터 존재해 왔다.
광자의 개수는 보존되지 않는다. 광자는 충분한 에너지만 있으면 얼마든지 만들어낼 수 있다.
빛의 양자화: 빛도 물질이다
독자들에게 이미 광자라는 용어는 매우 익숙하겠지만, 실제로 광자의 동역학을 기술하는 양자역학적 파동 방정식이 무엇인지 물어보면 답하기가 쉽지 않을 것이다.
쉽게 말해서, 광자의 “슈뢰딩거 방정식”은 무엇인가?
결론부터 말하면, 직접적인 의미에서 광자의 “슈뢰딩거 방정식”이란 것은 없다.
이 말의 의미를 깨닫기 위해서 슈뢰딩거 방정식이 무엇을 주는지 생각해 보자. 슈뢰딩거 방정식은 입자가 공간에 퍼져서 출렁거리는 확률을 준다. 하지만 빛, 즉 전자기장은 원래부터 공간에 퍼져서 출렁거린다. 이러한 전자기장의 공간적인 출렁거림을 기술하는 방정식은 맥스웰 방정식Maxwell’s equations이다. 하지만 맥스웰 방정식은 고전역학적 파동 방정식이다.
우리에게 필요한 것은 전자기장의 세기가 양자역학적으로 출렁거리는 것을 기술하는 새로운 파동 방정식이다.
이해를 돕기 위해서, 1차원에서 진동하는 끈의 동역학을 생각해 보자.
끈의 진폭을 \(u(x,t)\)라고 할 때, 끈의 해밀토니안은 다음과 같이 쓰일 수 있다.
$$H=\frac{1}{2}\int_{0}^{L} dx \left[
\left(\frac{\partial u}{\partial t}\right)^2
+c^2\left(\frac{\partial u}{\partial x}\right)^2
\right]$$
여기서 끈은 양쪽 끝인 \(0\)과 \(L\)에 묶여 있다. 즉, \(u(x=0,t)=u(x=L,t)=0\)이다. 그리고 여기서 \(c\)는 끈의 출렁거림의 이동 속도이다.
끈의 출렁거림을 기술하는 고전역학적인 파동 방정식은 위 해밀토니안에서 유도될 수 있다.
$$\frac{\partial^2 u}{\partial t^2}-c^2\frac{\partial^2 u}{\partial x^2}=0$$
이 고전역학적인 파동 방정식의 해는 다음과 같다.
$$u(x,t)=\sum_{p=1}^\infty u_p(t) \sin{(k_p x)}$$
여기서 끈의 진폭 \(u_p(t)\)은 다음과 같이 쓰일 수 있다.
$$u_p(t)=u_p e^{-i\omega_p t} +u_p^* e^{i\omega_p t}$$
위에서 파수 \(k_p\)과 진동수 \(\omega_p\)는 다음과 같이 주어진다.
$$k_p=\frac{p\pi}{L},\;\;\; \omega_p=ck_p$$
여기서 끈의 진폭의 크기, 즉 \(u_p\)과 \(u_p^*\)는 위 고전역학적 파동 방정식에 의해서 결정되지 않는다. 끈의 진폭은 파동 함수가 아니다. 따라서 끈의 진폭은 파동 함수와 다르게 제곱한 값을 전공간에 대해서 적분했을 때 그 값이 1이 될 필요가 없다. 그렇다면 무엇이 끈의 진폭을 결정하는 것일까?
끈의 진폭은 에너지에 의해서 결정된다.
$$H=2L \sum_{p=1}^\infty \omega_p^2 u_p^* u_p$$
위 공식에 따르면 끈의 진폭이 양자화되면 에너지가 양자화된다. 이제 거의 목적지에 다 왔다.
편의상, 끈의 진폭을 표시하기 위해서 새로운 변수 \(a_p\)를 도입하자.
$$a_p=\frac{1}{\sqrt{2L\omega_p}} u_p$$
이제 끈의 동역학을 기술하는 해밀토니안은 다음과 같이 쓰인다.
$$H=\sum_{p=1}^\infty \omega_p a_p^* a_p
=\frac{1}{2}\sum_{p=1}^\infty \omega_p (a_p^* a_p +a_p a_p^*)$$
참고로, 위 맨 오른쪽 공식에서는 양자화를 위한 정지 작업으로 \(a_p\)과 \(a_p^*\)의 순서를 대칭적으로 표현하였다.
이제 드디어 끈의 진폭을 양자화시킬 단계에 도달했다. 진폭을 나타내는 변수를 다음과 같이 연산자로 바꾸어 보자.
$$a_p=\sqrt{\hbar} \hat{a}_p,\;\;\; a_p^*=\sqrt{\hbar} \hat{a}_p^\dagger$$
끈의 양자역학적 해밀토니안은 새롭게 정의된 연산자로 다음과 같이 쓰인다.
$$H=\frac{\hbar}{2} \sum_{p=1}^\infty \omega_p (\hat{a}_p^\dagger \hat{a}_p +\hat{a}_p \hat{a}_p^\dagger)$$
이제 양자화를 위해서 \(\hat{a}_p\)와 \(\hat{a}_p^\dagger\) 사이에 교환 관계commutation relation를 할당하는 일이 남았다.
$$[\hat{a}_p, \hat{a}_p^\dagger]= \hat{a}_p\hat{a}_p^\dagger-\hat{a}_p^\dagger\hat{a}_p=1$$
최종적으로 끈의 양자역학적 해밀토니안은 다음과 같이 얻어진다.
$$H=\hbar \sum_{p=1}^\infty \omega_p \left(\hat{a}_p^\dagger \hat{a}_p +\frac{1}{2}\right)$$
자, 이 해밀토니안, 어디선가 본 적이 있지 않은가?
위 해밀토니안은 앞선 “믿기 힘든 양자 [12]: 많음, 다름, 그리고 양자”에서 보았다. 바로 란다우 해밀토니안Landau Hamiltonian이다.
기억을 되살려 보면, 란다우 해밀토니안은 등간격으로 배치된 에너지 준위를 가지며, \(\hat{a}_p\)와 \(\hat{a}_p^\dagger\)는 그러한 에너지 준위 사이를 이동할 수 있는 소위 사다리 연산자ladder operator, 구체적으로 각각 내림과 올림 연산자이다.
이 사실을 이용해서 앞선 끈의 해밀토니안의 에너지 고유값을 쓰면 다음과 같다.
$${\cal E}=\hbar \sum_{p=1}^\infty \omega_p \left( n_p+\frac{1}{2} \right)$$
여기서 \(n_p\)는 0 혹은 양의 정수이다.
위 결론은 다음과 같이 해석될 수 있다.
끈의 진폭은 그것이 주는 에너지가 기본 에너지 단위, 즉 \(\hbar\omega_p\)의 정수 배가 되는 형식으로 양자화된다. 이것은 마치 모종의 새로운 입자가 존재해서 하나 생성될 때마다 \(\hbar\omega_p\)의 에너지가 소요되는 것으로 해석될 수 있다. 이 경우, 올림 및 내림 연산자는 입자를 생성creation 및 소멸annihilation시키는 연산자로 재해석될 수 있다.
이 모종의 새로운 입자는 바로 끈 양자이다.
빛 양자, 즉 광자도 비슷하게 생성된다.
빛을 양자화하기 위해서는 항상 그렇듯이 빛이 가지는 에너지로부터 출발한다.
전자기장의 해밀토니안은 다음과 같이 주어진다.
$$H=\frac{1}{2}\int d^3 {\bf r} \left( {\bf E}^2+{\bf B}^2 \right)$$
여기서 \({\bf E}\)와 \({\bf B}\)는 각각 전기장과 자기장이다.
이제 전기장과 자기장을 스칼라와 벡터 퍼텐셜로 표시하면 다음과 같다.
$$H=\frac{1}{2}\int d^3{\bf r}\left[ \left( \nabla\phi+\frac{1}{c}\frac{\partial{\bf A}}{\partial t} \right)^2 +(\nabla\times{\bf A})^2 \right]
=\frac{1}{2}\int d^3{\bf r}\left[ \left( \nabla\phi \right)^2 +\left(\frac{1}{c}\frac{\partial{\bf A}}{\partial t} \right)^2 +(\nabla\times{\bf A})^2 \right]$$
위에서 우변의 마지막 표현식은 부분 적분integration by parts을 통해서 얻어졌다. 사실 부분 적분을 한 번 더 적용하면 \((\nabla\phi)^2=\rho\phi\)이라는 사실을 보일 수 있다. 여기서 \(\rho\)는 전기 전하의 밀도이다. 현재 우리는 전기 전하 혹은 전류가 전혀 없는 자유 공간에서 전자기장이 가지는 에너지에 관심을 가지고 있다. 따라서 이 마지막 항은 현재 무시할 수 있다.
결국 전자기장의 해밀토니안은 다음과 같이 쓰인다.
$$H=\frac{1}{2}\int d^3{\bf r}\left[ \left(\frac{1}{c}\frac{\partial{\bf A}}{\partial t} \right)^2 +(\nabla\times{\bf A})^2 \right]$$
벡터 퍼텐셜의 파동 방정식은 위 해밀토니안으로부터 얻어질 수 있다.
$$\left(\frac{\partial^2}{\partial t^2} -c^2\nabla^2 \right){\bf A}=0$$
사실 위 파동 방정식은 소위 쿨롱 게이지Coulomb gauge라는 조건 \(\nabla\cdot{\bf A}=0\))에서 얻어진다.
자, 이제 전자기장의 동역학과 앞서 설명한 끈의 동역학 사이의 유사성이 슬슬 보이기 시작한다. 즉, 둘 다 매우 유사한 형태의 파동 방정식을 만족한다. 유사성을 더욱 부각시키기 위해서 벡터 퍼텐셜을 다음과 같이 표현해 보자.
$${\bf A}=\sum_{\bf k} \left(
{\bf A}_{\bf k} e^{i({\bf k}\cdot{\bf r}-\omega_k t)}
+{\bf A}_{\bf k}^* e^{-i({\bf k}\cdot{\bf r}-\omega_k t)}
\right)$$
여기서 빛의 진동수는 \(\omega_k=c|{\bf k}|\)이다. 사실 빛은 두 가지 다른 편광polarization 방향을 가진다. 따라서 벡터 퍼텐셜은 편광 방향을 고려해서 다음과 같이 쓰일 수 있다.
$${\bf A}=\sum_{{\bf k},\lambda} \left(
{\bf A}_{{\bf k},\lambda} e^{i({\bf k}\cdot{\bf r}-\omega_k t)}
+{\bf A}_{{\bf k},\lambda}^* e^{-i({\bf k}\cdot{\bf r}-\omega_k t)}
\right)$$
여기서 \(\lambda=1,2\)는 편광 방향을 나타내는 변수이다.
이제 위 벡터 퍼텐셜을 전자기장의 해밀토니안에 집어 넣고 계산하면 다음과 결론에 이를 수 있다.
$$H=2\sum_{{\bf k},\lambda} \left(\frac{\omega_k}{c}\right)^2 {\bf A}_{{\bf k},\lambda}^* \cdot {\bf A}_{{\bf k},\lambda}
=\sum_{{\bf k},\lambda} \left(\frac{\omega_k}{c}\right)^2 \left({\bf A}_{{\bf k},\lambda}^* \cdot {\bf A}_{{\bf k},\lambda} + {\bf A}_{{\bf k},\lambda}\cdot {\bf A}_{{\bf k},\lambda}^* \right)$$
빛의 양자화는 끈의 경우와 유사하게 벡터 퍼텐셜을 연산자로 바꾸면 된다.
$${\bf A}_{{\bf k},\lambda}=c\sqrt{\frac{\hbar}{2\omega_k}} \hat{a}_{{\bf k},\lambda} \hat{\epsilon}_{{\bf k},\lambda},\;\;\;
{\bf A}^*_{{\bf k},\lambda}=c\sqrt{\frac{\hbar}{2\omega_k}} \hat{a}^\dagger_{{\bf k},\lambda} \hat{\epsilon}_{{\bf k},\lambda}$$
여기서 \(\hat{\epsilon}_{{\bf k},\lambda}\)는 빛의 편광 방향을 나타내는 단위 벡터이다.
이제 광자를 기술하는 최종 해밀토니안은 다음과 같다.
$$H=\hbar \sum_{{\bf k},\lambda} \omega_k \left( \hat{a}^\dagger_{{\bf k},\lambda}\hat{a}_{{\bf k},\lambda} +\frac{1}{2}\right)$$
자, 이것으로 빛이 양자화되었다.
여기서 한 가지 기억해야 할 중요한 사실이 있다. 광자의 동역학을 기술하는 양자역학적 파동 방정식은 슈뢰딩거 방정식과 다르게 파동 함수가 아니라 광자의 개수를 조절하는 연산자의 형태로 주어진다. 앞선 “믿기 힘든 양자 [6]: 양자 삼위일체 2부”에서 배웠듯이 연산자의 동역학은 슈뢰딩거 방정식이 아니라 하이젠베르크Heisenberg equation 방정식에 의해서 기술된다. 이런 의미에서 광자의 “슈뢰딩거 방정식”은 없다.
하지만 하이젠베르크 방정식은 슈뢰딩거 방정식과 완벽하게 동일하다. 따라서 하이젠베르크 방정식을 쓴다고 해서 새로운 종류의 양자역학이 탄생하는 것은 아니다. 다만, 전자기장의 경우에 파동 함수라는 개념이 편리하지 않을 뿐이다. 구분의 편의를 위해서, 파동 함수를 통한 보통의 양자화를 제1 양자화first quantization, 생성 및 소멸 연산자를 이용한 새로운 양자화를 제2 양자화second quantization라고 부른다.
좋다. 우리는 빛을 양자화해서 광자를 얻었다.
그런데 광자를 기술하는 해밀토니안을 자세히 들여다보면 굉장히 이상한 점이 하나 있다.
진공에 무한이 숨어있다.
카시미르 효과: 진공은 요동친다
광자를 기술하는 해밀토니안에 따르면 설사 광자의 개수가 정확히 0이라고 하더라도 기본적으로 존재하는 에너지가 있다. 바로 0점 에너지zero-point energy라고 불리는 진공의 에너지이다.
$${\cal E}=\frac{\hbar}{2}\sum_{{\bf k},\lambda} \omega_k$$
묻지도 따지지도 말고 0점 에너지를 계산해 보자.
광자가 길이 \(L\)을 가지고 떨어진 두 거울 사이의 1차원 공간에 갇혀있다고 상상해 보자.
$${\cal E}=\hbar\sum_{\bf k} \omega_k=\hbar c \sum_p k_p=\hbar c \sum_{p=1}^\infty \frac{p\pi}{L}$$
(편광에 관련된 자유도는 파수에 대한 합을 단순히 2배 증가시키는 효과를 준다.) 위에서 주목할 중요한 사실은 거울이 빛을 완벽하게 반사한다는 가정하에 광자의 파수가 다음과 같이 양자화된다는 것이다.
$$k_p=\frac{p\pi}{L}$$
자, 이제 구체적으로 0점 에너지가 어떤 값을 가지는지 계산해 보자.
$${\cal E}=\frac{\pi\hbar c}{L} \sum_{p=1}^\infty p
=\frac{\pi\hbar c}{L}(1+2+3+4+\cdots)$$
앗, 무한이 나타났다!
위 수식에서 나타난 수열의 합은 명백하게 무한이다. 그렇다면 진공의 에너지는 무한이라는 소리인가?
어쩌면 그럴 수도 있을 것이다.
진공의 에너지가 무한이라고 하더라도 그것은 어찌 보면 단순히 에너지의 기준에 불과하다. 만약 진공의 에너지가 아무런 물리적으로 측정가능한 결과를 가져오지 않는다면, 설사 그것이 무한이더라도 그냥 무시하면 될 것이다.
하지만 진공의 에너지는 실제 물리적으로 측정가능한 결과를 가져올 수 있다.
바로 카시미르 효과이다.
이 글의 도입부에서 이미 언급되었듯이 앞선 수열의 합이 다음과 같다고 주장한 사람이 있었다.
$$S=1+2+3+4+\cdots=-\frac{1}{12}$$
그 사람은 바로 라마누잔이었다
이 미친 생각을 이해하기 위해서 라마누잔의 논리를 따라가 보자. 우선 다음과 같은 라마누잔 합이 유한한 결과를 준다고 가정해 보자.
$$S=1+2+3+4+\cdots$$
만약 그렇다면 위 수식의 양변에 4를 곱해도 될 것이다.
$$4S=4+8+12+16+\cdots$$
이제 위 두 수식을 좌변은 좌변끼리, 우변은 우변끼리 빼 보자.
$$-3S=1-2+3-4+5-6\cdots$$
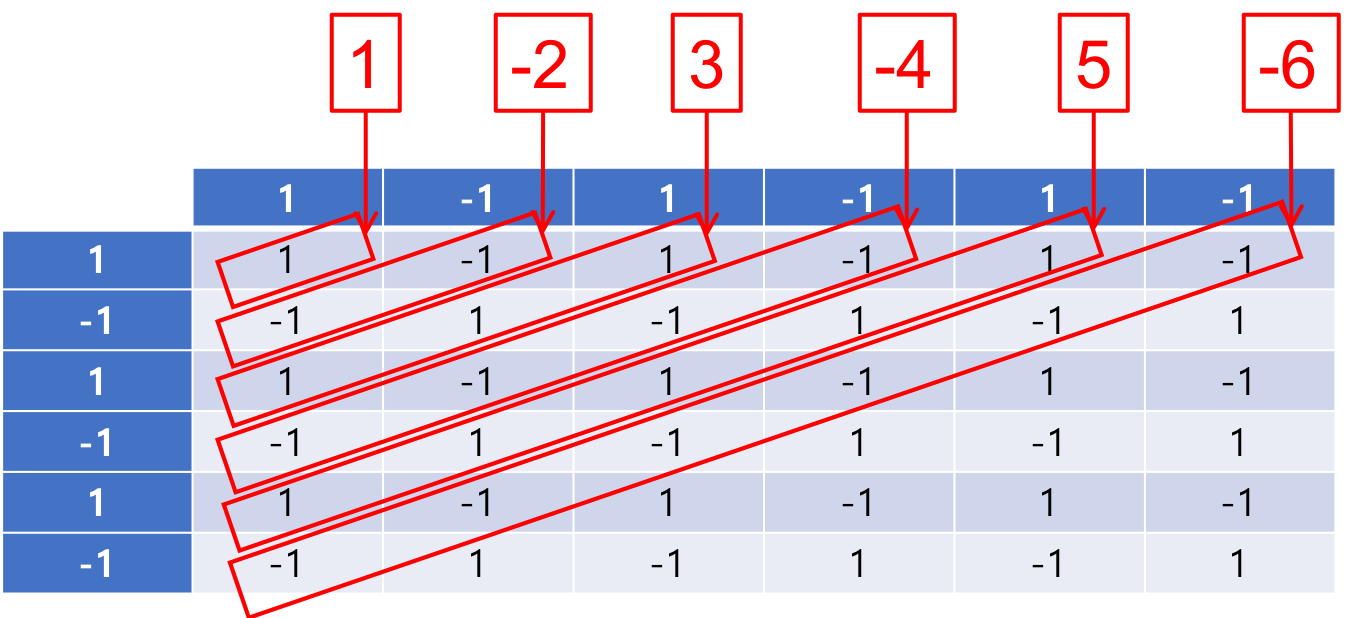
그런데 곰곰이 잘 생각해 보면 위 수식의 우변은 다음과 같이 쓸 수 있다.
$$1-2+3-4+5-6\cdots=(1-1+1-1+1-1+\cdots)^2=s^2$$
참고로, 위 수식은 다음과 같은 “곱셈 표”를 보면 이해하기 쉽다.
[그림9]의 곱셈 표는 진한 색으로 표시된 맨 위 칸에 있는 수열, \(1, -1, 1, -1, 1, -1, \cdots\)과 맨 왼쪽 칸에 있는 수열, \(1, -1, 1, -1, 1, -1, \cdots\)을 하나씩 곱해서 표의 각 칸을 채우는 것으로 이해할 수 있다. 보는 바와 같이, 빨간색 상자로 묶인 대각선 상의 숫자들의 합은 차례로 \(1, -2, 3, -4, 5, -6, \cdots\)으로 이어지는 수열을 이룬다.
이제 우리에게 남겨진 숙제는 다음 수열의 합을 구하는 것이다.
$$s=1-1+1-1+1-1+\cdots$$
재미있게도 \(s\)는 우리에게 매우 익숙한 등비 수열의 공식을 써서 구할 수 있다. 즉, \(s\)는 초기 값이 \(a=1\)이고, 매번 \(r=-1\)이라는 비율이 곱해지는 수열이다.
$$s=\frac{a}{1-r}=\frac{1}{2}$$
그렇다면 다음과 같은 결론에 이를 수 있다.
$$-3S=s^2=\frac{1}{4}$$
결국 라마누잔 합은 다음과 같이 주어진다.
$$S=-\frac{1}{12}$$
참고로, 위에서 언급한 라마누잔 합은 리만 제타 함수Riemann zeta function의 일종이다. 리만 제타 함수는 다음과 같이 정의된다.
$$\zeta(s)=\sum_{p=1}^\infty p^{-s}=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots$$
따라서 위에서 언급한 라마누잔 합은 \(S=\zeta(-1)\)이다.
위 라마누잔의 논리의 허점을 지적하기 전에 라마누잔의 답이 맞다고 가정해 보자. 그렇다면 진공의 에너지는 다음과 같이 주어진다.
$${\cal E}=\frac{\pi\hbar c}{L}\zeta(-1)$$
진공의 에너지 자체는 측정할 수 없다. 하지만 진공의 에너지가 외부 변수, 특히 공간의 크기에 따라서 변하는 정도는 측정가능하다. 이것은 다름 아니라 카시미르 힘이다.
$$F=-\frac{d{\cal E}}{dL}=\frac{\pi\hbar c}{L^2}\zeta(-1)$$
카시미르 힘은 음수이다. 다시 말해서, 진공을 담고 있는 두 거울은 그 거리가 줄어드는 방향으로 힘을 받는다.
자, 이제 라마누잔 합이 말도 안 되는 논리라고 생각하는 사람을 위해서 조금 더 정상적인 논리를 펴 보자.
당연한 말 같지만 앞선 라마누잔 합이 발산하는 이유는 더하는 숫자가 계속 커지기 때문이다. 이것을 막으려면 더하는 숫자에 모종의 인자를 곱해서 결국 숫자가 줄어들게 만들면 될 것이다. 이러한 목표 하에 다음과 같은 수열의 합을 생각해 보자.
$$S(\alpha)=\sum_{p=1}^\infty p e^{-\alpha p}$$
여기서 \(\alpha\)는 높은 진동수 혹은 파수의 효과를 억제하는 모종의 차단막cutoff이다.
사실 이러한 차단막이 있는 것은 물리적으로 매우 자연스럽다. 왜냐하면 아무리 좋은 거울이라고 하더라도 무한히 높은 진동수의 빛을 완벽하게 반사할 수는 없기 때문이다. 나중에 보겠지만 \(\alpha\)의 구체적인 값은 중요하지 않다. 다른 효과에 의해서 상쇄되기 때문이다.
일단 현 단계에서는 \(\alpha\)에 의해서 수열의 숫자가 더 이상 발산하지 않고 줄어들기 시작하는 차단 지수cutoff index \(p_c=1/\alpha\)가 있다는 사실이 중요하다. 그리고 차단 지수에 해당하는 차단 파수cutoff wavenumber \(k_c\)가 있다는 사실이 중요하다.
$$k_c=\frac{p_c\pi}{L}=\frac{\pi}{L\alpha}$$
위 수열은 \(\alpha\)가 0보다 크기만 하면 절대적으로 수렴한다. 문제는 라마누잔 합이 \(\alpha\)가 정확히 0인 경우에 얻어진다는 사실이다. 이 문제는 나중에 생각하기로 하고 일단 앞으로 진행해 보자.
위 수식을 잘 들여다보면 \(S(\alpha)\)가 어떤 등비 수열을 \(\alpha\)에 대해서 미분하면 얻어질 수 있다는 것을 깨달을 수 있다.
$$S(\alpha)=-\frac{\partial}{\partial \alpha}\left( \sum_{p=1}^\infty e^{-\alpha p} \right)
=-\frac{\partial}{\partial \alpha} \left( \frac{e^{-\alpha}}{1-e^{-\alpha}} \right)$$
위에서 우변의 마지막 표현식은 등비 수열의 공식으로부터 얻어졌다. 미분과 기타 연산 작업을 조금 더 하면 우리는 다음과 같은 결론에 이를 수 있다.
$$S(\alpha)=\frac{1}{4\sinh^2{(\alpha/2)}}$$
여기서 \(\sinh{(x)}\)는 쌍곡사인hyperbolic sine이라고 불리는 함수이다.
우리는 \(\alpha\)가 0에 가까운 상황에 관심이 있으므로, 위 공식을 \(\alpha\)가 작은 극한에서 전개해 보자.
$$S(\alpha)=\frac{1}{\alpha^2}-\frac{1}{12}+\cdots$$
위 공식을 이용해서 에너지를 표현하면 다음과 같다.
$${\cal E}=\frac{\pi\hbar c}{L}S(\alpha)
=\frac{\pi\hbar c}{L}\left( \frac{1}{\alpha^2}-\frac{1}{12}+\cdots \right)$$
이제 앞에서 정의한 차단 파수 \(k_c\)를 이용해서 \(\alpha\)를 다시 표현하면 다음과 같다.
$${\cal E}=\hbar c \left( \frac{k_c^2}{\pi}L-\frac{\pi}{12}\frac{1}{L}+\cdots \right)$$
차단 파수는 물리적으로 매우 자연스럽기는 하지만 현 단계에서는 임의로 선택한 양에 불과하다. 따라서 가능하다면 우리는 이 양에 대한 의존성을 제거하고 싶다.
다행히 우리는 재미있는 요령을 하나 쓸 수 있다.
두 개의 거울로 이루어진 우리의 시스템이 사실은 훨씬 더 큰 거울 상자 안에 들어 있다고 상상해 보자. 그리고 이 큰 거울 상자의 길이를 \(U\)라고 해 보자. 앞서 구한 에너지는 시스템 안의 에너지이다. 그럼 시스템 밖의 에너지는 무엇일까?
$${\cal E}^\prime=\hbar c \left( \frac{k_c^2}{\pi}(U-L)-\frac{\pi}{3}\frac{1}{U-L}+\cdots \right)$$
여기서 시스템 밖은 길이가 \((U-L)/2\)인 두 개의 또 다른 거울 상자로 볼 수 있다는 사실을 썼다.
이제 시스템 안과 밖의 에너지를 모두 더한 전체 에너지는 다음과 같이 주어진다.
$${\cal E}_{\rm tot}={\cal E}+{\cal E}^\prime=\hbar c \left( \frac{k_c^2}{\pi}U-\frac{\pi}{12}\frac{1}{L}-\frac{\pi}{3}\frac{1}{U-L}+\cdots \right)$$
위에서 우변의 첫 번째 항은 여전히 \(k_c\)에 의존하기는 하지만 더 이상 \(L\)에는 의존하지 않는다. 이 항은 힘에 아무런 영향을 주지 않으므로 무시할 수 있다. 반면에 우변의 세 번째 항은 \(U\)가 \(L\)에 비해서 엄청나게 크다면 역시 무시할 수 있다. 결론적으로 물리적으로 의미 있는 에너지는 앞서 라마누잔 합을 이용해서 구한 결론과 정확히 일치하게 된다.
$${\cal E}_{\rm tot}=\frac{\pi\hbar c}{L}\zeta{(-1)}$$
위에서, 다시 한번, \(\zeta{(-1)}=-1/12\)이다.
3차원에서 발생하는 카시미르 효과도 비슷하게 계산해 볼 수 있다.
$${\cal E}=\hbar\sum_{\bf k}\omega_k=\hbar c \iint dk_x dk_y
\sum_{p=1}^\infty \sqrt{k_x^2+k_y^2+\left(\frac{p\pi}{L}\right)^2}$$
자세한 유도 과정 없이 답만 쓰면 아래와 같다.
$${\cal E}=-\frac{\pi^2\hbar c}{6L^3}\zeta{(-3)}$$
여기서 \(\zeta{(-3)}=1/120\)이다. 위 공식에서 알 수 있듯이, 3차원 카시미르 힘도 1차원과 마찬가지로 음수이다.
정리해 보자.
아무것도 존재하지 않을지라도 진공은 양자역학적으로 요동치고 있다. 이러한 양자요동quantum fluctuation은 진공의 에너지를 무한으로 만든다. 하지만 묘하게도 무한으로 발산하는 진공의 에너지는 카시미르 힘이라는 실제 물리적으로 측정가능한 효과를 만들어 낼 수 있다.
양자역학이란, 정말 믿기 힘들만큼 이상하다.
아, 그런데 상대성과 양자, 그리고 무한의 이야기는 아직 끝나지 않았다.
램 이동: 진공은 전자를 흔든다
또 다른 무한의 이야기는 수소 원자의 에너지 준위로부터 시작한다.
앞선 “믿기 힘든 양자 [11]: 양자 물질 상태”에서 우리는 슈뢰딩거 방정식을 풀어서 수소 원자의 에너지 준위를 정확히 구할 수 있었다. 묘하게도 이 정확한 에너지 준위는 간단한 보어의 원자 모형에서 얻어지는 결과와 완전히 같았다.
$$E=-\frac{Ry}{n^2}$$
여기서 \(Ry=me^4/2\hbar^2\)는 뤼드베리 에너지 단위 Rydberg unit of energy이고, \(m\)은 전자의 질량이다.
그런데 사실 위 수소 원자의 에너지 준위는 실제 실험 결과와 미세한 차이를 지닌다.
가장 중요하게, 위 에너지 준위 공식에 따르면 에너지는 주 양자수principal quantum number \(n\)에만 의존하며, 각운동량 양자수angular momentum quantum number \(l\)에는 전혀 영향을 받지 않는다. 구체적인 예로, 수소 원자의 에너지 준위 중에서 \(n=2\)인 상태는 두 개의 서로 다른 \(l\) 값, 즉 \(l=0,1\)을 가질 수 있다. 위 에너지 준위 공식에 따르면 이 두 가지 다른 상태는 정확히 똑같은 에너지를 가진다. 하지만 실험적으로는 그렇지 않다. 이러한 미세한 에너지 준위의 차이를 “미세 구조fine structure”라고 부른다.
이러한 미세 구조는 도대체 왜 발생하는 것일까?
답은 상대론적 효과이다.
다시 말해서, 슈뢰딩거 방정식 대신에 디랙 방정식을 풀면 미세 구조를 설명할 수 있다.
우선, 자세한 유도 과정 없이 디랙 방정식을 풀어서 수소 원자의 상대론적 에너지 준위를 정확히 구한 결과를 쓰면 다음과 같다. (복잡한 공식에 놀랄 준비를 하라!)
$$E=\frac{mc^2}{\sqrt{1+\frac{\alpha^2}{\left[n-(j+1/2)+\sqrt{(j+1/2)^2-\alpha^2}\right]^2}}}$$
여기서, 다시 한번, \(\alpha=e^2/\hbar c\)는 미세 구조 상수이다. 위에서 \(j\)는 소위 전체 각운동량 양자수total angular momentum quantum number라고 불리는 양인데, 거칠게 말해서 궤도와 스핀에 의한 각운동량을 더한 값이다. 구체적으로, \(j\)는 궤도 각운동량 \(l\)에 다음과 같이 두 가지 서로 다른 경우로 연결된다. 우선, \(l=0\)이라면 \(j=1/2\)이다. 그렇지 않고, \(l \geq 1\)이라면 \(j=l+1/2\) 혹은 \(j=l-1/2\)이다.
위 상대론적 에너지 준위 공식은 매우 복잡하다. 물리적인 직관을 위해서 미세 구조 상수 \(\alpha\)가 작아지는 극한, 즉 상대론적 효과가 작아지는 극한에서 에너지 준위 공식을 전개해 보자.
$$E=mc^2\left[
1-\frac{\alpha^2}{2n^2}
-\frac{\alpha^4}{2n^4}\left(\frac{n}{j+1/2}-\frac{3}{4}\right)
+\cdots\right]$$
위에서 우변 괄호 안의 첫 번째 항은 정지 에너지인 \(mc^2\)를 주고, 두 번째 항은 우리에게 익숙한 보어의 결과를 준다. 세 번째 항부터는 상대론적인 효과를 줄 수 있는데, 보는 바와 같이 이제 에너지 준위는 전체 각운동량에 의존하게 된다.
위 공식에 따르면, 앞서 든 예, 즉 수소 원자에서 주 양자수 \(n=2\)를 가지는 여러 상태들 중 적어도 하나의 준위는 에너지가 바뀌게 된다. 구체적으로, \(n=2, l=0\)인 상태는 스핀 각운동량을 고려하면 \(n=2, j=1/2\)를 가지는 상태인 \(2S_{1/2}\) 준위가 된다. 반면에 \(n=2, l=1\)인 상태는 스핀 각운동량을 고려하면 2가지 준위, 구체적으로 (1) \(n=2, j=1/2\)를 가지는 상태인 \(2P_{1/2}\) 준위와 (2) \(n=2, j=3/2\)를 가지는 상태인 \(2P_{3/2}\) 준위로 갈라지게 된다.
위 상대론적 에너지 준위 공식에 따르면, \(2S_{1/2}\)과 \(2P_{1/2}\) 준위는 아직도 에너지가 서로 같지만, 그것들과 \(2P_{3/2}\) 준위는 에너지가 다르게 된다.
좋다. 디랙 방정식은 수소 원자의 에너지 준위에 존재하는 미세 구조마저 잘 설명할 수 있다.
그런데 우리의 우주는 그렇게 호락호락하지 않다.
디랙 방정식의 예측과 다르게, 실험적으로는 \(2S_{1/2}\) 준위와 \(2P_{1/2}\) 준위 사이에도 아주 미세한 에너지 차이가 존재하기 때문이다. 이 또 다른 미세한 에너지 차이가 바로 램 이동Lamb shift이다.
그렇다면 램 이동은 도대체 왜 발생하는 것일까?
답은 진공의 양자요동이다.
다시 말해서, 진공의 양자요동은 전자를 이리저리 마구 흔듦으로써 에너지를 바꿀 수 있다.
자, 이제 램 이동을 구체적으로 이해해 보자.
우선, 전체 파동 함수는 원자에 묶인 전자의 파동 함수와 양자요동치는 진공의 파동 함수의 곱으로 이루어진다.
$$|\Psi\rangle=|\psi_{\rm atom}\rangle|0\rangle$$
진공의 양자요동은 전기장과 자기장을 요동치게 만든다. 다시 말해서, 진공 상태에서 전자기장이 가지는 에너지의 기대값expectation value은 카시미르 효과에서 설명한 바와 같이 0점 에너지이다.
$$\frac{1}{2}\langle0|({\bf E}^2+{\bf B}^2)|0\rangle=\frac{\hbar}{2}\sum_{{\bf k},\lambda} \omega_k
=\hbar\int\frac{d^3{\bf k}}{(2\pi)^3} \omega_k$$
여기서 대칭성에 의하면 전기장과 자기장의 제곱이 가지는 기대값은 동일하다. 이 성질을 이용해서 위 수식은 다음과 같이 조금 더 정리될 수 있다.
$$\langle 0| {\bf E}^2 |0\rangle=\frac{\hbar c}{2\pi^2}\int_0^\infty dk\; k^3
=\frac{\hbar}{2\pi^2 c^3} \int_0^\infty d\omega\; \omega^3$$
위 수식의 중간 표현식에서는 \(\omega_k=ck\)라는 성질을 썼고, 파수에 대해서 각도 적분을 수행했다. 맨 마지막 표현식에서는 편의 상 파수에 대한 적분을 다시 진동수에 대한 적분으로 바꾸었다.
한편, 전기장의 제곱의 기대값은 다음과 같이 푸리에 변환의 형태로 표현할 수 있다.
$$\langle 0| {\bf E}^2 |0\rangle=2\int_0^\infty \frac{d\omega}{2\pi}
\langle 0| |\widetilde{\bf E}(\omega)|^2 |0\rangle$$
여기서 \(\widetilde{\bf E}(\omega)\)는 \({\bf E}(t)\)의 푸리에 변환Fourier transform을 의미한다.
$$\widetilde{\bf E}(\omega)=\int_{-\infty}^\infty \frac{d\omega}{2\pi} e^{i\omega t} {\bf E}(t)$$
앞선 두 공식을 비교하면 우리는 다음과 같은 결론에 이를 수 있다.
$$\langle0||\widetilde{\bf E}(\omega)|^2 |0\rangle=\frac{\hbar}{2\pi c^3} \omega^3$$
이제 전기장의 양자요동에 의해서 전자의 위치가 어떻게 변하는지 알아보자.
원자 속에서 전자는 쿨롱 퍼텐셜의 영향을 받고 있다. 우리가 알고 싶은 것은 전기장의 양자요동으로 인해서 전자가 겪게 되는 여분의 위치 변화이다.
$$m\frac{d^2}{dt^2}\delta{\bf r}=e{\bf E}$$
위에서는 논의를 쉽게 하기 위해서 고전역학적 운동 방정식을 썼다.
푸리에 변환의 형태로 위 운동 방정식을 다시 쓰면 다음과 같다.
$$\delta{\bf r}(\omega)=-\frac{e}{m\omega^2}\widetilde{\bf E}(\omega)$$
여기서 위치 변화의 푸리에 변환은 다음과 같이 정의된다.
$$\delta{\bf r}(\omega)=\int^\infty_{-\infty}\frac{d\omega}{2\pi} e^{i\omega t} \delta {\bf r}(t)$$
이제 앞에서 구한 전기장의 요동을 기술하는 공식을 이용하면 위치 변화의 요동은 아래와 같이 얻어진다.
$$\langle0||\delta{\bf r}(\omega)|^2 |0\rangle
=\left(\frac{e}{m\omega^2}\right)^2\langle0||\widetilde{\bf E}(\omega)|^2 |0\rangle=
\left(\frac{\hbar}{mc}\right)^2
\frac{\alpha}{2\pi}\frac{1}{\omega}$$
여기서, 다시 한번, \(\alpha\)는 미세 구조 상수이다. 위 공식을 다시 진동수에 대해서 푸리에 변환하면 다음과 같은 결론에 이를 수 있다.
$$\langle0|\delta{\bf r}^2 |0\rangle
=2\int_0^\infty\frac{d\omega}{2\pi}
\langle0||\delta{\bf r}(\omega)|^2 |0\rangle
=\left(\frac{\hbar}{mc}\right)^2\frac{\alpha}{2\pi^2}
\int_0^\infty\frac{d\omega}{\omega}$$
그런데 이런! 위에서 진동수에 대한 적분은 무한대로 발산한다.
다시 말해서, 위 공식만 놓고 보면 진공은 전자를 무한히 세게 흔들어댈 수 있다.
무엇인가 잘못되었다.
만약 정말 그렇다면 진공의 양자요동은 원자 속 전자를 모두 원자 밖으로 튀어나오게 만들 것이고, 애초부터 원자란 것이 존재할 수 없기 때문이다.
다행히, 잘 생각해 보면, 우리의 앞선 계산은 다양한 근사를 포함하고 있다. 사실 앞선 계산은 전자의 진동수가 어떤 최대값과 최소값 사이에 놓일 때만 적용가능한 근사이다.
$$\int_0^\infty\frac{d\omega}{\omega}\rightarrow
\int_{\omega_{\rm min}}^{\omega_{\rm max}} \frac{d\omega}{\omega}
=\ln{\left(\frac{\omega_{\rm max}}{\omega_{\rm min}}\right)}$$
자, 그럼 진동수의 최대값과 최소값은 무엇인가?
우선, 우리의 계산은 고전역학적 운동 방정식에 의존한다. 따라서 \(\omega_{\rm max}\)는 대략적으로 상대성 이론이 적용되는 에너지 척도인 정지 에너지, 즉 \(mc^2\)에 의해서 결정될 것이다. 구체적으로, \(\omega_{\rm max}\approx mc^2/\hbar\)로 정할 수 있다.
반면에 우리의 계산은 쿨롱 퍼텐셜의 영향을 무시하고 진행되었다. 따라서 \(\omega_{\rm min}\)은 대략적으로 쿨롱 퍼텐셜에 의한 길이 척도인 보어 반지름Bohr radius, 즉 \(a_0=\hbar^2/me^2\)에 의해서 결정될 것이다. 구체적으로, \(\omega_{\rm min}=ck_{\rm min}\approx c\pi/a_0\)로 정할 수 있다.
$$\langle0|\delta{\bf r}^2 |0\rangle
=\left(\frac{\hbar}{mc}\right)^2
\frac{\alpha}{2\pi^2}
\ln{\left(\frac{\omega_{\rm max}}{\omega_{\rm min}}\right)}
\approx \left(\frac{\hbar}{mc}\right)^2
\frac{\alpha}{2\pi^2}
\ln{\left(\frac{1}{\pi\alpha}\right)}$$
이제, 이러한 전자의 위치 변화가 에너지에 어떤 영향을 끼치는지 알아보자.
우선, 전자의 위치 변화는 쿨롱 에너지에 다음과 같은 변화를 가져온다.
$$\Delta U=U({\bf r}+\delta{\bf r})-U({\bf r})
=\delta{\bf r}\cdot\nabla U({\bf r})
+\frac{1}{2}(\delta{\bf r}\cdot\nabla)^2 U({\bf r})
+\cdots$$
위에서 우변의 첫 번째 항은 양자요동이 공간의 방향에 의존하지 않으므로 사라진다. 결론적으로 진공의 양자진동으로 인한 쿨롱 에너지 변화의 기대값은 다음과 같이 주어진다.
$$\langle0|\Delta U|0\rangle=\frac{1}{2}\langle0|(\delta{\bf r}\cdot\nabla)^2|0\rangle\; U({\bf r})$$
여기서는 앞선 수식에서 점선으로 표시된 항들은 모두 무시하였다.
이제 다시 한번 양자요동이 공간의 방향에 의존하지 않는다는 성질을 쓰면 다음과 같은 결론에 이를 수 있다.
$$\langle0|\Delta U|0\rangle=\frac{1}{6}\langle0|\delta{\bf r}^2|0\rangle\ \nabla^2 U({\bf r})$$
다음 단계로 쿨롱 퍼텐셜에 라플라시안을 취하면 디랙 델타 함수Dirac delta function가 얻어진다.
$$\nabla^2 U({\bf r})
=-\nabla^2\left(\frac{e^2}{r}\right)
=4\pi e^2\delta{({\bf r})}$$
정리하면 다음과 같다.
$$\langle0|\Delta U|0\rangle=\frac{2\pi}{3}e^2\langle0|\delta{\bf r}^2|0\rangle\ \delta{({\bf r})}$$
이제 원자에 묶인 전자의 파동 함수를 포함한 전체 파동 함수에 대해서 쿨롱 에너지 변화의 기대값을 취하면 다음과 같다.
$$\langle\Psi|\Delta U|\Psi\rangle=\frac{2\pi}{3}e^2\langle0|\delta{\bf r}^2|0\rangle\cdot
\langle\psi_{\rm atom}|\delta{({\bf r})}|\psi_{\rm atom}\rangle
=\frac{2\pi}{3}e^2\langle0|\delta{\bf r}^2|0\rangle\cdot
|\psi_{\rm atom}(0)|^2$$
위에서 \(|\psi_{\rm atom}(0)|^2\)는 다름 아니라 전자가 원점에 존재할 확률이다.
최종적으로 진공의 양자요동에 의한 전자의 에너지 변화는 다음과 같이 쓰인다.
$$\Delta{\cal E}=\frac{mc^2}{3\pi}
\left(\frac{\hbar}{mc}\right)^3 \alpha^2
\ln{\left(\frac{1}{\pi\alpha}\right)}\;
|\psi_{\rm atom}(0)|^2$$
위 공식에 따르면 전자의 에너지 변화는 전자가 원점에 존재할 수 있을 때만 발생할 수 있다. 잘 생각해 보면, 이것은 각운동량 양자수가 0인 상태에서만 에너지가 변할 수 있다는 것을 의미한다.
매우 좋은 결과이다!
앞서 언급했듯이, 디랙 방정식에 따르면 \(2S_{1/2}\)과 \(2P_{1/2}\) 준위는 정확히 똑같은 에너지를 가져야 한다. 하지만 그 둘 사이에는 실제 아주 미세한 에너지 차이가 존재한다. 위 결과에 따르면, \(2P_{1/2}\) 준위는 각운동량 양자수가 1이기 때문에 에너지가 변하지 않지만 \(2S_{1/2}\) 준위는 각운동량 양자수가 0이기 때문에 에너지가 바뀌게 된다. 이것은 바로 램 이동이다.
아무것도 존재하지 않을지라도 진공은 정말 전자를 흔들 수 있다.
무한의 이야기는 계속된다
진공은 비어있지 않고, 요동치며, 전자를 흔든다.
그리고 이 모든 현상 뒤에는 무한이 숨어 있다.
이러한 무한을 없애는 방법은 없을까?
램 이동에 관한 앞선 논의는 물리적인 직관에 호소하는 근사 방법에 기반한다. 이 방법의 핵심은 무한을 없애기 위해서 진동수의 최대 및 최소값을 도입하는 것이다. 이것은 카시미르 효과를 설명하기 위해서 차단 파수를 도입한 것과 비슷하다.
사실 이러한 근사 방법이 개발되기 전인 1947년, 한스 베테Hans Bethe는 이미 조금 더 엄밀한 계산을 통해서 램 이동을 설명하는 데 성공했다. 베테의 성공에 고무된 물리학자들은 이후 그의 계산을 더욱더 엄밀하게 만들기 위해서 노력을 경주하게 된다.
이러한 노력을 통해서 성취하고자 했던 주요 목표는 진동수의 최대 및 최소값을 임의로 도입할 필요가 없는 자기정합적인 양자 이론을 세우는 것이었다.
결국 그러한 자기정합적인 양자 이론은 실제로 구축되게 되는데, 그것은 다름 아니라 바로 양자전기역학이다. 이후 양자전기역학은 현재 우리가 알고 있는 일반적인 양자 이론인 양자장론을 완성시키는 데 결정적인 역할을 하게 된다.
결론만 말하면, 양자전기역학을 포함해서 양자장론에서 발생하는 거의 모든 무한은 소위 재규격화renormalization라는 방법을 통해서 극복할 수 있다.
간단하게 말해서, 재규격화란 입자의 질량이나 전하를 적절하게 잘 재정의함으로써 무한을 극복하는 기술이다. 실제 베테의 계산에서도 질량의 재규격화가 핵심적인 아이디어다.
하지만 우리에게는 아직도 극복되지 않고 남아있는 무한이 있다. 바로 이 글의 초반부에서 언급한, 중력을 양자화시킬 때 나타나는 무한이다.
우리는 여전히 무한과 그 너머를 꿈꾼다.