생각하는 컴퓨터
컴퓨터가 등장한 뒤 우리의 삶은 크게 달라졌다. 우리나라가 월드컵에서 첫 골을 넣은 것이 언제였는지, 이웃나라의 GDP 순위가 어떻게 되는지와 같은 주제는 이제 대화가 아니라 검색의 대상이 되었다. 우리가 “일”이라 부르는 대부분의 것은 컴퓨터 앞에서의 어떤 작업이다. 우리는 점점 더 생각과 기억을 컴퓨터에 아웃소싱하고 있다.
수학에서도 컴퓨터의 영향력은 커지고 있다. 애플과 하켄은 이미 1970년대 4색문제1를 컴퓨터로 해결한 바 있다. 최근에는 극소수의 사람만 이해할 수 있었던 어떤 증명의 정확성을 컴퓨터가 재확인해 주기도 하고, 이 과정에서 중요한 증명의 결점을 찾아내기도 하였다. 또한, 증명 자체를 컴퓨터로 찾아내는 경우도 있다. 컴퓨터 운영체제나 연산장치의 설계를 컴퓨터가 확인하는 과정은 이제 필수적이다.
이러한 발전은 어디를 향하여 가는 것일까? 이미 인간은 정확성, 계산능력, 기억용량, 통신속도 등 많은 면에서 컴퓨터를 절대 따라잡을 수 없다. 이러다 보면 언젠가는 컴퓨터가 인간보다 뛰어난 수학자가 될 수 있을까? 혹시 인간의 영혼도 결국 하나의 컴퓨터에 불과한 것일까?
이번 글에서는 이러한 궁금증의 시작점에 있는 질문, “모든 수학 문제를 풀어주는 컴퓨터를 만들 수 있을까”에 대해 생각해 보고 이에 대한 앨런 튜링Alan Turing, 1912-1954의 해답을 알아보고자 한다.
모든 질문은 정지문제로 귀결된다
먼저 다음과 같은 정지문제를 생각해 보자.
“주어진 컴퓨터 프로그램이 유한한 시간 안에 정지할지 여부를 판단할 수 있는 컴퓨터가 있는가?”
예를 들어, 다음의 프로그램은 시작과 동시에 정지할 것이다.
프로그램 1. 인사
(1) “안녕?”을 출력하고 정지한다.
혹은 시간이 꽤 지난 후에야 정지하는 아래와 같은 경우도 있다.
프로그램 2. 100억 게임
(1) 변수 x에 1을 대입한다.
(2) x의 값을 하나 증가시킨다.
(3) x의 값이 100억보다 작다면 (2)로 돌아가고, 만일 그렇지 않다면 (4)로 간다.
(4) x의 값을 출력하고 정지한다.
프로그램이 무한루프에 빠져 영원히 정지하지 못하는 경우도 허다하다. 화장실 칸의 왼쪽과 오른쪽 벽에 각각 “반대쪽 벽을 보시오”라는 낙서를 써넣으면 앉은 사람을 무한루프에 빠뜨릴 것이다. 프로그램으로 이를 표현해 보자.
프로그램 3. 탁구
(1) “왼쪽”을 출력하고 (2)로 간다.
(2) “오른쪽”을 출력하고 (1)로 간다.
주어진 컴퓨터 프로그램이 유한한 시간 안에 정지할지 판별하는 것은 실용적으로도 매우 중요하다. 현대의 컴퓨터 프로그래밍 언어 번역기(컴파일러)는 이 과정을 상당히 효율적으로 하여 프로그램의 버그를 미리 차단한다. 혹시 이러한 작업을 완벽하게 해 내는 컴파일러가 있을까? 한번 다음의 프로그램을 생각하여 보자.
프로그램 4. 골드바흐 추측
(1) x에 2를 대입한다.
(2) x의 값을 2만큼 증가시킨다.
(3) 만일 2 ≤ p ≤ q ≤ x를 만족하는 두 소수 p, q가 존재하여 x = p + q를 만족하면 (2)로 돌아간다; 그러한 p, q가 없다면 (4)로 간다.
(4) 정지한다.
처음의 두 단계가 유한한 시간 안에 끝나는 것은 당연하다. 세 번째 단계는 어떨까. 자연수 x가 주어졌을 때 우리는 p = 1, 2, 3, 4, 5, … 와 같이 증가시켜 가면서 p와 x – p가 동시에 소수가 되는 경우가 있는지 확인하면 된다. 주어진 수가 소수인지 컴퓨터로 판별하는 방법은 많이 알려져 있다. 따라서 (3)의 단계도 유한한 시간 안에 끝난다. 하지만 (3)의 결과에 따라 우리는 (2)를 반복할 수도, 혹은 (4)로 갈 수도 있다. 그리고 이 프로그램이 영원히 (2)와 (3)을 반복한다는 것은 다음의 명제와 동일하다.
“2보다 큰 모든 짝수는 두 개의 소수의 합으로 표현할 수 있다.”
이 명제는 바로 1742년 크리스티안 골드바흐Christian Goldbach, 1690-1764가 제시한 골드바흐 추측이다. 이 추측은 2021년 현재까지도 난공불락의 난제로 남아있으며, 따라서 프로그램 4가 정지하는지 여부를 아는 사람은 아직 세상에 없다.
이렇게 모든 수학 문제는 정지문제의 형태로 표현할 수 있다. 바꾸어 말해, 프로그램의 정지여부를 결정하는 기계를 만든다면 이 기계는 수학의 모든 문제를 해결할 수 있다. 수학과 정지문제의 연관성은 20세기 초 다비드 힐버트David Hilbert, 1862-1943와 빌헬름 애커만Wilhelm Ackerman, 1896-1962에 의하여 정확하게 제시되었다. 두 수학자는 “어떠한 수학 문제가 주어져도 참과 거짓을 판단할 수 있는 기계가 있는가?”라는 결정문제를 제시하였는데, 이는 정지문제와 논리적으로 같다.
튜링의 (의도적인) 오답
튜링은 1936년 발표한 논문 “계산 가능한 수에 대하여, 그리고 결정문제에의 응용”에서 힐버트—애커만의 결정문제를 완전하게 해결한다. 그 자체로 계산과학의 전설이 된 이 논문에서 튜링은 컴퓨터(튜링 기계), 하드웨어와 소프트웨어의 구별, 계산가능성, 결정 가능성 등 계산과학의 현대적인 개념을 엄밀하게 정의하였다. 게오르그 칸토어Georg Cantor, 1845~1918의 대각논법에 기반한 튜링의 증명 테크닉은, “계산”이라는 작업의 한계를 규정짓는 인류의 유일한 방법이라 할 수 있다.
정지문제를 엄밀하게 다루기 위하여, 우리는 프로그램 p와 입력 i가 주어질 때마다 함수값 halt(p,i)를 다음처럼 정의하여 보자.
(1) 만일 p에 i를 입력하여 프로그램이 정지한다면 halt(p,i) = 정지.
(2) 만일 p에 i를 입력하였을 때 프로그램이 정지하지 않는다면 halt(p,i) = 무한.
논의의 편리를 위하여 우리는 계산, 프로그램, 컴퓨터 이 세 단어를 비슷한 의미로 사용하려 한다. 정지문제의 목표는 함수 halt(p,i)를 임의의 (p,i)에 대하여 계산해 내는 것이다. 가장 순진한 방법은 p라는 프로그램에 i를 대입하여 답을 기다리는 것이다. 만일 기다림이 언젠가 정지한다면 우리는 halt(p,i) = 정지 라는 결론을 얻는다. 하지만 우리는 얼마나 기다려야 할까? 만일 프로그램이 10년, 100년, 10억 년을 넘게 돌아간다 하더라도 우리는 섣불리 halt(p,i) = 무한 이라 결론지을 수는 없다. 11억 년을 지난 후에 멈출 수도 있으므로.
이를 대비하여 우리는 동시에 세상의 모든 글 q1, q2, q3, … 를 나열한다. 글이란 결국 알파벳과 같은 기호의 나열이니 충분히 가능한 일이다. 우선 한 글자 짜리 글은 금방 다 나열될 것이다. 그다음은 두 글자… 아주아주 오랜 시간이 지나면 이러한 글 중에는 헤밍웨이의 소설이나 성경 전체도 있을 것이다.
이러한 각각의 과정에서 우리는 j = 1, 2, 3, … 번째 나열된 글 qj가 다음 명제의 증명인지 확인한다.
“프로그램 p에 입력 i를 대입하면 무한하게 돌아간다. 즉, halt(p,i) = 무한 이다.”
잘 알려진 사실에 따르면, 주어진 글이 주어진 명제를 증명해내는지 여부는 쉽게 판단할 수 있다. 따라서 프로그램이 무한하게 돌아가는 경우에도 우리는 적절한 qj가 halt(p,i) = 무한 임을 계산해 주는 것이다. 이제, 프로그램 p에 i를 입력하여 컴퓨터를 돌리는 동시에, 세상의 모든 글 q1, q2, q3, … 를 하나하나 컴퓨터에게 해석하게 하다 보면 우리는 언젠가 halt(p,i)값이 정지인지 무한인지 판별하게 되는 것이 아닐까.
하지만 튜링은 곧 이 답이 오답임을 지적한다. 튜링보다 앞선 쿠르트 괴델Kurt Gödel, 1906-1978의 결과에 따르면 수학 체계에는 증명도 반증도 불가능한 명제가 있기 때문이다. 만일 “halt(p,i) = 무한 이다”라는 명제가 하필이면 증명도 반증도 불가능한 괴델의 명제라면, 학수고대하는 증명 qj는 영원히 오지 않을 것이다.
다시, 칸토어
이 오답을 극복하기 위하여 튜링은 함수가 자연수보다 많다는 칸토어의 아이디어를 이용한다. 먼저, 다음과 같은 함수 f를 모두 고려하여보자.
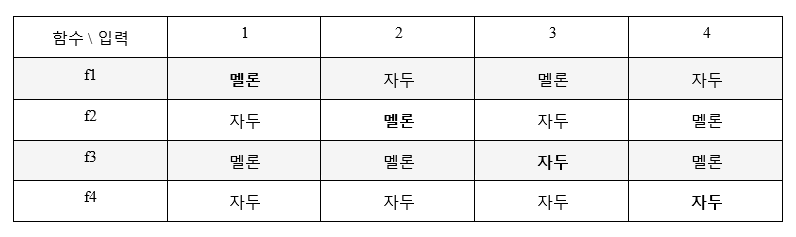
f : {1,2,3,…} → {자두, 멜론}
우리는 모든 함수를 f1, f2, f3, … 처럼 나열하는 것이 불가능하다는 것을 보이고 싶다. 결론을 부정하여, 아래처럼 그러한 나열이 가능하다고 가정하여 보자.
이제 각각의 i = 1, 2, 3, 4, … 에 대하여 함수 g(i)의 값이 fi(i)의 값과 다르도록 정의하여 보자.
즉 첫 번째 표의 대각선 값 f1(1), f2(2), f3(3), … 에서 자두와 멜론을 서로 바꾸어주면 우리는 g(1), g(2), g(3), … 의 값을 얻는다. 칸토어의 발견은, g가 첫 번째 표의 어떤 행에도 등장할 수 없다는 것이다. 예를 들어, g(3)은 멜론이고 f3(3)은 자두이므로 g와 f3는 서로 다른 함수이다. 마찬가지로 g는 f1, f2, f3, … 중 어느 것과도 같을 수 없다. 따라서, 모든 함수를 f1, f2, f3, … 처럼 나열했다는 우리의 가정은 틀렸다. 자연수는 하나, 둘, 셋, … 나열할 수 있지만 함수는 그렇게 할 수 없다.
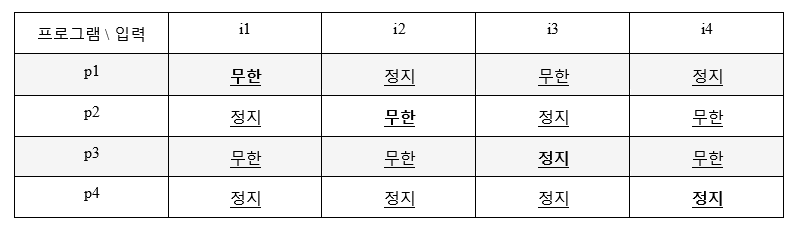
튜링의 기막힌 아이디어는 이 논법을 정지문제에 그대로 적용하는 것이다. 먼저 세상의 모든 프로그램을 p1, p2, p3, … 와 같이 나열하여 보자. 프로그램 (즉, 코드) 역시 유한한 글이므로 이렇게 나열하는 것이 가능하다. 각각의 프로그램 p와 각각의 입력 i에 대하여 halt(p, i)의 값이 다음과 같다고 가정하여 보자.
예를 들어, 프로그램 halt(p1, i1) = 무한 인데 이는 p1에 i1를 입력할 경우 무한루프에 빠진다는 의미이다. 마찬가지로 halt(p4,i4) = 정지 이므로 p4에 i4를 입력하면 정지하게 된다.
이제 모순을 이끌어 내기 위하여, 위의 표를 모두 계산해 내는 프로그램이 있다고 하자. 칸토어의 대각논법과 매우 흡사하게, 우리는 halt라는 프로그램에 간단한 작업을 추가하여 새로운 프로그램 q를 만들 수 있다.
프로그램 q
(1) 입력 ix를 받아들인다. 여기서 x = 1, 2, 3, … 중 하나이다.
(2) 만일 halt(px,ix) = 무한 이라면, q(ix) = 777을 출력하고 정지한다.
(3) 만일 halt(px,ix) = 정지 라면, 단계 (4)로 이동한다.
(4) 단계 (3)으로 이동한다.
위에서 보았듯이 p1에 i1을 입력하면 무한루프에 빠진다. 따라서 halt(p1,i1)=무한 이고 q(i1)은 777의 값을 계산하면서 정지한다. 이는 halt(q, i1) = 정지 임을 의미한다. 또한 halt(p4,i4) = 정지 이므로 q(i4)는 (3)단계와 (4)단계를 오가며 무한루프에 빠지는 코드이다. 다시 말해, halt(q,i4)는 무한 이다.
이제, 대각논법의 교훈처럼 이러한 행은 halt(p,i)를 계산하는 표에 절대로 나타나지 않는다. 즉 q는 p1, p2, p3, … 어떤 것과도 같을 수 없다. 이는 p1, p2, p3, … 가 모든 프로그램을 나열한다는 가정에 모순이고, 따라서 프로그램의 정지여부를 나타내는 halt를 기계적으로 계산하는 방법은 없다. 세상의 모든 프로그램은 기계적으로 나열할 수 있지만, 프로그램의 정지여부는 그렇게 할 수 없다.
수학은 완전할까
힐버트는 수학의 토대에 대한 세 가지의 질문을 던졌다고 알려져 있다. 완전성 문제, 일관성 문제, 결정가능성 문제가 그것이다. 힐버트에게 실망스럽게도 세 가지 모두 불가능함이 차례대로 밝혀졌다. 주어진 명제의 증명가능성을 기계로는 결정할 수 없다는 것이 바로 튜링의 결과이다. 이에 앞서 괴델은, 합리적인 수학체계에 증명도 반증도 불가능한 명제가 있다는 제1불완전성정리를 증명하였고, 이로써 첫 번째 질문을 부정한다. 또한 수학체계에 모순이 없다는 일관성을 그 체계 내에서 증명하는 것이 불가능하다는 내용이 괴델의 제2불완전성 정리이며, 이는 힐버트의 두 번째 질문을 부정한다.
한편 튜링의 의도적인 오답이 말하는 바는 정지문제를 통하여 약한 형태의 제1불완전성정리를 증명할 수 있다는 것이다. 만일, 모든 참인 명제를 증명할 수 있다면 정지문제의 답도 존재하기 때문이다. 바꾸어 말해, 어떤 프로그램의 정지여부는 우리의 수학체계로 증명도 반증도 불가능한 명제인 것이다.
튜링의 아이디어를 이용하면 “우리의 수학체계에서 절대 계산해 낼 수 없는 함수”를 만들 수도 있다. 튜링 기계에서 상태라는 개념은 현대 컴퓨터의 메모리에 해당한다. 자연수 n = 1, 2, 3, … 이 주어졌을 때 입력 값을 포함하여 n개의 상태를 가지는 튜링 기계는 유한할 것이다. 이러한 튜링 기계가 언젠가는 정지하는 경우만을 추려냈을 때, 얼마나 많은 단계를 거치고 나서 정지할까?
이러한 단계의 최대값을 우리는 부지런쟁이 함수Busy Beaver Function BB(n)으로 정의한다. 사실, 프로그램이 정지하는지 여부조차 우리는 알기 어려운데, 정지하는 경우를 추려낸 다음에 그 계산 단계를 계수하는 것이 쉬울 리 없다. BB(1) = 1, BB(2) = 6, BB(3) = 21, BB(4)=107까지는 어렵지 않게 알아낼 수 있지만, BB(5)부터는 그 값이 4백만보다 크다는 것만이 알려져 있다. BB(6)은 10의 36,534 제곱보다도 더 크다. 골드바흐 추측은 BB(27)을 계산하는 것보다 쉽고, 정수론의 더 중요한 난제인 리만 가설은 BB(744)의 계산보다 쉽다는 것이 알려져 있다. 현대수학 체계에 모순이 있는지 여부는 아직 아무도 모르지만, 적어도 BB(748)의 계산보다는 쉽다.2
어떤 함수들은 잘 정의되어 있지만 계산하는 것이 불가능하다. 그리고 어떠한 수학 명제들은 참이지만 증명이 불가능하다. 무슨 의미일까. 인간의 지성에 한계가 있다는 뜻일까? 엄밀한 증명에 기반하는 수학에 어떤 태생적인 한계가 있다는 것일까? 그렇지 않다. 튜링과 괴델의 결과를 지성, 혹은 수학의 한계로 이해하는 것은 대표적인 오독이다. 두 결과 모두 수학에서 기계적인 계산의 범위를 다룰 뿐이며, 수학은 그 범위를 분명히 뛰어넘고 있다. 인간이 기계만 못하다는 회의를 느끼는 날이라면, 괴델의 이 문구3를 음미하여 보면 어떨까.
“수학이 인간의 마음보다 더 크거나,
혹은 인간의 마음이 기계보다 우월하다.”
– 쿠르트 괴델