유한 확산 집합체: 패턴의 성장에 대한 모델

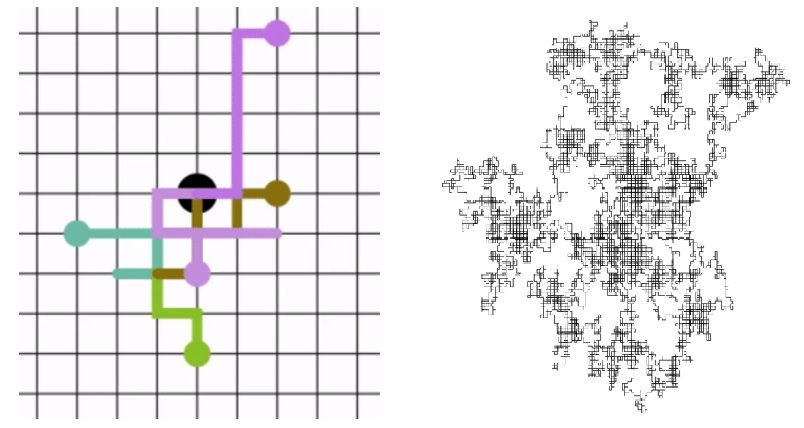
자연계에서는 눈송이, 형석의 대칭적인 성장, 은하수, 태풍, 소라 껍데기의 나선 모양, 사막의 사구의 초승달 모양 등 다양한 패턴이 관측됩니다. 그리고 많은 경우 이러한 패턴들은 성장을 합니다. [그림1]부터 [그림4]까지는 성장하고 있는 다양한 패턴을 보여줍니다. 예를 들어 [그림1]을 보면, 가운데에서 시작해서 점점 바깥 쪽으로 뻗어 나가는 형태를 볼 수 있는데, 이때 무작위로 뻗어 나가지 않고 특정한 패턴을 유지하면서 뻗어 나갑니다. 이렇게 패턴을 유지하면서 성장하는 것, 즉 패턴의 성장을 확률 모형을 이용하여 수학적으로 나타낼 수 있습니다. 이 글에서는 확률 모형 중 하나인 유한 확산 집합체^{Diffusion-Limited Aggreation}에 대해서 알아보려고 합니다.

^그림1  황산구리 용액에서 전착^{電着, Electrodeposition 그림2}  고전압 절연체에서 방전
Wikipedia 

[그림1]부터 [그림4]가 보여주는 것은 황산구리 용액에서 전착^{電着, Electrodeposition}, 고전압 절연체에서 방전, 리튬이온 전지에서 나뭇가지 모양의 생장물, 희박한 박테리아의 성장 등입니다. 이들의 공통점은, 마치 무한히 먼 곳의 입자가 무작위로 돌아다니다가 하나씩 와서 달라불어서 집합체가 자라는 것 같이 성장을 한다는 것입니다. 이렇게 먼 곳에서 입자가 하나씩 오는 과정을 확산이라고 합니다. 그리고 이렇게 먼 곳에서 무작위 행보를 하던 입자가 확산의 과정을 거쳐 집합체를 형성하는 것을 설명하는 수학적인 모델이 1981년에 토마스 위튼과 레너드 샌더에 의해서 제시된 유한 확산 집합체라는 것입니다.[1] 확산이나 무작위 행보들에 대해서는 다음 절들에서 좀 더 구체적으로 설명하려고 합니다.

리튬이온 전지를 사용함에 따라 전해액에서 나뭇가지 모양의 생장물이 자라나게 됩니다. 이 생장물이 자라나서 양극, 음극을 연결하게 된다면 전지는 고장 나고 폭발할 가능성도 있습니다. 유한 확산 집합체를 이용해서 이 현상을 분석할 수 있습니다. 그리고 앞에서 예를 들었듯이 다른 많은 물리적 현상을 유한 확산 집합체를 이용해서 설명 가능하고, 유한 확산 집합체를 연구하는 것은 중요한 의미를 가집니다.

무작위 행보^{Random Walk}

유한 확산 집합체에 대해서 자세히 알아보기기 앞서 무작위 행보^{Random Walk}에 대해서 알아봅시다. 무작위 행보는 수학적 공간에서 잇따른 무작위 걸음에 의한 경로를 나타내는 수학적 대상입니다. 특별한 경우로서 \(d\)차원 정수 격자^{\(d\)-dimensional interger lattice} \(\mathbb{Z}^d = \{(x_1, x_2, \cdots, x_d) : x_1, \cdots, x_n \in \mathbb{Z} \}\)에서의 단순^Simple 대칭^Symmetric 무작위 행보에 대해 설명하겠습니다. (여기서 \(\mathbb{Z}\)는 정수 전체의 집합입니다.) 이는 \(n\)차원 정수 격자 위에서의 열 \((S_n: n=0,1,…)\)으로 나타낼 수 있는데, \(S_n\)이 \(n\)번째 단계에서의 무작위 행보의 위치를 나타냅니다. \(S_0\)는 처음에 시작하는 위치이고, 이 무작위 행보는 각 단계마다 인접한 격자점으로(단순^Simple) 동등한 확률(대칭 ^Symmetric)로 이동합니다.

단순 대칭 무작위 행보를 계속 진행하고 멀리서 관찰하는 것을 생각해봅시다. 진행하는 단계의 수가 커지고 격자 사이의 거리가 줄어듦에 따라 이 무작위 행보의 이산적인 경로가 연속적인 경로로 수렴합니다. 이 극한이 브라운 운동^{Brownian Motion}입니다. 브라운 운동은 1827년 스코틀랜드의 식물학자 로버트 브라운^{Robert Brown}에 의해서 발견되었습니다. 브라운이 물에 떠 있는 꽃가루에서 나온 작은 입자가 수면 위를 불규칙적으로 계속 움직이는 것을 발견한 것이 시초입니다. 알베르트 아인슈타인^{Albert Einstein}은 1905년 브라운 운동에 대한 정량적 이론을 만들었습니다. 프랑스의 물리학자 장 바티스트 페랭^{Jean Baptiste Perrin}은 아인슈타인의 분석을 성공적으로 증명하여, 이 공로로 1926년 노벨 물리학상을 받았습니다. 1930년대 노버트 위너^{Nobert Wiener}가 아인슈타인의 브라운 운동 모형을 확률 과정^{Stochastic process}으로 변형시켰으며, 이를 위너 과정^{Wiener process}라고 부릅니다. 수학에서 브라운 운동을 말할 때는 위너 과정을 말합니다.

유한 확산 집합체^{Diffusion-Limited Aggregation}

유한 확산 집합체는 무한히 먼 곳에서 입자가 하나씩 무작위 행보를 하다가 집합체에 인접하게 되면, 집합체에 이 입자가 붙어서, 집합체가 자라나는 모델입니다. 유한 확산 집합체는 \(d\)차원 정수 격자 \(\mathbb{Z}^d\)의 부분집합의 열 \((A_n: n=0,1,…)\)으로 나타낼 수 있습니다. \(A_n\)은 \(n\)번째 단계에서 유한 확산 집합체를 나타내며 격자점들의 집합입니다. \(A_0\)는 초기의 유한 확산 집합체입니다. 각 단계에서 먼 곳에서 시작한 입자가 격자 위에서 단순 대칭 무작위 행보를 하다가, 유한 확산 집합체와 인접하게 되면, 무작위 행보를 멈추고, 유한 확산 집합체가 이 인접한 자리를 포함하여 커지게 됩니다.

2차원 유한 확산 집합체를 수식을 이용해서 설명하겠습니다. 초기값 \(A_0=\{ 0 \}\)이라 합시다. 즉, 이 유한 확산 집합체는 원점에서 시작합니다. \(n+1\)번째 단계의 유한 확산 집합체 \(A_{n+1} = A_n \cup \{ a_{n+1} \}\)으로 주어집니다. \(n\)번째 단계 \(A_n\)에서 이웃한 격자점 \(a_{n+1}\)이 추가되었습니다. 여기서 \(a_{n+1}\)은 확률 분포 \(\mathcal{H}_{\partial A_n}\)을 따라 선택이 됩니다. 이를 \(a_{n+1 } \sim \mathcal{H}_{\partial A_n} \left( \cdot \right)\)으로 표현합니다. \(\partial A_n\)은 집합 \(A_n\)의 바깥 경계이며, \(A_n\)의 외부에 있는 점 중에서 \(A_n\)과 이웃해 있는 점들의 집합입니다. 수식으로 표현하면 \(A\)의 바깥 경계는 \( \partial A = \{ y \in \mathbb{Z}^2 \backslash A : \exists x \in A, y \sim x \}\)입니다.

유한 확산 집합체에 대해서 알려진 성질은 많지 않습니다. 유한 확산 집합체가 공 모양으로 성장하지 않는다는 것에 대한 증명은 아직 없습니다. 해리 케스턴^{Harry Kesten}은 \(d\)차원 유한 확산 집합체의 가지들의 성장률이 \(n^{\frac{2}{d+1}}\)이하임을 증명하였습니다.[4,5]  아직 해결되지 않은 문제들로 유한 확산 집합체가 안정화하는가, 성장률이 얼마인가, 가지의 개수가 몇 개인가, 프랙탈 차원이 얼마인가 등이 있습니다.

비격자^off-lattice 유한 확산 집합체와 프랙탈 차원

앞에서 유한 확산 집합체는 격자 위에서 정의되었습니다. 비슷하게 유한 확산 집합체를 격자에서 벗어나 정의할 수 있습니다. 이를 비격자^off-lattice 유한 확산 집합체라고 부릅니다. 다음과 같은 방법으로 정의할 수 있습니다. 처음 시작할 때 하나의 반지름 \(a\)인 입자에서 시작합니다. 각 단계마다 먼 곳에서 같은 크기의 입자를 하나씩 놓고, 확산^diffusion을 하게 만듭니다. 즉, 무작위 방향으로 길이 \(a\)만큼 이동을 반복하게 합니다. 그러다가 이 입자가 집합체와 인접하게 되면 이동을 멈추고, 집합체에 붙게 합니다. (약간 다른 방법으로 정의할 수도 있습니다. 입자를 무작위 방향으로 길이 \(a\)만큼 이동을 반복시키는 대신, 브라운 운동을 하게 합니다. 그리고 입자가 집합체와 인접하면 브라운 운동을 멈추고, 집합체에 붙게 합니다.)

유한 확산 집합체의 프랙탈 차원에 대해서 알아봅시다. 프랙탈 차원은 음이 아닌 정수로 정의된 차원을 음이 아닌 실수로 확장한 개념으로, 프랙탈이 공간을 얼마나 조밀하게 채우는지 나타내는 양입니다. 프랙탈 차원 \(D\)는 입자의 개수 \(n\), 집합체의 크기 \(r\)에 대해서 \(n=r^D\)로 주어집니다. (프랙탈 차원을 정의하는 방법은 여러 가지가 있으며, 이 글에서의 정의는 하우스도르프 차원입니다.) 비격자 유한 확산체의 경우, 2차원에서 \(D \approx 1.71\),[6,7]  3차원에서 \(D \approx 2.5\)로 알려져 있습니다. 이에 대한 엄밀한 증명이 아직 있지는 않습니다. 수치 시뮬레이션 결과가 8개 이상의 공간의 차원에서 행해졌으며 공간의 차원 \(d\)가 커질 경우 \(D \rightarrow d-1\)인 결과를 얻었습니다.

격자위에서 유한 확산 집합체의 프랙탈 차원은 비격자인 경우와 다릅니다. 2차원 정방형 격자 위에서의 유한 확산 집합체의 경우 시뮬레이션을 통해 프랙탈 차원 \(D\)는 약 3/2임이 보여졌습니다. 해리 케스턴은 2차원의 경우 \(D\geq \frac{3}{2}\)를 엄밀하게 증명하였습니다.[8]

헤이스팅스-레비토브^{Hastings-Levitov} 접근법

앞에서의 정의대로 격자 위에서의 모델 또는 비격자 모델을 다루기는 어려운 점이 있습니다. 유한 확산 집합체에서 새로운 입자가 붙는 위치가 정해지는 것은 조화측도^{Harmonic measure}를 따릅니다. (측도는 수학의 개념으로 질량, 부피, 사건의 확률 등을 일반화시킨 개념입니다. 확률론에서 유클리드 공간 \(\mathbb{R}^n\)의 ^{유계bounded} 부분집합의 경계의 조화측도는 이 부분집합 내부에서 브라운 운동이 시작해서 경계에 도착할 확률로 주어집니다.) 헤이스팅스^{M.B. Hastings}와 레비토브^{L.S. Levitov}는 이 성질을 이용해서 2차원인 경우에 대해 새로운 정식화를 만들었습니다.[9]

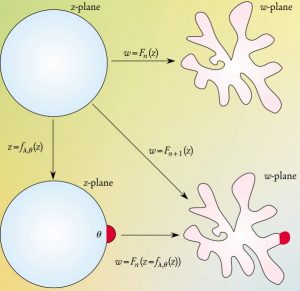
2차원 평면은 복소평면(복소수로 이루어지는 평면. \(x\)좌표가 복소수의 실수부, \(y\)좌표가 복소수의 허수부)으로 생각할 수 있습니다. \(n\)개의 입자로 이루어진 집합체를 생각해봅시다. 리만 사상 정리에 의해 단위원을 이 집합체의 경계로 보내는 등각사상 \(w=F_n (z)\)가 존재합니다. (등각사상은 각도를 보존하는 사상(함수)으로, 정의역의 두 곡선 \(l_1, l_2\)가 이루는 각이 이들의 상 \(l_{1}’, l_{2}’\)이 이루는 각과 항상 같습니다.) 헤이스팅스와 레비토브는 이 등각사상 \(F_n (z)\)를 표현하는 간단한 알고리즘을 만들었습니다. 단위원을 작은 혹이 붙어 있는 단위원으로 보내는 함수 \(f_{\lambda_{n+1}, \theta_{n+1}}\)를 생각해봅니다. 여기서 \(\lambda_{n+1}\)는 혹의 크기, \(\theta_{n+1}\)는 혹이 붙어있는 위치(각도)를 나타냅니다. 그러면 등각사상 \(F_n (z)\)이 \(n\)개의 입자로 이루어진 집합체를 나타낸다면, \(n+1\)개의 입자에 대해서는 등각사상 \(F_{n+1} (z) = F_n ( f_{\lambda_{n+1}, \theta_{n+1}} (z) ) \)로 나타내어집니다. 매개변수 \(\alpha\)는 0이상 2이하의 실수입니다. 각 단계에서 \(\lambda_{n+1} = \lambda \| F’_{n+1} (e^{i \theta_{n+1}}) \|^{-\frac{\alpha}{2}} \), \(\lambda\)는 고정된 양의 실수이고, \(\theta_{n+1}\)는 0, \(2\pi\) 사이의 값으로 균등한 확률로 선택됩니다.

앞 문단에서 정의한 모델이 헤이스팅스-레비토브(\(\alpha\)) 모델입니다. \(\alpha=0\)일때 많은 성질이 알려져있습니다. \(\alpha=0\)이면 \(\lambda_{n}=\lambda\)로 고정된 값을 가집니다. 헤이스팅스-레비토브(0) 모델은 끝 가지가 하나입니다. 그리고 척도구성극한^{Scaling limit}이 원판이고, 작은 입자 극한^{Small particle limit}은 브라운 그물^{Brownian web}입니다.[11]  \(n\)번째 입자의 평균 크기는 약 \(e^{cn}\)입니다. 여기서 \(c\)는 상수를 나타냅니다.

마치며

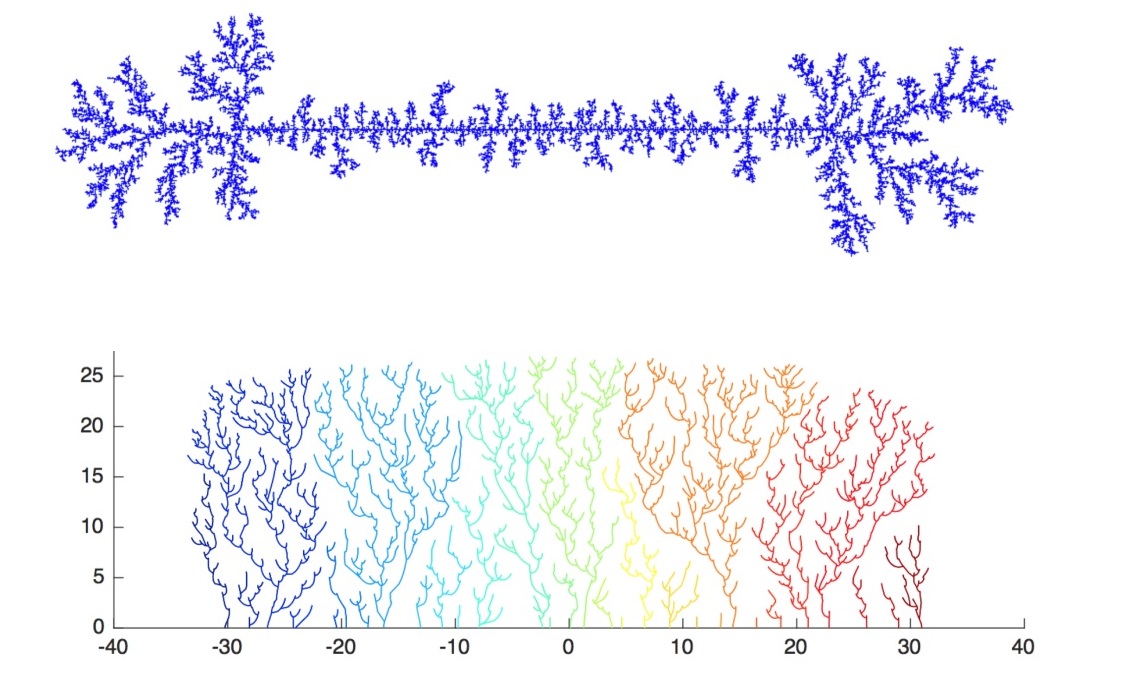
유한 확산 집합체는 자연계의 많은 현상을 설명할 수 있는 모델입니다. 수학적으로 많은 것이 엄밀하게 밝혀지지는 않았습니다. 최근 정상 유한 확산 집합체^{Stationary Diffusion-Limited Aggregation}에 대한 여러 성질이 밝혀졌습니다. 2차원에서 길이 \(n\)의 선분이나 원통의 밑면(원)에서 시작하는 유한 확산 확산체는 2차원 격자의 상반평면 \(\mathbb{Z} \times \mathbb{Z}_+\) 위의 정상 유한 확산 집합체로 수렴합니다.[12]

정상^Stationary 헤이스팅스-레비토브 모델도 앞에서처럼 등각사상을 이용해서 정의할 수 있습니다. 원에서 시작하지 않고 직선에서 시작해서 자라나는 모델입니다. 2차원에서 \(x\)축에서 시작하는 정상 헤이스팅스-레비토브 모델을 생각해봅시다. 만약 \(y\)축을 \(N\)을 단위로 스케일하고 \(x\)축을 \(\sqrt{N}\)을 단위로 스케일한다면, \(N\rightarrow \infty\)에 따라 가지의 끝에서 \(x\)축으로 가는 경로는 브라운 운동의 그래프로 수렴합니다. 여기서 브라운 운동의 그래프의 하우스도르프 차원은 3/2으로 케스턴이 밝힌 한계인 3/2와 일치합니다.[13]