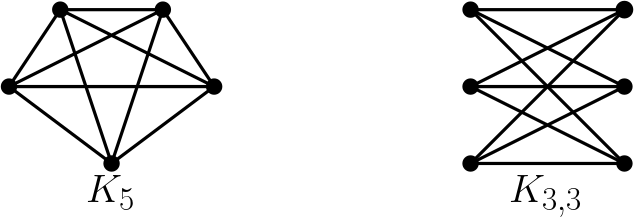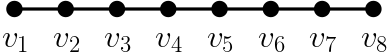듬성한 그래프 [2] : 그래프 마이너 구조정리에 대하여

지난 연재에서는 듬성한 그래프 모임을 다루는 데 중요한 나무-폭^tree-width에 대해 알아보았습니다. 나무-폭이 작은 그래프 모임은 기본적인 듬성한 그래프 모임 중 하나로 최대 독립집합 등의 알고리즘 문제들을 다항식 시간에 해결할 수 있음을 보았습니다. 반면, 나무-폭이 큰 그래프에서는 반드시 큰 격자 그래프를 마이너 포함관계로 찾을 수 있다는 격자 그래프 마이너 정리^{grid-minor theorem}에 대해서도 알아보았습니다.

나무-폭과 관련된 여러 이론이 형성된 배경에는 바그너^K.Wagner의 추측이 있습니다.
1970년에 바그너는 그래프 마이너 포함관계와 관련된 흥미로운 추측을 하였습니다 [9]. 임의의 무한 그래프 나열 \(G_1, G_2, \ldots \)가 있으면 반드시 \(G_i\)가 \(G_j\)의 마이너가 되는 두 그래프 \(G_i, G_j (i<j)\)들이 존재한다는 것이 이 추측입니다.로버트슨^N.Robertson과 시무어^{P. Seymour}는 이 추측을 1980-2010년 동안 23편의 그래프 마이너 프로젝트 논문들을 통하여 해결하였고 [6], 이를 해결하는 과정에서 나무-폭과 관련된 여러 가지 이론들을 개발하게 됩니다. 특별히 중요하게 사용된 결과는 특정한 그래프 하나를 그래프 마이너 포함관계로 포함하지 않는 그래프 모임들의 구조를 표현해 주는 그래프 마이너 구조정리^{Graph structure theorem}로 이에 대해서 이번 시간에 다루어보도록 하겠습니다. 이러한 그래프 모임들이 듬성하다는 것은 오래전부터 알려져 있었습니다 [7].

바그너의 추측^{Wagner’s conjecture}

먼저 바그너의 추측에 대해서 조금 더 살펴보도록 하겠습니다. 일반적으로 그래프 마이너 포함관계를 점과 선을 지워서만 얻는 부분 그래프 포함관계로 바꾸어서 생각한다면, 이 추측이 참이 아니라는 것을 쉽게 알 수 있습니다. 가령 아래 [그림1]과 같이 모든 원 그래프들을 \(G_1, G_2, \ldots \)라고 놓으면 무한 그래프 나열이 됩니다.

이 때, 하나의 원 그래프는 크기가 다른 원 그래프의 부분그래프가 되지 못하기 때문에 \(G_i\)가 \(G_j\)의 부분그래프가 되는 \(G_i, G_j(i<j)\)가 존재하지 않는다는 것을 알 수 있습니다. 하지만 작은 원 그래프는 큰 원 그래프에서부터 선을 축약해서 만들어낼 수 있으므로, 그래프 마이너 포함관계에 대해서는 하나가 다른 것의 마이너가 되는 두 그래프를 찾아낼 수 있습니다. 바그너의 추측은 이러한 성질이 임의의 무한 그래프 나열에 대해서 성립한다는 것을 주장하고 있습니다.

이러한 추측을 하게 된 배경에는 쿠라토스키의 정리^{Kuratowski’s theorem}가 있습니다. 평면 그래프는 평면에 선을 교차하지 않으면서 그릴 수 있는 그래프를 말합니다. 아래 [그림2] 두 개의 그래프는 대표적으로 평면 그래프가 아닌 그래프들입니다.

주어진 평면그래프에서 마이너 연산을 적용하여 작은 그래프를 얻으면 새로운 그래프도 다시 평면그래프가 됩니다. 점을 지우거나 선을 지우는 경우는 자명하고, 선을 축약하는 경우에는 축약하는 선 주변에 미세한 근방을 통하여 새로운 교차점 없이 두 점에 연결되어 있던 선들을 한 곳으로 모을 수 있습니다.

평면 그래프가 아닌 그래프 중에서 그래프 마이너 포함관계에 대해 가장 아래에 있는 그래프들은 어떤 그래프들일까요? 여기서 어떤 그래프가 가장 아래에 있다는 말은, 이 그래프 자체는 평면그래프가 아니나, 마이너 연산을 하나만 취해도 평면 그래프가 되는 그래프를 말합니다. 1930년에 쿠라토스키^{K. Kuratowski}는 저런 그래프들은 \(K_5\)와 \(K_{3,3}\) 두 개만 존재한다는 것을 보였습니다. 다르게 표현하면, 주어진 그래프가 평면 그래프일 필요충분조건이 \(K_5\)와 \(K_{3,3}\)를 그래프 마이너 포함관계로 가지지 않는다는 것이고, 이를 쿠라토스키의 정리라고 부릅니다 [4].

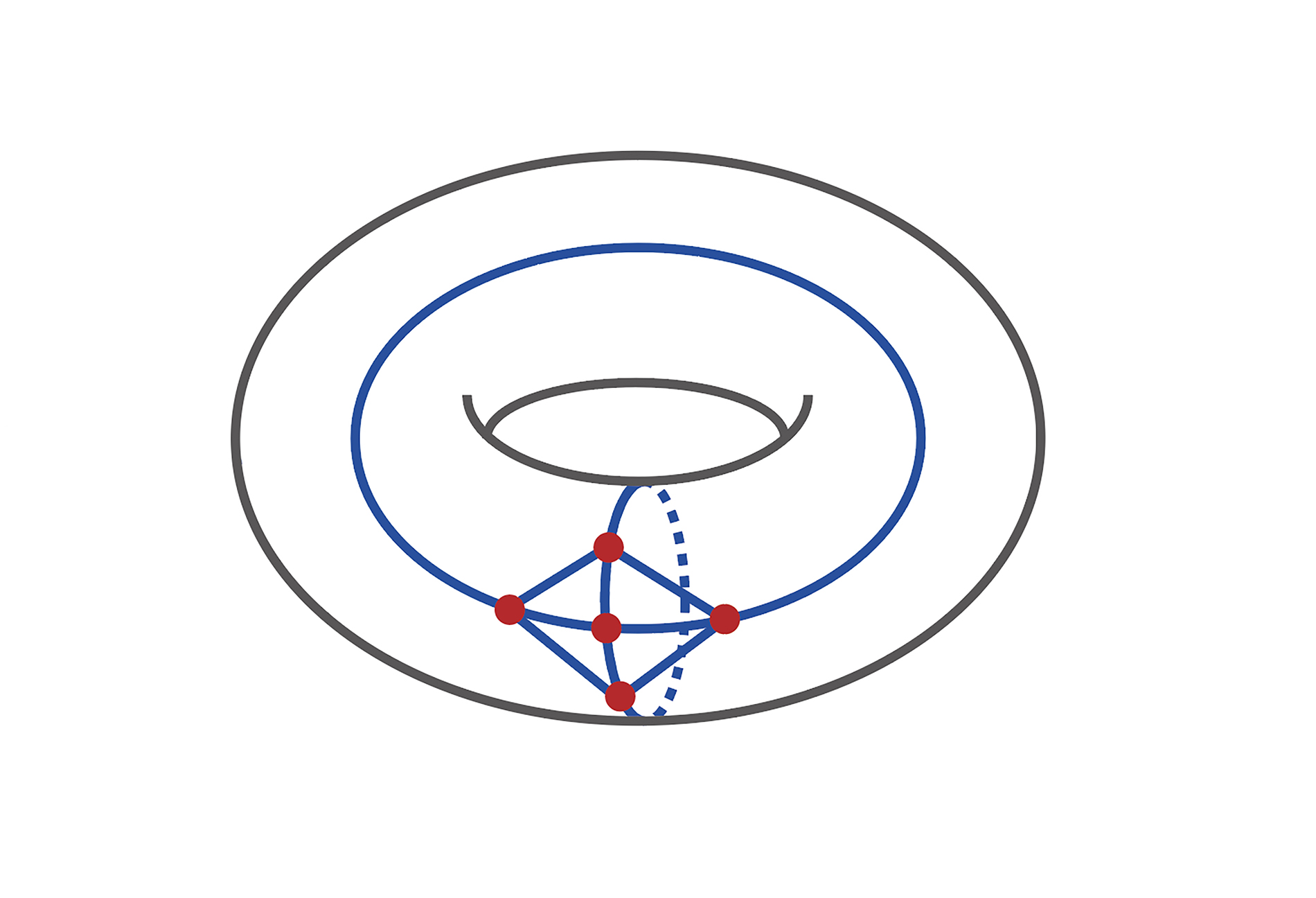
이러한 평면 그래프의 성질을 자연스럽게 다른 곡면에 매립되는 그래프들의 모임에 대해 바꾸어서 생각해 볼 수 있습니다. 가령, 토러스^torus라고 불리는 도너츠 형태의 곡면을 생각해 보겠습니다. 토러스에 선을 교차하지 않고 그릴 수 있는 그래프들의 모임도 비슷한 이유로 그래프 마이너 포함관계에 대해 닫혀있음을 알 수 있습니다. 토러스에 선을 교차하지 않고 그릴 수 없는 그래프 중에서 마이너 포함관계에 대해 가장 아래에 있는 그래프들은 어떤 그래프들이 될까요? 흥미롭게도, 이러한 리스트는 완벽하게 알려지지 않은 상태이고, 최소한 \(17523\)개의 서로 다른 그래프들이 존재한다는 것이 알려져 있습니다 [8]. 평면 그래프와 매우 다른 양상을 보여줍니다. 다른 곡면에 대해서도 비슷한 연구들이 진행되어 왔습니다. 아래 [그림3]은 토러스에서 \(K_5\) 그래프가 선을 교차하지 않으면서 그릴 수 있음을 보여줍니다.

  [그림3] / 셀루

그렇다면 과연 토러스에 선을 교차하지 않고 그릴 수 없는 그래프 중에 마이너 포함관계로 가장 아래에 있는 그래프들이 유한개만 있을지, 아니면 무한히 많을지 궁금해할 수 있습니다. 바그너의 추측이 맞는다는 것을 알게 되었으므로, 이를 이용하여 그러한 그래프가 유한개만 존재한다는 것을 알 수 있습니다. 토러스에 선을 교차하지 않고 그릴 수 없는 그래프 중에 마이너 포함관계로 가장 아래에 있으면서 서로 다른 그래프들이 \(G_1, G_2, \ldots \) 이라고 가정하고 이 모임이 무한하다고 가정해 보겠습니다. 바그너의 추측이 참이기 때문에, \(G_i\)가 \(G_j\)의 마이너가 되는 두 그래프 \(G_i, G_j(i<j)\)가 존재합니다. 그러면 \(G_j\)에서 마이너 연산을 통해 \(G_i\)를 얻었는데, \(G_i\)도 아직 토러스에 그릴 수 없는 그래프이므로 \(G_j\)가 가장 아래에 있는 그래프였다는 사실에 모순이 됩니다. 그러므로 위의 모임은 유한하다는 결론을 얻게 됩니다. 같은 이유로 그래프 마이너 연산에 닫혀있는 임의의 그래프 모임에 대해 이 모임 밖에 있는 그래프 중 가장 아래에 있는 것은 항상 유한개임을 알 수 있습니다.

그렇다면 바그너의 추측이 참이라는 것을 어떻게 증명할 수 있었을까요? 임의의 무한 그래프 나열을 고려해야 하므로 때문에 증명하기 매우 어려운 주장처럼 느껴집니다. 그래프 나열 \(G_1, G_2, \ldots \)이 주어져 있다고 가정해 봅시다. 만약 \(G_1\)을 제외한 \(G_2, G_3, \ldots\) 그래프 중에서 \(G_1\)을 그래프 마이너 포함관계로 가지는 그래프가 하나라도 있다면 원하는 쌍이 나오게 됩니다. 그러므로 \(G_2, G_3, \ldots\) 모든 그래프가 \(G_1\)을 그래프 마이너 포함관계로 가지지 않는다는 것을 가정할 수 있습니다. 로버트슨과 시무어는 이러한 관찰에서 고정된 그래프 하나를 그래프 마이너 포함관계로 가지지 않는 그래프들이 어떤 식으로 형성될 수 있는 지를 정확하게 표현해내었고, 이를 이용하여 언젠가는 비슷한 그래프 구조가 반복되는 시점이 존재한다는 것을 증명하게 됩니다.

이렇게 해서 나오게 된 것이 임의의 그래프 하나를 그래프 마이너 포함관계로 가지지 않는 그래프들에 대한 구조를 설명해 주는 그래프 마이너 구조정리입니다. 이 정리는 바그너의 추측이 참임을 증명하는 데 중요한 역할을 하기도 하였지만, 다른 그래프 문제를 해결하는 데에도 중요하게 사용되고 있습니다. 이 정리를 정확히 표현하는 것은 짧은 글에서는 어려운 일이지만, 어떤 아이디어를 통해 진행되었는지 살펴보도록 하겠습니다.

그래프의 분리^separation와 얽힘^tangle

그래프 \(G\)가 주어져 있다고 가정해 보겠습니다. \(G\)에서 두 개의 점 부분집합의 쌍 \((A,B)\)에 대해 (1) \(A\cup B\)가 \(G\)의 모든 점들을 포함하고, (2) \(A\setminus B\)와 \(B\setminus A\)를 연결하는 \(G\)의 선이 존재하지 않으면, \((A,B)\)를 그래프의 분리라고 부르겠습니다. 분리 \((A,B)\)에 대해 \(A\)와 \(B\)의 교집합의 크기, 즉 \(|A\cap B|\)를 이 분리의 위수^order라고 하겠습니다.

위수가 작은 분리를 하나 생각해 보겠습니다. 가령 주어진 분리 \((A,B)\)의 위수가 \(2\)이라고 가정해 보겠습니다. 서로서로 모든 쌍이 연결된 점 집합은 나무-폭이 큰 부분 그래프를 생성하게 됩니다. 만약에 서로서로 모든 쌍이 연결된 크기 6의 점 집합 \(S\)가 있다면, \(A\setminus B\)와 \(B\setminus A\) 사이에는 선이 없기 때문에 \(S\)는 반드시 \(A\)와 \(B\) 둘 중 한 곳에 완전히 속해 있어야 한다는 관찰할 수 있습니다.

조금 전에는 위수가 \(2\)인 분리 \((A,B)\) 하나에 대해서만 관찰을 하였습니다. 일반적으로 주어진 그래프에서 위수가 2인 분리가 아주 많이 있을 수 있습니다. 각각의 이러한 분리 \((A,B)\)에 대해 \(A\)와 \(B\) 중에 어느 쪽에서 \(S\)를 가졌는지 정보를 줄 수 있고, 이 정보를 통해 \(S\)가 어디에 있는지를 알 수 있습니다. [그림4]를 보면 각 분리 \((A,B)\)에서 \(S\)가 어느 쪽에 있는지 화살표로 그려져 있습니다.

이러한 정보를 통해 주어진 그래프에서 잘 분해가 되지 않는 부분이 어디에 있는지를 알려주는 개념이 로버트슨과 시무어에 의해 정의된 얽힘^tangle입니다 [5]. 위수가 \(\ell\)인 얽힘 \(\mathcal{T}\)는 주어진 그래프 \(G\)에서 위수가 \(\ell\)보다 작은 분리들의 모임 중 (1) \((A,B)\)가 \(G\)에서 위수가 \(\ell\)보다 작은 분리라면, \((A,B)\)와 \((B,A)\) 중 반드시 하나는 \(\mathcal{T}\)에 들어가 있어야 한다는 조건과, (2) \((A_1, B_1), (A_2, B_2), (A_3, B_3)\in \mathcal{T}\)이면, \(A_1, A_2, A_3\)들로 생성되는 그래프의 부분 그래프들을 합쳤을 때 전체그래프가 되지 않아야 한다는 조건을 만족하는 것입니다. 얽힘 \(\mathcal{T}\)는 이에 속한 모든 분리 \((A,B)\)들이 잘 분해되지 않는 하나의 부분을 동시에 가리키게끔 정의되었습니다.

얽힘은 나무-폭과 상반되는 성질을 가지고 있습니다. 나무-폭은 숫자가 작을수록 그래프가 잘 분해될 수 있음을 의미합니다. 하지만 위수가 작은 얽힘은 쉽게 만들 수 있습니다. 가령 \(V(G)\)가 \(G\)의 전체 점 집합일 때, \(\mathcal{T}=\{(\emptyset, V(G))\}\)는 위수가 0인 얽힘이 됩니다. 하지만 얽힘의 위수를 계속해서 올릴 수 없다는 것을 관찰할 수 있습니다. 가령 나무 그래프에서는 위수가 3인 얽힘을 만들 수 없습니다. 예로 아래 [그림5]와 같은 나무 그래프를 고려해 보고, 여기에 위수가 3인 얽힘 \(\mathcal{T}\)가 존재한다고 가정해 보겠습니다.

각 \(i\in \{1, 2, \ldots, 8\}\)에 대해 \(A_i=(\{v_1, \ldots, v_i\}, \{v_i, \ldots, v_8\})\)은 위수가 1인 분리입니다. 하지만 조건 (2)에 의해 \(A_1\)의 앞 뒤를 바꾼 분리는 \(\mathcal{T}\)에 들어갈 수 없고, 조건 (1)에 의해 \(A_1\)이 반드시 \(\mathcal{T}\)에 들어가야 합니다. 비슷하게 \(A_8\)도 \(\mathcal{T}\)에 들어갈 수 없습니다. \(A_i\) 형태의 분리 중 얽힘에 들어가는 최대의 \(j\)를 택해 보겠습니다. 그러면 선택에 의해 \(A_{j+1}\)은 \(\mathcal{T}\)에 들어가지 않게 되고, 그러므로 조건 (1)에 의해 앞뒤를 바꾼 \(A_{j+1}^*=(\{v_{j+1}, … v_8\}, \{v_1, … v_{j+1}\})\) 가 \(\mathcal{T}\)에 들어가게 됩니다. 마지막으로 위수가 2인 분리 \(B=(\{v_j, v_{j+1}\}, \{v_1, \ldots, v_8\})\)을 고려해 보면, 조건 (2)에 의해 이것의 앞뒤를 뒤집은 분리는 \(\mathcal{T}\)에 들어갈 수 없습니다. 하지만 이 분리가 \(\mathcal{T}\)에 들어가게 되면 \(A_j, A_{j+1}^*, B\) 세 개의 분리가 조건 (2)를 위반하게 됩니다. 그러므로 \(\mathcal{T}\)라는 얽힘은 존재할 수 없습니다. 마지막 논리에서 얽힘을 위한 조건 (2)에서 왜 세 개의 그래프가 왜 필요한지 조금은 알 수 있으리라 생각됩니다.

주어진 그래프에서 위수가 가장 큰 얽힘의 위수를 그래프의 얽힘-수라고 부릅니다. 신기하게도 주어진 그래프의 나무-폭(\(tw(G)\))과 얽힘-수(\(tn(G)\))는 아주 예외적인 경우를 제외하면 일반적으로 다음과 같은 관계를 갖고 있습니다 [5].

\(tn(G)\le tw(G)+1\le \frac{3}{2}tn(G).\)

풀어서 얘기해보면, 위수가 큰 얽힘이 존재하면 나무-폭이 크고, 반대로 나무-폭이 크면 위수가 큰 얽힘이 반드시 존재한다는 것입니다.

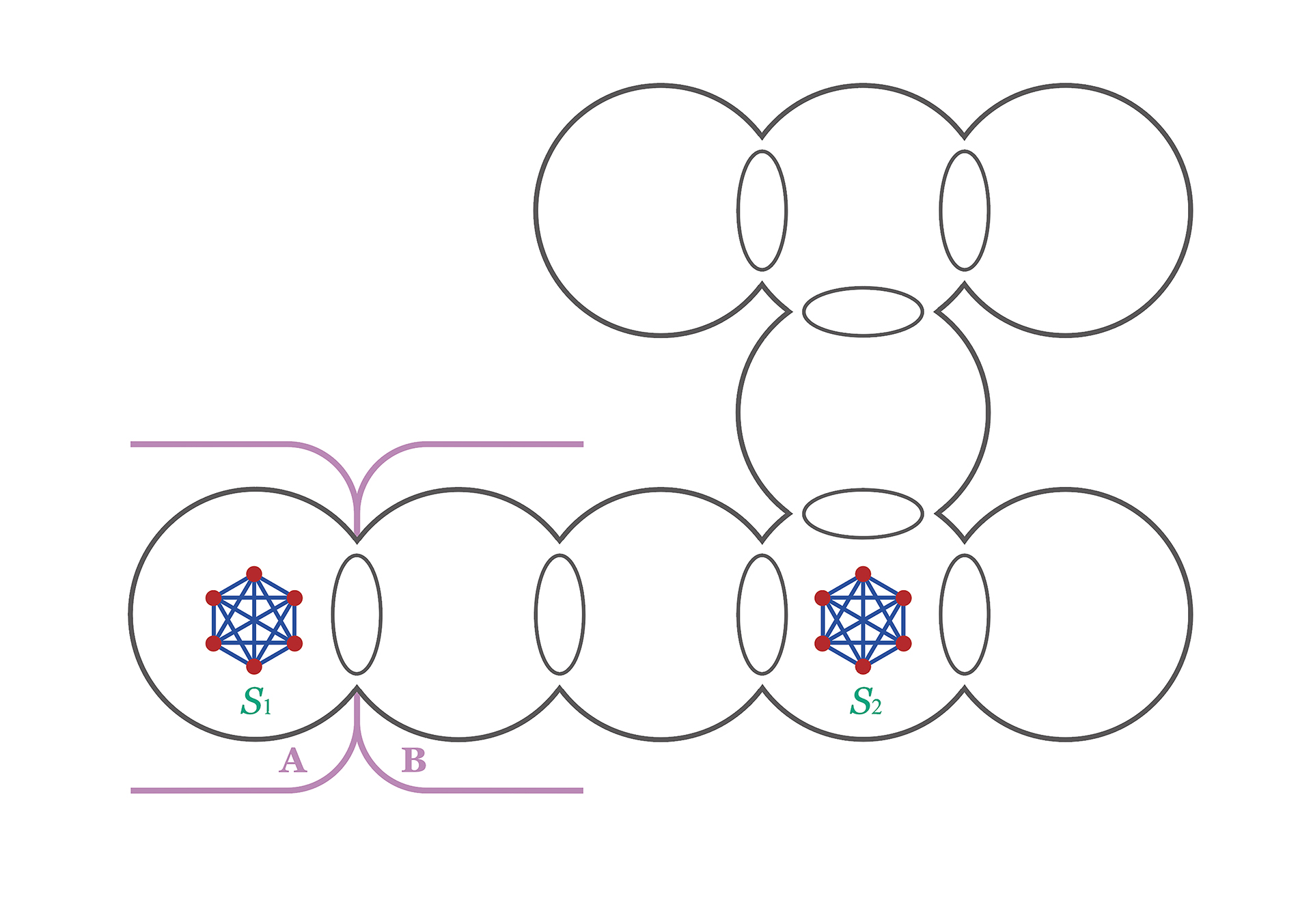
다시 얽힘으로 돌아가 보면, 얽힘은 그래프에서 분해하기 어려운 부분이 있는 곳을 가리켜주는 지시자의 역할을 한다고 볼 수 있습니다. 일반적으로 분해하기 어려운 두 부분이 아래 그림처럼 서로 다른 영역에서 나타날 수 있습니다. 이런 경우 \((A, B)\) 분리에서 보면 \(S_1\)에 대한 얽힘에는 \((B,A)\) 분리가 들어가는 반면 \(S_2\)에 대한 얽힘에는 \((A,B)\) 분리가 들어가서 얽힘에서 구분이 됩니다.

[그림6] / 셀루

그래프에서 분해가 잘 안 되는 부분을 최대한 표현한 것들은 포함관계로 최대인 얽힘^{inclusion-wise maximal tangle}들입니다. 로버트슨과 시무어는 이러한 얽힘이 나무의 구조를 이용해서 모두 구분할 수 있다는 정리를 증명하였고, 이것을 나타내는 분해를 얽힘-나무 분해^{tangle-tree decomposition}라고 부릅니다.

그래프 마이너 구조정리로 돌아와 보면, 어떤 그래프 \(H\)를 그래프 마이너 포함관계로 포함하지 않고 있다는 것을 가정하고 있습니다. 이 때, 최대 얽힘 대신 적절한 위수의 얽힘을 구분하는 얽힘-나무 분해를 택하면, 그 위수로 분해하기 어려운 그래프들로 나누어집니다. 이렇게 나누어진 조각들은 나무-폭이 높기 때문에, 지난 연재에서 보았던 격자그래프 마이너 정리를 이용하여 적절히 큰 격자그래프를 그래프 마이너 포함관계로 얻을 수 있습니다.

이 격자 그래프를 둘러싸서 다른 많은 점이나 선들이 붙어있을 수 있습니다. 어떤 점이나 선들은 격자 그래프에서 아주 먼 곳을 연결할 수도 있고, 아니면 매우 가까운 점들을 연결하고 있을 수도 있습니다. 하지만 첫 번째 형태의 점이나 선들이 많이 존재한다면, 없다고 가정한 \(H\)를 만들어낼 수 있어서 모순을 유도할 수 있습니다. 그러므로 그러한 점이나 선들은 소수만 존재할 수 있으며 관련된 점들을 지우고 나면 나머지 부분은 적당한 곡면에 매립할 수 있다는 것을 증명할 수 있습니다. 이렇게 해서 구조정리가 완성됩니다.

이 구조정리를 이해해 보면, 고정된 \(H\)에 대해 \(H\)를 그래프 마이너 포함관계로 포함하지 않는 그래프들은 결국 약간의 점을 지우고 나면 어떤 곡면에 선을 교차하지 않고 매립된 그래프들이 기본 골격이 되는 그래프 모임이 됨을 알 수 있습니다. 여기서 필요한 곡면의 종수^genus는 \(H\)에 대한 함수로 상한됩니다. 그래서 이를 기반으로 많은 문제를 해결할 수 있습니다.

방향그래프로의 확장

이제까지는 그래프에서 선에 특별한 방향이 설정되지 않은 무방향 그래프를 다루었습니다. 그래프의 두 점 \(u\)와 \(v\)사이에 있는 선에 \(u\to v\)의 방향이 설정된 그래프를 고려해볼 수 있습니다.그래프 마이너 구조정리와 비슷한 이론이 방향 그래프에서도 나타나지 않을까 생각해 볼 수 있습니다. 그러기 위해서는 다양한 개념들이 새롭게 필요하게 됩니다.

먼저 선을 마음대로 축약하는 것은 복잡한 상황을 만들어 냅니다. 보통 무방향 그래프에서 선을 축약하는 것은 위상적인 성질을 비슷하게 유지합니다. 가령 원 그래프가 축약하는 선을 포함하여 존재하고 있으면 축약한 후에는 비슷한 원 그래프가 남아 있게 됩니다. 하지만 원 그래프가 없었는데 축약하는 선 때문에 새로 생기는 일은 없습니다. 하지만, 방향 그래프에서는 방향을 따라서 제자리로 돌아오는 원 그래프를 생각한다면, 아래 그림과 같이 축약하는 선이 방향이 반대여서 원 그래프가 아니었다가 이를 축약함으로써 없애버리고 새로운 원 그래프를 만들어낼 수 있습니다.

이를 방지하기 위해 만들어진 개념이 나비-축약^{butterfly-contraction}입니다. 나비-축약은 \(x\to y\) 선을 축약할 때 (1) \(x\)에 이 선 외에는 모두 들어오는 선만 있거나, 또는 (2) \(y\)에 이 선 외에는 모두 나가는 선만 있을 때만 축약을 하는 것입니다. 예제[그림7]는 (1)과 (2)를 둘 다 만족하지 않음으로 나비-축약이 아닙니다. 나비-축약과 선 또는 점을 지워서 얻어지는 그래프를 원래 그래프의 나비-마이너^{butterfly-minor}라고 부릅니다.

2001년에 존슨^{T. Johnson}, 로버트슨, 시무어, 토마스^{R. Thomas}는 나무-폭과 비슷한 방향 나무-폭^{directed tree-width}를 정의하고 방향 그래프의 방향 나무-폭이 매우 크면 원형 격자 그래프를 나비-마이너로 가짐을 추측하였습니다 [2]. 이 추측은 시간이 흘러 2015년에 카와라바야시^{K. Kawarabayashi}와 크로이쳐^{S. Kreutzer}가 함께 참임을 증명하였습니다 [3].

저는 2016년부터 카와라바야시와 크로이쳐와 함께 나비-마이너 이론에 대해 연구를 진행하고 있습니다. 최근에 방향 그래프에서 얽힘을 정의하고 이에 대한 얽힘-나무 구조를 만들어 내어 이에 대한 논문을 발표하였습니다 [1]. 그래프 구조정리와 비슷한 결과를 방향 그래프에서 만들어내는 것은 앞으로 남아 있는 큰 연구계획 중 하나입니다.

다음 마지막 연재에서는 그래프 마이너 포함관계를 완화하여 만든 얕은 그래프 마이너 포함관계에 대해 알아보고 이를 이용하여 한 그래프를 마이너 포함관계로 가지지 않는 그래프 모임을 확장하는 모임들에 대해 알아보도록 하겠습니다.