듬성한 그래프 [3] : 얕은 마이너로 표현되는 그래프 모임들

이번 글은 “듬성한 그래프” 라는 제목으로 준비한 연재의 마지막 글입니다. 첫 번째 연재에서는 나무-폭^tree-width이 작은 그래프 모임들에 대해 알아보았고, 두 번째 연재에서는 특정한 그래프를 그래프 마이너 연산으로 가지지 않는 그래프 모임들에 대해 알아보았습니다. 특정한 그래프를 그래프 마이너 연산으로 가지지 않는 그래프 모임들은 평면그래프 모임이나 특정한 종수^genus의 곡면에 선을 교차하지 않고 그릴 수 있는 그래프들의 모임들을 포함하였습니다. 그 외에 흥미로운 예제를 찾자면, 그래프를 유클리드 3차원 공간에 매립할 때 어떤 두 개의 원 부분그래프도 고리를 만들지 않게 매립할 수 있는 그래프들을 생각해볼 수 있습니다. 이러한 그래프들은 고리 없이 매립가능한 그래프^{linklessly embeddable graph}라 불리며 이러한 그래프들의 모임이 그래프 마이너 연산에 닫혀있다는 것이 알려져 있습니다. 이 그래프 모임은 완전그래프 \(K_6\)를 포함한 특정한 그래프 7개를 그래프 마이너 연산으로 가지지 않는 그래프로 특성화된다는 것이 로버트슨^{N. Robertson}, 시무어^{P. Seymour}, 토마스^{R. Thomas}에 의해 증명되었습니다 [12].

반면에 그래프 마이너 연산으로 닫혀있지 않지만, 여전히 듬성한 그래프 모임들도 많이 있습니다. 이러한 그래프 모임들의 예제 두 개를 살펴보겠습니다.

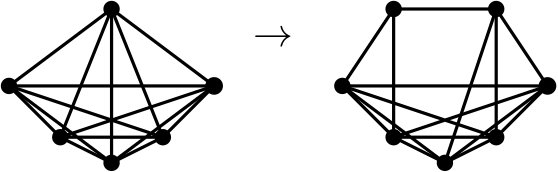
그래프에서 한 점에 연결된 선의 개수를 이 점의 차수^degree라고 합니다. 고정된 상수 \(k\)에 대해, 모든 점의 차수가 \(k\) 이하인 그래프들의 모임을 생각해볼 수 있습니다. 이러한 그래프들은 항상 선의 개수가 \(\frac{k}{2}n\)개 이하가 되기 때문에, 듬성한 그래프 모임을 이루게 됩니다. 하지만 선을 축약하면 점의 차수가 커질 수가 있기 때문에, 이 모임은 그래프 마이너 연산에 닫혀있지 않습니다. 또한 임의의 완전그래프 \(K_n\)에서 각 점을 아래[그림1]와 같이 두 점으로 나누는 연산을 반복적으로 수행하면 모든 점의 차수가 \(3\) 이하가 되게끔 만들어 줄 수 있습니다. 이 과정을 반대로 수행하는 것을 고려해보면, 차수가 \(3\) 이하인 그래프들의 모임에서 모든 완전그래프들을 그래프 마이너로 생성할 수 있다는 것을 알 수 있습니다. 즉, 어떤 \(H\)를 가져와도 \(H\)를 마이너로 가지지 않는 그래프 모임은 위 그래프 모임을 완전히 포함할 수 없습니다.

다른 형태의 듬성한 그래프 모임을 알아보기 위해 책 매장^{book embedding}을 생각해 보겠습니다. 아래[그림2]를 참조하면 되겠습니다.

유클리드 \(3\)차원 공간에서 한 직선을 공통으로 경계를 가지는 유한 개의 반평면들의 모임을 고려해 보겠습니다. 주어진 그래프 \(G\)에서, 모든 점은 경계 직선 위에 놓은 후 \(G\)의 선들은 주어진 반평면들 중에 하나를 통해 연결할 때 어떤 두 선도 교차하지 않고 그리는 것을 \(G\)의 책 매장이라고 합니다. 이때 이러한 책 매장을 구성하기 위해 필요한 최소의 반평면 개수를 주어진 그래프의 책 두께^{book thickness} 라고 정의합니다. 이는 1970년대에 캐넨^{P. C. Kainen}과 올만^{L. T. Ollmann}에 의해 정의되었으며 [6, 12], RNA 구조를 분석하는 등의 수리생물학에 사용되며 관심을 받았습니다 [5]. 위 그림은 완전그래프 \(K_5\)의 책 두께가 \(3\) 이하임을 보여줍니다.

책 두께가 \(k\) 이하인 그래프가 책 매장된 상태를 보면 각각의 반평면에 매장된 부분은 평면에 매장된 것으로 볼 수 있으므로, 각 반평면에 나타나는 선의 개수는 \(3n\)개 이하가 되고, 총 선의 개수는 \(3kn\)개 이하가 됨을 알 수 있습니다. 그러므로 책 두께가 \(k\) 이하인 그래프들의 모임은 듬성하다는 것을 알 수 있습니다. 블랭켄쉽^{R. Blankenship}은 \(K_n\)의 책 두께는 \(\lfloor n/2\rfloor\)보다 같거나 크지만 \(K_n\)의 각 선들을 적당히 긴 길 그래프^path들로 대치시키면 책 두께를 \(3\) 이하로 만들 수 있음을 보였습니다 [1]. 원래 \(K_n\)을 대치된 그래프에서 마이너로 얻을 수 있기 때문에, 책 두께가 \(3\) 이하인 그래프 모임이 그래프 마이너 연산에 닫혀있지 않고, 임의로 큰 완전그래프를 그래프 마이너로 생성할 수 있음을 보여줍니다.

자연스럽게 이러한 다양한 그래프 모임들이 공통으로 갖는 구조적 성질이 있지 않을까 궁금해할 수 있습니다. 이에 대해 2008년에 네세트릴^{J. Nesetril}과 오소나 데 멘데즈^{P. Ossona de Mendez}[그림3]는 얕은 마이너 개념을 도입하여 익스팬션이 상한 된 그래프 모임^{bounded expansion class}을 정의하였고, 앞에서 얘기한 그래프 모임들은 모두 익스팬션이 상한된 그래프 모임들이라는 것을 보였습니다. 이러한 그래프 모임은 여러 가지 다양한 성질을 공유함을 알게 되었고, 이런 성질들은 알고리즘 고안 등에 사용되었습니다. 이에 관한 얘기를 나누어 보도록 하겠습니다.

얕은 마이너와 익스팬션이 상한 된 그래프 모임

다시 언급하면, 어떤 그래프 \(H\)가 그래프 \(G\)의 마이너라는 것은 \(H\)를 \(G\)에서부터 점, 선을 지우거나 선을 축약하는 연산을 반복적으로 하여 얻을 수 있다는 것입니다. 이것을 다음과 같이 다른 방법으로 동등하게 정의할 수 있습니다. 아래[그림4]를 참조하면 되겠습니다.

\(H\)의 점 집합이 \(\{w_1, w_2, \ldots, w_t\}\)라고 할 때, \(G\) 안에서 서로 만나지 않으면서 공집합이 아닌 점 집합들 \(S_1, S_2, \ldots, S_t\)을 찾는데 1) 각 \(S_i\)로 만들어지는 부분그래프가 연결되어 있고, 2) \(H\)에서 \(w_i\)와 \(w_j\)가 연결되어 있으면 \(G\)에서 \(S_i\)와 \(S_j\)사이를 연결하는 선이 있는 점 집합들이 있다고 가정해 보겠습니다. 그러면 \(\bigcup _{1\le i\le t}S_i\)에 속하지 않은 점들을 모두 지우고, 각 \(S_i\)들을 선 축약을 반복적으로 하여 한 점으로 축약시킨 후, 필요 없는 선들을 지움으로써 \(H\)를 마이너로 얻을 수 있음을 알 수 있습니다. 사실 이러한 점 집합들 \(S_1, S_2, \ldots, S_t\)이 있을 필요충분조건이 \(H\)가 \(G\)의 마이너라는 것을 쉽게 알 수 있고, 이를 그래프 마이너 포함관계의 정의로 사용하여도 무방합니다.

주어진 그래프 \(G\)에서 두 점 \(v, w\) 사이의 거리^distance는 두 점을 연결하는 경로 중 가장 최소의 선의 개수를 쓰는 최단 경로의 선의 개수로 정의하고, \(\operatorname{dist}_G(v,w)\)로 표기합니다.\(V(G)\)를 전체 점 집합이라고 할 때, 주어진 그래프의 반경^radius은 \(\min_{v\in V(G)} \left(\max_{w\in V(G)\setminus \{v\}} \operatorname{dist}_G(v,w)\right)\)으로 정의합니다. 즉, 어떤 기준점 \(v\)에서 모든 점까지의 거리가 \(d\) 이하가 되게 잡을 때 \(d\)값을 최소로 만들 수 있는 점에서의 \(d\)값이 반경이 됩니다.

그래프 \(H\)가 그래프 \(G\)의 \(d\)-얕은 마이너^{\(d\)-shallow minor}라는 것은 그래프 마이너의 정의에서 \(S_1, S_2, \ldots, S_t\)를 각각 그 집합으로 만들어지는 그래프가 반경이 \(d\) 이하가 되게 잡을 수 있다는 것으로 정의합니다. 위 그림에 나온 예제는 \(G\)가 \(H\)를 \(2\)-얕은 마이너로 가지고 있음을 보여 줍니다. 일반적으로 깊이의 제한이 없이 택하는 그래프 마이너에 비해 얕은 마이너에서는 깊이의 제한을 두어 마이너를 택하여 얕다는 표현을 사용하고 있습니다.

\(0\)-얕은 마이너를 택하는 것은 각 \(S_i\)를 한 점으로 택하는 것을 얘기하므로, 선이나 점을 지워서만 얻는 부분그래프를 얻는 것과 동일하게 됩니다. 그리고 \(d\)가 점의 총 개수보다 큰 수로 택하면, 반경에 특별히 제한이 없는 것으로 볼 수 있으므로, 일반적인 그래프 마이너로 볼 수 있습니다. 그러므로 \(d\)-얕은 마이너는 이 두 개의 그래프 연산을 여러 가지 단계로 쪼갠 개념으로 볼 수 있습니다.

네세트릴과 오소나 데 멘데즈는 얕은 마이너를 통해 익스팬션이 상한 된 그래프 모임^{bounded expansion class}를 다음과 같이 정의하였습니다 [8]. 그래프 모임 \(\mathcal{C}\)에 대해 모든 자연수 \(d\)와 \(\mathcal{C}\)에 속한 그래프 \(G\)의 \(d\)-얕은 마이너 \(F\)에 대해 \(\frac{|E(F)|}{|V(F)|}\le f(d)\)를 항상 만족하는 함수 \(f\)가 존재하면 \(\mathcal{C}\)를 익스팬션이 상한 된 그래프 모임^{bounded expansion class}으로 정의합니다.

앞에서 본 예제들을 한 번 살펴보겠습니다. 먼저 고정된 \(H\)를 그래프 마이너 포함관계로 가지지 않는 그래프 모임을 생각해 보겠습니다. 이 모임에 있는 그래프 \(G\)를 고른 후 이의 \(d\)-얕은 마이너 \(F\)를 택하면 \(F\)도 당연히 \(H\)를 마이너로 가지지 않습니다. 그러므로 이 경우에는 \(f(d)\)를 \(d\)와 상관없이 \(H\)를 마이너로 가지지 않는 그래프에서 최대 선의 개수를 점의 개수로 나눈 수로 택할 수 있고, 그래서 익스팬션이 상한된 그래프 모임이라는 것을 알 수 있습니다. 가령 \(n\)개 점을 갖는 평면그래프는 최대 \(3n\)개의 선을 가지기 때문에 모든 \(d\)에 대해 \(f(d)=3\)으로 정의한 함수를 통해 평면 그래프들의 모임이 익스팬션이 상한 된 그래프 모임이라는 것을 알 수 있습니다.

이번에는 고정된 상수 \(k\)에 대해 모든 점의 차수가 \(k\) 이하인 그래프 모임을 생각해 보겠습니다. 이러한 모임에 속한 그래프 \(G\)를 고른 후 이의 \(d\)-얕은 마이너 \(F\)를 택해 보겠습니다. \(V(F)=\{w_1, w_2, \ldots, w_t\}\)일 때, \(d\)-얕은 마이너의 정의에 의해 \(G\) 안에서 조건 1)과 2)를 만족하는 서로 만나지 않는 점 집합 \(S_1, S_2, \ldots, S_t\)들이 존재합니다. 특히 각 \(S_i\)로 만들어지는 부분그래프의 반경이 \(d\) 이하이고 각 점의 차수가 \(k\) 이하여서, \(S_i\)에 속한 총 점의 개수가 \(1+k+k^2+ \cdots +k^{d}\) 개로 상한됨을 알 수 있습니다. 그리고 \(S_i\)의 각 점은 다른 집합 중 최대 \(k\)개로만 선을 가질 수 있으므로, \(S_i\)에서 \(\{S_j:1\le j\le t\}\)의 서로 다른 집합들로 나갈 수 있는 선의 총 개수가 어떤 상수 \(c\)에 대해 \(c\cdot k^{d+1}\)개 이하가 됩니다.그러므로 이러한 집합들을 축약시켜 만들어진 \(F\)는 차수가 평균적으로 이 값 정도 되므로 \(f(d)\)를 이 값으로 잡아줄 수 있고 (\(k\)는 고정된 상수로 취급), 이러한 모임이 익스팬션이 상한 된 그래프 모임이 된다는 것을 알 수 있습니다.

책 두께가 \(k\) 이하인 그래프 모임이 익스팬션이 상한 된 그래프 모임이라는 것을 증명하는 것은 조금 더 복잡합니다. 이에 대한 증명은 [Theorem 8.3, 10]를 참조하면 되겠습니다.

그러면 다음으로 익스팬션이 상한된 그래프 모임들의 공통적인 성질에 대해 알아보도록 하겠습니다.

나무-폭 색칠^{tree-width coloring}과 약한 색칠수^{weak coloring number}

익스팬션이 상한 된 그래프 모임의 두 가지 대표적인 성질은 나무-폭 색칠^{tree-width coloring}과 약한 색칠 수^{weak coloring number}로 설명할 수 있습니다.

평면그래프의 모임은 잘 알고 있는 익스팬션이 상한 된 그래프 모임입니다. 4색 정리를 통해서 임의의 평면그래프는 각 집합 안에서 선이 존재하지 않는 네 개의 독립집합^{independent set}으로 나눌 수 있음을 알 수 있습니다. 하지만 이러한 사실이 어떤 알고리즘적인 응용을 주기는 어려운데, 이유는 두 개의 다른 부분집합 사이의 관계에 대해 아무런 설명을 해 주지 않기 때문입니다.

그러면 혹시 적당한 개수의 점 집합들 \(T_1, T_2, \ldots, T_x\)를 택하는데 이들 중에 어떤 두 집합 \(T_i, T_j\)를 택해도 \(T_i\cup T_j\)가 좋은 성질을 가지면서 \(\bigcup_{1\le i\le x}T_i\)가 전체 점 집합이 되는 집합들을 찾을 수 있을까 질문을 던져볼 수 있습니다. 만약에 이런 성질을 갖는 집합들이 있다면, 모든 선의 양 끝점은 목록에 있는 두 개의 집합에 들어가게 되므로 `좋은 성질’을 이용한 어떤 응용을 기대해 볼 수 있습니다.

그룬바움^{B. Grunbaum}은 1973년에 처음으로 일반적인 그래프 색칠을 일반화한 나무-색칠^{acyclic coloring} 개념을 제안합니다 [4]. 그래프의 나무-색칠은 점들을 \(k\)개로 색칠하는 데 어떤 두 개의 색으로 만들어진 부분그래프를 보아도 각 연결성분이 나무가 되게 하는 색칠을 말합니다. 나무-색칠 수^{acyclic chromatic number}는 이렇게 색칠하는 데 필요한 최소의 수를 일컫습니다. 그룬바움은 평면그래프의 나무-색칠 수가 9 이하임을 보였고, 5 이하임을 추측하였습니다. 1979년에 보로딘^{O. V. Borodin}은 이 추측을 증명하였습니다 [2].

나무가 나무-폭이 1임에 착안하여, 이러한 색칠개념을 확장하여 고안된 개념이 \(p\)-나무-폭 색칠^{\(p\)-tree-width coloring}입니다. 주어진 그래프 \(G\)의 점들을 \(k\)개로 색칠하는데, \(p\)보다 같거나 작은 \(p’\)에 대해 \(p’\)개의 집합들을 합집합해서 만들어지는 부분그래프의 나무-폭이 항상 \(p’-1\) 이하가 되면 이를 \(p\)-나무-폭 색칠이라고 정의합니다. 2004년에 데보스^{M. DeVos} 외 6명은 처음으로 이 개념을 생각하였으며, 고정된 그래프 \(H\)와 임의의 자연수 \(p\)에 대해 항상 어떤 상수 \(y=y(H, p)\)가 존재하여 \(H\)를 그래프 마이너로 포함하지 않는 그래프들의 모임의 \(p\)-나무-폭 색칠수가 최대 \(y\) 이하가 됨을 증명하였습니다 [3]. 이 증명에는 두 번째 연재에서 보았던 그래프 마이너 구조정리가 사용되었습니다. 그룬바움의 결과는 평면그래프와 \(p=2\)일 때만 얘기를 해 주니 훨씬 확장된 셈입니다.

그러면 어떤 모임들이 모든 \(p\)에 대해 \(p\)-나무-폭 색칠 수가 상한될까요? 흥미롭게도 네세트릴과 오소나 데 멘데즈는 그래프 모임이 익스팬션이 상한될 필요충분조건이 모든 \(p\)에 대해 \(p\)-나무-폭 색칠 수가 상한된다는 것을 보였습니다 [8].

이러한 성질은 가령 \(H\)-부분그래프 찾기^{\(H\)-subgraph isomorphism}문제를 풀 때 사용될 수 있습니다. \(H\)-부분그래프 찾기 문제는 주어진 그래프 \(G\)에서 \(H\)와 똑같이 생긴 부분그래프가 있는지 없는지를 판단하라는 질문입니다. 만약 \(G\)에 특별한 정보가 없다면 \(|V(H)|\)개 점에 해당하는 모든 부분집합을 고려해서 테스트해 볼 수 있지만, 이는 \(|V(G)|^{|V(H)|}\)의 시간이 최소 들기 때문에, 매우 비효율적입니다. 만약에 \(|V(H)|\)-나무-폭 색칠 수가 어떤 상수 \(C\)로 상한 된다는 것을 알고 이를 다항식 시간에 얻어낼 수 있다고 가정해 보겠습니다. 이 중에 \(|V(H)|\)개의 색을 골라 합쳐보면 \(|V(H)|\)-나무-폭 색칠 수의 정의에 의해 이 부분의 나무-폭이 최대 \(|V(H)|-1\)이라는 것을 알 수 있습니다. 그렇다면 이 부분에서 \(H\)와 똑같이 생긴 부분그래프가 있는지 확인하는 것은 선형시간에 할 수 있습니다. 만약에 \(H\)와 같이 생긴 부분그래프가 존재한다면, \(|V(H)|\)개의 부분을 골라서 확인하는 중 한 번은 반드시 나타나야 합니다. 그래서 전체 알고리즘을 선형시간 알고리즘을 \({C \choose |V(H)|}\)번 돌려서 구성할 수 있음을 알 수 있습니다.

다음은 약한 색칠 수에 대해 알아보겠습니다. 먼저 평면그래프에서는 이미 알아본 것처럼 선의 개수가 항상 (점의 개수)x3으로 상한 됩니다. 선의 개수는 각 점의 차수를 모두 합한 다음 절반을 택한 것과 같아지므로, 평면그래프는 항상 차수가 6 이하인 점이 있다는 것을 알 수 있습니다. 사실 조금 더 자세히 들여다보면, 차수가 5 이하인 점이 있다는 것도 알 수 있습니다.

이를 이용하면 평면그래프를 다음과 같이 한 점씩 지워나갈 수 있습니다. 처음 주어진 평면그래프를 \(G_1\)이라고 하고, 여기서 차수가 \(5\) 이하인 점을 \(v_1\)이라고 했을 때, \(v_1\)을 지워서 \(G_2\)를 만들면 다시 평면그래프가 되고, 그래서 다시 \(G_2\) 안에서 차수가 \(5\) 이하인 점 \(v_2\)가 존재합니다. 이 과정을 반복하면, 차수가 \(5\) 이하인 점을 계속 지워서 한 점이 되게 만들 수 있습니다.

이러한 성질을 일반화하여 만들어진 개념이 약한 색칠 수입니다.주어진 그래프에서 점들을 일렬로 배치한 나열 \(L\)을 생각해 보겠습니다. 이 때, \(u\)가 \(v\)보다 먼저 나타난다면 \(u<_L v\)로 표기하겠습니다.이런 나열을 고려했을 때 \(u<_L v\)인 \(u,v\)에 대해 \(v\)에서 \(u\)로 가는 길이가 최대 \(k\)의 경로 중 중간에 나오는 점들이 모두 \(L\)에서 \(u\)보다 뒤에 나오게 되는 경로가 존재하면, \(u\)가 \(v\)로부터 \(k\)-접근 가능^{weak \(k\)-accessible}하다고 정의합니다. 주어진 그래프 \(G\)의 약한 \(k\)-색칠 수^{weak \(k\)-coloring number}가 \(t\) 이하인 것은 모든 점에서 \(k\)-접근가능한 점들의 개수가 \(t\) 이하가 되는 나열 \(L\)이 존재하는 것으로 정의합니다. 이러한 관점에서 보면 평면그래프는 약한 \(1\)-색칠 수가 \(5\) 이하라고 할 수 있습니다.

어떤 그래프 모임에서 모든 \(k\)에 대해 약한 \(k\)-색칠 수가 항상 상한 될까요? 흥미롭게도 주^{X. Zhu}는 그래프 모임이 익스팬션이 상한될 필요충분조건이 모든 \(k\)에 대해 약한 \(k\)-색칠 수가 상한 된다는 것을 증명하였습니다 [13].

약한 색칠 수가 상한 된다는 성질은 나무-폭 색칠보다 훨신 더 유용하게 사용되지만 간단하게 설명하기는 어렵습니다. 가령 최근에 저는 지벳^{S. Siebertz}과 필립죽^{M. Pilipczuk}과 함께 나무-폭 색칠을 일반화한 계수-폭 색칠^{rank-width coloring}을 정의하였고, 예를 들어 평면 그래프들에서 거리가 \(d\) 이하인 점들의 쌍에 선을 추가하여 만들어지는 조밀한 그래프들의 모임은 \(p\)-계수-폭 색칠 수가 항상 상한 됨을 보였습니다 [7]. 이러한 증명에서 약한 색칠 수가 상한 된다는 성질을 매우 중요하게 사용하였습니다.

독립집합 문제를 다시 들여다보기

첫 번째 연재에서 최대 독립집합 문제에 대해서 알아보고, 나무-폭이 상한되는 그래프 모임에서는 다항식 시간에 해결할 수 있음을 보였습니다. 이를 익스팬션이 상한 된 그래프 모임으로 확장을 할 수 있을까요? 이에 대한 답은 부정적인데, 이유는 이미 평면그래프에서 최대 독립집합 문제가 NP-hard, 즉 다항식 시간에 해결하는 것을 기대하기 어렵다는 사실을 알고 있기 때문입니다.

그렇지만, 생각할 수 있는 영역을 넓히기 위해 최대 독립집합 문제를 세분화하여 \(k\)-독립집합 문제를 고려해볼 수 있습니다. 이 때 \(k\)는 고정된 상수이며, 이 문제는 주어진 그래프에 \(k\)크기의 독립집합이 존재하는 지를 묻는 질문이 됩니다. 이러한 것을 문제의 매개변수화라고 합니다. 간단히 관찰할 수 있는 사실은 이 문제를 \(k\)와 상관없이 (가령 \(k=\sqrt{n}\)라 할지라도) 그래프 크기에 대한 다항식 시간에 해결할 수 있다면 최대 독립집합도 다항식 시간에 해결할 수 있습니다. 그러므로 평면그래프에서 \(k\)-독립집합 문제를 다항식 시간에 해결하기를 기대하기는 어렵습니다.

다만, \(k\)에 대한 지수함수를 허용한다면 어떨까요? 가령 점의 개수가 \(n\)개인 평면그래프에 대해 \(k^k n^2\) 시간에 해결할 수도 있습니다. 이러한 여지는 아직 남아있다는 것입니다. 사실 이러한 시간에 해결할 수 있는 알고리즘은 쉽게 얻을 수 있습니다. 평면그래프에서 4색 정리를 알고 있지만, 일반적인 교과서에 나오는 5색 정리를 이용하면 다항식 시간에 \(5\)개의 독립집합으로 쉽게 나눌 수 있습니다. 그러므로 그중에 하나가 \(k\)크기 이상이면, 질문에 `맞다’고 답을 할 수 있습니다. 그렇지 않다면 나누어진 5개의 독립집합의 크기가 각각 \(k-1\) 이하라는 것이고, 전체 점의 개수가 \(5k-5\)개 이하라는 결론이 나옵니다. 이 경우는 모든 \(k\)크기의 점 집합을 잡아서 테스트해 보아도 \({5k-5\choose k}\)정도의 시간이 들기 때문에, 적절한 상수 \(c\)와 함수 \(f\)에 대해 \(f(k)n^c\)시간에 전체 문제를 해결할 수 있음을 알 수 있습니다.

이렇게 \(f(k)n^c\) 형태의 수행시간을 가지는 알고리즘을 \(k\)에 대한 매개변수 알고리즘^{fixed parameter tractable algorithm}이라고 부릅니다. 이러한 알고리즘이 존재한다면 작은 \(k\)에 대해서는 효율적으로 문제를 해결 가능하다고 생각할 수 있습니다. \(k\)-독립집합에 대한 매개변수 알고리즘의 존재성이 익스팬션이 상한 된 그래프 모임에도 존재함이 증명되었습니다. 그 외 익스팬션이 상한된 그래프 모임에서 사용할 수 있는 여러 가지 알고리즘들에 관심이 있다면 네세트릴과 오소나 데 멘데즈 두 분이 쓰신 『Sparsity』[그림5] 책을 읽어보길 권장해 드립니다 [9].

세 번의 연재 동안 듬성한 그래프 모임들의 분류에 대해 다루어 보았습니다. 평면 그래프들과 나무 그래프들에서 관찰할 수 있는 많은 성질이 여러 가지 형태의 듬성한 그래프 모임들로 확장이 된다는 것을 알 수 있었습니다. 수학자들이 2차원 구조물에 대해 연구를 하다 보면 특정한 곡면에 매립된 형태의 그래프를 다루면서 새로운 사실을 증명해 내는 경우들이 많습니다. 연재에서 살펴본 것과 같이 이러한 그래프 모임들이 익스팬션이 상한 된 그래프 모임들로 확장이 되는 것을 알고 있다면 연구한 것들을 더 확장할 수 있는지 고민해 볼 수 있을 것입니다. 그래프이론에 관심 있는 독자들에게 유익한 연재였기를 바랍니다.