단백질 접힘 이야기

2021년 과학계를 뒤집어 놓은 뉴스를 꼽으라면 “알파폴드^AlphaFold의 성공”이 반드시 들어갈 것이다. 알파폴드는 이세돌에게 4:1로 승리를 거둬 세상을 놀라게 한 알파고^AlphaGo를 만든 딥마인드^DeepMind가 개발한 과학 연구 프로그램이다. 알파고가 2017년 바둑계에서 은퇴를 선언하면서 딥마인드는 이제 단백질 접힘^{protein folding}이라는 과학 문제에 도전하기로 결정한다. 그리고 약 3년의 세월이 흐른 후, 알파폴드는 지금까지 인간이 이뤄 놓은 것보다 더 훌륭한 답을 내놓았다. 이 글에서는 이 알파폴드의 업적을 이해하는 것을 목표로 단백질 접힘 문제를 소개해 보고자 한다.

우선 단백질의 중요성에 관해 이야기해보자. 많은 사람이 “단백질”이라는 단어를 들으면 단백질 파우더나 콩, 달걀 등 식품을 떠올리기 마련이다. 그도 그럴 것이 단백질은 우리가 반드시 섭취해야 하는 영양소로, 제대로 섭취하지 않으면 병에 걸리거나 심지어 사망할 수도 있다. 단백질은 생체 내에서 다양한 역할을 감당하는데, 흔히 알려진것처럼 근육 등 여러 구조를 만드는 데에도 사용되지만, 생체 내의 화학 반응을 매개하고, 이런저런 물질을 수송하고, 생체 내 물질 균형을 맞추는 등 생체 내 핵심적인 기능들을 수행한다. 단백질이 올바르게 작동하지 않으면 세포가 살아갈 수 없다.

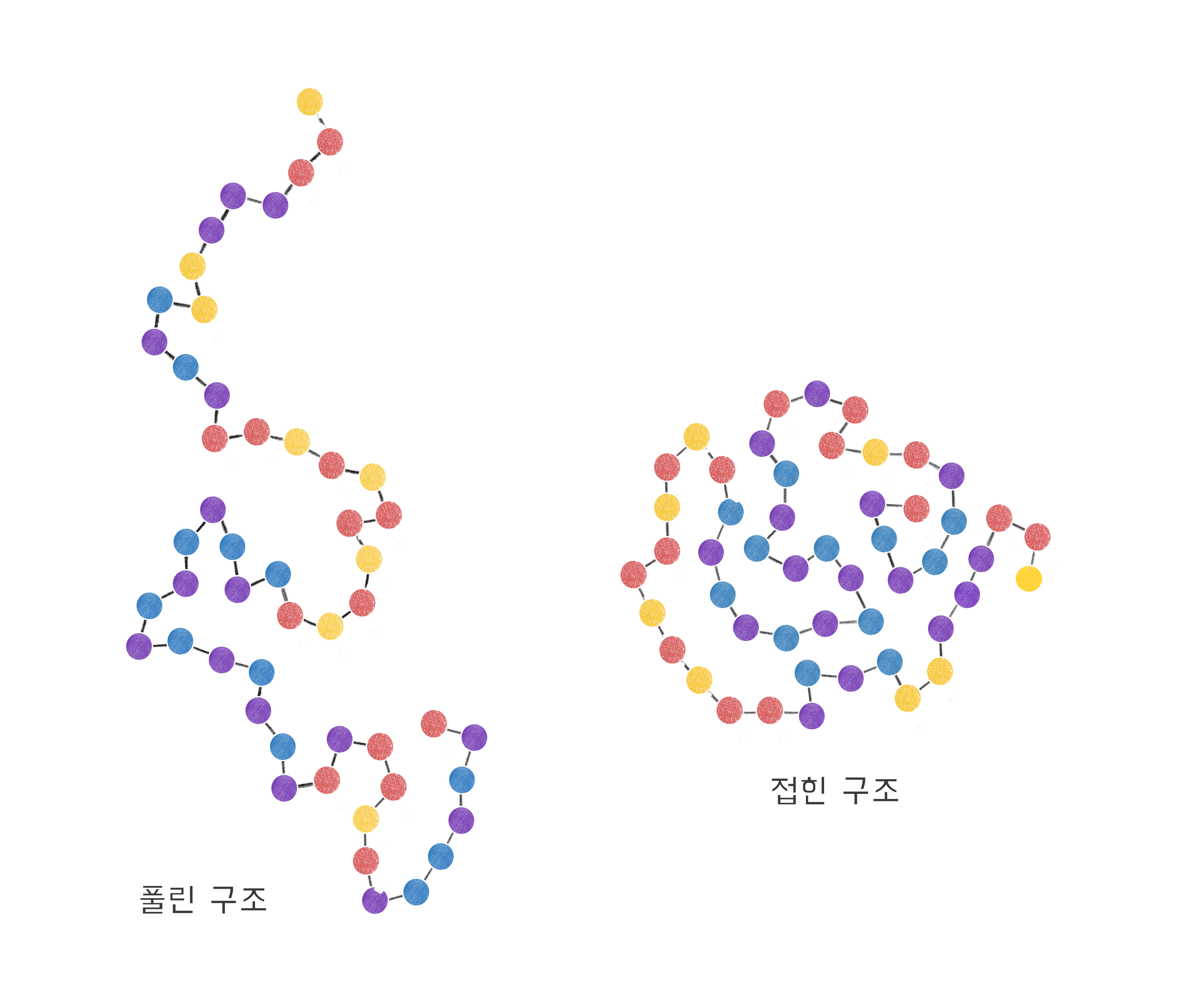
화학적으로 보자면 단백질은 고분자의 일종으로, 단위체들이 서로 화학 결합으로 연결되어 긴 끈과 같은 형태를 이루고 있다[그림1]. 비유하자면 진주 구슬이 쭉 꿰어져 있는 목걸이인데, 아직 목에 걸기 전의 구조, 그러니까 양 끝이 연결되지 않은 구조를 떠올려 보면 도움이 될까? 단백질을 구성하는 단위체(진주 구슬)를 아미노산^{amino acid}이라 부른다. 그런데 이 아미노산은 한 가지 종류가 아니라 다양한 종류가 있다. 보통 유전자에 기록된 정보를 기준으로 스무 가지 종류라고 하지만 실제 생체 내에서는 그보다 더 다채로운 선택이 가능한 것으로 알려져 있다. 각 단백질은 다양한 아미노산이 서로 다른 순서로 꿰어진 구조로 되어 있고, 이렇게 일렬로 연결된 아미노산 정보를 가리켜 단백질의 서열^sequence이라고 부른다.

각 아미노산은 다른 아미노산과 여러 가지 상호작용을 할 수 있다. 서로 밀어낼 수도 있고, 서로 잡아당길 수도 있다. 이때 밀고 당기는 정도도 아미노산의 종류마다 달라진다. 이렇게 아미노산끼리 다양한 상호작용을 한 결과 단백질은 단단한 3차원 구조를 이루게 된다[그림1]. 이렇게 단백질의 1차원 서열이 3차원 구조를 형성하는 과정을 “단백질 접힘”이라고 부른다. 그리고 이렇게 결정된 구조를 고유 구조^{native structure}라고 부르는데, 이 고유 구조가 각 단백질의 기능을 결정한다. 마치 인간이 설계한 기계도 설계자의 의도대로 구조를 유지하고 있어야 제대로 기능을 수행하는 것과 같다. 이 말은 반대로, 만약 단백질이 제대로 된 구조를 이루지 못하면 그 기능을 제대로 해내지 못할 것이라는 이야기가 된다. 따라서 생체 내의 단백질들은 자신의 고유 구조를 항상 유지하고 있어야 한다.

“단백질 접힘 문제”란 바로 이 단백질 접힘과 관련된 문제를 가리킨다. 단백질 접힘 문제에는 원리를 묻는 문제가 있고, 개별적인 분자에 적용되는 또 다른 문제가 있다. (1) 이론상 단백질 서열 하나가 가질 수 있는 구조는 매우 많을 수 있다. 그런데 단백질에 눈이 달린 것도 아닌데 어떻게 그중에서 하나를 골라 항상 그 구조를 유지할 수 있을까? 이는 특정 단백질에만 적용되는 문제가 아니라 모든 단백질의 접힘 원리를 탐구하는 문제라 할 수 있고, 이 글에서는 “첫 번째” 단백질 접힘 문제로 부르겠다. (2) 단백질의 구조로부터 단백질의 기능 및 작동 원리를 파악할 수 있기 때문에 현대 생물학에서는 개별 단백질의 구조 정보를 아는 것이 중요하다. 그런데 실험적으로 구조를 결정하는 것은 비용과 노력이 많이 들어가기 때문에 모든 단백질의 구조 정보를 실험적으로 결정해 둔다는 것은 불가능하다. 그래서 특정 단백질의 서열을 알고 있을 때 그것만으로 구조를 예측할 수 있다면 단백질 연구에 큰 도움이 될 것이다. 이것을 “두 번째” 단백질 접힘 문제라고 하자.

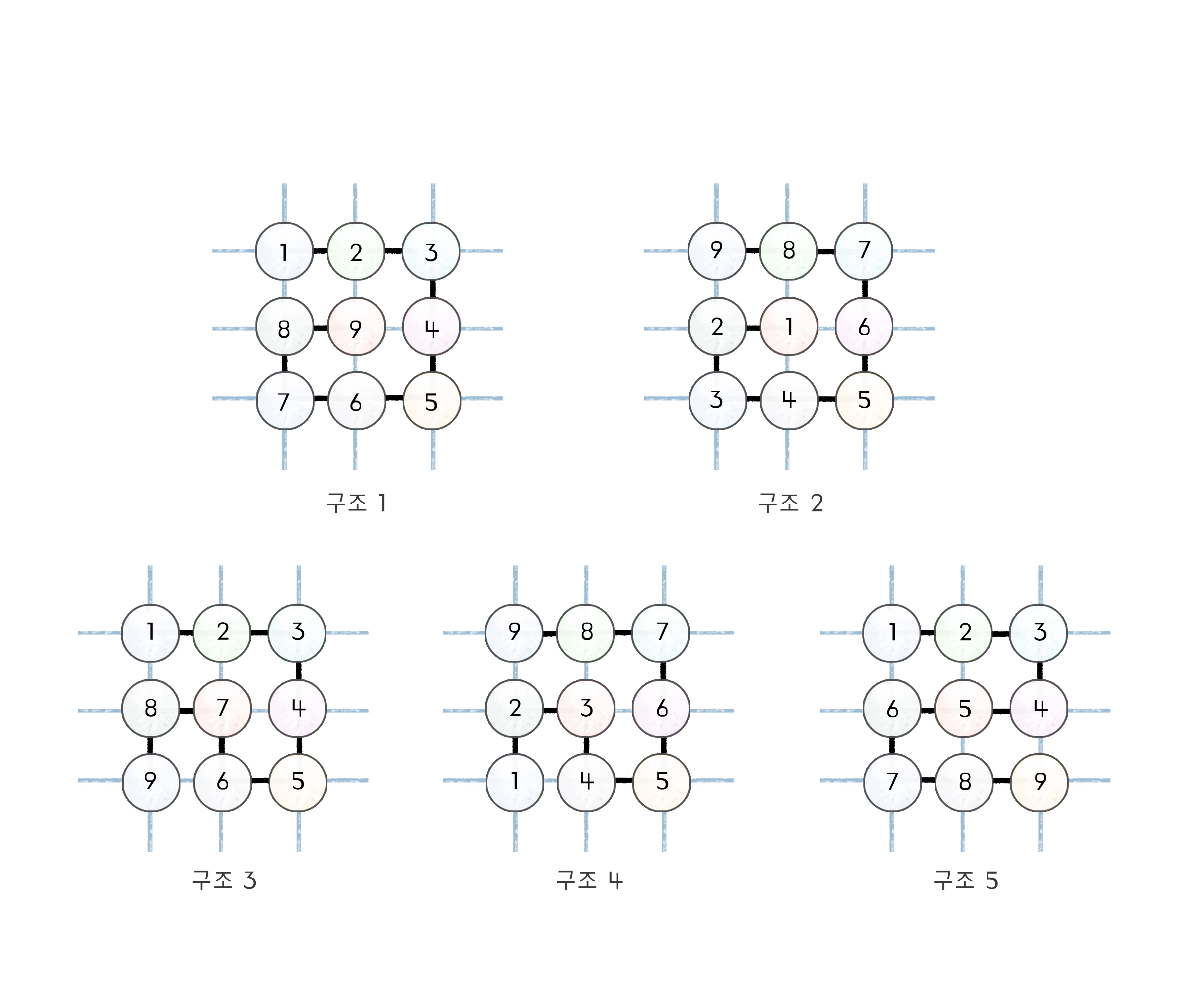
첫 번째 단백질 접힘 문제부터 살펴보자. 3차원 공간 안에서 하나의 단백질 서열이 가질 수 있는 모든 구조를 다 살펴보는 것은 어렵기 때문에, 단순한 모형을 사용하여 문제에 접근해 보겠다. 단백질을 아미노산 구슬이 꿰어 있는 긴 끈으로 보되, 바둑판 위에 올려놓는 것이다. 그리고 각 아미노산 구슬은 선과 선이 만나는 점에만 존재할 수 있고, 구슬과 구슬을 연결하는 끈의 길이가 바둑판의 한 칸에 해당한다고 가정하자[그림2]. 이를 2차원 격자 단백질 모형^{lattice protein model}이라고 한다. 그중에서도 특히 9개 아미노산으로 구성된 단순한 단백질을 생각해 보자. 이 단백질이 가장 빽빽한 구조를 이룰 수 있는 경우는 3×3 공간에 빼곡하게 채우는 것이다. 서로 연결된 아미노산 구슬들을 순서대로 집어넣어 3×3 공간을 다 채울 수 있는 경우의 수는 총 스무 가지다. (이를 해밀턴 경로^{Hamiltonian path}라 하는데, 해밀턴 경로의 수를 세는 것도 꽤 흥미로운 수학적 문제이다.) 이 중 회전 관계에 있거나 거울상 관계에 있는 것들을 제외하면 다섯 개만 남는다[그림3]. 이 구조들을 “뭉친 구조”라고 부르자.

이제 이 단백질 모형의 열역학을 생각해 보자. 서로 끈으로 연결되어 있지 않은 구슬끼리 옆 칸에 놓이게 되면 두 구슬의 종류에 따라 서로 좋아할 수도 있고, 싫어할 수도 있다. 좋아하는 경우 에너지가 더 안정해진다고, 즉 더 낮아진다고 할 수 있고, 싫어하는 경우 에너지가 더 불안정해진다고, 즉 더 높아진다고 할 수 있다. 이를 수학적으로 다루기 위해 각 접촉마다 에너지를 할당할 수 있고, 이러한 구슬-구슬 접촉 에너지를 모두 더하면 해당 단백질이 그 구조를 이룰 때 갖는 에너지 \(E\)를 계산할 수 있다. 한편, 동일한 에너지를 갖는 구조를 다 모아 그 개수를 \(W\)라 한다면, 해당 에너지에 대한 엔트로피 \(S\)는 다음과 같은 식으로 구할 수 있다.

\begin{equation}
     S = k_{\textrm{B}} \ln W
\tag{1}\end{equation}

여기서 \(\ln\)은 자연로그 기호이고, \(k_\textrm{B}\)는 볼츠만 상수라 불리는 상수이다. 이제 에너지와 엔트로피를 다음과 같이 결합하여 헬름홀츠 에너지 \(A\)를 얻는다.

 \begin{equation}
     A = E – TS = E – k_\textrm{B} T \ln W
\tag{2}\end{equation}

여기서 \(T\)는 계의 온도를 가리킨다. 열역학 법칙에 따르면, 계는 헬름홀츠 에너지가 제일 낮은 상태를 선호한다.

이제 단백질의 거동을 이해할 준비가 끝났다. 다시 우리의 3×3 격자 단백질로 돌아가서, 우선 이 단백질을 구성하는 아미노산이 전부 동일하다고 가정하자(동종중합체^homopolymer). 다섯 개의 뭉친 구조는 접촉의 수가 4개로 동일하기 때문에[그림3], 한 접촉당 에너지가 \(\varepsilon\)이라면 에너지는 \(4\varepsilon\)으로 구할 수 있다. 그리고 이 에너지를 갖는 구조의 수는 \(W = 5\)이므로, 뭉친 상태의 헬름홀츠 에너지는 \(A_\text{뭉침} = 4\varepsilon – k_\textrm{B}T \ln 5\)로 구할 수 있다. 한편, “펼친 구조”는 단백질 분자 내부에 아무런 접촉도 생기지 않는 구조로 볼 수 있다([그림2]와 같은 경우). 이 경우 접촉 에너지가 없으므로 \(E = 0\)이다. 또한 이런 구조는 뭉친 구조에 비해 훨씬 많은 수가 존재할 수 있으므로, 이 펼친 구조의 수를 \(N\)이라 한다면(\(N > 5\)), 펼친 상태의 헬름홀츠 에너지는 \(A_\text{펼침} = -k_\textrm{B}T \ln N\)으로 쓸 수 있다. 뭉친 상태와 펼친 상태 중 어느 상태를 선호하는가는 두 헬름홀츠 에너지 중 어느 쪽이 낮은가에 의해 결정된다. \(A_\text{뭉침} < A_\text{펼침}\)이면 뭉친 상태를 선호할 것이고, \(A_\text{뭉침} > A_\text{펼침}\)이면 펼친 상태를 선호할 것이다. 뭉친 상태를 선호할 조건을 식으로 써보면,

\begin{equation}
  4\varepsilon – k_\textrm{B} T \ln 5 < -k_\textrm{B} T \ln N
\tag{3}\end{equation}

이 되고, 이로부터 온도 \(T\)에 대한 조건을 찾으면 다음과 같다.

 \begin{equation}
     T < -\frac{4\varepsilon}{k_\textrm{B}} \ln \left(\frac{N}{5}\right)
\tag{4}\end{equation}

만약 접촉 에너지 \(\varepsilon\)이 양수라면 음수 온도가 나오므로 뭉친 상태를 선호하는 온도를 찾을 수 없다. 이는 직관적으로도 이해할 수 있는데, 접촉 에너지가 양수라는 것은 접촉이 없는 상태에 비해 더 높은 에너지를 갖는다는 뜻이고, 구슬끼리 서로 접촉하기 싫어하는 상황을 의미한다. 따라서 모든 온도 범위에서 그냥 펼친 상태로 존재하는 것을 선호한다. 반면, 접촉 에너지 \(\varepsilon\)이 음수라면 위 부등식을 만족하는 온도 범위에서는 뭉친 상태를, 만족하지 않는 온도 범위에서는 펼친 상태를 선호하게 된다.

아주 간단한 모형을 이용하여 온도에 따라 뭉친 상태와 펼친 상태를 왔다 갔다 할 수 있는 단백질을 만들어 보았다. 그러면 이게 단백질의 접힘 현상을 완전히 설명할까? 아쉽게도 그렇지 않다. 이 모형에 따르면 다섯 개의 구조가 모두 뭉친 상태에 대응하는데, 실제 단백질 접힘에서는 단 하나의 고유 구조만이 접힌 상태로 존재한다. 실제로 단백질은 9개의 아미노산 구슬보다 더 많은 수의 아미노산 단위체로 구성되므로, 충분히 긴 단백질을 생각해 보면 뭉친 상태에 속할 수 있는 구조의 수가 상당히 많아지게 된다. (물론 펼친 상태로 존재하는 구조는 훨씬 더 많아진다!) 따라서 이 뭉침-펼침 전이만으로는 단백질의 접힘 현상을 설명할 수 없다.

실제 단백질은 다양한 종류의 아미노산으로 구성되어 있으므로, 이번에는 우리의 2차원 격자 단백질에서 각 구슬의 종류가 다양하다고 생각해 보자(이종중합체^{heteropolymer}). 이제 단백질의 서열이 중요해진다. 가장 쉬운 예로 두 가지 종류의 구슬 A, B가 가능하다고 가정하면, 9개의 구슬을 줄줄이 꿸 때 AAABBBAAA와 같이 꿸 수도 있고, ABABABABA와 같이 꿸 수도 있고, AABABBABA와 같이 꿸 수도 있으니 말이다. 가능한 구슬의 종류가 \(M\)가지이고 단백질을 이루는 구슬의 개수가 \(N\)개라면, 가능한 서열의 수는 \(M^N\)으로 구할 수 있다. 9개의 구슬을 가진 우리의 단백질이라면, 두 가지 종류의 구슬만으로도 \(2^9 = 512\)가지의 서열을 만들어낼 수 있다. 그 모든 서열을 다 따져보는 것은 힘들고, 하나만 골라서 뭉침-펼침 전이가 어떻게 달라지는지 살펴보자.

AAABABAAB라는 서열을 생각해 보자[그림4]. 그리고 구슬의 접촉 에너지를 다음과 같이 가정한다(이 때 \(\varepsilon_0 > 0\)).

\begin{equation}
  \varepsilon_{\textrm{AA}} = -2\varepsilon_0,\quad \varepsilon_{\textrm{AB}} = -\varepsilon_0, \quad \varepsilon_{\textrm{BB}} = -3\varepsilon_0
\tag{5}\end{equation}

즉, 구슬끼리 만나면 기본적으로 안정화가 되지만, 그 안정화되는 정도가 서로 만난 구슬의 종류마다 달라진다. 이제 저 서열을 넣어서 각 뭉친 구조마다 에너지를 계산해 보면 다음과 같다.

\begin{equation}
  \text{구조 1:} -9\varepsilon_0, \quad\text{구조 2:} -5\varepsilon_0, \quad\text{구조 3:} -8\varepsilon_0, \quad\text{구조 4:} -5\varepsilon_0, \quad\text{구조 5:} -8\varepsilon_0
\tag{6}\end{equation}

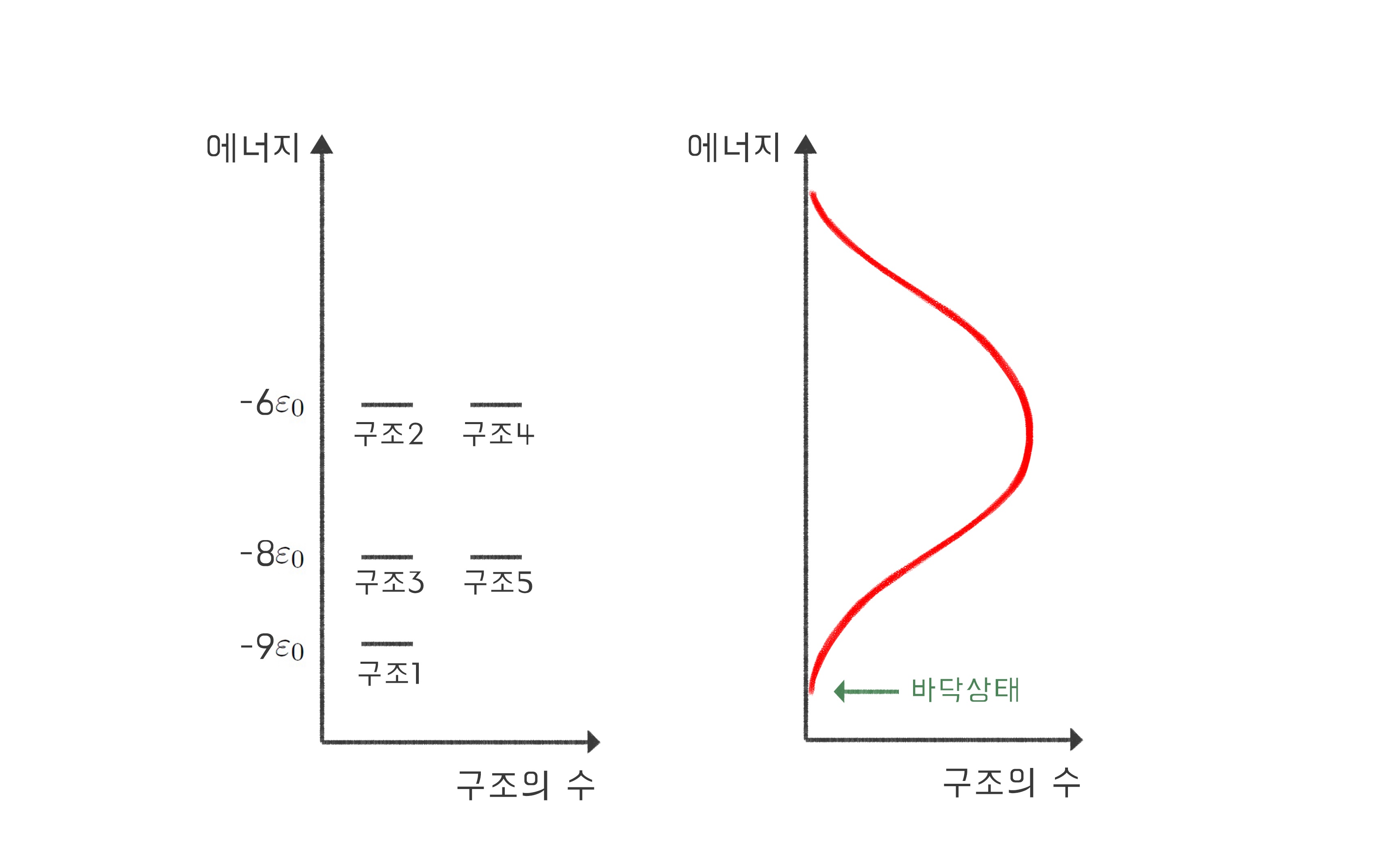
이렇게 단위체의 종류를 다양하게 만드는 것만으로도 뭉친 구조들 사이의 에너지가 달라지는 효과가 있다. 이를 일반화하기 위해, 이번에는 길이가 제법 긴 고분자를 생각해 보자. 고분자가 가질 수 있는 구조별로 에너지를 계산하고, 각 에너지에 해당하는 구조의 수를 세보면 일반적으로 [그림5]와 같은 관계를 얻게 된다.[1] 여기서 알 수 있는 것은 가장 에너지가 낮은 상태(“바닥 상태”)에는 한두 개의 구조만 존재할 수 있다는 점이다. 이제 단백질 접힘은 올바르게 묘사된 것일까?

아쉽게도 그렇지 않다. 앞서 헬름홀츠 에너지의 차이는 “경향성”을 알려준다고 언급했다. 즉, 여러 상태가 존재할 때 헬름홀츠 에너지가 가장 낮은 상태는 가장 높은 확률로 존재할 수 있는 상태일 뿐이다. 다른 상태 역시 확률이 조금 더 낮을 뿐 존재할 수 있다. 이때 확률은 볼츠만 인자^{Boltzmann factor} \(p(A)\)로 계산할 수 있다.

\begin{equation}
      p(A) \propto e^{-A/k_\textrm{B}T} = e^{-E/k_\textrm{B}T + S/k_\textrm{B}} = We^{-E/k_\textrm{B}T}
\tag{7}\end{equation}

이러한 확률이 존재하기 때문에 [그림5]와 같은 상황에서 온도가 0 K이 아니라면 바닥 상태 외의 상태들도 존재할 확률을 갖게 된다. 특히 바닥 상태 다음으로 안정한 상태는 헬름홀츠 에너지가 바닥 상태와 거의 다르지 않기 때문에 바닥 상태 못지않은 확률을 갖게 될 것이다. 바닥 상태의 구조와 다른 구조가 바닥 상태 못지않은 확률로 존재한다면, 역시 상온에서 단일한 구조로 존재하는 단백질 접힘을 표현하기에는 부족하다. 따라서 단위체의 종류를 다양하게 만드는 것만으로는 상온에서 단 하나의 구조로만 존재하는 “단백질 접힘”을 묘사할 수 없다.

그렇다면 단백질 접힘을 올바르게 묘사할 수 있는 방법은 무엇일까? [그림5]와 같은 상황에 가장 낮은 에너지 상태를 추가하되, 기존의 에너지 상태들과 간격^gap을 띄도록 하면 된다[그림6]. 이 간격이 충분히 크다면 상온에서도 가장 낮은 에너지 상태로 존재할 확률을 거의 100%에 가깝게 만들 수 있다. 이 모형을 흔히 깔때기 모형^{funnel model}이라 부른다. 바닥 상태는 에너지가 매우 안정하고 그 상태에 포함되는 구조의 수가 매우 적기에 깊은 빨대 모양을 이루는 반면, 불안정한 상태들은 그보다 에너지가 한참 높으면서 그 안에 포함되는 구조의 수가 많기 때문에 넓고 얕은 모양을 나타내어, 이 둘을 결합하면 깔때기와 같은 모양을 띠기 때문이다. 많은 수의 실제 단백질들이 이러한 깔때기 모양의 에너지 분포를 갖는다는 것이 알려져 있다.[2,3]

앞서 살펴본 것처럼 단순히 단위체의 종류를 다양하게 만드는 것만으로는 이런 깔때기 모양을 만들 수 없지만, 일부 서열은 자연스레 깔때기 모양의 에너지 분포를 갖는다는 것이 알려져 있다. 문제는 대부분의 랜덤한 서열은 [그림5]와 같은 에너지 분포를 갖는다는 점이다. 깔때기 모양의 에너지 분포를 가져야 무의미한 구조들을 최소화하고 세포 내 자원의 낭비를 막을 수 있으므로, 아마 자연은 자연 선택을 통해 깔때기 모양의 에너지 분포를 갖는 서열들을 계속해서 선택해 온 것으로 보인다. 이로써 첫 번째 단백질 접힘 문제, 즉 단백질의 접힘이 어떻게 가능한지에 관한 질문은 어느 정도 해결되었다고 하겠다.

자, 그렇다면 두 번째 단백질 접힘 문제, 즉 개별 단백질에 대해 서열 정보만으로 고유 구조를 예측하는 문제는 어떻게 접근할 수 있을까? 연구 현장에서 과학자들이 사용하는 예측 프로그램은 대개 주어진 서열의 단백질에 대해 여러 가지 구조를 가상으로 만든 후, 각 구조의 에너지를 나름의 방법으로 예측하여 가장 낮은 에너지를 갖는 구조를 고유 구조로 예측하는 식으로 작동한다. 이 때 각 구조의 에너지를 예측하는 방법은 여러 가지가 존재하는데, 대표적인 방법으로는 다음과 같은 방법을 쓸 수 있다. 두 가지 종류의 원자가 거리에 따라 에너지가 어떻게 달라지는지 모델을 세운 후, 단백질 구조 내에 있는 모든 원자들에 대해 원자-원자 거리를 계산하고, 앞서 세운 모델에 집어넣어 각각 에너지를 계산한 후 그 모든 에너지를 합산하면 구조의 전체 에너지가 나올 것이다. 문제는, 이 때 에너지를 계산하는 모델이 100% 정확할 수 없다는 점이다. 원자들의 상호작용은 미묘한 환경 차이에 의해서도 변화할 수 있다. 그 모든 환경 차이를 다 반영하여 모델을 세우는 것은 불가능한 일이기 때문에, 이러한 예측 프로그램들은 필연적으로 오차를 포함할 수밖에 없다. 만약 우리가 에너지를 정확하게 계산하는 게 목표라면, 현재의 기술로는 아직 가야할 길이 멀다.

하지만 구조를 정확하게 예측하는 게 목표라면, 꼭 에너지 계산이 정확하지 않아도 된다(!). 첫 번째 단백질 접힘 문제에서 찾아낸 원리를 떠올려보자. 깔때기 모형으로 논의한 것처럼 일반적으로 고유 구조의 에너지는 다른 구조들의 에너지보다 훨씬 낮고, 그 사이에는 큰 에너지 간격이 있다. 따라서 개별 구조의 에너지 예측이 어느 정도 오차를 포함한다 하더라도 간격만 재현할 수 있다면 이론상 고유 구조를 정확하게 예측할 수 있다. 그래서 알파폴드 이전에도 과학자들은 여러 방법을 사용하여 꽤 많은 단백질의 고유 구조를 성공적으로 예측해 왔고, 처음 컴퓨터로 예측을 시작한 이래 정확도는 계속해서 향상되어 왔다. 물론 모든 단백질에 대해 성공을 거둔 것은 아니었고, 예측이 잘 안 맞는 어려운 분자들도 존재했다. 아마 이들은 과학자들이 사용하는 비교적 단순한 에너지 예측 모델이 처리할 수 없는 복잡한 상호작용들이 포함되어 있을 것이다.

알파폴드가 대단한 것은 바로 이 어려운 분자들까지 높은 정확도로 고유 구조를 찾아낸다는 점이다. 알파폴드는 인간처럼 특정한 에너지 예측 모델을 가정하고 시작하는 것이 아니라, 주어진 데이터 내의 패턴을 (인간이 이해할 수 없는 형태로) 학습하여 새로운 데이터가 주어졌을 때 예측을 내놓는 식으로 작동한다. 따라서 알파폴드의 성공 여부는 얼마나 많은 데이터를, 그리고 얼마나 다양한 데이터를 학습하느냐에 달려 있다. 그런데 단백질의 구조는 현대 생물학에서 워낙 중요한 역할을 하기 때문에 이미 신뢰할 만한 다양한 데이터가 다량 축적되어 있었고(10만 개 이상), 그 데이터를 잘 활용한 결과 알파폴드는 인간이 상상할 수 없는 복잡한 상호작용들도 전부 패턴으로 학습할 수 있었던 것이다. 알파폴드의 정확도가 워낙 높다 보니, 심지어 최근에 나오는 단백질 논문 중에는 구조를 실험으로 결정하지 않고 알파폴드 예측 구조를 기준으로 논의를 진행하는 논문들도 있다. 즉, 알파폴드 덕분에 단백질 접힘의 두 번째 문제에도 큰 진전이 있었다 할 수 있겠다.

오늘 이 글에서는 단백질 접힘이라는 현상을 중심으로 이론가들이 고민해 온 문제들을 소개했다. 단백질 접힘은 생명 현상을 이해하는데 중요한 현상이므로, 그 원리가 어떻게 되는지도 이해해야 했고, 또 개별 분자에서 단백질 접힘이 어떻게 일어나는지도 예측할 수 있어야 했다. 우리는 동일한 단위체로 구성된 동종고분자도, 서로 다른 단위체로 구성된 이종고분자도 그것만으로는 단백질 접힘을 설명할 수 없고, 결국 깔때기 모양의 에너지 분포를 갖는 “특별한” 서열들만 단백질 접힘 현상을 잘 나타낸다는 것을 배웠다. 또한, 이러한 간격 덕분에 100% 정확한 에너지 계산 모델이 아니더라도 개별 단백질 분자의 고유 구조는 꽤나 정확하게 찾을 수 있음을 알았다. 단백질 접힘을 연구해 온 이론가들은 이제 알파폴드 이후 시대에 무엇을 연구해야 하는지를 고민하고 있다. 고유 구조가 존재하지 않는 비정형 단백질^{intrinsically disordered protein}이나, 여러 단백질들이 서로 달라붙어 형성하는 단백질 복합체^{protein complex} 등이 유력한 차세대 주제로 보인다. 이제 이 분야에서 어떤 흥미로운 논의가 시작될지 기대가 된다.