최근, 국제도량형총회에서 인위적으로 만든 백금-이리듐의 ‘킬로그램원기’를 기준으로한 정의를 폐지하고, 질량의 단위인 킬로그램(kg)을 플랑크 상수의 값을 사용하는 새로운 정의를 결정하였습니다.
인위적으로 만든 물질의 값에 근거한 표준이 아닌 자연법칙에서 나온 물리 상수들의 값들을 고정함으로써 7개의 기본단위를 새로운 정의로 바꾸는 역사적인 결정이 있었습니다. 길이의 단위인 미터의 정의도 변경이 있었는데 이에 관련한 내용과 빛의 속력의 값의 결정 등 잘 알려져 있지 않은 이야기들을 소개해 드리도록 하겠습니다.[1] [2] [3]
1. 기본단위의 새로운 정의
2018년 11월 13일부터 16일까지, 프랑스 파리에서 개최된 국제도량형총회 CGPMConférence Générale des Poids et Mesures 제26차 회의에서 7개의 단위를 ‘정의하는defining’ 물리 상수들의 값을 고정함으로써 7개 기본단위의 새로운 정의를 채택하였습니다. 그 물리 상수들의 값과 관련된 단위들을 다음 [표1] 에 나타내었습니다.
이 새로운 정의로 인하여 비로소, 백금-이리듐 합금제의 질량 원기와 같은 인위적으로 만든 원기의 표준값에 근거하던 인공물 척도, 물질의 성질 혹은 측정에 관한 서술을 하지 않아도 되는 물리상수 들에만 기반으로 하는 온전한 7개의 단위의 정의가 마련된 것입니다.
[표1] SI 기본단위와 그에 관련된 물리상수
|
기본량의 명칭 |
단위 |
정의와 관련되는 물리상수 |
기호 |
고정한 물리상수 값 |
단위 |
|
|
명칭 |
기호 |
|||||
|
시간 |
초 |
s |
세슘Cs의 초미세 전이 주파수 |
\(\Delta\nu _{c_{s}}\) |
9 192 631 770 |
Hz = s-1 |
|
길이 |
미터 |
m |
진공에서 빛의 속력 |
c |
299 792 458 |
m s-1 |
|
질량 |
킬로그램 |
kg |
플랑크 상수 |
h |
6.626 070 15 \(\times 10^{-34}\) |
J s |
|
전류 |
암페어 |
A |
기본전하 |
e |
1.602 176 634 \(\times 10^{-19}\) |
C |
|
열역학 온도 |
켈빈 |
K |
볼츠만 상수 |
k |
1.380 649 \(\times 10^{-23}\) |
J K-1 |
|
물질량 |
몰 |
mol |
아보가드로 상수 |
\(N_{A}\) |
6.022 140 76 \(\times 10^{23}\) |
mol-1 |
|
광도 |
칸델라 |
cd |
시감효능 |
\(K_{cd}\) |
683 |
lm W-1 |
7개 기본단위에 대한 새로운 정의들은 2018년 11월 16일에 CGPM에서 합의되어, 2019년 5월 20일부터 발효되었습니다. 5월 20일이 발효되는 날짜로 선정된 이유는 세계 최초의 다자간 협의였던 1875년 미터협약이 조인된 날을 기념하는 ‘세계 측정의 날’이기 때문입니다.
다만 새로운 정의가 도입되는 시점에서는 이전의 정의들과 일관성을 유지하도록 각별한 주의가 기울여졌으며 또, 이들의 정의를 실현하기 위하여 최첨단 과학기술이 도입되었고 정확한 정의의 실현을 위한 지침이 추천되어 있으며, 보다 정확한 정의의 실현을 위한 연구는 계속되고 있습니다.
2. 미터의 역사[4]와 정의
프랑스 혁명과 혁명 전쟁의 어려운 시기 중인 1792년부터 1798년까지 6년간의 두 측량팀이 겪은 죽음을 무릅쓴 고난의 지구 자오선의 측량 결과에 따라, 북극에서 적도까지의 거리의 천만 분의 1의 길이로 백금원기가 만들어지고[그림1] 이 원기에 가장 가까운 길이의 백금-이리듐 원기[그림2]가 만들어져 이에 근거한 미터의 정의가 정해졌습니다.
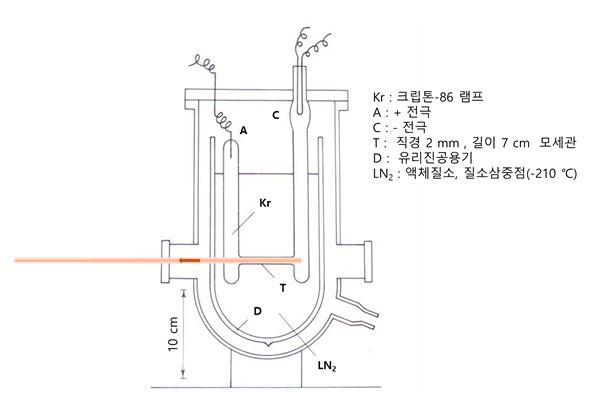
이후, 재난으로 인해 ‘국제 미터원기‘의 파괴될 위험성과 원기에 그어진 눈금의 선폭에 의한 정확한 측정의 한계, 열팽창으로 인한 길이의 변화 등의 문제 때문에, 파괴되어도 재현이 가능한 크립톤-86 램프[그림3]의 주황색 파장의 진공 파장 값에 근거한 미터로 1960년에 다시 개정되었습니다.
1972년 빛의 속력이 정확하게 측정됨에 따라, 미터정의자문위원회 1973년 회의에서 빛의 속력 값이 결정되고, 1975년 제15차 국제도량형총회 CGPM에서 빛의 속력은 불확도가 없는 권고값으로 정해짐에 따라, 1983년 제17차 국제도량형 총회에서 ‘미터는 빛이 진공에서 1/299 792 458 초 동안 진행한 경로의 길이이다.’로 정하였습니다.
2018년 제26차 국제도량형총회에서의 자연의 물리상수의 값들을 고정하고 이들 물리상수에 기반한 국제단위계의 7개 단위들을 정의함과 더불어 미터 정의에 대해서도, ‘빛의 속력’에 근거한 이 1983년의 “미터의 정의”에서 자세하게 표현하지 않았던, “초”의 정의에 관련된 문장을 더 첨부함으로써 미터의 정의를 아래와 같이 온전한 문장으로 수정하였습니다.
‘미터(기호: m)는 길이의 SI 단위이다. 미터는 진공에서의 빛의 속력 c 를 m s-1 단위로 나타낼 때 그 수치를 299 792 458로 고정함으로써 정의된다. 여기서 초(기호: s)는 세슘주파수 \(\Delta\nu _{c_{s}}\) 를 통하여 정의된다.’
이와 같은 정의로는 미터 정의를 현실적으로 어떻게 실현하는지, 또 정밀한 길이 측정은 어떻게 이루어지는지 알 수가 없습니다.
이를 위하여 국제도량형위원회 CIPM의 길이 정의 자문위원회 CCL에서는 다음과 같은 방법을 미터 정의의 현실적인 구현과 활용(길이 측정)에 사용할 것을 추천하고 있습니다.
3. ‘미터 정의’의 실현 방법(길이 측정법)
새로이 미터 정의가 제정됨에 따라서, 미터를 실현하기 위해서는 1차적인 두 가지 방법과 2차적인 3가지 방법을 길이정의자문위원회에서는 추천하고 있습니다.
1차적으로 미터의 정의를 실현하는 방법은 빛의 이동시간을 직접 측정하여 빛의 속력을 곱하여 얻는 방법이며 또 다른 방법은 간접적으로 이동시간을 측정하는 방법으로서 주파수(또는 진공파장) 안정화된 레이저를 사용한 간섭계를 이용하는 방법입니다.
또, 미터를 실현하기 위한 2차적인 방법으로써는 나노측정학을 위하여, 실리콘 단결정의 격자상수(d220 면의 격자상수는 192.015 571 4(32) \(\times10^{-12}\) m, 상대불확도 : 1.6 \(\times10^{-8}\))[6]와 X-선 간섭계를 이용하는 방법, 실리콘 격자상수와 투과형 전자현미경을 이용하는 방법, 실리콘 표면의 단원자 계단 높이를 사용하는 방법 등 3가지 방법이 있습니다.
이에 대한 더 자세한 내용은 본 원고에서는 지면 관계상 다루지 않고 다음의 기회를 기다리기로 하겠습니다.
3-1. 미터의 정의를 실현하기(길이 측정) 위한 1차적 방법
빛의 속력과 시간 초(s)의 정의에 근거한 미터정의의 기본방정식은 다음과 같습니다.
\(L= c\bullet \Delta t\)
여기서, c는 진공에서 빛의 속력, c = 299 792 458 m s-1이며,
\(\Delta t\) 는 길이가 L인 기하학적 경로를 따라 빛의 이동한 시간입니다. 따라서 길이 단위의 실현은 빛의 이동 시간 측정과 연결됩니다.
이것은 장거리(예: 달까지 거리 측정) 측정에서는 높은 상대 정확도로 직접 측정을 할 수 있지만, 일반적인 거리 범위에서는 매우 짧은 시간 간격(예를 들면, 1 m 는 빛이 약 3.3 ns = 3.3\(\times10^{-9}\)s , 1 mm의 경우는 약 3.3 ps = 3.3\(\times10^{-12}\)s 동안 빛이 이동한 거리에 상당한다.)이므로 짧은 시간 측정은 어려운 일이기 때문에 간접적인 이동 시간 측정이 더 나은 정확도를 제공합니다.
따라서, 미터의 정의는 다음과 같은 방법으로 실현할 수 있습니다.
a) 빛의 이동 시간을 직접 측정하거나
b) 빛의 이동 시간의 간접 측정법으로
빛의 이동 시간을 간접적으로 측정하는 방법으로는 간섭계를 이용하는 방법이 있는데, 이는 주파수 \(\nu\)의 평면 전자기파의 진공 파장 \(\lambda\)를 길이 측정의 기준으로 이용하는 방법입니다. 이 파장 \(\lambda\)의 값은 \(\lambda = c/\nu\)의 관계식과 진공에서 빛의 속력 값 c = 299 792 458 m s-1를 사용하여 측정된 빛(레이저)의 주파수 \(\nu\)값으로 나누어 얻을 수 있습니다. 또, ‘국제도량형위원회 CIPM에서 추천하는 레이저 복사선 목록(CIPM LoF)‘에 있는 복사선의 파장을 사용할 수 있습니다.
3-1-1. 빛의 이동 시간의 직접 측정법
빛의 이동 시간을 직접 측정하려면 타이밍 프로세스에 사용되는 기준 신호를 만들기 위해 빛을 펄스 형태로 만들 필요가 있습니다.
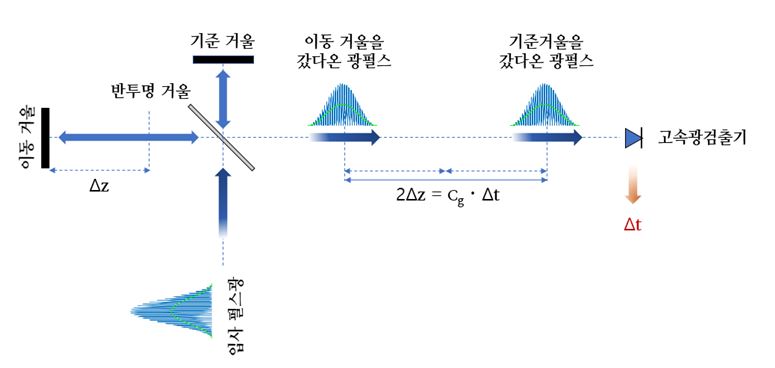
[그림4]는 광 펄스를 이용하여 길이 측정을 설명하고 있는 그림입니다. 입사 광 펄스가 서로 다른 길이의 두 경로를 이동하여 광검출기에 도달하게 됩니다. 그러면, 두 광 펄스 간의 시간 지연을 직접 측정하여 길이를 측정할 수가 있습니다.
그림의 광 펄스 안의 촘촘한 신호는 광 강도(전자기장의 제곱에 비례)의 광의 위상을 나타낸 것으로, \(\lambda/2\)가 한 주기가 됩니다. 광 펄스 내부의 녹색 곡선은 광검출기가 감지하는 광 펄스의 평균 광 강도를 나타냅니다. 광검출기는 너무 빠르게 변화하는 광의 위상은 감지할 수가 없고, 평균 광 강도(녹색 곡선)만 감지하여 반응합니다.
광검출기가 반응하는 펄스 형의 두 광 강도 사이의 시간 지연 \(\Delta t\)를 측정하면 길이를 결정할 수 있습니다. 길이 L을 나타내는 측정 경로와 기준 경로 간의 차이 \(\Delta z\)은 다음과 같습니다.
\(L= \Delta z=c _{g}\bullet \left ( \Delta t/2 \right )\)
여기서, \(\Delta t\)를 2 로 나눈 것은 지연시간 \(\Delta t\)는 측정하려고 하는 거리를 왕복한 시간이기 때문입니다. \(c_{g}\)는 광 펄스의 군속도(群速度)group velosity입니다. 진공 상태에서 \(c_{g}\)는 c와 동일합니다. 공기 중에서는\(c_{g}\)는 \(c_{g}=c/n_{g}\)이며, 여기서 \(n_{g}\)는 공기의 군 굴절률(群屈折率)group refractive index of air이며, 빛의 단일파장의 연속파를 사용할 때(간섭계)에 사용하는 위상 굴절률phase refractive index of air \(n_{p}\)와는 다릅니다. 그러나 군 굴절률은 위상 굴절률 공식을 사용하여 다음의 관계식으로 계산할 수가 있습니다.
\(n_{g}\left ( \lambda \right )= n_{p}\left ( \lambda \right )-\lambda \bullet \left ( dn_{p} /d\lambda \right )\)
빛의 이동 시간을 직접 측정하는 대표적인 예는 지구에서 달까지의 거리 측정입니다. 1969년 7월 21일 아폴로APOLLO, Apache Point Lunar Laser-ranging Operator-11호 달 탐사선이 달까지의 거리 측정을 위하여, 수직으로 입사해야 되돌아오는 평면 반사거울 대신에, 입사한 광로에 나란하게 되돌아오는 반사경인 코너큐브프리즘 세트를 달 표면에 처음 설치한 이후에, APOLLO-14호(1971년), APOLLO-15호(1971년) 등의 탐사선들도 프리즘 세트를 달 표면에 설치해 놓았습니다. 프랑스에서 만든 반사경 세트들도 러시아 달 탐사선 Luna-17호(1970년), Luna-21호(1973년)를 통해 올려졌습니다.
Q-스위칭된 루비 레이저와 2.7 m 직경의 망원경을 이용한 측정시스템으로 달에 설치한 반사경까지의 거리 측정하였고, 거리 측정 정확도는 15 cm(달거리 38만 km로 나눈 통계적 A형의 측정불확도 : 4.0\(\times10^{-10}\), 1\(\sigma\))이였으며[7],
이는 당시 ”크립톤 램프의 특정 스펙트럼선의 진공 파장에 기반을 둔 미터 표준“의 측정 불확도(±4\(\times10^{-9}\), 3\(\sigma\)) 보다 더 작은 값이었습니다. 이때 빛의 속력은 1958년 마이크로파 간섭계를 이용한 측정값 (299 792 500 ± 100) m s-1(통계적 A형의 측정불확도 : 3.3\(\times10^{-7}\), 1\(\sigma\))를 사용하였습니다.[8] 달거리 측정값이 빛의 속력의 값에 의존하므로 보다 정확한 빛의 속력의 값이 필요하였습니다.
최근, 가장 진보된 달거리 측정 스테이션인 아파치 지점 관측소(APOLLO, 텍사스 오스틴 대학의 맥도날드 관측소)는 그 이후, 3.5 미터 망원경과 532 nm Nd:YAG 레이저(100 ps 펄스 지속 시간, 115 mJ / 펄스, 반복률 20 Hz)로 구성된 측정 시스템으로 개선한 후, 달까지 거리 측정의 통계적 A형 측정 불확도, ± 1.1 mm(상대측정 불확도 : 2.9\(\times10^{-12}\))를 얻을 수 있었습니다.[9] [10]
달까지의 거리 측정은 장거리에서의 왕복 시간 측정이고, 그 중간 경로가 거의 진공에 가까워 공기 굴절률 영향이 작으므로, 이와 같이 정확한 측정할 수가 있었습니다.
그러나, 실제 지구상에서의 어떤 거리나 길이를 빛의 이동 시간의 직접 측정하는 방법은 대기의 굴절률, 불균질성 및 가변성 때문에 측정 불확도에 한계가 있으며, 빛이 너무 빠르기 때문에 극히 짧은 시간을 측정해서 길이를 아는 방법은 정교한 광 펄스의 시간 측정 장치로도 어려운 기술입니다.
그러므로 다른 대안의 측정법으로 빛의 이동 시간의 간접 측정법인 간섭계를 이용한 길이 측정에 대해 이야기하겠습니다.
3-1-2. 빛의 이동 시간 간접 측정법(광 간섭계)
일반적으로 백 미터 미만의 길이를 측정하는 경우뿐만 아니라 정확하게 길이를 측정하기 위해서는 간섭계를 사용합니다.
그 예로서, 2015년 9월, 4 km의 길이의 간섭 팔를 갖는 마이켈슨형의 최첨단의 레이저 주파수제어 간섭계를 사용한 최초의 중력파 측정이 이루어졌습니다. 2개의 블랙홀이 하나로 병합되면서 태양의 3배 질량에 상당하는 에너지가 중력파로 변환되었다고 하는데, 공간이 왜곡되어 지구상에서 \(10^{-21}\) 정도의 상대적 스트레인의 크기를 갖는 중력파 신호를 최초로 관측하고, Caltech(미국)의 바리시B. C. Barish, 서런Kip. S. Thirne, MIT의 바이스R. Weiss등은 2017년 노벨 물리학상을 수상한 바 있습니다.[11]이처럼 극초고감도의 길이 관련량의 측정은 간섭기술이 아니면 거의 어려운 일인 것입니다.
광학 간섭계는 빛의 중첩(간섭)을 기반으로 하는 측정 방법입니다. 빛은 측정 경로(z 방향으로 정의)를 따라 전파되는 단일 파장을 갖는 평면 전자기파로 간주합니다. 간섭 현상을 이해하기 위해 간단한 코사인 신호로 광의 전기장을 표현하면, 다음과 같습니다.
\(E\left ( z,t \right )= A\bullet cos \left ( \varphi \right ) = A\bullet cos\left ( k\bullet z+\delta \right )\)
여기서, A 는 전기장의 진폭, \(\varphi\)는 위상, \(\omega\) 는 각 주파수, k는 파수이며, \(\delta\)는 초기 위상입니다. 파장 \(\lambda\), 빛의 속도 c, 주파수 \(\nu\) 및 파수 k 사이의 관계는 다음과 같이 주어집니다.
\(k = 2\pi /\lambda\) 및 \(c= \nu \bullet \lambda\)
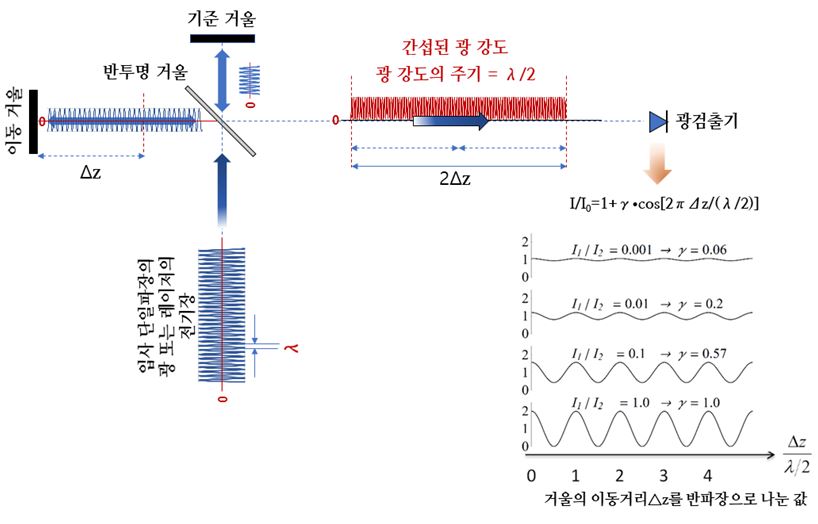
길이측정 간섭계를 나타낸 [그림6] 에서는 [그림4]와 같은 펄스 광이 아닌 연속적으로 발진하며 하나로 파장으로 안정화된 광을 렌즈를 이용하여 평행 광으로 만들어 사용합니다.
입사된 광(광강도 : \(I_{0}\))이 반투명거울에서 반반으로 나누어져 그 반은 기준 거울에서 반사하고, 그 반은 광로의 길이가 다른 이동 거울을 입사한 후 다시 반사합니다. 되돌아온 두 광은 반투명거울에서 합쳐져 광 간섭이 일어나고 광검출기 위치에서는 광 경로차를 만들고 그에 상당하는 광 위상 차이가 발생하며, 이동 거울의 거리에 따라 광 강도가 변화를 하게 되는데 광검출기에서 이 변화를 측정하게 됩니다.
입사한 한 광이 광검출기에 도달할 때, 다른 길이를 이동한 광과의 경로 차이에 때문에 생기는 시간 지연에 대한 광 강도는 다음과 같이 됩니다.
\(I = I_{0}\left [ 1+\gamma \bullet cos\left ( 2\pi \Delta z/\left ( \lambda /2 \right ) \right ) \right ]= I_{0}\left [ 1+\gamma \bullet cos\left ( \Delta \varphi \right ) \right ]\)
여기서, 검출된 광 강도의 가시도 \(\gamma\) 는 되돌아온 두 광의 강도 비\(\left ( I_{1}/I_{2}\right )\) 와 관련이 있습니다. [그림6]의 오른쪽에는 이것을 나타내었습니다. 이동길이 \(\Delta z\)와 이에 상응하는 광 강도의 위상 차이 \(\Delta \varphi\) 사이의 관계식인 위의 식을 이용하여 길이 측정을 실현할 수가 있습니다.
위의 식에서 오른쪽 두 항의 코사인의 위상값을 비교해 보면 다음과 같이 됩니다.
\(\Delta\varphi = 2\pi \Delta z/\left ( \lambda /2 \right )\)
\(\Delta z = \left ( \Delta \varphi /2\pi \right )\bullet \left ( \lambda /2 \right )= \left ( n+\varepsilon \right )\bullet \left ( \lambda /2 \right )\)
측정할 이동 길이 \(\Delta z\)는 위상 측정장치에서 측정된\(\Delta \varphi\)값을 2\(\pi\) 로 나눈 값, \(\Delta \varphi /2\pi\) (\(\Delta \varphi /2\pi\)은 자연수이며, 정수 n과 소수 \(\varepsilon\) 의 합, \(=\left (n+\varepsilon \right )\)으로 나타낼 수가 있으며)에 반파장 \(\lambda/2\)을 곱하여 얻을 수가 있습니다.
정밀한 위상측정 전자장치를 사용하면, 위상값의 1/1,000 정도(\(\varepsilon\)를 1/1,000)까지는 측정할 수 있으므로, 헬륨-네온레이저(파장 633 nm)를 사용한 레이저 간섭계에서는 (633 nm/2)\(\bullet\) (1/1,000) \(\approx\)0.3 nm의 분해능으로 측정이 가능합니다.
또, 이동 거울의 좌우 이동 방향에 따른 부호 값을 갖는 이동길이를 측정하기 위해서는 기준 거울에 적당한 높이의 차이를 갖는 스텝형의 두 반사면을 만들고 각각으로 기준면으로 하는 두 간섭 신호를 만들거나 적절한 편광 소자들을 사용하여 간섭의 광 강도의 신호가 기존 코사인 신호와 위상이 90도 다른 또 다른 하나의 사인파의 신호를 만들고 이 두 신호를 이용하여, 2-방향성 계수기를 이용하면 좌우의 방향을 알 수 있는, -와 + 부호를 갖는 거리 값을 읽을 수 있게 됩니다.
3-1-3. 공기 굴절률 측정과 길이 측정값 보정
실제 공기 중에서 광을 이용한 길이 측정을 할 때에는 파장 \(\lambda\) 가 진공 파장이 아니기 때문에 다음과 같이 굴절률 보정하여 사용하여야 합니다.
\(\Delta z= \left [ \left ( \lambda /2 \right )\bullet \left ( n+\varepsilon \right ) \right ]/n_{p}\)
간섭계를 진공이 아닌 대기 중에서 사용하기 때문에 공기 굴절률(위상 굴절률, \(n_{p}\))은 1 이 아니며, 사용하는 파장, 대기의 온도, 압력, 습도 및 대기 중의 탄산가스의 양 등의 값에 따라 바뀝니다. 이들의 관계식을 처음으로 공식화한 것을 Edlen-공식[12]이라고 합니다. 그 후 여러 연구자들의 연구결과를 취합하여 만든 Cidder-공식이나 수정된 Edlen-공식이 사용되고 있는데 미국, 국립표준기술연구소(NIST)에서는 2001년부터 이들 공식을 종합하여 각 변수에 따른 굴절률 변환 공식을 웹[13]에 공개하고 있습니다.
다음의 두 가지 방법으로 공기 굴절률을 측정할 수 있습니다.
(i) 압력, 온도, 습도 및 공기 중의 \(CO_{2}\) 함량 등에 대한 측정한 값을 사용하여 n 에 대한 굴절률 실험식을 이용하여 계산에 의하거나
(ii) 측정 경로를 따라 굴절률을 직접 측정 (공기 굴절계)
방법 (ii)는 양쪽 면이 평행한 관의 양 단면을 평행한 광학유리 판을 부착하여 빛이 관통할 수 있도록 만든 평행한 진공 유리관을 빛의 측정 경로에 동축으로 배치하고 유리관의 알려진 기하학적 길이에 대해, 공기 중의 빛의 경로와 진공 상태의 빛의 경로 사이의 차이를 측정하여 굴절률 값을 측정할 수 있습니다.
위상 굴절률 값의 한 예로서, 표준 조건 (대기압 101,325 Pa, 공기 온도 20 oC, 상대습도 50% RH 및 공기 중의 이산화탄소량 400 ppm\(CO_{2}\))에서 빛의 파장 633 nm에 대해 공기의 위상 굴절률은 약 1.000 271 37입니다. (앞서 말씀드린 바와 같이, 펄스 광이나 변조된 광을 사용하는 장거리 측정에서는 군 굴절률을 사용하여야 하며, 이때, 군 굴절률은 1.000 279 27 입니다.)
따라서, 공기 중의 길이 측정에서 위상 굴절률을 무시하면 1 m 에서 약 0.27 mm의 효과가 나타나며, 측량용 거리 측정기나 펄스 광원을 이용한 거리 측정을 할 경우에는, 1 m 에서 약 0.28 mm의 차이가 나는 효과가 나타납니다.
표준 실험실 조건에서 환경 매개변수의 변화에 대한 공기 굴절률 (파장 633 nm)의 감도는 [표2] 에 나와 있습니다. 예로서, [표2] 에서 온도 감도를 고려해 보면, 길이 측정에서 대기온도 값이 20 oC에서 +1 oC가 올라가면, 길이의 측정값은 –0.92\(\times10^{-6}\) (1 m 에 0.92 μm) 만큼 줄어들게 됩니다.
[표2] 공기 굴절률의 표준상태에서의 감도 계수
| 영향 인자 | 표준 상태에서의 값 | 공기 굴절률 감도계수 | |
| 1 | 대기온도 | 20 oC | -9.2\(\times10^{-7}\) \(K^{-1}\) |
| 2 | 대기압 | 101,325 Pa | +2.7\(\times10^{-9}\) \(Pa^{-1}\) |
| 3 | 대기중 \(CO_{2}\) 함량 | 400 ppm | +1.4\(\times10^{-10}\)(ppm)\(^{-1}\) |
| 4 | 습도 | ||
| 4-a | 상대습도 | 50 %RH | -8.7\(\times10^{-9}\)(%RH)\(^{-1}\) |
| 4-b | 이슬점 | 9.27 oC | -1.5\(\times10^{-8}\) \(K^{-1}\) |
| 4-c | 수증기압 | 1168 Pa | -1.8\(\times10^{-10}\) \(Pa^{-1}\) |
기압과 기온은 높은 감도계수를 갖는데, 상대적으로 큰 일교차로 인한 온도 변화는 가장 중요한(가장 민감한) 변수임을 알 수 있습니다. 이상에서는 공기 굴절률에 의한 길이 측정에서의 보정과 측정오차에 대해 말씀드렸습니다.
한편, 줄자나 자와 같이 등 간격의 눈금선들이 그으져 있는 것을 선기준물이라고 하고, 강철이나 세라믹 등으로 양 단면을 평행한 광학 거울면으로 가공해 놓은 게이지블록을 길이의 단면기준물이라고 합니다. 이들 길이를 측정할 수 있는 간섭계를 각각 동적 간섭계와 정적인 간섭계로 나눌 수가 있는데, 이에 대한 자세한 기술은 [부록Ⅰ] 에 나타내었습니다.
이들 간섭계의 광원으로 사용하는 주파수(또는 진공파장)를 안정화한 레이저를 사용하면 정확한 길이 및 관련량 들을 측정할 수가 있습니다.
이와 같이, 미터의 실제 구현이나 간섭계를 사용한 길이 측정을 위하여, 국제도량형위원회에서 추천한 표준기준주파수(CIPM LoF, List of Standard Reference Frequency Values)와 SRS(초의 2차 표현) 표준 주파수 값을 단일 목록으로 작성하여 사용할 것을 추천하고 있습니다. 추천한 레이저들에 대한 상세한 내용을 [부록Ⅱ]에 게재하였습니다.
4. 빛의 속력 측정과 물리 상수
빛을 이용한 길이 측정에서는 빛의 속력의 값이 아주 중요합니다. 그러므로, 오랫동안 과학계에서는 빛의 속력 측정을 위한 다양한 방법과 아이디어들을 동원하여 빛의 속력의 값들을 찾아내었습니다. 최종적으로는 1972년, 미연방표준국의 NBS의 에벤슨 그룹이 메탄안정화헬륨-네온레이저 (\(CH_{4}/He-Ne\; Laser\), 3.39 μm)의 주파수를 직접 측정하고 또 크립톤램프의 표준파장선을 기준으로 하는 간섭계로 파장을 측정하여 두 값을 곱한 빛의 속력 c을 측정함으로서, 기존의 빛의 속력에 대한 많은 연구 결과에 의한 측정값들은 이제 역사적인 값이 되었습니다. (참고 : 물리학에서는 ”speed of light“를 ”빛의 속력“으로 번역하고, 빛의 속력은 크기만 있고 방향이나 시작점이 없는 스칼라이며, 시작점과 방향과 크기를 모두 갖는 벡터량인 ”velocity of light“ 를 ”빛의 속도“로 번역합니다.)
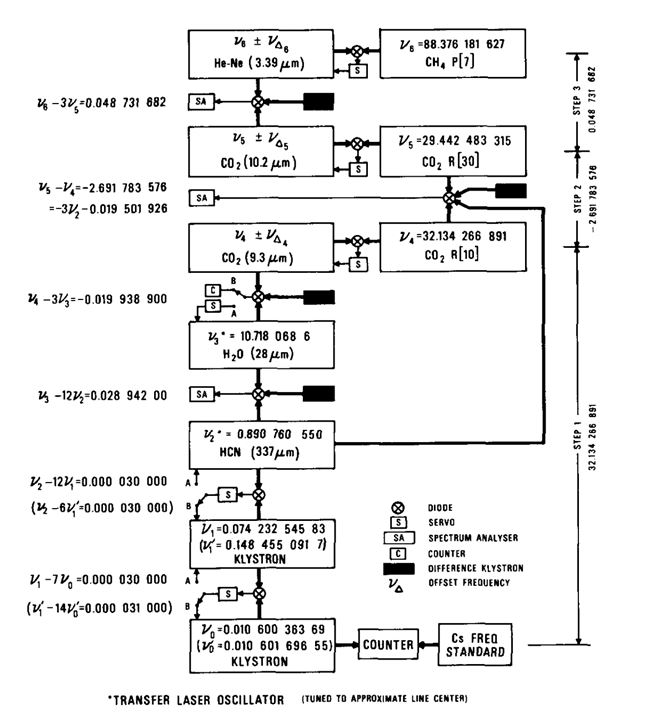
에벤슨그룹이 사용한 적외선 광주파수 측정시스템[그림7]을 “주파수합성체인frequency synthesic chain이라는 하는데, 적당한 점-접촉 믹서 다이오드를 사용하면, 안정화된 레이저들의 연결 체인과 마이크파에서 동작하는 클라이스트론 주파수 소스들을 이용하여 NBS 주파수 표준에서부터 29 THz(10.3 μm)의 \(CO_{2}\)레이저, 그리고 88 THz(3.39 μm)의 메탄 안정화 레이저까지 직접 고조파 생성 및 주파수 혼합이 가능하게 됩니다.
이들은 5종류의 레이저와 5개의 클리이스트론을 3단계 측정 과정에서 사용하였습니다. 세슘 원자시계에서 나오는 10 MHz 주파수 기준신호를 시간 베이스로 한 보간-주파수 계수기로 X-밴드의 클라이스트론 주파수를 측정하고 또, 그 하모닉스를 이용하여 그 위의 클라스트론의 주파수에 위상 동기시키고, 같은 방법으로 차례로 HCN-레이저, \(H_{2}O\)–레이저, \(CO_{2}\)–레이저들을 안정화하여 최종적으로 메탄 안정화 레이저 주파수에 동기하여 주파수를 측정하여 다음과 같은 값을 갖는다고 보고하였습니다.
\(\nu\left ( CH_{4} \right ) = \left ( 88\; 376\: 181\: 627\: \pm \: 50 \right )\) kHz \(\left (\delta \nu /\nu = \pm\: 6\: \times 10^{-10}\right )\)
이들 그룹이 사용한 시스템은 고정밀의 주파수 및 위상 제어기술과 여러 개의 주파수 기준들이 사용된 거대한 측정시스템이였습니다.
오늘날에는 레이저 주파수 제어기술이 발전하여 이 주파수합성체인을 대체하여, [그림 8]과 같은 팸토초 레이저를 사용한 레이저주파수콤laser frequency comb이라고 하는 1 대의 레이저광 주파수 측정시스템으로 모든 레이저의 광주파수를 측정할 수가 있게 되었습니다. 이에 대한 공로로 2005년 미국 JILAJoint Institute for Laboratory Astrophysics의 존 홀 박사와 독일 Max Plank 연구소의 핸쉬 박사가 공동으로 노벨상을 수상한 바 있습니다.
빛의 속력을 측정할 때 가장 큰 오차의 요인은 당시 길이표준으로 사용하는 크립톤 파장 값의 불확도와 그 스펙트럼선의 비대칭성이였습니다.
에벤슨그룹은 파장 측정 기준으로 사용한 크립톤 파장값(\(\lambda\) = 605 780. 210 6 pm)을 임의로 무게중심값으로 보고 메탄안정화헬륨-네온레이저 파장값을 측정하였습니다.
\(\lambda\left ( CH_{4} \right ) = \left ( 3\; 392\: 231.\: 376\: \pm \: 0.012 \right )\) pm \(\left (\delta \lambda /\lambda = \pm\: 3.5\: \times 10^{-9}\right )\)
이 두 값, 즉 주파수와 파장을 곱하여 빛의 속력을 계산하여 다음과 같은 값을 얻었다고 발표하였습니다.[14][15][16]
\(c=\lambda \cdot \nu = \left ( 299\: 792\: 456.2\: \pm \: 1.1 \right )\) m s-1 \(\left (\delta c /c = \pm\: 3.5\: \times 10^{-9}\right )\)
여기서, 보고한 상대불확도, \(\delta c/c\) 의 불확도는 크립톤 램프의 파장 불확도에 기인하는 값입니다.
또, 이들은 파장 측정에서 기준의 크립톤 파장 값을 크립톤 스펙트럼의 피크 값을 대표한 값이라고 한다면, 메탄 안정화 레이저의 파장 값은 다음과 같다고 보고하였습니다.
\(\lambda\left ( CH_{4} \right )_{peak} = \left ( 3\; 392\: 231.\: 404\: \pm \: 0.012 \right )\) pm \(\left (\delta \lambda /\lambda = \pm\:3.5\: \times 10^{-9}\right )\)
\(c=\lambda \cdot \nu = \left ( 299\: 792\: 458.7\: \pm \: 1.1 \right )\) m s-1 \(\left (\delta c /c = \pm\: 3.5\: \times 10^{-9}\right )\)
이들 그룹이 최초로 발표한 빛의 속력의 측정값(299 792 456.2 ± 1.1 m s-1)은 우리가 사용하고 있는 299 792 458 m s-1) 과 다르다는 것을 알고 궁금할 것입니다.
아래에 빛의 속력의 값이 결정되는 과정을 소개하겠습니다.
에벤슨그룹 NBS(B)의 빛의 속력 측정이 보고되고, 국제도량형위원회 CIPM의 미터정의자문회의 CCDM의 조속한 연구 종용에 따라 각국의 표준연구기관에서는 메탄 안정화 헬륨-네온 레이저의 파장 측정 등을 빠르게 진행하였고, NRC(캐나다), BIPM, NPL(영국), NBS(G: Gaitherburg 미국) 등에서도 파장 측정에 관한 연구결과들을 보고하였습니다. 에벤슨그룹 NBS(B)의 파장 측정값은 두 파장 값의 평균값이 받아들여졌습니다.
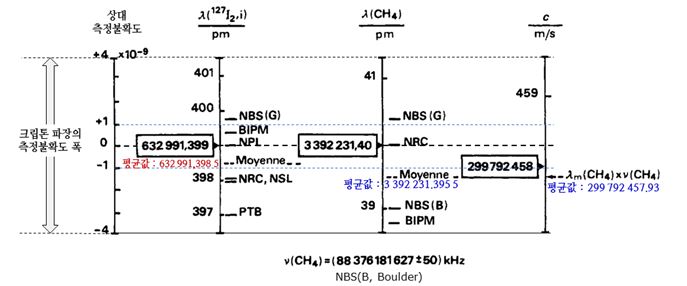
에벤슨, (레이저주파수콤의 업적으로 노벨물리학상을 수상한) 존 홀 등 빛의 속도 측정에 관련한 표준기관의 과학자들이 참석한 1973년 CCDM회의에서 BIPM국장 테리앙 J. Terrien은 각국 표준기관들이 보고한 측정 데이터[표3]들을 취합 · 정리[그림9]하여 발표하고, 같은 회의에서 만장일치로, 다음과 같은 값들을 결정하였습니다.[17][18]
각국의 관련 연구기관에서 측정한 요오드안정화헬륨-네온레이저, 메탄안정헬륨-네온레이저의 파장값을 평균하고 그 값을 반올림을 하여 각각, 632 991.399 pm 와 3 392 231.40 pm 로 할 것으로 결정하고, 에벤슨그룹이 측정한 메탄안정화레이저의 주파수 88 376 181 627 kHz(\(\delta\nu /\nu \: =\: \pm \, 6\times 10_{}^{-10}\))의 값을 이용하여, 파장의 평균값과 주파수 값을 곱하여 빛의 속력의 값을 299 792 457.9 m s-1으로 계산하고, 이를 반올림한 정수로 299 792 458 m s-1로 정할 것을 미터정의자문회의 1973년 회의에서 만장일치로 결정하고, 그 파장 측정의 기준이였던 크립톤 파장의 상대불확도와 같은 \(\pm\: 4\times 10^{-9}\) 로 빛의 속력의 불확도(\(\pm \: 1.1\) m s-1를 나타내었습니다.
[표3] 여러 실험실의 메탄안정화헬륨-네온레이저(CH4, P(7), Band \(\nu\)3) 파장 측정
|
|
연구기관 |
진공파장(\(\lambda\) ) 값, pm |
불확도, pm |
|
1 |
NBS(G) |
3 392 231.404(a, b) |
\(\sigma_{m}\) = 0.013 |
|
2 |
NBS(B) |
3 392 231.390 (a) |
\(\sigma_{m}\) + \(\delta\) = 0.012 |
|
3 |
NRC(캐나다) |
3 392 231.40 (b, c) |
\(\sigma_{m}\) = 0.02 |
|
4 |
BIPM |
3 392 231.388 |
\(\sigma_{m}\) + \(\delta\) = 0.017 |
|
파장값 |
평균값 |
3 392 231.395 5 |
|
|
반올림값 |
3 392 231.40 |
|
|
(주) \(\sigma_{m}\)은 평균값의 표준편차, |
그 후, 1975년 제15차 국제도량형총회 CGPM에서의 빛의 속력에 대한 권고값(CR, 103 및 Metrologia, 1975, 11, 179-180)의 결의사항 2 에 따라, 빛의 속력 c = 299 792 458 m s-1 값을 사용할 것을 결의하였습니다. 즉, 측정불확도가 없는 빛의 속력 값으로 나타낸 것입니다. 이것으로 물리상수 빛의 속력 값이 정해진 것입니다.
이상과 같은 과정을 거쳐서 과학계의 오랜 숙제였던, 자연의 물리상수 중에 가장 중요한 빛의 속력에 대한 고정된 값이 결정된 것입니다. 이후 빛의 속력의 값은 국제단위계 SI뿐만 아니라 과학의 전반에 걸쳐서 지대한 영향을 미치게 되었습니다.
빛의 속력 값이 정해지고 빛의 속력에 근거한 미터의 정의가 결정되는 데에는 인류가 발명한 ”레이저“라는 특별한 빛의 탁월한 특성을 이용할 수 있었기 때문에 가능하였습니다.
오늘날의 과학문명에서 미터(m)와 레이저의 쓰임은 이루 다 헤아릴 수가 없습니다.
大哉라, 미터 표준의 쓰임이여, 그 오묘할 진져 !
부록Ⅰ. 길이 측정을 위한 동적 및 정적 간섭계
길이의 선기준물인 줄자나 자와 같이 등 간격의 눈금선들이 그으져 있는 것들의 길이를 측정하기 적합한 동적 간섭계(광학적 기본 구성은 본문의 [그림3]과 같습니다.)가 있고, 단면기준물인 게이지블록의 길이를 측정하기 위해 고안한 정적인 간섭계가 있습니다.
본문의 [그림6] 에서와 같은 간섭계의 이동 거울에 현미경을 부착하고 그 아래 설치한 선기준물의 눈금의 중앙부를 현미경으로 관측할 수가 있도록 만들면, 자와 같은 선기준물들을 눈금 간격을 측정할 수 있는 간섭계가 될 수 있습니다. 이때, 현미경은 이동 거울과 함께 눈금 사이를 이동하면서(동적), 눈금의 중심간의 간격도 측정할 수가 있게 됩니다. 아래 [그림Ⅰ-1]은 반도체 웨이퍼의 위치를 제어하는 스테이지의 xy축의 2차원적인 이동 거리를 측정할 수 있는 상용의 동적인 레이저 간섭계 사진입니다.
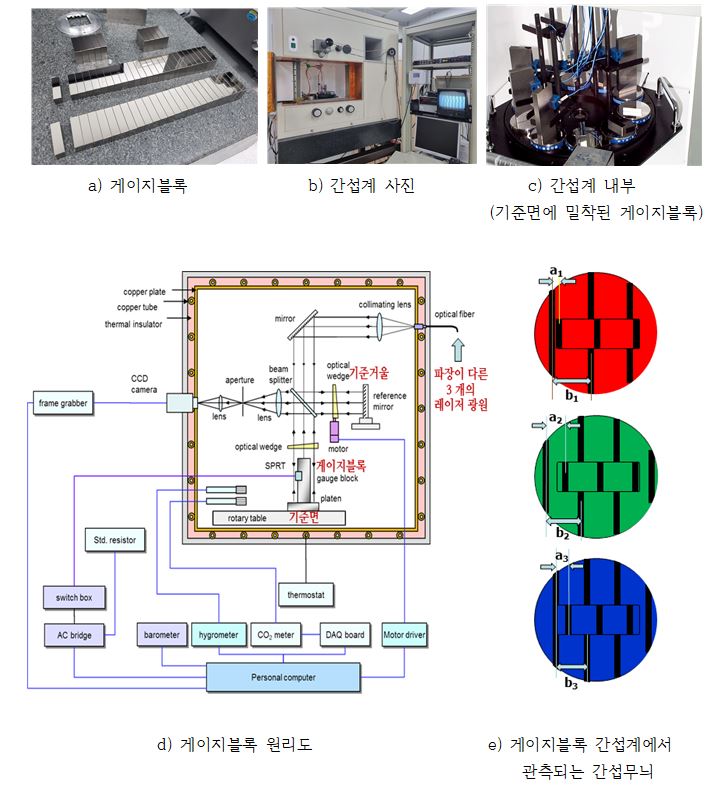
한편, 동적 간섭계와는 달리, 정적인 간섭계는 이동하는 부분이 없이 기준 거울과 측정하고자 하는 면들이 모두 정적으로 고정되어 있습니다. 대표적인 정적간섭계인 게이지블록간섭계를 [그림Ⅰ-2]에 나타내었습니다.
[그림Ⅰ-2]의 간섭계 [그림d]를 보면, 게이지블록의 아랫면은 기준면에 광학적으로 부착되어 있어 그 사이의 갭은 nm 이하 값으로 알려져 있는데 기준면은 게이지블록과 같은 재질의 금속제의 광학적 평면을 갖고 있습니다.
이들 둘 사이에는 반데르발스 힘과 물의 수소 결합에 의해 부착된다고 알려져 있으며 진공이 유지될 정도로 강한 힘으로 밀착됩니다. 그러므로, 게이지블록의 아래면과 밀착된 기준면은 동일한 평면으로 간주하고 간섭측정을 하게 됩니다.
[그림Ⅰ-2.e]에서 둥근원 안의 간섭무늬는 기준면(게이지블록의 아랫면과 기하학적으로 동일면으로 간주됩니다.)과 기준 거울 사이의 간섭무늬이며 직사각형 안의 간섭무늬는 게이지블록 윗면과 기준 거울 사이의 간섭무늬이다.
그림에서와 같이 간섭무늬를 CCD 카메라의 이미지로 얻었을 때, 게이지블록의 길이, \(L_{i}\) 은 다음과 같습니다.
\(L_{i}= \left [ \left ( \lambda _{i}/2 \right )/n_{pi} \right ]\bullet \left ( n_{i}+a_{i}/b_{i} \right )\) , i = 1, 2, 3
여기서 i = 1, 2, 3 값을 가지며 서로 다른 3개의 파장의 레이저 광원 1, 2, 3 을 나타냅니다. \(n_{p_{i}}\) 는 각 파장에서의 공기의 위상 굴절률이며, \(n_{p_{i}}\) 의 값들 결정하기 위해서 본문에서 설명한 바와 같은 두 가지 방법 중의 하나로 굴절률을 측정합니다.
\(\lambda _{i}\) 는 이들 레이저 광원의 진공파장 값들이며, \(n _{i}\) 는 정수이며, [그림Ⅰ-2.e]에서 보는 바와 같이, \(a _{i}\), \(b _{i}\) 는 각각 간섭무늬 어긋남과 간섭무늬의 간격입니다.
측정실험에서 정수 \(n _{i}\) 은 측정할 수가 없으므로 합치법이라는 방법으로 결정합니다. 각 파장에 따른 길이 측정값 \(L _{1}, L _{2}, L _{3}\) 의 평균값으로 게이지 블록의 길이 L을 결정하게 됩니다.
부록Ⅱ. 간섭측정 등에 사용되는 레이저 복사선의 목록, CIPM LoF
간섭계에서는 파장(주파수)을 기준으로 하여 길이를 측정하므로 파장이 안정화된 레이저 광원을 사용하여야 합니다. 미터의 실제 구현이나 간섭을 이용한 길이 측정을 위하여, 국제도량형위원회에서 추천하는 표준기준주파수(CIPM LoF, List of Standard Reference Frequency Values)와 SRS(초의 2차 표현) 표준 주파수 값을 단일 목록으로 작성하고, 새로운 후보 표준 주파수를 추천하여 주기적으로 업데이트하여 공개하고 있습니다.[20]
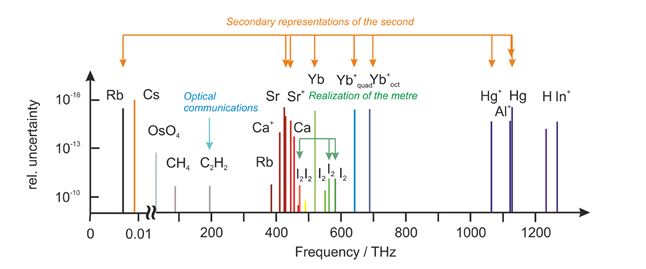
[그림Ⅱ-1]은 미터 실현, 광통신 파장표준 및 SRS(초의 2차 표현)으로 사용되는 CIPM 추천 주파수 목록(2017년 기준)을 그림으로 나타내었으며, 또 [표Ⅰ-1]에는 LoF의 일부를 나타내었습니다.
[표Ⅰ-1] 미터정의 실현 및 광통신표준을 위한 레이저 주파수(파장) 목록(CIPM LoF)
|
용도 |
광 주파수(THz) |
부분 불확도 |
진공파장 nm |
레이저/흡수선 |
|
미터정의 |
494.886 516 4 |
3.9\(\times 10^{-9}\) |
605.780 210 3 |
\(_{}^{86}\textrm{Kr},\; \; 5 d_{5}-2p_{10}\) |
|
473.612 7 |
1.5\(\times 10^{-6}\) |
632.9908 |
He-Ne, 비-안정화 Ne, \(3s_{2}-2p_{4}\) |
|
|
473.612 353 604 |
2.1\(\times 10^{-11}\) |
632.991 212 58 |
He-Ne/\(I_{2}\), |
|
|
551.580 162 400 |
4.5\(\times 10^{-11}\) |
543.515 663 608 |
He-Ne/\(I_{2}\), \(b_{10},\;R\left ( 106 \right ), 28-0\) |
|
|
563.260 223 513 |
8.9\(\times 10^{-12}\) |
532.245 036 104 |
2f(Nd-YAG)/\(I_{2}\), |
|
|
광통신 |
194.369 569 384 |
2.6\(\times 10^{-11}\) |
1 542.383 712 38 |
\(_{}^{13}\textrm C{_{2}}H_{2}\), \(P\left ( 16 \right ) \; \left ( \nu _{1} +\nu_{ 2}\right )\) |
미터 실현을 위한 추천된 레이저 주파수 표준 값의 CIPM LoF 목록의 일부 광원을 사용하는 각국의 국가표준 실험실(예, 한국표준과학연구원, 길이표준그룹)은 최소한 10년마다 한번은 ‘국제 주요 비교 프로그램 CCL-K11’에 참여하여야 합니다.
이 비교 실험으로 명시된 불확도 내에서 관련 광주파수 표준을 실현하는 실험실의 능력을 테스트받게 됩니다. 이것으로 그 실험실이 유지 관리하는 광주파수 표준이 국제적 표준과 동등함을 인정받게 됩니다.
참고문헌
-
국제단위계(SI) 제9판(한국어판), KRISS/SP—2020-011, 한국표준과학연구원 발행, 2020
-
SI Brochure, 9th edition(2019), Appendix 2, Mise en Pratique for the Definition of the METRE in the SI, Consultative Committee for Length, 2019
-
Fritz Riehle, Patrick Gill, Felicitas Arias and Lennart Robertsson, The CIPM list of recommended frequency standard values: guidelines and procedures, Metrologia 55, 188, 2018
-
Le Bureau International Des Poids et Mesures 1875-1975, BIPM, 1975
-
小泉袈裟勝 度量衡의 歷史 原書房, 1977
-
CODATA Recommended Values of the Fundamental Physical Constants: 2010
- P. L. Bender, D. G. Currie, R. H. Dicke, D. H. Eckhardt, J. E. Faller, W. M. Kaula, J. D. Mulholland, H. H. Plotkin, S. K. Poultney, E. C. Silverberg, D. T. Wilkinson, J. G. Williams, C. O. Alley, SCIENC 182, No. 4109, 229-238. 19, October 1973, The Lunar Laser Ranging Experiment.
- K. D. Froome, A New Determination of the Free-Space Velocity of Electro-magnetic Waves, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 247, No. 1248 (Sep. 9, 1958), pp. 109-122
- T. W. Murphy, Lunar laser ranging: the millimeter challenge, Rep. Prog. Phys. 76 (2013) 076901 (21 pp) 2013
- T. W. Murphy Jr, et. al., ‘APOLLO: millimeter lunar laser ranging’, Class. Quantum Grav. 29 (2012) 184005 (11 pp)
- B. P. Abbott, et al., Observation of Gravitational Waves from a binary black hole merger, Phys. Rev. Lett. 116, 061102, 2016
- B. Edlén, "The refractive index of air," Metrologia 2, 71-80 (1966)
- NIST, Engineering Metrology Toolbox, https://emtoolbox.nist.gov/Wavelength/Edlen.asp
- K.M. Evenson, J. S. Wells, F. R. Peterson, B. L. Danielson and G. W. Day, R. L. Barger and J. L. Hall, Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser, Phy. Rev. Lett. V29, 19, 1346, 1972
- K.M. Evenson, J. S. Wells, F. R. Peterson, B. L. Danielson and G. W. Day, Accurate frequencies of molecular transitions used in laser stabilization: the 3.39 μm transition in CH4CH_{4}and the 9.33 μm and 10.18 μm transitions in CO2 CO_{2}, Appl. Phys. Lett., Vol. 22, No. 4, 192, 1972
- R. L. Barger, J. L. Hall, Wavelength of the 3.39 μm laser-saturated absorption line of meyhane, Appl. Phys. Lett., Vol. 22, No. 4, 196, 1972
- J. Terrien, Wavelength standards, optical frequency standards, and the velocity of light, Nouv. Rev. Optique, 1973, t. 4, no 4, pp. 215-220, Bureau International des Poids et Meaures Pavillon de Breteuil, F-92310, Sevres
-
Comite International des Poids et Mesures, Comite Consultatif pour La Definition du METRE, 5e Session-1973 (13-15 Juin), Bureau International des Poids et Meaures Pavillon de Breteuil, F-92310, Sevres
- K.M. Baird, D.S. Smith, W.E. Berger, Wavelength of The CH4CH_{4} line at 3.39 μm, Opt. Comm. 7, 2, 107, 1973
- BIPM 2018 Recommended Values of Standard Frequencies,
www.bipm.org/en/publications/mises-en-pratique/standardfrequencies.html