나노계측학을 위한 X-선 간섭계와 실리콘 격자상수

2019년 SI 단위계가 새로 제정됨에 따라서, 길이자문위원회^{CCL, Consultative Committee for Length}에서 미터 정의 실현을 위해 추천하는 일차적인 방법 두 가지를 이전 글에서 살펴보았습니다. 각각 빛의 이동시간을 직접 측정한 뒤 빛의 속력을 곱하는 방법과 광주파수 안정화 레이저를 사용한 간섭계를 이용하는 측정하는 방법으로, 이전 글 “미터의 정의와 레이저”에서 확인할 수 있습니다.

이번 글에서는 나노계측학에서 미터 정의를 실현하기 위한 이차적인 방법에 대해 알아보고자 합니다. 속도(빛의 속력)과 시간(초)을 정확히 정의하거나 파장이 긴(~수백 나노미터) 광 간섭계를 이용하면 길이(미터)를 정의할 수 있지만, 실제로 나노미터 이하의 물체의 길이를 측정하는 데 늘 적합한 것은 아닙니다. 

광속은 299,792,458m/s로 정의되어 있으므로, 단순히 빛과 시계를 이용하여 원자 크기를 표현하는 길이 단위인 옹스트롬(10^-10m)이나 나노미터(10^-9m) 수준에서 길이를 정의하고 측정하려면 시간을 10^-17초나 10^-18초 수준까지 정확히 측정할 수 있어야 합니다. 이는 현존하는 기술로 불가능하지는 않지만 대단히 어렵기 때문에 나노계측학에서 길이를 측정하기 위한 보다 현실적이고, 기술적으로 유용한 이차적인 방법이 필요합니다.

이를 위해 고안된 방법은 단결정 물질의 격자 상수를 정밀하게 측정하여, 이를 나노미터 수준에서 길이의 단위로 사용하는 것입니다. 이때 주로 실리콘 단결정이 사용됩니다. 본 글에서는 (1)실리콘 단결정의 격자상수와 X-선 간섭계를 이용하는 방법, (2)실리콘 격자상수와 (주사)투과전자현미경을 이용하는 방법, (3)실리콘 단원자 계단과 주사탐침현미경을 이용하는 방법[1]에 대하여 살펴보겠습니다.

1. 실리콘 단결정과 X-선 간섭계

실리콘은 현대 반도체 산업의 가장 핵심적인 재료로, 동위원소를 포함한 불순물 정제, 단결정 성장 및 가공 기술이 고도로 발달되어 있습니다. 따라서 동일한 시료를 재현하는 데에 유리하고, 이는 길이의 표준으로 채택하는 데 대단히 유용한 특성입니다.

X-선 간섭계^{XRI, X-Ray Interfeometer}는 주어진 단결정 물질의 격자 간격을 측정하기 위한 기술로 1960년대에 본즈^Bonse와 하트^Hart[2,3]가 처음 제안했습니다. 이들은 진공에서 고전압으로 가속시킨 초고속 전자를 구리로 만든 양극 타겟에 충동시켜 얻은 구리의 특성 X-선인 Kα-선(파장: 0.154 nm)과 실리콘 결정 (220)면의 간격 d₂₂₀(0.192 nm, 브래그 회절각: 23.6°)를 이용해 실험하였습니다. 실험을 통해 X-선 굴절률 측정, 작고 복잡한 물질의 정확한 두께측정, 생물학적 재료의 X-선 위상차현미경, 극히 작은 결정 격자의 뒤틀림 측정, 분산표면의 측정을 실현하였습니다. 또한 몰리브덴의 특성 X-선인 Kα-선(0.0709 nm, 브래그 회절각: 10.6°)를 이용하여 실리콘 격자상수 측정과 길이의 2차 표준을 위한 연구 등도 제안하였습니다.[3]

이후 1973년 NBS(현 NIST, 미국립표준기술원)의 R. D. Deslattes와 A. Henins에 의해 실리콘 격자상수 d₂₂₀가 처음으로 정밀하게 측정되었습니다.[4] 이들은 당시 길이표준이었던 크립톤 램프의 파장에 소급성을 갖는 요오드안정화 헬륨-네온 레이저^{129I2 stabilized He-Ne Laser, k-peak}로 교정한, 네온의 이득곡선 램딥^{Lamb dip}에 주파수 안정화된 헬륨-네온 레이저 파장의 광원을 사용한 파브리-페로^Fabry-Perot 간섭계와 X-선 간섭계를 이용하였습니다.

1990년대에 들어와서 X-선 간섭계를 이용한 연구는 질량 측정표준 연구를 지원하는 아보가드로 상수를 결정하기 위한 대규모 프로젝트의 일환으로, 실리콘 (220) 결정면의 격자 간격 d₂₂₀을 측정하는 방향으로 진행되었습니다.[5,6] 격자상수를 측정하는 것 외에도 불순물 함량 함수의 변동도 조사되었습니다.[7,8] 이들의 연구 결과로 Si d₂₂₀ 격자 간격에 대한 여러 값이 발표되었고[9], 최종적으로 d₂₂₀격자 간격이 CODATA[10,11]에도 게재되었습니다.

X-선 간섭계를 사용한 연구는 아보가드로 상수 측정[12]이나, 미터 정의의 2차적 현시 방법과 함께 새로운 킬로그램의 현시나 밀도 측정표준을 위한 실리콘 단결정의 표준구 연구^{standard sphere} 등 오늘날에도 지속적으로 진행되고 있습니다.[13]

실리콘의 단결정

처음 X-선 간섭계에 실리콘 단결정이 이용된 이래로, 1970년대의 NBS의 측정 이후, 1980년대 초 PTB의 연구실에서도 실리콘 단결정의 d₂₂₀ 격자 간격이 측정되어 길이측정에 대한 참조 표준데이터로 사용하기에 충분하다는 점이 알려졌습니다. 이후 실리콘 (220) 결정면은 X-선 간섭계에서 주로 사용되는 결정면이 되었습니다.[14]

X-선 간섭계 제조에 사용되는 실리콘 단결정은 플로팅존^{floating zone}법으로 성장하여 탄소 및 산소 함량으로 인한 점-결함 농도가 10¹⁵cm^-3 미만인 초순수, 도핑되지 않은 무전위의 실리콘 결정입니다.([그림1]) 불순물 함량은 적외선 또는 질량 분석, 중성자 활성화 또는 X-선 형광분석기, 분광타원기 등을 포함한 다양한 기술을 사용하여 개별적으로 결정할 수 있습니다. 더블 크리스탈 XRT^{Double crystal X-ray topography}는 10^-8의 불확도로 격자 균질성을 검사하는 데 사용할 수 있으며, 사용된 결정은 원하는 경우 격자상수가 알려진 결정과 비교할 수 있습니다.

다이아몬드와 같은 결정구조를 갖는 실리콘 결정은 [그림2]와 같은 정사면체^{Tetrahedral structure} 구조를 기본으로 하는 결정입니다. 14족 원자인 실리콘의 최외각 전자는 4개이고, 이들이 공유결합을 하므로 결정구조는 정사면체^{tetrahedral structure}가 기본 구조(a)이고, 이들이 8개 모여서 만들어진 결정구조가 단위셀을 만듭니다(b, c). X-선 간섭계에서 주로 사용하는 결정면은 (220)면이고, (d)에서는 푸른 선이 결정면을 나타냅니다. 원자 안의 숫자는 바닥 면에서부터 높이를 나타냅니다.

짧은 사선이 (220)결정면이고 인접한 사선까지 거리가 격자상수 d₂₂₀입니다. 격자상수 d₂₂₀로부터 단위셀의 격자상수 a는 a = √8·d₂₂₀로 정해지며, d₁₀₀ = 0.25a와 같은 관계가 있고, 이들 값 역시 참조표준 데이터로 사용될 수 있습니다.

X선 간섭계와 간섭계의 정렬

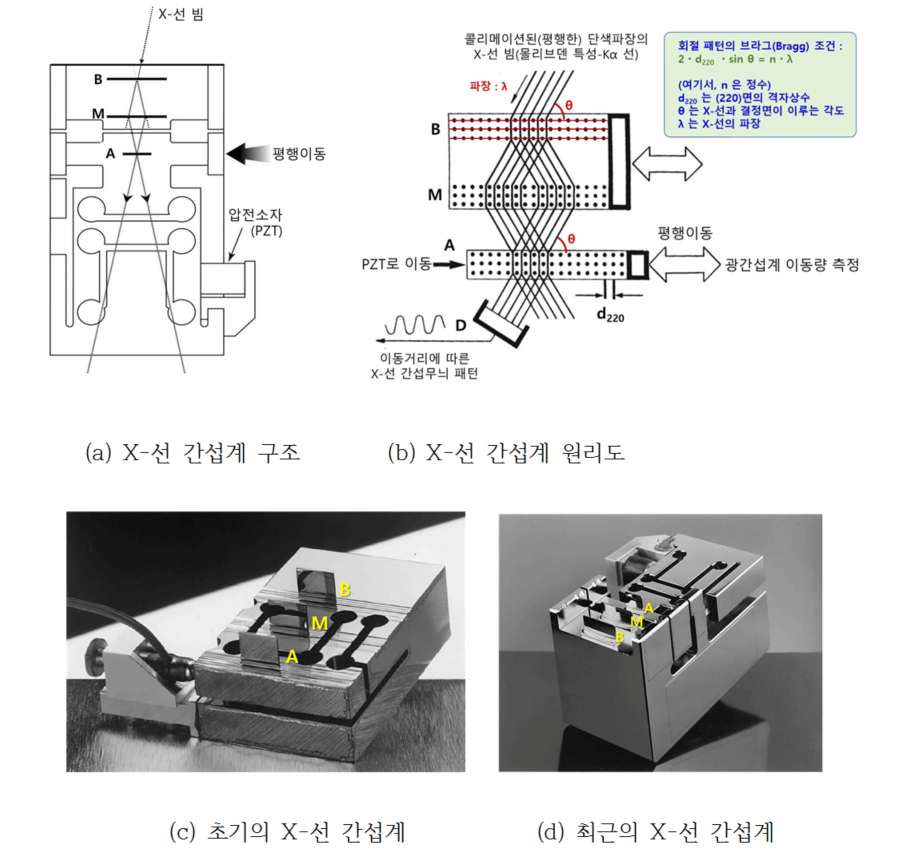
X-선 간섭계에서는 원자의 결정 간격으로부터 나노미터 스케일의 눈금자를 얻을 수 있습니다. 이는 [그림3]처럼 X-선 빔, 모놀리식^monolithic의 3개의 라멜라^{Lamella, 얇은 결정의 판}와 X-선 빔으로 구성되는 X-선 간섭계로 실현할 수 있습니다.

X-선 간섭계의 X-선 회절빔의 광로는 마하-젠더^Mach-Zehnder 광간섭계와 유사한 구조이므로, 초기 개발 시부터 실리콘 단결정 위에 한 덩어리로 만들어진 등간격의 평행한 3개의 라멜라(얇은 결정의 판)를 각각 빔 스플리터(B), 미러(M) 및 분석기(A)라고 명명하고 있습니다.

[그림3]의 (b)는 (a)의 X-선 간섭계 부분만 확대하여 자세히 본 그림입니다. 콜리메이션된 단색파장의 X-선 빔은 빔스플리터 라멜라-B에서 브래그 조건에 맞는 2개의 회절빔이 나오고 이들은 각각 두 번째 라멜라-M에서 다시 각각 2개의 X-선 회절빔을 만듭니다. 안쪽의 2개의 X-선 빔은 분석기 라멜라-A에서 간섭무늬를 만듭니다.

라멜라와 X-선 빔 사이의 각도 θ가 다음과 같은 브래그 조건을 만족하는 각도로 정밀조정되면, 간섭무늬의 간격은 X-선 빔의 파장과 무관하게 격자상수에 비례하는 X-선 간섭무늬를 얻을 수 있습니다.

브래그^Bragg 조건 : 2·d₂₂₀·sinθ = n·λ

라멜라-A 위치에서, 격자 간격 d₂₂₀와 같은 X-선 간섭 줄무늬와 라멜라-A의 격자는 두 개의 같은 간격의 줄무늬가 만드는 무아레 간섭무늬와 같은 줄무늬를 만들어 그 일부가 X-선 검출기에서 검출됩니다. 라멜라-A를 압전소자를 이용하여 평행이동 시키면, X-선 검출기에서는 격자 간격 d₂₂₀의 주기를 갖는 정현파의 강도의 변화를 감지하게 됩니다. 라멜라-A의 이동거리 L은 L = m_x·d₂₂₀ = (m_xi+ε_x)·d₂₂₀과 같이 표현할 수 있습니다. 여기서 m_x는 X-선 검출기에서 계수한 간섭무늬 개수이며, m_xi은 강도 변화의 개수로 정수이며, ε_x는 강도 변화의 위상에 해당하는 소수입니다.

[그림3]의 (c)에서 보는 바와 같이 등간격의 평행한 3개의 라멜라, X-선 선원, 검출기 등의 구성 요소를 정밀하게 정렬해야 하는 까다로운 허용 오차로 인해 모놀리식 구조를 가진 대부분의 X-선 간섭계가 1개의 큰 단결정으로부터 가공됩니다.

간섭계에서 실리콘 단결정 블록을 수백 μm 두께의 등간격의 평행한 라멜라 3개를 남기고 블록의 상단은 가공됩니다.

라멜라의 면은 X선이 회절될 수 있는 결정학적 평면(220)에 수직으로 배열됩니다. 세 번째 라멜라-A 주변에는 라멜라 면에 평행한 힘을 가하면 라멜라-A가 변위되어 평행이동할 수 있도록 결정의 바닥면은 [그림3]의 (c),(d)와 같이 가공됩니다.

몰리브덴의 특성 X-선인 Kα-선을 발생시키고 파라볼릭^parabolic형 반사식 콜리메이터로 평행으로 시준된 X-선 빔을 회절 평면에 대한 브래그 각도 θ로 빔 스플리터 라멜라-B에 입사시켜 첫 번째 라멜라-B에서 회절되어 2개의 회절빔이 나오도록 레이저 간섭계를 사용하여 아주 정밀하게 각도 θ를 정렬합니다.

COXI의 동작원리

X선 간섭계를 이용한 나노길이 및 나노 변위측정이나, 나노미터 변위측정기의 교정을 위해 광간섭계와 결합된 X-선 간섭계^{COXI, Combined Optical and X-ray Interferometer}시스템은 영국의 국립물리연구소 NPL[15,16]이 처음 구축했습니다.

이것은 X-선 간섭계를 사용하여 주파수 안정화 헬륨-네온^He-Ne 레이저의 레이저 파장과 실리콘의 격자상수 값을 연결지음으로써 미터에 대한 소급성을 확립하는 것입니다. 또 장거리 측정(최대 ±1mm)은 광학 간섭계를 사용하여 구현하며, 단거리의 초정밀 측정은 버니어 스케일과 유사한 원리로 작동하는 X-선 간섭계를 사용해 구현합니다.

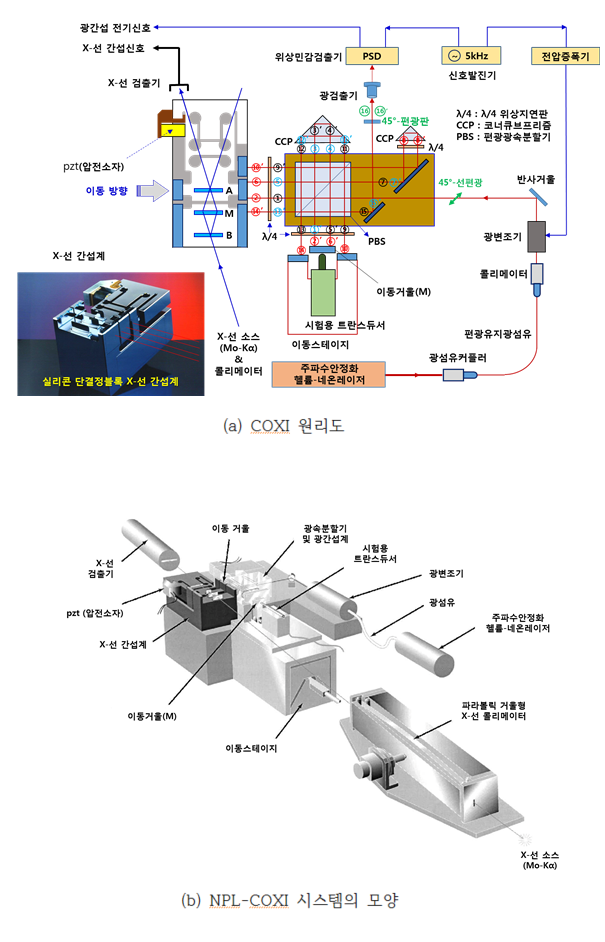
[그림4]의 (a)와 (b)에서 광간섭계와 결합된 X-선 간섭계, COXI시스템의 작동 원리와 장치를 확인할 수 있습니다. 전술한 바와 같이 [그림4]에서, X-선 간섭계에 부착된 PZT(압전소자)를 이용하여 A-라멜라를 ΔL만큼, 평행이동 시키면 X-선 검출기에서 실리콘 격자상수 d₂₂₀ ≅ 192nm 주기(λ_d220)로 X-선 간섭 신호가 주기적으로 나타납니다.

[그림4]의 광간섭계의 원리를 살펴보겠습니다. 일반적으로 1개의 레이저 광파장을 이용하는 호모다인 간섭계일 경우에는 간섭무늬의 신호대잡음비(S/N비)가 낮아서 측정의 정확도가 제한됩니다. 이때 레이저 광을 변조^modulation하고 검출된 간섭무늬 신호를 다시 복조^demodulation하여 사용하면 S/N비를 개선하는 것이 가능합니다. 이를 위하여 [그림4]의 발진기, 전압증폭기, 광변조기, 위상민감검출기^{PSD, Phase Sensitive Detector} 등과 같은 전자 소자들이 사용됩니다.

주파수가 안정화된 헬륨-네온 레이저 광을 이용하여 광섬유커플러, 편광유지광섬유 및 콜리메이터를 통한 평행광의 레이저 빔은 광변조기에서 광주파수가 5kHz로 주파수 변조되고 반사거울에서 반사하여 광간섭계로 입사됩니다. 입사하는 광의 편광이 수평면에 대해 45° 선편광이 되도록 콜리메이터를 회전하여 편광각을 조정합니다.

광간섭계에는 지면에 수평인 편광의 빔 성분은 투과하고 수직인 방향의 편광된 빔(광속)은 반사시키는 편광광속분할기 PBS와 광의 위상을 90°((λ/4)에 해당한다) 지연시키는 (λ/4)판, 입사한 빔을 평행으로 되반사시키는 코너큐브프리즘 CCP등의 광학소자로 구성되어 있습니다.

(λ/4)판을 1번 통과한 빔의 편광은 수평, 또는 수직 편광에서 원편광으로, 원편광의 빔은 선편광으로 바뀌며, 2번 통과한 빔은 수직편광은 수평편광으로, 수평편광은 수직편광으로 바뀌게 됩니다.

45° 선편광된 주파수 안정화된 레이저 빔은 PBS에서 수평 편광과 수직 편광성분으로 나뉘어져 각각 PBS를 통과하거나 반사하며 광학소자에 따라 각각의 광로로 진행합니다. 최종적으로 광검출기 앞에 45°방향으로 편광된 편광판을 통과하면 각각 이 방향으로 편광된 성분만이 통과한 두 빔이 간섭을 일으켜 간섭무늬를 만듭니다. 각각의 광경로를 살펴보면 다음과 같습니다.

지면에 수평 편광 성분의 레이저광 빔은 다음과 같이 진행합니다.([그림5-(a)])

여기서 검은색은 수평편광을, 푸른색은 수직편광을, 붉은색은 원편광을, 녹색은 45° 선편광을 나타냅니다.

PBS통과→①→(λ/4)→②→A-라멜라 측면 반사면의 아래부분 반사→(λ/4)→PBS반사→③→④→PBS반사→⑤→(λ/4)→⑥→A-라멜라 측면 반사면 윗부분 반사→(λ/4)→PBS 통과→⑦→(λ/4)→⑧→PBS 반사→⑨→(λ/4)→⑩→(고정된)오른쪽 거울면 반사→(λ/4)→PBS 통과→⑪→⑫→PBS 통과→⑬→(λ/4)→⑭→(고정된)왼쪽 거울면 반사→(λ/4)→PBS 반사→⑮→거울 반사→45°-편광판 통과→⑯

한편, 지면에 수직편광 성분의 레이저 빔은 다음과 같이 진행합니다.([그림5-(b)])

PBS반사→①’→(λ/4)→②‘→가운데 이동거울(M) 왼쪽면 반사→(λ/4)→PBS통과→③’→④‘→PBS통과→⑤’→(λ/4)→⑥‘→가운데 이동거울(M) 오른쪽면 반사→(λ/4)→PBS반사→⑦’→(λ/4)→⑧‘→(λ/4)→PBS통과→⑨’→(λ/4)→⑩‘→(고정된) 윗쪽 실리콘 측면 반사면 반사→(λ/4)→PBS반사→⑪’→⑫‘→PBS반사→⑬’→(λ/4)→⑭‘→(고정된)M-라멜라 측면반사면 반사→(λ/4)→PBS통과→⑮’→거울 반사→45°-편광판 통과→⑯‘

각 반사면을 반사한 수평 편광빔⑯과 수직편광 빔⑯‘은 광검출기 앞의 45° 편광판을 통과하여 같은 각도로 편광되어 있으므로, 서로 간섭하여 이를 검출하는 광검출기에서는 이동하는 A-라멜라 측면 반사면이나 이동하는 광간섭계의 이동거울(M)의 이동량에 따라 간섭무늬가 주기적으로 변동하는 신호를 검출하게 됩니다.

COXI를 이용한 실리콘 단결정의 격자상수 측정

광간섭계에서는 A-라멜나의 이동량(ΔL)에 따른 광 간섭무늬가 나타난다. A-라멜라 측면 반사면에서 수평 편광된 레이저광 빔(파장, λ)이 두 번 반사하므로, (λ/2)/2 = λ/4 파장 주기로 간섭무늬가 생성되어 이를 계수함으로써, X-선 간섭무늬의 계수량과 비교해 다음과 같이 실리콘 격자상수를 측정할 수 있습니다.

ΔL = m_x∙(λ_d220) = m_opt∙(λ/4) 이므로

λ_d220 = d₂₂₀ = (m_opt/m_x)∙(λ/4) 이 됩니다.

여기서 λ_d220, λ, m_x, m_opt는 각각 X-선 간섭무늬 파장(격자상수 d₂₂₀와 같다), 사용한 안정화 레이저 광파장, X-선 간섭무늬의 개수 및 광간섭 무늬의 개수를 나타냅니다.

[그림6]은 두 간섭무늬 비율을 측정하는 예를 보여줍니다. 녹색은 광 간섭무늬, 빨간색은 X-선 간섭무늬, m_opt, m_x는 각각 광 간섭무늬와 X-선 간섭무늬의 개수입니다. 그림에서 정수 m_x = m_opt = 0인 부분(가상적으로 정함)부터 m_opt = 1인 점에서, 가상적인 값 m_x = 10.3을 찾아냅니다. 여기서 d₂₂₀ = (λ/4)*10.3으로 계산됩니다.

실제, 요오드분자(¹²⁷I₂)의 초미세 구조선 f-성분에 주파수 안정화된 요오드안정화 헬륨-네온 레이저의 파장을 간섭계에 광원으로 이용하였을 경우, 파장 λ = 632. 991 212 58nm이다. ΔL = 110.77μm 를 이동하였을 때, m_opt = 770이며 이에 상응하는 X-선 간섭무늬 개수 m_x는 m_x = m_xi + ε_x = 576,898 + 0.33이며 1.67 × 10^-8의 상대 불확도를 측정하기 위해서는, X-선 간섭무늬의 계수값 소수 부분 ε_x을 0,01 이내의 정확도로 반복 측정하여 얻어야 합니다.

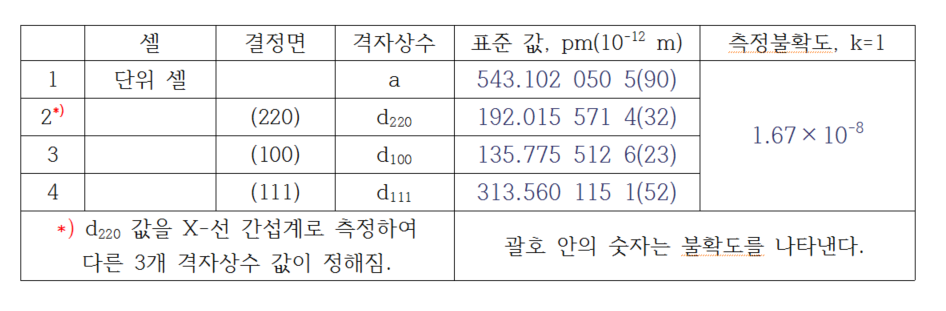
이렇게 반복 측정하여, 얻어진 (220)면의 격자상수는, d₂₂₀ = 192.015 571 4(32) × 10^-12m (상대 불확도 σ = 1.67 × 10^-8)이며, 이로 환산한 단위셀의 격자상수 a는 a = √8·d₂₂₀ = 543.102 050 5(87) × 10^-12m(상대 불확도 σ = 1.67 × 10^-8)가 됩니다.

COXI를 이용한 트랜스듀서 교정

표면거칠기 측정이나 진원도 측정, 나노길이 측정에는 초정밀 트랜스듀스가 사용됩니다. 지금부터는 X-선 간섭계를 이용하여 트랜스듀스를 교정하는 예를 살펴보겠습니다. 길이의 미소 변위량을 초정밀 측정하는 데 사용하는 트랜스듀서를 교정하기 위해서는 [그림4]와 같이 광간섭계의 이동거울(M) 뒷면에 트랜스듀서 센서를 부착합니다. 이후 이동거울을 지지하는 이동스테이지를 이동시켜 두 반사거울과 이동거울(M) 사이에 변위 ΔL를 주면, 광간섭계와 트랜스듀서 센서는 변위를 감지하여 측정됩니다.

광간섭계와 트랜스듀서 센서가 각각 측정한 두 변위량은 부호는 다르지만 같은 값입니다. X-선 간섭계의 입장에서 보면, 아직 라밀라-A의 움직임이 없었으므로, X-선 검출기에서 관측된 X-선 간섭무늬는 없습니다.

이 간섭계의 이동거울(M)의 변위량(ΔL)과 같은 값만큼 라멜라-A를 이동시키고 X-선 간섭무늬를 계수하면 라멜라-A의 변위량을 측정할 수 있고, 광간섭계는 두 기준면 중 하나인 라멜라-A의 반사면이 이동거울(M)과 같은 방향으로 이동하였으므로 광 간섭무늬는 원래의 위치로 되돌아옵니다. 전체 이동한 광 간섭무늬의 개수는 0이 됩니다.

즉, 트랜스듀서가 측정한 변위량이 라멜라-A의 변위에 상당하는 X-선 간섭무늬 개수가 됩니다. 그러므로, A-라멜라를 움직인 거리를 X-선 간섭계로 측정할 수 있고, 이로써 트랜스듀서의 측정 변위의 감도를 교정할 수 있습니다.

여기서, X-선 간섭계는 라멜라-A(의 측면 거울)의 이동량에만 감응하고, 트랜스듀서는 이동거울(M)의 이동량에만 감응하지만, 광간섭계는 라멜라-A(의 측면 반사면)의 이동거리와 이동거울(M)의 이동량이 같은 방향, 같은 양일 때는 두 이동량 모두에 반응하여 서로 상쇄되므로 간섭무늬 이동이 없어집니다.

측정의 실례로, 표준과학연구원에서 실리콘 결정의 변위를 측정한 X-선 간섭계의 간섭무늬와 피교정용 길이측정용 트랜스듀서인 LVDT^{Linear Variable Displacement Transducer, 선형 가변 변위 변환기} 변위에 대한 출력 신호를 [그림7]에서 확인할 수 있습니다.

X-선 간섭무늬의 한 피치의 간격은 전술한 바와 같이 격자간격 d₂₂₀ = 192.015 571 4(32) × 10^-12m(상대 불확도 : σ = 1.67 × 10^-8)이므로. 이값에 X-선 간섭무늬의 개수를 곱하여 트랜스듀서의 감도를 측정할 수 있습니다.

2. 실리콘 격자상수와 (주사)투과전자현미경

실리콘 단결정의 d₂₂₀ 격자상수의 값과, a = √8·d₂₀₀, d₁₀₀ = 0.25a , d₁₁₁ = (1/√3)a의 관계식을 이용하여 (100), (111)면의 격자상수 d₁₀₀, d₁₁₁를 계산하고, 이 값들을 이용하여 (주사)투과전자현미경^{STEM, Scanning Transmission Electron Microscpe([그림7])}의 배율 교정하거나 (S)TEM 내부의 CCD 카메라 배율을 교정하고 이들을 사용하여 미소 시료의 크기를 측정하는 방법이 미터의 정의를 실현하는 이차적인 방법이 됩니다.

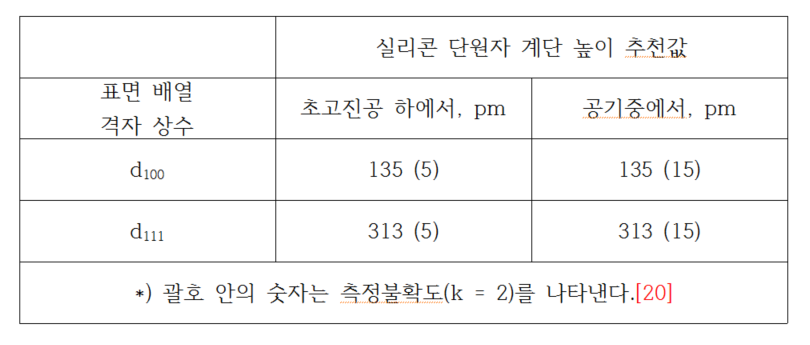
앞서 설명한 COXI에서 측정한 실리콘의 격자상수 d₂₂₀ 값을 기반으로 하여 [표1]에 실리콘 결정면의 격자상수를 정리하였습니다.

투과형전자현미경 TEM에서는 반도체 산업이나 표면과학에서 많이 사용하는 실리콘 결정면인 (100), (001)면이나 (111)면의 격자상수 d₁₀₀, d₀₀₁ 및 d₁₁₁값를 이용하여, TEM이나 그 내부의 CCD카메라의 배율 교정하는 데 사용할 수 있습니다. 실제 예시를 살펴보겠습니다.

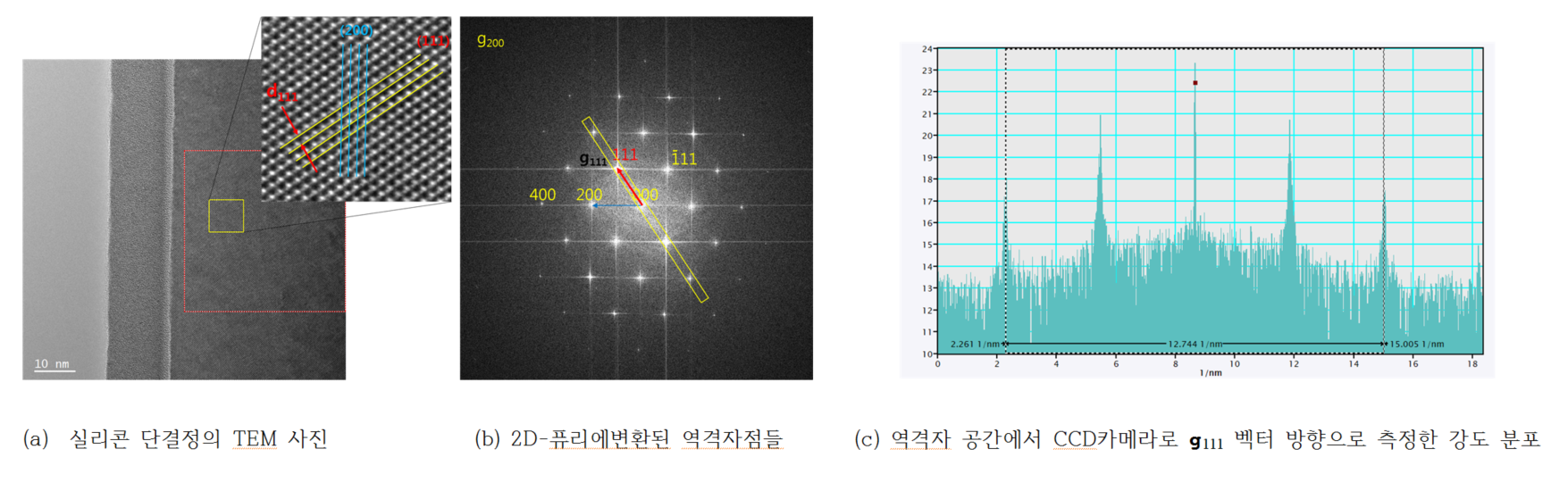
[그림9]는 STEM으로 실리콘 단결정의 이미지를 측정한 사진입니다. (a)의 푸른 선은 실리콘 (200)결정면을 나타내고 노란 선은 실리콘 (111)결정면을 나타냅니다. (b)는 2차원-퓨리에 변환된 역격자점을 나타내는데 (a)의 (111)결정면과 상응하는 것은 (b)에서 이에 수직인 선이 g₁₁₁ 벡터(역격자 공간에서 격자점 (000)에서 격자점 (111)까지의 벡터)로 나타나고, g₁₁₁ 벡터와 나란하게 CCD 카메라의 강도분포를 측정한 것을 (c)에 나타냅니다.

(c)에서 5개의 피크 사이의 거리는 12.7441/nm이고 두 피크 사이의 거리는 (12.7441/4)/nm = 3.186025/nm 이므로, (111)면의 격자간격 d₁₁₁는 이값과 역수의 관계가 있으므로, CCD카메라로 측정한 격자간격은 d₁₁₁ = 1/(3.186 025/nm) = 0.313 871nm가 됩니다.

표1에서 d₁₁₁의 표준값은 0.313 560 115 1nm이므로, TEM 내부의 CCD카메라로 측정한 값의 상대적 오차는 -1.0*10^-3(-0.1%)임을 알 수 있습니다.

이와 같은 방법으로 TEM의 측정배율을 교정하고, 교정된 TEM으로 나노구조를 측정함으로써, 나노계측학에서 실리콘 격자상수와 TEM를 이용한 미터 정의를 실현할 수 있습니다.

3. 실리콘 단원자 계단과 주사탐침현미경

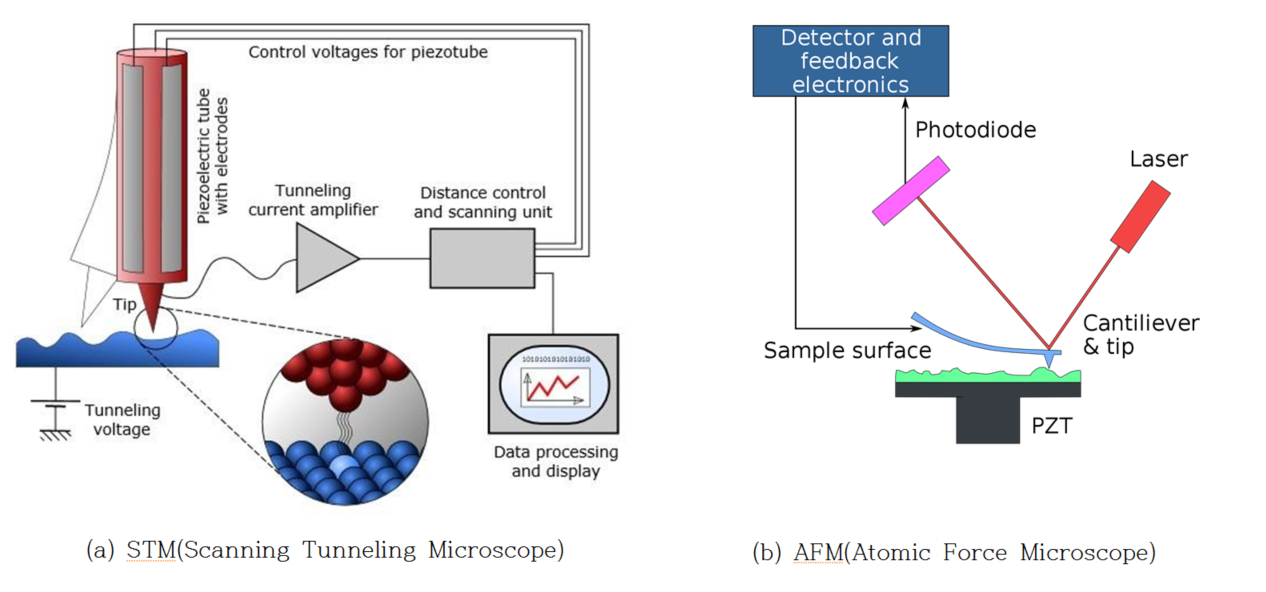
nm영역이나 sub-nm영역에서 작동하는 원자 크기의 분해능을 갖는 주사터널링현미경 STM이나 원자력현미경 AFM 등([그림10] 참고)과 같은 주사탐침현미경 SPM^{Scanning Probe Microscope}의 수직 변위를 측정하기 위해서는 단원자층 또는 다원자층 결정구조의 표준계단 시편을 기준 길이로 사용합니다.

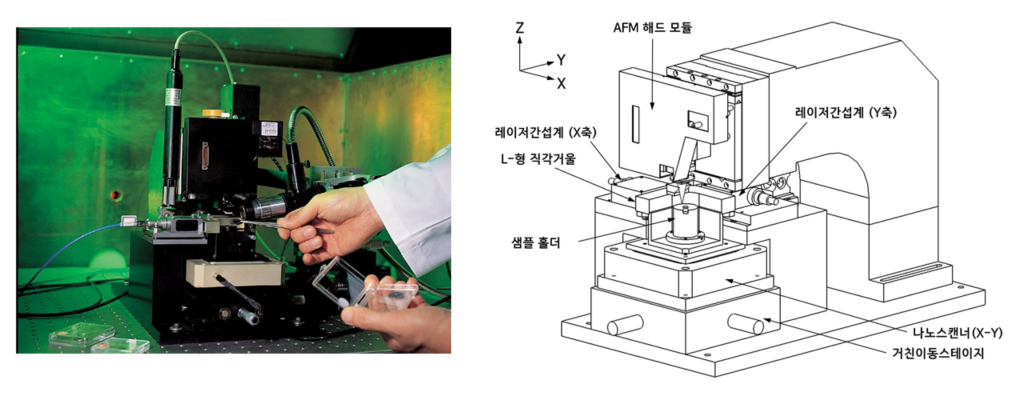
정밀한 나노변위의 계측은 마이크로미터 및 나노미터 범위의 1D, 2D 및 3D 격자 표준의 교정을 위해서, 레이저 광 간섭계와 연결되어 측정표준의 소급성이 보증되는 계측학적-원자력현미경 M-AFM^{Metrological Atomic Force Microscope}이 사용됩니다.([그림11] 참고)

특히, 다수의 동일한 격자 구조에 대해 측정하는 더 큰 스캐닝 범위를 가진 AFM의 경우, 평균 피치 측정에 대해 달성 가능한 측정불확도는 ~pm(10^-12m)범위에 있습니다. 그러나 두 개의 측면 위치 또는 수직으로 분리된 두 개의 평면(스텝 높이) 사이의 거리 측정은 nm(10^-9m) 미만의 측정불확도로 제한됩니다. 이 불확도는 변위 간섭계의 비선형성, Abbe-오프셋, 표면 거칠기^{surface roughness}, 파형^waveness 또는 프로브-샘플 상호작용 등에 의해서 발생합니다.

실리콘(Si) 위의 이산화규소(SiO₂)을 기반으로 하는, 상업적으로 이용 가능한 스텝 높이 표준시편에서 실현되는 가장 작은 스텝높이는 6nm 범위입니다. 그러나 이러한 SiO₂/Si 계단높이 표준시편의 측정불확도, u(k=1)은 약 0.5nm로 상대적으로 AFM의 해상도에 비해 상당히 큽니다.[20]

이와 같은 계단높이 표준시편의 측정불확도는 단일벽 및 다중벽 탄소나노튜브^{SW-CNT, MW-CNT}, 분자, 벌키한 볼, 폴리머, 박막 및 평평한 표면에 놓인 DNA 등을 명확하게 분해하는 AFM 이미지로 측정 가능한 높이의 측정 정확도를 제한합니다. 이러한 한계를 극복하고 AFM의 측정값을 교정하기 위해서는 새로운 기준시편이 요구됩니다. 즉, 더 미세한 계단이나 구조를 보여주며 더 작은 측정불확도를 갖는 자연 상수와 관련된 표준시편이 필요합니다.

결정 표면은 주어진 결정학적 방향의 표면에 있는 원자 사이의 고정된 거리, 소위 자연 상수를 갖고 있으며, 결정학적 평면 세트와 수직 방향으로 일정 높이의 계단을 가지고 있습니다. 결정학적 평면의 패밀리로부터 형성된 단원자 계단 사이의 간격은 유용한 범위인 0.1nm에서 0.3nm 사이의 값을 가지고 있습니다.

그러므로, 국소화된 나노구조의 높이 측정을 위한 나노계측학적 기준으로, (111) 및 (100) 방향을 가진 표면이 있는 단결정 실리콘의 사용할 수 있습니다. 표면과학의 연구에서는 실리콘 결정의 (001) 방향을 기준으로 하는 반면, 반도체 산업에서는 (100) 평면을 기준으로 합니다. 하지만 계측학적인 관점에서 볼 때 둘은 동일합니다.

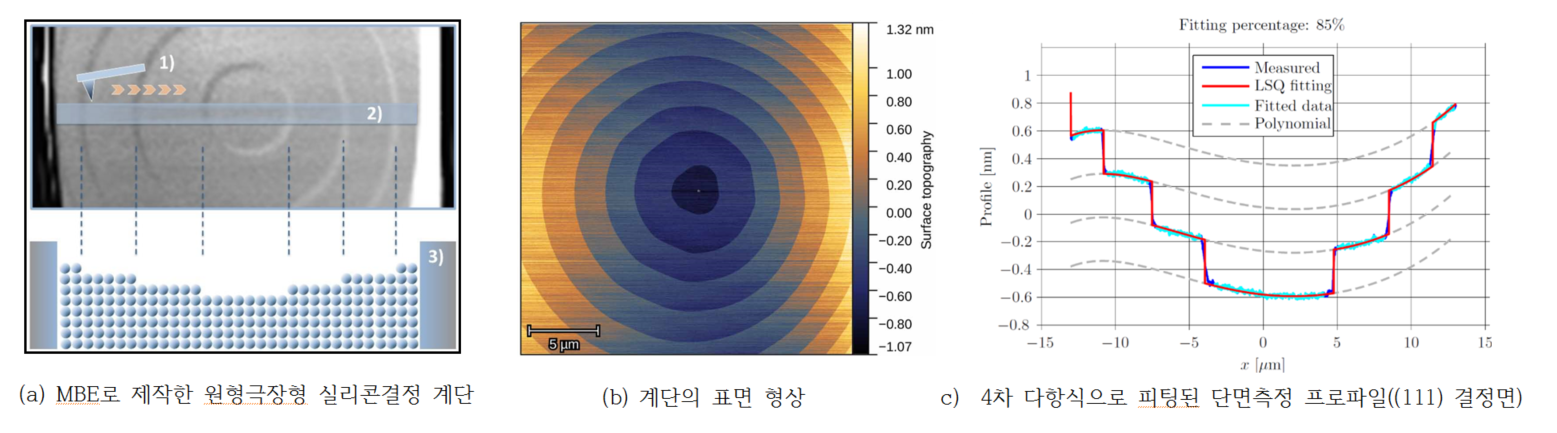
그림12]의 (a), (b)는 MBE^{Molecular Beam Epitaxy}로 제작한 실리콘(²⁸Si) 단원자 계단의 기하학적인 지형 형상이며, (c)는 AFM으로 측정한 실리콘 (111) 결정면 계단 측정의 결과입니다.

실제 측정에서 평면인 결정면을 측정하여도 측정 범위가 수μm 이상이면, AFM의 캔틸레버나 STM에서는 튜브^tube형 pzt 스캐너 등의 비선형적 이동으로 인해 직선의 값이 아닌 곡선으로 휘어지는 현상이 나타납니다. 이 측정 프로파일의 휨을 보정하는 즉, 측정한 원본 프로파일에서 휨의 피팅 방정식을 제거하여 보정하면 단면 계단 형상을 비교적 정확하게 얻을 수 있습니다.

그러므로, 최적 피팅(여기서는 4차 다항식 피팅)을 이용하여 계단의 높이를 보정하여 측정할 수 있습니다. 그 결과 d_111(cor) = (0.3137 ± 0.0038) nm, 즉 상대 측정불확도 u(d_111(cor))는 1.2%입니다.[21] 이와 같은 방법으로 실리콘 단원자 계단을 높이로 AFM, STM 등과 같은 SPM을 교정하여 나노계측학에서 나노크기의 나노구조물을 측정할 수 있습니다.

[표2]에는 여러가지 측정오차 오인을 고려하여 길이자문위원회^CCL에서 추천하는 실리콘 단원자 계단의 높이값을 나타내었습니다.

지금까지 나노계측학에서 사용하는 높이표준 시편으로서 실리콘 단결정의 단원자 계단의 높이를 이용해 미터의 정의를 실현하는 방법에 대해 알아보았습니다.

나가며

이번 글에서는 나노계측학에서 사용하는 미터 정의의 이차적인 실현 방법을 살펴보았습니다. 구체적으로 실리콘 단결정의 격자상수 d₂₂₀(격자상수: 0.119 nm)와 X-선 간섭계를 이용하는 방법, 실리콘 결정 배열이 만드는 격자상수와 (주사)투과형전자현미경을 이용하는 방법, 실리콘 단원자 계단 표준시편을 이용하여 원자 크기의 분해능을 갖는 현미경인 AFM이나 STM과 같은 SPM을 교정하거나 이를 이용하는 방법에 대해 알아보았습니다.

이들 방법을 이용하여, 미터 표준에 소급성을 갖는 실리콘 결정의 격자상수를 나노계측학에 사용되는 각종 현미경의 교정에 적용하여, nm 또는 Sub-nm 수준의 미세구조물을 측정하는 현미경들의 측정한계에 가까운 ~10pm 이하의 측정정확도를 보증할 수 있게 되었습니다.

또, 플로팅존법으로 결정 성장된 초고순도의 실리콘 단결정으로 만든 표준구와 X-선 간섭계는 새로운 SI 정의에 따른 킬로그램의 구현, 밀도 표준, 아보가드로 측정에서도 지대한 역할을 하고 있음을 알 수 있습니다. 이와 관련된 또 다른 흥미 있는 측정 이야기는 질량분야 전문가들의 아티클이나 논문에서 찾아볼 수 있을 것입니다.