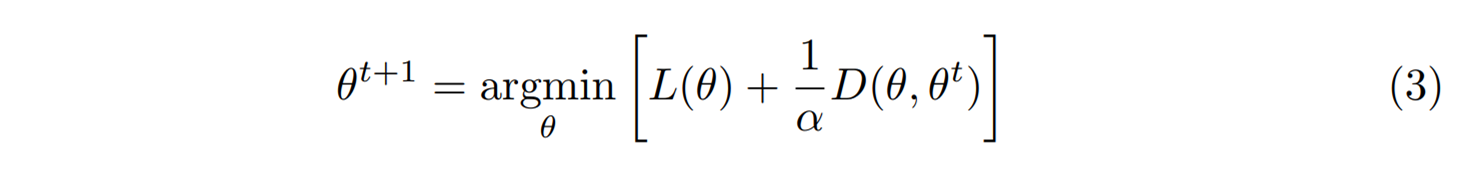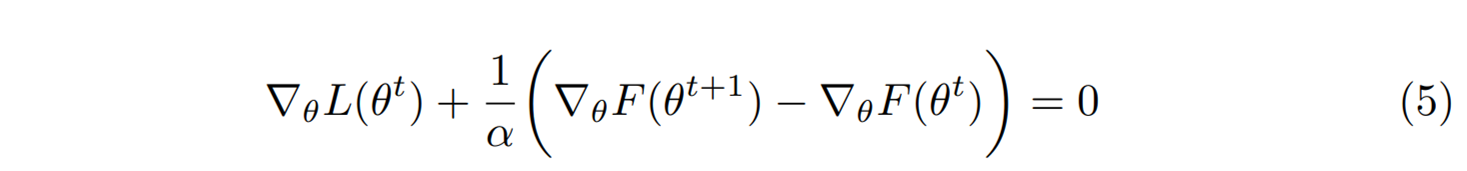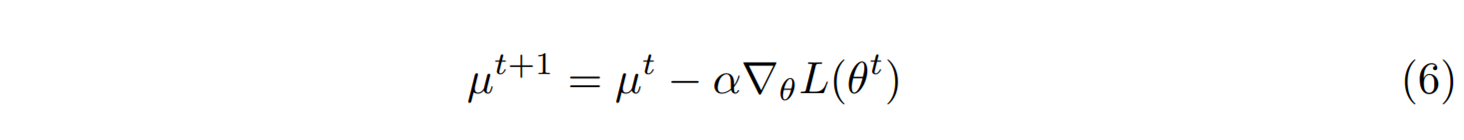정보기하학과 머신러닝 [3]: 거울 하강법

앞선 두 개의 글 “확률모형 사이의 거리”와 “충분통계량과 f-거리”에서 우리는 쿨백-라이블러 거리^{Kullback-Leibler divergence}의 특별함에 대해서 이야기 하였다. 이 거리는 지수족^{exponential family} 확률모형의 브레그만 거리^{Bregman divergence}임과 동시에 충분통계량^{sufficient statistic}에 대해 불변이다. 이번 글에서는 머신러닝의 최적화 과정에 정보기하학이 어떻게 멋지게 쓰일 수 있는지 살펴보고자 한다.

머신러닝은 주어진 데이터에 대해서 모형의 매개변수인 \(\theta = (\theta_1, \theta_2, \cdots, \theta_n)\)를 조정해서 목적함수 \(L(\theta)\)를 최적화하는 과정으로 생각할 수 있다. 이를 실현하는데 핵심적인 역할을 하는 것이 바로 경사하강법^{gradient descent}이다. 이는 목적함수의 기울기를 살피면서 목적함수를 줄이는 또는 늘리는 방향으로 매개변수를 \(\theta^t\)에서 \(\theta^{t+1}\)으로 갱신한다. 목적함수의 최소점을 찾는 경우는 다음과 같은 수식으로 표현할 수 있다.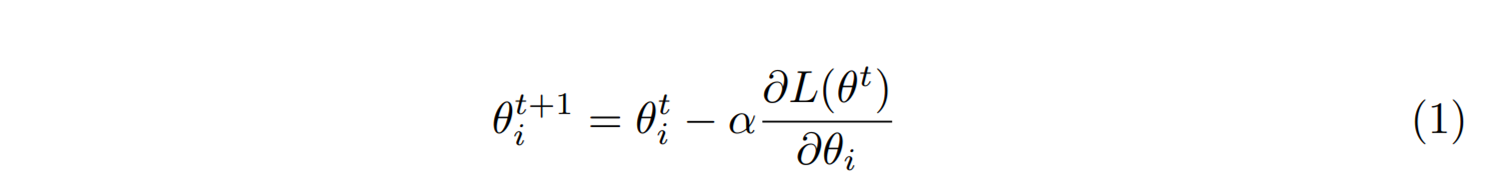

이 경사하강법을 더 정교하게 만든 자연스러운 경사하강법^{natural gradient descent} 이 있다.[1] 

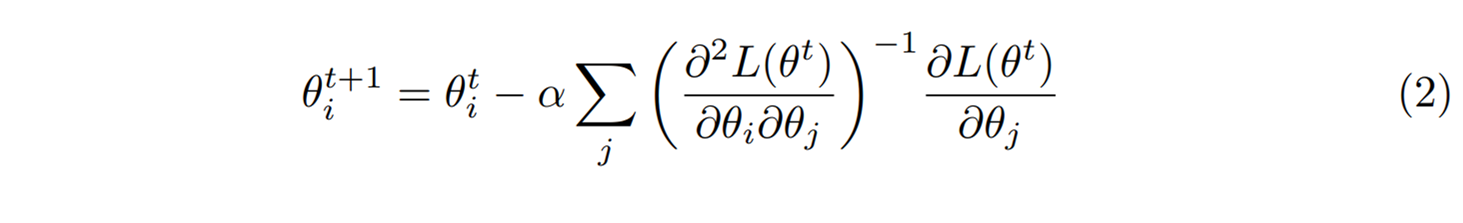이는 목적함수의 곡률 \(H_{ij}(\theta^t) \equiv \partial^2 L(\theta^t) /\partial \theta_i \partial \theta_j\)를 염두에 두면서 매개변수를 갱신하기 때문에 최소점에 더 효과적으로 접근할 수 있다. 물론 세상에 공짜는 없어서 곡률을 계산하고 역수를 취하는 과정에서 계산 비용을 더 지불해야 한다. 자연스러운 경사하강법은 매개변수의 척도 변화에 대해서도 불변인 공식이 된다. 가령 \(\theta\)를 2배로 만드는 새로운 매개변수 \(\tilde{\theta}\)를 생각하면 식 (1)과는 다르게 식(2)는 \(\theta\)만 \(\tilde{\theta}\)로 고치면 된다. 이렇게 척도 변화에 대해서 불변이 되기 위해서 자연스러운 경사하강법의 곡률은 \(\partial^2 G(\theta^t) /\partial \theta_i \partial \theta_j\)의 형태이기만 하면 되므로 꼭 \(G=L\)일 필요는 없다.

자명한 작동원리를 가지는 경사하강법을 다음과 같이 해석해 볼 수도 있다.

여기서 \(D(\theta, \theta^t) = ||\theta – \theta^t ||^2\)를 \(\theta\)와 \(\theta^t\) 사이의 유클리드 거리의 제곱으로 정의해 보자. 그러면 위 최적화 과정은 \(\theta^t\) 근방에서 가장 작은 \(L(\theta)\)를 갖는 \(\theta\)를 찾아서 \(\theta^{t+1}\)으로 갱신하자는 것이다. \(\theta^t\)에 가까운 \(\theta\)를 찾고 있기 때문에 테일러 근사 \(L(\theta) \approx L(\theta^t) + \nabla_\theta L \cdot (\theta – \theta^t)\)를 이용할 수 있고, 위 최적화의 해는 식 (1)이 됨을 확인할 수 있다. 이번에는 \(D(\theta, \theta^t)\)를 브레그만 거리로 한번 정의해 보자.

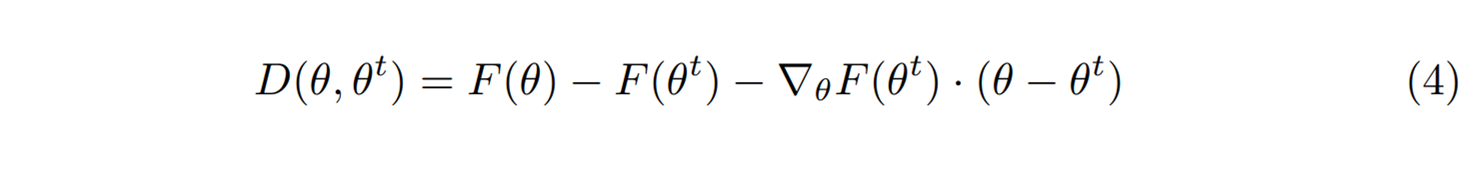이는 오목함수 \(F(\theta)\)가 주어졌을 때, \(\theta\)에서의 함수값과 \(\theta^t\)에서 테일러 근사로 어림한 함수값 사이의 차이로 정의된다. 이렇게 정의한 브레그만 거리는 \(\theta = \theta^t\)에서만 \(D(\theta^t, \theta^t)=0\)이 된다. 위에서 언급한 유클리드 거리의 경우는 사실 \(F(\theta)= ||\theta||^2\)의 특별한 경우로 생각할 수 있다. 이제 일반적인 브레그만 거리인 식 (4)를 이용해서 식 (3)의 최적화 해를 다시 찾아 보자.

이 최적화 조건이 조금 복잡하게 보일 수 있는데, 오목함수 \(F(\theta)\)의 기울기에 해당하는 새로운 변수 \(\mu = \nabla_\theta F\)를 도입해 보자. 오목함수 \(F(\theta)\)는 모든 \(\theta\)에서 다른 기울기 값을 가지기 때문에 \(\mu\)는 \(\theta\)의 켤레가 되는 새로운 변수^{conjugate variable}가 된다. 위 최적화 조건을 새로운 변수로 표현하면 다음의 경사하강법이 된다.

얼핏보면 경사하강법처럼 보이는데, 여기서 \(\nabla_\theta L\)은 \(\theta\)에 대한 기울기이지 \(\mu\)에 대한 기울기가 아님을 주의해야 한다. 흥미로운 사실은 이 식은 마치 경사하강법처럼 보이는데 사실은 자연스러운 경사하강법을 내포하고 있다.[2] 이를 조금 더 자세히 살펴보자. 오목함수 \(F(\theta)\)의 르장드르 변환^{Legendre transformation}에 해당하는 또다른 오목함수 \(G(\mu)\)를 생각하자.

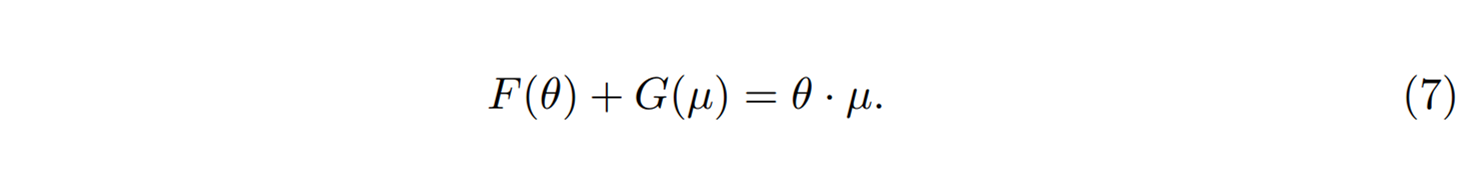이 관계는 \(\theta\)와 \(\mu\)의 쌍대성^duality을 준다.

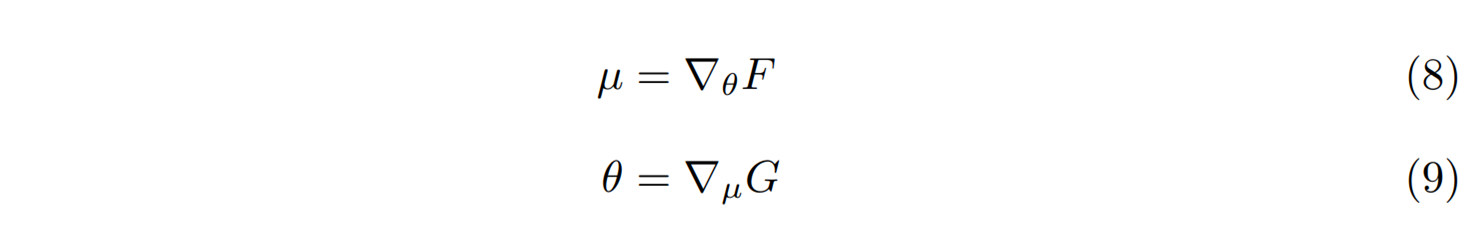이제 체인법칙을 이용해서 \(\theta\)에 대한 기울기 \(\nabla_\theta L\)을 \(\mu\)에 대한 기울기로 표현해 보자.

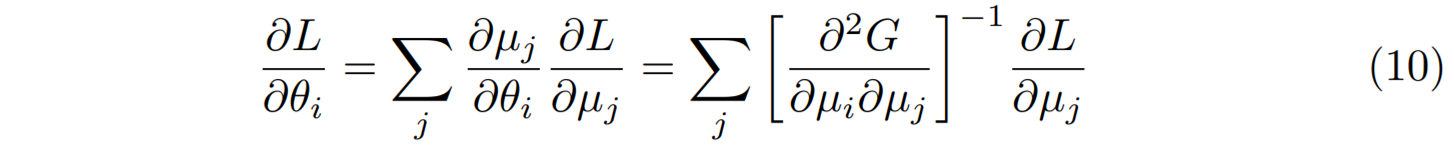위 유도과정에서 \(\theta_i = \partial G/\partial \mu_i\)을 이용했다. 그러면 경사하강법처럼 보이던 식 (6)이 사실은 자연스러운 경사하강법이라는 것을 확인할 수 있다.

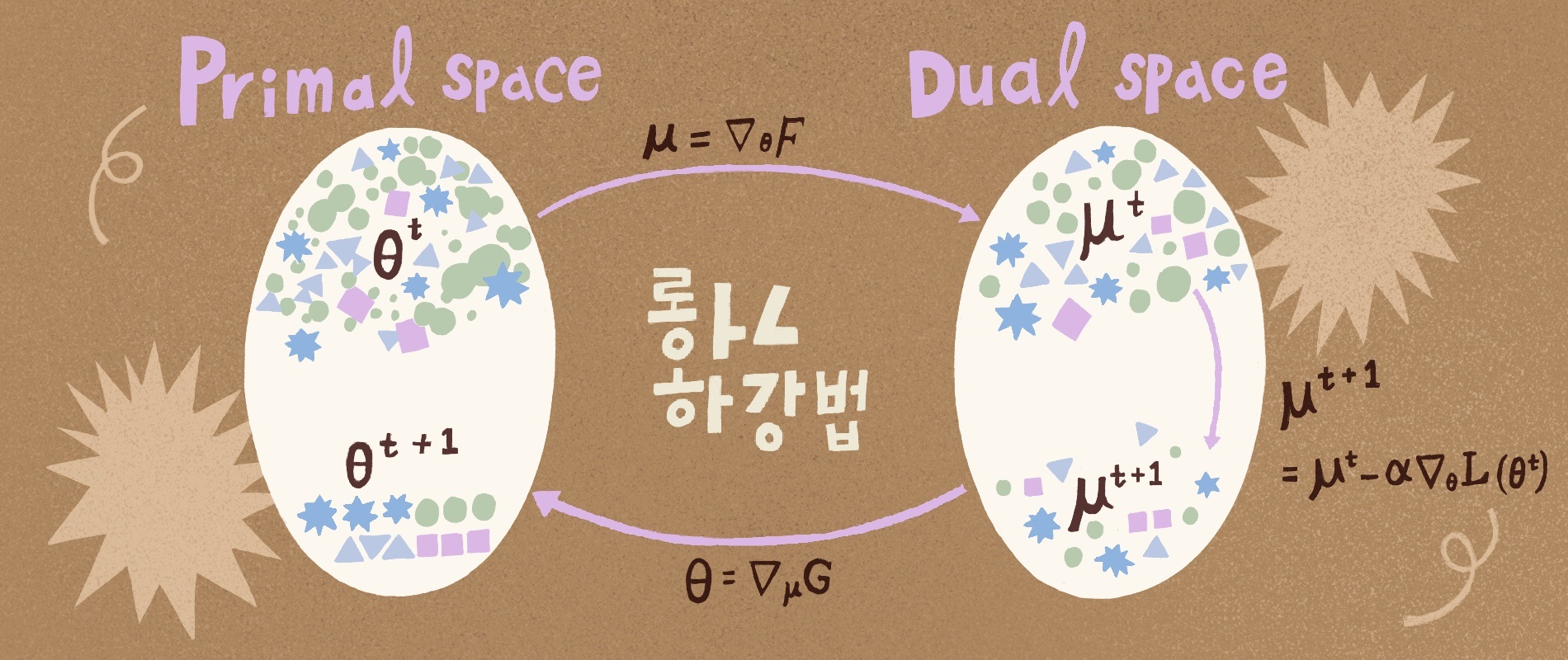
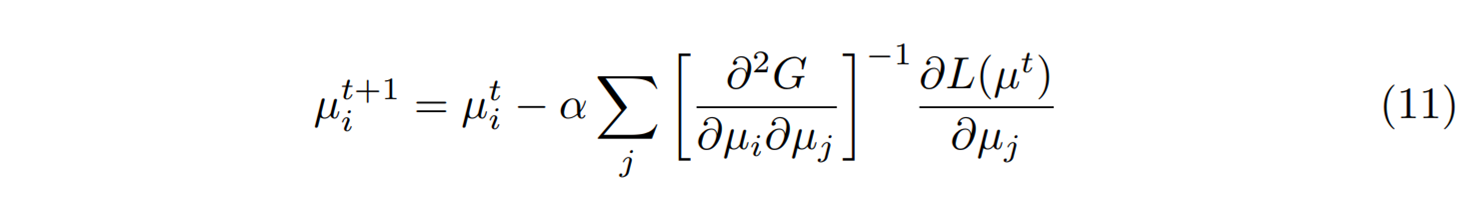만약 우리가 원래공간과 쌍대공간을 오갈 수 있다면, 곡률계산이 없는 경사하강법을 쓰면서 자연스러운 경사하강을 할 수 있게 되었다. [그림1]에 보인 것처럼 이 과정을 다음의 세 단계로 정리해 볼 수 있다. (i) 원래공간의 현재 \(\theta^t\)를 쌍대공간의 \(\mu^t\)로 변환한다. (ii) 그리고 경사하강법을 통해 \(\mu^{t+1}\)를 갱신한다. (iii) 갱신된 \(\mu^{t+1}\)을 원래공간의 \(\theta^{t+1}\)로 역변환한다. 쌍대공간을 이용한 이 갱신을 거울하강법^{mirror descent}이라고 부른다.

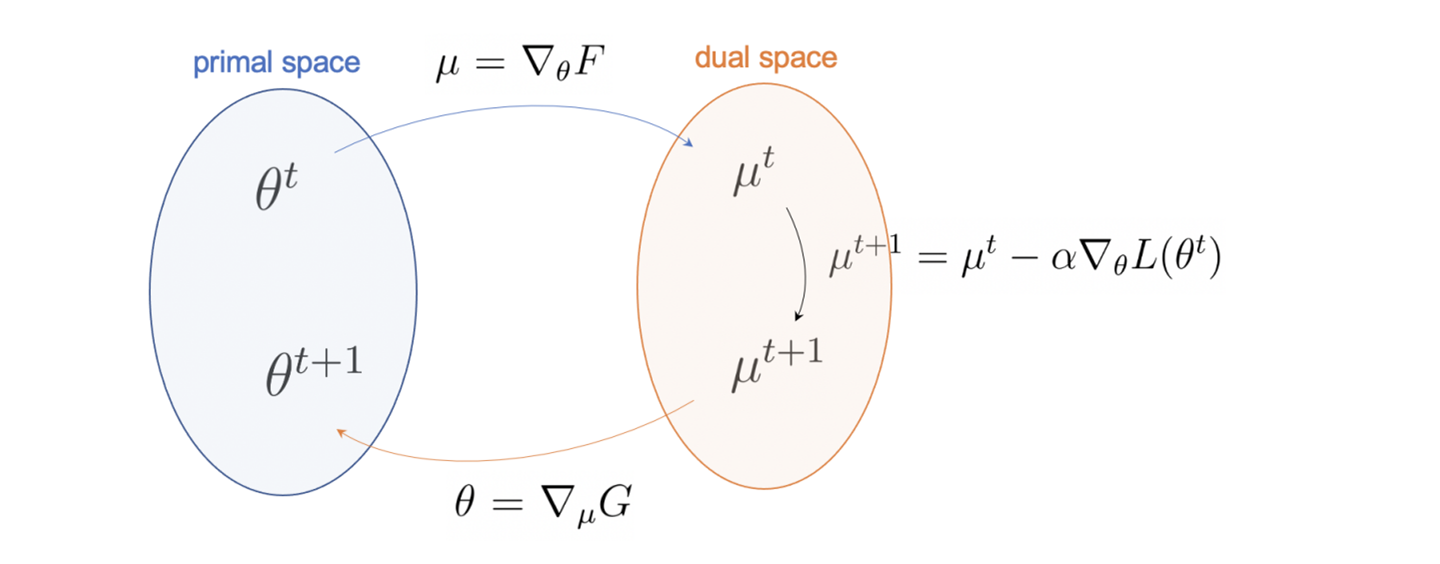
실제 곡률을 계산하지 않고도 자연스러운 경사하강을 할 수 있다.  여기서도 공짜는 없는 것이 쌍대공간에서 갱신한 \(\mu^{t+1}\)을 원래공간으로 가져와야 우리가 원하는 모형의 매개변수 \(\theta^{t+1}\)을 얻게 된다. 이는 함수 \(G(\mu)\)를 알아야 기울기에 해당하는 \(\theta^{t+1} = \nabla_\mu G(\mu^{t+1})\)을 계산할 수 있다. 이 역변환이 가능한 특별한 경우가 하나 있다. 바로 브레그만 거리 \(D(\theta, \theta’)\)을 정의하는 오목함수를 다음과 같이 \(p\)-norm으로 정의할 때이다.

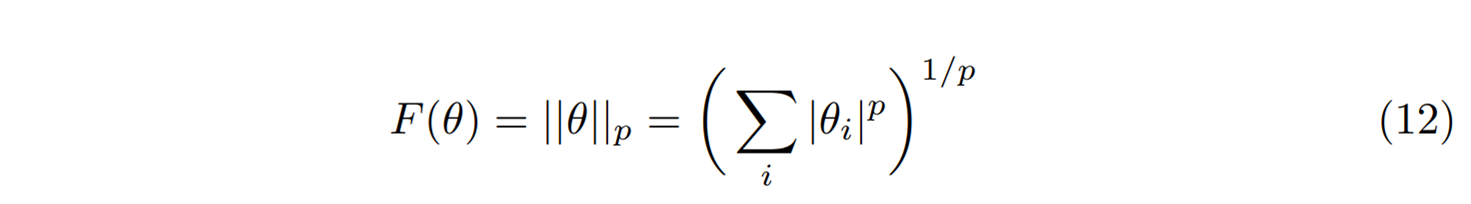이 경우 이 함수의 켤레가 되는 함수가 \(q\)-norm임이 수학적으로 이미 알려져 있기 때문이다.[3] 여기서 \(p\)와 \(q\)는 \(1/p+1/q=1\)을 만족한다. 따라서 \(G(\mu) = ||\mu||_q\)를 알고 있는 경우이므로 역변환이 가능하게 된다. 여기서 \(p=q=2\)인 경우는 원래공간과 쌍대공간이 일치하는 자기쌍대성^self-duality을 보이는 경우로 곡률을 고려하지 않는 경사하강법에 해당한다. 이렇게 \(p\)-norm을 이용한 거울경사를 딥러닝에 적용하면 일반적인 경사하강법에 비해서 학습 후 일반화가 더 잘 된다는 보고가 있었다.[4]

한 가지 아쉬운 점은 매개변수 \(\theta\)와 \(\theta’\)사이의 거리 \(D(\theta, \theta’)\)이 데이터와는 상관없는 모형공간에서만 정의된 것이다. 데이터 \(x\)의 분포가 주어진 문제에서 모형의 확률분포 \(P(x; \theta)\)를 찾는 머신러닝을 생각해 보자. 이 경우 매개변수가 다른 두 모형들 사이의 거리는 다음의 쿨백-라이블러 거리로 자연스럽게 정의한다.

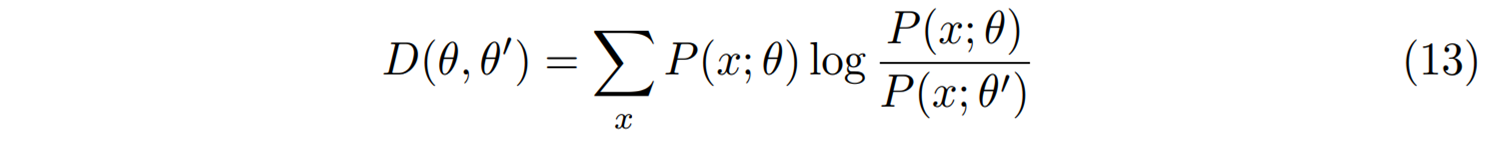이렇게 정의한 브레그만 거리는 데이터에 의존하게 된다. 이를 이용하면 데이터를 살피면서 모형의 매개변수를 갱신할 수 있는 가능성이 열린다. 물론 이 경우 쌍대공간으로의 변환과 본래공간으로의 역변환에 어려움이 생긴다. 우리의 확률모형 \(P(x; \theta)\)가 지수족인 경우는 \(\theta\)에 대응하는 쌍대공간의 켤레변수 \(\mu = \mathbb{E}[x]\)가 기대값이 되므로 쌍대공간으로의 변환을 쉽게 할 수 있다. 그리고 쌍대공간에서의 갱신 이후 생기는 역변환의 어려움은 갱신된 \(\mu^{t+1}\)가 \(\mu^t\)에서 많이 벗어나지 않는 경우이므로 \(G(\mu)\)를 \(\mu^t\)에서의 테일러 근사를 이용해서 해결할 수 있다. 우리는 최근 이 아이디어를 발전시켜서 홉필드 모형^{Hopfield model}을 거울경사를 이용해서 효과적으로 학습할 수 있음을 보였다.[5]

세 번의 글을 통해서 정보기하학과 머신러닝에 대한 이야기를 해 보았다. 먼저 확률모형들 사이의 “자연스러운” 거리를 정의해 보았다. 이는 유클리드 공간에서 정의되는 피타고라스 정리와 같은 식을 만족하고, 충분통계량에 대해서도 불변이 되는 거리가 되었다. 그리고 머신러닝에서 매개변수를 갱신하는 경사하강법에서 목적함수의 곡률을 염두에 두는 자연스러운 경사하강을 소개하였다. 마지막으로 매개변수의 쌍대공간을 이용한 거울하강법에 대해서도 알아 보았다. 데이터에 숨어 있는 규칙을 찾은 학문인 머신러닝에서 모형들 사이의 거리, 목적함수의 곡률과 같은 기하학적 개념들이 사용되는 것은 필연적으로 보인다. 머신러닝의 발전에 핵심적인 역할을 하고 있는 기하학, 특히 정보기하학에 대한 관심이 조금 생겼기를 바라면서 연재를 마친다.

연재기사

[SF와 나 (1)] 어느 과학자가 SF를 쓰는 이유
[SF와 나 (2)] 20세기 중반 SF 소설에 그려진 인공지능
[SF와 나 (4)] 내가 SF를 즐기는 방법
[SF와 나 (5)] 나는 어쩌다 SF를 읽게 되었고, 앞으로도 읽게 될 것인가?