2022 필즈상 수상자 위고 뒤미닐-코팽

들어가며: 네모의 꿈

2022년에 필즈상을 수상한 위고 뒤미닐-코팽^{Hugo Duminil-Copin}의 업적을 본격적으로 소개하기에 앞서, 그가 확률론적 방법론으로 주로 다뤄 온 격자 모형^{Lattice Model}들에서 나타나는 확률기하학^{Random Geometry}적 현상들과 수리물리학적 테마들을 포괄적으로 소개해 보고자 한다.

게임 ‘마인크래프트^MineCraft‘를 플레이해 보면 격자 구조의 특징을 긴밀히 알게 된다. 구름도, 산도, 나무도 정육면체 블록들로 이루어져 있는 게임속 세계에서 플레이어들은 건축학이나 3D 모델링에 대한 지식이 없이도 블록을 쌓기만 하면 원하는 모양을 근사하게¹ 만들어 낼 수 있고, 인터넷을 조금만 검색해 봐도 현실에 존재하는 복잡한 건축물들을 게임 속에서 재현한 수많은 예를 찾을 수 있다. 이러한 편리함에 따르는 한계도 분명 명확한데, 원하는 모양에 곡선이 조금이라도 섞여 있다면 구현해 낼 수 있는 결과물은 잘해도 근사할² 뿐 완벽할 수 없다는 것이다.

가장 간단한 예로, 마인크래프트에서 일정 크기 이상의 원을 만드는 것은 주어진 지름에 맞추어 밑그림을 그려주는–즉, 원의 방정식을 주어진 해상도로 이산화^discretize하여 풀어주는–앱 없이는 거의 불가능하게 느껴진다. 다시 말하면, 직선과 직각만이 존재하는 정사각 격자 위에 원을 그린다는 것은 부자연스럽게만 보이는데, 과연 그럴까?

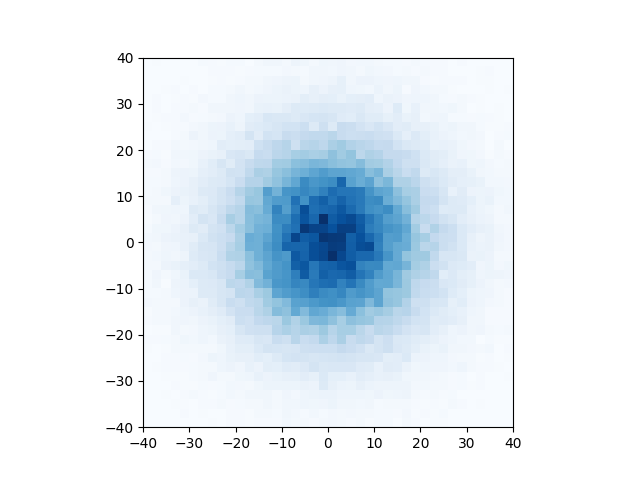
정사각 격자 위에 원을 그리는 잘 알려진 방법을 하나 소개하고자 한다. 먼저, 원의 중심이 될 정사각형을 하나 선정한 다음, 그 블록에 맞붙은 4개의 정사각형 중 하나를 균일한 확률로 골라 이동한다. 그 후에도 계속 4개의 이웃들 중 하나를 균일하게 골라 움직이기만 하면 된다. 놀랍게도, 이 과정을 여러 번 시행하여 (예를 들어) 100걸음 이후 위치를 히스토그램으로 나타내보면 깔끔한 원형 봉우리를 그리는 것을 쉽게 실험해 볼 수 있다.(그림1)

즉, 위의 단순한 무작위 보행^{Simple Random Walk}은, 격자 위에서 아주 자연스러워 보이는 이웃이라는 구조만을 사용하지만, 격자 위 네모만을 알며 살아가는 이들에게는 설명조차 못할 회전대칭성을 보이기 시작한다. 이처럼, 융통성 없는 격자 구조에 뗄 수 없이 얽매여 있는 것처럼 보이는 확률적 모형들에서도 특정한 조건이 갖춰지면 격자 구조를 뛰어넘는 대칭성이 축척^scale이 커질수록, 시행의 횟수가 많아질수록 창발하는^emerge 듯 보이는 경우가 많다. 다만, 무작위 보행의 회전대칭성은 중심극한정리^{Central Limit Theorem}라는 확률론의 핵심 정리를 사용해 비교적 쉽게 보일 수 있지만, 대부분의 다른 격자 모형에서 비슷한 결과를 엄밀하게 증명하는 것은 매우 어려운 일일 뿐이다. 축척이 커질수록 급격히 증가하는 경우의 수–예를 들어, 하나의 무작위 보행은 동서남북을 100번 고르는 가짓수인 \(4^{100}\)개의 보행들 중 하나일 뿐이다–에도 불구하고 나름대로의 확연한 질서가 생긴다는 매혹적인 명제는 곧 엄밀한 증명을 위해서는 그 수많은 경우의 수를 어떤 식으로든 모두 고려해야 한다는 수학적 부담으로 다가오기 때문이다.

사실, 잠시 생각해 보면 우리는 사실 게임 밖에서도 완벽한 원을 본 적이 한 번도 없음을 알 수 있다. 어떻게 그려보아도, 우리는 모니터의 픽셀–이들도 격자 구조를 가진다–이나 컴퍼스의 떨림, 심지어는 종이의 분자 구조에 얽매인 불완전한 원을 보고 있지 않은가? 그럼에도 불구하고, 우리는 이러한 격자를 촘촘하게 만드는 축척 극한^{scaling limit}을 통해 원이라는 아름다운 개념에 다가서며, 현실의 근사한 원들을, 완벽한 추상적인 원의 실현으로 이해한다. 격자 모형들에서 창발하는 대칭성도 비슷한 맥락으로 이해해 보려 노력할 수 있다. 과연 이 모형들은, 구현에 필수적인 격자 구조 같은 세부사항을 초월하는, 보편성^universality을 가지는 연속체 상 이론에 지배받고 있는 것일까? 뒤미닐-코팽의 많은 업적들은 이러한 궁금증에서 출발한다고 볼 수 있다.

격자로 (못) 만들다: 이징^Ising 모형과 \(\Phi^{4}\) 모형

무작위 추출^{random sampling}의 문제로 돌아가 보자. 위에서 사용된 ‘균등한 확률로 네 개의 방향 중 하나를 뽑은’ 결과는 이산 균등 분포^{discrete uniform distribution}를 가지며, 주사위나 동전 던지기를 통해 만들어 낼 수 있는 우리에게 익숙한 무작위성의 형태이다. 이 가장 기본적인 분포에서 ‘유한개의 선택지’를 ‘균등한 확률’로 ‘하나씩’ 뽑는다는 조건들 중 하나만 바뀌어도 정의하거나 실현하는 것은 주의를 요하며, 이런 경우에 격자는 꽤나 자연스러우면서도 매력적인 만들기 도구로 떠오른다. 일례로 무한히 많은 0과 1 사이 실수들 중 하나를 균등한 확률로 뽑는 작업은, 보통 0과 1 사이 (현대 64비트 컴퓨터라면) 10여 개 자리까지 내려가는 소수들 중 하나, 즉 실선 위 격자점 중 하나를 뽑는 작업으로 구현된다. 이런 근사는 기초적이고 자연스럽지만, 엄밀하게 다루려면 벌써 사용하는 확률론의 공리계에 대한 주의를 요한다.³

‘하나씩’ 추출한다는 조건을 바꾸면 어떨까? 수학에서는 다수의 수량을 하나로 조직하는 데 함수를 사용한다. 확률적으로 추출된 함수, 즉 확률장^{random field}은 많은 분야에서 자연스럽게 나타나는 개념이지만, 무한히 많은 입력값을 가지는 함수를 추출하는 것은 일반적으로 정의하기도, 다루기도 매우 까다로운 일이다. 0과 1 사이 모든 실수를 입력받는 함수 \(f\), 즉 \(x\)축의 선분 \([0,1]\) 위 그래프 \(y=f(x)\)를 무작위로 그린다고 생각해 보라! 이대로는 너무나 막연하게 느껴지지만, 다르게 말하면 \(f\)의 형태에 따른 가중치를 추가적으로 줌으로써⁴ 다채로운 성질을 가진 확률장을 추출하길 기대해 볼 수 있다는 이야기도 된다.

이번에도 \([0,1]\)같은 무한집합 대신 그에 근사하는 촘촘한 격자 \(\Lambda\) 위 격자점들을 입력값으로 받는 함수 \(f\)들을 고려하면 일단 추출은 시도해 볼 수 있을 것이다. 일반적으로, 추출된 함수 \(f\)마다 바라는 성질을 가졌는지 수량화하는 양숫값 에너지 혹은 해밀토니안 \(H(f)\)이 주어진다고 가정하면, 함수\(f:\Lambda\to\mathbb{R}\)를 지수함숫값 확률가중치

\[
\exp\left(-\beta H(f)\right)
\]
를 주어 추출할 수 있다. 여기서 \(\beta>0\)는 물리적으로 온도의 역수에 해당하는, 낮은 에너지에 대한 선호도를 조정하는 매개변수이다. \(\beta\)가 높을수록 (온도가 낮을수록) 에너지가 낮은 \(f\)를 추출할 확률이 상대적으로 높아진다.

예를 들면, \(\Lambda\)의 각 격자점에 단순히 \(+1,-1\) 중 하나를 대응시키는 함수 \(f\)를 생각해 볼 수 있다. 이러한 함수는 가장 대표적으로 자성을 가진 물체를 모형화할 때 등장한다. 미시적인 자성인 스핀^spin을 가지는 입자들이 서로 정렬하려는 경향이 모여 거시적인 자성이 나타난다는 원리를 단순화된 모형에 구현하기 위해, 격자점 \(x\in\Lambda\) 위 스핀값 \(f(x)\in\{+1,-1\}\)들이 정렬한 정도에 따라 확률을 부여하는 것이다. 전자기학에 큰 족적을 남긴 물리학자 렌츠^Lenz가 처음 소개한 후[14] 그의 학생 이징^Ising이 본격적으로 다루기 시작한 이징 모형^{Ising model}에서, 에너지 \(H(f)\)는 스핀값이 불일치하는 이웃들의 수, 즉

\[
H(f)=\#\{\{x_{1},x_{2}\}|x_{1}\text{과 }x_{2}\text{는 }\Lambda\text{에서 이웃, }f(x_{1})\neq f(x_{2})\}
\]
로 주어진다.

즉, 스핀이 더 정렬되어 있을수록 에너지가 낮아져 더 안정성이 있는 구성이며, 확률적으로 더 높은 가중치를 가진다. 이러한 확률적인 스핀들의 분포가 거시적으로 자성을 띠려면, 우세하는 자성이 수많은 격자점들을 넘어 전달될 수 있어야 한다. 예를 들어 격자의 가장자리의 스핀들을 \(+1\)로 고정했을 때, 격자의 중심에 있는 스핀들이 \(+1\)이 될 확률이 \(1/2\)보다 커야 한다. 이런 식으로 가장자리의 자성이 격자가 촘촘해질 때 살아남는지를 생각해 볼 수 있는데, 이징은 1차원에서는 자성이 소실됨을, 즉 어떤 \(\beta>0\)에서도 중앙의 스핀이 \(+1\)일 확률은 격자점이 많아질수록 \(1/2\)로 수렴함을 증명하였다.[13] 하지만, 파이얼스^Peierls는 2차원 이상에서는 \(\beta\)가 특정 양수값보다 커지면 중앙에 있는 스핀이 가장자리 스핀의 방향을 가리킬 확률이 격자점의 수와 상관없이 \(1/2\)보다 큰 값으로 유지됨을 보였다.⁵[16] 즉, 특정한 퀴리 온도^{Curie point} 이상에서 자성을 잃어버리는 현실의 자석과 같은 상전이^{phase transition}의 존재를 도출한 것이다.

그 이후, 1944년에 온사거^Onsager는 2차원에서 정사각 격자 위 이징 모형의 해법과 임계점^{critical point}의 값 \(\beta_{c}=\frac{1}{2}\log(1+\sqrt{2})\)를 밝혀냈는데[15], 이는 모형의 수많은 자유도에도 불구하고 정밀한 결과들을 내는데 성공한 매우 놀랍고 희귀한 결과였다. 곧 양^Yang은 온사거의 결과들에 기반해 자발적 자기화^{spontaneous magnetization}, 동등하게는 격자 중앙의 스핀이 \(+1\)일 확률을 모든 \(\beta\)에서 계산해 냈고[20], 이 값이 \(\beta\)에 따라 연속적으로 변해 \(\beta\leq\beta_{c}\)에서 \(0\)이라는 사실, 즉 상전이의 연속성^continuity을 증명해 냈다.

이러한 2차원 이징 모형에 대한 정밀한 결과들에도 불구하고, 3차원의 이징 모형에 대해서는 비슷한 정밀도나 정량성을 가진 결과들을 찾기 힘든데, 일례로 임계점 \(\beta_{c}\)의 값도 아직 알려져 있지 않다. 그럼에도 불구하고, 뒤미닐-코팽과 동료들은 미해결 문제로 남아있던 3차원에서의 이징 모형 상전이의 연속성을 보였다.[3] 상전이의 연속성은 물리적으로 말하자면 자석의 온도가 높아질수록 (\(\beta\)가 낮아질수록) 자성이 줄어들어 임계점에서 갓 사라짐을 말한다. 이는 수많은 격자점을 넘어 자성이 전파되는 미임계^sub-critical 상태와 장거리에 자성이 확실히 소실되는 초임계^{super-critical} 상태 사이에 특징적인 임계 체제^{critical regime}가 존재함을 시사한다.

가능한 함숫값의 범위가 일반적인 실수로 확대된다면 어떻게 될까? 비슷하게 이웃간 값의 차이를 통제하기 위해

\[
H(f)=\sum_{x_{1}\text{과 }x_{2}\text{는 이웃}}\left(f(x_{1})-f(x_{2})\right)^{2}
\]
와 같은 에너지식을 사용할 수 있다. 이번에도 가장자리 격자점들에는 상수값 \(f\equiv0\)을 정해두자. 이렇게 추출되는 이산적 함수 \(f:\Lambda\to\mathbb{R}\)는 확률통계에서 가장 핵심이 되는 다변수 정규분포^{multivariate normal distribution}를 따르는데, \(\Lambda\)가 촘촘해지는 축척 극한 아래 무질량^massless 가우시안 자유장^{Gaussian free field}이라는 대상으로 수렴한다는 사실이 알려져 있다 (일반적으로는 2차항을 더해 유질량^massive 체제도 고려한다). 달리 말하면, 가우시안 자유장은 확률적으로 함수⁶를 추출한다는 의도에 가장 깔끔하고 명백하게 부합하는 대상 중 하나라고 할 수 있다.

가우시안 자유장은 구현의 세부사항들이 연속체 상에서 소실되는 현상, 즉 보편성의 좋은 예이기도 하다. 1차원 가우시안 자유장은 \(f(0)=f(1)=0\)을 만족하는 확률적 연속 함수로, \([0,1]\)을 이산화한 후 위와 같은 에너지식을 사용해 추출할 수도 있지만, 앞서 소개한 무작위 보행을 1차원에서 시행하여 추출할 수도 있다. 즉 \(f(0)=0\)에서 출발해 다음 격자점으로 넘어갈 때마다 \(1\)을 더하거나 빼는데, 마지막에 \(f(1)=0\)로 돌아오지 않으면 버리고 다시 시작한다. 이렇게 얻어진 두 확률적 함수들 \(f\)를 같은 축척으로–예를 들어, \(f(1/2)\)의 분산이 \(1\)이 되게–그리면 축척 극한 아래 같은 확률적 그래프로 수렴함이 알려져 있다. 이웃간 값의 차이를 통제한다는 정성적인 의도의 두 가지 구현이 같은 결과를 낳는 것이다.

이러한 보편성은 가우시안 자유장이라는 연속체 상 이론의 자연스러움을 시사하지만, 어떤 면에서는 너무 강력해서, 이웃간 값 사이 비슷한 간섭이 있는 격자 모형이라면 결국 가우시안 자유장에 지배를 받는 것이 아닌지 고려해 보아야 한다는 이야기도 된다. 이런 예로서는 사실 앞서 소개한 임계체제에서의 이징 모형도 들 수 있고, 특히 가우시안 자유장에 기반한 모형이라면 더욱 그럴 텐데, 가우시안 자유장의 에너지식에 4차항을 더해 정의한 \(\Phi^{4}\) 모형이 바로 그러한 예이다. 격자 위 임계 이징 모형과 \(\Phi^{4}\) 모형은 4차원 이상에서 축척 극한 아래 가우시안 자유장과 같은 보편성 부류^{universality class}에 속할 것이라 예측되어 왔고, 이는 5차원 이상에서는 아이젠먼^Aizenman과 프뢸리히^Fröhlich에 의해 증명되었다.[1,11]

뒤미닐-코팽은 아이젠먼과 함께, 수십 년 간 미해결로 남아있던 4차원의 경우, 즉 이 모형들이 격자가 촘촘해질 때 가우시안 자유장으로 기술된다는 예측을 증명하였다.[2] 이는 연속성 이외의 임계 체제에서의 양태가 아직도 거의 알려져 있지 않은 3차원 이징 모형과 달리 가우시안 자유장으로서의 정량적인 양태까지도 보이는 수렴 결과라고 볼 수 있다.

2차원의 풍부함: 침투^Percolation 모형들과 등각대칭성

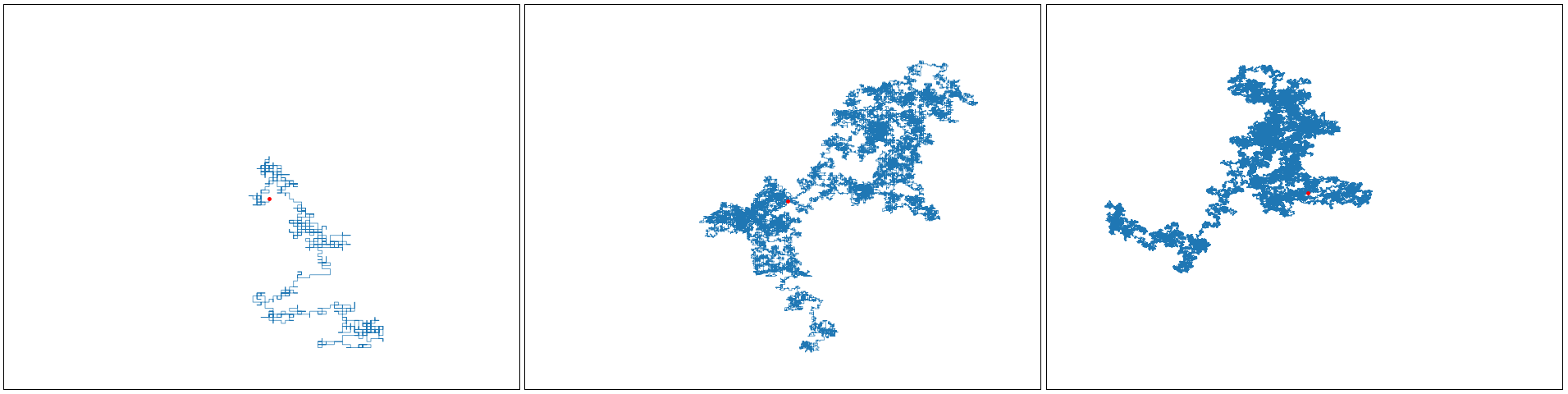
먼저 소개한 무작위 보한행은 대칭성과 확률성이 결합했을 때 얼마나 다채로운 그림을 그려내는지 보여주는 예라고 할 수 있다. 흔히 우리는 대칭성의 예로서 원이나 나비 등의 정적인 도형들을 생각하지만, 회전 대칭과는 거리가 멀어 보이는 무작위 보행의 표본들도 확률적인 의미의 회전대칭성을 가진다. 이 표본을 회전시킨⁷ 표본이 추출될 확률이 거의–즉, 격자가 촘촘해질수록–같다는 것이다. 무작위 보행은 사실 확률적으로 중요한 의미를 가지는 또 하나의 대칭성인 축척불변성^{scale invariance}도 가지는데, 예를 들어 시작점에서 반지름이 2인 원을 나갈 때까지 무작위 보행이 그린 궤적을 두 배 축소하는 축척 변환을 취하면 반지름이 1인 단위원을 나갈 때까지 추출된 보행과 거의 같은 확률 분포를 가진다.(그림2)

이러한 회전과 축척 변환은 모두 각을 보존하는 등각 변환^{conformal transformation}이라는 공통점이 있다. 2차원은 등각 변환이 풍부한 것이 특징인데, 리만 사상 정리^{Riemann Mapping Theorem}에 따르면 단위원(안의 영역)은 등각 변환을 통해 임의의 구멍 없는 평면 위 영역 \(\Omega\)로 변환될 수 있다. 확률적인 의미에서의 등각대칭성^{conformal symmetry}은 이렇게 많은 등각 변환을 거쳐도 확률 분포가 변하지 않는다는, 회전과 축척불변성을 포함하는 강력한 성질이며, 축척 극한 아래 무작위 보행에서 창발함이 질 알려져 있다. 즉, \(\Omega\)에 촘촘한 정사각 격자를 깔아 영역을 탈출할때까지 추출한 무작위 보행은, 단위원을 탈출하는 무작위 보행을 리만 사상을 통해 변환한 결과물과 확률 분포가 거의 같다.

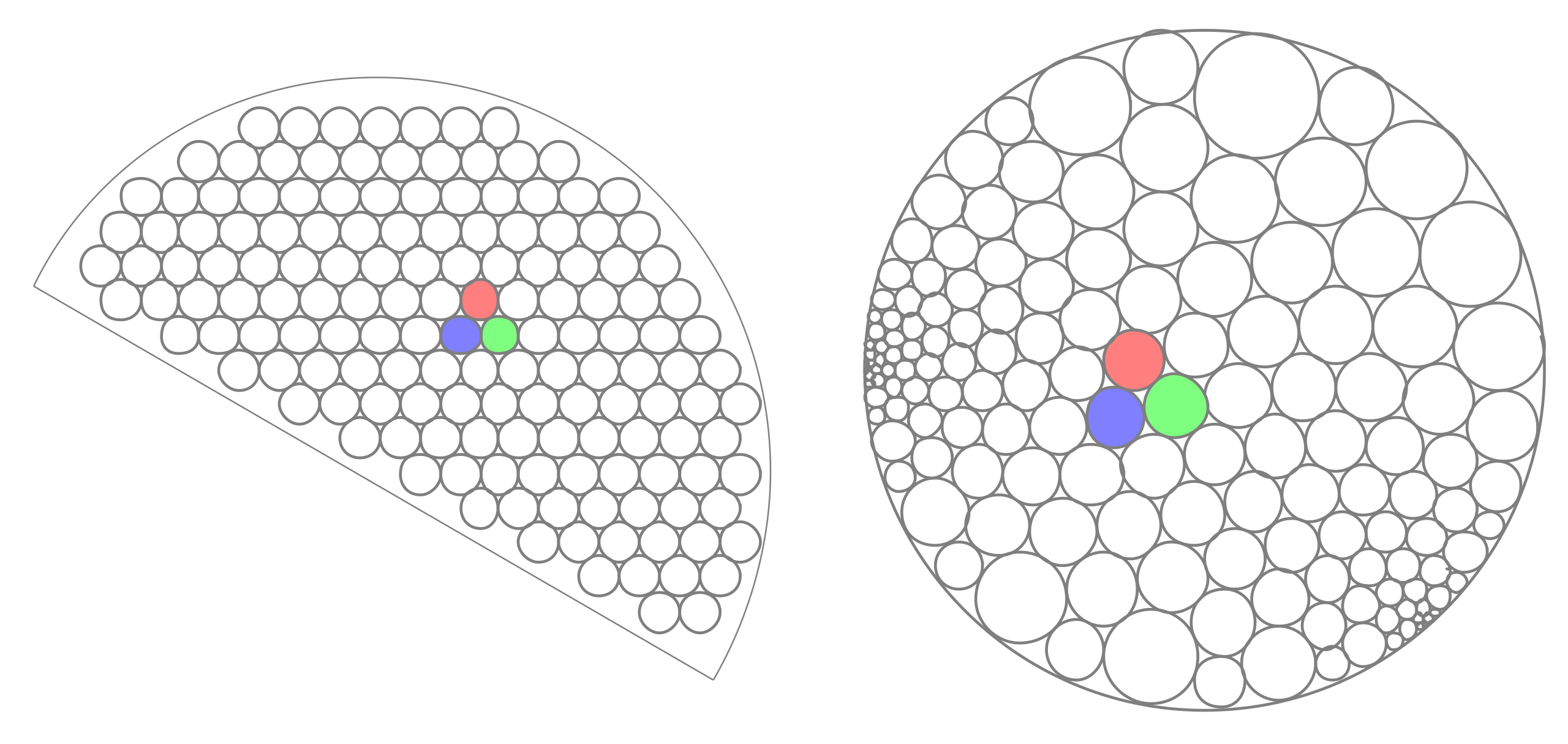
이산화라는 테마에 맞게 로딘^Rodin과 설리번^Sullivan의 정리[17]⁸를 빌려 표현하자면 다음과 같다. \(\Omega\) 안에 작은 원들을 빼곡히 채우면, 원들 사이의 인접 관계를 변하지 않게 하면서도 개별적인 원을 확대/축소해 단위원 안을 빼곡히 채우게 변환할 수 있고, 채워진 원들이 더 촘촘해질수록 역시나 이 변환은 리만 사상 정리가 보장하는 \(\Omega\)와 단위원 사이의 등각 변환에 가까워진다.(그림3) 무작위 보행의 예에서 \(\Omega\) 안의 궤적을 그 속을 채운 작은 원들을 지나가는 부분들로 분할해 생각하면, 각각의 부분 궤적은 단위원 속에 채워진 대응하는 원을 지나가는 부분 궤적과 회전 및 축척 변환을 거치면 비슷할 것이라 생각해 볼 수 있는데, 다르게 말하면 무작위 보행처럼 회전과 축척불변성을 보이는 모형들에서 그보다 강력한 등각대칭성을 기대하는 것이 마냥 무리한 일은 아니라는 말도 된다.

풍부한 등각 변환들 덕에 등각대칭성은 2차원 모형들을 다루는 물리학과 수학에 중요한 요소가 되었다. 연속 상전이를 거치는 모형들의 임계 체제는 축척 극한 아래 등각대칭성을 보일 것으로 기대되는데, 등각 변환의 수가 많다는 말은 곧 대칭성이 제공하는 정보가 많다는 말도 되기 때문이다. 구체적으로는, 많은 임계 체제의 2차원 격자 모형들은 1변수족, 즉 매개변수 하나로 결정되는 보편성 부류에 속할 것으로 예측된다. 거칠게 말하면, 이 매개변수의 값 하나로 모형의 축척 극한을 기술하는 이론이 정해진다는 것이다.

예를 들어 임계 체제의 2차원 이징 모형을 생각해 보자. 앞서 소개하였듯 이 경우에는 상전이의 연속성 및 많은 정량적 결과들이 20세기 중반부터 알려지기 시작했다. 이징 모형에서 영역의 가장자리를 두 부분으로 나누어 스핀을 각각 \(+1,-1\)로 고정했을 때, 같은 스핀으로 이루어진 두 가장자리 군집들은 중간에서 만나 경계 곡선^interface을 형성한다. 뒤미닐-코팽은 지도교수 스미르노프^Smirnov 및 동료들과 함께 이 경계 곡선이 축척 극한 아래 슈람-뢰브너 전개^{Schramm-Loewner Evolution}라는 확률적 곡선으로 수렴함을 증명하였으며[7], 여기서 보편성 부류를 결정하는 매개변수 \(\kappa\)의 값은 3으로 정해진다.(그림4)

흔히 SLE로 일컬어지는 슈람-뢰브너 전개는 무작위 보행과는 대조적으로 자기가 이미 그린 궤적을 가로지르지 않는 곡선들–경계 곡선들은 자연적으로 이 성질을 가진다–의 극한을 기술할 것이라 기대되는데, 예를 들어 매번 4개의 이웃 중 하나를 고르는 무작위 보행 대신 이미 지나가보지 않은 이웃들만 고르는 자기회피보행^{Self-Avoiding Walk}은 매개변수가 \(\kappa=8/3\)인 SLE로 수렴할 것이라 기대된다. 간단한 정의와는 달리 이 모형의 분석은 쉽지 않은데, 뒤미닐-코팽은 대표적으로 물리학자 닌하위스^Nienhuis가 1982년에 추측했던, 벌집 격자가 촘촘해질 때 자기회피보행의 수를 점근적으로 세는 문제를 박사과정 중 스미르노프와 해결한 바 있다.[10]

물론 경계 곡선이 SLE라고 추측하는 데에는 고려되는 모형들이 연속 상전이를 거치며 임계 체제가 등각대칭성을 보이는 것이 전제되는데, 수학적으로는 모두 일반적으로 간단치 않은 증명의 대상이다. 이렇게 연속 상전이를 보일 것으로 예측되어 온 모형들 중 포투인-케스텔라인^{Fortuin-Kesteleyn, FK} 침투^Percolation 모형들이 있다. 침투 모형은 비균질한 매질을 확률적으로 구현한 격자 모형으로, 확률적으로 열리고 닫히는 격자의 변들을 통해 양 끝 사이 물질이 투과할 수 있는지, 즉 연결된 열린 변들의 군집^cluster으로 양 끝이 연결될 수 있는지가 주요한 질문이 된다. 매개변수 \(q\geq1\)가 정해졌을 때, \(q\)-FK 침투 모형은 정사각 격자 변들의 집합 \(\Lambda_{\text{edges}}\)의 부분집합인 열린 변들의 집합 \(E\subset\Lambda_{\text{edges}}\)를 확률적으로

\[
\mathbb{P}_{p,q}[E]\propto\left(p/(1-p)\right)^{\#E}q^{(\text{열린 군집의 수})}
\]
의 가중치를 주어 추출한다. \(0\leq p\leq1\)는 이징 모형에서 온도의 역할에 대응하는 변수로, 뒤미닐-코팽은 박사과정 중 베파라^Beffara와 함께 \(p=\sqrt{q}/(1+\sqrt{q})\)일 때 이 모형이 상전이를 거친다는 것을 증명했다.[5]

놀랍게도, \(q\)에 대해 연속적으로 변하는 듯 보이는 가중치식이지만, \(q\) 값이 조금만 바뀌어도 FK-침투 모형의 정체성은 근본적으로 바뀌는데, \(q\) 값이 다른 FK-침투 모형들은 서로 다른 보편성 부류에 속할 것으로 예측된다.[19] 구체적으로는, 정확히 \(1\leq q\leq4\)일 때 FK-침투 모형은 연속 상전이를 보이며, 그 임계 체제에서의 경계 곡선⁹은 서로 다른 매개변수의 SLE로 수렴할 것이라는 것이다. 앞서 소개한, 정성적으로 유사하지만 정량적으로 분명히 다른 세 개의 모형들이 같은 보편성 부류에 속하는 경우와 대비된다.

수학자 슈람^Schramm의 영감으로 제안된[18] SLE의 대두 전에 물리학에서는 2차원 임계 모형들을 등각장론^{Conformal Field Theory}이라는 체계를 통해 분류하고 분석했다.[6] 경계 곡선의 기하적 특성에 대해 주목하는 대신, 등각장론은 장론^場論적 관점을 택해서, 일단 보편성 부류가 정해지면 (매개변수 \(c\)가 정해지면) 멀리 떨어진 두 격자점이 같은 군집으로 연결될 확률이 점근적으로 감소하는 속도 등을 예측해 낸다. 현재는 등각장론과 SLE는 본질적으로 같은 보편성 부류들을 바라보는 두 관점으로 볼 수 있다는 사실이 수학적으로 많은 부분 설명되었다.[4] 즉 FK-침투 모형들은 이렇게 모형들이 ‘다르게 등각대칭일 수 있는 방식들’을 보여주는 구체적인 예로서 기능하고 있는 것이다.

임계 FK-침투 모형들은 등각대칭성을 보일 것이 예측되지만, 이징 모형과 연관된 \(q=2\)의 경우를 제하고 그런 수준의 정밀성을 가지는 결과들의 수학적 증명은 요원했다. 뒤미닐-코팽은 동료들과 함께 이에 대한 부분적 결과들을 차근차근 쌓아나가고 있는데, 대표적으로 2차원 FK–침투 모형에 대해 예측되어 온 대로 \(q>4\)일 때 이 상전이가 불연속임을[12], 그리고 \(q\leq4\)일 때 상전이가 연속임을[9] 증명했다. 더 나아가, 뒤미닐-코팽과 동료들은 최근에 FK-침투 모형의 장론적 회전대칭성, 즉 두 격자점이 열린 군집으로 연결될 확률이 격자가 촘촘해질수록 두 점 사이 거리에 의해서만 정해진다는 결과를 발표했다.[8] 그는 필즈상 수상 강연에서 ‘본인 생애에는 불가능할’ 것이라 농담했지만, 확률기하학자들의 숙원인 등각대칭성의 증명은 지난 10년 사이 눈에 띄게 가까워진 것이다.(그림5)

끝맺으며

뒤미닐-코팽 교수는 2011년 스위스 제네바 대학에서 박사학위를 받은 후, 얼마 되지 않아 동 대학에서 교수가 되었다. 앞서 소개한 그의 업적들은 대부분 그가 학위를 마친 지 10년 이내, 혹은 학위 중에 발표되었고, 이런 행보에서 엿볼 수 있듯 그는 연구결과들의 우수함뿐만 아니라 연구활동의 활발함과 폭넓음으로도 명성이 높다. 필자가 근처인 로잔에서 박사과정을 밟으며 제네바 대학에 세미나를 들으러 갈 때 본 뒤미닐-코팽 교수는 언제나 끊임없는 방문 연구자들과 토의하는 모습으로 기억에 남았다. 아니나 다를까, 아직 세부적인 연구 주제나 방향을 잡기 전에도 익히 들어 알고 있었던 미해결제들인 3, 4차원 이징 모형의 상전이나 4차원 \(\Phi^{4}\) 모형의 건설불가능성 문제가, 다양하면서도 그의 이름이 빠지지 않는 연구진들에 의해 풀렸다는 소식을 하나씩 듣는 것은, 학생으로서 사뭇 경외심을 가지게 하면서도 예비 수학자로서 고무적으로 다가온 경험이었다. 또한 그의 광범위한 논문, 저술 및 강의들의 포괄성과 접근성은 필자에게 후배 연구자로서 수학에서의 소통을 어떻게 해야 할지에 대한 귀감이 되어 왔다. 그와 동료들이 찾아내는 놀라운 결과들은 앞으로도 활발히 계속될 것이라고 믿으며, 다시 한 번 필즈상 수상을 축하드린다.