휘어진 공간의 극한은 어떻게 생겼을까

들어가며

학교에서 배우는 수학적인 개념들 중에서도 극한은 매우 중요하게 다루어집니다. 이 문장으로 글을 시작하려고 보니, 정말 그런지 의구심이 생겨서 (끊임없이 질문이 생기는 것은 수학자와 어린아이의 공통점일 것입니다) 2023학년도 수능시험 문제를 펼쳐 보았습니다. 그랬더니 바로 1번 문제에 실수의 무리수 승 (\(2^{\sqrt{2}}\))이 등장합니다. 이 수는 2에다 \(\sqrt{2}\)로 수렴하는 유리수 승을 취하였을 때 극한이 존재함을 보임으로써 정의할 수 있습니다. 2번 문제는 한층 더하여 “\(\displaystyle{\lim_{x \to \infty}\frac{\sqrt{x^2-2}+3x}{x+5}}\)의 값은?” 하고 연속함수의 극한에 대해서 묻고 있습니다. 이와 같이 어떤 나열의 극한, 즉 어떤 대상들을 극으로 몰고 갔을 때 무엇인가를 향하여 접근한다는 개념은 우리에게 낯설지 않습니다. 중고등학교 교과과정에서 이 대상들은 대개 수열의 항이거나, 혹은 서로 다른 \(x\) 값들에 대한 함숫값이지요.

그런데 숫자만 나열할 수 있는 것은 아닙니다. 수학이라는 단어에 數^{셈 수}가 들어 있다고 해서, 논리적인 언어인 수학으로 표현할 수 있는 것들이 단지 숫자에 그치는 것은 아니니까요. 어떤 대상들을 나열해 놓았을 때 극한으로 수렴하는 현상은 수학의 많은 분야에서 매우 다양한 형태로 나타납니다. 이 대상들은 함숫값이 아니라 함수들 자체일 수도 있고, 심지어는 그 함수들의 정의역에 해당하는 공간들일 수도 있습니다.

재미있게도 어떤 대상의 극한을 취함으로써 그 대상이 어떤 성질을 지녔는지가 역으로 드러나기도 합니다. 한 컵의 물을 떠다 놓고 관찰해 본다면, 컵의 안쪽만 볼 때와는 다르게 물이 컵에 닿은 경계면으로 다가갈수록 표면장력이 두드러지며 수면을 휘어지게 만들고 있습니다. 이 물컵을 냉동실에 넣어 온도를 낮추면서 물이 얼음에 가까워지는 변화를 관찰할 수도 있겠습니다. 그럼으로써 물분자의 특징인 수소 결합에 대해서 더 잘 알게 되겠지요. 마치 울타리로 둘러싸인 목장 안쪽에서 평화롭게 풀을 뜯고 있는 양들은 한없이 온순하게만 보이다가도, 울타리 가까이로 내몰아 보면 (=양떼의 극한을 취하면) 비로소 양들이 숨긴 진짜 성질이 드러나는 것에 비유할 수 있겠지요. 물론 어떤 상황에서든 순하고 태평한 양떼일 수도 있습니다. 반면에 어떤 양은 숨겨 놓은 뿔을 드러낼 수도 있습니다. 심지어는 울타리 안에만 사는 얌전한 양인 줄 알았더니 용감하게 목장을 뛰쳐나갈 수도 있습니다. 극한을 취해 보면 양들이 어떤 동물인지를 진정으로 이해하게 되는 것입니다.

미분기하학자의 관점에서, 이 글에서는 리만다양체, 그 중에서도 리치 곡률이 제한된 리만다양체를 양떼로 삼아 보겠습니다. 이 양떼목장이 과연 어떤 곳일까 하는 질문은 역사적으로 여러 저명한 수학자들의 관심사였으며 현재도 활발히 연구되고 있습니다. 리만다양체와 리치 곡률이 무엇인지와 리치 곡률이 미분기하학 내외로 어떤 중요성을 가지는지는 아래에서 개략적으로 다루어집니다. 지면의 한계로 엄밀한 정의와 수식은 상당 부분 생략하고, 개념을 전달하는 데 집중하고자 합니다.

거리 공간, 그중에서도 리만다양체

하나의 집합 안에서도 두 점간의 거리를 잴 수 있는 방법은 다양합니다. \(x\)축과 \(y\)축을 가진 실평면(\(\mathbb{R}^2\))을 예로 들어 보겠습니다. 좌표축에 평행한 직선만 따라가며 격자 형태로 거리를 잰다면 (이 거리를 택시 거리^{taxi metric}라 합니다), 두 점 \((x_1, y_1), (x_2, y_2)\) 사이의 거리는 \(|x_1 – x_2| + |y_1 – y_2|\)입니다. 반면 조금 더 익숙한 방식으로 두 점 사이의 최단 직선거리를 잰다면, 거리는 피타고라스 정리에 의하여 \(\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\)가 됩니다. 후자가 우리가 가장 흔히 생각하는 거리공간^{metric space}으로서의 실평면에 해당합니다. 마찬가지로 피타고라스 정리에 의해 거리가 주어지는 일반적인 차원의 실공간(\(\mathbb{R}^n\))도 생각할 수 있습니다.

\(\mathbb{R}^n\)은 거리공간들 중에서도 직관적이고 단순하여 가장 잘 이해된 공간입니다. 리만다양체^{Riemannian manifold}는 국소적으로 이러한 \(\mathbb{R}^n\)과 기하학적 성질이 같은 공간입니다. 수학적으로 조금 더 정확한 설명을 부연하자면, 먼저 미분다양체^{Differentiable manifold}는 국소적으로 \(\mathbb{R}^n\)과 미분동형인 공간을 의미합니다. 즉 \(n\)차원 미분다양체 상의 어느 점이든 마치 \(n\)차원 실공간처럼 보이는 근방^neighborhood을 가지고 있다는 의미입니다. 여기에 거리나 각도, 곡률, 길이, 부피 같은 기하학적 개념까지 고려된 것, 즉 리만 계량^{Riemannian metric}을 더한 것이 리만다양체입니다.

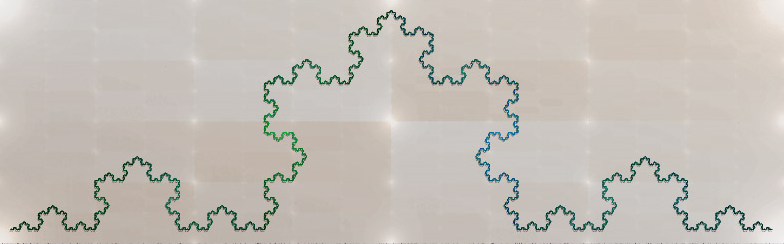
부드러운 곡선의 한 점에서 접선을 정의할 수 있고 곡면에 접면을 정의할 수 있듯이, \(n\)차원 리만다양체는 어떤 점이든 \(n\)차원 접공간^{tangent space}을 가집니다. 이 접공간은 유일하게 결정되며 \(\mathbb{R}^n\)과 같습니다. 이것은 리만다양체만의 특별히 좋은 성질로, 일반적으로도 성립하는 것은 아닙니다. 예를 들어 아래와 같은 눈송이 모양의 코흐 곡선^{Koch snowflake}을 보겠습니다. 어느 점에서든 접하는 방향이 계속해서 변하고 있어 접선이 유일하게 결정되지 않지요.

어떤 거리공간이 \(n\)차원이리라고 기대할 때, 접공간이 잘 정의되며 \(\mathbb{R}^n\)과 같은 점들만 골라서 모아 놓은 집합을 정규점 집합^{regular set}, 그렇지 못한 점들의 집합을 특이점 집합^{singular set}이라고 부를 수 있습니다. 리만다양체는 모든 점이 정규점이고, 코흐 곡선은 모든 점이 특이점입니다. 일반적으로 정규점 집합이 클수록 수학자들이 잘 알고 있는 리만다양체에 가깝고, 특이점 집합이 클수록 난해한 양상을 띠는 것이지요. 그렇다면, 매우 순한 양떼처럼 보이는 리만다양체들의 극한으로 나타나는 공간들 또한 리만다양체일까요? 그렇지 않다면, 극한 공간은 과연 얼마나 큰 특이점 집합을 가지고 있을까요?

다양체의 휘어짐: 리치 곡률

속 시원한 해답이 있다면 좋겠지만, 안타깝게도 한두 마디로 대답하기에는 너무나 방대하고 난해한 질문입니다. 두 가지 문제가 발생하기 때문입니다.

첫 번째 문제는 리만다양체들은 끝도 없이 다양한 양상을 보일 수 있어, 이대로는 양떼목장이 아니라 동물원에 가깝다는 것입니다. 질문과 해답이 유의미하려면 관심사를 조금 더 좁히는 것이 좋습니다. 그러므로 리만다양체들 중에서도 리치 곡률^{Ricci curvature}이 제한되는 경우를 살펴보겠습니다. 가독성을 위하여, 리치 곡률의 엄밀한 정의보다는 기하학적 의미와 중요성을 위주로 설명하도록 하겠습니다.

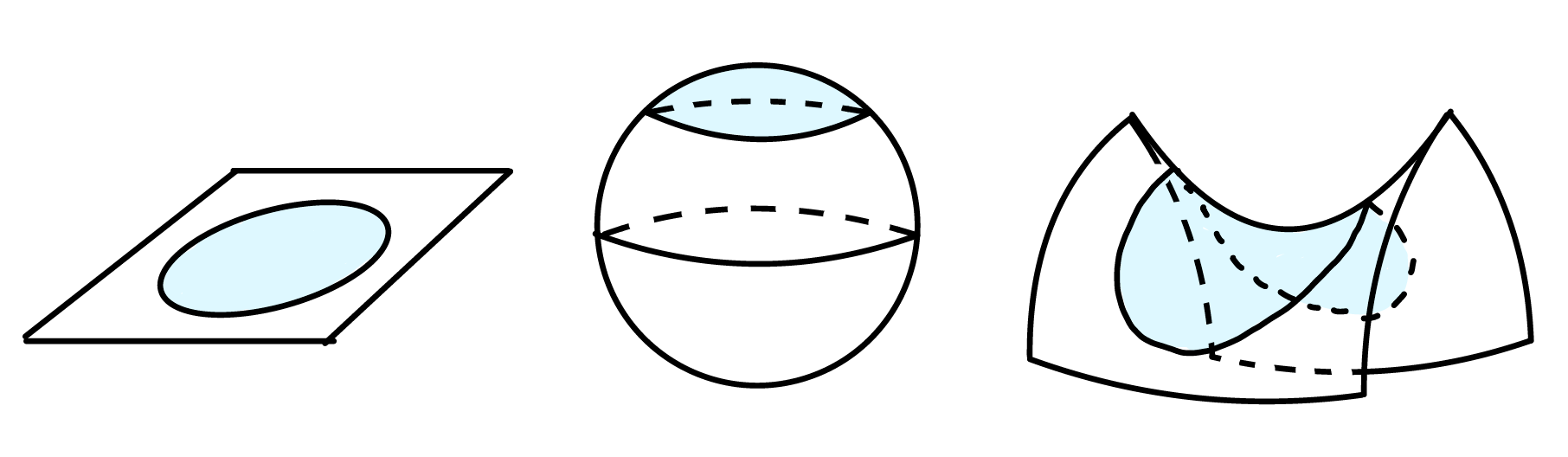
다음과 같이 세 개의 2차원 리만다양체들을 떠올려 봅시다. 앞서 살펴본 실평면 \(\mathbb{R}^2\), 반지름이 1인 구 \(\mathbb{S}^2\), 그리고 말안장과 같이 휘어진 다양체인 쌍곡 공간^{hyperbolic space} \(\mathbb{H}^2\)입니다. 이제 각각의 다양체 위에 한 점 \(p\)를 잡고, 그 점으로부터 거리가 \(r\)이내인 영역의 넓이를 생각해 봅시다. 이 넓이는 2차원에서 반지름 \(r\)인 공^ball의 부피^volume에 해당하므로, \(\mathrm{Vol}_2(B_p(r))\)로 표기하겠습니다.

실평면에서 반지름 \(r\)인 원 안의 넓이는 \(\pi r^2\)입니다. 구에서도 약간의 계산을 통해 \(\mathrm{Vol}_2(B_p(r))=2\pi (1-\cos r)\)임을 얻을 수 있습니다. \(\cos r = 1-\frac{1}{2!}r^2 + \frac{1}{4!}r^4 + \cdots\)라는 테일러 전개를 대입하면, 대략 \(\mathrm{Vol}_2(B_p(r)) \approx \pi r^2 – \frac{\pi}{12} r^4\)이 되어 실평면에서 계산한 \(\pi r^2\)보다 작을 뿐 아니라, \(r\)에 따른 증가 속도가 느립니다. 이것은 구의 리치 곡률은 1, 실평면의 리치 곡률은 0이기 때문입니다. 일반적으로 리치 곡률이 클수록 부피는 작아집니다. 마찬가지로 \(\mathbb{H}^2\)에서는 \(\mathrm{Vol}_2(B_p(r))=2\pi (\cosh r-1) \approx \pi r^2 + \frac{\pi}{12} r^4\)임이 알려져 있어 \(r\)에 따라 \(\pi r^2\)보다 빠르게 증가합니다. \(\mathbb{H}^2\)의 리치 곡률은 \(-1\)로 실평면의 0보다 작고, 따라서 부피는 큰 것이지요.

이 세 가지 계산은 부피 증가에 대한 비숍-그로모프의 단조성 공식^{Bishop-Gromov monotonicity formula}의 특수한 경우입니다. 리치 곡률이 \(k\) 이상인 리만다양체와 리치 곡률이 정확히 \(k\)인 (그리고 단일 연결된^{simply connected}) 리만다양체의 부피 증가 속도를 비교하면, 전자가 후자보다 부피가 느리게 증가합니다. 비숍-그로모프 공식을 포함하여 여러 가지 단조성 공식이 기하학적 해석학 전반에서 유용하게 쓰입니다. 곡률흐름에서의 단조성 공식에 대해 언급된 최경수 교수님의 HORIZON 기사 “곡면의 열방정식 [1]: 에너지가 줄어들면 단순해진다”와 최범준 교수님의 HORIZON 기사 “등주부등식, 곡률흐름 그리고 질량”을 함께 읽어 보시면 좋으리라 생각됩니다.

수학사의 난제들에 관심이 많은 독자라면, 리치 곡률이라는 이름에서 리치 흐름^{Ricci flow}을 연상할지도 모릅니다. 실제로 리치 흐름은 리만다양체의 시간에 따른 변화를 뜻하는 곡률흐름이 리치 곡률에 의해 주어지는 경우를 말합니다. 식으로 쓰면 다음과 같습니다. 시간 \(t\)에서의 리만 계량을 \(g(t)\)리치 곡률을 \(\mathrm{Ric}(g(t))\)라고 쓸 때, 리치 흐름의 식은 \(\frac{\partial}{\partial t} g(t) = -2 \mathrm{Ric}(g(t))\)입니다. 이 리치 흐름을 사용하여 3차원 위상수학의 오랜 난제인 푸앵카레 추측을 해결할 수 있으리라고 해밀턴^Hamilton이 제안하고 페렐만^Perelman에 의하여 증명이 완성된 것은 21세기 수학의 가장 유명한 성과들 중 하나지요.

리만다양체의 리치 곡률은 수리물리학에 있어서도 대단히 중요합니다. 앞서 살펴본 \(\mathbb{R}^2\), \(\mathbb{S}^2\), \(\mathbb{H}^2\)과 같이 리치 곡률이 상수인 다양체를 아인슈타인 다양체^{Einstein manifold}라 합니다. 아인슈타인 다양체는 상대성 이론에서 중력장에 의한 시공간의 휘어짐을 기술하는 아인슈타인 방정식의 해가 됩니다. 아인슈타인 방정식에 대하여 오성진 교수님께서 설명해 주신 HORIOZN 기사 “블랙홀 안에서는 어떤 일이 벌어질까?: 특수 상대성 이론에서 블랙홀까지”를 함께 읽으시는 것 또한 권해 드리고 싶습니다. 또한 초끈이론에서 시공의 축소화 모델인 칼라비-야우 다양체^{Calabi-Yau manifold}도 아인슈타인 다양체의 특별한 예에 해당합니다.

리치 곡률의 의미와 중요성에 대해 살펴보았으니, 이제 리만다양체의 극한에 대한 질문에 따라오는 두 번째 난점을 다루어 보겠습니다.

거리 공간들 사이의 거리

앞선 질문에 대답하는 데 또 다른 난점은, 다양체들의 극한을 취하는 방법을 적절히 정하는 것도 못지않게 어려운 문제라는 겁니다. 숫자의 나열이 극한값으로 수렴하는 것은 의미가 명확하지만 (실수 수열 \(\{a_n\}\)이 \(a_\infty\)로 수렴한다는 것은 \(n\)이 무한대로 향할 때 \(|a_n – a_\infty|\)가 0으로 향한다는 의미이지요), 두 리만다양체, 나아가 두 거리 공간의 차이가 0으로 간다는 것은 어떻게 정의하여야 할까요?

두 거리 공간 \(X,Y\)가 또 다른 거리 공간 \(Z\) 안에 들어 있는 부분공간^subspace인 경우, \(X\)와 \(Y\) 사이의 거리는 다음과 같이 잴 수 있습니다. 먼저 \(X\)의 점들 중 \(Y\)에서 가장 멀리 떨어진 것을 찾고 이 거리를 기록합니다. 이제 \(Y\)에서 똑같이 반복합니다. 이 두 거리 중에 더 큰 것을 \(Z\) 내에서 잰 하우스도르프 거리^{Hausdorff distance}라 합니다. 수식으로는 \(d_H^Z(X,Y) = \max \{ \sup_{x\in X} \inf_{y \in Y} d(x,y), \sup_{y \in Y} \inf_{x\in X} d(x,y) \}\)와 같이 나타낼 수 있겠지요.

이제 일반적으로 \(X,Y\)가 주어진 경우, \(X,Y\)를 부분공간으로 가지는 \(Z\) 중에서 \(d_H^Z(X,Y)\)를 가능한 작게 만들어 봅니다. 즉, \(X,Y\)의 그로모프-하우스도르프 거리^{Gromov-Hausdorff distance}는 \(d_{GH} (X,Y) = \inf_{Z} d_H^Z(X,Y)\)라고 정의됩니다.

리치 곡률을 공부하는 데 그로모프-하우스도르프 거리가 적절한 이유는 그로모프의 옹골성 정리^{compactness theorem}가 극한의 존재성을 보장하기 때문입니다. 이 정리에 따르면, 리치 곡률의 하한을 갖는 리만다양체들의 나열이 있으면 항상 어떤 부분나열^subsequence은 그로모프-하우스도르프 거리 하에서 어떤 거리 공간으로 수렴합니다.

따라서, 앞서 제기한 “리만다양체들의 극한은 또다시 리만다양체인가? 그렇지 않다면, 특이점 집합은 얼마나 클까?”하는 질문이 수학적으로 조금 더 명확해졌습니다. 리치 곡률이 제한된 리만다양체의 그로모프-하우스도르프 극한이 존재한다는 것을 알았으니, 이 극한 거리 공간의 특이점 집합에 대한 질문이 되지요.

리치곡률이 제한된 다양체들의 극한

정규점에서는 접공간이 존재하며 \(\mathbb{R}^n\)과 같음을 떠올려 볼 때, 특이점에서도 접공간이 존재하는지, 그리고 비록 \(\mathbb{R}^n\)처럼 \(n\)개나 되는 직선 방향에 대하여 대칭은 아니더라도 \(k(\leq n)\)개의 직선 방향에 대하여 대칭인지 물을 수 있습니다. 이제 특이점 전체의 집합을 \(\mathcal{S}\), 접공간이 최대 \(k\)개의 직선 방향으로 대칭적인 특이점의 집합 (즉, 어떤 거리 공간 \(X,Y\)에 대해서도 접공간이 \(\mathbb{R}^{k+1} \times X\) 형태가 될 수 없는 특이점의 집합)을 \(\mathcal{S}^k\)라 표기하겠습니다. \(\mathcal{S} = \cup_{k \geq 0} \mathcal{S}^k\)라는 것을 정의로부터 알 수 있습니다. 또한 \(k\)가 작아질수록 접공간은 \(\mathbb{R}^n\)에서 멀어질 것이고, 따라서 특이점은 점점 예측하기 어려운 양태를 보이게 되겠지요.

\(n\)차원 리만다양체들의 리치 곡률이 하한을 가질 뿐 아니라 부피도 양의 하한을 가질 경우, 치거^Cheeger와 콜딩^Colding이 극한 거리 공간의 특이점 집합에 대하여 중요한 사실을 증명하였습니다. (이때 \(\dim\)은 하우스도르프 차원^{Hausdorff dimension}을 뜻합니다. 실공간 \(\mathbb{R}^n\)만이 아니라 일반적인 거리 공간에 대해 정의할 수 있는 차원입니다. 정확한 정의는 분량상 생략하나, \(k\)가 클수록 공간이 커지며 \(\mathbb{R}^n\)의 차원은 \(n\)인 등 일반적인 직관과 일치합니다.)

\(\dim \mathcal{S} \leq n-2,\)
\(\dim \mathcal{S}^k \leq k.\)

따라서 특이점 집합은 극한 공간 전체에 비하여 상당히 작은 부분이 됩니다. 예를 들어 전체 공간이 2차원이라면 특이점 집합은 0차원, 즉 이산적인 점들의 모임입니다. 전체 공간이 3차원이라면 특이점 집합은 최대 1차원이 됩니다.

그런데 이것이 과연 특이점 집합에 대해 얻어낼 수 있는 최상의 정보일까요? 특이점 집합은 어쩌면 이보다도 더 작은 것이 아닐까요? 4차원에서 1차원 이상의 특이점이 발견되지 않았기 때문에, 특이점 집합은 사실 최대 \((n-4)\)차원일 것이라는 가설이 생겨났습니다. 이를 ‘여차원 4 가설^{codimension 4 conjecture}‘이라 합니다. 리치 곡률과 부피의 하한에 더하여 리치 곡률이 상한도 갖는 경우, 여차원 4 가설은 치거^Cheeger와 네이버^Naber에 의해 증명되었습니다.

\[\dim \mathcal{S} \leq n-4.\]

예를 들어 \(n=3\)인 경우에는 \(\mathcal{S}=\emptyset\)이 되어, 극한 공간은 특이점을 갖지 않고 또다시 리만다양체가 됩니다. \(n=4\)인 경우 특이점 집합은 이산적인 점들의 모임입니다. 이와 같이, 리치 곡률이 제한된 리만다양체들의 극한은 아주 작은 집합(여차원 4 이상인 집합)을 제외하면 리만다양체들과 거의 같은 구조를 가집니다.

글을 마치며

리만다양체의 극한에 대해서 이 글에서 소개한 것은 지극히 일부에 불과하며, 이외에도 수많은 연구가 진행되어 왔습니다. 위에서 다룬 치거, 콜딩, 네이버의 결과들은 타원형 편미분 방정식 및 양적 층화^{quantitative stratification}를 주요 방법론으로 삼고 있습니다. 반면에 곡률흐름(특히 리치 흐름)을 통하여 극한을 공부하는 방법도 가능합니다. 이 글에서는 극한 공간의 특이점 집합이라는 한 면모에만 집중하였지만, 극한 공간의 위상수학적 성질도 여러 수학자들의 관심사입니다. 한편으로 극한 공간들은 RCD 공간^{RCD space}이라는 특별한 해석학적 성질도 가지고 있는 거리 공간이며, RCD 공간 또한 활발한 연구의 주제입니다. 이 밖에도 리치 곡률 대신 다른 종류의 곡률이 제한되는 경우의 연구, 실다양체가 아닌 복소다양체의 극한에 대한 연구 등, 기하학 내에서도 공간의 극한에 대한 수학자들의 궁금증과 해답은 그야말로 무궁무진합니다.

기하학 외적으로도, 심지어는 수학만이 아니라 다른 학문 및 실생활에 있어서도 비단 숫자만이 아닌 다양한 객체들의 극한을 고려하게 되는 경우가 얼마든지 있을 것입니다. 이와 같이 서로 다른 상황에서 어떤 비슷한 맥락이 나타나는지 눈여겨보시는 것도 이 글의 독자분들께 하나의 즐거움이 될 수 있으면 좋겠다고 생각하며 글을 마칩니다.