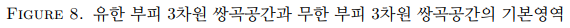세상은 계속해서 변하지만 와중에 변하지 않는 것들도 있습니다. 이번 연재에서는 수학적 대상인 3차원 쌍곡 공간의 변형과 그에 대한 저항, 즉 강직성에 대해 다루고자 합니다. 아래에서 정의할 3차원 쌍곡 공간은 기하학, 위상수학, 동역학 및 정수론 등 수학의 여러 분야에서 등장하는 중요한 대상입니다. 하나의 3차원 쌍곡 공간은 때로는 또다른 3차원 쌍곡 공간으로 변형될 수 있고, 또 그럴 수 없을 때도 있습니다. 주어진 3차원 쌍곡 공간이 변형될 수 없는지, 혹은 어떠한 변형만을 갖는지에 대한 성질을 우리는 강직성이라 부릅니다. 유한 부피를 갖는 3차원 쌍곡 공간은 변형될 수 없다는, 약 50년 전 모스토우의 강직성 정리[2,3,4]에서 출발하여, 무한 부피에서의 강직성을 규명한 최근 연구결과[1]까지 소개하고자 합니다.
3차원 쌍곡 공간이란?. 3차원 쌍곡 공간이란, 곡률이 인 3차원 공간을 의미하며 3차원 쌍곡 다양체hyperbolic 3-manifold라고도 불립니다. 형식적으로 3차원 쌍곡 공간을 정의하기보단, 우리가 어떻게 3차원 쌍곡 공간을 얻을 수 있는지를 묘사함으로써 이를 상상해보고자 합니다.
여러가지 도넛면을 얻는 방법 3차원도, 쌍곡 공간도 아니지만 우리에게 친숙한 도넛면을 생각해 봅시다. 도넛에서 속을 비워낸 도넛면은 2차원 대상으로, 원환체 라고도 불립니다. 도넛 면을 아래 그림과 같이 잘라보면 사각형을 얻을 수 있습니다. 이를 정확히 반대로 진행하면, 사각형의 마주보는 각 변을 붙여 도넛면을 얻을 수 있기도 합니다.
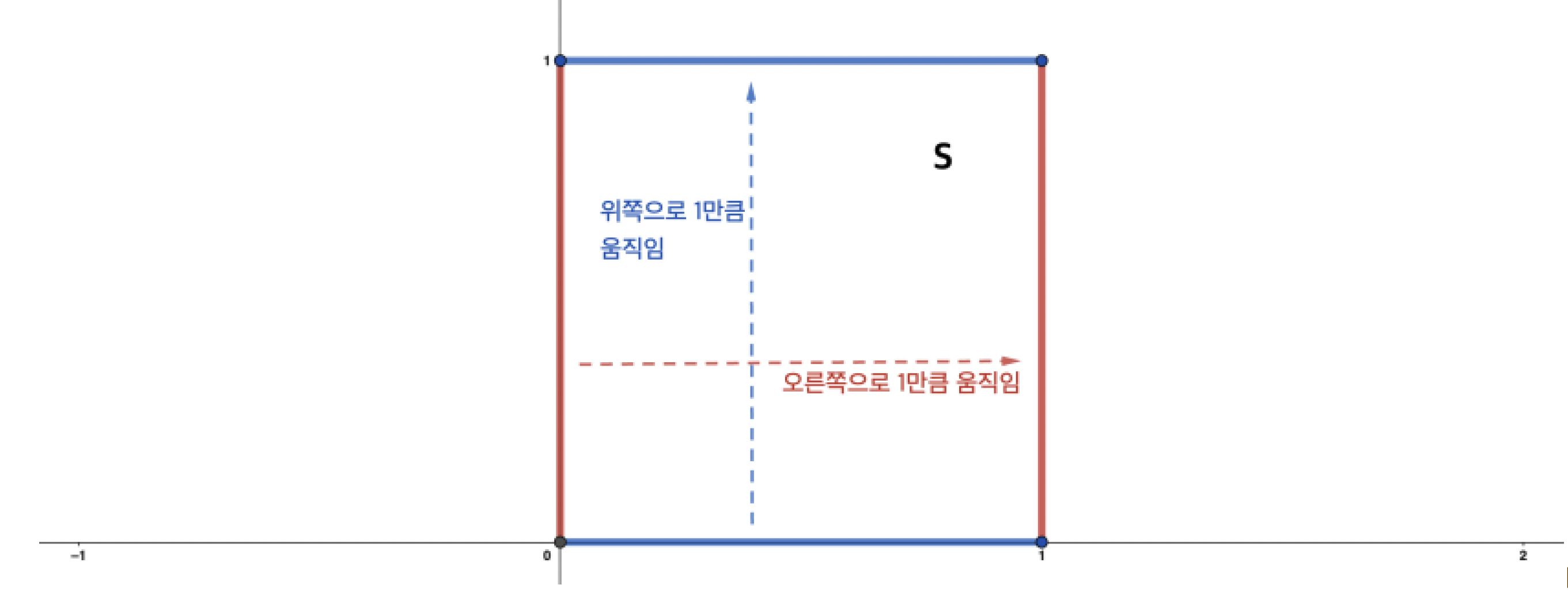
이제 사각형을 평면에 놓아봅시다. 여기에서 평면은, 유클리드 평면이라고도 불리는, 무한한 평면입니다. 예로, 평면 위에서 네 꼭짓점을 갖는 정사각형 S를 생각해 봅시다. 이제 “마주보는 각 변을 붙이는 것”은, “오른쪽으로 1만큼 움직이는 것”과 “위로 1만큼 움직이는 것”에 대응됩니다. 한 가지 주목할 점은, “마주보는 각 변을 붙이는 것”은 정해진 정사각형에서 논의가 되는 “붙임”이지만, “오른쪽으로 1만큼 움직이는 것”과 “위로 1만큼 움직이는 것”은 평면 전체에서 논의되는 “움직임”이라는 것 입니다.
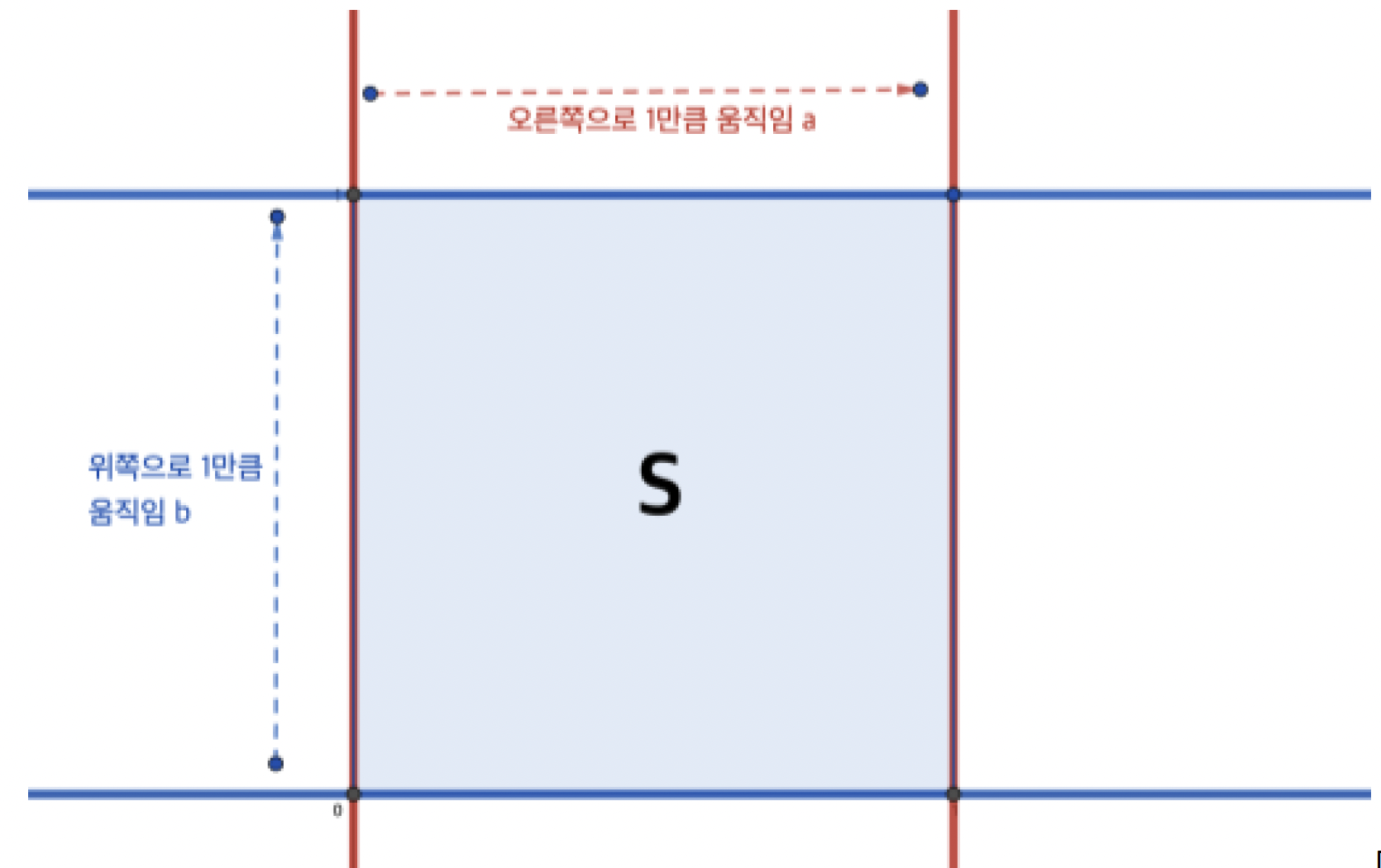
역으로, 평면 위에서 “오른쪽으로 1만큼 움직이는” 움직임 a와, “위쪽으로 1만큼 움직이는” 움직임 b를 생각해 봅시다. 움직임 a는 원점 을 지나는 y축을 오른쪽으로 1만큼 움직여
을 지나고 y축에 평행한 직선으로 보냅니다. 움직임 b는 원점
을 지나는 x축을 위쪽으로 1만큼 움직여
을 지나고 x축에 평행한 직선으로 보냅니다.
자, 이제 우리는 x축, y축과 이를 a, b로 움직여 얻은 직선들이 앞서 생각했던 정사각형을 형성한다는 것을 확인할 수 있습니다. 또, 각각의 움직임 a와 b는, 우리가 정사각형에서 도넛면을 얻을 때 정사각형의 마주보는 각 변을 서로 대응시키는 것, 즉 붙이는 것으로 이해할 수 있습니다. 즉, 평면 위에서 두 “움직임”을 고려함으로써 정사각형 S와 도넛면을 얻어낼 수 있고, 이 도넛면은 정사각형 S가 평면의 부분공간으로서 갖는 기하구조를 그대로 가지게 됩니다. 이같은 이유로, 정사각형S를 해당 도넛면의 “기본영역”이라고 합니다.
기본영역의 의미와 “변을 붙이는 것”을 어떻게 움직임으로 이해할 수 있는지 조금 더 자세히 살펴보고자, 위 예시에서의 기본영역인 정사각형 S를 평면 전체의 일부로서 생각해보도록 하겠습니다. 움직임 a와 움직임 b, 그리고 a와 b의 “역 움직임”인 왼쪽으로 1만큼 움직이는 것과 아래쪽으로 1만큼 움직이는 것, 총 네 가지의 움직임을 이용하여 정사각형 S를 움직여 볼 수 있습니다. 예를들어, 정사각형 S를 오른쪽으로 1만큼 세번, 아래쪽으로 1만큼 한번 움직이면을 네 꼭짓점으로 갖는 정사각형을 얻을 수 있습니다. 이처럼 움직임 a, b와 그들의 역 움직임들을 적절히 사용하여 정사각형 S를 계속해서 움직이다 보면, 모든 정수 n, m에 대해서 (n, m), (n+1, m), (n+1, m+1), (n, m+1)을 네 꼭짓점으로 갖는 정사각형을 얻을 수 있습니다. 이렇게 정사각형 S를 움직임으로써 얻어진 정사각형 조각들은 아래의 두 가지 특징을 갖습니다:
(1) 정사각형 조각들 전부를 모아보면 평면 전체를 덮어버립니다.
(2) 두 정사각형 조각은 겹치지 않거나, 한 변 혹은 한 꼭짓점에서만 만납니다.
즉, 정사각형 조각들은 평면 전체의 타일링을 구성합니다. 마치 화장실 바닥처럼 말입니다. 움직임 a, b는 정사각형 S를 다른 한 조각으로 옮길 뿐 아니라, 정사각형 S위의 한 점을 다른 한 조각 내의 한 점으로 보냅니다. 반대로, 평면 위의 임의의 한 점이 있다면, 위의 성질(1)에 의해 이는 하나의 정사각형 조각에 포함되며, 따라서 이를 움직임 a, b를 통해 적절히 움직여 정사각형 S안에 넣을 수 있습니다. 또, 성질 (2)는 정사각형 S가 이러한 성질을 만족하는 가장 작은 단위의 정사각형임을 의미합니다. 정사각형 S보다 조금 작은 정사각형은 움직임 a, b를 아무리 적용해도 평면 전체를 채울 수 없고, 만일 정사각형 S보다 조금 큰 정사각형을 움직여 평면을 가득 채운다면, 두 조각이 한 변보다 더 두꺼운, 면의 일부를 공유하기 때문입니다. 이는 우리가 정사각형 S를 기본영역이라 일컫는 이유를 설명합니다.
기본영역을 생각함으로써 우리는, 평면 위의 두 움직임 a, b가 실제로 도넛면을 만들 때 정사각형의 마주보는 변을 붙이는 것에 대응됨을 확인할 수 있습니다. 평면 위의 두 점이 있을 때 만약 한 점에 움직임 a, b를 적용하여 다른 한 점이 된다면 그 두 점을 “같은 점”으로 취급해보도록 하겠습니다. 예를 들어, (0.5, 0.3)에 a를 한번, 그리고 b를 두번 적용하면 (1.5, 2.3)이 되므로, 이 두 점은 “같은 점”입니다. 위의 성질 에 의해, 평면 위 임의의 점은 정사각형 S의 한 점과 “같은 점” 입니다. 이제 정사각형 S의 점들 중 “같은 점”이 무엇인지 살펴본다면, 성질 (2)에 의해 정사각형 S의 한 변 위의 각 점은 마주보는 변의 마주보는 점과 “같은 점”임을 확인할 수 있습니다. 예를 들어, (0, 0.5)는 (1, 0.5)와 같은 점이며, (0.3, 0)은 (0.3, 1)과 같은 점입니다. 평면 위에서 “같은 점”들을 “하나의 점”으로 생각하여, “다른 점”들만 모아놓아 보도록 하겠습니다. 앞선 관찰을 통해, 이는 정사각형 S위에서의 점들 중 “같은 점”들을 “하나의 점”으로 생각하여 모아놓는 것과 동일하며, 실제로 정사각형 S의 마주보는 각 변에서 마주보는 각 점들을 “하나의 점”으로 간주하는 것, 즉 마주보는 각 변을 “붙이는 것”으로 이해할 수 있습니다.
따라서 평면 위에서 움직임 a, b를 생각하면, 움직임 a, b를 통해 서로에게 이동할 수 있는 평면 위의 점들을 하나의 점으로 생각함으로써 기본영역인 정사각형 S의 마주보는 각 변을 붙이는 것과 같습니다. 즉, 움직임 a, b를 통해 기본영역의 기하구조가 입혀진 도넛면을 얻게 됩니다.
이와 같이 평면 위의 두 움직임을 생각함으로써 우리는 다양한 도넛면을 얻을 수 있습니다. 예를 들어, 이번에는 평면 위에서 오른쪽으로 2만큼 움직이는 움직임 a’와 위로 1만큼 움직이는, 전과 동일한 움직임 b를 생각해 봅시다. 이번에는 움직임 a’가 y축을 오른쪽으로 2만큼 움직여 (2, 0)을 지나고 y축에 평행한 직선으로 보냅니다. 따라서 두 움직임 a’, b로부터 얻어지는 평면 위 도형은 (0, 0), (2, 0), (2, 1), (0, 1)을 네 꼭짓점으로 갖는 직사각형이며, 마찬가지로 두 움직임 a’, b가 직사각형의 마주보는 각 변을 붙임으로써 우리는 또다른 도넛면을 얻습니다.
자, 지금까지 우리는 움직임 a, b와 움직임 a’, b를 생각하여 도넛면을 두개 얻었는데요. 과연 이 두 도넛면은 같은 도넛면일까요 다른 도넛면일까요? 여기에서 “같은 도넛면”이라고 함은 두 도넛면이 평면으로부터 갖는 기하구조가 동일함을 의미합니다.
기하구조가 동일하다는 뜻은, 형식적으로는 두 도넛면 사이에 “거리를 보존하는 사상”이 존재함을 의미합니다. 간단히 이야기하여, 만일 두 기하구조가 동일하다면 “넓이”, “부피”, “가장 짧은 루프의 길이” 등 여러가지 기하적인 성질들이 같아야 할 것입니다. 역으로, 만일 다른 기하적인 성질이 나타난다면 두 기하구조는 “다른 기하구조”가 될 것입니다. 움직임 a, b로부터 얻은 도넛면은 각 변의 길이가 1인 정사각형의 기하구조를 가지므로, 넓이가 1이라고 할 수 있습니다. 그러나 움직임 a’, b로부터 얻은 도넛면은, 넓이가 2인 직사각형으로부터 기하구조를 얻었으므로 2의 넓이를 갖습니다. 만일 두 도넛면이 같은 기하구조를 가졌다면, 두 도넛면은 같은 넓이를 가져야 하므로, 두 도넛면은 “다른 도넛면”입니다.
이처럼, 움직임 a, b로 만든 도넛면 를 생각한 후 움직임 a를 움직임 a’로 바꾸어 움직임 a’, b로 새로운 도넛면을 만든다면, 이를 도넛면
의 “변형”이라고 합니다. 변형된 도넛면은
와 다른 도넛면, 즉, 같지 않은 도넛면이므로, 우리는 이 변형을 “자명하지 않은 변형”이라고 합니다.
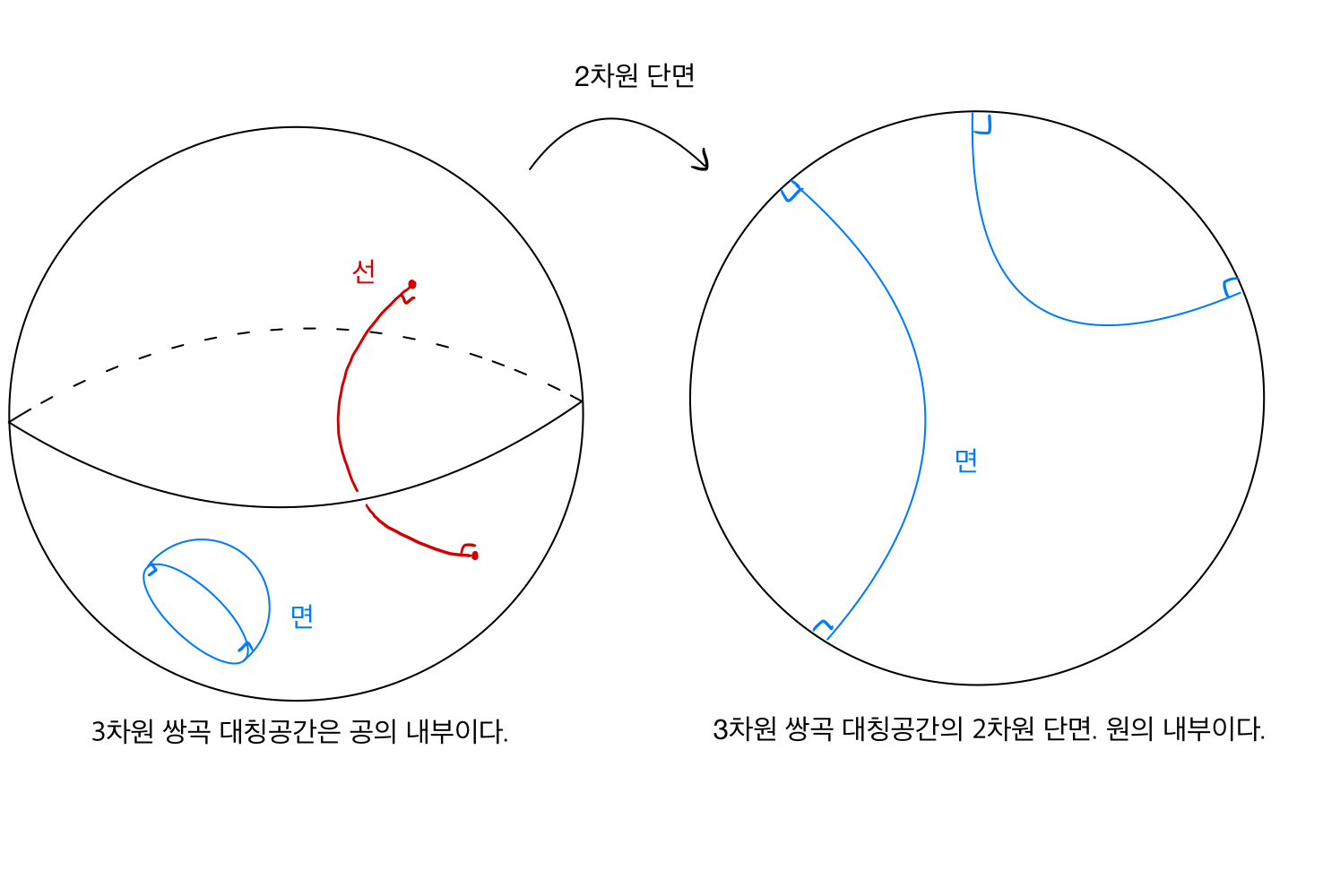
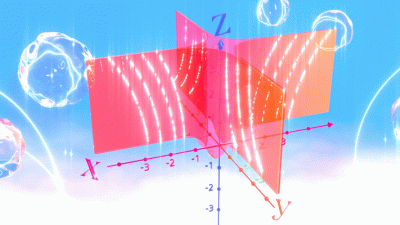
3차원 쌍곡공간을 얻는 방법 앞서 우리는 도넛면이라는 대상을 평면 위의 두 움직임으로 생각함으로써, 도넛면의 기하구조와 이의 변형을 생각할 수 있었습니다. 자, 이제 3차원 쌍곡 공간으로 돌아와보도록 하겠습니다. 앞서 “평면”은 도넛면에 평면기하구조를 입히는 역할을 하였습니다. 3차원 쌍곡 공간을 만드는 과정에서도 마찬가지로 쌍곡기하구조를 입히는 역할을 수행하는 특정 3차원 공간을 필요로 합니다. 이를 우리는 3차원 쌍곡 대칭 공간 라고 하며, 속이 꽉 찬 3차원 공에 일정한 곡률 -1을 갖는 기하구조가 주어진 것으로 정의될 수 있습니다.
형식적으로 3차원 쌍곡대칭공간 를 정의하기 보단, 에서 선과 면이 어떤 형태를 가지는지를 살펴봄으로써 이를 묘사해보고자 합니다. 우리가 일반적으로 상상하는 반듯한 3차원 공간 (유클리드 공간)에서 선은 반듯한 직선, 면은 반듯한 평면으로 나타납니다. 그러나 의 기하구조는 곡률 -1을 가지도록 휘어져있기 때문에, 선과 면이 우리가 반듯한 공간에서 상상하는 것과는 달리 휘어진 형태를 띕니다. 에서의 선은 공의 경계면에 수직한 반원으로, 에서의 면은 공의 경계면에 수직한 반구로 나타납니다. 비록 우리는 공의 형태로 쌍곡대칭공간을 이해하고 있지만 여기에서의 기하 구조는 공의 가장자리로 갈 수록 거리가 급격히 멀어지고 있는 양상을 띄고 있어 무한한 부피를 갖게 됩니다. 아래 그림에서처럼, 앞으로는 2차원 단면을 생각하여 그림을 그리도록 하겠습니다.
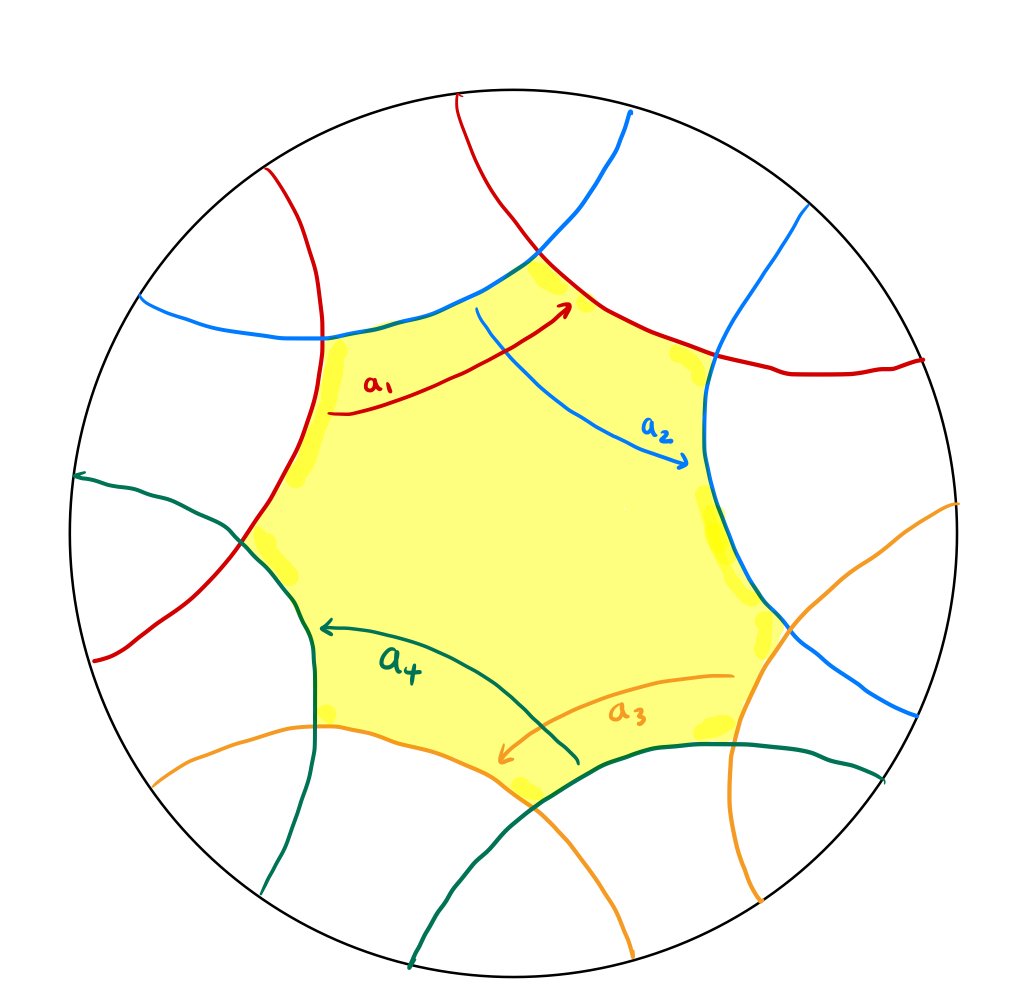
도넛면에서와 마찬가지로, 우리는 3차원 쌍곡대칭공간 에서의 여러 움직임을 가지고 3차원 쌍곡공간을 만들 수 있습니다. 평면에서의 움직임이 선을 선으로 보내어 특정 영역(위 예시에서의 정사각형, 직사각형)을 만들었던 것 처럼, 에서의 움직임은 면을 면으로 보내어 특정 영역을 만들어낼 수 있습니다. 따라서 도넛면 예시에서 정사각형 또는 직사각형을 얻어냈던 것 처럼, 우리는 아래와 같이 3차원 쌍곡대칭공간 에서 특정 입체 영역을 형성할 수 있고, 입체 영역의 각 면들을 붙여 3차원 쌍곡공간을 얻을 수 있습니다.
또, 에서의 움직임 으로 얻어진 3차원 쌍곡공간
이 있을 때, 움직임
중 일부 또는 전체를 다른 움직임
으로 바꾸어 또다른 3차원 쌍곡공간
‘을 얻을 수 있습니다. 마찬가지로
‘을
의 “변형”이라고 생각할 수 있습니다. 도넛면에서와는 달리, 3차원 쌍곡공간의 변형을 정의하기 위해서는 추가적인 논의가 필요합니다. 이는 글의 후미에 자세히 다루도록 하겠습니다.
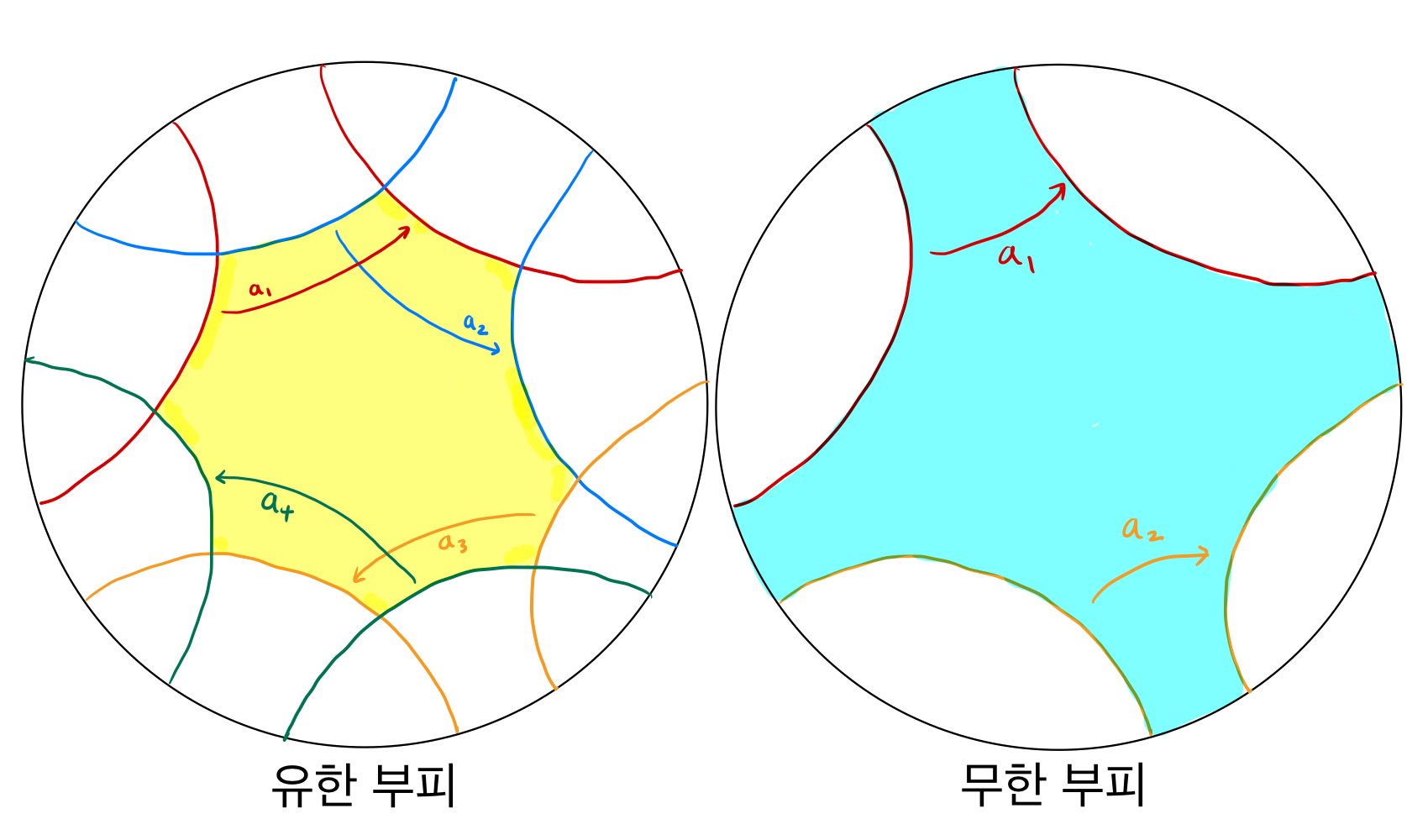
유한 부피, 무한 부피 제목에서 확인할 수 있듯이, 본 연재에서의 관심사는 한 3차원 쌍곡공간이 유한한 부피를 가질 때 혹은 무한한 부피를 가질 때 어떠한 강직성을 확인할 수 있는지에 대한 것입니다. 이를 위해 앞서 묘사된 3차원 쌍곡공간을 얻어내는 과정에서 공간의 부피를 어떻게 상상할 수 있을지 살펴보고자 합니다.
다시 2차원 예시로 돌아와보겠습니다. 평면에서 두 움직임을 골라 도넛면을 만들었을 때, 우리는 [FIGURE 3]와 [FIGURE 4]에서처럼, 움직임들이 만들어내는 기본영역의 넓이를 도넛면의 넓이로 간주할 수 있음을 확인하였습니다. 위 두 상황에서는 각각 기본영역이 정사각형과 직사각형으로, 1과 2라는 유한한 넓이를 가지고 있었습니다.
그렇다면 무한한 넓이를 만들어내는 상황은 무엇일까요? 아마 눈치채신 독자 분들도 계시겠지만, 움직임 하나만을 가지고 공간을 만들어낼 수 있습니다. 예를 들어, 도넛 면을 만들 때와 달리 오른쪽으로 1만큼 움직이는 단 하나의 움직임 a만을 생각해 보도록 하겠습니다. 이는 y축을 (1, 0)을 지나고 y축에 평행한 직선으로 보냅니다. 이외의 다른 움직임은 없으므로, 움직임 a가 기본 영역을 결정합니다. 즉, 기본 영역은 y축과 이에 평행하고 (1, 0)을 지나는 직선이 형성하는, 무한히 길고 너비가 1인 띠가 기본영역이 되며, 무한한 넓이를 갖습니다. 움직임 a는 이 무한한 띠의 양 끝을 붙이는 역할을 합니다. 이렇게 움직임 a로부터 만들어진 공간은 무한히 뻗어 나가는 원통면이 되겠습니다.
이제 3차원 쌍곡공간의 예시로 돌아와보도록 하겠습니다. 3차원 쌍곡대칭공간 에서의 움직임 으로 만들어지는 3차원 쌍곡공간
의 부피는 마찬가지로 움직임
이 형성하는 기본영역의 부피로 간주할 수 있습니다. 따라서 공간
의 부피가 유한한지 혹은 무한한지 여부는 움직임
이 유한한 부피의 기본영역을 형성하는지 혹은 무한한 부피의 기본 영역을 형성하는지에 의해 결정됩니다.
유한 부피 3차원 쌍곡공간의 강직성: 모스토우 강직성 정리 이제 우리는 본 연재에서의 첫 번째 강직성 정리인 모스토우 강직성 정리를 받아들일 준비가 되었습니다.
(모스토우 강직성 정리). 유한한 부피를 갖는 3차원 쌍곡공간은 비자명한 변형을 갖지 않는다.
위 정리에서 등장하는 용어 중 “유한한 부피를 갖는 3차원 쌍곡공간”에 대해서는 앞서 논의한 바가 있습니다. 그러나 위에서 언급되었듯이, 3차원 쌍곡공간의 “변형” 또는 “비자명한 변형”이 무엇인지에 대해서는, 도넛면에서의 상황과 달리 추가적인 논의가 필요합니다.
주어진 3차원 쌍곡공간 이, 3차원 쌍곡대칭공간 에서의 움직임
으로부터 만들어졌다고 합시다. 앞서 움직임
대신 다른 움직임
을 생각하여 새로운 3차원 쌍곡공간
’을 얻어내는 것을
의 변형이라 일컬은 바 있습니다. 그러나 도넛면을 만들던 상황과는 달리, 단순히 주어진 움직임
을 다른 움직임
으로 대체하는 것 만으로 항상 새로운 3차원 쌍곡공간을 얻어낼 수 있는 것은 아닙니다.
무엇이 도넛면에서의 상황과 차이를 가져올까요? 평면 위의 움직임으로 도넛면을 만드는 예시로 잠깐 다시 돌아가 보도록 하겠습니다. 전과 동일하게, 평면 위에서 오른쪽으로 1만큼 움직이는 것을 움직임 , 위쪽으로 1만큼 움직이는 것을 움직임
라고 하겠습니다. 우리는 앞서 두 움직임
,
로부터 넓이가 1인 도넛면
를 얻었습니다. 또, 움직임
를 오른쪽으로 2만큼 움직이는 새로운 움직임
‘로 대체하여, 두 움직임
’,
로부터 넓이가 2인 도넛면
‘을 얻었습니다. 앞서 우리는 두 움직임
,
를
’,
로 대체하는 것을 도넛면
의
’로의 변형이라 묘사한 바 있습니다.
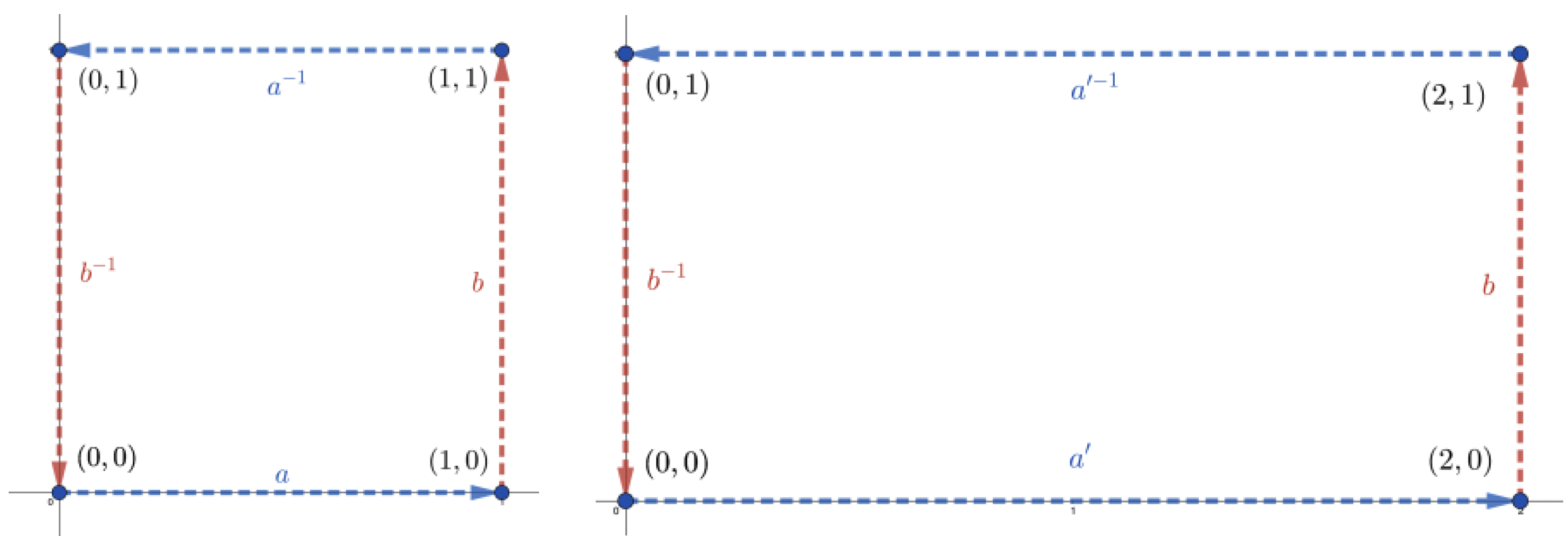
여기에서 추가적인 논의 없이 도넛면을 잘 변형시킬 수 있었던 원인 중 하나는, ,
를
’,
로 대체하는 것이 움직임들 간의 역할을 잘 보존해주기 때문입니다. 구체적으로, 평면 위의 원점 (0, 0)에
를 적용하면 (1, 0)이, 그리고 또 b를 적용하면 (1, 1)이 됩니다. 그리고
의 역 움직임인
, 즉 왼쪽으로 1만큼 움직이는 것을 적용하면 (0, 1)이 되며,
의 역 움직임인
, 즉 아래로 1만큼 움직이는 것을 적용하면 (0, 0)이 되어 제자리로 돌아옵니다. 즉, 원점 (0, 0)에
,
,
,
를 순차적으로 적용했더니 우리는 원래의 위치로 돌아왔습니다.
자, 이제 를
’로 바꾸고 b는 그대로 유지하는, 앞서 묘사된 변형을 생각해 봅시다. 이 변형은 순차적으로
,
,
,
를 적용하는 과정을 순차적으로
’ ,
,
,
를 적용하는 과정으로 대체합니다. 그러나, (0, 0)에
’을 적용하면 (2, 0)이, 그리고
를 적용하면 (2, 1)이, 여기에
을 적용하면 (0, 1)이, 마지막으로
을 적용하면 원래의 (0, 0)으로 돌아옵니다. 즉, 도넛면 예시에서는 단순히 움직임을 잘 대체해 주는 것이 각 움직임 간의 역할을 잘 보존하게 됩니다.
그러나 이는 3차원 쌍곡공간에서는 더 이상 성립하지 않습니다. 즉, 주어진 움직임 을 임의의 다른 움직임
으로 대체하는 것이 각 움직임 간의 역할을 항상 잘 보존해주는 것은 아닙니다.
따라서 3차원 쌍곡공간의 변형 {}
{
}을 정의할 때에는, 대체되는 움직임
이 기존의 각 움직임 간의 역할을 잘 보존하여 움직임
으로부터 어떠한 3차원 쌍곡공간
’이 얻어진다는 것이 전제되어야 합니다.1 이 상황에서 변형 {
}
{
}이 비자명한 변형이라는 것은 두 쌍곡공간
과
‘이 다른 기하구조를 가진다는 것을 의미하며,
과
‘이 동일한 기하구조를 가질 때 우리는 변형 {
}
{
}을 자명한 변형이라고 합니다. 앞서 도넛면 예시에서처럼, 동일한 기하구조란 형식적으로는
과
‘사이에 거리를 보존하는 사상이 존재함을 뜻하며, 두 공간이 완전히 동일한 기하적인 성질을 가지고 있음을 의미합니다. 이제 모스토우 강직성 정리를 우리가 그간 이해한 언어로 다시 기술할 수 있습니다.
(모스토우 강직성 정리). 3차원 쌍곡대칭공간 위의 움직임
이 유한부피 3차원 쌍곡공간 M을 만들어낸다고 하자. 만약 위의 움직임
이 있어서
을
으로 대체하는 것이 각 움직임 간의 역할을 잘 보존하여, 새로운 움직임
으로부터 또 하나의 3차원 쌍곡공간 M’을 얻는다면, 새로이 얻어진 3차원 쌍곡공간 M’은 원래의 쌍곡공간 M과 동일한 기하구조를 갖는다.
3차원 쌍곡공간은 곡률이 -1인 3차원 공간이라 간단히 정의되지만, 정의가 갖는 추상성으로 인해 구체적으로 어떠한 3차원 쌍곡공간들이 존재하고, 이들이 어떠한 성질을 가지는지 자세히 이해하는 데에는 많은 노력이 필요합니다. 앞서 묘사된, 3차원 쌍곡대칭공간 위에서의 움직임들을 상상하여 쌍곡공간을 얻어내는 것은, 어떠한 3차원 쌍곡공간이 존재할 수 있는지 그 예시를 구체적으로 제공해줍니다. 그러나 서로 다른 움직임들이 만들어낸 공간 중 동일한 기하구조를 갖는 공간과 그렇지 않은 공간을 구별하는 것은 또다른 문제입니다. 상대적으로, 두 공간의 기하구조가 다름을 확인하는 것은 같음을 확인하는 것 보다 간단히 해결될 수 있습니다. 도넛면 예시에서 넓이만을 비교해 보았듯이, 여러가지 기하적인 성질들 중 단 하나라도 다르다는 것을 확인하면 충분하기 때문입니다. 그러나 두 공간의 기하구조가 같음을 보이는 것은 몇 가지 기하적인 성질을 공유함을 확인하는 것으로 충분하지 않으며, 많은 경우 더 깊고 복잡한 논의를 필요로 합니다. 이러한 맥락에서, 모스토우 강직성 정리는 유한한 부피를 갖는 3차원 쌍곡공간을 대칭공간 위에서의 일련의 움직임들로부터 만들어내었을 때, 이 움직임들을 간의 역할을 잘 보존하는 어떠한 변형을 수행하더라도 결과적으로 기존과 동일한 기하구조만을 얻을 수 있다는 중요한 함의를 가집니다. 즉, 유한 부피를 갖는 3차원 쌍곡공간의 모임은 서로간의 역할이 전혀 보존될 수 없는 일련의 움직임들을 묶음으로 모아놓은 것과 같습니다. 이는 결과적으로 유한 부피 3차원 쌍곡공간은 하나, 둘, 셋, 처럼 셀수 있는 만큼, 즉 정수 갯수만큼 존재한다는 것을 의미합니다.
이후 연재에서는 모스토우 강직성 정리에서 중요하게 관찰할 수 있는 현상이 무엇인지 소개하고, 이를 통해 무한 부피를 갖는 3차원 쌍곡공간의 강직성을 어떻게 다룰 수 있는지를 논의하고자 합니다. 끝으로 무한 부피의 3차원 쌍곡공간의 강직성에 대한 최근 연구결과를 소개하는 것으로 연재를 마무리할 계획입니다.
연재
3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [1]
3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [2]
3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [3]
참고문헌
[1] Dongryul M. Kim and Hee Oh. Rigidity of Kleinian groups via self-joinings. Invent. Math, pages 1-12,2023.
[2] George Mostow. Quasi-conformal mappings in n-space and the rigidity of hyperbolic space forms. Inst. Hautes Etudes Sci. Publ. Math., (34):53-104, 1968.
[3] George Mostow. Strong rigidity of locally symmetric spaces. Annals of Mathematics Studies, No. 78. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo, 1973.
[4] Gopal Prasad. Strong rigidity of Q-rank 1 lattices. Invent. Math., 21:255-286, 1973.







 를 정의하기 보단,
를 정의하기 보단,