3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [3]

지난 연재에서는 클라인 군 이라는 대수적 대상을 통해 3차원 쌍곡공간을 상상하고 이해하는 방법을 살펴보았습니다. 3차원 쌍곡공간의 변형은 두 클라인 군 사이의, 군의 구조를 보존하는 대응관계로 이해할 수 있었는데요. 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 유한한 부피를 가질 때, 클라인 군 \(\Gamma\)의 변형 \(\rho : \Gamma \to \Gamma’\)가 항상 동일한 기하구조를 갖는 3차원 쌍곡공간을 만들어낸다는, 모스토우 강직성 정리의 증명을 개괄적으로 살펴보았습니다. 본 마지막 연재에서는, 만약 3차원 쌍곡공간이 무한한 부피를 가질 때에는 강직성을 어떻게 논의할 수 있는지 이해해 보고자 합니다.

극한 집합과 경계사상 . 지난 연재에서, 모스토우 강직성 정리 증명의 핵심은 1) 클라인 군의 변형 \(\rho : \Gamma \to \Gamma’\)로부터 경계사상 \(f : \mathbb{S}^2 \to \mathbb{S}^2\)를 유도한 후, 2) 경계사상 \(f\)가 2차원 구면 \(\mathbb{S}^2\) 위에서 둥글함을 보존함을 보이는 것, 즉 등각사상임을¹ 보이는 것입니다.

자, 이제 일반적인 클라인 군 \(\Gamma\)를 생각해 봅시다. 특히 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 무한한 부피를 가진다고 해봅시다. 클라인 군의 변형 \(\rho : \Gamma \to \Gamma’\)에 대해, 모스토우 강직성 정리를 살펴본 우리에게 떠오르는 자연스러운 질문은 위의 1), 2)가 성립하냐는 것입니다. 즉, 일반적인 클라인 군 \(\Gamma\)와 그 변형 \(\rho : \Gamma \to \Gamma’\)에 대하여,

                     (1) 경계사상 \(f : \mathbb{S}^2 \to \mathbb{S}^2\)가 존재하는가?
                     (2) 경계사상 \(f : \mathbb{S}^2 \to \mathbb{S}^2\)가 등각사상인가?   

첫째로, 일반적인 클라인 군 \(\Gamma\)와 변형 \(\rho : \Gamma \to \Gamma’\)에 대해 아주 많은 경우 경계사상이 존재한다는 것이 알려져 있습니다 ^[13]. 그러나 (1)에서와 완전히 동일한 형태로 경계사상이 주어지지는 않습니다. 그 이유는 모스토우 강직성 정리 증명에서 경계사상을 얻어냈던 방법에서 알 수 있는데요. 다시 상기해 보자면, 대칭공간 \(\mathbb{H}\)의 경계 \(\mathbb{S}^2\) 위의 점 \(x \in \mathbb{S}^2\)에 대해, 클라인 군 \(\Gamma\)의 원소로 이루어진 어떤 수열 \(\gamma_{n}\)이 있어서 점 \(o \in \mathbb{H}\)에 대해 대칭공간 \(\mathbb{H}\)위의 수열 \(\gamma_{n} (o)\)가 \(x\)로 수렴할 때, \(f(x) \in \mathbb{S}^2\)를 수열 \(\rho(\gamma_{n}) (o)\)의 극한으로 정의함으로써 경계사상 \(f\)를 얻어내었습니다.

그러나 여기에서 한 가지 맹점은 바로, 주어진 점 \(x \in \mathbb{S}^2\)에 대해, 클라인 군 \(\Gamma\)의 원소로 이루어진 수열 \(\gamma_{n}\)이 있어서 수렴 \(\gamma_{n} (o) \to x\)이 성립하냐는 것인데요. 만약 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 유한한 부피를 갖는다면 경계 위의 임의의 점 \(x \in \mathbb{S}^2\)에 대해 직전의 명제가 성립한다는 것이 알려져 있습니다만, 일반적인 클라인 군 \(\Gamma\)에 대해서는, 즉 \(\Gamma \setminus \mathbb{H}\)가 무한한 부피를 가질 때에는 항상 성립하는 명제는 아닙니다. 즉, 클라인 군 \(\Gamma\)에 대해 3차원 쌍곡공간 \(\Gamma\ \setminus  \mathbb{H}\)가 무한 부피를 갖는 경우, 수열 \(\gamma_{n} \in \Gamma\)에 대해 \(\mathbb{H}\)에서의 수열 \(\gamma_{n} (o)\)가 수렴할 수 있는 \(\mathbb{S}^2\)의 점들이 \(\mathbb{S}^2\) 전체를 항상 이루는 것은 아닙니다. 경계사상을 유도하는 과정에서 알 수 있듯 \(\mathbb{H}\)의 부분집합으로서의 \(\Gamma\)-궤적 \(\Gamma (o) = \{\gamma (o) : \gamma \in \Gamma \}\)가 집적될 수 있는 \(\mathbb{S}^2\) 위의 점들은 중요한 역할을 수행하기에, 우리는 이러한 집적점들의 집합에 이름을 붙였습니다. 이것이 바로, 클라인 군 \(\Gamma\)의 극한 집합입니다.

\(\mathbf{Definition}\) 1 (극한집합). 클라인 군 \(\Gamma\)에 대해, 극한집합 \(\Lambda_{\Gamma} \subset \mathbb{S}^2\)는 \(\mathbb{S}^2\) 위의 점들 중 \(\mathbb{H}\) 내의 \(\Gamma\)-궤적 \(\Gamma (o)\)가 집적되는 점들의 집합입니다.

만일 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 유한한 부피를 가진다면, 극한집합은 \(\mathbb{S}^2\) 전체와 같습니다, 즉, \(\Lambda_{\Gamma} = \mathbb{S}^2\). 그러나 극한집합이 아주 작은 부분집합인 경우도 있습니다. 백형렬 교수님의 지난 Horizon 글 “자유를 원한다면 탁구를 쳐라“에서는 탁구보조정리를 통해 주어진 군이 자유군임을 확인할 수 있음에 대한 멋진 소개가 있었는데요. 뭉뚱그려 이야기하여 만약 클라인 군 \(\Gamma\)가 탁구보조정리가 적용될만한 여지가 있어 자유군이라면 (이를 Schottky subgroup이라고 합니다) 극한집합 \(\Lambda_{\Gamma}\)는 \(\mathbb{S}^2\) 위의 칸토어 집합이 됩니다. 특정 규칙을 통해 원으로 구면을 채우는 수학적 대상인 “아폴로니안 원 채우기” 역시 클라인 군의 극한집합 중 하나입니다.

이제 클라인 군 \(\Gamma\)의 변형 \(\rho : \Gamma \to \Gamma’\)를 생각해 봅시다. 극한집합의 정의에서 알 수 있듯이, 비록 질문(1)에서와 같이 경계사상 \(f\)를 경계 \(\mathbb{S}^2\) 전체에서 정의되도록 얻을 수는 없겠습니다만, 우리는 자연스레 경계사상 \(f\)가 \(\Gamma\)의 극한집합 \(\Lambda_{\Gamma}\) 위에서 정의되도록 얻을 수 있을지 기대해볼법 합니다. 그렇다면 \(\Lambda_{\Gamma}\)위에서 정의된 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)란 무엇일까요? 모스토우 강직성 정리의 증명에서 살펴본 것처럼,경계사상이란, 클라인 군의 원소 \(\gamma \in \Gamma\)가 대칭공간 \(\mathbb{H}\)의 경게에서 작용하는 방식이 클라인 군의 변형 \(\rho\)에 의해 어떻게 바뀌는지를 묘사해줍니다. 이를 식으로 써보면, 모든 \(\gamma \in \Gamma\)에 대해 아래의 등호가 성립함을 의미합니다: 

그러나 앞서 살펴본 것 처럼 일반적인 클라인 군의 경우 경계사상은 극한집합 위에서 논의되어야 합니다. 이같은 관찰로부터, 우리는 일반적인 클라인 군과 변형에 대해 경계사상을 아래와 같이 정의합니다.

\(\mathbf{Definition}\) 2 (경계사상). 클라인 군 \(\Gamma\)와 변형 \(\rho : \Gamma \to \Gamma’\)에 대해, 사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)가 모든 \(\gamma \in \Gamma\)와 \(x \in \Lambda_{\Gamma}\)에 대해

주어진 클라인군과 변형에 대해 위의 정의대로의 경계사상이 존재하는지 역시 간단한 문제는 아닙니다만, 아주 많은 경우 경계사상이 존재함이 알려져있습니다^[13].

무한부피 쌍곡공간의 변형과 강직성 . 모스토우 강직성 정리의 증명은 결국 경계사상이 등각사상임을 보이는 것으로 마무리됩니다. 이는 무한부피의 상황에서도 마찬가지인데요. 일반적인 클라인 군 \(\Gamma\)와 변형 \(\rho : \Gamma \to \Gamma’\)가 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)를 가질 때, \(f\)가 \(\mathbb{S}^2\) 전체로 확장될 수 있고, 이러한 확장이 등각사상이라면 변형된 3차원 쌍곡공간 \(\Gamma’ \setminus \mathbb{H}\)는 원래의 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 동일한 기하구조를 갖게됩니다. 즉 어떤 등각사상 \(F: \mathbb{S}^2 \to \mathbb{S}^2\)가 존재하여 \(F\) 와 \(f\)가 \(\Lambda_{\Gamma}\)에서 일치한다면, 변형된 3차원 쌍곡공간 \(\Gamma’ \setminus \mathbb{H}\)가 기존의 공간 \(\Gamma \setminus \mathbb{H}\)와 동일한 기하구조를 갖는 것이지요.  따라서 일반적인 클라인 군과 변형에 대하여도, 강직성에 대한 질문은 경계사상이 등각사상으로 확장될 수 있는지에 대한 질문으로 치환됩니다. 그러나 유한부피의 상황과는 달리, 클라인 군 \(\Gamma\)에 대해 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 무한한 부피를 갖는다면, 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)가 등각사상으로 확장될 수 없는 변형 \(\rho : \Gamma \to \Gamma’\)도 아주 많이 존재할 수 있습니다. 예를 들어 몇몇 종류의 클라인 군 \(\Gamma\)에 대해서는, 등각사상으로 확장될 수 없는 경계사상을 갖는 많은 종류의 변형 \(\rho : \Gamma \to \Gamma’\)이 알려져 있습니다.

따라서 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 유한한 부피를 가질 때, 클라인 군 \(\Gamma\)의 임의의 변형 \(\rho : \Gamma \to \Gamma’\)에 대해 \(\Gamma’ \setminus \mathbb{H}\)가 \(\Gamma \setminus \mathbb{H}\)와 동일한 기하구조를 가진다는 모스토우 강직성 정리와는 달리, 무한부피 3차원 쌍곡공간에 대해서는 다른 형태로 강직성에 대한 질문이 기술되어야 할 것입니다. 즉, 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)가 무한한 부피를 갖는다면, 클라인 군 \(\Gamma\)에 대해, “어떠한 성질을 갖는 변형 \(\rho : \Gamma \to \Gamma’\)이 결과적으로 변형된 쌍곡공간 \(\Gamma’ \setminus \mathbb{H}\)에 기존의 \(\Gamma \setminus \mathbb{H}\)와 동일한 기하구조를 주게될까?”가 강직성에 대한 적절한 질문일 것입니다. 달리 기술한다면, 주어진 클라인 군 \(\Gamma\)와 변형 \(\rho : \Gamma \to \Gamma’\)이 “어떤 추가적인 성질”을 만족할 때 변형된 3차원 쌍곡공간 \(\Gamma’ \setminus \mathbb{H}\)가 기존의 것과 동일한 기하구조를 갖게될지를 규명하는 것이 무한부피 3차원 쌍곡공간의 강직성에 대한 질문이라고 할 수 있겠습니다. 이는 반대로 이야기하면, 주어진 클라인 군이 어떠한 변형만을 가질 수 있는지를 논하는 의미에서의 강직성이라고도 이해할 수 있겠습니다. 이에 대한 예시로, 설리반 준등각 강직성 정리^{Sullivan’s quasiconformal rigidity theorem, [11]}가 있습니다.

\(\mathbf{Theorem}\) (설리반 준등각 강직성 정리). 클라인 군 \(\Gamma\)가 대칭공간 \(\mathbb{H}\)의 경계 \(\mathbb{S}^2\) 전체를 극한집합으로 갖는다고 하자, 즉, \(\Lambda_{\Gamma} = \mathbb{S}^2\). 변형 \(\rho : \Gamma \to \Gamma’\)의 경계사상 \(f : \mathbb{S}^2 \to \mathbb{S}^2\)가 구면 위에서 둥글함을 어느정도 보존해 준다면, 즉, 모든 원을 거의 원과 가깝게 보내는, 준등각사상이라면, \(f\)는 반드시 등각사상이며 따라서 \(\Gamma’ \setminus \mathbb{H}\)는 \(\Gamma \setminus \mathbb{H}\)와 동일한 기하구조를 갖는다.

설리반의 준등각 강직성 정리는 원래 “경계사상이 구면 전체에서 정의되는 준등각 사상이고, 극한집합 외부에서 등각사상임”을 가정하는, 위 명제보다 더 강한 형태를 띄고있었습니다. 그러나 비교적 최근 알포스 측도 추측^{Ahlfors’ measure conjecture, [2]}가 해결됨에 따라 ^[5],[4],[1] 위의 명제만이 설리반의 증명을 필요로하는 부분이 되었습니다.

극한집합이 전체가 아닐 때 . 이제 더 일반적인 상황인, 클라인 군 \(\Gamma\)의 극한집합 \(\Lambda_{\Gamma}\)가 구면 전체를 채우지 않는 경우를 살펴보도록 하겠습니다. 한 가지 자연스러운 질문은 이 경우에도 만약 주어진 변형 \(\rho : \Gamma \to \Gamma’\)의 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)가 (설리반 준등각 강직성 정리에서 처럼) 둥글함을 어느정도 보존해 줄 때, 과연 \(f\)가 구면 전체에서의 등각사상으로 확장되는지, 즉 변형된 공간 \(\Gamma ‘ \setminus \mathbb{H}\)가 기존의 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 동일한 기하구조를 가지는지입니다. 이는 비록 본 연재에서 소개하지는 않았지만, 그로모프와 써스턴이 모스토우 강직성 정리를 증명한 아이디어^[6],[12]가 무한 부피의 상황에도 논의될 수 있는지에 대한 질문과도 맞닿아 있습니다. 이는 최근 필자의 지도교수님이신 오희 교수님과의 연구^[8]에서, 3차원 쌍곡공간의 강직성을 이해하는 새로운 관점을 제시함으로써 규명해 내었는데요, 개략적으로나마 이를 소개하며 본 연재를 마치도록 하겠습니다.

극한집합의 원형 조각 . 본 질문에 앞서, 극한집합 \(\Lambda_{\Gamma}\)가 구면 \(\mathbb{S}^2\) 전체가 아닐 경우 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)가 둥글함을 잘 보존한다는 것이 무얼 의미하는지에 대한 논의가 선험되어야 합니다. 설리반 준등각 정리에서처럼 극한집합이 구면 전체고, 그에따라 경계사상이 구면 전체에서 정의된 경우엔 구면 위의 원들이 거의 원으로 보내질 때 경계사상 \(f\)가 둥글함을 잘 보존한다고 할 수 있을 것입니다. 그러나 극한집합이 구면 전체가 아닐 경우는 어떨까요? 이 경우, 극한집합은 면적이 없는 구면 위의 아주 작은 집합입니다. 따라서 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\) 역시 아주 작은 영역에서만 정의가 되어있기 때문에, “원”을 경계사상 \(f\)로 보내는 것이 거의 불가능하게 됩니다.

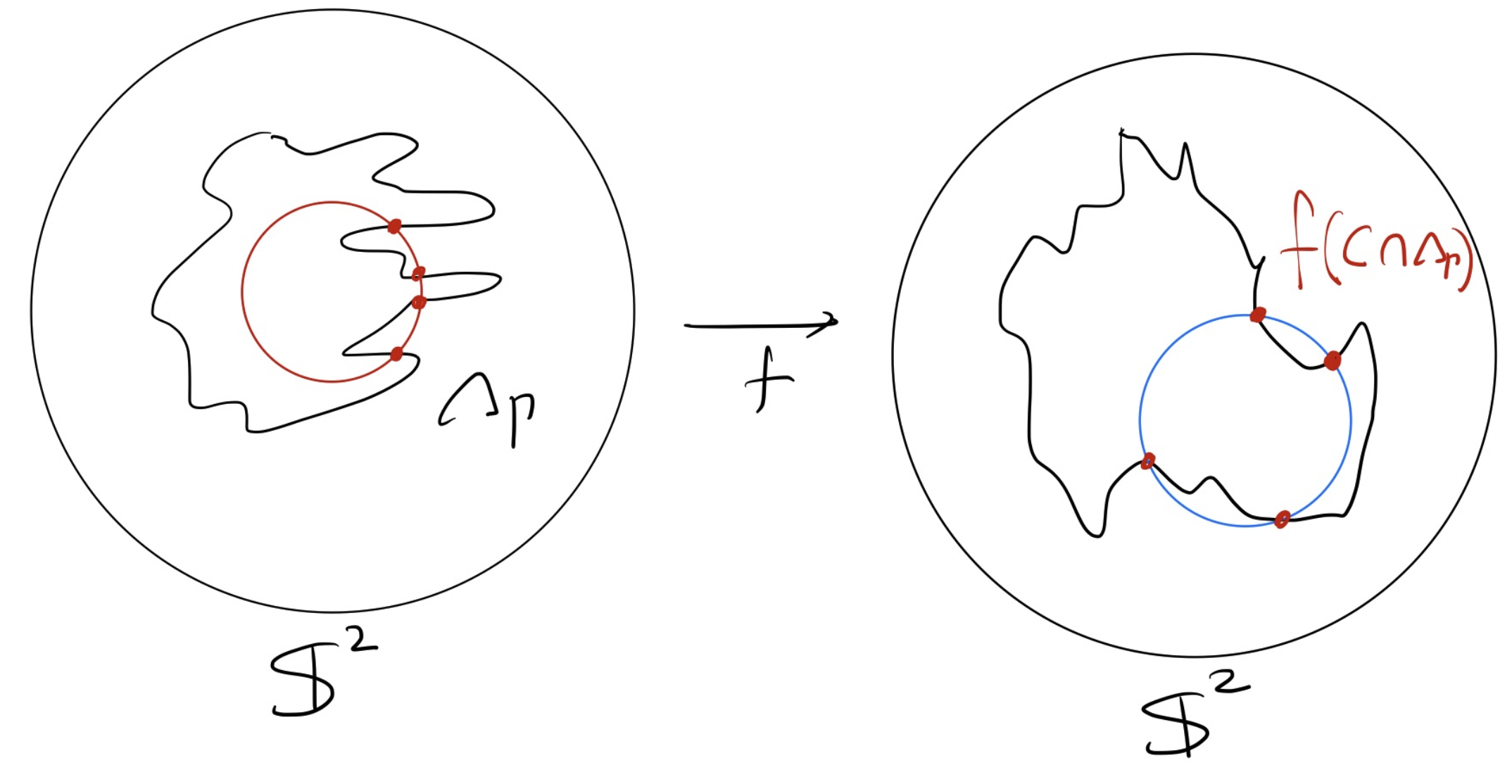
대신, 우리는 구면 위의 원 \(C \subset \mathbb{S}^2\)에 대하여, 극한집합 \(\Lambda_{\Gamma}\)의 원형 조각 \(C \cap \Lambda_{\Gamma}\)를 생각해 볼 수 있습니다. 또, 경계사상 \(f\)는 극한집합 \(\Lambda_{\Gamma}\) 위에서 정의되어 있으므로, 원형 조각을 \(f\)로 보내어 \(f(C \cap \Lambda_{\Gamma})\)를 논할 수 있습니다. 극한집합 \(\Lambda_{\Gamma}\)가 이미 구면 위의 아주 작은 부분이기 때문에, 원형 조각 \(C \cap \Lambda_{\Gamma}\) 역시 아주 원 \(C\)의 아주 작은 조각이며, 대부분의 경우 칸토어 집합과 같은 형태를 띄고 있습니다.

이같은 맥락에서, 아주 작은 영역인 극한집합 \(\Lambda_{\Gamma}\)에서 경계사상이 정의되어있을 경우엔, 경계사상이 둥글함을 얼마나 잘 보존하는지를 경계사상 \(f\)가 원형조각들을 얼마나 잘 유지하는지로 이해할 수 있는데요. 이에 대한 강직성 정리를 대략적으로 기술하자면 아래와 같습니다. 이는 복소수와 관련하여 등장하는 “교차비”라는 개념을 사용하여서도 기술될 수 있습니다만, 자세한 설명은 생략하도록 하겠습니다.

\(\mathbf{Theorem}\) A (무한 부피 강직성 정리 ^[8]). 만일 클라인 군의 변형 \(\rho : \Gamma \to \Gamma’\)의 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)이 아주 많은 원형조각 \(C \cap \Lambda_{\Gamma}\)을 원으로 보낸다면, 즉 각 원형조각 \(C \cap \Lambda_{\Gamma}\)마다 \(f(C \cap \Lambda_{\Gamma})\)가 어떤 원에 포함된다면, 경계사상 \(f\)는 구 전체로 확장될 수 있으며 그 확장은 등각사상이고, 그에따라 두 쌍곡공간 \(\Gamma’ \setminus \mathbb{H}\)와 \(\Gamma \setminus \mathbb{H}\)는 동일한 기하구조를 갖는다.

본 글의 나머지 부분에서는, 무한 부피 쌍곡공간의 변형과 강직성을 이해한 새로운 시각을 설명함으로써 위의 강직성 정리가 어떻게 증명되었는지 개략적으로나마 살펴보겠습니다.

강직성을 바라보는 새로운 관점 . 위의 강직성 정리의 증명은, 공간이 음의 곡률을 가지고 휘어져 있다는 사실에 기반한 기존의 여러 강직성 정리와는 다른 관점을 가지고 있습니다. 그것은 바로 주어진 클라인 군 \(\Gamma\)와 그 변형 \(\rho : \Gamma \to \Gamma’\)로부터 고차원의 특정한 공간을 생성하여 그 위에서의 동역학을 관찰하는 것입니다. (더 정확히는, 고-랭크 균질 공간^{higher rank homogeneous space} 입니다.)

고차원, 고랭크 공간 . 이를 위해 지난 연재를 상기해 보자면, 우리는 대칭공간 \(\mathbb{H}\) 위의 모든 움직임을 모아놓은 집합을 \(G\)라고 표기하였고, \(G\)는 군 이라는 대수적 구조를 가지고 있었습니다. 이제 우리는 이 \(G\)의 원소들로 이루어진 순서쌍들을 생각해 볼 것입니다. 즉, 아래와 같이 정의된 집합을 생각해 봅시다:

군 \(G\)가 대칭공간 \(\mathbb{H}\)의 움직임들을 모아놓은 집합이므로, \(G \times G\)는 \(\mathbb{H}\) 위의 점들로 이루어진 순서쌍들의 집합 \(\mathbb{H} \times \mathbb{H} := \{ (o_1, o_2) : o_1, o_2 \in \mathbb{H} \}\) 위의 움직임들을 모아놓은 것이라 생각할 수 있습니다. 마찬가지로 \(G \times G\)도 군의 구조를 갖는데요, 어려운 용어를 쓰자면 이는 랭크가 2인 리 군입니다.

굳이 이러한 이야기를 하는 이유는, 이 랭크가 2라는 것이, 공간 \(\mathbb{H} \times \mathbb{H}\)가 갖는 기하학적 특성과도 연관이 있기 때문입니다. 대칭공간 \(\mathbb{H}\)는 곡률 \(-1\)을 갖는 3차원 공간이었지요. 그렇다면 이들이 쌍을 이루어 만드는 공간 \(\mathbb{H} \times \mathbb{H}\)는 \(3 + 3 = 6\)차원의 공간일 것입니다. 그러나 곡률은 얘기가 좀 다릅니다. 공간 \(\mathbb{H}\)에서 어떤 `선’ \(L\)을 생각해 봅시다. 그러면 이제 쌍으로 이루어진 공간 \(\mathbb{H} \times \mathbb{H}\)에서는 선 \(L\)의 점들로 이루어진 순서쌍들을 또 생각할 수 있습니다. 즉, 아래 집합을 생각할 수 있습니다.

그런데 선 \(L\)을 실수선 처럼 생각해보면, 위의 집합 \(L \times L\)은 두 실수로 이루어진 순서쌍들을 모아놓은 집합으로 간주할 수 있습니다. 어딘가 익숙한 모양새인데요. 바로 우리가 (유클리드) 평면을 \(\mathbb{R}^2\), 즉 실수 \(\mathbb{R}\)이 쌍을 이루어, 평면 위의 한 점을 두 실수의 쌍으로 생각하는 것과 동일한 과정입니다. 즉, 위의 집합 \(L \times L\)은 \(\mathbb{H} \times \mathbb{H}\) 내부의 “평면”이 되겠습니다. 이런 평면은 \(\mathbb{H} \times \mathbb{H}\) 내에 아주 많이 존재합니다. 그런데 평면은 말 그대로, 평평한 영역이지요. 따라서 공간 \(\mathbb{H} \times \mathbb{H}\)는 음의 곡률을 갖지 않습니다. 더불어, 평면은 2차원의 대상인데요. 여기에서 나타나는 2는 앞서 언급된 랭크 2와 같은 의미를 갖습니다.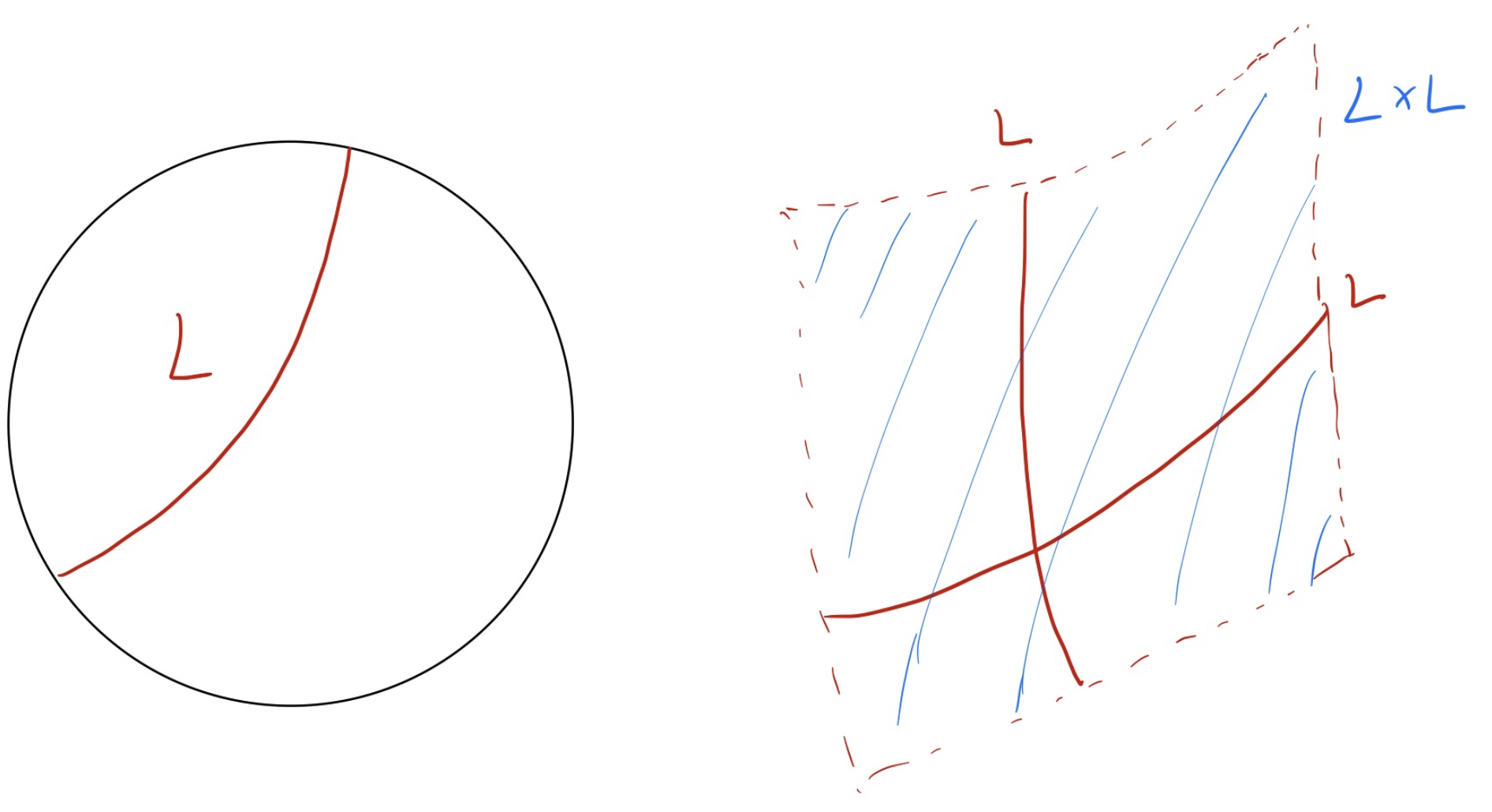

\begin{equation} (0.1)\quad\quad\quad
\Gamma_{\rho} := \{ (\gamma, \rho(\gamma)) \in G \times G : \gamma \in \Gamma\}.
\end{equation}

이를 클라인 군 \(\Gamma\)를 변형 \(\rho\)로 자가 결합하여 얻어졌다고 하여, 자가 결합 군 이라고 부르는데요. 클라인 군 \(\Gamma\)로부터 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)를 얻었던 것 처럼, 자가 결함 군 \(\Gamma_{\rho}\)로부터 아래와 같은 공간을 얻습니다:

여기에서, \(\Gamma_{\rho} (o_1, o_2) = \{ (\gamma(o_1), \rho(\gamma)(o_2)) : \gamma \in \Gamma \}\)는 공간 \(\mathbb{H} \times \mathbb{H}\)에서 쌍 \((o_1, o_2)\)의 \(\Gamma_{\rho}\)-궤적입니다.

자가 결합 군 \(\Gamma_{\rho}\)의 정의에서 알 수 있듯이, 이는 기존의 클라인 군 \(\Gamma\)와 변형된 클라인 군 \(\rho(\Gamma)\)가 각각 \(\mathbb{H} \times \mathbb{H}\)의 왼쪽과 오른쪽에 작용하는 형태를 띄고 있습니다. 변형 \(\rho\)의 강직성이 곧 두 3차원 쌍곡공간 \(\Gamma \setminus \mathbb{H}\), \(\rho(\Gamma) \setminus \mathbb{H}\)의 기하구조가 같은지 다른지에 대한 질문이라는 것을 고려한다면, 위의 자가 결합 군과 이로부터 얻어지는 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)를 상상하는 것이 어색하게 다가오진 않는데요. 실제로 여기에서 소개하고자 하는 강직성에 대한 새로운 관점은, 자가 결합 군을 생각함으로써 주어진 변형의 강직성 문제를 고-랭크 공간의 동역학적에 대한 질문으로 치환하는 데에 있습니다.

강직성과 고-랭크 공간의 기하구조 . 변형 \(\rho : \Gamma \to \Gamma’\)에 대하여 만약 두 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 \(\rho(\Gamma) \setminus \mathbb{H} = \Gamma’ \setminus \mathbb{H}\)가 동일한 기하구조를 가진다고 해 봅시다. \(\Gamma_{\rho}\)의 생김새 (0.1)로부터, 만일 두 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 \(\rho(\Gamma) \setminus \mathbb{H}\)가 동일한 기하구조를 갖는다면 \(\Gamma_{\rho}\)가 만들어내는 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)는 (수학적으로 엄밀한 표현은 아니지만) 소위 좌-우가 대칭적인, 아주 똑바르게 생긴 단순한 구조를 가지고 있을 것입니다. 반면 두 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 \(\rho(\Gamma) \setminus \mathbb{H}\)가 다른 기하구조를 갖는다면 \(\Gamma_{\rho}\)의 \(\mathbb{H} \times \mathbb{H}\)위로의 작용이 불-균형적이어, \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)는 복잡하게 엉켜있는 기하구조를 가지고 있을 것입니다.

그렇다면 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)의 구조가 단순하게 생겼는지, 복잡하게 엉켜있는지는 어떻게 알 수 있을까요? 우리 일상 속 상황을 비유로 한번 상상해 봅시다. 여러분이 자동차를 타고 어디론가 가고 있다고 상상해 봅시다. 만약 아주 반듯하게 똑바로 나있는 고속도로를 달린다면, 우리는 그저 앞만 보고 달려갈 뿐입니다. 주변의 모습도 앞으로 이동함에 따라 앞에 있던 것들이 옆으로 오는 정도이겠죠. 꽤나 지루한 장면의 변화일 것입니다. 그런데 굽이굽이 굽어있는 도로를 달린다면 어떨까요? 커브도 돌면서 새로운 장면도 등장할 거고, 다리 밑을 지날 땐 다리의 아랫부분도 보여지겠지요. 이처럼 공간이 단순한 구조를 가지고 있다면 공간 내에서 이동하며 관찰할 수 있는 것이 단조로울 것이고, 공간이 복잡한 구조를 가지고 있다면 공간 내에서 이동함에 따라 공간의 아주 많은 것들을 관찰할 수 있을 것입니다.

조금 다른 비유를 들어볼까요? 롤러장으로 가봅시다. 자가 결합 군 \(\Gamma_{\rho}\)의 생김새에서 알 수 있듯이, 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)는 두 클라인 군 \(\Gamma\), \(\rho(\Gamma)\)가 각각 \(\mathbb{H} \times \mathbb{H}\)의 왼쪽과 오른쪽에 작용하여 얻어진 공간입니다. 우리가 롤러장에서 왼발과 오른발에 똑같은 종류의 롤러스케이트를 신고, 왼발 오른발 똑같이 움직인다면, 아마 아주 똑바로 앞으로 나아가겠지요. 저 끝으로 곧게 나아갈 것입니다. 이는 \(\Gamma_{\rho}\)가 \(\mathbb{H} \times \mathbb{H}\)의 양쪽에 균형적으로 작용하는 상황, 즉 두 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 \(\rho(\Gamma) \setminus \mathbb{H}\)가 동일한 기하구조를 갖는 상황을 비유한 것입니다. 반대로, 왼발과 오른발에 다른 종류의 롤러스케이트를 신고, 왼발과 오른발이 제각각 멋대로 움직인다면 어떻게 될까요? 이리저리 움직이며 롤러장 곳곳을 헤집고 다닐 것입니다. 모두의 주목을 받겠지요. 이는 \(\Gamma_{\rho}\)가 \(\mathbb{H} \times \mathbb{H}\)의 양쪽에 불균형적으로 작용하는 상황을 비유한 것으로, 두 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 \(\rho(\Gamma) \setminus \mathbb{H}\)의 기하구조가 다른 상황이 되겠습니다.

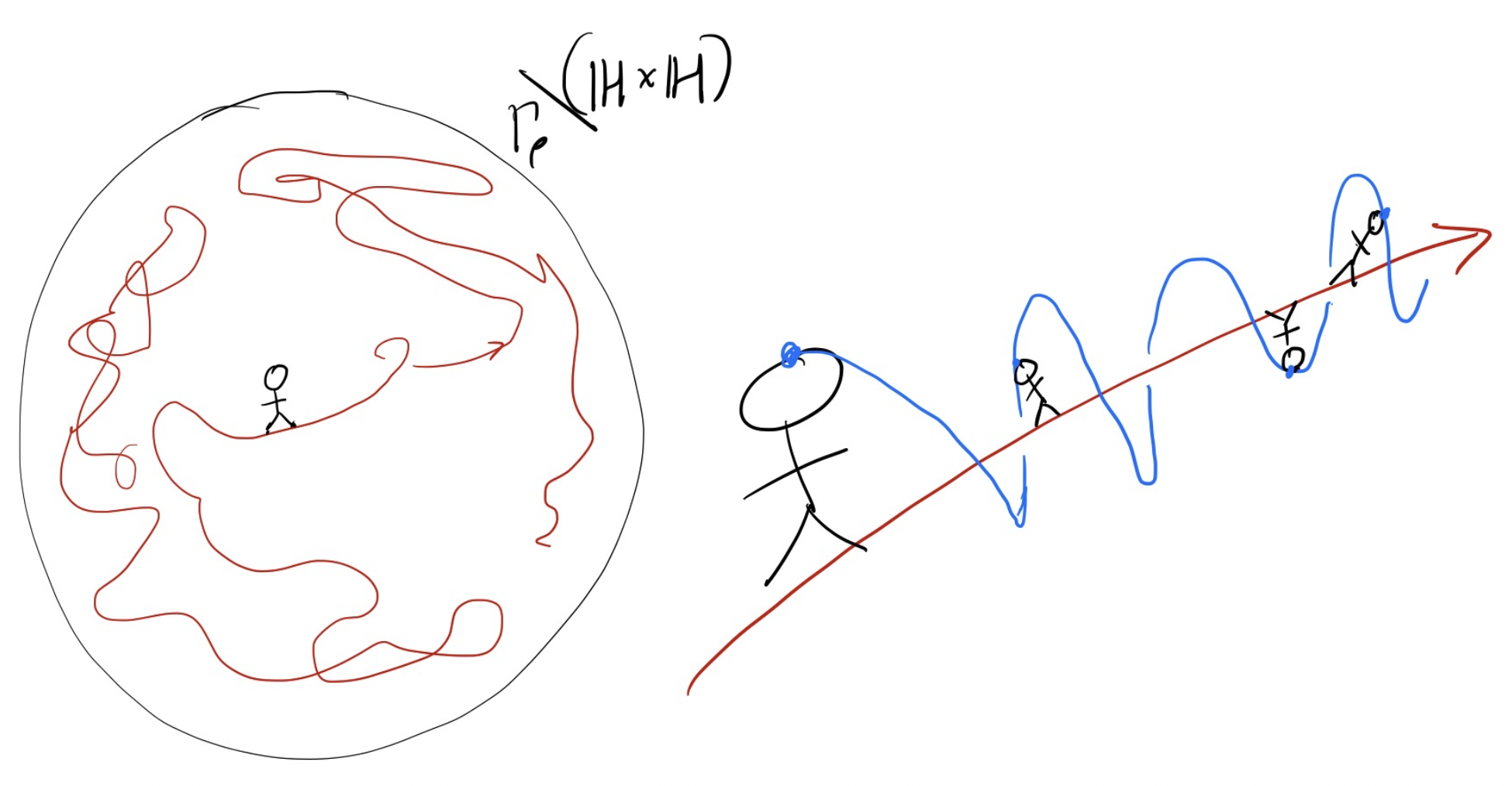
위에서의 비유를 조금 더 수학적으로 이야기 하도록 하겠습니다. 만일 클라인 군의 변형 \(\rho : \Gamma \to \Gamma’\)로부터 얻어진 변형된 쌍곡공간 \(\rho(\Gamma) \setminus \mathbb{H}\)가 기존의 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 다른 기하구조를 가질 때, 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\) 내의 관측자가 한 점에서 출발하여 특정 방향으로 계속해서 이동하다 보면 공간의 상당한 부분을 모두 지나며 관측하게 될 것입니다. 즉, 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\) 위의 어떤 1차원 흐름이 공간을 (정확히는 공간 내의 중요한 부분을) 가득 채워 나가게 되는 것이지요. 이를 수학적인 용어로는 1차원 흐름이 위상적으로 전이적이라고 ^{topologically transitive} 하는데요. 클라인 군의 변형이 기하구조가 다른 쌍곡공간을 만들어 낼 때 이러한 1차원 흐름의 동역학적 성질을 함의한다는 것은, 클라인 군의 변형에 대한 강직성 문제를 고-랭크 공간에서의 동역학적 현상으로 해석할 수 있다는 관점을 제시합니다.

경계에서 일어나는 일 . 이제 강직성 정리 \(\mathbf{Theorem}\) \(\mathbf{A}\)로 다시 돌아가 봅시다. 본 강직성 정리가 의미하는 바는, 클라인 군의 변형 \(\rho : \Gamma \to \Gamma’\)의 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)가 아주 많은 원형 조각 \(C \cap \Lambda_{\Gamma}\)를 원으로 보낼 때 변형된 쌍곡공간 \(\rho(\Gamma) \setminus \mathbb{H}\)가 기존의 \(\Gamma \setminus \mathbb{H}\)와 같은 기하구조를 갖는다는 것인데요. 이 결론에 도달하기 위해선 앞서 논의한 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\) 위에서의 1차원 흐름의 동역학적 성질과 경계사상 \(f\)의 거동사이의 연관성을 규명하여야 할 것입니다.

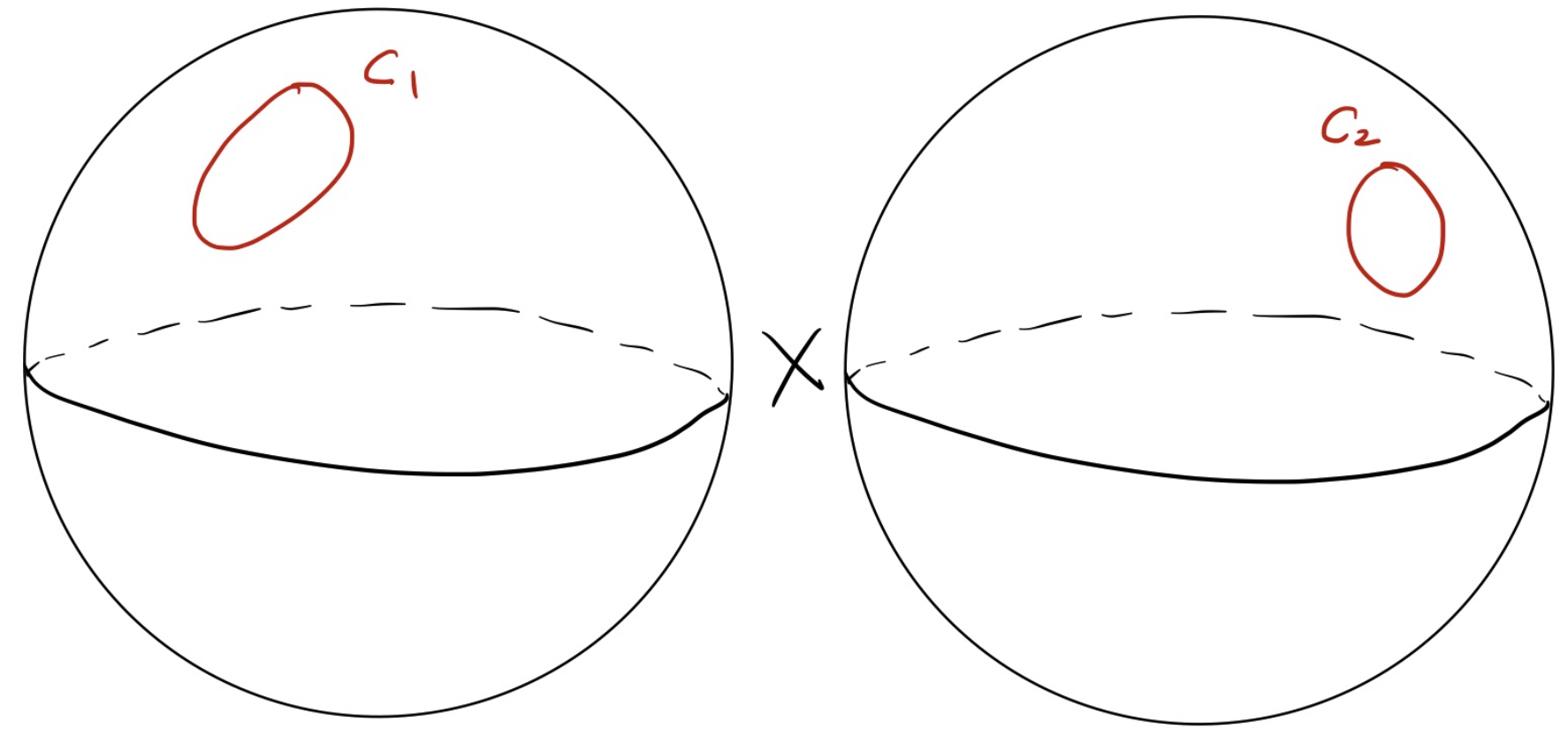
앞서 우리는 대칭공간 \(\mathbb{H}\)의 경계를 2차원 구 \(\mathbb{S}^2\)로 이해한 바 있습니다. 그렇다면 \(\mathbb{H}\)의 점들의 순서쌍들로 이루어진 공간 \(\mathbb{H} \times \mathbb{H}\)의 경계는, 마찬가지로 \(\mathbb{S}^2\)의 점들의 순서쌍으로 이루어진 \(\mathbb{S}^2 \times \mathbb{S}^2\)라고 할 수 있겠지요. 앞서 \(\mathbb{S}^2\) 위에서 원을 생각했던 것처럼, \(\mathbb{H} \times \mathbb{H}\)의 경계 \(\mathbb{S}^2 \times \mathbb{S}^2\)에서는 두 원의 순서쌍들을 생각할 것입니다. 즉, 두 원 \(C_1, C_2 \subset \mathbb{S}^2\)에 대해서 순서쌍 \((C_1, C_2)\)을 생각할 것입니다. 위에서 언급된 것 처럼, 강직성 정리 \(\mathbf{Theorem}\) \(\mathbf{A}\)의 증명은 클라인 군의 변형과 고-랭크 공간 위 1차원 흐름의 동역학, 그리고 \(\mathbb{S}^2 \times \mathbb{S}^2\) 위의 원의 순서쌍 사이의 연관성을 규명함으로써 이루어지는데요. 이를 개략적으로 묘사해 보도록 하겠습니다.

만약 주어진 변형 \(\rho : \Gamma \to \Gamma’\)으로부터 얻어진 변형된 쌍곡공간 \(\rho(\Gamma) \setminus \mathbb{H}\)가 쌍곡공간 \(\Gamma \setminus \mathbb{H}\)와 다른 기하구조를 갖는다면, 위에서 살펴보았던 것 처럼 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)에 어떤 1차원 흐름이 (위상적으로 전이적이어) \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)의 상당한 부분을 가득 채우게 됩니다. 이러한 1차원 흐름의 동역학적 성질이 경계 \(\mathbb{H} \times \mathbb{H}\) 위의 두 원으로 이루어진 순서쌍들에 대해 특별한 함의를 갖는데요. 그것은 바로 아주 많은 경우 두 원 \(C_1, C_2 \subset \mathbb{S}^2\)으로 이루어진 쌍 \((C_1, C_2)\)에 \(\Gamma_{\rho}\)의 원소들을 적용하여 이리저리 움직이다 보면, 웬만한 쌍들 \((D_1, D_2)\)에 모두 가까이 다가갈 수 있다는 것입니다.

반면, 위 강직성 정리 \(\mathbf{Theorem}\) \(\mathbf{A}\)에서의 가정처럼, 만일 경계사상 \(f : \Lambda_{\Gamma} \to \mathbb{S}^2\)가 아주 많은 원형조각 \(C \cap \Lambda_{\Gamma}\)를 원으로 보낸다면 어떨까요? 만약 어떤 원형조각 \(C \cap \Lambda_{\Gamma}\)에 대해 \(f(C \cap \Lambda_{\Gamma})\)가 또 다른 원 \(D\)에 들어간다고 해 봅시다. 우리는 쌍 \((C, D)\)를 생각할 수 있습니다. 그러나 쌍을 이루는 두 원 \(C, D\)는, \(C\)의 조각을 \(f\)로 보냈을 때 \(D\)에 들어가도록 만들어졌다는 특별한 관계를 갖습니다. 따라서 \((C, D)\)를 자가 결합 군 \(\Gamma_{\rho}\)로 이리저리 움직여 얻어내는 쌍들 역시 특별한 관계를 가지고 있고, 이는 쌍 \((C, D)\)를 움직여 가까이 다가갈 수 있는 또 다른 원들의 쌍이 제한적임을 의미하게 됩니다.

정리해보자면, 만약 변형 \(\rho\)로부터 얻어진 쌍곡공간의 기하구조가 기존의 것과 다를 때, 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\) 위의 특정 1차원 흐름이 갖는 동역학적 성질은, 원으로 이루어진 많은 수의 쌍 \((C_1, C_2)\)에 대해 이를 \(\Gamma_{\rho}\)로 이리저리 움직이다 보면 거의 모든 원의 쌍 \((D_1, D_2)\)에 가까이 갈 수 있다는 것을 함의합니다. 반면, \(\mathbf{Theorem}\) \(\mathbf{A}\)의 가정에서 처럼 경계사상이 원형 조각들에 대해 둥글함을 잘 보존한다면, 아주 많은 수의 쌍 \((C, D)\)에 대해 이를 \(\Gamma_{\rho}\)로 이리저리 움직여도 가까이 갈 수 없는 쌍들이 존재하게 됩니다. 즉, 이 두 현상은 동시에 일어날 수 없다는 것을 의미하지요. 따라서 클라인 군의 변형 \(\rho\)의 경계사상이 극한집합의 원형 조각들에서 둥글함을 잘 보존하고 있다면, 사실 \(\rho\)가 만들어내는 변형된 쌍곡공간은 기존의 쌍곡공간과 동일한 기하구조를 가져야 한다는 결론에 도달하게 됩니다. 이로써 강직성 정리 \(\mathbf{Theorem}\) \(\mathbf{A}\)가 증명되는 것이지요. 아주 개략적으로 살펴보았습니다만, 위의 논증은 클라인 군의 경계집합이 갖는 기하학적 성질에 대한 여러 수학자들의 연구 결과에 기반하여 이루어집니다.

새로운 관점 그 이후 . 위에서 살펴보았듯, 클라인 군의 변형 \(\rho : \Gamma \to \Gamma’\)의 강직성에 대한 문제를, 자가 결합 군 \(\Gamma_{\rho}\)를 생각한 후 고-랭크 공간 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\)에서의 동역학적 관점으로 바라보는 것은 기존의 모스토우 강직성 정리의 증명과는 사뭇 다른 느낌을 주는데요. 앞서 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\) 위의 1차원 흐름의 동역학적 성질이 강직성 정리를 증명하는 데에 역할을 했던 것처럼, 이러한 새로운 관점은 자가 결합 군 \(\Gamma_{\rho}\)로부터 등장하는 추가적인 동역학적 관찰들이 주어진 변형 \(\rho\)에 대해 더 많은 이야기를 해주지는 않을까 하는 기대를 안겨줍니다.

이는 정말인데요. 조금 더 수학적인 용어들을 사용하여 예를 들어보도록 하겠습니다. 만일 변형 \(\rho\)가 소위 볼록코-컴팩트 convex cocompact 라고 불리는 종류의 클라인 군 사이의 변형이라면, 자가 결합 군 \(\Gamma_{\rho}\)는 아노소프 군 이라는 대상이 됩니다. 이 경우 \(\Gamma_{\rho} \setminus (\mathbb{H} \times \mathbb{H})\) 에는 위의 1차원 흐름이 더욱 풍성한 동역학적 성질을 가진다는 것이 알려져 있습니다. 예를 들어, 에르고딕성이 알려져 있는데요 ^[3],[10]. 이와 더불어 자가 결합 군 \(\Gamma_{\rho}\)의 패터슨-설리반 측도라는 것이 어떤 특정한 형태로 나타날 수 있다는 관찰을 통해, 만약 변형 \(\rho\)가 기하구조가 달라지는 쌍곡공간을 만들어 낼 때, 극한집합 \(\Lambda_{\Gamma}\)의 원형 조각들의 둥글함이 얼마나 보존될 수 있는지에 대한 정량적인 관찰 역시 가능해 집니다 ^[9].

또, 자가 결합 군 \(\Gamma_{\rho}\)의 동역학적 성질을 통해 강직성을 규명하는 이같은 관점은, 사실 공간 \(\mathbb{H}\)가 음의 곡률 \(-1\)을 가지고 휘어져있다는 사실에 아주 의존하는 것은 아닙니다. 따라서 클라인 군이 아닌 보다 일반적인 종류의 군에 대해 여러 형태의 강직성에 대한 질문을 생각해볼 여지를 제공해주기도 합니다 ^[7].

연재를 마치며 . 이렇게 총 세 편의 글을 통해 3차원 쌍곡 공간의 강직성에 대해 개략적으로나마 살펴보았습니다. 유한 부피를 갖는 3차원 쌍곡공간에 대한 모스토우 강직성 정리에서부터, 무한 부피의 상황에서의 강직성 정리까지, 강직성에 대한 질문을 어떻게 이해하고 답할 수 있을지를 확인해 보았는데요. 독자분들께 공간의 강직성이라는 것이 수학적으로는 저렇게 이해할 수 있구나 하는 메세지가 조금이나마 전달되었기를 바라는 마음을 담아, 이만 연재를 마치도록 하겠습니다. 감사합니다.

연재
3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [1] 
3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [2]
3차원 쌍곡 공간의 강직성: 유한 부피에서 무한 부피까지 [3]