초전도 양자컴퓨터의 물리적 구현

들어가며

최근 몇 년 사이 IBM과 Google의 양자컴퓨터가 특정 문제를 슈퍼컴퓨터보다 빠르게 계산했다는 소식이 종종 들려온다. 그러나 매번 얼마 지나지 않아 더 뛰어난 고전컴퓨터 알고리즘이 개발되어 슈퍼컴퓨터가 앞섰다는 소식도 함께 전해지곤 한다. 이렇게 엎치락뒤치락 발전하다 보면 언젠가는 양자컴퓨터의 유용성을 실증할 날이 오지 않을까? 양자컴퓨터의 유용성에 대해서는 Horizon의 이전 글 [1] [2] 에 잘 설명되어 있어, 이번 글에서는 IBM과 Google을 필두로 빠르게 발전하고 있는 초전도 양자컴퓨터의 물리적 구현 방법을 소개한다. 샹들리에처럼 생긴 희석식 극저온 냉각기에 부착되어 동작하는 초전도 양자컴퓨터의 동작원리부터 시작해서 시스템 성능 향상과 확장을 위해 어떤 노력들이 이루어지고 있는지 함께 살펴보도록 하자. 

왜 초전도체로 양자컴퓨터를 만들까?

초전도 양자컴퓨터는 초전도 물질로 만들어진 전자회로이다. 고전컴퓨터는 회로의 전압상태로 비트 정보를 표현하지만, 이 장치는 회로의 양자상태로 큐비트 정보를 표현한다는 점이 특별하다. 비트와는 달리 큐비트는 0과 1을 동시에 표현하는 중첩 상태를 나타낼 수 있고, 큐비트끼리 서로 얽혀 있다면 한 큐비트의 측정 결과가 다른 큐비트 상태에 영향을 미치기도 한다. 이러한 중첩과 얽힘이라는 특성 덕분에 양자컴퓨터만의 독특한 연산 방식이 가능하다. 중첩과 얽힘의 중요성에 대해 알고 싶은 독자는 Horizon의 이전 글 [3] 을 참조하기 바란다. 그러나 큐비트 정보는 외부와의 상호작용으로 쉽게 손상될 수 있어 전자회로의 에너지가 외부로 방출되지 않도록 해야 한다. 따라서 전기저항이 0인 초전도체로 전자회로를 제작해야만 양자컴퓨터가 안정적으로 동작할 수 있다.

초전도 회로의 양자상태를 이해하기 위해서 초전도체의 특성을 알아야 한다. 1957년, 바딘^{J. Bardeen}, 쿠퍼^{L. N. Cooper}, 슈리퍼^{J. R. Schrieffer}는 임계온도 이하에서 저항 없이 전류가 흐르는 초전도 현상을 설명하기 위해 전자가 짝을 이루는 쿠퍼쌍^{Cooper pair} 개념을 도입하였다. 전자는 페르미온 입자이기 때문에 파울리 배타원리에 의해 서로 같은 상태에 있을 수 없지만, 쿠퍼쌍은 보존의 특성을 지녀 초전도체 내 모든 쿠퍼쌍이 결맞음^coherence을 유지한 채 하나의 상태로 집단적으로 행동한다. 이 특성 덕분에 초전도체 내의 모든 쿠퍼쌍을 하나의 거시적인 양자시스템으로 간주할 수 있으며, 더 나아가 초전도 회로의 전류나 전압 역시 하나의 양자상태로 표현이 가능하다.

초전도 LC 회로는 어떤 양자상태를 가질 수 있을까?

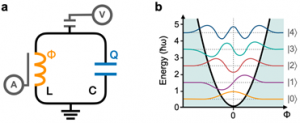
간단한 예시를 통해 초전도 회로의 양자상태를 이해해보자. 그림 1a에 그려진 LC 회로는 인덕터와 축전기로 구성된다. 회로의 유도용량이 \(L\), 정전용량이 \(C\)일 때, 회로에 흐르는 전류 \(I\)와 축전기에 저장된 전하량 \(Q\)는 서로를 이끌며 공진주파수 \(\omega=1/\sqrt{LC}\)로 진동한다. 그리고 전류는 인덕터를 관통하는 자기선속 \(\Phi=LI\)을 유도한다. 먼저 전하량과 자기선속의 관계를 살펴보자. 인덕터의 전압은 패러데이 법칙에 따라 시간에 따른 자기선속의 변화율 \(V_L=d\Phi/dt\)로 결정되고, 축전기의 전압은 저장된 전하량과 비례하는 \(V_C=Q/C\)의 관계를 가진다. 병렬회로에서 두 전압의 크기는 같기 때문에 아래의 전하량-자기선속 관계식을 얻을 수 있다.

 \(Q=C\frac{d\Phi}{dt}.\)

이 전하량과 자기선속의 관계는 우리에게 익숙한 입자의 운동량 \(p\)와 위치 \(x\)의 관계인 \(p=m\frac{dx}{dt}\)와 유사하여 종종 정전용량 \(C\)를 입자의 질량 \(m\), 자기선속 \(\Phi\)를 입자의 위치 \(x\)로 비유하기도 한다.

LC회로의 헤밀토니안은 다음과 같이 축전기에 저장된 에너지 \(E_C\)와 인덕터에 저장된 에너지 \(E_L\)의 합으로 표현된다.

 \(H_{LC}=E_C+E_L=\frac{Q^2}{2C}+\frac{\Phi^2}{2L}.\)

운동량과 위치에 대한 비유를 생각해보면, 축전기 에너지 \(E_C\)를 운동에너지, 인덕터 에너지 \(E_L\)을 퍼텐셜 에너지에 해당한다. 이러한 유사성을 이용해 양자역학 수업 시간에 배우는 입자의 조화운동^{harmonic motion}에 대한 슈뢰딩거 방정식 해를 LC 회로에 적용할 수 있다. (양자 조화진동자에 관한 자세한 설명은 Horizon에 기재된 글 [4] 을 살펴보는 것을 추천한다.) 그 결과로 자기선속에 대한 조화운동 퍼텐셜 에너지와 양자화된 상태함수는 그림 1b와 같다. 상태함수의 절댓값 제곱이 자기선속의 확률분포를 나타낸다는 사실을 바탕으로, 노란색으로 그려진 가장 낮은 에너지 상태인 \(|0\rangle\)을 살펴보자. 그림에서 보이듯이 자기선속이 0인 확률이 가장 높고 자기선속이 양수인 경우와 음수인 경우가 동일한 위상으로 중첩되어 있다. 인덕터의 자기선속은 전류와 비례하기 때문에 \(|0\rangle\) 상태에서는 시계 방향으로 흐르는 전류와 반시계 방향으로 흐르는 전류가 확률분포에 따라 중첩되어 있다는 것을 의미한다. 동일한 방식으로 다음으로 에너지가 낮은 보라색의 \(|1\rangle\) 상태함수를 해석해보면, 자기선속, 즉 전류는 \(|0\rangle\) 상태에 비해 상대적으로 큰 값을 가지고 있으며, 시계 방향으로 흐르는 전류와 반시계 방향으로 흐르는 전류가 180도의 위상 차이로 중첩되어 있다는 것을 확인할 수 있다. 전하량의 경우, 운동량과 위치의 관계처럼 전하량의 상태함수와 자기선속의 상태함수가 서로 푸리에 변환 관계에 있다. 따라서 각 에너지 상태에서 전하량이 어떻게 중첩되어 있는지는 독자들이 큰 어려움 없이 직접 생각해볼 수 있을 것이다.

조셉슨 정션은 왜 필요할까?

우리는 LC회로를 큐비트로 사용할 수 있을까? 예를 들어, 가장 낮은 두 에너지 상태인 \(|0\rangle\)과 \(|1\rangle\)만으로 양자정보를 표현하고 이를 제어할 수 있을까? 아쉽게도 일반적인 방법으로는 불가능하다. 초전도 큐비트의 상태 제어는 그림 1a에서 보이듯이 교류 전압 또는 교류 자기장(전류) 마이크로파를 회로에 인가하는 방법을 사용한다. 마이크로파의 주파수가 양자화된 에너지 간격(공진 주파수)과 일치하면, 마이크로파 진폭에 비례하는 속도로 상태 전이가 발생한다. 만약 \(|0\rangle\) 상태로 초기화된 LC회로에 공진 주파수의 마이크로파를 가하면 서서히 \(|1\rangle\) 상태로 전이하게 된다. 그러나 그림 1b에서 보이듯이, LC회로의 양자상태는 모두 동일한 에너지 간격을 가지기 때문에 \(|1\rangle\)에서 \(|2\rangle\)로의 상태 전이도 발생한다. \(|0\rangle\)과 \(|1\rangle\) 이외의 상태는 큐비트 정보로 간주되지 않기 때문에 오류로 취급되며, 이는 LC 회로가 큐비트 시스템으로 사용되기 어려운 이유가 된다. 따라서 초전도 회로의 에너지 등간격성을 깨뜨릴 방법이 필요하다.

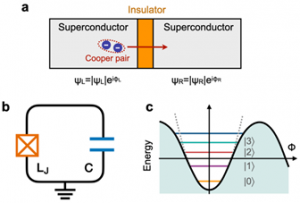
그 방법이 조셉슨 정션을 활용하는 것이다. 조셉슨 정션은 두 초전도체 사이에 금속, 반도체, 절연체 등 수 nm의 얇은 비-초전도체가 삽입되어 있는 회로 요소이다(그림 2a). 절연층이 중간에 끼어 있더라도 두께가 충분히 얇다면 터널링 현상을 통해 전하 운반자인 쿠퍼쌍이 통과할 수 있어 전기저항 없이 전류가 흐른다. 터널링 확률은 좌우 초전도체 쿠퍼쌍의 양자상태 위상차이 \(\phi=\phi_R-\phi_L\)에 의존하며 이에 따라 조셉슨 정션에 흐르는 전류 \(I_J\)와 전압 \(V_J\)은 다음과 같이 주어진다.

\(I_J=I_c \sin \phi, \ V_J=\frac{\hbar}{2e}\frac{d\phi}{dt}\)

흥미롭게도 조셉슨 전압을 \(\Phi\equiv\hbar\phi/2e\) 변수로 다시 정리하면 패러데이 법칙과 같은 꼴인 \(V_J=d\Phi/dt\)로 쓰일 수 있는데 여기서 \(\Phi\)는 초전도체 폐회로를 통과하는 자기선속에 해당한다. 또한 조셉슨 정션은 전류와 자기선속이 비선형적인 관계를 가지는 비선형 인덕터임을 쉽게 확인할 수 있다.

조셉슨 정션의 헤밀토니안은 전류와 전압의 곱을 시간에 대해 적분한 것과 축전기 에너지의 합으로 써진다.

\(H_{JJ}=\frac{Q^2}{2C}-\frac{\hbar I_c}{2e}\cos \phi\)

여기서 \(C\)는 조셉슨 정션 자체의 정전용량이며, 그림 2b와 같이 병렬로 축전기를 연결하여도 \(C\)값만 증가할 뿐 동일한 형태의 헤밀토니안을 가진다. 그림2c는 자기선속 \(\Phi=\hbar\phi/2e\)에 대한 코사인 형태의 퍼텐셜 에너지를 보여준다. 에너지가 낮을 때는 거의 포물선 형태를 띠지만, 에너지가 높아질수록 이 포물선 형태가 양 옆으로 벌어진다. 이는 높은 에너지 상태에서 에너지 간격이 점점 좁아지는 결과를 만들고, 깨어진 에너지 등간격성 덕분에 선택적인 양자상태 제어가 가능하다.

그림 2c의 \(|0\rangle\)과 \(|1\rangle\) 양자상태를 살펴보면, \(\phi\)가 0 근처에서만 확률을 가지기 때문에 \(\cos \phi \approx 1-\phi^2/2\)로 근사할 수 있다. 상수를 제외하고 퍼텐셜 에너지를 다시 써보면 \(E_J \approx \left(\frac{\hbar I_c}{4e}\right)\phi^2=\left(\frac{e I_c}{\hbar}\right)\Phi^2\)로 정리되는데, 이를 LC 회로의 인덕터 에너지 \(E_L\)과 비교해보면 조셉슨 정션의 유도용량은 \(L_J\approx\hbar/(2eI_c)\)에 해당한다. 이렇듯 낮은 에너지 상태에서는 조셉슨 정션을 단순한 선형 인덕터로 이해할 수 있다. 더 나아가, \(|0\rangle\)과 \(|1\rangle\)의 양자상태 제어를 위한 공진주파수도 \(\omega = 1/\sqrt{L_J C}\)로 계산할 수 있다. 참고로, 양자상태의 상태함수를 전류의 중첩으로 해석할 때 LC회로에서는 전류가 인덕터의 자기선속 \(\Phi\)와 비례하지만, 조셉슨 정션에서는 전류가 \(I_c \sin \phi = I_c \sin(2e\Phi/\hbar)\)의 관계를 가지고 있어 초전도체 폐회로의 자기선속 \(\Phi\)에 비례하지 않을 뿐만 아니라 주기성을 가진다는 점을 유의해야 한다.

초전도 큐비트의 종류

앞서 설명한 것처럼 에너지의 등간격성을 깨뜨려줄 수 있는 조셉슨 정션은 초전도 큐비트 구현에 핵심적인 회로 요소이다. 지금부터는 조셉슨 정션에 축전기와 인덕터를 추가하여 만들 수 있는 두 가지 종류의 초전도 큐비트를 소개하겠다. 먼저 그림 2b에 그려진 회로는 조셉슨 정션에 축전기를 병렬로 연결한 전하 큐비트^{charge qubit}이다. 앞서 언급한대로 축전기를 추가하더라도 위의 조셉슨 정션 헤밀토니안 \(H_{JJ}\)와 형태가 동일하다. 그림 2c에 보이는 \(|0\rangle\)과 \(|1\rangle\) 상태에 정보를 담아 큐비트로 사용하며, 축전기에 저장된 평균 쿠퍼쌍 (전자쌍) 개수로 두 상태가 구분되어 전하 큐비트라 명명되었다. 엄밀하지는 않지만 \(|0\rangle\)은 축전기에 쿠퍼쌍이 없는 상태, \(|1\rangle\)은 유한한 쿠퍼쌍이 존재하는 상태로 이해해도 된다. 전하 잡음에 취약하다는 단점이 있지만 축전기의 용량을 늘림으로써 전하 잡음 효과를 완화할 수 있다. 축전기 정전용량이 큰 전하 큐비트는 특별히 트랜스몬^transmon이라 부르며 현재 가장 널리 사용되고 있는 초전도 큐비트 종류이다.

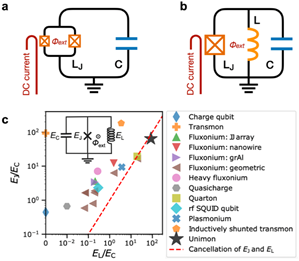
단일 조셉슨 정션 대신 두 조셉슨 정션을 병렬로 연결한 SQUID^{superconducting quantum interference device}를 사용하면 주파수 조절이 가능한 전하 큐비트를 구현할 수 있다(그림 3a). 직류 전류로 SQUID 폐회로를 통과하는 자기장을 조절하여 초전도체의 위상을 바꿀 수 있고, 간섭 효과에 의해 SQUID를 지나는 조셉슨 전류 진폭\(I_c\)조절이 가능해진다. 초전도 큐비트의 에너지 간격, 즉 공진주파수가 \(L_J\approx\hbar/(2e I_c)\)에 의존한다는 점을 생각해본다면, 외부 전류로 실시간 공진주파수 제어가 가능하다는 것을 알 수 있다. 주파수 조절 가능성은 다양한 큐비트 상호작용 및 양자게이트를 구현할 수 있다는 장점이 있지만, 외부 자기장 잡음에 취약하다는 단점도 존재한다. 참고로 현재 IBM은 고정 주파수 트랜스몬 큐비트 구조로, Google은 주파수 조절 트랜스몬 큐비트 구조로 양자프로세서를 개발하고 있다.

다음으로 소개할 플럭스 큐비트^{flux qubit}는 그림 3b에서 보이는 회로로, 조셉슨 정션에 인덕터를 병렬로 연결하여 구현한다. 조셉슨 정션과 인덕터가 폐회로를 이루기 때문에 \(\phi_{ext}\)로 퍼텐셜 에너지의 형태 조절이 가능하다. 구체적인 헤밀토니안은 아래와 같이 인덕터 에너지가 추가된 형태이다.

\(H_{Flux}=\frac{Q^2}{2C}-\frac{\hbar I_c}{2e}\cos \phi +\frac{1}{2L}\left(\frac{\hbar}{2e}(\phi+\phi_ {ext})\right)^2\)

퍼텐셜 에너지는 포물선 이차함수에 음수 부호의 코사인 함수가 더해진 꼴인데, 외부 자기장 \(\phi_{ext}\)을 0에서부터 조금씩 변화시켜 보면 자기선속 \(\phi\)가 양수와 음수인 영역에 퍼텐셜 우물이 하나씩 만들어진다. 양자상태 \(|0\rangle\)과 \(|1\rangle\)은 두 퍼텐셜 우물에 가둬져 자기선속^{magnetic flux}으로 구분되기 때문에 플럭스 큐비트로 불린다. 그리고 자기선속과 전류의 관계성 덕분에 \(|0\rangle\)과 \(|1\rangle\)이 초전도 회로에 흐르는 전류 방향으로 구분된다고 해석할 수도 있다. 즉, \(|0\rangle\)은 축전기를 기준으로 반시계방향으로 전류가 흐르는 상태, \(|1\rangle\)은 시계방향으로 전류가 흐르는 상태로 이해하면 된다. 참고로 외부 자기장을 \(\phi_{ext}=\pi/2\)이 되도록 설정하면 자기 잡음에 영향을 덜 받고 전하 큐비트에 비해 훨씬 넓은 에너지 비-등간격성을 가지고 있어 많은 장점을 가진다 [5]. 그럼에도 본질적으로 자기 잡음에 취약하기 때문에 유도용량 \(L\)을 키운 회로가 주로 사용되며 이러한 플럭스 큐비트를 특별히 플럭소니움^fluxonium이라고 부른다. 하지만 코일과 같은 기하학적인 인덕터로는 원하는 정도의 유도용량을 달성하기 힘들어, 조셉슨 정션을 직렬로 연결하거나 나노와이어를 사용하는 등 키네틱 유도용량^{kinetic inductance}을 활용한다.

이 외에도 그림 3c에 보이듯이 조셉슨 에너지 \(E_J\), 축전기 에너지 \(E_C\), 인덕터 에너지 \(E_L\)의 비율을 조절하거나 [6] , \(Y-\Delta\) 형태와 같은 독특한 초전도 회로 네트워크를 구성하는 [7] 등 외부 잡음에 강인한 큐비트를 만들기 위한 노력이 계속 되고 있으며 최근에는 1ms 이상의 양자 결맞음 시간을 가진 초전도 큐비트가 보고되었다 [8].

초전도 양자프로세서의 구성

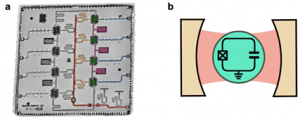
그림 4a는 필자가 양자게이트 연구 [9] 를 위해 사용한 트랜스몬 기반 양자프로세서 칩 사진이다. 이 사진을 통해 초전도 양자프로세서의 구성을 살펴보도록 하자. 초록색으로 표시된 요소들은 각 트랜스몬 큐비트를 구성하는 축전기에 해당하며, 이 축전기들은 축전기 사이에 위치한 조셉슨 정션으로 연결되어 있다. 그림 2b의 회로와 비교해보라. 큐비트들은 보라색으로 표시된 커플링 공진기를 통해서 정전^capacitive 방식으로 상호작용한다. 참고로 상호작용이 너무 강해지지 않도록, 인접한 큐비트들은 서로 다른 공진 주파수를 갖도록 설계한다. 그리고 양자게이트와 양자상태 측정은 각각 파란색으로 표시된 드라이브 라인과 빨간색으로 표시된 버스^bus 라인에 마이크로파 펄스를 주사하여 구현한다. 드라이브 라인은 각 큐비트마다 독립적으로 제작되어 개별적인 양자게이트 구현이 가능하다. 반면 양자상태 측정의 경우에는, 노란색 리드아웃 공진기마다 공진주파수가 다르다는 점을 이용해 여러 주파수의 마이크로파 펄스를 버스 라인에 동시에 주입하여 여러 큐비트의 양자상태를 한번에 측정한다. 양자상태 측정 원리를 간단히 설명해보면 다음과 같다. 그림 4b에 도식화하여 그려진 것처럼 초전도 큐비트는 노란색 리드아웃 공진기의 전자기장과 상호작용한다. 이 상호작용 때문에 공진기의 공진주파수가 큐비트 상태에 따라 살짝 변화한다. 이점을 활용하여 버스 라인을 통해 주입되었다가 반사되는 마이크로파 펄스 신호의 세기나 위상 변화를 측정하여 큐비트 \(|0\rangle\)과 \(|1\rangle\) 상태를 구별할 수 있다. 

그림 4. a, 트랜스몬 기반의 초전도 양자프로세서 사진.
b, 큐비트와 리드아웃 공진기의 상호작용 도식화.

초전도 양자컴퓨터의 오류 원인 및 개선 방안

복잡한 문제를 빠르고 정확하게 연산할 수록 더 좋은 컴퓨터이다. 이를 기준으로 생각해보면, 양자컴퓨터의 성능 지표로는 큐비트 수, 큐비트 연결성, 게이트 동작시간, 게이트 오류율 등을 꼽을 수 있겠다. 현재 초전도 양자컴퓨터의 수준을 요약하면 다음과 같다. 2023년 말 IBM은 1,121개의 초전도 큐비트 양자프로세서인 Condor를 공개했으며, 이는 현재 가장 큰 규모의 양자프로세서이다. 또한, 많은 연구 그룹에서 단일 큐비트 게이트의 경우 5 ~ 30ns 동작 시간에 0.01% 수준의 오류율을, 이중 큐비트 게이트의 경우 30 ~ 200ns 동작 시간에 0.1% 수준의 오류율을 보고하고 있다. 시스템 확장성는 나중에 다루도록 하고, 여기서는 게이트 오류의 발생 원인과 개선 방안을 살펴보도록 하자.

앞서 설명한대로 초전도 양자컴퓨터에서는 마이크로파 펄스를 주사하거나 전류로 큐비트 회로를 통과하는 자기장을 변화시키는 방식으로 양자게이트를 구현한다. 오류의 종류는 크게 1) 불완전한 양자게이트 교정^calibration이나 원치 않는 큐비트 간 상호작용으로 인한 유니터리 오류와 2) 외부환경과의 상호작용으로 인한 비유니터리 오류로 분류된다. 대부분의 유니터리 오류는 마이크로파 펄스와 전류의 파라미터를 정밀하게 조정하거나 튜너블 커플러를 사용해 상호작용 세기를 제어함으로써 어느 정도 해결할 수 있다. 그러나 비유니터리 오류는 큐비트가 외부 환경과 상호작용하면서 양자적인 결맞음^coherence을 잃게 되는 경우로, 해결이 쉽지 않다. 큐비트의 결어긋남 특성은 주로 두 가지 시간 척도로 대표된다.

1. T1 이완 시간: 큐비트가 외부로 에너지를 방출하여  \(|1\rangle\)에서 \(|0\rangle\) 상태로 바뀌는데 걸리는 시간.
2. T2 위상 어긋남 시간: 큐비트가 외부 환경과 양자적으로 얽히거나 잡음에 의해 에너지 간격이 흔들려 \(|0\rangle\)과 \(|1\rangle\) 상태의 위상 결맞음을 잃는데 걸리는 시간.

이러한 T1과 T2 시간은 큐비트의 안정성에 중요한 영향을 미치며, 양자컴퓨터의 성능을 결정하는 핵심 요소이다. 대표적인 결어긋남 원인 세 가지와 이를 해결하기 위한 전략을 소개한다.

에너지 손실: 초전도 양자프로세서를 제어하려면 외부와 도선으로 연결해야 하므로 에너지가 외부로 빠져나갈 수 밖에 없다. 이를 극복하기 위해서는 특정 주파수만 통과하도록 하는 대역필터나 에너지가 단방향으로만 흐르도록 하는 회로 요소를 개발하여 활용할 수 있다. 또한, 회로 요소가 초전도체로 만들어졌더라도 주변 산화막과 기판은 저항을 가지고 있어 유전 손실이 발생한다. 미시적으로 생각해보면, 그림 5에 보이는 산화막이나 공정 과정에서 남은 잔여물 내 결함이 특정 에너지 간격을 가진 2-레벨 양자시스템에 해당한다. 만약 주변 결함의 에너지 간격이 초전도 큐비트와 유사하면 공진에 의해 큐비트의 에너지를 빼앗는 원인이 된다. 따라서 유전 손실이 적은 물질을 기판으로 사용하고, 공정과정에서 산화막과 잔여물을 깨끗이 제거하는 것이 중요하다. 최근에는 주변 결함의 에너지 간격을 전기장으로 제어하여 초전도 큐비트를 보호하는 연구가 활발히 진행 중이다. 마지막으로, 큐비트의 동작 주파수를 낮게 설계하면 전자기장 잡음이 증가하기는 하지만 유전 손실을 줄일 수 있다.

 

전자기장 잡음: 초전도 큐비트는 외부 전자기장 환경에 민감하게 반응한다. 전하 잡음이나 회로를 통과하는 자기장 잡음이 초전도 큐비트의 에너지 간격을 바꾸어 위상 어긋남 오류를 일으킨다. 이를 방지하려면 전자기장 잡음이 적은 전력 소스를 사용하고, 뮤메탈 및 초전도 자기장 쉴드를 사용하여 외부 자기장 잡음을 차단하는 것이 필수적이다. 그리고 큐비트에 인가되는 전압과 자기장에 바이어스를 주어 큐비트의 에너지 간격 변화가 최소화되는 최적의 조건^{sweet spo}t에서 큐비트를 동작시키는 것이 도움이 된다. 보다 근본적으로는 그림 3c와 같이 축전기, 인덕터, 조셉슨 정션의 값을 조절해 외부 잡음에 강한 최적의 초전도 큐비트를 설계하는 연구가 필요하다. 정전용량을 키워 전하 잡음 효과를 줄인 트랜스몬 큐비트와 유도용량을 키워 자기장 잡음 효과를 줄인 플럭소니움 큐비트가 좋은 예가 되겠다.

열 잡음: 다른 양자시스템에서도 마찬가지겠지만, 열 잡음은 초전도 양자프로세서에서 특히 중요한 문제이다. 주변 온도가 상승하면 초전도 에너지 갭 이상의 열에너지가 발생하게 되고, 이는 초전도 현상의 중요한 역할을 하는 쿠퍼쌍이 깨져 준입자^{quasiparticle}로 변화하는 원인이 된다. 준입자 수의 증가는 시스템 내 저항을 만들어내며 에너지 손실과 위상 결어긋남을 발생시킨다. 최근 연구에서는 알루미늄이나 나이오븀보다 초전도 에너지 갭이 큰 탄탈륨을 사용하여 양자프로세서를 제작하였을 때 결맞음 시간이 향상된다는 결과가 일관성 있게 보고되고 있다. 또한 고에너지 방사선으로부터 쿠퍼쌍을 보호하기 위해 적외선, 자연 방사선, 우주선 등에 대한 필터나 쉴드를 사용하는 것이 중요하다. 열에 의한 또 다른 문제는 큐비트가 리드아웃 공진기, 커플링 공진기 등과 상호작용하기 때문에 발생한다. 주변 온도가 높아지면 공진기 내부의 광자 수가 보즈-아인슈타인 통계에 따라 분포하게 되는데, 광자 수에 따라 큐비트 에너지 간격이 조금씩 달라진다. 즉, 열 광자 수 분포에 의해 큐비트의 에너지 간격이 흔들리고 이는 위상 어긋남을 발생시킨다. 따라서 큐비트 주변 요소들을 높은 공진 주파수로 설계하여 열 잡음의 효과를 줄이는 것이 도움이 된다.

 

초전도 양자컴퓨터의 양자오류보정

현재 초전도 단일 큐비트 게이트의 오류는 0.01% 수준, 이중 큐비트 게이트의 오류는 0.1% 수준까지 낮아졌다. 그러나 실용적인 양자 알고리즘을 실행하기 위해서는 많은 수의 양자게이트 작용이 필요하며, 이로 인해 누적된 오류는 연산결과의 신뢰성을 낮춘다. 궁극적으로는 큐비트의 결맞음 시간을 늘려 고전컴퓨터의 오류 발생률인 \(10^{-16}\) 수준까지 오류율을 낮춰야 하겠지만, 현재로서는 뚜렷한 돌파구가 없다. 그래서 큐비트 자체의 오류율을 낮추는 노력과 동시에 양자오류보정 코드를 사용하여 오류를 수정하고자 한다. 오류보정의 핵심 아이디어는 오류율이 충분히 낮다면 여러 큐비트에서 동시에 오류가 발생할 확률이 하나의 큐비트에서 오류가 발생할 확률보다 작다는 것이다. 여러 물리 큐비트를 묶어 양자오류보정 코드를 구성하면 오류를 검출하고 보정할 수 있는 논리 큐비트를 만들 수 있으며, 구성하는 물리 큐비트의 수가 늘어날수록 논리 큐비트의 오류율을 낮출 수 있다. 양자오류보정 원리에 대해 더 자세히 알고 싶다면 Horizon 이전 글을 탐독해 보길 권한다 [11].

양자시스템마다 활용할 수 있는 큐비트 상호작용 방식이 달라 구현에 용이한 양자오류보정 코드도 다르다. 초전도 양자프로세서에서는 일반적으로 인접한 큐비트 간의 상호작용만 가능하여 이 상호작용만으로 오류 검출과 보정이 가능한 표면 코드 구현을 목표로 한다. 표면 코드의 결함 감내 임계치는 약 1%인데, 이는 물리 큐비트 당 오류율이 1%보다 낮아야지만 큐비트 수를 늘려 논리 큐비트의 오류율을 낮출 수 있다는 것을 의미한다. 즉, 상태 초기화, 양자게이트, 양자상태 측정, 피드포워드 등 양자오류보정 과정 전체의 오류율을 1% 이하로 만들어야 오류보정이 의미가 있다. 게다가 이론적으로는 프로세서의 큐비트 수가 늘어나더라도 물리 큐비트의 오류율은 일정하다고 가정하지만, 실제로는 시스템 복잡도 증가로 물리 큐비트의 오류율이 증가한다. 따라서 양자오류보정을 통해 논리 오류율을 낮추는 것은 매우 어려운 일이다. 좋은 소식은 2024년 Google 연구팀이 105-큐비트 초전도 양자프로세서를 사용하여, 거리-3 표면코드(17 큐비트), 거리-5 표면코드(49 큐비트), 거리-7 표면코드(97 큐비트)로 확장할 때마다 논리 오류율이 약 2.15배씩 감소하는 실험 결과를 얻었다는 것이다 [12]. 상당한 노력에도 불구하고 오류율은 여전히 \(10^{-3}\) 수준으로 가야 할 길은 멀지만 양자오류보정 시대의 시작을 알리는 중요한 성과라고 생각한다.

실험적인 노력 외에도, 양자오류보정 코드를 구현하는데 필요한 물리 큐비트 수를 줄이기 위한 연구가 활발히 진행되고 있다. 중요한 연구결과 두 가지만 소개하겠다. 첫째, 초전도 양자컴퓨터의 경우 일반적으로 Z 오류(위상 반전) 발생 확률이 X 오류(비트 반전)보다 높다는 사실을 이용하여, 기존 표면 코드를 개선한 XZZX 표면 코드가 제안되었다 [13]. 이 코드는 오류편향 정보를 활용하여 직사각형 형태의 코드를 구성함으로써 결함 감내 임계치를 높이고 오류 검출의 오버헤드를 줄일 수 있다. 둘째, 기존 표면 코드에 비인접한 초전도 큐비트 간의 상호작용을 추가하여 논리 큐비트 구현에 필요한 물리 큐비트 수를 상당히 줄일 수 있는 BB 코드가 제안되었다[14].  그림 6 참조. 예를 들어, 기존 표면 코드를 사용하여 0.1%의 물리 큐비트 오류율을 \(10^{-7}\)의 논리 오류율로 낮추기 위해서는 약 3,000개의 물리 큐비트가 필요하지만, BB코드를 사용하면 288개의 물리 큐비트로 가능하다. 이는 양자오류보정에 필요한 물리 큐비트 수를 크게 줄일 수 있다는 희망적인 결과이다. IBM연구팀은 이 코드를 실제로 구현하기 위해 비인접 큐비트 커플러를 포함한 새로운 양자 프로세서를 개발에 힘쓰고 있다고 밝혔다. 이 외에도, 일반적인 양자오류보정 코드로는 보정할 수 없는 동시 오류 발생, \(|0\rangle\)과 \(|1\rangle\) 이외의 양자상태로의 누출 오류 등을 처리하기 위한 여러 가지 방법론이 제시되고 있다.

 

초전도 양자컴퓨터의 확장성

마지막으로 초전도 양자프로세서의 확장성에 대해서 살펴보도록 하자. 먼저, 초전도 양자프로세서를 구성하는 요소의 물리적인 크기부터 생각해보자. 앞서 말했듯이, 전하 잡음과 자기 잡음의 효과를 최소화하기 위해서는 초전도 큐비트의 정전용량이나 유도용량을 키워야 한다. 이로 인해 칩 위의 초전도 큐비트가 차지하는 면적이 커질 수 밖에 없으며, 일반적으로 수백 \(\mu\)m 정도의 크기를 가진다. 비유전율이 높은 물질이나 키네틱 유도용량이 높은 물질을 사용하면 회로 요소의 표면적을 줄일 수 있지만, 대부분의 경우 더 큰 에너지 손실을 유발하여 큐비트 결맞음 시간에 악영향을 끼친다. 또한, 초전도 양자프로세서 요소의 공진주파수가 일반적으로 수 GHz임을 고려하면 마이크로파 한 파장의 길이가 수 cm에서 수십 cm에 이른다. 따라서 커플링 공진기, 리드아웃 공진기를 굽이굽이 말아서 제작하더라도 이들이 차지하는 면적이 작지 않다. 그러므로 초전도 양자프로세서의 집적도를 높이기 위해서는 정전용량이나 유도용량이 크면서도 에너지 손실이 적은 물질을 찾고, 새로운 방식의 초전도 큐비트를 설계하는 등의 돌파구가 필요하다.

현재 초전도 양자프로세서의 집적도를 높이는 방법은 큐비트, 커플링 공진기, 리드아웃 공진기, 드라이브 라인 등을 서로 정전capacitive 또는 유도 inductive 방식으로 연결해 3차원 적층을 하는 것이다. 일반적인 반도체 공정과 유사하게, 레이어를 서로 마주 보게 한 플립 칩 기술과 초전도체로 제작된 실리콘 관통 전극(TSV; Trough-silicon via)을 통해 위아래의 레이어를 연결하는 기술을 사용한다 (그림 7). 주로 냉간 용접이 가능한 초전도 인듐을 사용하여 칩 간격을 벌려 적층하는데, 인듐의 무른 성질 때문에 간격 조절에 어려움이 있다. 칩 간격에 따라 위아래 요소 사이의 상호 정전용량이 크게 변해 큐비트 공진주파수가 바뀌거나 상호작용 세기가 변화하는 등의 문제가 발생한다. 이를 해결하기 위해 무르지 않은 물질을 덧대거나 추가하여 칩 간 간격을 유지하는 방법들이 제안되고 있다.

 

하지만 초전도 양자 프로세서 칩 자체의 크기를 늘리는 데는 공정 장비와 웨이퍼 크기의 한계가 있다. 또한 큐비트 수가 늘어날 수록 제어와 측정 과정에서 발생하는 열이 많아져 희석식 극저온 냉각기의 냉각 용량이 걸림돌이 된다. 이를 해결하기 위한 대안으로 여러 개의 초전도 양자프로세서 칩과 희석식 냉각기를 연결하는 모듈러 아키텍처가 주목받고 있다 (그림 8). 한번에 큰 프로세서를 만드는 것과 비교해서 작은 프로세서 여러 개를 만드는 것이 수율과 성능 면에서 유리하다. 따라서 초전도 양자 프로세서 칩을 높은 신뢰도로 연결하는 모듈러 기술이 개발되면, 단순히 큐비트 수를 늘리는 것뿐만 아니라 시스템 복잡도에 따른 물리 큐비트 오류율 증가 문제도 해결할 수 있을 것이다. 이는 물리 큐비트 오류율을 낮게 유지해야 하는 양자오류보정 기술에도 도움이 되어 결함감내 양자컴퓨터를 구현하는 데 중요한 돌파구가 될 것으로 기대한다.

 

마치며

초전도 양자컴퓨터의 물리적 구현 방법을 살펴보며 여러 어려움과 진행중인 노력들에 대해 이야기해보았다. 현재 초전도 양자컴퓨터가 자랑하는 1,121 큐비트는 우리가 몇 만원이면 살 수 있는 외장 디스크의 저장 용량에 비해 한없이 작은 숫자이며, 높은 오류율로 계산 결과조차 믿기 어려운 쓸모 없는 장치로 생각될 수도 있다. 그런데 양자컴퓨터를 사용해서 양자 알고리즘과 양자 시뮬레이션을 시연했다는 논문들이 심심치 않게 보이기 시작했다. 언제쯤 일상생활에서 양자컴퓨터의 유용성을 체감하게 될지는 모르겠지만, 최근의 발전 속도는 상당히 놀랍다. 우리는 양자회로 설계, 소재, 공정 방법, 잡음 환경 등 다방면의 연구를 통해 큐비트의 결맞음 시간을 늘리고 오류율을 낮추는 방법들을 하나둘씩 알아가고 있다. 또한, 이론적 발전을 통해 양자오류보정에 필요한 자원의 양도 점차 줄여가며 결함감내 양자컴퓨터 구현에 한 발짝씩 다가가고 있다. 결함감내 양자컴퓨터 구현이 불가능하다는 물리학적 근거가 없기 때문에, 언젠가는 구현될 수 있을 것이라고 기대해본다. 역사의 한복판에서 기술의 발전을 지켜보는 일은 즐거운 일이다. 이 글이 여러분이 이러한 발전을 지켜보고 이해하는 데 조금이나마 도움이 되었기를 바란다.