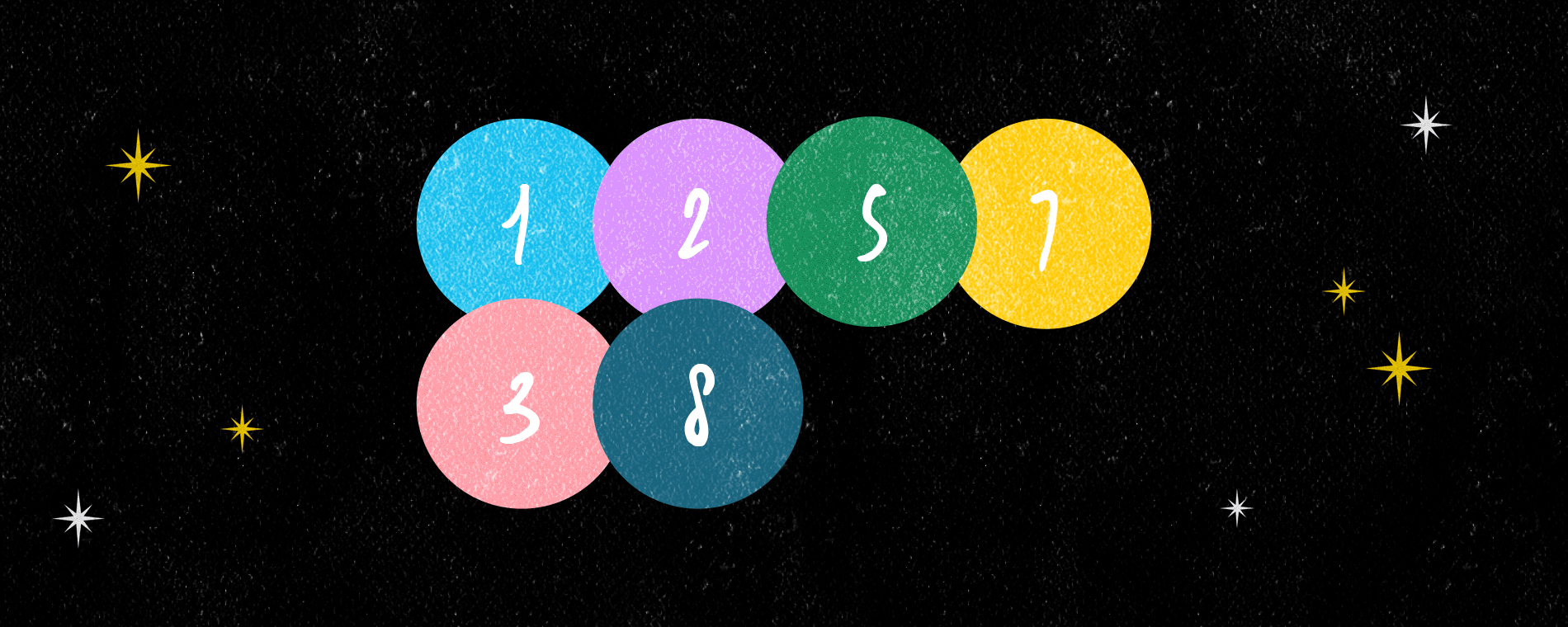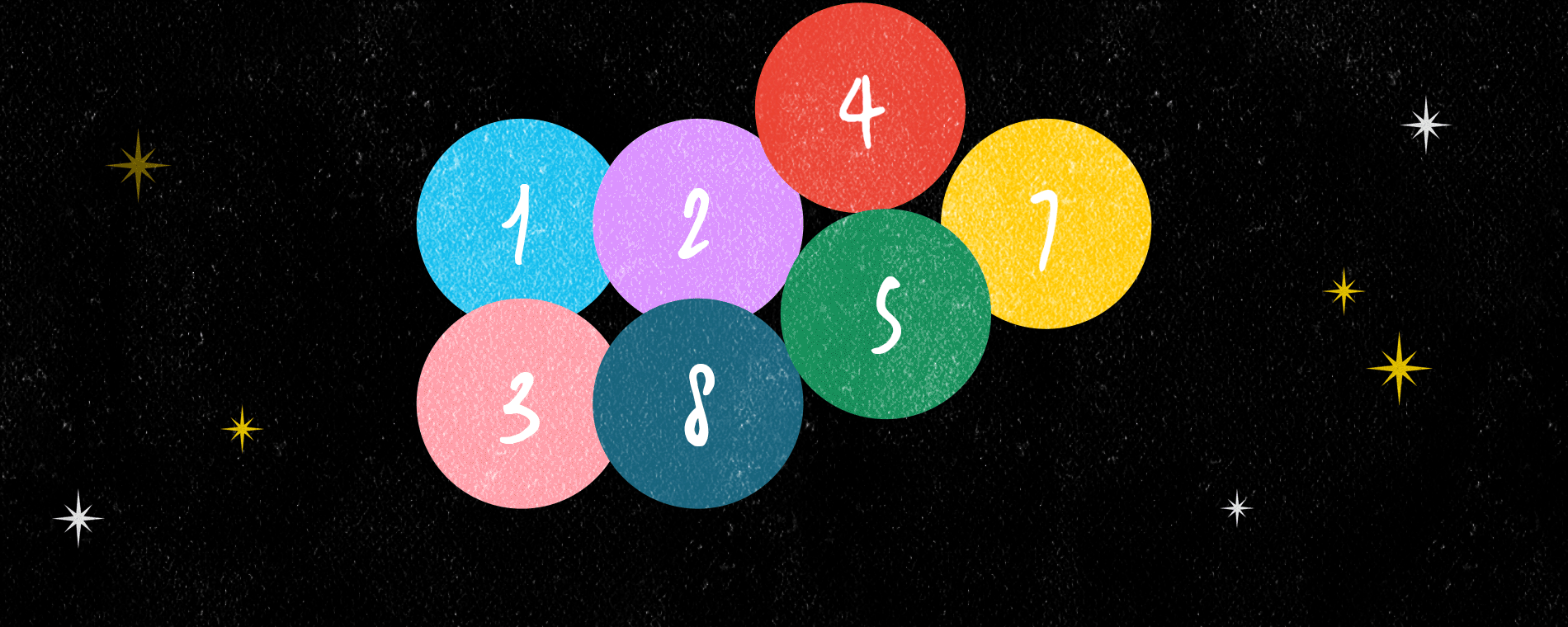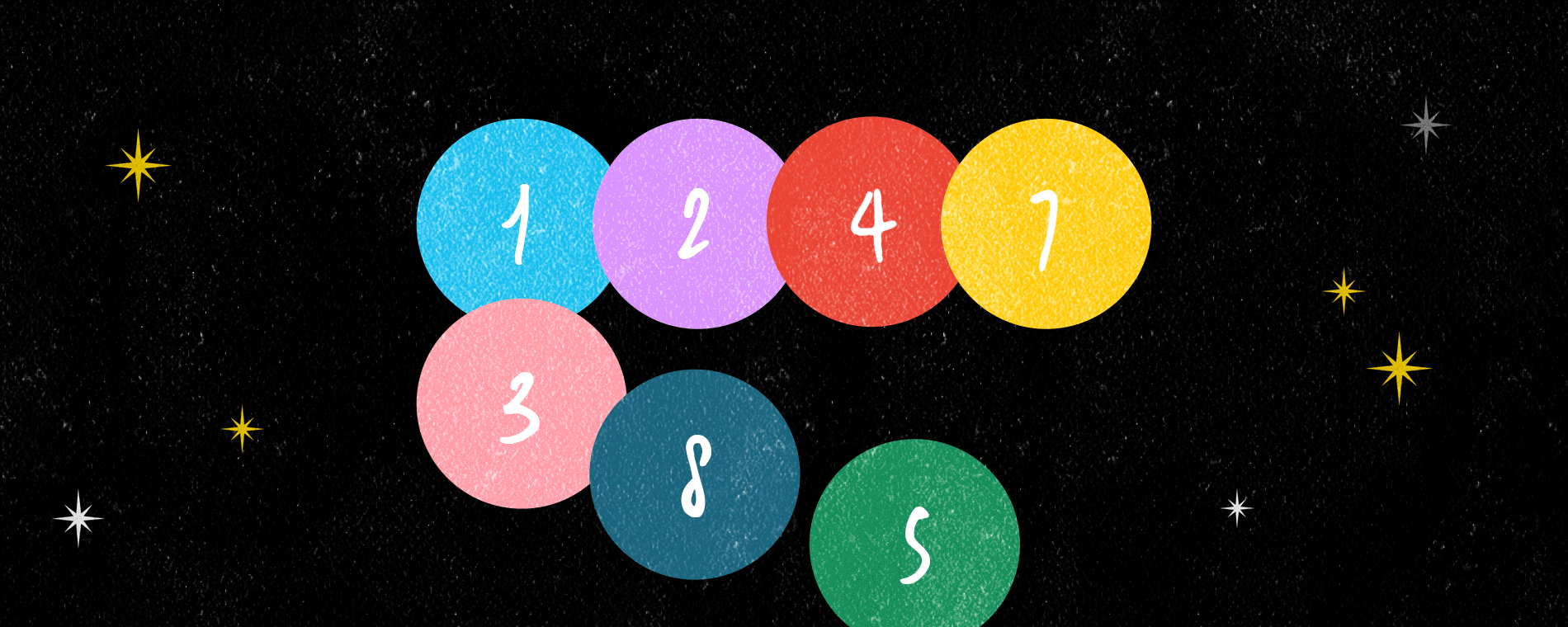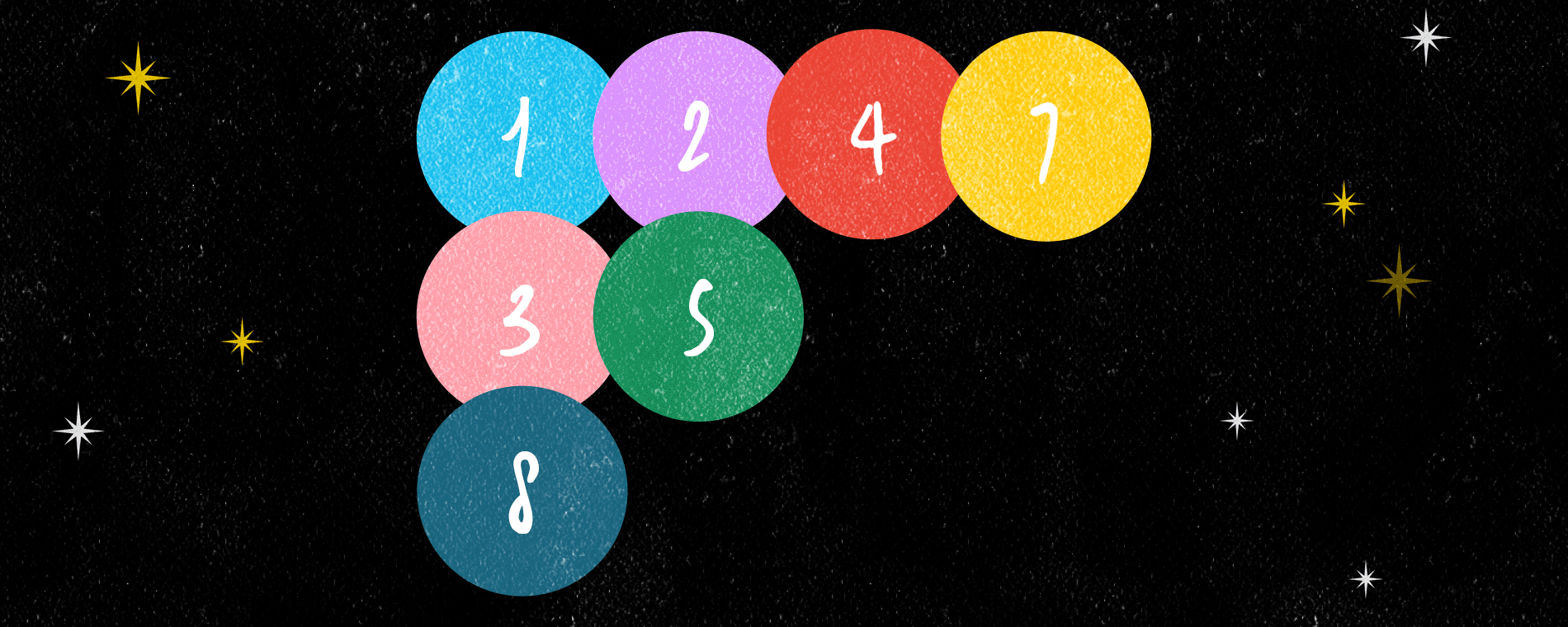영 타블로

대칭군의 불변량에 관한 1901년 연구논문에서 앨프리드 영은 자연수들의 (특정한) 배열을 소개했다. 이제 영 타블로라고 불리는 이 배열은 대칭군의 표현론, 대칭함수 이론은 물론 슈베르트 계산이론에서도 중요한 역할을 하고 있다. 대수적 조합론의 중심에 위치하고 있는 영 타블로의 역할을 역사적으로 중요한 몇 가지 주제를 통해서 살펴본다.

영 타블로^{Young Tableau}는 표현론, 대수학, 기하학 모두에서 보편적으로 등장하는 유용하고 흥미로운 조합적 대상이다. 대칭군 및 일반선형군의 표현, 대칭함수, 슈베르트 계산이론 등에서 자연스럽게 나타나며, 엄밀한 정의는 뒤에 살펴볼 것이다. 영 타블로와 연관된 셈 공식을 발견하거나 해석하는 것은 대수적 조합론^{algebraic combinatorics}의 핵심적인 주제이다. 영 타블로라는 이름은 1901년에 그 개념을 처음으로 제시한 수학자 앨프리드 영^{Alfred Young}의 이름에서 따 온 것이다. 이 글에서는 먼저 영 타블로가 연구되게 된 동기를 제공한 불변량 이론을 살펴보고, 영 타블로가 어떤 것인지 둘러본 후, 그 응용과 일반화를 알아보고자 한다.

1. 영 타블로가 만들어진 배경은 불변량 이론

영은 처음에는 불변량 이론을 공부하기 위한 목적으로 대칭군^{symmetric group}의 표현을 이해할 필요성을 느꼈고, 그런 과정에서 영 타블로를 발견했다. 따라서 먼저 불변량 이론의 역사적 흐름을 간단히 짚어보자. 불변량 이론^{invariant theory}이란 벡터 공간과 같은 대수적 다양체 위에서 군의 작용^action을 연구하는 이론이다. 가장 고전적인 결과는 주어진 선형군이 작용할 때 변하지 않는 다항식을 묘사한다. 예를 들어 대칭군 \(S_3\)가 세 개의 변수 \(x_1,x_2,x_3\)로 생성된 다항식 공간에 작용하는 경우를 생각해보자. 이 때,
\[x_1^2x_2+x_2^2x_3+x_3^2x_1+x_2^2x_1+x_3^2x_2+x_1^2x_3\]
와 같은 다항식은 \(S_3\)의 임의의 원소를 통해 변수를 치환하여도 불변이다. 이러한 다항식을 대칭다항식^{symmetric polynomial}이라고 하며 대수학이나 조합론 등에서 매우 중요한 대상이다.

헤르만 바일^{Hermann Weyl}은 자신의 저서 『The Classical Groups: Their Invariants and Representations (1939)』에서 불변량 이론에 기여한 중요한 몇몇 수학자들을 언급했다.

• 아서 케일리

아서 케일리^{Arthur Cayley, 1821-1895}는 불변량 이론의 창시자로 여겨진다. 그는 처음으로 군^group을 현대대수학의 추상적인 방식으로 정의했는데, 케일리 이전의 수학자들에게 군이란 치환군^{permutation group, 대칭군의 부분군}만을 의미하였다. 케일리는 1846년 발표한 논문에서 행렬식^determinant에 관한 사고를 더욱 일반적인 불변량의 관점에서 바라보는 시각을 제시했다.

그의 이름이 붙은 정리들 중 특히 현대대수학에서의 케일리 정리와 선형대수학에서의 케일리-해밀턴 정리가 유명하다. 일반적으로 케일리 정리는 다음을 의미한다.

예를 들어 대칭군 \(G=S_3\)를 생각해보자. 원소들을 순환치환^cycle의 형태로 모두 나열하면 \[G=\{\epsilon, (1 2), (1 3), (2 3), (1 2 3), (1 3 2)\}\]이다. 이들 각각의 원소를 다시 \(S_G\)의 한 원소로 생각할 수 있는데, 그것들이 \(G\)의 각 원소에 좌측곱셈^{left multiplication}으로 곱해지는 작용을 생각하는 것이다. 예컨대 \((1 2)\)는 \(S_G\)의 한 원소로서, \(G\)의 원소들을 순서대로 \[\{(1 2)\epsilon, (1 2)(1 2), (1 2)(1 3), (1 2)(2 3), (1 2)(1 2 3), (1 2)(1 3 2)\}\]로 치환하는 것이다. 즉 \(G\)는 자기 자신에 작용하는 \(G\)- 작용(\(G\)-action on \(G\))이다.

• 다비트 힐베르트

다비트 힐베르트^{David Hilbert, 1862-1943}는 그의 1890년/1892년 논문을 통해 불변량 이론의 역사에서 정점을 찍게 된다. 갈루아 이론에서 군 \(G\)의 작용에 대해 불변인 원소를 찾는 것은 중요한 문제인데, 19세기 후반에 그런 불변 집합을 단지 특별한 몇몇 경우의 유한한 생성원소^generator를 통해 이해할 수 있음이 밝혀졌다. 따라서 주어진 불변 집합이 유한한 원소들로 생성되기 위한 필요충분조건을 찾는 것은 불변량 이론의 가장 핵심적인 문제였고, 힐베르트는 매우 일반적인 충분조건을 찾아냄으로써 그 문제를 해결하였다. 그를 통해 불변량 이론은 거의 사장되는 것처럼 보였다.

• 아돌프 후르비츠

힐베르트의 업적 이후에도 불변량 이론을 꾸준히 연구하는 소수의 수학자들이 있었다. 그중 아돌프 후르비츠^{Adolf Hurwitz, 1859-1919}는 1897년 연구를 통해 불변량 이론에서 새롭고도 중요한 기여를 하게 된다. 그는 유니타리안 기교^{Unitarian trick}라 불리는, 콤팩트 리 군^{Lie group} 위에서의 적분을 통해 불변량을 만들 수 있음을 보였다.

• 앨프리드 영

앨프리드 영^{Alfred Young, 1873-1940}은 특이하게도 35살부터 성직자로서 여생을 보냈다. 그의 불변량 이론에 관한 일련의 논문들은 대부분 성직자이던 시절 쓰인 것이다. 대칭군의 표현에서 중요한 업적을 남겼으며 이에 대해서는 이어서 설명하도록 한다.

2. 영 타블로란?

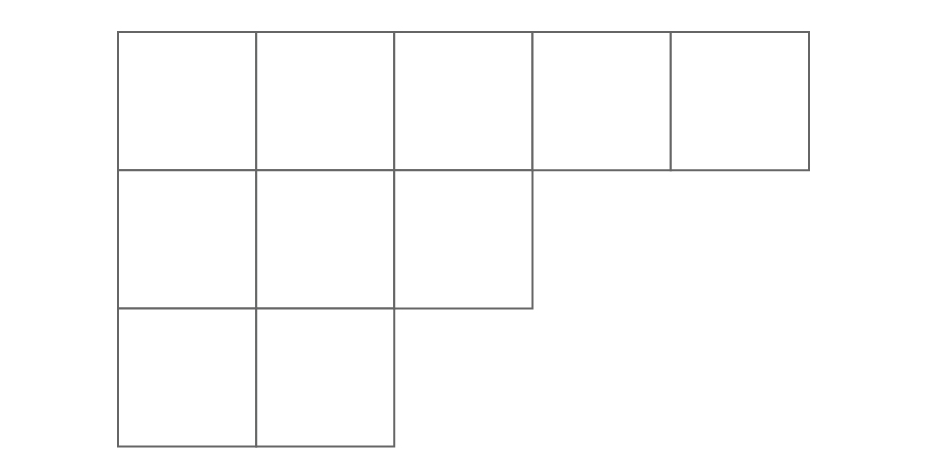
먼저 영 타블로가 어떤 것인지 예를 들어 살펴보기로 하자. 어떤 자연수를 여러 자연수의 합으로 쓰는 것을 분할이라고 부른다. 예를 들어 \(10=5+3+2\)이므로, \(\lambda=(5,3,2)\)는 \(10\)의 분할이다. 분할이 있으면 아래 그림과 같은 상자를 쌓아만든 모양을 만들 수 있는데 이것을 영 다이어그램^{Young diagram}이라고 부른다.

즉 \(\lambda = (\lambda_1,\lambda_2,\cdots,\lambda_l)\)가 자연수 \(k\)의 한 분할(partition), 즉 \(k=\lambda_1+\lambda_2+\cdots+\lambda_l\)과 \(\lambda_1\ge \lambda_2\ge\cdots\ge\lambda_l> 0\)을 만족한다고 하자. 이때 \(\lambda\)의 영 다이어그램^{Young diagram}은 각 \(i\)번째 행마다 \(\lambda_i\)개의 칸을 왼쪽 정렬하여 차례로 배열한 그림이다. 그래서 \(\lambda\)를 이 영 다이어그램의 모양이라고도 부른다.

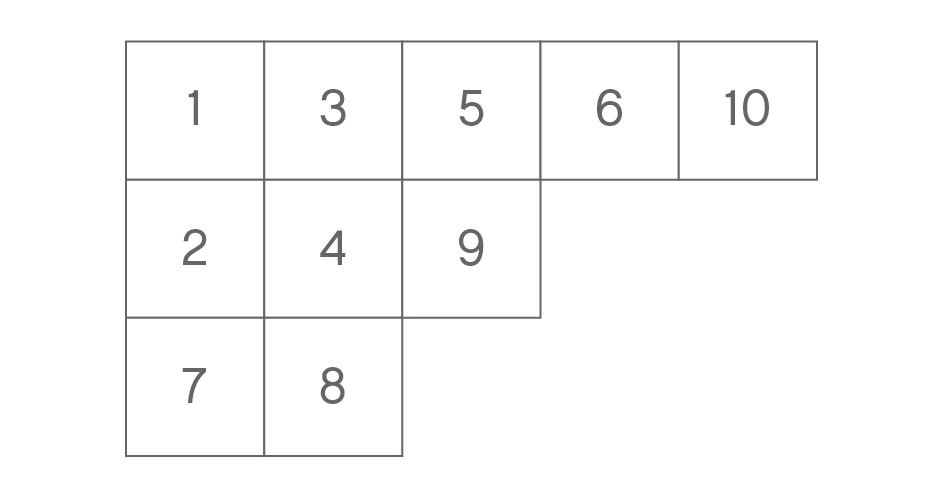
총 \(k\)개 상자로 만들어진 영 다이어그램이 있을 때 그 상자 안에 아래 두 규칙을 만족시키면서 \(1\)부터 \(k\)까지의 자연수를 채우는 방법을 생각해보자.

· 가로로 이웃한 두 상자가 있으면 오른쪽 상자의 값이 왼쪽 상자 값보다 커야 한다.
· 세로로 이웃한 두 상자가 있으면 아래 상자의 값이 위의 상자 값보다 커야 한다.

예를 들어 아래 그림은 위의 영 다이어그램에 이 두 규칙이 맞도록 자연수를 채운 것이다.

이러한 방법을 모양 \(\lambda\)의 표준 영 타블로^{standard Young tableau}라고 부른다. 표준 영 타블로는 영 다이어그램의 각 칸에 1부터 \(k\)까지의 서로 다른 자연수를 쓰되, 각 행과 열이 모두 증가 수열을 이루도록 한 것이다.

이제 \(f^\lambda\)를 모양 \(\lambda\)의 가능한 모든 표준 영 타블로의 개수라고 하자. 뒤에서 공식을 살펴보겠지만, \(f^{(5,3,2)}=450\)이다.

영은 1900년부터 1952년까지 『On quantitative substitutional analysis』라는 제목으로 9개의 시리즈 논문을 발표했다. 이 중 마지막 아홉 번째 논문은 그의 사후 길버트 로빈슨^{G. de B. Robinson}에 의해 출판되었다. 대칭군에 관한 일련의 논문들이지만, 그 제목은 영이 불변량 이론을 염두에 두고 있었음을 말해준다. 그 중 1900년 출판되었고 1901년 수정된 첫 번째 논문에 현재 영 타블로라 불리는 수학적 대상이 처음 소개되었다.

• 대칭군의 표현

군 \(G\)의 표현^{representation}이란 어떤 집합 위에서의 \(G\)-작용이다. 예를 들어 앞서 살펴본 케일리 정리는 \(G\)가 자기자신에 작용하는 표현의 한 예이다. 자연스럽게 기약 표현^{irreducible representation}도 정의할 수 있는데, 더 작은 부분 표현을 갖지 않는 표현을 의미하며, 복소수체 \(\mathbb{C}\) 위에서 정의된 군 대수^{group algebra}의 표현은 기약 표현들의 직접곱^{direct product}로 표현할 수 있다.

복소수체 \(\mathbb{C}\)와 \(G=S_3\)인 경우 케일리 정리에 등장하는, \(\mathbb{C}[G]\) 위에 \(G\)가 작용하는 표현을 생각해보자. 기저^basis 표현을 사용한다면 \[\mathbb{C}[G] = \mathbb{C}\{\epsilon, (1 2), (1 3), (2 3), (1 2 3), (1 3 2)\}\]와 같은 6차원 벡터 공간이며 \(G\)는 각 기저에 좌측곱셈으로 작용한다. 이 표현은 기약 표현이 아닌데, 부분공간 중 \(G\)에 불변인 공간이 있기 때문이다. 예를 들어 대칭함수를 생각했던 것과 동일한 방식으로 \((1 2)\)에서 시작해 \(G\)의 작용으로 만들어질 수 있는 원소들을 모두 더하면 \[\mathbb{C}\{\epsilon+(1 2)+(1 3)+(2 3)+(1 2 3)+(1 3 2)\}\]와 같은 1차원 \(G\)-불변 부분공간을 얻을 수 있다. 다른 방식으로 계수를 각 원소의 홀짝성에 따라 정하면
\[\mathbb{C}\{\epsilon-(1 2)-(1 3)-(2 3)+(1 2 3)+(1 3 2)\}\]와 같은 또 다른 1차원 \(G\)-불변 부분공간을 얻는다. 물론 더 높은 차원의 부분공간도 있는데, 다음은 2차원 \(G\)-불변 부분공간의 한 예이다.\[\mathbb{C}\{\epsilon+(1 2)-(1 3)-(1 3)(1 2), (2 3)+(2 3)(1 2)-(1 2)(1 3)-(1 3)\}\]차원이 높아지면 복잡한 것처럼 보이지만 이들은 모두 영의 멱등원소^idempotent라는 특별한 대상을 사용하여 체계적으로 만들 수 있다. 다음은 기약 표현과 관련한 중요한 사실이다.

• 대칭군의 조합론적 표현

이제 대칭군 \(S_n\)의 표현을 생각해보자. 앞서 \(S_n\)의 기약 표현의 개수는 \(S_n\)의 켤레류 개수와 같다는 사실을 언급했다. 대수학에서 \(S_n\)의 모든 켤레류는 순환치환 유형^{cycle type}으로 유일하게 결정된다는 간단한 사실을 생각하면 그 개수는 다시 \(n\)의 분할의 개수와 같아진다. 따라서 \(S_n\)을 기저로 하는 벡터 공간은 \(n\)의 분할 개수만큼의 기약 부분공간으로 분할될 것이다. 영은 1901년과 1923년 논문에서 다음과 같은 사실들을 `조합적으로’ 증명했다.

여기서 조합적인 방법이라 함은 이미 알려졌던 간단한 사실들만을 이용해 순전히 초등적이고 직접적인 방식으로 증명했다는 것이다. 영과 비슷한 시기에 활동한 수학자 페르디난트 프로베니우스^{Ferdinand Frobenius, 1849-1917}는 군의 지표를 통해 표현을 연구하는 지표 이론^{character theory}을 통해 일반적인 군을 연구하고 있었다. 간단히 말해 지표^character란 군의 각 원소를 연관된 행렬의 대각합^trace과 대응시켜주는 함수로서, 군의 표현에 관한 핵심적인 정보를 담고 있는 대상이다.

영이 밝힌 사실 중 일부는 지표 이론에서 당연하게 유도되는 결과였다. 그러나 프로베니우스는 일반적인 이론을 만드는데 치중한 반면, 영은 대칭군이라는 아주 특정한 군에 대해서 지표 이론을 사용하지 않고 직접적이고 조합론적인 방법으로 접근했다는 차이가 있다. 프로베니우스는 지표 이론 없이 이러한 결과들을 유도해낸 영의 논문을 접하고 크게 놀랐으며, 후에 자신의 이론을 사용해 대칭군에 관한 영의 결과들을 다시 증명했다. 프로베니우스의 제자인 이사이 슈어^{Issai Schur, 1875-1941}는 이를 더 발전시켜 일반적인 선형군의 다항식 표현 이론에 기여했으며, \(GL_n(\mathbb{C})\)의 기약 표현에 대한 지표는 슈어 함수^{Schur function}로 알려져 있다.

3. 영 타블로는 어디에 쓰일까?

이제 영 타블로의 몇 가지 응용에 대해 살펴보자.

• 로빈슨-쉔스티드 알고리즘

앞서 \(\mathbb{C}S_n = \bigoplus_\lambda f^\lambda S^\lambda\)와 \(f^\lambda=\dim S^\lambda\)가 성립한다는 사실을 언급했다. 따라서 차원을 비교해보면
\[n! = \sum_\lambda (f^\lambda)^2\]
이라는 공식을 얻는다. 이 공식을 조합적으로, 즉 일대일대응을 통해 보일 수 있지 않을까? 1938년 길버트 로빈슨^{Gilbert Robinson}과 1961년 크레이그 쉔스티드^{Craige Schensted})가 독립적으로 찾아낸 로빈슨-쉔스티드 알고리즘^{Robinson-Schensted Algorithm}은 그런 일대일대응을 직접적으로 보여준다.

좌변은 \(\{1,2,\cdots,n\}\)의 치환의 개수, 우변은 가능한 모든 표준 영 타블로 쌍의 개수를 의미한다. 따라서 하나의 치환에 의해 어떤 표준 영 타블로 쌍이 유일하게 결정되고 그 역도 성립하면 공식이 증명된다. 예를 들어 \(k=8\)인 경우 치환이 \[\pi=\left(\pi(1),\pi(2),\cdots,\pi(8)\right)=\left(1 3 5 8 2 7 4 6\right)\]
와 같이 주어졌다고 하자. 이제 표준 영 타블로를 만드는데 어떤 규칙에 따라 수와 칸을 하나씩 추가해 나간다. 아래 그림은 일곱 번째 단계에서 4를 추가하는 과정을 나타낸 것이다.

먼저 앞 여섯 단계에서 만들어진 표준 영 타블로에 4를 추가하는데 가장 첫 번째 행에 추가한다. 표준 영 타블로는 모든 행이 증가 수열을 이루어야 하므로 7 뒤에 4를 추가할 수는 없다. 그런 경우 다른 자리를 찾아야 하는데, 4는 1, 2, 5의 위치에 들어갈 수 있다. 그 중 가장 뒤쪽인 5의 자리에 추가하고, 5는 그 다음 두 번째 행에 추가한다. 그런데 두 번째 행에서 역시 5는 8 뒤에 위치할 수 없으므로 8을 대체하여 들어가고 8은 그 다음 행에 추가한다. 세 번째 행은 아무 수도 없으므로 8을 그대로 추가할 수 있고 4를 넣는 단계가 끝난다. 여섯 번째 단계의 결과로서 처음 주어졌던 표준 영 타블로 역시 1, 3, 5, 8, 2, 7을 위 규칙에 따라 차례로 추가하여 얻어졌음을 알 수 있다. 마지막으로 6은 5 오른쪽에 추가될 것이다.

한편 이와 별개로 다른 표준 영 타블로를 만드는데, 그것은 이 첫 번째 표준 영 타블로가 만들어지는 과정에서 똑같은 영 다이어그램 위에 칸이 어떤 순서로 추가되었는지를 기록하기만 하면 된다. 결과적으로 우리는 하나의 치환에 대응하는 유일한 영 타블로 쌍을 하나 얻었고, 거꾸로 그 정보를 통해 치환을 유일하게 복원할 수도 있다.

쉔스티드는 원래 주어진 치환에서 가장 긴 증가/감소 수열을 찾을 목적으로 연구를 하다 이 알고리즘을 발견했다. 위의 예에서 \(\left(1 3 5 8 2 7 4 6\right)\) 속 가장 긴 증가수열은 \(\left(1 3 5 7\right)\)이고, 가장 긴 감소수열은 \(\left(8 7 6\right)\)인데, 이것들의 길이인 4와 3은 각각 알고리즘을 통해 만들어지는 영 다이어그램의 첫 번째 행과 열의 크기와 같다.

• 고리 길이 공식

\(f^\lambda\)를 계산하는 것은 어떤 경우 매우 중요하며, 앞서 \(f^\lambda = n!\det{\left[\frac{1}{(\lambda_i-i+j)!}\right]_{ij}}\)라는 공식을 알아보았다. 그러나 이 공식은 행렬식이 포함되어 계산이 매우 복잡하고 실용적이지 않다. 고리 길이 공식^{hook length formula}은 \(f^\lambda\)를 계산하는 아주 간단한 공식이다.
\[f^\lambda = n! / \prod h_{ij}\]
여기서 \(h_{ij}\)는 영 다이어그램에서 \((i,j)\) 위치에 있는 칸의 고리 길이^{hook length}, 즉 \((i,j)\) 칸 그 자신을 포함해 \(\Gamma\) 모양의 고리에 속하는, 오른쪽과 아래쪽 칸들의 개수와 같다. 3.2 에서 살펴보았던 예의 경우
\[f^{(5,3,2)} = \frac{10!}{7\cdot 6\cdot 4\cdot 2\cdot 4\cdot 3\cdot 2}=450\]
과 같이 계산할 수 있다. 비교적 간단한 공식이지만 일대일대응을 이용하는 완전히 조합론적인 증명은 1997년이 되어서야 발견되었다.

4. 영 타블로를 더 확장한 것도 있을까?

• 슈어 다항식

\(\lambda = (\lambda_1,\lambda_2,\cdots,\lambda_l)\)가 자연수 \(k\)의 한 분할(partition), 즉 \(k=\lambda_1+\lambda_2+\cdots+\lambda_l\)과 \(\lambda_1\ge \lambda_2\ge\cdots\ge\lambda_l> 0\)을 만족한다고 하자. 1841년 모리츠 야코비^{Moritz Jacobi}, 그리고 1901년 이사이 슈어가 제안한 슈어 다항식^{Schur polynomial}은 다음과 같이 정의된다.
\[s_\lambda(x_1,x_2,\cdots,x_n) = \det \left[x_i^{\lambda_j+n-j}\right]_{ij} / \det \left[x_i^{n-j}\right]_{ij}\]
슈어 다항식은 대칭다항식이며, 모든 대칭다항식을 모은 공간의 기저^basis가 된다.

슈어 다항식은 조합적인 방식으로도 표현할 수 있다. 준표준 영 타블로^{semistandard Young tableau}란 표준 영 타블로와 마찬가지로 영 다이어그램에 수를 채워 넣는데, 표준 영 타블로와 달리 각 행은 약한 증가 수열을 이루고 각 열은 강한 증가 수열을 이루어야 한다. 모든 슈어 다항식은

\(s_\lambda = \sum_T x^T,\qquad T\) : 준표준 영 타블로

와 같이 표현할 수 있다. 예를 들어
\[s_{(2,1)}=x_1^2x_2+x_1x_2^2+x_1^2x_3+x_1x_3^2+2x_1x_2x_3+\cdots\]
이며, 위에서 각각의 항은 차례로 준표준 영 타블로

에 대응된다.

• 리틀우드-리차드슨 수

리틀우드-리차드슨 수^{Littlewood-Richardson number}는 다음과 같이 대수학, 기하학 등 다양한 분야에서 보편적으로 등장하는 계수 \(c_{\lambda\mu}^\nu\)이다.

  · 슈어 함수의 곱
\[s_\lambda(\mathbf{x})s_\mu(\mathbf{x}) = \sum_\nu c_{\lambda\mu}^\nu s_\nu(\mathbf{x})\]
  · 대칭군의 기약표현의 곱
\[S^\lambda \cdot S^\mu = (S^\lambda\otimes S^\mu)\uparrow_{S_n\times S_m}^{S_{n+m}} = \sum _\nu c_{\lambda\mu}^\nu S^\nu\]
  · \(GL_n(\mathbb{C})\)의 기약 다항식 표현의 텐서 곱
\[E^\lambda \otimes E^\mu \simeq \bigoplus_\nu c_{\lambda \mu}^\nu E^\nu\]
  · 그라스마니안^Grassmannian \(Gr(n,m)\)의 슈베르트 류^{Schubert class}의 컵 곱
\[\sigma_\lambda \cdot \sigma_\mu = \sum_\nu c_{\lambda\mu}^\nu \sigma_\nu\]

슈어 다항식과 마찬가지로 리틀우드-리차드슨 타블로^{Littlewood-Richardson tableau}로 불리는 비틀린^skew 형태의 일반화된 타블로의 개수가 리틀우드-리차드슨 수와 같음이 알려져 있다. 이러한 조합적 해석을 통해 리틀우드-리차드슨 수에 관한 여러 가지 다양한 성질들을 증명할 수 있다.

• 슈어-P함수

1911년 슈어가 제안한 슈어 P-함수^{Schur P-function}는 표지되고 이동된 준표준 타블로^{marked shifted semistandard tableau}를 통해 슈어 다항식과 비슷하게 정의되는 다항식이다. 슈어 함수들의 곱을 슈어 함수들의 곱으로 표현할 때 나타나는 계수(리틀우드-리차드슨 수)가 중요한 의미를 가진 것과 같이, 슈어 P-함수의 구조 상수^{structure constant} \(f_{\lambda\mu}^\nu\)도 여러 관련 분야에서 중요한 의미를 가지는 수이며 적절하게 비틀린 형태의 타블로를 통해 셀 수 있음이 알려져 있다. 이 수는 다음과 같은 다양한 대상과 관련이 있다.

  · 대칭함수의 부분환 \(\Gamma\)
\[P_\lambda(\mathbf{x})P_{\mu}(\mathbf{x})=\sum_{\nu}f_{\lambda\mu}^\nu P_\nu(\mathbf{x})\]
  · 직교 최대 등방 그라스마니안^{orthogonal maximal isotropic Grassmannian}의 코호몰로지환 \(H^{*}(OG(n+1,2n+2))\)
\[\tau_\lambda \tau_\mu = \sum_\nu f_{\lambda\mu}^\nu \tau_\nu\]
  · \(\mathcal{S}_n\)의 사영 표현^{projective representation}

• 그 외

관심 있는 대상에 따라 일반화된 타블로를 생각할 수 있으며 준^quasi-, 아핀^affine-, 리 유형^{Lie type}, 양자^quantum- 등 다양한 접두어와 수식어가 붙을 수 있다. 예컨대 \(K\)-이론에서는 슈어 P-함수의 경우처럼 표지되고 이동된 준표준 타블로를 사용하는데, 칸 하나에 하나 이상의 수가 들어갈 수 있는 식으로 일반화된다.