병 진단의 정확성과 오진 가능성
혈액검사만으로 암을 비롯한 각종 질병의 발생 여부를 알아낼 수 있다고 한다. 간단한 채혈만으로 중대한 질환을 예측할 뿐만 아니라 정확도가 90%이상이라니 대단하다는 생각이 든다.
그런데 종종 오진으로 인한 뉴스가 보도되는 것을 보면 병 진단의 정확성에 대한 우려도 든다. 그리고 검사결과 병에 걸린 것으로 판정받았을 때, 실제로 그 병에 걸려있지 않을 가능성도 있다. 왜냐하면 실제로는 그 병에 걸리지 않았지만 병에 걸린 것으로 오진하는 경우가 있기 때문이다.
이제 검사결과 병에 걸린 것으로 진단 받았을 때, 실제로 그 병에 걸렸을 가능성이 어떻게 되는지 알아보도록 하자.
조건부 확률의 뜻
병에 걸린 것으로 진단 받았을 때 실제로 병에 걸렸을 가능성을 계산하기 위해서는 조건부확률의 개념이 필요하다. 조건부 확률이 생소한 독자도 있을텐데, 기본 개념은 간단하다. 보통의 확률은 ‘어떤 사건 A가 일어난 확률’을 말하는데 비해, 조건부 확률은 ‘어떤 사건 B가 일어났다고 했을 때, 사건 A가 일어날 확률’을 말한다.
예를 들어 남녀 학생이 함께 있는 교실에서 임의로 한 명을 뽑을 때, 뽑힌 학생이 안경을 쓴 학생일 확률은 보통의 확률이다. 그런데 남학생이 뽑혔을 때, 그 학생이 안경을 쓴 학생일 확률은 조건부 확률이다. 왜냐하면 남학생이 뽑혔다는 (또는 남학생 중에서 뽑았다는) 조건하에 안경을 쓴 학생일 확률을 구하는 것이기 때문이다.
우리가 알아보려고 하는 확률도, 단순히 병에 걸려있을 확률을 구하는 것이 아니라, 검사를 받아서 병에 걸린 것으로 진단결과가 나왔다는 조건하에 실제로 그 병에 걸려 있을 확률을 구하는 것이므로 조건부 확률이 된다. 이제 조건부 확률에 대하여 좀 더 알아보자.
조건부 확률의 계산
조건부 확률을 요약하여 기호로 나타내면 다음과 같다.
이때, 조건부 확률의 계산에 대하여 다음 공식이 성립한다.
위 공식에서 \(Pr(A)\)는 사건 A가 일어날 확률이고, \(Pr(A\cap B)\)는 두 사건 \(A\)와 \(B\)가 동시에 일어날 확률을 뜻한다. 다음 예를 생각해보자.
예 새로 이사 온 옆집 아주머니가 딸과 함께 나오는 것을 우연히 마주쳤다. 반가워서 인사를 나누었는데 아주머니가 애가 하나 더 있다고 했다. 그 애가 딸일 확률은 얼마일까? 단, 아들과 딸을 낳을 확률은 각각 \(\frac { 1 }{ 2 } \)이라고 하자.
첫 번째 해설 그냥 단순하게 생각해서 아들과 딸 중 하나일 것이므로, 딸일 확률은 \(\frac { 1 }{ 2 } \)이라고 하면 틀린다. 왜냐하면 ‘딸이 하나 있다’는 가정이 있기 때문이다. 그러면 어떻게 해야 될까? 우선 애가 2명인 경우 첫째, 둘째의 남녀 구성을 따져보면 다음과 같이 4가지 경우가 있다.
아들-아들, 아들-딸, 딸-아들, 딸-딸
그런데 딸이 1명 있으므로, 위의 4가지 경우에서 아들-아들인 경우는 제외된다. 따라서 가능한 경우는 딸이 적어도 1명 있는 ‘아들-딸, 딸-아들, 딸-딸’의 3가지 경우이다. 3가지 경우 중에서 다른 아이도 딸일 확률, 즉 딸이 2명인 경우는 1가지이다. 그러므로 딸이 이미 1명 있을 때, 다른 아이도 딸일 확률은 \(\frac { 1 }{ 3 } \) 이다.
두 번째 해설 이번에는 예를 위의 조건부 학률의 공식을 이용하여 해결해보자. 우선 위 예의 상황을 요약하면 다음과 같이 된다.
- 아주머니에게 자녀가 2명 있다.
- 자녀 2명 중 1명은 딸이다.
- 자녀 2명 중 1명이 딸이라는 가정 하에, 나머지 자녀도 딸일 확률은 얼마인가?
이제 사건 A와 B를 각각 다음과 같이 정의하자.
- 사건 A: 자녀 2명 중에 딸이 적어도 1명 있다.
- 사건 B: 자녀 2명이 모두 딸이다.
따라서 구하고자 하는 확률은 ‘자녀 2명 중 1명이 딸이라는 가정 하에, 자녀 2명이 모두 딸일 확률’과 같고, 이것을 기호로 나타내면 \(Pr(B |A)\)이다. 이제 각각의 확률을 구하면 다음과 같다.
\(Pr(A)=\frac{3}{4},\) \(Pr(B)=\frac{1}{4},\) \(Pr(A \cap B)=Pr(B)=\frac{1}{4}\)
따라서 구하고자 하는 확률은 \(Pr(B|A)=\frac{Pr(A\cap B)}{Pr(A)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}\)이다.
위 예에서 옆집 아주머니가 “애가 하나 더 있다”고 말하지 않고 “(애가 둘인데) 이 아이의 동생이 한 명 있다”고 말했다면 확률은 달라진다. 아이가 2명인 경우, 첫째-둘째의 남녀 구성 4가지 중에서 첫째가 딸인 경우는 ‘딸-아들’과 ‘딸-딸’의 2가지다. 그리고 이 2가지 경우 중에서 둘째가 딸일 확률은 \(\frac { 1 }{ 2 } \)이다. 이처럼 “이 애 말고 애가 하나 더 있다”고 말하는 것과 “이 애의 동생이 하나 있다”고 말하는 것은 정보의 질적인 면에서 큰 차이가 있다.
병 진단 오진율
이제 병 진단의 오진율에 대하여 알아보자. 우선 정확한 진단에는 2가지 경우가 있음을 알아둘 필요가 있다. 하나는 실제로 병에 걸렸을 때, 병에 걸렸다고 정확하게 판정하는 것이고, 다른 하나는 실제로 병에 걸리지 않았을 때, 병에 걸리지 않았다고 정확하게 판정하는 것이다.
조건부 확률을 이용하여 다음과 같은 경우 병 진단의 오진 확률을 구해보자.
병에 걸렸을 사건을 \(D\)라 하고, 병에 걸렸다고 양성판정을 하는 사건을 \(P\)라 하고, 병에 걸리지 않았다고 음성판정을 하는 사건을 \(N\)이라 하자. 병이 있을 때 병이 있다고 양성 판정할 확률은 \(Pr(P|D)\)이고, 병이 없을 때 병이 없다고 음성 판정할 확률은 \(Pr(N|{ D }^{ c })\)이다. 이제 각각의 확률을 구해보자.
우선 병에 걸릴 확률은 \(Pr(D)=\frac{5}{1000}=0.005\)이다. 그리고 주어진 조건에 의하여 각각의 확률은 다음과 같이 된다.
- 병이 있는 경우에, 병이 있다고 판정할 확률 : \(Pr(P|D)=0.95\)
- 병이 없는 경우에, 병이 없다고 판정할 확률 : \(Pr(N|D^c)=0.99\)
그리고 이 확률로부터 다음 확률도 알 수 있다.
- 병이 있는 경우에, 병이 없다고 판정할 확률 : \(Pr(N|D)=0.05\)
- 병이 없는 경우에, 병이 있다고 판정할 확률 : \(Pr(P|D^c)=0.01\)
구하려고 하는 확률 ‘검사 결과 병에 걸렸다고 판정을 받았을 때, 실제로 병에 걸렸을 확률’은 병에 걸렸다고 양성 판정을 받았다는 전제하에, 실제로 병이 있을 확률이다. 따라서 구하려고 하는 확률은 기호로 \(Pr(D|P)\)이다. 이 확률을 위의 값을 이용하여 구하면 다음과 같다.
\[\begin{align*}
\Pr(D|P)&=\frac{Pr(D\cap P)}{Pr(P)}=\frac{Pr(P\cap D) \cdot Pr(D)}{Pr(D\cap P)+Pr(D^c\cap P)} \\
&=\frac{Pr(P|D)\cdot Pr(D)}{Pr(P|D)\cdot Pr(D)+Pr(P|D^c)\cdot Pr(D^c)} \\
&=\frac{0.95 \times 0.005}{0.95 \times 0.005 + 0.01 \times 0.995} \\
&=0.323129
\end{align*}\]
따라서 구하려고 하는 확률 \(Pr(D|P)\)는 약 32.3%이다. 즉 이 병원에서 병이 있다는 판정을 받았다고 하더라도 실제로 환자가 그 병에 걸렸을 확률은 32.3%로 반도 안 된다.
병 진단 오진율에 대한 논의
병 진단의 오진율을 낮추고 정확도를 높이기 위해서는 ‘병이 없는데 병이 있는 것으로 잘못 판정하는 확률 \(Pr(P|{ D }^{ c })\)’와 ‘병이 있는데 병이 없는 것으로 잘못 판정하는 확률 \(Pr(N|D)\)’ 두 가지 확률을 모두 낮추어야 할 것이다. 이제 그 두 가지 확률을 각각 나누어 분석함으로써 각 확률의 영향을 알아보자.
우선 \(Pr(D)\)가 5%인 경우에, ‘병이 없는데 병이 있는 것으로 잘못 판정하는 확률 \(Pr(P|{ D }^{ c })\)’를 1%에서 0.1%로 10배 개선하면 ‘병이 있다는 판정을 받았을 때 실제로 병에 걸렸을 확률 \(Pr(D|P)\)’는 32.3%에서 82.7%로 급증한다(<표1>). 따라서 ‘병이 없는데 병이 있는 것으로 잘못 판정하는 확률’, 즉, 위양성False Positive의 확률이 \(Pr(D|P)\)에 큰 영향을 미친다고 볼 수 있다.
그런데 ‘병이 있는데 병이 없는 것으로 잘못 판정하는 확률 \(Pr(N|D)\)’를 5%에서 0.05%로 100배 개선해도 확률 \(Pr(D|P)\)는 32.3%에서 33.4%로 개선되는 정도가 미미하다(<표2>). 따라서 ‘병이 있는데 병이 없는 것으로 잘못 판정하는 확률’, 즉, 위음성False Negative의 확률은 \(Pr(D|P)\)에 큰 영향을 주지 않는다고 볼 수 있다. 따라서 진단의 정확도를 높이기 위해서는 위양성False Positive, 즉 병이 없을 때 병이 있는 것으로 잘못 판정하는 오류를 줄이는 것이 중요하다는 것을 알 수 있다.
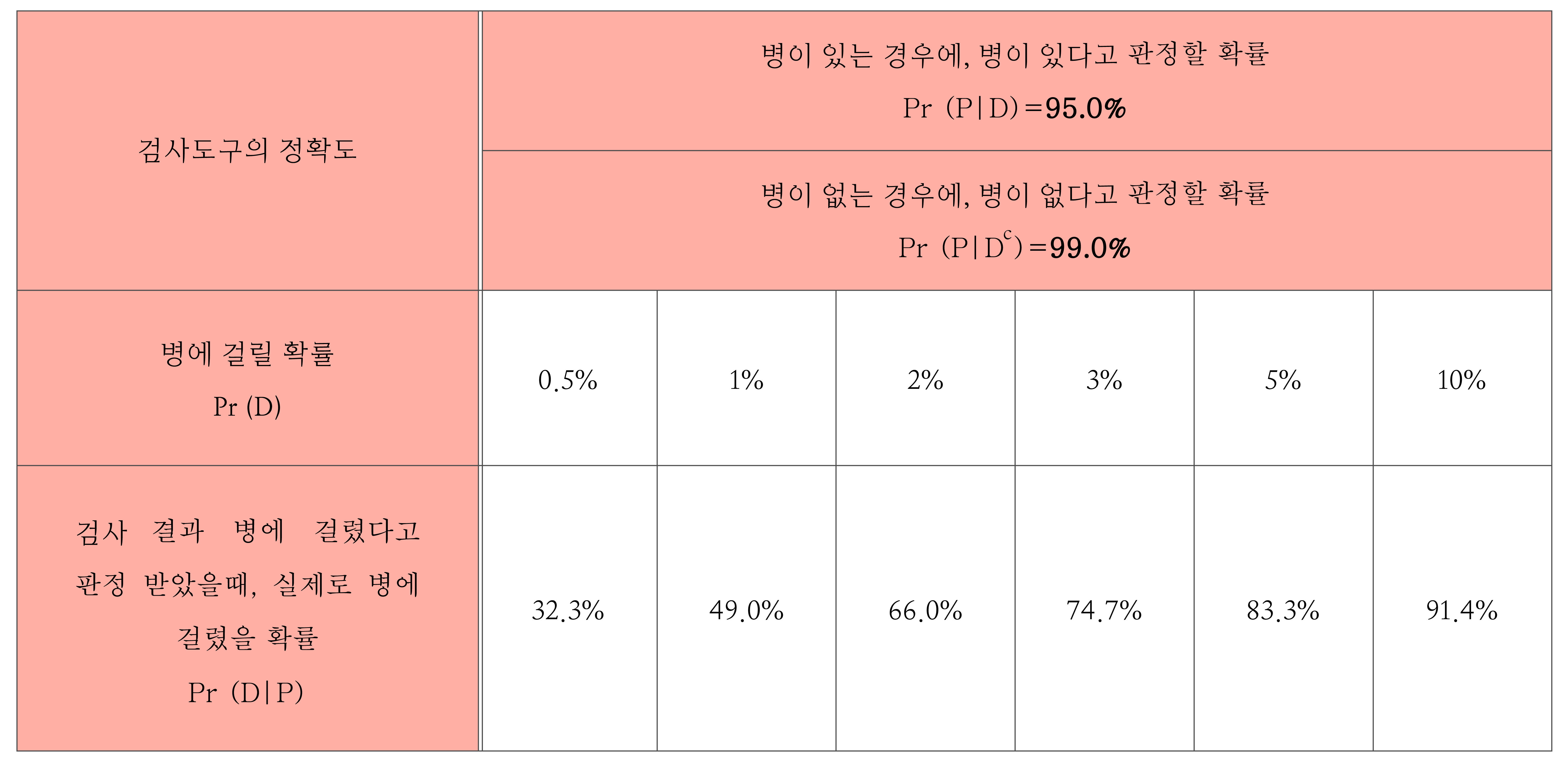
다음으로 병에 걸릴 확률 \(Pr(D)\)를 변경시켰을 때, \(Pr(D|P)\)가 어떻게 변하는지 알아보자. 그래서 ‘병이 없는데 병이 있는 것으로 잘못 판정하는 확률 \(Pr(P|{ D }^{ c })\)’와 ‘병이 있는데 병이 없는 것으로 잘못 판정하는 확률 \(Pr(N|D)\)’는 각각 5%와 1%로 고정시키고, 병에 걸릴 확률 \(Pr(D)\)를 주어진 0.5%에서 1%, 2%, 3%, 5%, 10%로 각각 높여보자. <표3>에서 알 수 있듯이, \(Pr(D)\)가 높아지면 \(Pr(D|P)\)가 급격히 높아짐을 알 수 있다. 따라서 위의 예에서 병에 걸린 것으로 판정받았을 때, 실제로 병에 걸려있을 확률이 32.3%로 낮았던 주요한 이유 중의 하나가 병에 걸릴 확률이 낮은 것임을 알 수 있다.
병 진단 오진율의 시사점
지금까지 조건부 확률을 이용하여 병 진단의 오진율을 계산해보고, 병 진단과 관련된 확률을 변경시켜 봄으로써 오진율에 영향을 미치는 중요한 요인과 조건이 무엇인지 알아보았다. 위의 논의를 다음과 같이 간단하게 요약, 정리할 수 있다.
첫째, 어떤 병에 걸릴 확률이 0.5% 정도로 낮은 경우에는 검사를 통해 ‘병이 있을 때 병이 있다’고 정확하게 진단할 확률이 95%이고, ‘병이 없을 때 병이 없다’고 정확하게 진단할 가능성이 99%로 높은 편이라 하더라도, 검사결과 병이 있는 것으로 판정받았더라고 실제로 그 병에 걸렸을 확률은 32.3%로 높지 않다는 점이다.
둘째, 어떤 병에 걸릴 확률이 5% 이상인 경우에는, 검사를 통해 ‘병이 있을 때 병이 있다’고 정확하게 진단할 확률이 95%이고, ‘병이 없을 때 병이 없다’고 정확하게 진단할 가능성이 99%로 높은 편이면, 검사결과 병이 있는 것으로 판정받았을 때 실제로 그 병에 걸렸을 확률이 80%이상으로 높다는 점이다.
이런 논의 결과로부터 검사를 통해 병의 유무를 판정하는 경우에, 그 병에 걸릴 확률이 어느 정도 되는지 확인하여 참고하는 것이 매우 중요함을 알 수 있다. 그리고 어떤 병에 대한 검사 결과를 바탕으로 병의 치료에 대한 중대한 결정을 내려야 할 경우에는 이 같은 여러 가지 가능성을 충분히 감안하는 신중함이 요구된다고 하겠다.
이 글은 <이승훈 교수의 실용수학>(이승훈, 경문사)의 내용을 보완한 것입니다.