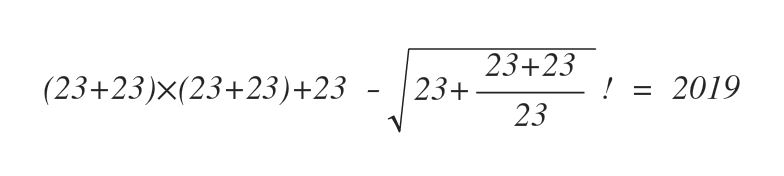1월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
1월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 이광현님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
다음과 같이 만들면 9개의 23으로 2019를 만들 수 있다.
\begin{align*}
&(23+23)(23+23) + 23 – \left(\sqrt{23+\frac{23+23}{23}}\right)! \\
&= 46\times46 + 23 – \sqrt{25}! \\
&= 2116 + 23 – 5! \\
&= 2139 – 120 \\
&= 2019
\end{align*}
이런 종류의 문제에 로그를 쓸 수 있다면 사실 23 다섯 개만으로 어떤 자연수든 만들 수 있다. 23에 제곱근을 \(n\)번 씌우면
\[
\sqrt{\sqrt{\cdots\sqrt{23}}} = (((23^{\frac12})\cdots)^{\frac12})^{\frac12} = 23^{\frac{1}{2^n}} = 23^{2^{-n}}
\]
이 되고, 여기에 밑이 23인 로그를 붙이면
\[
\log_{23} 23^{2^{-n}} = 2^{-n}
\]
이 된다. 다시 여기에 밑이 2인 로그를 붙이면
\[
\log_2 2^{-n} = -n
\]
이 되므로, 이 결과의 부호를 바꾸면 \(n\)이 된다.
세 개의 23으로 \(2 = (23+23)/23\)을 만들 수 있으므로, 제곱근 2019개를 씌운
\[
-\log_2 \log_{23} \sqrt{\sqrt{\cdots\sqrt{23}}}
\]
은 23 다섯 개로 2019를 만드는 식이다.
전산학에서 밑이 2인 로그를 \(lb\)로 나타내기도 하므로, 이 기호를 이용한다면
\[
-lb \log_{23} \sqrt{\sqrt{\cdots\sqrt{23}}}
\]
와 같이 단 두 개의 23으로 2019를 만들 수도 있다.
다음은 12월의 정답자로 선정된 이광현님의 해설입니다.
46*46 + 23 – 5! = 2019 로 풀었습니다.
9개의 23을 사용합니다.
(23+23)*(23+23)+23-(sqrt(23+(23+23)/23))! = 2019