곡면의 열방정식 [3] : 불량 흐름을 개선하는 일방통행

자동차도로는 보통 상행선과 하행선 두 가지 방향의 길이 있습니다만, 차량 한두대가 겨우 지나갈 수 있는 좁은 골목길은 상하행선을 지정하기 어렵습니다. 그래서 원활한 교통 흐름을 위해 좁은 길은 일방통행로로 지정하여 한 가지 방향으로 이동하도록 합니다. 한편 우리가 관찰해온 평균 곡률 흐름은 매몰된 곡면이라서 안과 밖이 구분됩니다. 따라서 마치 자동차가 상행 혹은 하행 두 가지 방향 중 하나의 방향으로 움직이듯이, 곡면 위의 각 점은 흐름에 따라 안쪽 바깥쪽 중 하나의 방향으로 움직입니다. 이때, 일방통행 도로와 같이 흐름이 안쪽 혹은 바깥쪽으로 움직이는 구역에서는 흐름이 여러 가지 좋을 성질을 가집니다. 이번 글에서는 일방통행하는 흐름의 특이점 분류와 불량 조건 문제에 관해 이야기하겠습니다.

미분 방정식의 미분 불가능한 해

이전 글 “곡면의 열방정식[2] : 위상 변화와 흐름의 운명”에서 여러 번 특이점을 지나 나누어지는 흐름을 예로 들었습니다. 그런데 특이점에서는 곡률이 발산하므로 미분이 불가능¹하다고 할 수 있습니다. 그런데 어떻게 미분 불가능한 흐름이 미분방정식의 해가 될 수 있을까요? 간단한 예로 함수열 \(u^n\)과 극한 \(u^\infty\)을 생각해보겠습니다.
\begin{align*}
& u^n(x,t)=:\sum_{k=1}^n k^{-1}e^{-k^2 t} \cos (kx) , && u^\infty(x,t)=:\sum_{k=1}^\infty k^{-1}e^{-k^2 t} \cos (kx).
\end{align*}

각각의 \(u^n\)은 무한번 미분 가능하며 열방정식 \(\partial_t u=\partial_x^2 u\)의 해이고, \(u^\infty\)로 수렴합니다.² 또한 \(t>0\)일 때, \(u^\infty\)은 무한번 미분 가능하고 열방정식을 만족합니다. 따라서 \(u^\infty\) 역시 열방정식의 해라고 생각하는 것이 합리적일 것입니다. 하지만 초기 값인 \(u^\infty(\cdot,0)\)은 미분 불가능하며 잘 정의되지 않아서³, 전통적인 관점에서 \(u^\infty\)을 열방정식의 해라고 부를 수 없습니다. 그래서 \(u^\infty\)과 같은 함수⁴를 열방정식의 약한 해^{weak solution}라고 부릅니다. 사실 이것은 약한 해의 정확한 정의가 아니며, 다양한 종류의 약한 해의 정의가 존재하지만, 지면이 많이 필요해서 생략하겠습니다.

미분방정식의 미분 가능한 해는 강한 해^{strong solution}라고 부르며, 강한 해도 약한 해의 일종으로 여깁니다. 대부분의 경우 강한 해의 존재성을 곧바로 증명하기 어려울 때, 약한 해는 해의 존재성을 먼저 보입니다. 그 후, 약한 해가 미분 가능함을 보임으로써 강한 해의 존재를 증명합니다. 하지만 위의 예제와 같이 모든 약한 해가 미분 가능한 것은 아니며, 약한 해의 미분 불가능한 점들을 모두 특이점이라고 부릅니다.

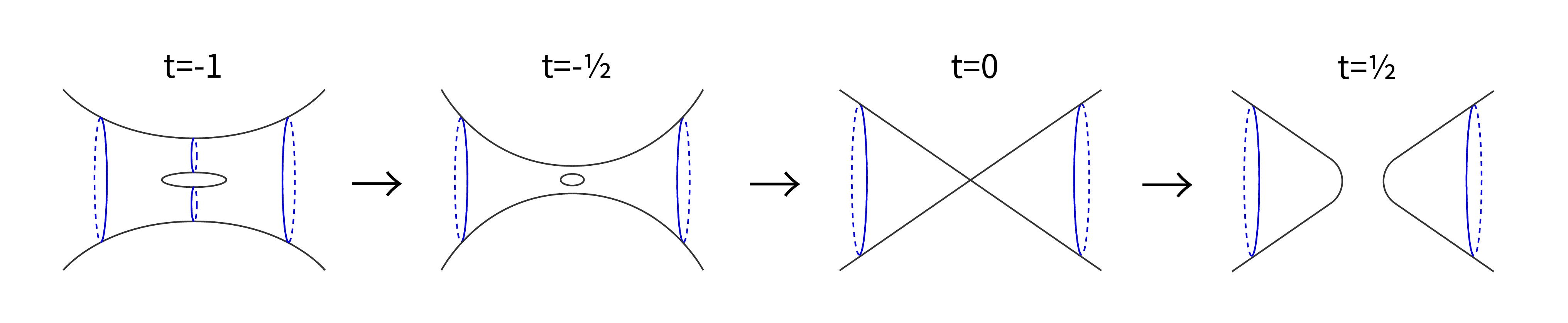
이전 글 “곡면의 열방정식[2] : 위상 변화와 흐름의 운명”의 아령 모양의 흐름과 같이, 평균 곡률 흐름은 사라지기 전에 특이점을 가지는 것이 일반적입니다. 특히 이전 글 “곡면의 열방정식[2] : 위상 변화와 흐름의 운명”에서 이야기 한 바와 같이 강한 해의 위상이 변화하는 순간 특이점이 발생하므로, 흐름으로 위상을 연구하기 위해서는 미분 불가능한 특이점을 허용하는 약한 흐름을 연구해야 합니다.

불량 조건 문제

중학교에서 연립일차방정식을 배울 때, 해가 존재하지 않으면 불능이고 해가 무한히 많으면 부정이라고 배웁니다. 예를 들어, \(ax+by=p\)와 \(cx+dy=q\)를 만족하는 해 \(x,y\)를 찾을 때, \(ad\neq bc\)라면 연립방정식의 해가 유일하게 존재하고, \(ad=bc\)라면 \(p,q\)에 따라 연립방정식은 부정 혹은 불능입니다.⁵ 따라서 우리는 \(ad=bc\)라면 연립방정식이 불량^ill-posed하고, \(ad\neq bc\)라면 연립방정식이 우량^well-posed하다고 이야기 할 수 있습니다.

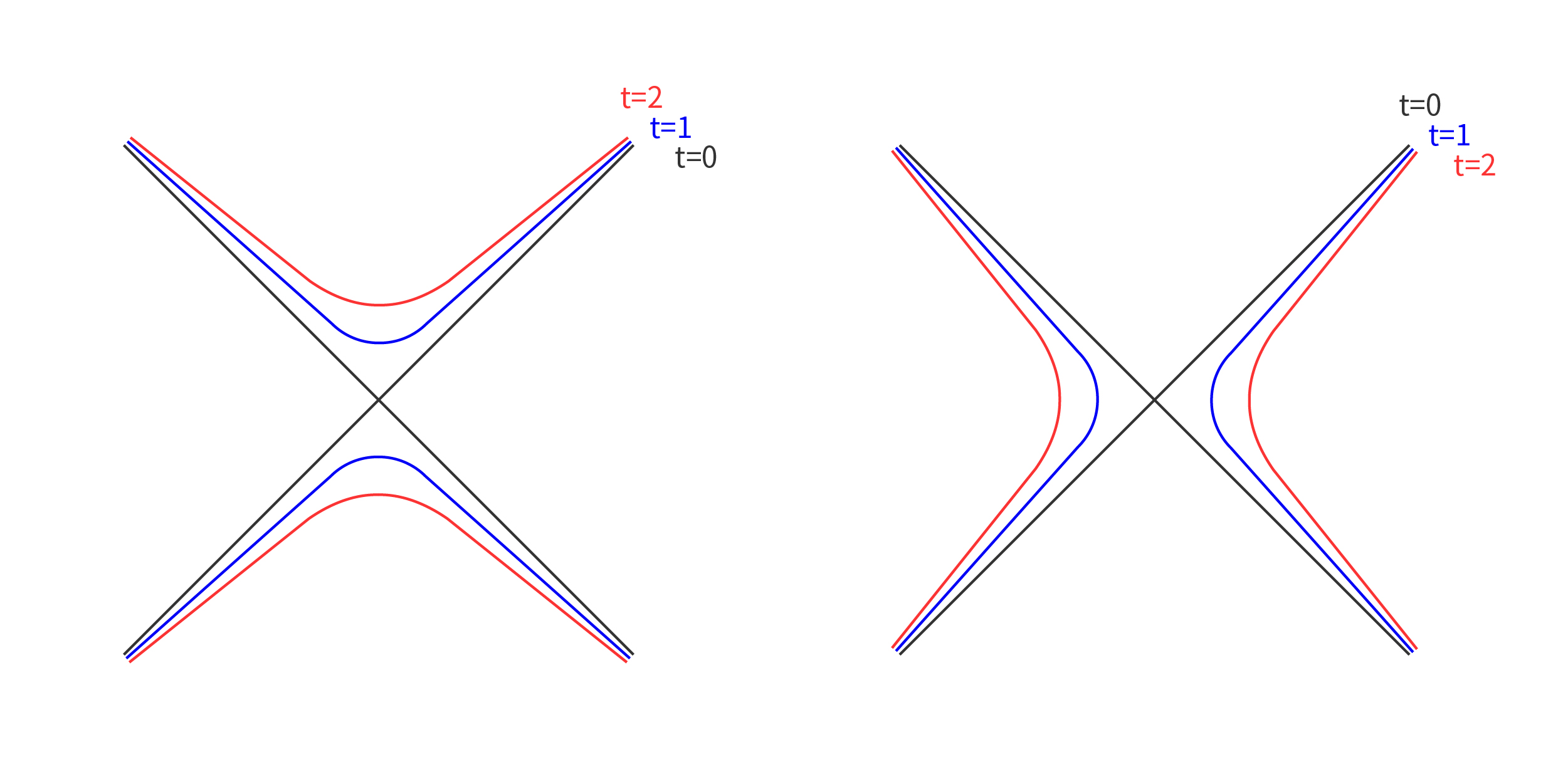
이와 마찬가지로 주어진 초기 곡면에서 시작하는 (약한) 흐름이 유일하게 존재한다면 우량하고, 그렇지 않다면 불량하다고 이야기합니다. 실제로 종종 원뿔인 곡면에서 시작하는 흐름은 무한히 많이 존재해서 불량합니다.([그림1]) 그런데 무한대에서 원뿔로 점근하는^{asymptotically conical} 자가수축자는 무한히 많고[10], 이들은 첫 특이 시간에 완벽한 원뿔이 됩니다.([그림2]) 결국 첫 특이 시간 이후에 흐름이 유일하게 결정되지 않아 불량합니다. 즉, 부드러운 초기 곡면에서 시작한 흐름조차 불량할 수 있습니다.

이 불량 흐름은 다양한 약한 흐름을 동시에 사용할 수 없어서 연구에 어려움이 있습니다. 앞서 언급한 것처럼 미분방정식은 다양한 종류의 약한 해를 정의할 수 있습니다. 평균 곡률 흐름 역시, 브라케 흐름과 약한 집합 흐름^{weak set flow}을 비롯하여 여러 가지 종류의 약한 흐름이 존재하고 각자의 성질이 있습니다. 그런데 만약 흐름이 우량해서 그들이 모두 동일하다는 것을 알 수 있다면, 각각의 약한 흐름의 성질을 모두 사용할 수 있습니다. 따라서 흐름이 우량할 조건을 찾고 어떤 특이점에서 국소적^local이라도 우량 조건을 만족하는지 확인하는 것이 중요합니다.

일방통행

공간에 매몰된 부드러운 닫힌 초곡면은 공간을 안과 밖으로 나눕니다. 즉, 매몰된 닫힌 초곡면은 안쪽 혹은 바깥쪽이라는 방향이 생깁니다. 그런데 한쪽⁶ 방향으로만 움직이는 흐름은 유일하게 존재한다는 것을 증명할 수 있습니다.⁷ 최근에 허쉬코비츠^Hershkovits교수님과 화이트^White교수님이[10] 흐름이 주어진 열린 시공간 집합에서 한쪽⁹ 방향으로 움직인다면 그 집합에서는 흐름이 유일하게 결정된다는 국소 우량성을 증명했습니다.

사실 안쪽으로만 움직이는 흐름은 찾기 쉽습니다. 만약 흐름의 평균 곡률 \(H\)가 항상 양수라면, 평균 곡률 흐름의 방정식 \(X_t=\Delta_g X=-H\nu\)에서 흐름이 안쪽으로만 움직이는 것을 관찰할 수 있습니다. 그리고 평균 곡률 \(H\)는 미분 부등식

\begin{equation}
\tag{(1)}
H_t\geq \Delta_g H+n^{-1}H^3,
\end{equation}
을 만족함이 알려져 있습니다. 따라서 닫힌 초기 곡면의 평균 곡률이 양수라면 최댓값 원리에 의해 \(H\)가 항상 양수임을 알 수 있습니다.¹⁰ 즉, 초기 곡면이 양의 평균 곡률을 가진다면, 흐름은 계속해서 양의 평균 곡률을 가지고 안쪽으로 움직입니다. 특이점에서 평균 곡률이 양의 무한대로 발산하여 존재하지 않지만, 약한 흐름이 계속해서 안쪽으로 일방통행하는 성질을 가지게 잘 정의할 수 있습니다.

일방통행하는 흐름은 여러 가지 좋은 성질을 가집니다. 먼저, 일방통행하는 흐름은 거의 모든 시간에서 특이점 집합의 여차원^codimension이 3이상 입니다.[8, 12,14]  즉, \(\mathbb{R}^3\)에서는 거의 모든 시간에 흐름이 부드러우며, \(\mathbb{R}^4\)에서는 거의 모든 시간에 흐름이 고립된 특이점을 가집니다.

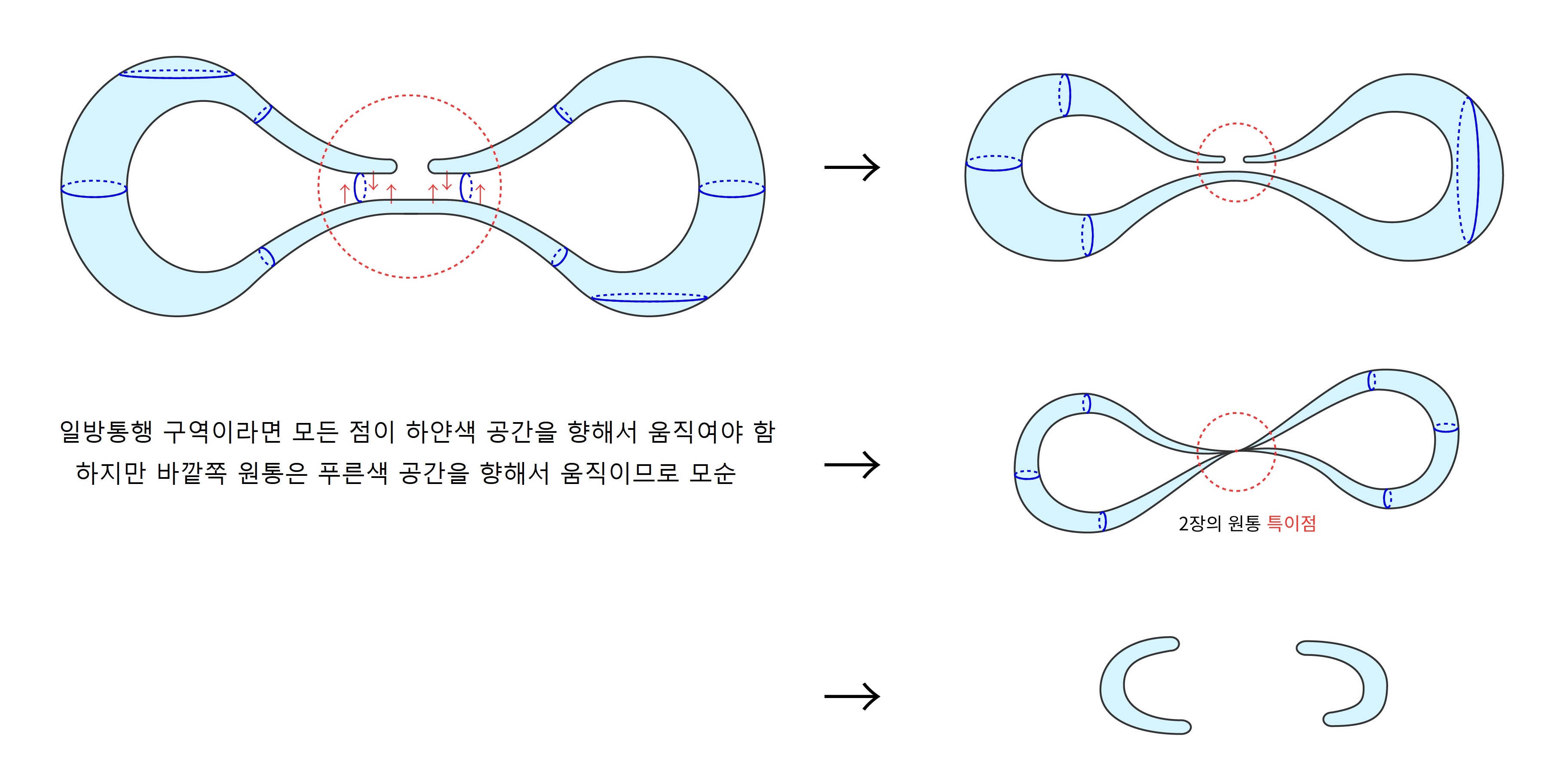
또한 일방통행하는 흐름의 특이점은 반드시 한 겹의 둥근 구 혹은 둥근 원통입니다. 이 성질은 국소적으로 일방통행해도, 해당 구역에서 성립합니다. 둥근 구와 둥근 원통만이 나오는 이유는 극한에서 얻을 수 있는 자가수축자가 양의 평균 곡률을 가지므로 \(\frac{|A|^2}{H^2}\)가 잘 정의되는데¹¹, \(\frac{|A|^2}{H^2}\)에 최댓값 원리를 적용하여 \(\frac{|A|^2}{H^2}\)가 상수임을 증명할 수 있습니다. 자세한 증명은 후이스켄^Huisken 교수님과 시네스트라리^Sinestrari 교수님의 논문[9]에 소개되어 있습니다. 한편 특이점이 한 겹인 것은 직관적으로 관찰할 수 있습니다. 예를 들어, [그림3]과 같이 두 겹의 원통을 고려하면, 서로 다른 방향으로 움직임을 관찰할 수 있습니다.

이런 일방통행하는 흐름의 좋은 성질은 일반적인^generic 흐름에 적용할 수 있을 것으로 예상됐습니다. 특히 후이스켄 교수님은 다음과 같이 추측했습니다.

주어진 매몰되고 부드러운 닫힌 초곡면 \(N_0\)에 대하여, \(N_0\)로 수렴하는 매몰되고 부드러운 닫힌 초곡면의 열 \(\{M_0^i\}_{i\in \mathbb{N}}\)이 존재하여, 각각의 초곡면 \(N^i_0\)에서 시작되는 우량 평균 곡률 흐름 \(M^i_t\)은 한 겹의 둥근 구 혹은 둥근 원통 특이점들만 가진다.

\(M^i_0\)은 \(N_0\)와 같은 위상을 가지므로, 후이스켄 추측이 참이라면 \(N_0\)에서 시작하는 흐름 대신 구와 원통만을 특이점으로 가지는 흐름 \(M^i_t\)을 이용하여 위상을 연구할 수 있습니다. 따라서 무한히 많은 자가수축자을 전부 연구하여 임의의 특이점에서의 위상 변화를 관찰할 필요 없이, 원통 특이점에서의 위상 변화만 관찰하면 됩니다. 이러한 주어진 곡면 근처의 곡면에서 시작하는 흐름을 일반적인 평균 곡률 흐름^{generic mean curvature flow}라고 합니다. 어째서 구와 원통을 제외한 모든 특이점을 일반적인 흐름으로 피해갈 수 있는지는 다음 글에서 논의하도록 하겠습니다.

둥근 구와 둥근 원통 특이점은 위상도 단순할 뿐만 아니라, 근처에서 흐름이 일방통행할 것으로 예상됩니다. 다음은 평균 볼록 인근^{mean convex neighborhood} 추측입니다.¹²

어떤 평균 곡률 흐름이 한 겹의 둥근 구 혹은 둥근 원통 특이점을 가진다면, 그 특이점을 포함하는 어떤 시공간 구역에서 일방통행한다.

위의 추측이 참이라면 일방통행하는 구역에서 흐름이 우량하므로, 후이스켄 추측에 등장하는 일반적인 흐름의 흐름이 우량함을 보일 수 있습니다. 일방통행 덕분에 위에서 언급한 바와 같이, 거의 모든 점에서 미분 가능함을 알 수 있습니다.

고대 흐름

우리는 평균 볼록 인근 추측을 증명하기 위해, 특이점 관찰에 도움이 되는 극한 흐름^{limit flow}이라는 개념을 도입해야 합니다. 이전 글 “곡면의 열방정식[2] : 위상 변화와 흐름의 운명”에서 흐름을 특이점에서 확대해서 어떤 자가수축자로 수렴하는 것을 알 수 있다고 하였습니다. 이것은 특이 시간으로 수렴하는 시간열의 곡면들을 확대해서 본 결과입니다. 하지만 우리는 보다 많은 정보를 얻기 위하여, 각각의 곡면을 확대하는 대신 흐름 자체를 시공상에서 확대하겠습니다. 예를 들어, 흐름 \(M_t\)를 시공간 특이점 \((x_0,t_0)\)으로 수렴하는 점열\((x_i,t_i)\)을 중심으로, 발산하는 양의 수열 \(\{\lambda_i\}_{ i \in \mathbb{N} }\)을 확대 계수로 이용하여 얻은 흐름열
\begin{equation*}
M^i_t= \lambda_i (M_{\lambda_i^2 (t-t_i) } -x_i)
\end{equation*}

을 생각합니다. \(M_t\)는 \(t=0\)부터 존재하므로, 각각의 흐름 \(M^i_t\)는 \(t=-\lambda^2t_i\)부터 존재함을 알 수 있습니다. 또한 모든 \(M^i_t\)은 시공간 원점\((0,0)\)을 포함합니다.¹³ 이때, 각각의 흐름 \(M^i_t\)은 평균 곡률 흐름이며, 만약 이 흐름열의 극한 \(\overline{M}_t\)가 존재한다면 마찬가지로 평균 곡률 흐름입니다. 이렇게 얻는 흐름을 극한 흐름이라고 합니다. 그런데 \(\lambda_i\)가 발산하므로 초기 시간 \(-\lambda_i^2t_i\) 역시 음의 무한대로 발산합니다. 따라서 극한 흐름은 모든 음의 시간 \(t\in (-\infty,0]\)에서 존재합니다.¹⁴ 

한편, 모든 음의 시간에 존재하는 흐름은 고대 흐름^{ancient flow}이라고 부릅니다. 따라서, 모든 극한 흐름은 고대 흐름이지만, 고대 흐름이 극한 흐름은 아닐 수 있습니다. 이런 모든 음의 시간에 존재하는 미분 방정식의 해를 고대 해라고 부르는데, 포뮬형 미분 방정식은 고대 해를 모두 찾을 수 있는 경우가 종종 있고, 이처럼 모든 고대 해를 찾는 것을 리우빌^Liouville 정리라고 부릅니다.

고대 흐름의 간단한 예로서 평면이나 최소 곡면과 같이 움직이지 않는 정지된 흐름을 생각할 수 있습니다. 또한, 자가수축자 \(\Sigma\)가 수축하는 흐름 \((-t )^{\frac{1}{2}}\Sigma\)을 생각할 수 있습니다. 예를 들어, 시간이 역행함에 따라 점점 커지는 둥근 구는 무한히 확대될 수 있고, 이는 고대 흐름의 일종입니다.

특이점에서 흐름을 확대하여 얻는 조정된 흐름과 마찬가지로, 고대 흐름 \(M_t\)을 수축하여 얻는 조정된 흐름 \(\bar M_\tau=e^{\frac{\tau}{2}}M_{-e^{-\tau}}\)을 고려하면 자가 수축하는 고대 흐름의 조정된 흐름은 자가수축자입니다. 또한 “곡면의 열방정식 [1]: 에너지가 줄어들면 단순해진다”에서 소개한 엔트로피는 흐름의 시간이 역행함에 따라 증가하는데, 음의 무한대에서 엔트로피가 유한하다면 특이점을 관찰할 때와 마찬가지로 조정된 흐름이 한 겹 혹은 여러 겹의 자가수축자로 수렴합니다.

그렇다면 한 겹의 둥근 구 혹은 둥근 원통 특이점에서 얻을 수 있는 극한 흐름을 조정하면 음의 무한대에서 어떤 자가수축자로 수렴할까요? 둥근 구와 둥근 원통의 엔트로피들은 모두 1.53을 넘지 못합니다. 이를 이용해서 한 겹의 구나 원통에서 얻은 극한 흐름은 음의 무한대에서도 엔트로피가 1.53을 넘지 못합니다. 한편 평면은 자가수축자 중 가장 작은 엔트로피값 1을 가집니다.¹⁵ 따라서 여러장의 자가수축자로 수렴한다면 엔트로피가 2이상이어야 하는데 1.53은 2보다 작으므로 한 겹의 자가수축자로 수렴합니다. 또한 3차원에 매몰된 자가수축자는 엔트로피가 작은 순서로 평면, 둥근 구, 둥근 원통입니다.[3] 이를 이용하며 3차원의 경우 고려했던 극한 흐름의 조정된 흐름은 음의 무한 시간에서 한 겹의 둥근 구 혹은 둥근 원통로 수렴합니다.¹⁶ 

그런데 평균 볼록 인근 추측이 참이 아니라면 어떤 극한 흐름이 존재할 수 있을까요? 주어진 한 겹의 구 혹은 원통 특이점 \((x_0,t_0)\)로 수렴하고 음의 평균 곡률을 가지는 점열 \((x_i,t_i)\)가 존재할 것입니다. 따라서, 그 점열에서 확대한 흐름열의 극한 흐름은 원통에서 양이 아닌 평균 곡률을 가집니다. 따라서, 어떤 고대 흐름이 존재해서 조정된 흐름이 음의 무한 시간에서 한 겹의 둥근 구나 둥근 원통으로 수렴하는데 어떤 점에서 음이 아닌 평균 곡률을 가져야만 합니다. 따라서 만약 한 겹의 구나 원통으로부터 나오는 조정된 고대 흐름이 양의 평균 곡률을 가진다면 모순이 되고, 평균 볼록 인근 추측이 참이 됩니다. 그런데 둥근 구는 닫힌 흐름으로서 양의 평균 곡률을 가지므로, (1)에서 논의한 대로 양의 평균 곡률을 가져야합니다. 따라서 원통으로부터 나오는 고대 흐름이 양의 평균 곡률을 가짐을 보이면 됩니다.

원통으로부터 나오는 고대 흐름의 분류

어떤 조절된 고대의 평균 곡률 흐름이 뒤에서¹⁷ 한 겹의 원통으로 수렴한다고 가정하겠습니다. 첫 번째로, 우리를 곤란하게 만드는 예상은 흐름이 고정된 원통으로 수렴하는 것이 아닌, 계속해서 도는 원통으로 수렴하는 것입니다. 이는 접흐름^{tangent flow}의 유일성을 묻는 질문입니다. 콜딩^Colding교수님과 미니코찌^Minicozzi교수님은 평균 곡률 흐름은 엔트로피가 단조 감소하는 기울기 흐름^{gradient flow}이라는 사실을 이용하여 접흐름의 유일성을 증명하였습니다.[7]¹⁸

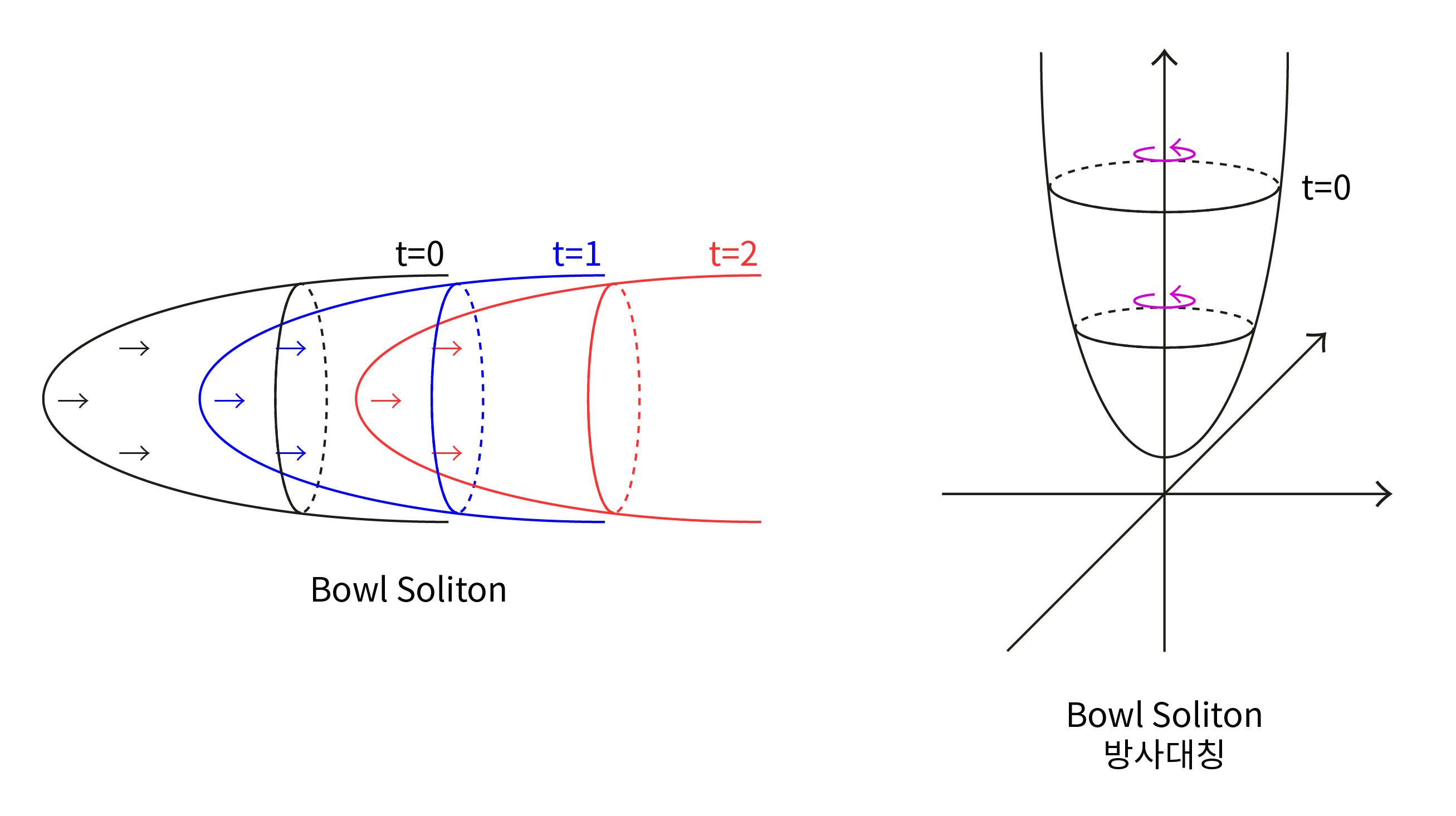
한편, 앙게넨트^Angenent 교수님, 다스칼로포울러스^{Daskalopoulos} 교수님과 세슘^Sesum 교수님은[1] 원통으로부터 나오는 볼록하고 부드러운 조정된 고대 흐름은 원통의 선형화 연산자의 불안정하거나 중립적인 고유 함수^{eigenfunction}에 의해 점근 행동^{asymptotic behavior}이 결정된다는 것을 보였습니다.¹⁹ 이를 바탕으로 저와 브렌들레^Brendle 교수님은 원통으로부터 나오는 볼록하고 부드럽고 닫혀있지 않은 고대 흐름은 자가수축하는 원통이거나 밥그릇 솔리톤^{bowl soliton}이라는 것을 증명하겠습니다. 밥그릇 솔리톤은 방사대칭인 함수의 그래프로서 볼록한 포물면처럼 생겼습니다. 또한 밥그릇 솔리톤은 크기와 모양을 유지한 채 한쪽 방향으로 움직이는 옮겨가는 자^translator의 일종입니다.([그림4])

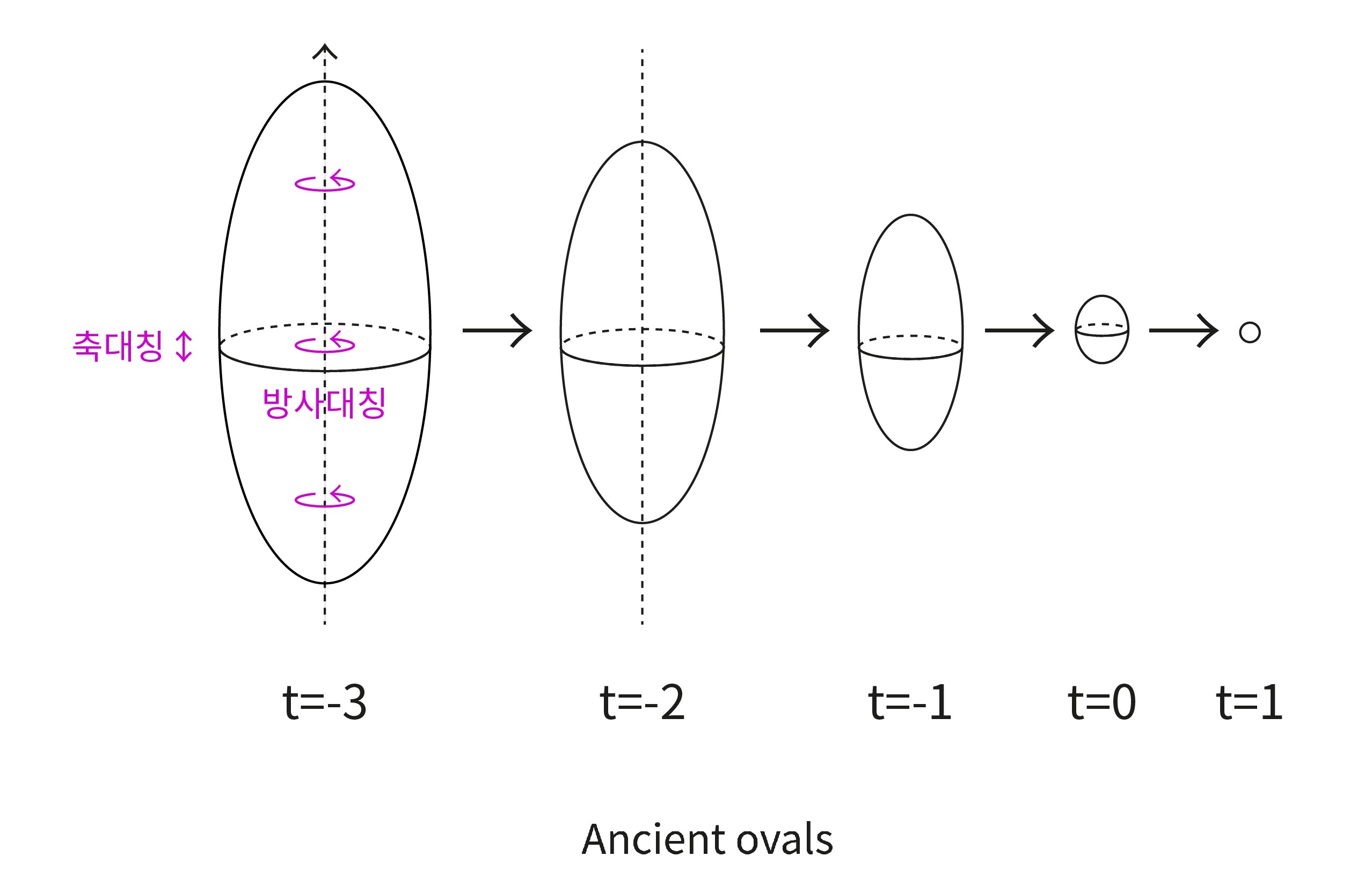
이를 이용하여, 앙게넨트-다스칼로포울러스-세슘 교수님은 원통으로부터 나오는 볼록하고 부드럽고 닫힌 고대 흐름은 자가수축자인 구이거나 고대의 계란형 흐름^{Ancient ovals}임을 증명하였습니다.[2] 고대의 계란형 흐름은 방사대칭인 흐름으로 양쪽 끝에 밥그릇 솔리톤이 달린 원통처럼 생겼습니다.([그림5])

이후, 허쉬코비츠 교수님, 하슬호퍼^Haslhofer 교수님과 저는 한 겹의 원통으로부터 나오는 3차원에 매몰된 조정된 고대 흐름은 위에서 설명한 자가수축하는 원통, 밥그릇 솔리톤, 혹은 고대의 계란형 흐름일 수밖에 없음을 증명하였습니다.[5] 세 가지 모두 볼록하고 방사대칭인 흐름으로 항상 양의 평균 곡률을 가집니다. 이로써 3차원에서 평균 볼록 인근 추측이 참임이 증명되었습니다. 그리고 저희는 화이트 교수님과의 협업으로 4차원의 한 겹의 목과 같은 원통 \(S^2\times \mathbb{R}\)으로 부터 나오는 고대 흐름 역시 위에 소개한 흐름이라는 것을 보였습니다.[6] 따라서 4차원에 매몰된 한 겹의 납작한 원통 \(S^1\times \mathbb{R}^2\)로부터 나오는 고대 흐름이 양의 평균 곡률을 갖는다는 것을 보인다면, 4차원 평균 볼록 인근 추측이 참임을 증명할 수 있습니다.

연재글
곡면의 열방정식 [1]: 에너지가 줄어들면 단순해진다
곡면의 열방정식 [2]: 위상 변화와 흐름의 운명
곡면의 열방정식 [4]: 손가락 위에서 돌아가는 농구공