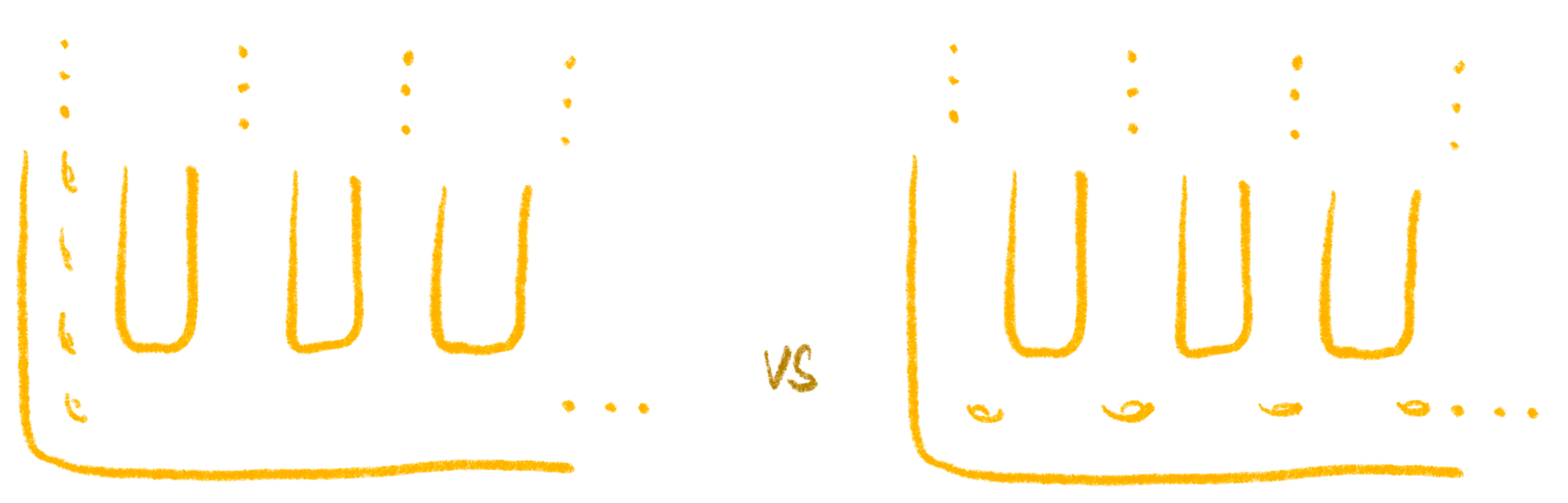그래프와 곡면의 동상이몽 [3]: 무한그래프와 무한곡면

우리는 유한한 세상에 살아가지만 그 너머의 무한한 세상에 대한 궁금증을 갖곤 한다. 처음 숫자를 배우는 아이에게는 어른에게 세상에서 제일 큰 수가 무엇이냐 묻는다. 밤하늘을 별은 우주의 끝을, 벽에 걸린 시계는 시간의 끝을 상상하는 통로가 되어준다. 등식 \(0.9999 \ldots =1\)에 관한 논의는 언제나 각종 커뮤니티를 뜨겁게 달구는 주제이다. 수학자들에게도 무한대와 무한소는 수학의 발전을 이끌었던 논란의 대상이었다.

우리는 지난 두 연재글 [6, 7] 에서 유한그래프와 유한곡면, 그리고 그 대칭군들에 대해 알아보았다. 유한그래프는 꼭짓점과 변의 개수가 유한해야 했고, 유한곡면은 구멍의 개수가 유한해야 했다. 그렇다면 “무한” 그래프와 “무한” 곡면에 대해서는 어떤 이야기들을 할 수 있을까? 

무한곡면

먼저 무한곡면부터 살펴보자. 무한히 많이 앉을 수 있는 \(\infty\)-인승 튜브를 떠올려보거나, 무한히 긴 원기둥에 무한히 많은 구멍이 뚫려 있는 “무한 플룻”같은 곡면을 생각해보면 되겠다.

그렇다면 서로 다른 두 무한곡면은 어떻게 구분할 수 있을까? 지난 두 번째 연재글 [7] 에서 도려낸 구멍과 뚫은 구멍의 차이를 알아보았었는데, 논의의 편의상 본 글에 등장하는 무한곡면의 모든 구멍은 뚫은 구멍이라고 생각하자. 그렇다면 무한곡면에서 뽑아낼 수 있는 두 가지 위상 데이터는 몇 인승인지 말해주는 “종수”와 그리고 “뚫린 구멍의 개수”일 것이다. 직관적으로, \(\infty\)-인승이면서 유한개의 구멍이 뚫린 곡면과, 유한인승이면서 무한개의 구멍이 뚫린 곡면은 위상적으로 다름을 예상해볼 수 있다. 하지만 두 곡면 모두 \(\infty\)-인승이라면, 혹은 모두 무한히 많은 구멍이 뚫려 있다면 어떨까?

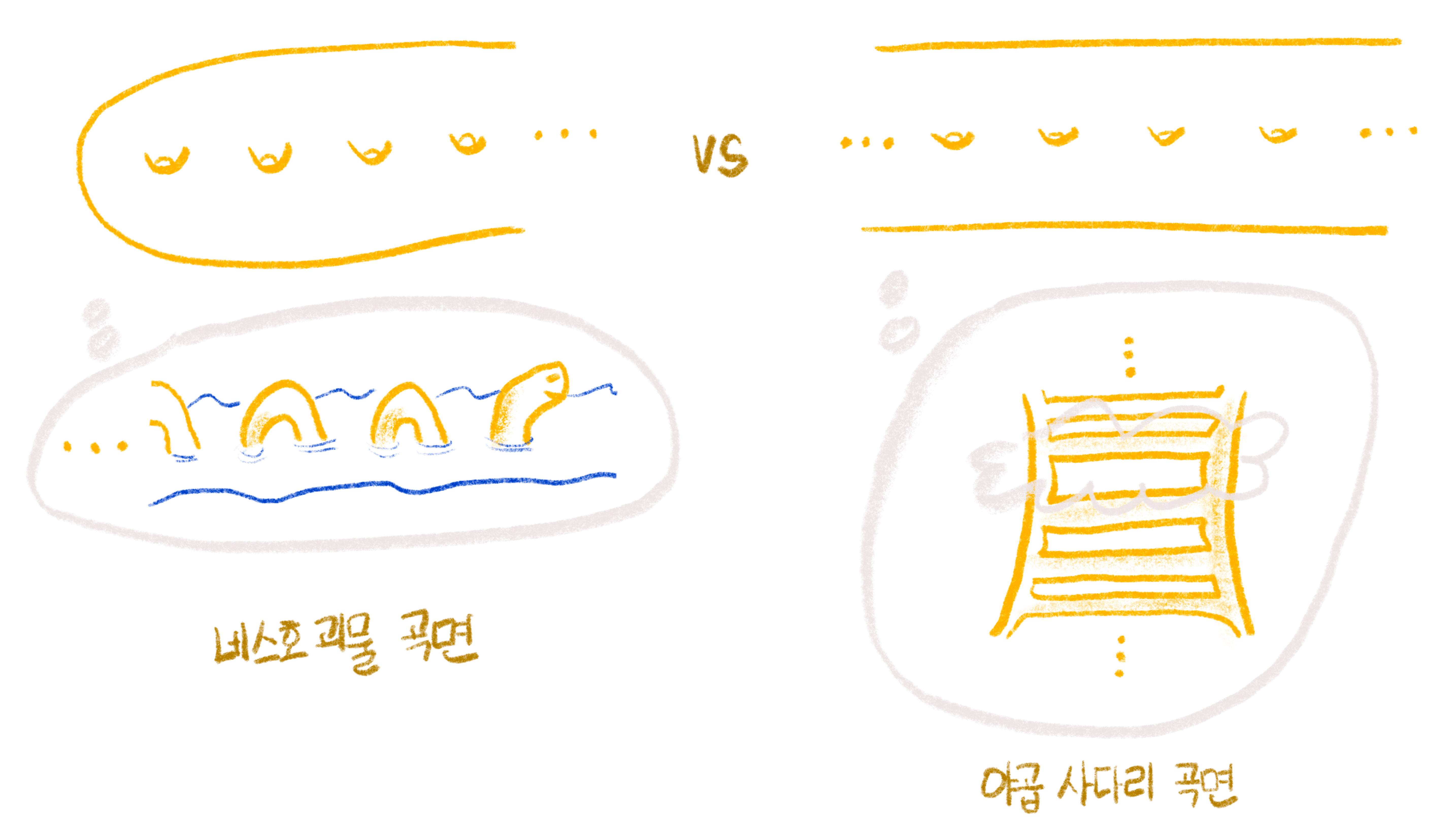
가령 그림 1의 두 곡면을 살펴보자. 

두 곡면 모두 \(\infty\)-인승임이 분명하다. 하지만 어떤 차이점이 보이는가? 네스호 괴물 곡면의 경우 아무 폐곡선 혹은 유한부분곡면을 따라 잘라내더라도 최대 한 덩어리만이 무한곡면이 된다. 반면 야곱 사다리 곡면의 경우 남은 두 덩어리 모두 무한곡면이 되도록 자르는 폐곡선이 존재한다. 마찬가지로, 그림 2의 에펠탑 곡면은 3개의 무한곡면 덩어리가 나오도록 자르는 유한부분곡면이 존재한다. 
 
  

우리가 방금 무엇을 발견했는가? 위 그림 1과 그림 2에 주어진 세 곡면들 모두 \(\infty\)-인승이고 구멍이 없으나, 위상적으로 다른 하나의 특징을 발견했다: “유한한 부분곡면”을 잡았을 때, 그 외부의 무한곡면의 ‘최대 개수’가 서로 달랐던 것이다. 이에 따라, 주어진 세 곡면은 모두 서로 위상적으로 다른 곡면이 된다.

직관적으로 보자면, 네스호 괴물 곡면은 무한으로 뻗어 나가는 방법이 하나이고, 야곱 사다리 곡면은 둘이며 에펠탑 곡면은 셋이라 서로 위상적으로 다르다고 볼 수도 있다. 이처럼 곡면 내에서 무한으로 나가는 독립적인 방향 각각을 한계^end라고 하고, 한 곡면의 모든 한계들을 모은 공간을 그 곡면의 한계공간^{end space}이라고 한다.

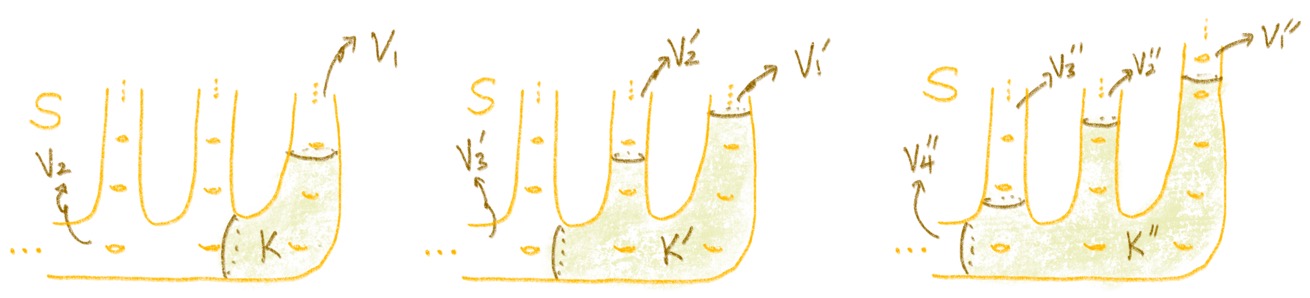
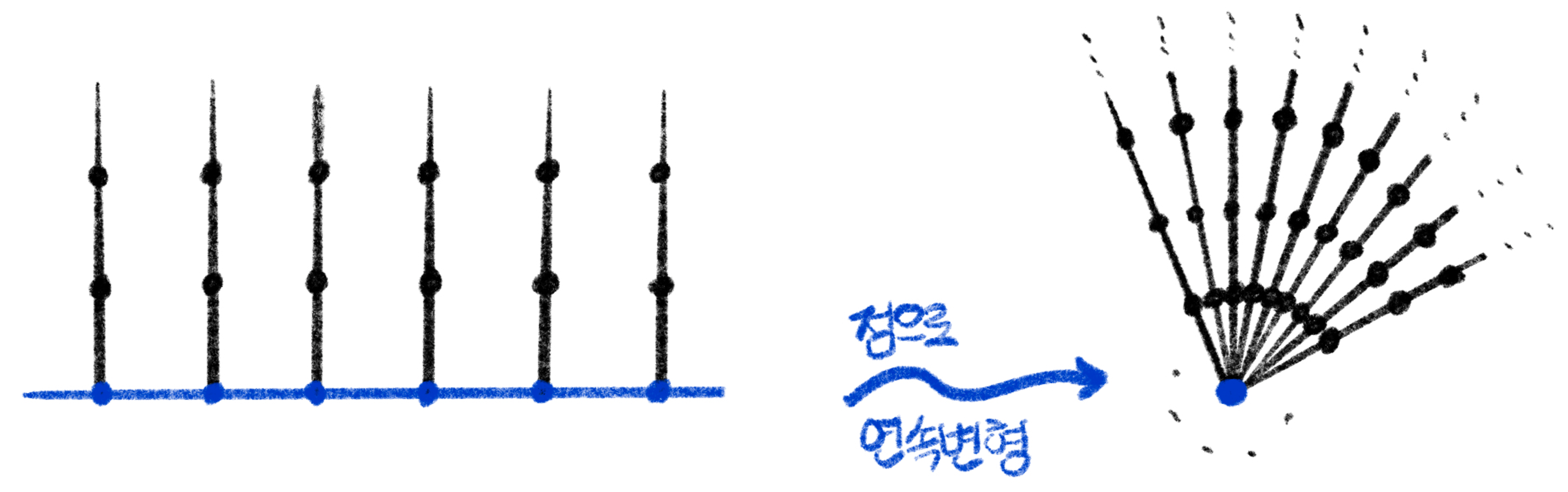
더 엄밀히 말하자면, 주어진 무한곡면 \(S\)의 한계 공간을 알고 싶으면 \(S\)의 유한부분곡면 \(K\)를 잡고 그 외부 \(S-K\)에 있는 무한부분곡면들을 보는데, 여기서 유한부분곡면 \(K\)의 크기를 늘리면 \(S-K\)의 크기가 작아지므로 \(K\)외부의 무한 곡면들의 크기도 작아지며, 심지어는 하나의 외부곡면이 두 개 이상으로 분화되기도 한다. 무한곡면 \(S\)의 한계공간은 바로 \(K\)를 점점 키워 나갈 때 \(K\)밖 무한부분곡면들의 “극한”이라고 볼 수 있다.
 

이 경우 외부무한곡면들이 \(V_1,V_2,V_3\)에서 \(V_1’,V_2’,V_3’\), 그리고 \(V_1’’,V_2’’,V_3’’\)으로 작아지지만, 분화되지는 않은 채 3개의 무한외부곡면을 유지하게 된다. 따라서 \(S\)의 한계공간은 3개의 점을 가진 집합이 된다.

예를들어, 그림 3과 같이 우리가 이때까지 본 무한곡면의 예시들은 유한부분곡면 \(K\)가 커져도 외부 무한곡면들이 분화없이 유지되는 경우이다. 위 예시를 일반화하여 한계의 수가 4개, 5개 등등인 곡면을 떠올려 볼 수 있을 것이다. 하지만 만약 한계의 개수마저도 무한한 경우는 어떨까? 이 경우에는 \(K\)가 커짐에 따라 외부무한곡면의 분화가 일어나기 시작한다. 그림 4를 보자.

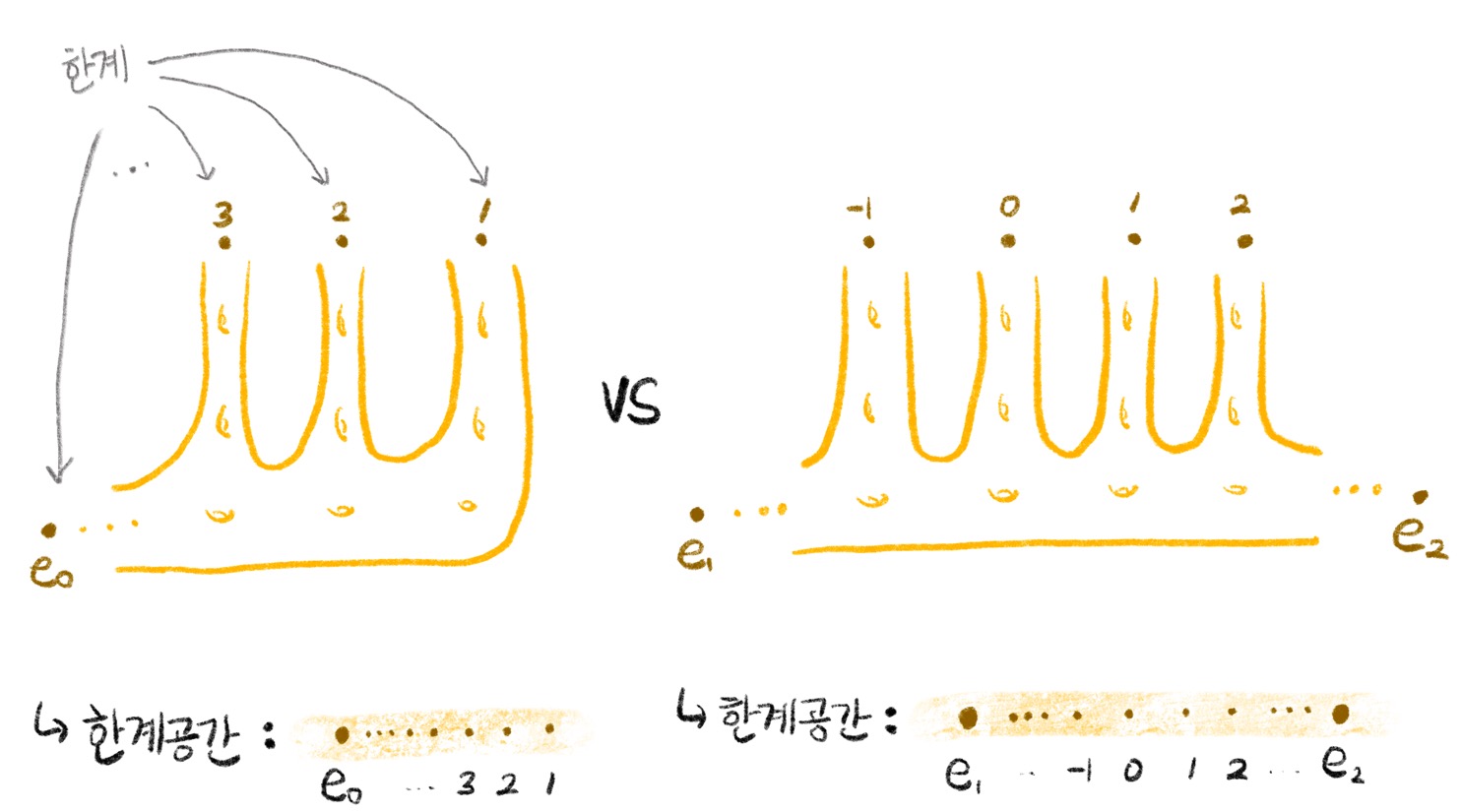
좌측의 그림과 같이 유한부분곡면을 \(K\)로 잡으면 외부무한곡면이 \(V_1\)과 \(V_2\) 두 개로 나오지만, \(K’\)으로 유한부분곡면을 확장하면 \(V_2\)가 \(V_2’\)과 \(V_3’\)으로 분화되어 \(K’\)은 총 3개의 외부무한부분곡면을 갖게된다. 마찬가지로 \(K’’\)을 잡으면 그 \(V_3’\)가 분화되어 \(V_3’’, V_4’’\)을 만들고 결국 \(K’’\)의 외부에는 4개의 외부무한부분곡면을 이루게 된다. 이러한 추세를 계속하다보면, 자연수의 집합과 같은 크기의 한계 공간이 만들어 진다.

무한개의 한계를 허용하기 시작하면, 이 무한한 한계를 한계공간 내에서 다르게 배열하는 것만으로도 여러가지의 무한곡면을 만들 수 있다. 그림 5를 보자. 왼쪽 곡면은 무한개의 한계가 있지만 그 무한개의 한계들이 \(e_0\) 방향을 향해서 축적되는 양상을 보이고, 오른쪽 곡면 역시 무한개의 한계가 있지만 두 방향으로 나뉘어 \(e_1\)과 \(e_2\)로 모두 축적되는 모습을 관찰할 수 있다. 이처럼 두 곡면 모두 무한개의 한계를 갖고 있지만 그 한계가 축적된 “모양”에 따라서 두 곡면을 구분 할 수 있음을 알 수 있다. 실제로, 무한곡면의 한계공간은 그 자체로 위상공간이 된다.

즉, 위 논의를 정리하자면, 서로 다른 한계공간을 갖고 있는 두 곡면은 위상적으로 다르다는 것이다. 그렇다면 다음과 같은 질문을 던질 수 있다. 만일 두 곡면의 한계공간마저 같으면 두 곡면은 위상적으로 같을까? 가령 다음 그림 6의 두 곡면을 비교해보자. 
   

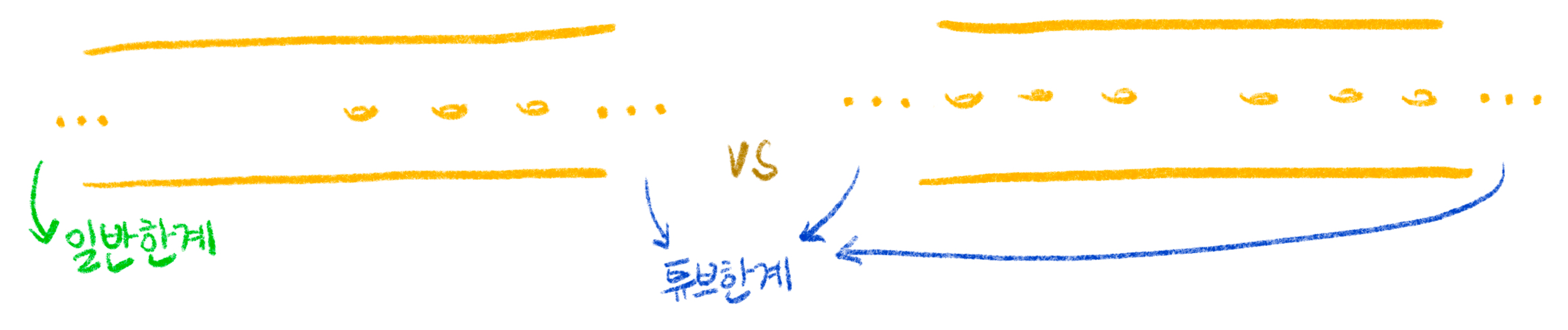
두 곡면 모두 각각 두 개의 한계를 갖는다. 하지만 왼쪽 곡면은 좌측으로 가다보면 어느 순간 튜브에 앉을 자리가 사라지는 반면, 오른쪽 곡면은 두 경계 모두 튜브의 앉을 자리가 무한히 제공되는 차이가 있다. 이처럼 한계에는 두 종류가 있다. 앉을 자리가 계속 제공되는 튜브한계와 앉을 자리가 어느 순간 제공되지 않는 일반한계. 이 두 종류의 한계를 구분하지 않으면 곡면을 정확하게 분류 할 수 없다. 여기서 바로 해볼 수 있는 관찰 하나는, 튜브한계가 존재하는 곡면은 \(\infty\)-인승이라는 것이다. 

자 그렇다면, 어떤 두 곡면이 서로 한계공간도 같고 튜브한계 공간끼리도 같다면 위상적으로 같은 곡면이 될까? 애석하게도 아니다. 예를 들어, 그림 7의 다음 두 곡면을 살펴보면, (종류를 무시한) 전체 한계공간이 같고, 그리고 튜브한계로 떼어 생각해보아도 두 곡면 모두 딱 한 개의 튜브한계를 갖고 있다. 
 

하지만 두 곡면은 위상적으로 서로 다른데, 왼쪽 곡면은 일반한계들이 축적되는 방향 또한 일반한계이나, 오른쪽 곡면은 튜브한계를 향해 일반한계들이 축적되고 있기 때문이다.

다시 말해, 튜브한계가 일반한계 안에 어떻게 자리 잡고 있는지, 그러니까 더 자세히 말하자면 한계공간 속 부분공간으로서 어떻게 위상적 공간으로 자리잡고 있는지에 대한 정보까지 정확하게 담아 내야 곡면을 분류 할 수 있다는 것이다. 자 이제 스무고개 놀이는 그만하고 무한곡면 분류 정리를 살펴보자:

정리 1.  두 곡면 \(S\)와 \(S’\)이 서로 위상동형일 필요충분조건은, \(S\)와 \(S’\)이 같은 종수를 갖고, 한계 공간 쌍 (전체 한계공간, 튜브한계공간)이 쌍으로서 위상동형¹ 인 것이다. 

즉 위 정리의 핵심은 종수, 한계 공간 쌍에 대한 정보가 곡면의 위상적 성질을 정확하고 충분하게 담아낸다는 것이다. 이는 사실 유한곡면 분류정리의 확장이라고도 볼 수 있다. 그 이유는 바로 뚫린 구멍이 일반한계에 대응 되기 때문이다. 유한 곡면은 유한인승이라 튜브한계가 없기 때문에 정리 1에 필요한 3개의 정보가 종수와 한계의 개수라는 2개의 유한한 숫자로 압축이 된다. 즉 같은 종수와 같은 한계의 개수를 가지는 유한곡면은 서로 위상동형이라는 결론을 얻게 된다. 그런데 여기서 한계의 개수가 곧 유한곡면의 뚫린 구멍의 개수와 같기 때문에 유한곡면의 분류정리를 다시 얻는다.

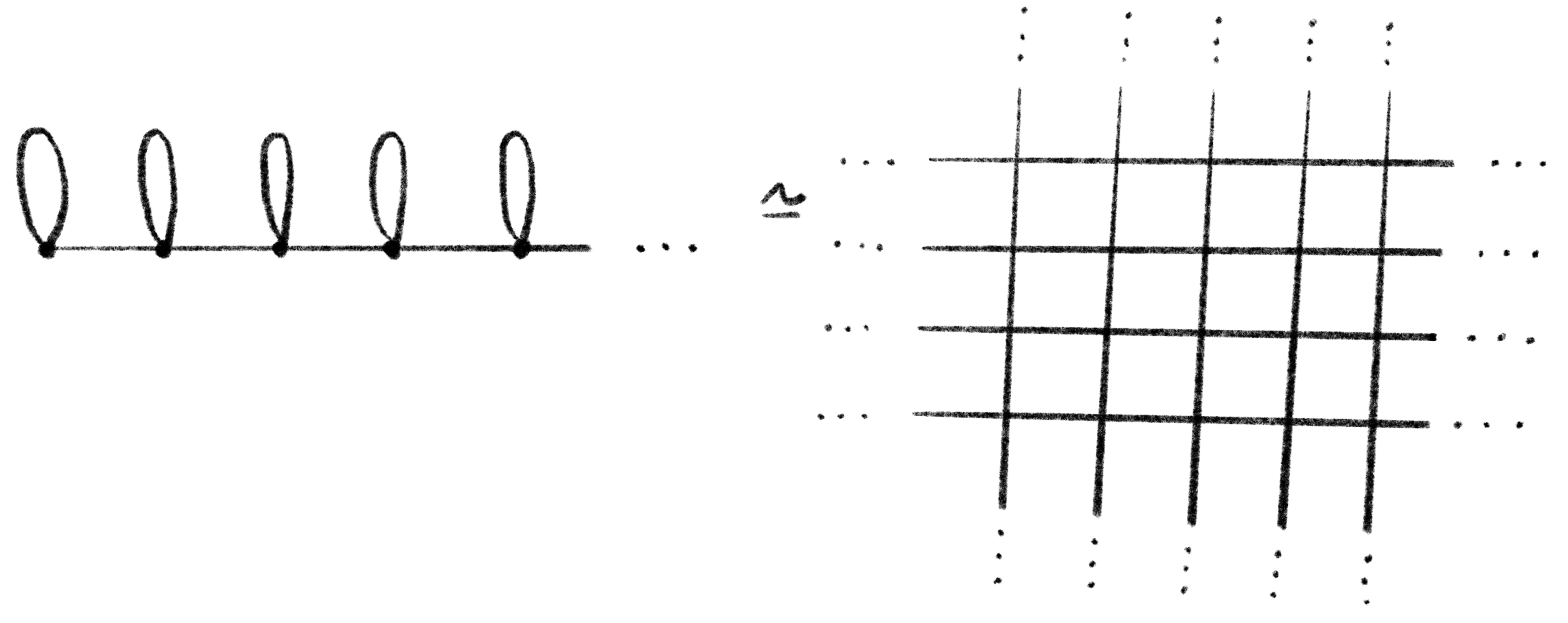
이 곡면의 분류정리가 얼마나 강력한지 하나의 알쏭달쏭한 예시를 통해 살펴보도록 하자. 다음 그림 8의 곡면들을 생각하자. 좌측은 네스호 괴물 곡면이고, 우측은 격자곡면으로서, 좌표 평면을 생각한 뒤 정수 점에 튜브와 같이 사람이 앉을 자리를 만들면 된다. 
 
  

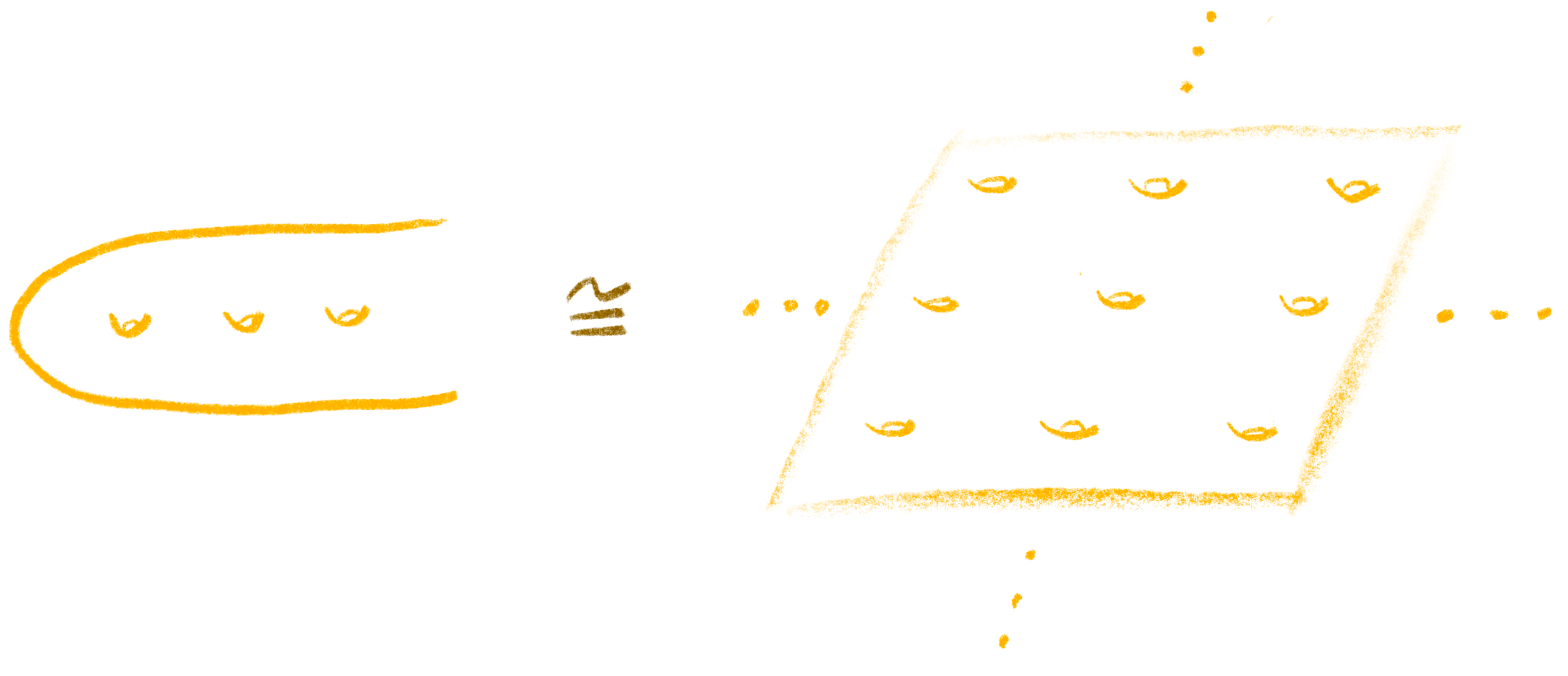
그렇다면 이 두 곡면 모두 \(\infty\)-인승인 곡면이 된다. 그렇다면 한계공간은 어떨까? 일단 네스호 괴물 곡면의 한계공간은 앞서 살펴 본 바와 같이 그냥 원소가 하나인 집합이 된다. 그렇다면 격자곡면의 한계공간은 어떨까? 한계공간의 정의는 무한으로 뻗어 나가는 방법의 수로 이해할 수 있다고 했지만, 여기서 더 엄밀한 정의의 유용함이 드러난다. 서두에서 밝힌 바와 같이 유한곡면을 잡고 그 유한곡면의 외부에 있는 무한곡면의 개수를 따져 보는 것이 한계공간의 정확한 정의이다. 그런데 오른쪽 격자곡면 같은 경우에는 어떠한 유한 부분곡면을 잡더라도 외부에 있는 무한곡면은 항상 하나만 존재한다. 따라서 오른쪽 곡면의 한계공간 역시 원소 한 개짜리 집합이 된다. 따라서, 정리 1에 의해서 결국 이 두 곡면은 서로 위상적으로 동형인 곡면이 된다. 이처럼, 분류정리는 두 곡면이 서로 같은지 다른지를 알아볼 때, 직관을 넘어서는 매우 유용한 정리이다.

다음은 이 곡면에 해당하는 대칭군에 대해서 잠시 살펴보도록 하자. 무한곡면 S의 사상류군은 유한곡면의 사상류군과 마찬가지로: 

\(\textrm{Map}(S):=\{S \to S \text{ 위상동형사상}\}/\text{연속변형}\)

으로 정의한다. 즉 정의가 유한곡면의 경우와 완전히 같다.

한편, 지난 연재 글 [7] 과 같이 위상동형사상 대신 연속변형동치 사상을 대칭으로 생각하여 곡면의 대칭군을 생각해 볼 수 있을 것이다. 하지만 이 경우에는 모든 무한곡면이 사실상 이파리가 (가산²)무한 개인 장미 그래프와 연속변형동치가 되므로, 무한곡면의 연속변형대칭 군은 단 하나, \(\textrm{Out}(F_\infty)\)로 굳어진다. 여기서 \(F_\infty\)는 차수가 (가산)무한인 자유군으로, [6] 에서 본 것 같이 이파리가 (가산) 무한개인 장미 그래프의 기본군이 된다. 수많은 곡면의 가짓수에 비해 생각보다 심심한 결과이니, 곡면의 대칭군은 사상류군으로 생각하기로 하자.


무한그래프

이번엔 무한그래프에 대해서 알아보자. 무한그래프라면 무한히 뻗은 나무, 또는 무한히 뻗어나가는 네비게이션 지도, 혹은 무한히 많은 사람들 사이의 친구관계를 나타낸 그림을 생각해볼 수 있겠다.

무한그래프는 사실 이제까지 보았던 무한곡면에 관한 논의를 그대로 따라가되, 그래프에 맞게 정의를 조금 수정해주면 된다. 예컨대 무한곡면에서는 일반한계와 튜브한계로 한계들을 구분 했다면, 무한그래프에서는 그림 9과 같이 일반한계와 루프한계로 구분하게 된다. 그리고 곡면에서처럼 종수를 세는 대신, 그 그래프의 “독립적인 루프”의 개수, 즉 기본군의 차수를 센다. 이를 간편히 그래프의 차수라고 부르도록 하자. 마찬가지로, 어떤 그래프가 루프한계를 가지려면 무한한 차수를 가져야 할 것이다.
 
 

아울러, 임의의 무한그래프를 모두 다루지는 않을 것이다. 대신, 

각 꼭짓점에 있는 변의 개수가 유한개인 그래프

만을 다룰 것이다. 이를 유한이웃 그래프라고 하고, 이런 그래프들은 국소적으로 항상 유한그래프로 나타낼 수 있어, 무한그래프 중 유한그래프와 가장 가까운 형태라고 할 수 있고 한계공간도 잘 정의된다. 유한이웃하지 않은 그래프로서, 다음의 무한그래프를 생각해보자. 
  

그림 10의 그래프는 한 꼭지점에 무한개의 변이 붙어 있다. 이 그래프 또한 한계공간을 생각할 수 있고, 직관적으로 중심에서 뻗어나가는 무한개의 반직선들이 한계공간의 원소를 이룰것이라 생각할 수 있다. 다만 문제는 무한성을 만드는 요소가 저 “바깥”방향 뿐 아니라, 내부의 점 주위에도 생겨서, 유한그래프로 근사하여 연구하고자 할 때 더 복잡해지게 된다. 이러한 근사의 까다로운 점을 피하기 위하여 우리는 유한이웃한 무한그래프만 살펴보도록 하자. 

그러면 유한이웃 무한그래프의 대칭군을 생각할 땐 이 유한이웃성을 잘 보존 하는 대칭이 무엇인지를 생각해 보아야 한다. 물론 위상동형은 이 유한이웃성을 잘 보존 하지만, 지난 1편의 글 [6] 에서와 같이 위상동형은 그래프에서 고려했을 때 너무 딱딱한 대칭이라고 관찰한 바 있다. 그래서 적당히 말랑한 대안으로 고려했던 것이 연속변형동치인데, 문제는 연속변형동치만으로는 이 유한이웃성을 유지할 수 없다는 것이다. 가령 다음 그림 11의 예시를 보자. 
   

그림 11의 왼쪽 그래프는 실수 수직선에서 시작하여, 그 직선의 정수점에 또 다른 반직선 들이 매달려있는 형태이다. 각 꼭짓점에 닿아있는 변의 개수가 2개 또는 3개이므로, 유한이웃성을 가짐을 관찰할 수 있다. 이 수직선을 점으로 줄이는 과정은 연속변형동치에 해당하며, 그 결과가 오른쪽 그래프이다. 하지만 이 그래프는 더 이상 유한이웃성을 갖고있지 않다. 따라서 유한이웃성은 일반적인 연속변형동치에 의해 보존되는 성질이 아니다. 그래서 우리는 연속변형동치 중 유한이웃성을 보존하는, 적합한³ 연속변형동치들만을 고려하기로 한다. 이 적합한 연속변형동치를 기준으로 유한이웃 무한그래프를 분류한 것이 바로 다음의 아얄라-도밍게즈-말케즈-킨테로⁴ 의 무한그래프 분류정리이다. 

정리 2 ([2]). 두 유한이웃 무한그래프 \(G\)와 \(G’\)가 서로 적합한 연속변형동치로 같을 필요충분조건은, 두 그래프의 차수가 갖고 두 그래프의 한계공간 쌍 (전체 한계공간, 루프한계공간) 이 서로 위상동형인 것이다. 

무한곡면에서 논의 했던 것처럼, 정리 2를 이용하면 다음의 두 무한그래프들이 적합한 연속변형동치로 같다는 것을 보일 수 있다.
   

이 정리 2와 우리가 했던 관찰들에 따르면, 결국 어떤 유한이웃 무한그래프 $G$의 대칭군은, 알곰-크피르와 베스트비나⁵의 논문 [1] 에서 제시한 것처럼 다음과 같이 정의하는 것이 바람직해 보인다: 

\(\textrm{Map}(G):= \{G \to G \text{ 적합한 연속변형동치}\}/\text{적합한 연속변형}\)

여기서 적합한 연속변형이란 연속변형과정에서 나오는 사상들이 적합성을 유지하는 연속변형을 말한다.


무한그래프와 무한곡면
: 덴-닐슨-베어정리?

무한곡면과 무한그래프는 많이 닮아 있다. 그렇다면 무한곡면과 무한그래프의 대칭군 사이에는 어떤 관계가 있을까? 가령 [7] 의 유한한 경우에서 보았던 것처럼 덴-닐슨-베어 정리가 존재할까? 즉, 무한곡면 \(S\)에 대응하는 어떤 그래프 \(G\)가 있어서 자연스러운 사상 \(\textrm{Map}(S) \to \textrm{Map}(G)\)을 만들 수 있을까? 유한곡면에서의 논의를 그대로 따라가면 일단 무한곡면의 (위상동형)사상류군 \(\textrm{Map}(S)\)에서 무한곡면의 연속변형대칭 사상군으로 가는 사상을 찾을 수는 있다. 하지만 앞서 관찰한 바와 같이, 무한곡면의 연속변형대칭 사상군은 곡면의 종류에 관계없이 모두 \(\textrm{Out}(F_\infty)\)가 나오게 된다. 

그렇다면 조금 더 본질적으로 무한곡면의 대칭군과 무한그래프의 대칭군을 이어주는 사상은 없는 것일까? 모든 무한곡면에 대해서는 아직 밝혀지지 않았지만, 만일 곡면에 무한히 많은 “도려낸 구멍”을 허용하면, 그래프와 적합한 연속변형동치로 같은 곡면들을 완전히 분류 할 수 있게 된다. 이러한 그래프-곡면 쌍에 대해서는 곡면의 대칭군에서 그래프의 대칭군으로 가는 사상을 잡을 수 있음이 알려져 있다([4].)


: 강직성

한편 이런 생각을 해 볼 수 있다. 이렇게나 많은 종류의 곡면들이 있는데, 이 곡면의 대칭군들은 서로 다 다를까? 다시 말해, 어떤 곡면의 대칭군만 보고서 그 곡면을 알아맞힐 수 있을까? 이러한 종류의 문제를 수학에서는 강직성 문제라고 부른다. 유한곡면과 무한곡면의 사상류군은 강직성을 가짐이 알려져 있다. 즉, 주어진 두 (유한/무한) 곡면에 대해 그들의 사상류군이 동형이면, 그 곡면들은 서로 위상동형이어야 한다.

하지만 그래프는 어떨까? 일단 유한그래프는 강직성이 성립한다. [6] 에서 논의했던 것처럼, 유한그래프의 대칭군은 유한차수 자유군의 외부 자기동형사상군, \(\textrm{Out}(F_n)\)이었다는 것을 기억하자. 즉, 두 그래프 \(G,G’\)을 가져와서 그들의 차수가 각각 \(n\)과 \(m\) 이라고 할 때, 따라서 두 그래프의 대칭군이 동형이라는 것은

\(\textrm{Out}(F_n)\)과 \(\textrm{Out}(F_m)\)이 동형

이라는 말이 된다. 그런데 컬러와 보흐만⁶의 논문 [3] 에 따르면 \(\textrm{Out}(F_n)\)은 \(n\)이 달라짐에 따라 서로 다 다른 군이 된다는 것이 알려져 있다. 따라서, 위 동형사상은 곧 \(n=m\)을 시사한다. 그런데 또 [6] 에서 임의의 유한그래프는 그것의 생성나무를 통해서, 차수만큼의 잎이 있는 장미그래프와 연속변형동치임을 보였었다. 마침 \(n=m\)이니, \(G\)와 \(G’\)는 같은 이파리 개수의 장미그래프로 연속변형동치가 가능하고 따라서 그 공통의 장미그래프를 거치면 \(G\)와 \(G’\)은 서로 연속변형동치로 같게 된다. 다시 말해, 유한그래프의 대칭군은 강직성을 갖는다.

그렇다면 무한그래프는 어떨까? 놀랍게도 무한그래프의 대칭군은 강직성이 성립하지 않는다. 즉, 서로 다른 두 무한그래프들이 동형인 대칭군을 갖는 경우가 존재한다.

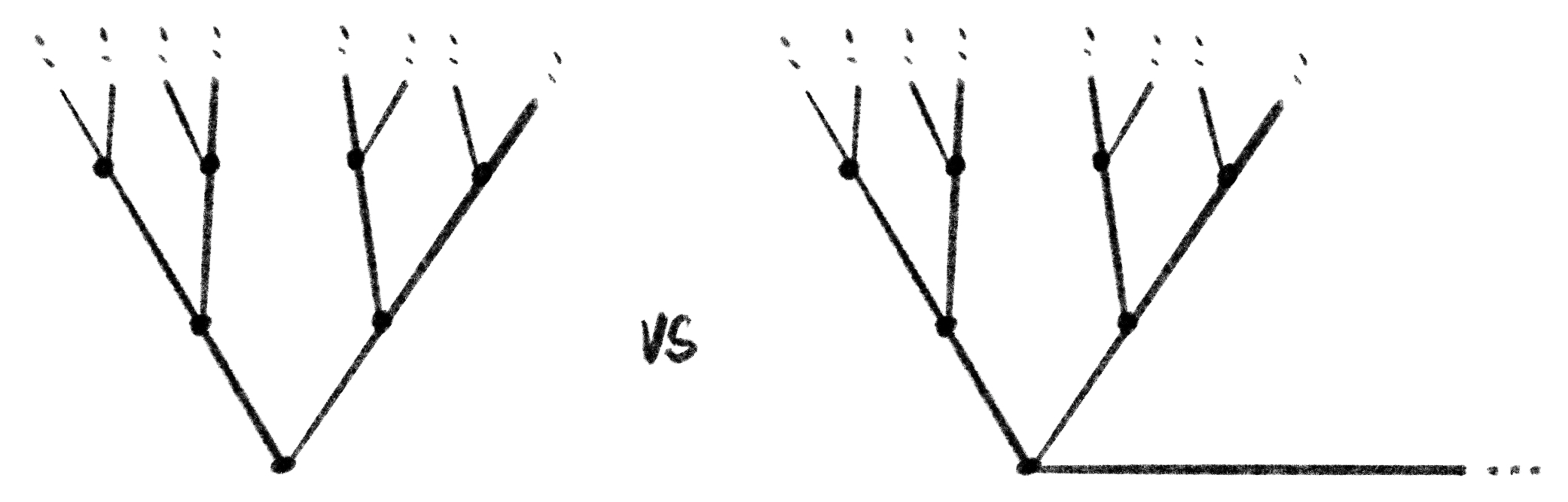
이 반례를 자세히 살펴보도록 하자. 그림 13을 보자.  
  

왼쪽의 그래프는 칸토어 나무이고 다른 하나의 그래프는 “밧줄달린” 칸토어 나무로서, 하나의 반직선이 칸토어 나무에 추가로 붙은 형태이다. 두 그래프의 한계공간이 서로 다르기 때문에, 정리 2에 의해 두 그래프는 적합한 연속변형동치로 다른 그래프임을 알 수 있다. 하지만 그들의 대칭군은 모두 칸토어 집합 \(\mathcal{C}\)의 위상동형사상군⁷ \(\textrm{Homeo}(\mathcal{C})\)로 같게 된다. 왜인지 살펴보자. 일반적으로, 어떤 그래프 \(T\)가 나무인 경우(즉 차수가 0인 경우)에는 그 대칭군이 그 나무의 한계공간 \(E(T)\)의 위상동형 사상군 \(\textrm{Homeo}(E(T))\)가 된다. 그림 13의 첫 번째 그래프의 한계공간은 칸토어 집합 \(\mathcal{C}\)이고, 두 번째 그래프의 한계공간은 칸토어 집합에 하나의 외딴 점을 넣은 \(\mathcal{C} \cup \{\ast\}\)이 된다. 그런데 \(\mathcal{C} \cup \{\ast\}\)의 자기위상동형사상은 이 외딴 점 \(\ast\)를 자기자신으로 보낼 수 밖에 없어서, 결국 이 집합에서 외딴 점을 삭제한 C의 위상동형 사상으로 볼 수 있게 된다. 이는 곧 

\(\textrm{Homeo}(\mathcal{C})\)와  \(\textrm{Homeo}(\mathcal{C} \cup \{\ast\})\)이 서로 동형

임을 의미하게 된다. 따라서 우리는 어떤 서로 다른 그래프가 같은 대칭군을 갖는 것을 확인했으니, 이것이 무한그래프의 대칭군의 강직성에 대한 반례가 된다.


그래프와 곡면의 동상이몽

그래프와 곡면은 서로 매우 닮아있는 것으로 보인다. 어떤 곡면을 보면 그에 대응하는 그래프를 상상해 볼 수 있고, 어떤 그래프를 보면 반대로 그에 대응하는 곡면을 상상해 볼 수 있다. 그 외관적 유사성(同像⁸) 때문에 그 둘 사이의 이론도 실제로 비슷한 점이 많다. 하지만 그 둘은 이따금 놀라운 차이점(異夢⁹)들을 보여주곤 한다. 가령 바로 앞에서 언급한 강직성 문제처럼 말이다.

지난번 연재 [7] 에서 밝혔던 것 같이 그래프와 곡면 사이에는 모종의 사전이 존재함을 연구자들이 믿고 있다. 마치 우리가 한글과 영어를 서로 번역 할 때 그 둘을 완벽하게 번역할 수 없는 것처럼, 그 사전은 매우 불완전하다. 실제로, 곡면의 세계와 그래프의 세계는 서로 닮은 듯 보이지만 그들의 대칭군의 구조를 깊이 파헤쳐나가면 다른 부분이 많다. 그래프와 곡면을 함께 공부하는 기하군론 학자로서 느끼는 즐거움은, 바로 익숙한 것에서 다름을 발견하고 낯선 것에서 익숙함을 발견하는 것이다. 그리고 그래프와 곡면 각각의 세계 안에서 유한한 경우와 무한한 경우의 공통점과 차이점을 보는 것도 재미있다. 우리가 무한을 이해하려 할 때 그것을 유한한 것들로 근사를 시키곤 하지만, 때로는 그 유한한 경우들에 대한 정보들로 무한한 경우를 설명할 수 없는 경우가 있고, 사실은 이러한 부분이 무한곡면과 무한그래프 연구의 의미에 무게를 실어주는 지점들이다. 

지금까지 세 번의 연재를 통해 그래프와 곡면, 그리고 이들이 유한한 경우와 무한한 경우에서 각각 어떤 대칭군을 가지는지 살펴보았다. 필자는 특히 무한한 경우에 관심이 많은데, 이는 기하군론 내에서도 최근 젊은 연구자들이 많이 유입될 만큼 활발히 연구되고 있는 분야이기도 하다. 우리는 유한한 땅을 밟으며 유한한 시간을 살아가지만, 그럼에도 불구하고 무한한 세계를 꿈꾸고 동경할 자유가 있다는 사실을 기억했으면 좋겠다. 

“If I find in myself desires which nothing in this world can satisfy, the only logical explanation is that I was made for another world.”
— C.S. Lewis [5]