성서 다음으로 가장 많이 인쇄된 책이 무엇일까요? 기원전 300년경 유클리드Euclid가 집필한 수학책 “원론”이 바로 그 주인공입니다. 원론은 알렉산드리아를 중심으로 당시 헬라스 세계의 기하학적인 지식을 엮어 총 13권으로 구성되었습니다.1 유클리드 이전에도 몇몇 그리스 수학자들이 원론과 비슷한 방식의 책을 펴낸 것으로 알려졌지만 대부분 소실되었고, 원론만이 전해지고 있습니다. 오늘날까지 전수된 대부분의 고대 지식이 그렇듯 원론은 오랜 시간 가장 중요한 수학 교과서로 애용됐습니다. 그래서 이 책에는 성서 다음으로 가장 많이 인쇄된 책, 뉴턴의 프린키피아 구성에 모델이 된 책, 인류의 기하학적인 지식을 2천 년 가까운 시간 동안 거의 독점적으로 제공한 책과 같은 화려한 수식어들이 따릅니다.
그러나 성서의 원본이 남아 있지 않듯 원론의 원본도 남아 있지 않습니다. 기원후 1-2세기경의 몇몇 파피루스 조각들과 기원후 5-6세기 경의 아주 짧은 단편을 제외하면, 현재 옥스포드대학 보들레이언 도서관이 소장하고 있는 888년경 만들어진 양피지 코덱스MS. D’Orville 301가 유클리드 원론의 가장 오래된 사본입니다. 원본과 무려 천 년이 넘는 시차가 있는 셈입니다.
오늘날 우리가 원론을 읽을 수 있게 된 것은 19세기 말 덴마크의 고전학자 하이베르그Johan Ludvig Heiberg, 1854-1928의 입지전적 노력 덕분입니다. 하이베르그는 그리스어 필사본들을 비교 대조하여 유클리드 원론뿐 아니라 그리스 수학자들이 저술한 대다수 주요 저서들의 원본과 가장 유사한 것으로 추정되는 결정판critical edition을 내놓았습니다. 현대어로 번역된 그리스 수학의 주요 저서들 대부분이 하이베르그에게 큰 빚을 지고 있는 셈입니다. 하지만 애석하게도 하이베르그는 글의 복원에 집중하였을 뿐 원본에 수록되었을 그림의 본래 모습을 찾으려 애쓰지는 않았습니다. 대신 하이베르그는 글에 대한 이해를 돕기 위해 그가 살았던 시대의 기준에 따라 그림을 재구성하였습니다. 그 결과 오늘날 현대어 번역본의 그림에는 2천 년이 넘는 기하학의 역사에서 일어났던 여러 변화가 반영되어 있지 않습니다.
그러나 그리스어, 아랍어, 라틴어 등으로 쓰인 수백 개가 넘는 필사본을 관찰해보면 원론의 그림이 다양하게 변화해왔으며, 그러므로 그림 또한 역사 연구의 대상이 될 수 있음을 알 수 있습니다. 저는 그림의 역사에 관한 연구를 통해 인류가 글이라는 수단뿐 아니라 그림이라는 시각적 수단을 활용해 어떻게 지식을 창조하고 전수하였는지 연구하고 있습니다. 이번 연재 글에서는 제가 하고 있는 연구 중 하나인 유클리드 원론의 인쇄본들에서 볼 수 있는 그림의 변화를 소개하고자 합니다.
루카 파치올리와 제자의 초상
제가 좋아하는 그림에서부터 이야기를 풀어볼까 합니다. 그림에서 수사복을 입은 중앙의 인물은 프란체스코회 수사였던 루카 파치올리Luca Pacioli c.1447-1517로 알려져 있습니다. 파치올리 옆에 서 있는 청년이 누구인지는 정확히 밝혀지지 않았지만, 미술사가들은 그가 파치올리의 제자일 가능성이 높다고 보고 있습니다. 그래서 이 그림에는 <루카 파치올리와 제자의 초상 Portrait of Luca Pacioli and Disciple>이라는 제목이 붙었습니다.
그림에서 파치올리는 오른손으로 유클리드라고 적힌 서판 위에 도형을 그리고 있고 왼손으로 유클리드 원론의 한 정리를 짚고 있습니다. 아마도 13권에 있는 명제일 가능성이 높습니다. 그 옆에 파치올리 자신이 저술한 산술서 <Summa de Arithmetica>는 펼치지 않은 채로 놓여있어 원론과 대비를 이룹니다. 더불어 천장에 매달린 투명한 입체 모형이 그림에 기하학적인 색채를 더합니다.
그러나 이 그림이 더욱 흥미로운 이유는 하단의 도구들 때문입니다. 하단의 도구들은 파치올리와 제자를 향하지 않는 대신 이 그림을 마주하게 될 사람을 향해 놓여 있어, 마치 당신도 “나처럼” 당신만의 도형을 직접 그려보라고 초대하고 있는 것처럼 보입니다.
이러한 초대는 파치올리가 활동했던 16세기 초엽부터 원론의 그림에 일어난 많은 변화를 예고하는 것이기도 합니다. 유클리드 원론의 첫 번째 인쇄본은 1482년 랏돌트Erhard Ratdolt가 베니스에서 만들었습니다. 하지만 랏돌트가 제작한 인쇄본 속 그림들은 기존 라틴어 필사본들에서 제시된 그림들과 거의 유사했습니다. 14세기부터 크게 유행했던 노바라의 캄파누스Campanus of Novara 라틴어 필사본들이 첫 인쇄본을 위한 훌륭한 저본底本 역할을 했기 때문입니다. 그는 손으로 그렸던 그림들을 목판이나 동판을 활용해 복제 생산하는 기술적인 발전에 더 많은 관심을 쏟았습니다.
16세기에 나타난 변화
그러나 초기 간행본incunabula의 시기를 지나 16세기에 접어들자, 필사본과는 비할 수 없이 저렴해진 인쇄판 원론이 등장해 기하학적인 지식이 필요한 곳으로 구석구석 퍼져나갔습니다. 이러한 변화는 원론의 그림을 변화시키는 결과를 낳게 되었습니다. 원론은 더 이상 수도원의 케케묵은 고문서실 안에만 갇힌 책도 아니고, 소수의 특권을 가진 사람들만이 접근할 수 있는 책도 아니게 되었습니다.
인쇄판 원론이 필사본보다 더 많은 사람에게 퍼져나간 것은 크게 두 측면에서 두드러집니다. 첫째 원론을 실용적으로 적용한 다양한 분야의 장인들이 원론을 읽게 되었고, 둘째 원론의 연역체계를 통해 논리적 훈련을 한 유럽의 대학생들이 원론을 읽게 되었습니다. 예를 들어, 알브레히트 뒤러Albrecht Dürer 1471-1528는 뉘른베르크와 베네치아에서 접했던 원론을 바탕으로 화가, 대장장이, 채석공, 조각가, 목수 등 측정기술을 필요로 한 대부분의 장인을 위한 일종의 실용 기하학 책Underweysung der messung mit dem zirckel un richt scheyt 1525을 펴냅니다. 즉 원론이 수학자뿐만 아니라 미술, 건축, 공예를 비롯한 여러 분야의 장인들을 위한 기하학 책으로 확대된 것입니다. 또한 옥스포드대학을 비롯한 초기의 유럽 대학들에서는 원론의 13권 중 평면기하를 주로 다루는 1~6권의 내용을 가르치는 경우가 많았고, 학생들도 졸업을 위해 최소한 1권의 내용을 숙지하는 시험을 통과해야 했던 것으로 알려져 있습니다.
이렇듯 이전보다 원론에 대한 독자의 수준과 관심사가 다양해지자, 원론의 편집자들은 독자의 여러 요구와 필요를 충족시키기 위해, 오랫동안 큰 변화 없이 반복적으로 필사해온 그림을 변형시키기 시작하였습니다. 이 변화의 양상은 크게 두 가지 측면으로 요약해 볼 수 있습니다. 첫째는 컴퍼스를 비롯한 도구의 사용이 더 빈번해졌다는 것이고, 둘째는 점선을 비롯한 여러 보조표시visual auxiliaries가 도입되었다는 점입니다. 이 두 가지 변화를 제대로 감상하기 위해서는 라틴어 필사본들에서 제시되었던 원론의 그림과 인쇄본들에서 제시된 그림을 비교해 보는 것이 좋겠습니다.
컴퍼스와 자를 이용한 작도
필사본에서는 컴퍼스를 쓴다고 직접적으로 명시된 적이 없었습니다. 필사본에 등장하는 원이 매끄럽게 그려졌고 직선은 반듯하게 그려졌다는 점을 고려할 때, 이를 그리기 위해 컴퍼스와 자가 동원되었을 것이라고 짐작해볼 수는 있습니다. 그러나 필사본의 그림을 그렸던 제작자들은 이처럼 도구를 활용해 쉽고 효과적으로 작도하는 방법을 소개한 적이 없습니다. 대부분의 그림은 선행적으로 소개된 기하학적 지식에서부터 연역적으로 도출된 가상의 작도를 통해 만들어진 것처럼 제시되었습니다.
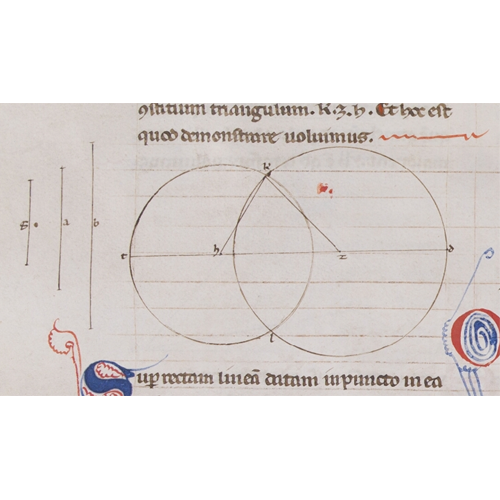
원론 1권의 22번째 명제는 이 점을 잘 보여줍니다. 22번째 명제는 세 선분이 주어졌을 때, 세 선분을 변으로 갖는 삼각형을 작도하는 문제를 다루고 있습니다. 물론 세 선분의 길이가 삼각부등식을 만족해야 한다는 점이 선결조건으로 제시되어 있습니다. 그리스어 필사본에서부터 라틴어 필사본에 이르기까지 대부분의 필사본에서 소개하는 방법을 요약하면 다음과 같습니다.
- 반직선을 세 선분에 상응하게 분할합니다.
- 두 번째 선분의 왼쪽 끝점을 중심으로 첫 번째 선분을 반지름으로 갖는 원을 그립니다.
- 두 번째 선분의 오른쪽 끝점을 중심으로 세 번째 선분을 반지름으로 갖는 원을 그립니다.
- 삼각부등식에 따라 이 두 원은 서로 만나게 되는데 그중 하나의 교점을 두 원의 중심과 연결하면 우리가 원했던 삼각형을 얻는다.
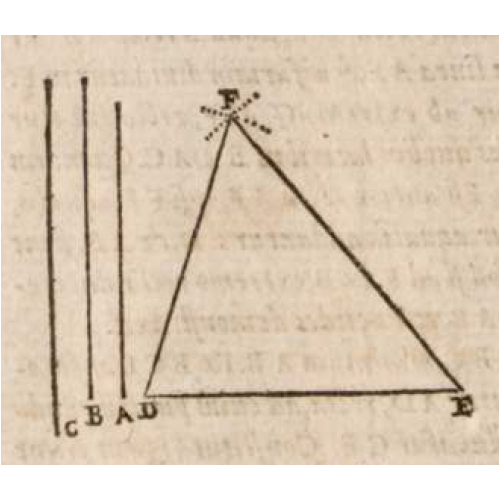
이 작업을 위해 필요한 모든 작도 행위는 철저히 22번째 명제 이전까지 소개된 정의, 공리, 공준 그리고 21개의 명제에만 기반을 둡니다. 따라서 이 삼각형의 작도는 원론의 연역체계 안에 기반을 둔 지식 중심의 작도로 볼 수 있습니다. 그에 반해 16세기 초엽의 인쇄본들은 새로운 그림을 제시하기 시작합니다. 이 그림은 연역체계에 속박되지 않고 컴퍼스를 이용한 더욱 쉽고 효과적인, 오늘날 중학교에서 배울 법한 방법에 따라 소개됩니다.
- 컴퍼스를 이용하여 두 번째 선분의 길이를 복제하여 다시 그립니다.
- 이 복제된 선분의 왼쪽 끝점에서 컴퍼스를 사용해 첫 번째 선분의 길이를 복제하여 짧은 호를 그립니다.
- 다시 이 복제된 선분의 오른쪽 끝점에서 컴퍼스를 사용해 세 번째 선분의 길이를 복제하여 짧은 호를 그립니다.
- 그 결과 원했던 삼각형을 얻게 됩니다.
컴퍼스의 반복적인 사용에서 알 수 있듯 이때 삼각형의 작도는 도구 중심의 작도로 변화하였습니다. 컴퍼스를 사용하는 과정에서 복제해야 할 길이가 좁혀지거나 늘어나지 않고 동일하게 유지된다고 할 때, 이제 기하학에 조예가 깊지 않은 누구라도 쉽게 도형을 작도할 기회를 얻게 된 셈입니다.
인쇄본의 그림들이 더욱 많은 보조표시를 갖게 되었다는 점도 주목할만한 변화입니다. 보조표시의 대표적인 예로 점선과 상응 표식correspondence markers을 들 수 있습니다.
필사본에서는 도형을 표현하기 위해 점선이 사용된 사례가 없었습니다. 오늘날 우리는 흔히 입체도형을 그릴 때 보이지 않는 부분을 표현하기 위해 점선을 사용하지만, 유클리드의 원론에서 이러한 용례는 적어도 17세기에 이르러서야 발견됩니다. 필사본 전통에서는 입체를 표현하기 위해 대게 점선을 사용하는 대신 입체를 펼쳐서 묘사하는 방식이 사용되었습니다. 이를테면 구를 표현할 때 점선을 사용해 입체감을 부여하는 대신 앞면과 뒷면을 붙여서 8자의 형태로 도형을 제시하는 것이지요. 16-17세기의 인쇄본들에서 사용된 점선은 입체를 표현하기 위한 목적뿐만 아니라 실선과의 차별을 통해 더욱 다양한 논의를 전개하기 위해 사용되었습니다. 예를 들어 아래 그림에서와 같이 두 변이 일직선에 놓여있음을 표현하기 위해 혹은 귀납법적 가정의 상황을 묘사하기 위해 점선이 사용되었습니다.
점선의 도입과 더불어 동일한 크기의 선분이나 각의 상응 관계를 표시하는 표식들도 원론의 필사본보다는 인쇄본에서 더욱 자주 발견할 수 있습니다. 오늘날 우리가 평행한 두 직선에서 엇각이나 동위각의 합동 관계를 표현하기 위해 흔히 사용하는 각 표시들도 원론의 초기 인쇄본의 유산이라고 볼 수 있습니다.
글에서 독립한 그림
결론적으로 이러한 그림의 변화가 지향하는 바는 연역적인 그림에서 개별적인 그림으로, 글에 의존적인 그림에서 자기충족적인 그림으로의 전환입니다. 이로 인해 원론을 읽는 방식에도 변화가 생기게 됩니다.
원론의 궁극적인 가치는 연역체계 안에서 정의와 공리와 공준2 등의 기본원칙을 토대로 기하학적인 지식을 쌓았다는 점입니다. 따라서 원론은 처음부터 순서를 따라 읽도록 설계된 셈입니다. 그림 또한 연역체계를 바탕으로 제시됐습니다. 그러나 도구를 활용하여 도형을 작도하기 시작한 이후, 그림은 연역체계로부터 분리되어 개별적으로 존립할 수 있게 되었습니다. 덕분에 독자들이 필요한 부분만 발췌해서 읽는 것이 가능해졌습니다. 16세기 후반 예수회 소속이었던 클라비우스Christopher Clavius 1538-1612의 원론에서 필요한 부분을 발췌해서 읽는 독해를 돕기 위해 목차와 색인 그리고 참고 명제 표시와 같은 여러 편의장치를 도입한 것이 그 예입니다. 이제 원론은 기하학적 지식의 저장고일 뿐 아니라 기하학적 지식의 사전이라는 성격도 동시에 갖게 됩니다.
또한 그림에 도입된 여러 보조장치는 독자로 하여금 텍스트를 읽지 않고도 그림으로부터 가능한 많은 기하학적 정보를 도출해내는 독해를 가능하게 하였습니다. 오랫동안 원론 안에서 그림은 글의 시각적인 보조에 불과했습니다. 그래서 중세의 원론 필사본 중에는 그림을 생략한 축약본이 상당수 만들어졌습니다. 그러나 그림이 점선을 비롯한 여러 장치를 갖추면서부터, 완벽하지는 않더라도 그림이 어느 정도 스스로를 설명할 수 있는 자격을 갖추게 되었습니다. 독자들은 원론에서 글을 읽는 것보다 그림으로부터 더욱 직관적이고 효과적으로 기하학적인 정보를 읽어낼 수 있게 되었습니다. 오늘날 학생들이 기하학 문제를 풀 때, 도형에 대한 설명을 거의 제대로 읽지 않고 그림만 이용해서 문제를 풀다가 틀리는 것도 궁극적으로 그림이 기하학적인 정보들을 거의 완비하고 있다고 믿게 된 이러한 변화에 기인합니다. 그림이 글이라는 대변인을 거칠 필요 없이 스스로 이야기를 시작한 셈입니다.
저는 이 흐름을 2300년에 걸친 원론의 역사 속에서 시각적 지식visual knowledge이 문자적 지식textual knowledge으로부터 (완전히 분리되지는 않더라도) 독립하기 시작하는 중요한 지점으로 보고 연구를 진행하고 있습니다. 다음 글에서는 원론의 필사본 전통으로 거슬러 올라가 글의 번역이 그림의 번역에 어떤 영향을 미치게 되었는지를 다루어 보고자 합니다. 그림은 번역의 대상인가? 그렇다면 그림의 번역은 어떤 층위들 속에서 이루어지는가? 등이 핵심적인 질문이 될 것입니다.