이전 글 “유클리드 원론 속 그림의 역사 [2]: 그림을 어떻게 번역할 것인가?”에서 우리는 원론의 그림들이 번역되는 여러 양상을 살펴보았습니다. 원론의 번역가들이 그림의 번역을 놓고 고민한 것 못지않게, 세대를 이어 원론을 전달해야 했던 필사가들도 그림을 베끼는 데 있어 독특한 문제에 직면하게 됐습니다. 이번 글에서는 번역이라는 요소가 도입되기 전 그림들이 어떻게 전수되어 왔는지를 살펴보려고 합니다.
먼저 이 글에서 다룰 그리스어 필사본들에 대해 간략히 소개할 필요가 있겠습니다. 비잔틴제국의 필사가들이 원론의 기하학적 지식을 보존하기 위해 사본들을 만들어 둔 덕분에 오늘날 그리스어 필사본들이 남아있을 수 있었습니다. 만일 고대 그리스 세계의 지식을 수집하고 보존하려 했던 비잔틴 제국의 각고의 노력이 없었다면, 유클리드의 원론뿐 아니라 고대 그리스의 수많은 고전들 중 상당 부분이 소실되었을 것입니다. 그만큼 비잔틴 시기의 필사본들은 고대 그리스 세계의 지식 전수에 있어서 중대한 역할을 했습니다. 물론 그 이후로도 계속해서 그리스어 사본들이 만들어졌지만, 우리가 원론의 역사에서 특별히 주목해야 할 것은 원론을 복원하는 데 결정적인 역할을 한 여섯 개의 사본입니다. 이 사본들은 대략 9-12세기 사이의 시기에 필사되었고, 현재 각각 바티칸, 옥스포드, 피렌체, 볼로냐, 파리, 비엔나의 도서관에 소장되어 있습니다.
19세기 말 고전문헌학자 하이베르그J. L. Heiberg는 이 여섯 개의 사본을 중심으로 여러 그리스어 필사본들을 비교하여, 지금은 소실되고 없는 유클리드 원론을 복원해 나갔습니다. 하지만 그가 복원작업에 그림들을 포함시키지 않았기 때문에 필사본들의 그림을 서로 비교하는 연구는 최근에 와서야 시작되고 있습니다.1 물론 하이베르그가 필사본들의 그림을 비교하는 작업을 생략한 것에 대해 변론할 여지도 있습니다. 아마도 그리스어 필사본들에서 제시된 그림들이 근대 이후 기하학에 등장한 그림들과는 사뭇 차이가 있었기 때문일 것입니다. 오늘날 우리가 기하학의 그림이라면 혹은 더 흔히 부르는 말로 도형이라면 응당 이러해야 한다고 기대하는 바를 필사본들의 그림들이 충족시키지 못한 탓입니다.
이 지점에서 우리가 물어야 할 질문은 간단해집니다. “그리스어 필사본들 속 도형의 독특한 면모는 필사 과정의 단순한 실수 때문인가 아니면 어떤 의도를 반영한 결과인가?” 이 질문을 염두에 두고 여섯 개의 주요 그리스어 필사본들 속 그림의 특징을 살펴보기로 하겠습니다.2
그리스어 필사본에서 가장 먼저 눈에 띄는 특징은 측도적 정확성이 결여된 도형들이 상당수 등장한다는 점입니다. 원론을 비롯한 고대 그리스 기하학에서는 변의 길이나 각의 크기를 사용해 넓이나 부피를 구하는 문제를 거의 다루지 않았습니다. 고대 그리스 기하학자들은 도형에 구체적인 수치정보를 부여하는 대신에 도형 간의 상응 관계를 밝히는데 더 많은 관심을 쏟았습니다. 이런 상황에서 그리스 기하학에서 측도적 정확성이란 대개 길이 얼마짜리 변을 실제로 그 길이에 맞게 그렸는가를 말하는 것이 아니라, 도형 A와 도형 B가 서로 크기가 상응하도록 그려졌는가를 의미합니다.
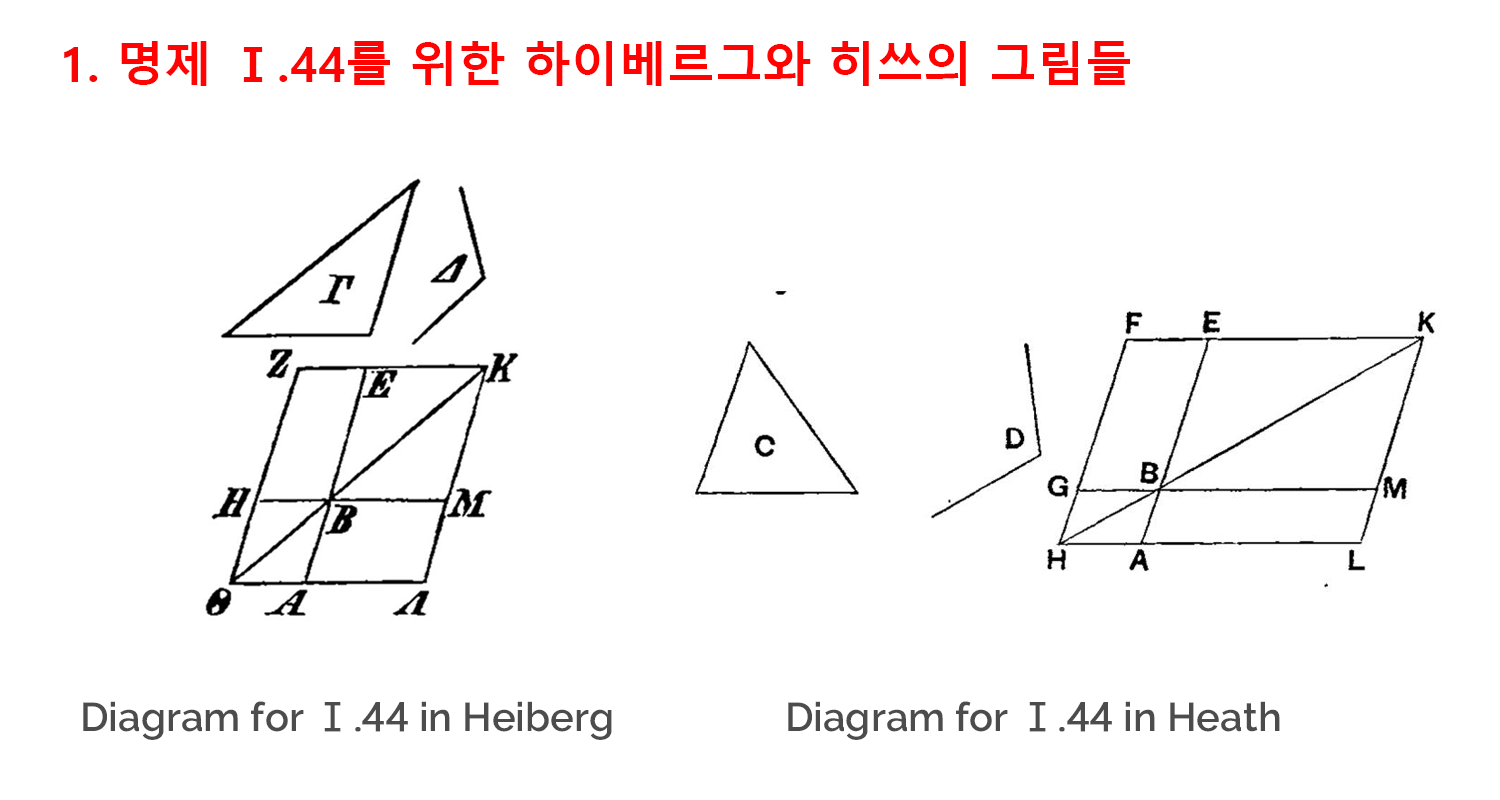
이 점을 가장 잘 드러내는 예는 소위 “넓이의 적용application of areas“이라는 아이디어를 담고 있는 1권의 44번 명제입니다. 이 명제에서 다루는 과제는 주어진 삼각형 C 와 같은 크기를 갖는 평행사변형 BALM을 주어진 선분AB 위에서 주어진 각 D를 통해 만드는 작업입니다.[1] 원론에서 제시하는 작도의 과정을 요약해 보면 다음과 같습니다.
- 주어진 삼각형 C와 같은 크기를 갖는 평행사변형 BEFG를 주어진 각과 같은 각 GBE를 통해 작도합니다(명제 I.42).
- 이때 선분 BE가 주어진 선분 AB의 연장선에 놓이게 합니다.
- 변 FG를 선분 AH가 변 BG나 변 EF와 평행할 수 있도록 점 H까지 연장합니다(명제 I.31).
- 점 H와 점 B를 연결하면, 각 BHG와 각 GFE의 합은 두 직각보다 작기 때문에 HB와 FE는 점 K에서 만나게 됩니다(공준 5: 평행선 공준).
- 선분 KL를 변 EA나 변 FH와 평행할 수 있도록 그립니다(명제 I.31).
- 사변형 HLKF는 평행사변형이 되고 HK는 그 평행사변형의 대각선이 됩니다.
- 평행사변형 ALMB는 평행사변형 BEFG와 넓이가 같고(명제 I.43), 평행사변형 BEFG는 주어진 삼각형 C와 넓이가 같습니다.
- 각 ABM은 각 GBE와 같고 (명제 I.15), 각 GBE는 주어진 각 D와 크기가 같습니다.
- 그러므로 주어진 삼각형 C와 넓이가 같은 평행사변형 ALMB를 주어진 선분 AB 위에서 주어진 각 D와 같은 각 ABM을 통해 작도하게 됩니다.
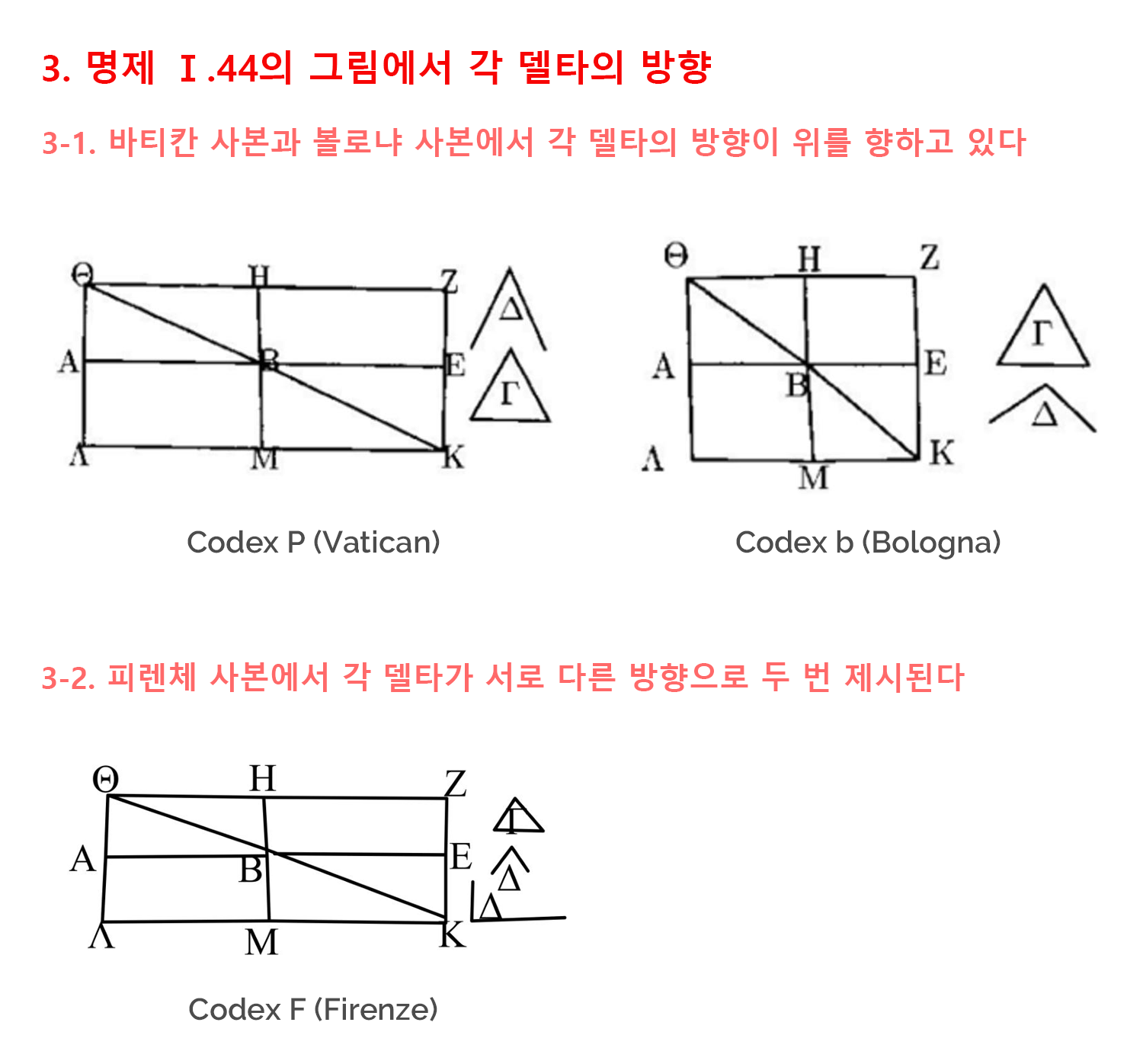
이 과정에서 주어진 삼각형 Γ과 평행사변형ΒΕΖΗ의 넓이가 갖도록 그려져야 함에도 불구하고, 그리스어 필사본들은 이 상응 관계에 어긋난 그림을 제시한 경우가 많았습니다. 이 글에서 관찰대상으로 삼고 있는 여섯 개의 주요 그리스어 사본들 중에서 파리와 비엔나에 소장된 사본을 제외한 나머지 네 개의 사본에서는 삼각형이 요구되는 것보다 더 작게 그려져 있습니다.[2] 예를 들어 바티칸, 옥스포드, 볼로냐, 피렌체에 소장된 필사본에서는 공통적으로 삼각형 Γ가 평행사변형 ΒΕΖΗ보다 더 작은 크기로 제시되었습니다.
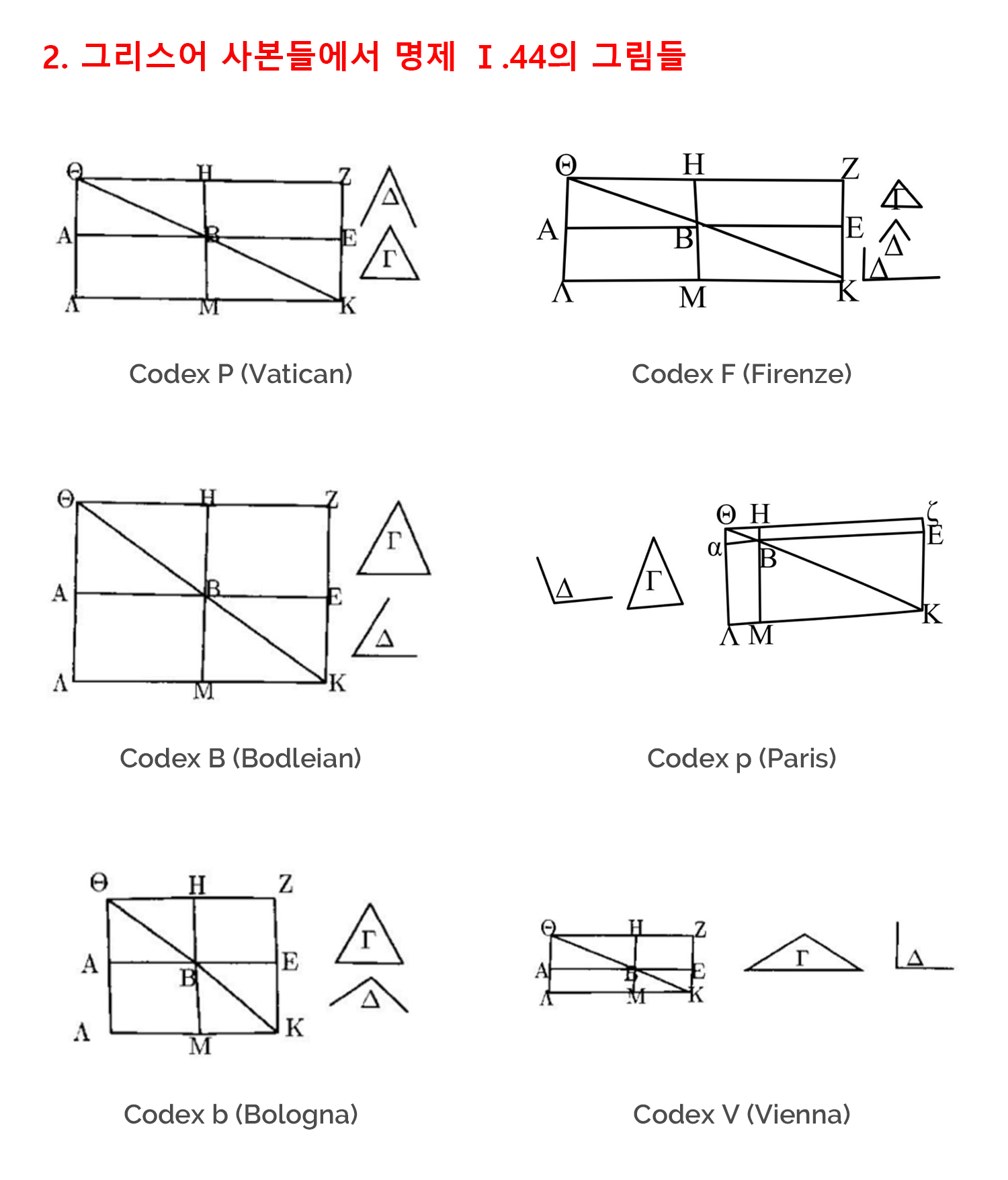
덧붙여서 각들의 상응 관계도 올바르게 그려지지 않았습니다. 위에서 요약한 작도과정에 따르면 각 Δ는 각 ΕΒΗ(혹은 각 ΑΒΜ)와 크기가 같아야 합니다. 만일 그림을 필사한 사람이 작도의 최종목표인 평행사변형을 직사각형 ΛΒ(ΑΛΜΒ)로 구현하게 되었다면, 각 ΕΒΗ는 직각이 됩니다. 그러나 비엔나 코덱스를 제외한 나머지 다섯 개의 필사본들은 각 Δ를 예각이나 둔각으로 그려서 두 각 사이의 상응 관계가, 적어도 그림에서는 분명하게 드러나지 않게 되었습니다.
그림과 작도의 과정을 더 면밀하게 들여다보는 독자라면 각 Δ가 그려진 방향도 독자들이 그림을 읽기에 편하지 않은 방향으로 주어졌다는 점도 발견할 수 있을 것입니다. 바티칸이나 볼로냐의 코덱스에서 각 ΕΒΗ는 각의 꼭짓점이 좌하향하는 반면에 각 Δ의 꼭짓점이 상향하고 있기 때문에, 독자들은 각 Δ가 어떻게 각 ΕΒΗ로 적용되는지 한 번 더 생각을 거치게 됩니다.[3-1] 이 불편을 덜고자 아마도 피렌체 코덱스는 상향하고 있는 각 Δ에 이어서 좌하향하는 각 Δ를 추가로 그려 넣었을 가능성이 높습니다.[3-2]
위의 그림에서 확인할 수 있는 것처럼 12세기의 비엔나 사본에 이르러서야 비로소 측도적 정확성에 맞게 그림의 수정이 이루어집니다. 그전까지, 즉 9-12세기까지 그리스어 필사본들의 도형은 거의 공통적으로 측도적 정확성을 결여하고 있었습니다.
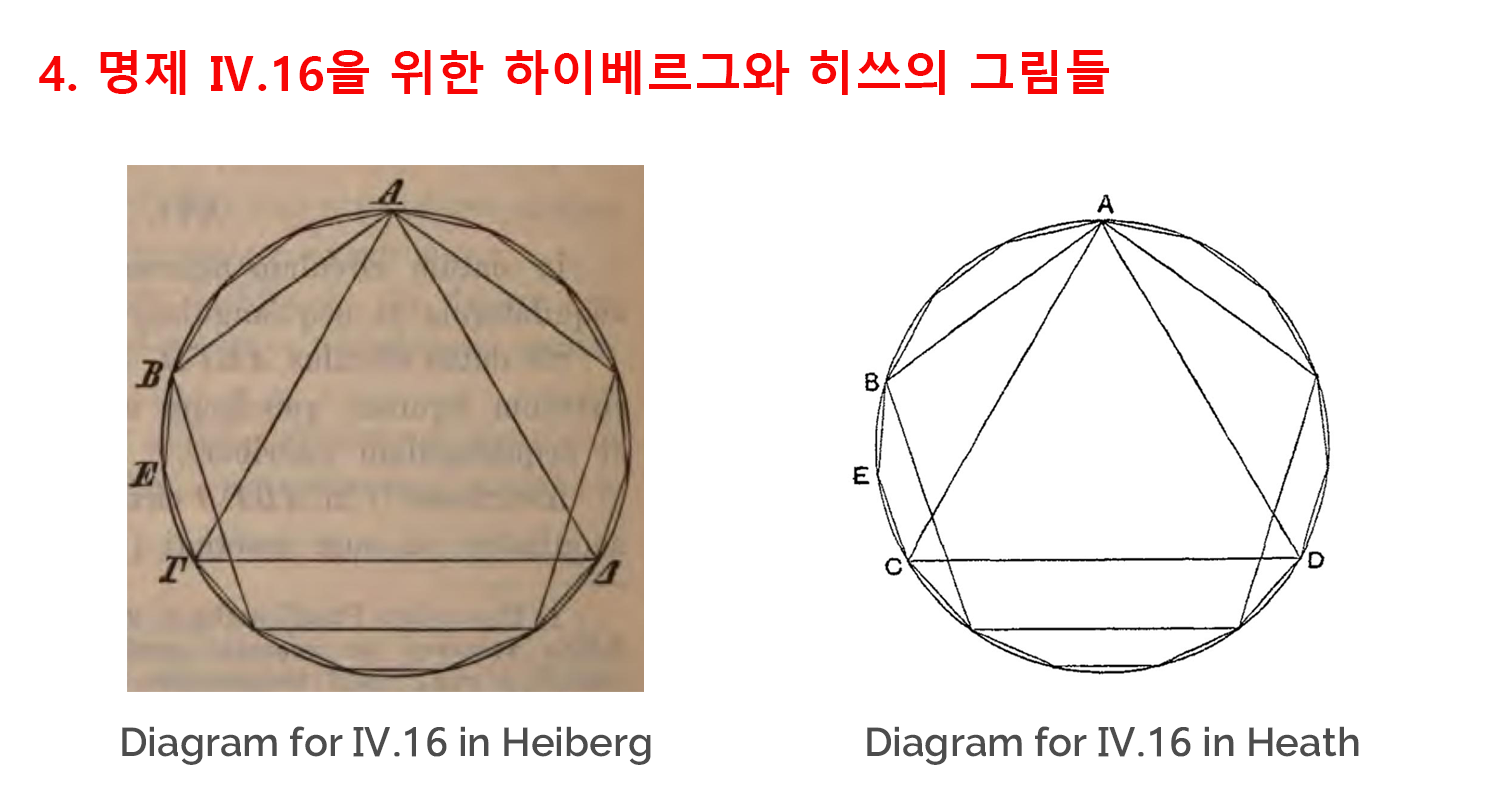
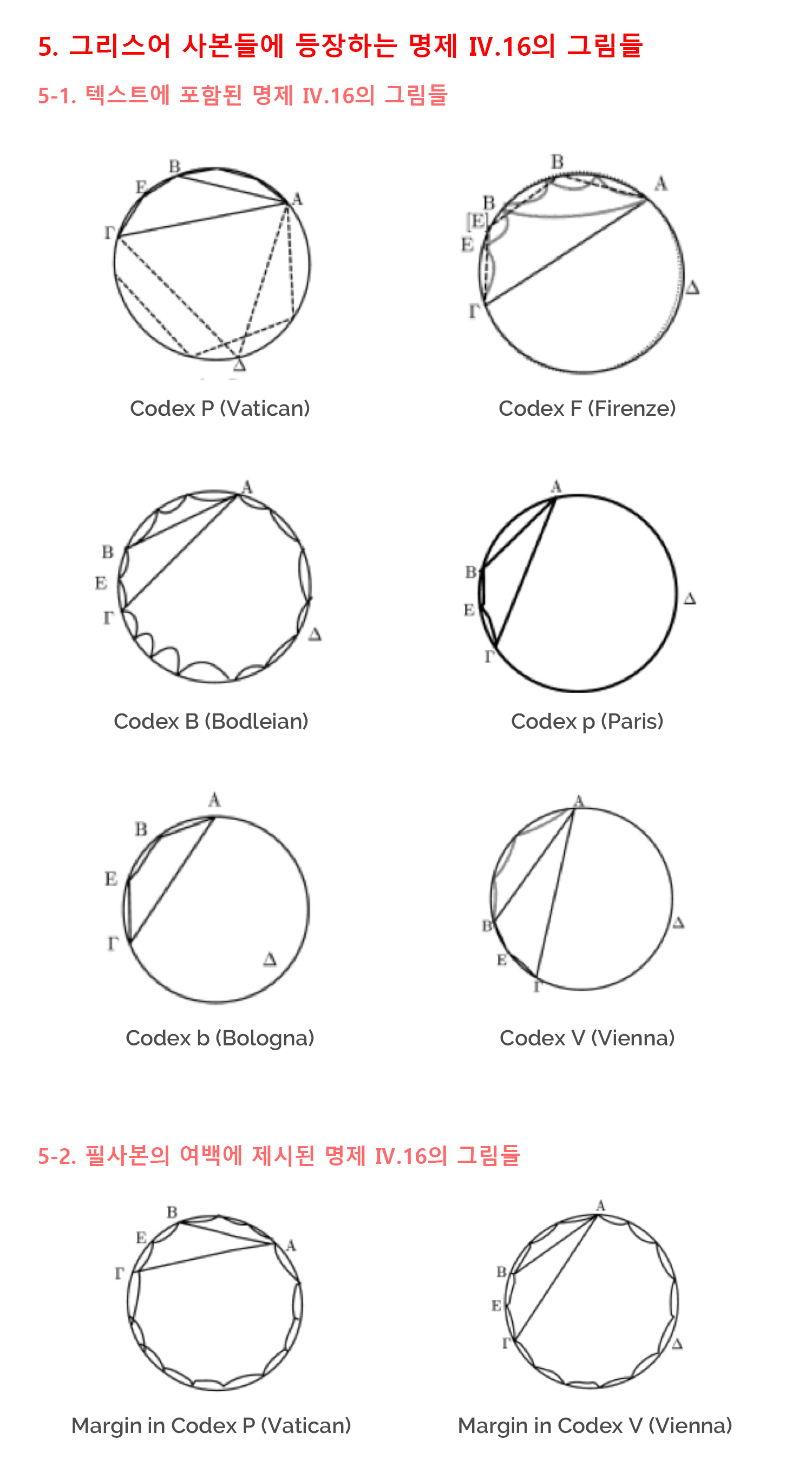
측도적 정확성과 더불어 시각적 정확성이 떨어지는 그림들도 등장합니다. 대표적인 예는 원론 4권의 마지막 명제 (Ⅳ.16)의 그림인데, 이 명제는 주어진 원 안에 내접하는 정15각형을 작도하는 문제를 다룹니다.
원론은 이 문제를 주어진 원 안에 내접하는 정삼각형 (전체 정15각형의 1/3을 차지)을 그린 다음 정오각형 (전체 정15각형의 1/5을 차지)을 그려서 그 차이에 해당하는 호 BC를 이등분함으로써 정 15각형의 한 변을 얻게 된다고 설명합니다.[4]
문제는 작도의 결과물로 얻게 되는 정 15각형을 그림으로 표현하는 과정에서 발생합니다. 15개의 변을 직선이 아니라 곡선의 형태로 표현했기 때문입니다.[5] 그래서 결과물이 정 15각형이라기보다는 흡사 15개의 톱니를 가진 바퀴처럼 보이기도 합니다.
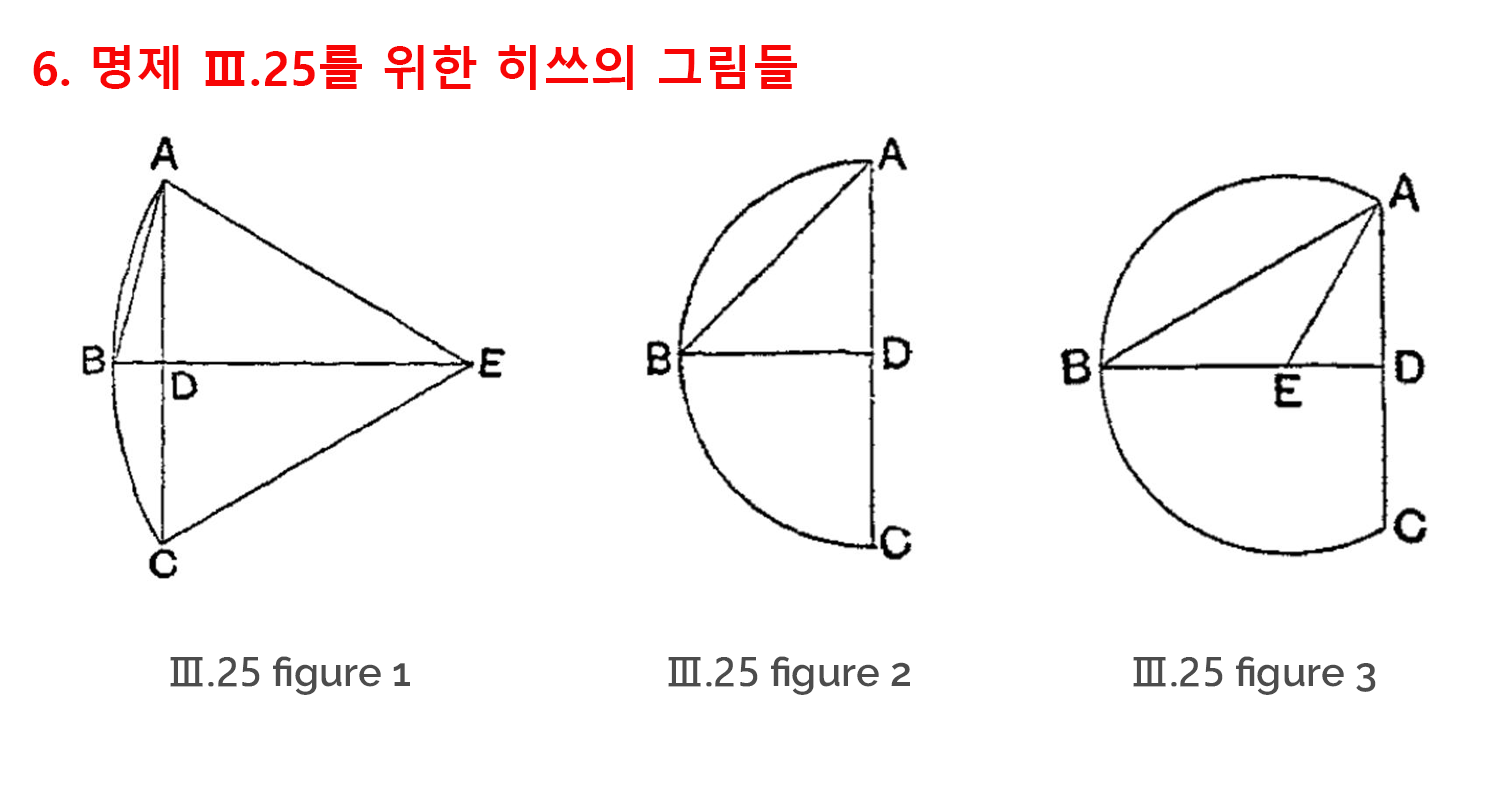
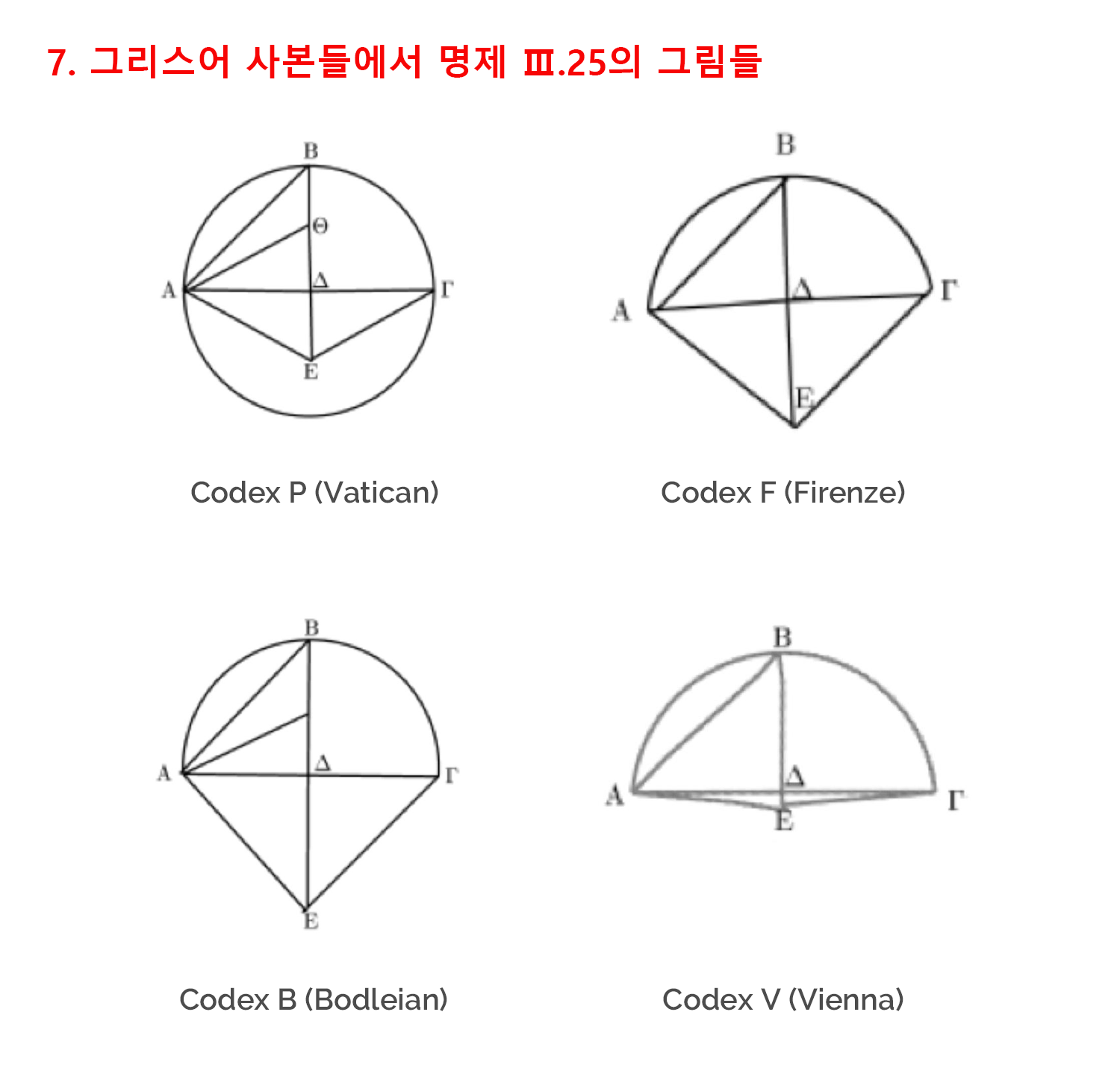
이처럼 필사가들이 시각적 정확성과 측도적 정확성에 크게 개의치 않으며 도형을 다루는 태도는 한 개의 그림으로 여러 경우를 동시에 표현한 그림에서 정점에 이르게 됩니다. 대표적으로 3권의 25번과 36번 명제들이 이에 해당합니다. 먼저 25번 명제는 활꼴이 주어졌을 때, 그로부터 원을 작도하는 문제를 다룹니다. 이 활꼴이 반원보다 크기가 작을 경우, 같을 경우, 클 경우에 따라 원의 중심도 각각 활꼴의 바깥, 활꼴의 선분 위, 활꼴의 내부에 놓이게 됩니다. 따라서 히쓰의 영어 번역본에서 보는 그림처럼 현대의 독자들은 각각의 경우를 표현하는 세 개의 그림들을 예상하게 됩니다.[6]
그러나 그리스어 필사본들은, 가령 바티칸 사본이나 옥스포드 사본은, 세 가지 경우를 하나의 원에 동시에 표현함으로써 한 경우를 만족하면 나머지 경우들에 대한 측도적, 시각적 정확성을 희생시킬 수밖에 없는 그림을 보여줍니다.[7]
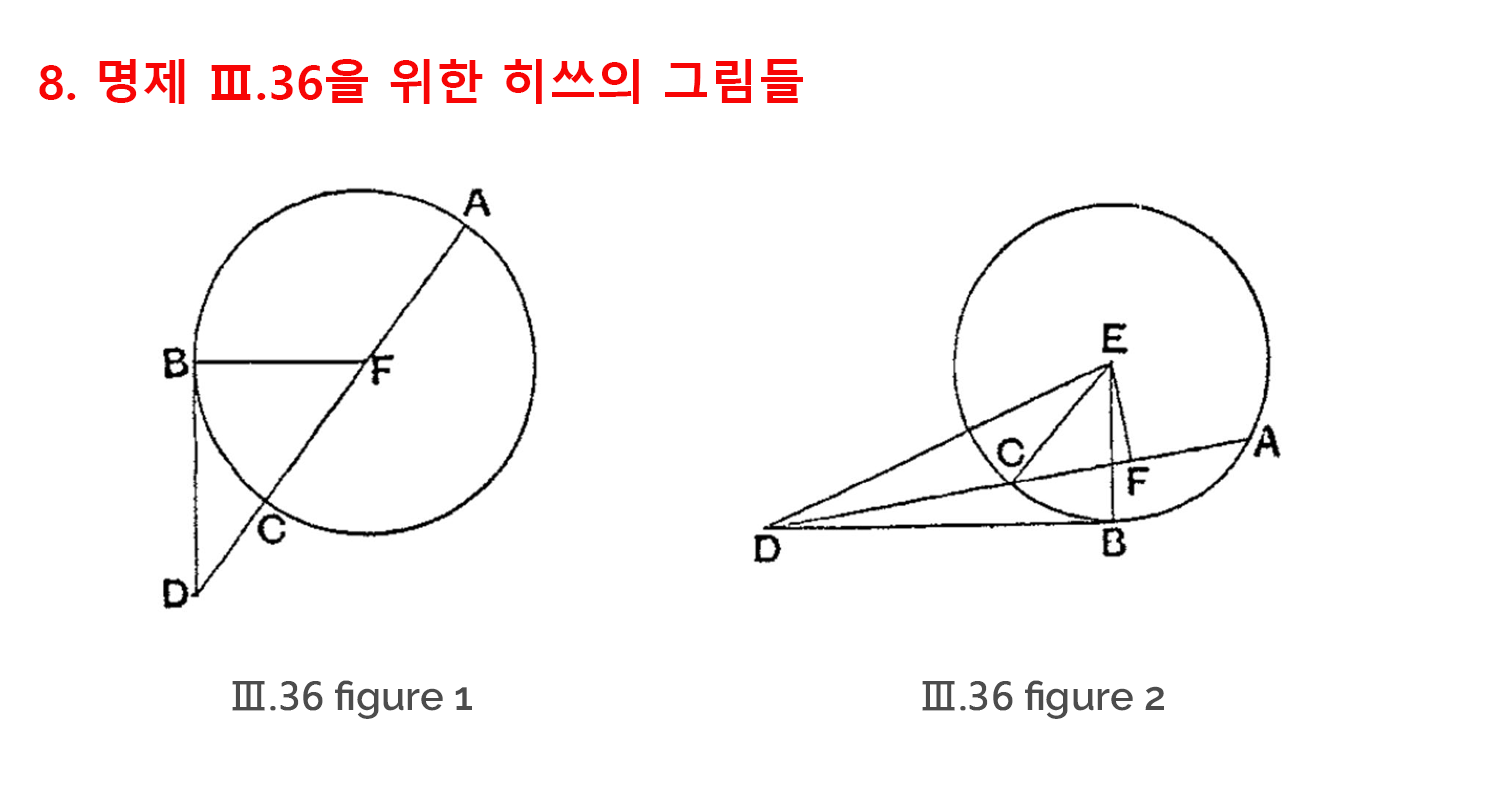
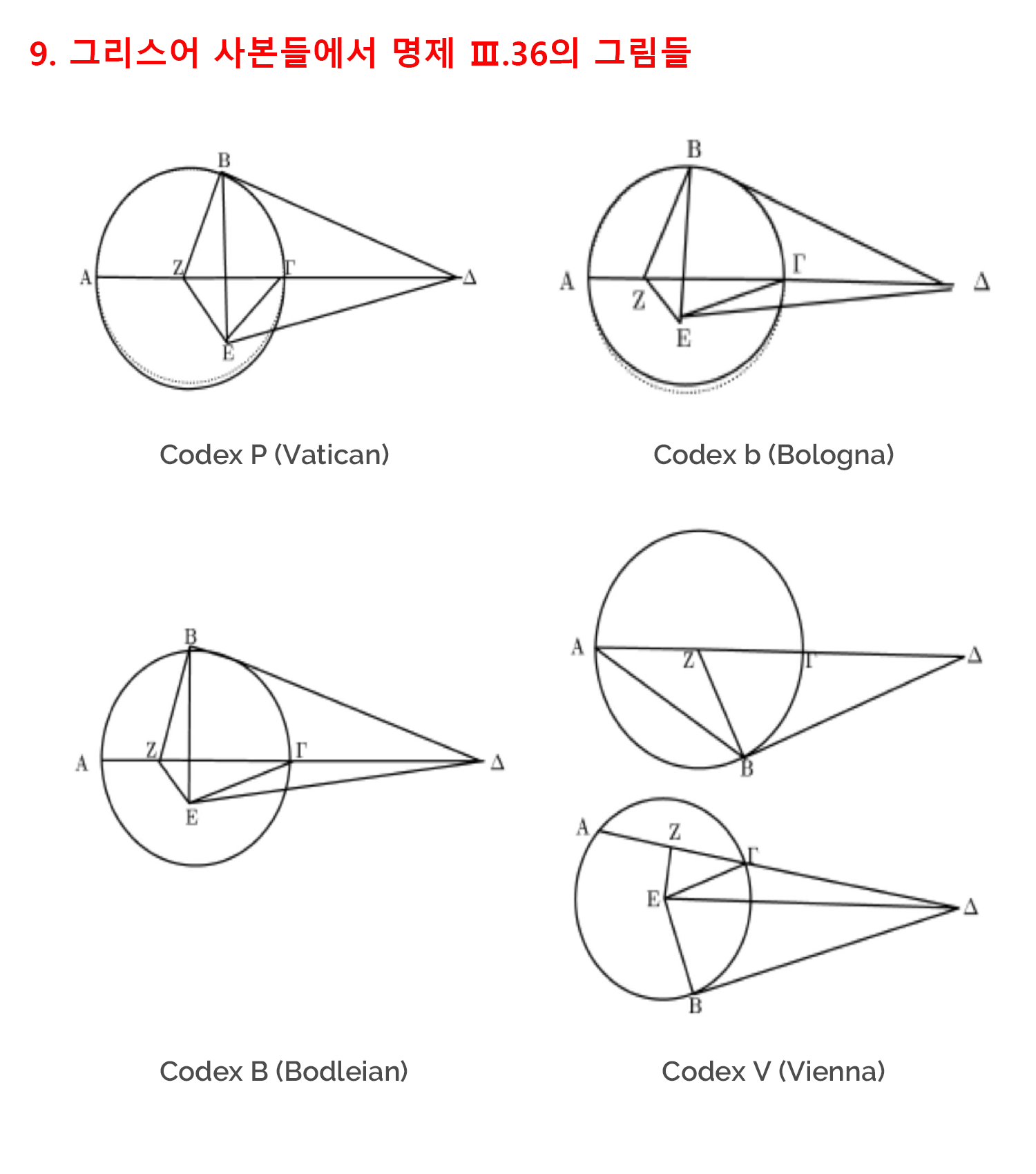
이와 비슷한 사례는 3권의 36번 명제에서도 발견됩니다. 이 명제는 원 밖의 한 점에서 접선과 할선을 그었을 때, 할선의 원 밖의 선분의 길이(DC)와 할선 전체의 길이(DA)의 곱은 접선의 길이(DB)의 제곱과 같다는 점을 설명합니다.
\[
\overline { DC } \cdot \overline { DA } ={ \overline { DB } }^{ 2 }
\]
이 명제의 증명은 할선이 중심을 지나는 경우와 중심을 지나지 않은 경우로 나누어 전개됩니다. 이 두 경우를 동시에 표현하는 것은 불가능하기 때문에 각각의 경우에 해당하는 두 개의 그림들이 각각 필요합니다.[8]
그러나 이번에도 그리스어 필사본들은 하나의 그림 안에 두 가지 경우를 모두 포함시켰기 때문에 같은 원에 중심이 2개 존재하게 됩니다.[9] 필연적으로 하나가 원의 중심이 되면 다른 하나는 중심에서 빗겨나 있게 되거나 (바티칸 사본) 아니면 절충해서 두 중심 모두 실제 원의 중심으로부터 떨어져 있게 됩니다 (옥스포드 사본).
왜 그리스어 필사본들에서 이와 같은 그림이 등장하게 되었는지 규명하기는 쉽지 않습니다. 다만 몇 가지 가능성을 생각해 볼 수 있습니다. 첫째는 유클리드의 원론에서는 하나의 경우(예를 들어 III.25에서는 활꼴이 반원보다 작을 경우)만을 다루었지만, 알렉산드리아의 테온Theon of Alexandria: c. AD.335–c.405과 같은 후대의 주석가나 편집자가 다른 경우들(반원과 같은 경우와 클 경우)을 추가했을 가능성입니다. 그렇다면 하나의 경우만을 표현하던 원래의 그림에 나머지 경우들이 덧붙게 되면서, 여러 경우를 동시에 표현하는 하나의 왜곡된 그림이 만들어지게 됩니다. 실제로 학자들은 오늘날 우리에게 전해지고 있는 원론이 유클리드가 원래 편집했던 원론보다 더 확장된 편집본일 것이라고 추정하고 있는데, 도형에 대해서도 이런 추가 작업이 이루어졌을 가능성이 있습니다. 그러나 문제는 텍스트의 어느 부분이 유클리드 시기부터 존재했던 것인지 아니면 후대의 편집자들의 보충 작업에 의한 것인지를 밝힐만한 증거가 충분하지 않다는 점입니다. 이런 상황에서 필사본들 간의 그림을 비교하는 연구는 이러한 판단을 내리는 데 도움이 될 수 있습니다. 필사본들 간의 그림을 비교하는 작업을 통해, 어떤 그림이 후대에 추가되었다고 추정할 수 있는 증거가 발견된다면, 이를 토대로 추가된 그림에 관한 텍스트 또한 후대에 추가된 것이라고 짐작할 수 있기 때문입니다.
다른 가능성은 원래 각각의 경우들을 표현하던 그림들이 따로 있었지만 이 그림들이 하나로 통합되었을 가능성입니다. 이러한 설명은 책의 형태변화에 주목한 해석입니다. 고대의 책들은 원래 파피루스의 두루마리Papyrus Rolls 형태로 존재하다가 대략 2-4세기 경에 점진적으로 양피지를 이용한 코덱스Parchment Codices로 전환되었습니다. 파피루스 두루마리에서는 코덱스처럼 페이지가 나누어져 있지 않았기 때문에 텍스트가 여러 열칼럼, Column들로 연속적으로 기술되었습니다. 원론보다 더 많은 두루마리와 코덱스가 남아있는 호메로스의 <일리아드>나 <오뒷세이아>의 두루마리 사본들을 참고해보면, 이야기 속 몇몇 장면들이 주로 그 장면이 등장하는 칼럼에 그림으로 삽입되었다는 점을 알 수 있습니다. 기본적으로 어떤 장면에 대한 일러스트레이션이 해당 장면을 기술하는 텍스트의 칼럼에 배속된 것입니다. 그러다가 두루마리가 코덱스로 전환되는 과정에서 두루마리의 칼럼들이 코덱스의 페이지로 새롭게 배열되어야 했기 때문에, 몇몇 칼럼의 그림들이 더 이상 독자적인 그림으로 존재하지 못하고 하나의 그림으로 통합되어 제시된 경우들이 발견됩니다. 만일 유클리드의 원론이 두루마리에서 코덱스로 변환될 때 비슷한 일이 일어났다면, 마찬가지로 도형들이 서로 겹쳐진 그림Superimposed figure으로 제시되었을 가능성을 배제할 수 없습니다. 아래에 각각의 경우를 나타내는 세 그림이 하나로 포개졌을 상황을 묘사해보았습니다.[10]
이외에도 그리스어 필사본의 독특한 그림들을 이해하는 데 도움이 될만한 몇몇 정황적인 설명이 가능하겠으나, 지금 남아있는 사본들보다 더 이른 시기에 만들어진 원론의 그리스어 필사본이 추가로 발견되기 전까지는 어떻게 이런 그림이 만들어지게 되었는지에 대한 판단을 유보하는 것이 좋을 것 같습니다. 그러나 한 가지 분명한 것은 그리스어 필사본의 그림들이 독자에게 그다지 친절한 안내를 제공하지 못했다는 점입니다. 앞서 살펴본 도형 간의 상응 관계나 정 15각형의 변과 원의 중심들처럼 시각적, 측도적으로 왜곡되었던 부분들의 교정은 결국 독자들이 텍스트를 읽을 때 비로소 가능해집니다. 반대로 말하자면 필요한 기하학적 상황을 텍스트가 묘사하고 있기 때문에, 그림은 어느 정도 측정과 비례라는 규범으로부터 일탈할 자유를 갖게 된 셈이기도 합니다.
오늘날에도 기하학 책에서 도형을 제시할 때, “도형이 비율대로 그려지지 않았다 Figures not drawn to scale“는 단서를 통해 도형이 텍스트의 관계를 올바르게 표현하지 못했을 가능성을 열어두고 있지만, 그리스어 필사본의 그림들이 기하학적 상황을 왜곡한 정도는 분명히 오늘날 독자들의 예상을 뛰어넘는 것입니다. 따라서 이 그림을 임시로 그리스어 필사본들의 “이상한 그림들”이라고 부르기로 하겠습니다.
이제 다시 서두에 말씀드렸던 핵심 질문으로 돌아가 보겠습니다. 이 “이상한 그림들”이 과연 필사가의 단순한 실수나 부주의에서 기인한 것일까요? 그렇다면 이 실수나 부주의가 왜 일회성으로 그치지 않고 몇 세기에 걸쳐서 반복되었을까요? 원론의 인쇄본들과는 달리 필사본들에는 어떤 서문이나 인사말도 쓰여 있지 않습니다. 인쇄본들에서 볼 수 있는 출판한 장소나 일자, 출판한 사람 등을 나타내는 그 흔한 간기刊記, Colophon조차 없는 경우가 허다합니다. 따라서 필사가들이 그림을 필사하면서 갖고 있었던 기하학적 도형들에 대한 그들의 태도는 한 번도 명시적으로 드러난 적이 없습니다.
이런 한계에도 불구하고 논의를 좀 더 진전시켜보면, 필사가가 아무리 자신이 필사하고 있는 사본을 충실하게 복제하려 했다 하더라도 한 사본의 실수나 부주의가 여러 필사본에 걸쳐 지속적으로 반복되었다고 보기에는 석연치 않은 구석이 있습니다. 만일 유클리드의 그림 자체가 처음부터 “이상한 그림”이었다면, 필사가들이 그 “이상한 그림들”을 자신들에게 전수된 대로 전달함으로써 그리스 기하학의 흔적을 훼손하지 않았다고 봐야 하지 않을까요? 그래서 그리스어 사본들 속 “이상한 그림들”의 반복적인 등장은 근현대 기하학의 세례를 받은 저의 선입견에 도전해왔습니다.
“왜 우리는 도형이 반드시 비례대로 그려져야 한다고 믿는가?”
우리에게 도형은 기하학적 논의를 위한 시각적 장치일 수 있지만, 그들에게 도형은 기하학적 논의를 체화하고 있는 논리적 장치일 수 있는 것이지요. 저는 지금 원론의 연역적 체계 안에서 텍스트가 구현하고 있는 논리적 증명을 담지한 기호로서의 도형을 상정해 보고 있습니다. 엄밀한 측정과 정확한 비례라는 가치는 시각적 장치로서의 도형에게는 필수적인 덕목이겠으나, 논리적 장치로서의 도형이라면 이야기가 달라지기 때문입니다.
그래서 저는 유클리드와 당대 고대 그리스 수학자들이 알던 기하학과 오늘날 우리가 아는 기하학 사이에 어떤 점이 여전히 궤를 같이하고 있고 또 어떤 차이가 있는지를 탐구 중입니다. 그들의 도형이 우리의 도형과 다르다는 것은, 그들이 학습하고 연구했던 기하학에 대한 경험과 수행이 오늘날 우리의 경험과 수행과는 다른 것일 수 있음을 암시합니다.
기하학 외에도 시각적 지식 혹은 시각적 재현을 도구로 삼아 추론reasoning을 만들어내는 여러 다른 분야가 있습니다. 예를 들어 고대의 지리학이나 천문학도 기하학만큼이나 텍스트로 된 지식과 함께 시각적 지식을 동반하는 학문입니다. 고대의 세계나 천체의 운동에 대한 시각적 묘사들이 실제와 얼마나 동떨어진 것이었는지는 벌써 친숙한 이야기가 되어버렸습니다. 그들이 자신들이 살고 있던 도시를 실제보다 더 크게 그렸다고 해서 혹은 태양이 지구를 돌고 있는 것으로 그렸다고 해서 그 시각적 묘사들이 전적으로 가치를 잃어버리는 것은 아닙니다. 그 왜곡된 시각적 재현 안에서도 그렇게 그리게 되었던 이유와 논리가 있기 때문입니다. 우리가 유독 기하학과 그 도형들에 대해서만 만고불변의 엄밀한 측정과 비례라는 가치를 강요할 필요는 없지 않을까요?
물론 과거의 시각적 재현들은 오늘날 우리의 기준에서 더 나은 시각적 재현에 의해 반박되고 결국에는 폐기되었습니다. 그러나 과학사가들에게는 이것이 반드시 “틀림”인 것만은 아니고 “다름”으로 받아들여지기도 합니다. 만일 우리가 마주하는 현상들에 대해 언제나 눈에 보이는 그대로의 시각적 재현만을 허락한다면, 서양미술사조의 사실주의를 제외한 여타의 다양한 노력을 모두 고사시키는 결과를 낳겠지요. 비록 “과학”이라는 이름이 가진 무게가 현상에 대한 하나의 궁극적 원리를 향해 수렴하도록 유도하지만, 같은 현상을 묘사하는 다양한 시각들은 과학을 더욱 다채롭게 만들기도 합니다.
위성의 정밀한 측정에 도움을 받은 구글맵을 켜놓고 우리 동네의 지리를 공부하는 것과, 내가 걸어 다니며 그렸던 우리 동네의 그림을 펼쳐놓고 지리를 공부하는 것은 전혀 다른 이야기가 됩니다. 어떤 그림을 그리고 사용하는가가 어떤 식으로 탐구를 할 것인지를 결정해 왔습니다.
이제 근원으로 올라가ad fontes 유클리드와 그리스 수학자들이 그들의 그림을 가지고서 어떻게 기하학이라는 지식체계를 만들어 냈는지 논의하는 일이 남았습니다. 그 전에 지금까지의 글들에서 거론하지 않았던 그러나 어쩌면 인쇄업자나 번역가나 필사가들 못지않게 중요한 역할을 담당했을 “독자들readers“이 남긴 그림들에 대해 살펴보고 넘어가려 합니다.