Are you really sure that a floor can’t also be a ceiling?
– M. C. Escher
M. C. 에셔Escher라는 그래픽 아티스트graphic artist가 있다. 에셔는 수학자와 과학자들 사이에서 특히 존경을 많이 받는 미술가 중 한 사람인데, 정작 주류 미술계에서는 오랫동안 그 가치를 인정받지 못했다. 여기에는 여러 이유가 있었다고 추정된다. 그 이유 중의 하나로, 에셔 작품의 주요 매체가 목판화woodcut나 금속판화lithograph인데 매체의 특성상 원칙적으로 무수히 많은 복제가 가능하기에 개별 작품의 희소성이 없었고 따라서 작품의 가격이 낮아 미술상들의 외면을 받았기 때문이라는 분석이 있다. 하지만 아마도 가장 중요한 이유는 당시 주류 미술 평론가들의 비판에서 드러나듯이 에셔의 작품이 과도하게 지적intellectual이고 서정적lyrical이지 않았기 때문이라고 한다. (여기서 드는 질문 하나, 예술은 반드시 감정을 나타내야 하는가?)
에셔가 천착했던 주제들은 매우 수학적이다. 이 주제들의 바탕에 면면히 흐르는 가장 중요한 수학적인 아이디어 두 개를 꼽으면 다음과 같다. 첫째 영어로 테셀레이션tessellation이라고 불리는 주제로, 반복되는 모양으로 공간을 채우는 방식에 대한 고찰이다. 이 주제는 물리학자들이 매우 좋아하는 공간의 대칭성 문제와 깊은 연관이 있다. 둘째 “불가능한 물체impossible objects”에 대한 상상이다. 여기서 “불가능하다”의 의미는 물체의 모든 부분이 불가능하다는 의미가 아니다. 물체의 부분 부분은 그 자체로서 이상하지 않지만, 그러한 부분들이 모여 만들어진 전체는 불가능하다는 것이다. 에셔가 이 주제에 천착하게 된 중요한 계기는 1953년 본인이 제작한 <상대성 Relativity>이라는 작품이다.
에셔의 <상대성>이 이상하게 보이는 이유는 서로 다른 중력이 작용하는 여러 공간이 하나의 장면 안에 겹쳐 있기 때문이다. 층계의 윗면과 아랫면 모두 사람이 다닐 수 있어, 어떤 사람의 바닥이 다른 사람의 천정으로 자연스럽게 연결된다. 부분 부분을 놓고 보면 이상하지 않지만 전체를 보면 현실에 존재할 수 없는 불가능한 구조이다. 다른 말로 표현하면, 공존할 수 없는 서로 다른 관점이 한 장면에 동시에 존재한다.
에셔의 <상대성>은 수학자 로저 펜로즈Roger Penrose와 그의 아버지인 생물학자 리오넬 펜로즈Lionel Penrose에게 깊은 인상을 남긴다. 이에 영감을 받은 두 사람은 1956년 “불가능한 물체: 특별한 종류의 착시 현상Impossible Objects: A Special Type of Visual Illusion”이라는 논문을 쓰고 이 논문의 사본을 에셔에게 보낸다. 이를 받아 본 에셔는 거꾸로 논문에 실린, 끊임없이 올라가는 계단의 이미지에 깊은 감동을 받는다. 이는 다시 1960년 에셔의 작품인 “상승과 하강Ascending and descending”의 탄생으로 이어진다.
특히 펜로즈의 논문에는 “가장 순수한 형태의 불가능성Impossibility in its purest form”이라고 일컬어지는 “불가능한 삼각형Impossible triangle”이 담겨 있었는데, 이는 이후 에셔의 “폭포Waterfall”를 비롯한 많은 작품에서 다양한 형태로 나타나게 된다[사실 불가능한 삼각형의 다른 형태는 이미 1934년에 스웨덴 미술가인 오스카 로이터스바르트Oscar Reutersvärd에 의해서 고안되었다]. 펜로즈의 “불가능한 삼각형”이 가장 순수하게 불가능한 이유는 다음과 같다. 우선 앞서 말했듯이 삼각형을 구성하는 세 개의 막대기는 각각의 관점에서 보았을 때 전혀 문제가 없을 뿐만 아니라 서로 다른 두 개의 막대기가 연결되는 방식에도 전혀 문제가 없다. 하지만 세 개가 모두 연결되어 하나의 전체를 만들 때, 그 전체는 명백하게 불가능해진다. 그리고 이러한 불가능성이 가능해지는(재미있는 표현이다!) 가장 작은 숫자는 바로 3이다. 따라서 “불가능한 삼각형”은 가장 순수하게 불가능하다. 인터넷에서 찾아보면 금방 알 수 있듯이 펜로즈의 “불가능한 삼각형”을 본뜬 다양한 불가능한 다각형들이 있는데, 물론 이것들은 가장 순수하게 불가능하지 않다(심지어는 독자 여러분들이 잘 알고 있지만 거의 분명히 눈여겨보지 않았을 확률이 높은 우리나라 어느 유명한 통신 회사의 로고도 “불가능한 물체”이다).
펜로즈의 “불가능한 삼각형”이 표현하는 하나의 전체는 단순히 불가능한 구조라는 의미를 넘어선다. “불가능한 삼각형”을 자세히 보고 있으면, 어느새 삼각형의 한 변에서 다른 변으로, 그리고 또 다른 변으로 돌아가며 삼각형을 눈으로 훑고 있는 자기 자신을 발견하게 될 것이다. 부분에는 없던 모종의 운동성이 전체에 부여되는 것이다. 이것이 아마도 에셔가 펜로즈의 “불가능한 삼각형”에서 영감을 얻어 그의 작품 “폭포Waterfall”에서 “영구 운동 기계perpetual motion machine”를 상상했던 이유일 것이다(물론 영구 운동 기계도 불가능하다). 그 의미를 약간 과장해서 해석하면, 펜로즈의 “불가능한 삼각형”은 아리스토텔레스의 유명한 명제인 “전체는 부분의 합보다 크다”를 가장 순수하게 시각적으로 표현하는 것이다.
여기까지 읽은 독자들은 필자가 얼마나 에셔의 작품과 펜로즈의 “불가능한 삼각형”을 좋아하는지 짐작할 수 있을 것이다. 이런 필자에게 에셔와 펜로즈에게서 받은 영감을 본인의 실생활에서 활용할 수 있는 기회가 생기게 되었다. 그것도 두 번.
첫 번째 기회는 2013년에 찾아왔다. 당시 새롭게 부임한 고등과학원 원장님[2018년 현재는 기초과학연구원IBS, Institute for Basics Science 원장님]이 그 이전까지 쓰던 고등과학원 로고를 새롭게 변경하고자 태스크포스 팀을 구성했는데, 필자가 팀장을 맡게 되었다. 그동안 간간이 고등과학원 내에서 자잘한 위원회의 위원을 맡아보기는 했지만 필자가 생각하기에 한 기관의 대표 이미지인 로고를 새롭게 창조하는 것은 차원이 다른 일이었다. 게다가 로고처럼 사람들 사이에서 호불호가 극명히 갈릴 수 있는 일은 잘하면 그만이지만 못하면 욕을 먹을 일이라 겁이 났다. 하지만 재미있겠다고 생각했다. 그래서 하겠다고 했다.
물론 로고는 필자 혼자 마음대로 결정할 수 있는 사안이 아니었다. 우선 로고를 전문적으로 디자인하는 전문 업체를 선정하기 위해서 태스크포스 팀의 이름으로 정식 입찰 공고를 내었다. 그 이후 복잡한 심사 과정을 거쳐서 한 디자인 업체를 선정했다. 최종 결과물을 얻기까지 3개월이라는 짧은 시간이 주어진 상황에서 이러한 행정절차를 완료하는 데에 너무 시간이 오래 걸린다고 생각했지만, 어쩔 수 없는 일이었다. 그리고 정작 중요한 작업은 이제부터 시작이었다.
고등과학원이라는 순수 이론과학 연구기관의 본질과 이상을 압축해서 표현하는 로고는 무엇을 담아야 할까? 아무리 간단한 것이라도 무엇을 창조해 본 사람은 새로운 것을 창조한다는 것이 얼마나 어려운지 알 것이다. 정말 새로운 것을 창조해내야 한다고 스스로를 다그칠수록 좋은 생각은 나지 않고, 좋은 생각이 나지 않을수록 더 다그치는 악순환이 시작된다. 마치 잠이 오지 않을 때, 잠을 자야 한다고 생각하면 할수록 잠이 더 오지 않는 것과 비슷하다. 의사들은 이럴 때 마음을 비워야 한다고 가르친다. 마음을 비우는 것은 마음먹은 대로 되지 않으므로, 오히려 잠자리에서 일어나서 딴짓을 하는 것이 도움이 된다. 책을 조금 읽든지, 물을 조금 마시든지, 아니면 아예 텔레비전을 조금 시청하든지, 마음을 비울 수 있는 그 어떤 딴짓을 하는 것이다.
자동차를 운전해서 출근하지 않았던 어느 날 (2013년 2월 5일이었다고 기억된다), 지하철을 타고 집으로 돌아가고 있었다. 지하철 좌석에 앉아, 새로운 로고를 위해서 고등과학원에서 필자와 동료 과학자들이 이루고 싶은 것이 무엇인지 생각해 보기로 했다. 이때 불현듯 불가능을 상상하는 것Imagine the impossible이라는 생각이 들었다. 여기서 불가능하다는 것은 진짜로 불가능하다는 것이 아니라, 불가능해 보여서 이전까지 아무도 시도해 보지 않았던 어떤 것에 도전한다는 의미이다. 이제 다음 질문. 불가능을 가장 잘 표현하는 이미지는 무엇일까?
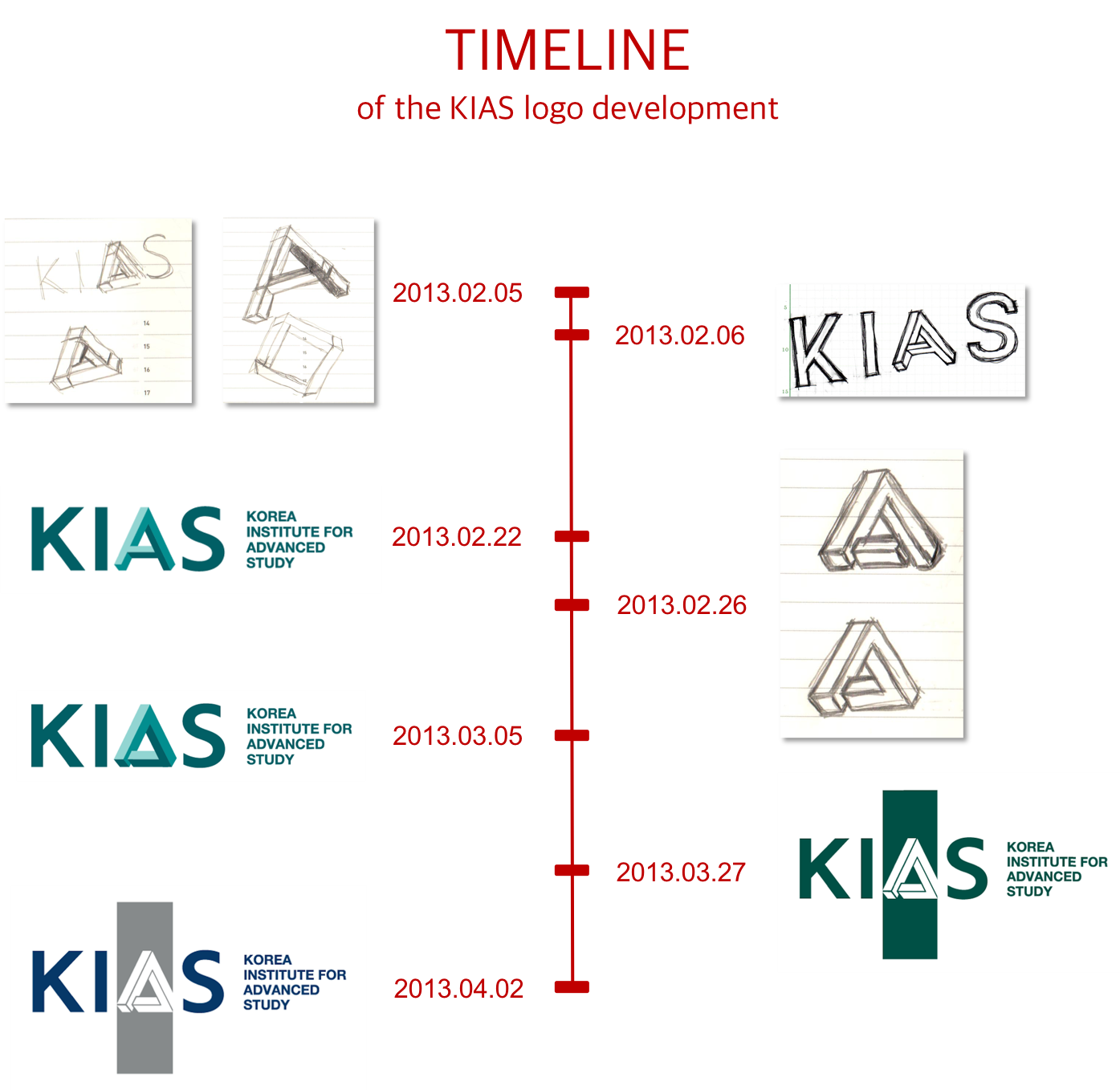
예상했겠지만 그 이미지는 바로 펜로즈의 “불가능한 삼각형”이다. 종종 로고에서 삼각형이 알파벳 A를 대신하는 경우가 있으므로, 고등과학원 영문 약자인 KIAS에서 A를 펜로즈의 “불가능한 삼각형”으로 치환하면 될 것 같았다. 그런데 수첩을 꺼내어 실제로 스케치를 해 보니 “불가능한 삼각형”이 제대로 된 A로 보이지 않았다. 그리고 생각보다 밋밋했다. 무언가 더 참신한 터치가 필요했다. 그래서 다음으로 생각한 아이디어는 “불가능한 삼각형”에 다리를 붙여서 진정한 의미의 “불가능한 A”를 만드는 것이었다. 재빨리 스케치를 해 보니 꽤 괜찮은 아이디어인 것처럼 느껴졌다. 스케치를 바탕으로 다음번 디자인 업체 실무진과 고등과학원 태스크포스 팀 사이의 로고 제작 회의에서 필자의 아이디어를 제안하였다. 반응은 좋았고 이 디자인으로 가기로 결정했다. 참고로 [그림4]는 고등과학원 로고의 개발 과정을 요약한 타임라인을 보여준다. 그림에 위에서 설명한 초기 아이디어에 관한 스케치도 담아 놓았으니 살펴보기를 바란다.
이 결정에 따라 디자인 업체에서 시안을 마련해 왔는데, 생각했던 것보다 더 마음에 들었다. 이제 이 아이디어로 최종 디자인을 확정하고 로고 디자인을 위한 디테일을 조정하는 단계에 접어들었다. 그런데 돌발 변수가 발생했다. 디자인 업체의 한 직원이 “불가능한 A”라고 구글에 검색해 보니 완전히 같은 디자인이 이미 존재하고 있는 것이었다. 이전까지 필자의 디자인에 이름을 붙이지 않았는데, 어느 시점부터 편의상 “불가능한 A”라고 부르기 시작했다. 이름이 생기니 자연스럽게 구글 검색을 할 수 있게 된 것이다. 김춘수의 “꽃”이라는 시처럼 “불가능한 A”는 “그의 이름을 불러주었을 때 그는 나에게로 와서 꽃이 되었다.” 하지만 그는 이미 알려진 꽃이었다(사실은 “불가능한 A”뿐만 아니라 불가능한 알파벳이 모두 있었다!). 디자인 업체에서는 이 디자인이 상표로 등록되어 있지 않았고, 그냥 A만 따로 쓰는 것이 아니라 KIAS의 일부분으로 쓰는 것이기 때문에 우리가 “불가능한 A”를 로고로 쓰는 데에 전혀 문제가 없다고 했다. 하지만 마음에 들지 않았다. 당시 로고 디자인에 참여했던 사람들은 과정을 알지만, 전혀 모르는 사람들에게 고등과학원 로고는 기존에 있던 아이디어를 베낀 것으로 보일 것이다. 디자인 팀에 시간을 조금 더 달라고 했다. 그리고 다시 한번 지하철을 탔다.
새 아이디어를 얻기 위해 다시 한번 고등과학원의 정체성에 대해서 생각해 보았다. 고등과학원의 이상이 불가능을 상상하는 것이라면, 그동안의 전통은 무엇인가? 이 시점에는 생각을 단순화하기로 했다. 이전 로고의 한 부분을 활용하여 고등과학원의 전통을 담아낼 수 있지 않을까? 그래서 이전 로고를 자세히 뜯어 보았다. 재미있게도 이전에는 큰 관심을 두지 않아 지각하지 못했지만, 이전 로고 속에 있는 A도 삼각형이었다! 엄밀하게 말해서, 삼각형의 한 변을 바닥으로 둔다고 할 때, 삼각형의 왼쪽 아래 모퉁이 한 부분을 잘라낸 모양이었다(사실 자세히 보면 이런 식으로 A를 표현하는 로고를 꽤 많이 찾을 수 있다). 좋다! 그렇다면 비슷하게 펜로즈의 “불가능한 삼각형”의 모퉁이 한 부분을 잘라내어 “불가능한 A”를 표현하면 어떨까? [그림4]를 참조하라. 그렇게 하면 고등과학원의 이상과 전통을 한꺼번에 담아낼 수 있을 것이다.
바로 이 디자인이 현재 고등과학원 로고의 바탕이 되었다. [그림4]에서 볼 수 있듯이 사실 원래 디자인은 “불가능한 A”가 다른 글자들(K, I, S)과 같이 단순하게 병렬되는 형태였는데, 나중에 “불가능한 A”가 세로로 긴 네모 상자 안으로 들어가 음각으로 나타나는 형태로 바뀌게 된다. 당시에 이 변화에 대해 상당히 고민을 많이 했는데 지금 보면 “불가능한 A”의 불가능성이 적절히 강조되면서도 글자 A로서의 역할도 잘할 수 있는 꽤 괜찮은 선택이었던 것 같다.
펜로즈의 “불가능한 삼각형”을 필자의 실생활에서 활용할 수 있는 두 번째 기회는 2016년에 찾아왔다. 매년 여름 국내 여러 대학교에서 응집물질물리를 전공하고 있는 대학원 학생들을 위해서 “응집물질물리 여름학교”가 열린다. 취지는 다음과 같다. 국내 많은 대학교에 물리학과가 있지만 개별 세부 전공으로 들어가면 해당 과목을 전문적으로 가르칠 수 있는 교수의 숫자가 매우 부족하다. 또 가르칠 수 있다고 하더라도 수강할 학생의 숫자가 한 자릿수로 매우 적기 때문에 해당 세부 전공에 관한 강의가 개설되지 못한다. 따라서 응집물질물리 분야의 방대함을 생각할 때 대부분의 응집물질물리 학생들은 우연히 그들이 속한 대학교에 있는 교수가 전공하고 있는 전문 분야 외에 다른 분야는 전혀 배울 기회가 없다. 심지어는 자기 지도 교수가 전공하고 있는 분야, 즉 학생 본인의 분야 외에는 전혀 배울 기회(때로는 의지 자체)가 없는 경우도 많다.
필자의 전공 분야는 응집물질물리 분야 중에서 강하게 상호작용을 하는 시스템인데, 줄여서 “강상관계strongly correlated systems”라고 한다. 다른 이름으로는 많은 입자의 문제, 즉 “다체 문제many-body problem”라고 알려져 있다. 모든 분야가 어렵지만, 다체 문제는 그중에서도 특히 어렵다고 알려진 분야이다. 따라서 다체 문제를 전공하는 교수가 상대적으로 적은데, 그만큼 국내에서 제대로 된 강의를 들을 수 있는 기회가 적다. 이 문제에 대해서 크게 걱정을 하고 있는 필자의 마음을 읽었는지, 응집물질물리 여름학교 조직위윈회는 필자에게 다체 문제에 관해서 강의를 해 줄 것을 부탁했다. 사실 2016년 이전에도 서너 번 다체 문제에 대해서 강의를 할 기회가 있었는데, 매번 할 때마다 다음에는 더 잘할 수 있을 것 같다고 생각했다. 그래서 이번에는 정말 준비를 잘 해보겠다고 결심했다.
응집물질물리에서 다루는 다체 문체는 사실 앞에 양자라는 단어가 생략된 “양자 다체 문제quantum many-body problem”이다. 따라서 다체 문제에 대한 필자의 강의는 기본적으로 양자역학에 대한 강의가 될 수밖에 없다. “믿기 힘든 양자 Incredible Quantum” 시리즈를 통해서 나중에 더 자세하게 얘기할 기회가 있겠지만, 다체 문제를 풀기 위해서는 양자역학의 다양한 수학적 형태를 다루어야 한다. 이전 연재 글에서 강조했듯이 양자역학은 기본적으로 파동 함수라는 관점에서 완벽하게 기술될 수 있다. 하지만, 양자역학은 파동 함수를 사용하지 않고도 기술할 수 있다. 사실 파동 함수 외에 두 관점이 더 있다. 하나는 “믿기 힘든 양자 Incredible Quantum [1]: 들어가며”에서 언급한 경로 적분path integral이고, 또 다른 하나는 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 언급한 연산자operator이다. 이렇게 양자역학을 바라보는 세 관점, 파동 함수, 경로 적분, 연산자는 서로 다르게 보이지만 본질적으로 같다. 이것이 바로 이번 글의 제목인 “양자 삼위일체quantum trinity”가 의미하는 바이다(사실 양자 삼위일체라는 이름은 이번 글을 쓰면서 필자가 고안한 이름이다).
필자는 다체 문제에 관한 강의 자료를 준비하면서, 어떻게 하면 양자 삼위일체(물론 그때는 이 이름이 없었지만)를 이미지로 잘 표현할 수 있을까 고민을 했다. 고민 끝에 불현듯 다시 펜로즈의 “불가능한 삼각형”이 머리에 떠올랐다. 그것은 공존하는 것이 불가능해 보이는 서로 다른 세 관점이 하나의 전체를 이루는 것이다. 그렇게 해서 만들어진 이미지가 [그림5]이다.
그렇다면 도대체 왜 양자 삼위일체의 세 관점은 본질적으로 같은 것일까? 이 질문에 답을 하기 위해서, 우선 파동 함수의 관점과 경로 적분의 관점이 같다는 것을 이해하도록 하자. 이 목표를 이룬 후에는 파동 함수의 관점이 연산자의 관점과 같다는 것을 이해하도록 하자.
경로 적분은 폴 디랙Paul Dirac의 초기 아이디어를 바탕으로 리처드 파인만Richard Feynman이 정립했다. 얘기를 시작하기 위해서 슈뢰딩거 방정식으로 다시 돌아가 보자. 잘 생각해 보면 지금까지 슈뢰딩거 방정식을 쓰기만 했지 어떻게 푸는지에 대해서는 전혀 얘기하지 않았다. 사실 슈뢰딩거 방정식을 실제로 푸는 것은 아주 특별한 경우를 제외하고는 매우 어렵다(이러한 특별한 경우 중에서 몇 가지를 이번 연재 글 중에서 얘기할 수 있을지 모르겠다). 하지만 다행히도 실제로 풀지 않고 얘기할 수 있는 것들이 생각보다 꽤 많다!
슈뢰딩거 방정식은 미분 방정식이다. “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 언급했듯이 미분 방정식은 어떤 함수의 미분값을 포함하는 방정식인데, 불행히도 2차 방정식의 근의 공식과 같은 일반적인 해법이 없다. 대신 슈뢰딩거 방정식을 약간 변형하여 미분이 필요 없는 형태로 바꿀 수는 있다. 바로 이 형태가 경로 적분이다. 거칠게 말하자면 경로 적분은 미분 방정식을 적분의 형태로 바꾼 것이다. 자, 이제부터 이 변형이 어떻게 가능한지 알아보자.
여러 파동 중에서 가장 중요한 파동은 정상파standing wave이다. 정상파가 중요한 이유는 시간이 흘러도 사라지지 않고 자기 자신의 형태를 유지하며 주어진 장소에 머무르기(영어 이름 그대로 standing) 때문이다. 정상파가 생기는 조건은 피리와 같은 얇은 관에서 공명 현상이 일어나는 조건과 같다. 수학적으로 말해서, “믿기 힘든 양자 Incredible Quantum [1]: 들어가기”에서 언급했듯이, 정상파를 얻기 위해서는 경계 조건에 맞추어 슈뢰딩거 방정식을 풀어야 한다. 조금 더 구체적으로 말해서, “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 언급했듯이, 정상파는 해밀토니안의 고유함수가 되는 조건으로부터 얻을 수 있다.
정상파는 여러 개 존재할 수 있으므로 편의상 \(n\)번째 정상파를 \(\varphi_n\)이라 부르고 그것의 에너지 고유값을 \(E_n\)이라고 부르도록 하자. 그렇다면 정상파의 조건은 다음과 같다.
\[
\hat{H}\varphi_n({\bf r})=E_n \varphi_n({\bf r})
\]현 시점에서는 위 방정식을 실제로 어떻게 풀 수 있는지에 대해서 고민하지 말자. 조금 무책임한 것 같지만, 어찌어찌해서 풀 수 있다고만 하자. 참고로 여기서는 해밀토니안이 시간에 따라 변하지 않는다는 가정을 했다. 따라서 위 정상파 방정식은 매 시간마다 모두 성립하는 방정식이다. 전문적으로 이러한 방정식을 “시간 독립적인 슈뢰딩거 방정식time-independent Schrödinger equation”이라고 부른다.
이제 정상파를 시간 미분을 포함한 완전한 형태로 쓰인 슈뢰딩거 방정식에 넣어보자. 우리의 목적은 정상파가 시간에 따라서 어떻게 변하는지 아는 것이다.
\[
i\hbar\frac{\partial}{\partial t}\varphi_n({\bf r},t)=\hat{H}\varphi_n({\bf r},t)=E_n \varphi_n({\bf r},t)
\]위 방정식에서는 시간에 대한 미분이 있으므로, 파동 함수의 시간 의존성을 명시적으로 표시하였다. 이 방정식의 해는 시간의 함수로 아주 쉬운 함수이다. 다시 말해서 시간 의존성은 “믿기 힘든 양자 Incredible Quantum [2]:가장 순수한 형태의 파동”에서 설명한 오일러의 공식에 의해서 기술된다.
\[
\varphi_n({\bf r},t)= e^{-iE_n t/\hbar} \varphi_n({\bf r})
\]약간 시적으로 표현하면, 정상파는 각각 자기 고유의 주파수\(\omega_n=E_n/\hbar\)를 가지고 진동하는 가장 순수한 형태의 파동이다.
당연한 말 같지만 임의의 파동이 항상 정상파인 것은 아니다. 그렇다면 초기에 어떤 임의의 파동이 있었다면[전문적으로 초기 조건initial condition이라 부른다] 그 파동은 시간에 따라 어떻게 변하는 것일까? 복잡한 질문인 것 같지만 생각보다 쉬운 해법이 존재한다. 임의의 파동이 시간에 따라 어떻게 변하는지를 즉각 예측하기는 어렵지만, 우리는 원칙적으로 모든 정상파들이 시간에 따라 어떻게 변하는지 알고 있다. 따라서 만약에 임의의 파동을 정상파들의 합으로 분해할 수 있다면, 시간이 흐른 후의 파동은 시간에 따라 각각 자기 고유의 주파수를 가지고 진동하는 정상파들을 다시 다 더하면 될 것이다.
위 내용을 수학적으로 표현하면 다음과 같다. 초기에 주어진 어떤 파동함수가 다음과 같이 정상파들의 합으로 분해된다고 하자.
\[
\psi_0({\bf r})=\sum_n c_n \varphi_n({\bf r})
\]그렇다면 시간이 흐른 후의 파동은 다음과 같이 쓰이게 된다.
\[
\psi({\bf r},t)=\sum_n c_n e^{-iE_n t/\hbar} \varphi_n({\bf r})
\]이것이 의미하는 바는, 정상파들을 모두 구할 수 있다면 원칙적으로 임의의 파동이 어떻게 시간에 따라서 변하는지, 즉 시스템의 동역학dynamics을 알 수 있게 된다는 것이다.
이 시점에서 다음과 같은 의문을 품는 독자가 있을지 모르겠다. 임의의 파동 함수는 언제나 정상파들의 합으로 완벽하게 분해될 수 있는가? 혹시 분해가 안 되고 남는 자투리가 생기지는 않을까? 다행히도, 여기서 자세하게 증명할 수는 없지만, 임의의 파동 함수는 언제나 하나의 자투리 없이 정상파들의 합으로 완벽하게 분해될 수 있다. 이 성질을 전문적으로 “정상파들은 완전성completeness을 지닌다”라고 표현한다.
이제까지 일반적인 해밀토니안에 대해서 얘기를 했다. 물리적인 직관을 얻기 위해서 실제로 풀 수 있는 해밀토니안에 대해서 위 결과를 적용해 보자. 앞서 언급했듯이 우리가 정확히 풀 수 있는 문제는 매우 제한적이다. 우리가 정확히 풀 수 있는 문제 중에서 가장 기본적이지만 중요한 문제는 입자가 상호작용하지 않고 자유롭게 날아다니는 시스템, 즉 자유 입자 시스템free particle system이다. 이 경우의 정상파는 다름 아닌 “가장 순수한 형태의 파동”인 평면파plane wave이고, 그것의 에너지 고유값은 다름 아닌 운동 에너지이다. 자유 입자 시스템에 대해서 위 논의를 적용한 결과를 단계별로 정리하면 다음과 같다. 편의상 논의를 1차원 문제로 국한시키자.
- 초기에 주어진 파동을 평면파로 분해한다. \[\psi_0(x)=\sum_k c_k e^{ikx}\]여기서 \(k\)는 파장의 역수인 파수wave number이다
- 분해된 평면파는 각각 자기 고유의 운동 에너지로 진동한다. \[e^{ikx} \rightarrow e^{i(kx-\omega_k t)}\]여기서 평면파의 주파수 \(\omega_k\)는 평면파의 운동 에너지 나누기 플랑크 상수이다.\[\omega_k= \frac{\hbar k^2}{2m}\]
- 시간이 흐른 후의 파동은 각각 따로 진동하는 평면파를 다시 더해서 얻어진다.\[\psi(x,t)=\sum_k c_k e^{i(kx-\omega_k t)}\]
위에서 매우 중요한 수학 아이디어가 하나 쓰였다. 어찌보면 과학과 공학에서 쓰이는 모든 수학 중에서 중요도로 따지면 미적분에 비할 수 있을 만큼 중요한 아이디어다. 그것은 바로 “푸리에 변환Fourier transform”이다.
푸리에 변환이란 무엇인가? 푸리에 변환을 쉽게 설명하면 다음과 같다. 어떤 음악이 연주되고 있다고 하자. 푸리에 변환은 이 음악 속에 섞여 있는 여러 음을 주파수별로 분해해서 각각의 음이 얼마나 세게 나타나는가를 알아내는 것이다. 이것을 머릿속에서 할 수 있다면 그야말로 완벽한 절대 음감sense of absolute pitch을 가진 것이다. 각각의 음으로 분해된 정보를 다시 조합해서 원래의 음악으로 복원할 수도 있는데, 이것을 “역 푸리에 변환inverse Fourier transform”이라고 한다. 이렇게 시간에 따라 변화하는 음악과 주파수별로 분해된 음의 세기 사이의 변환을 푸리에 변환이라고 한다.
시간과 주파수 사이의 푸리에 변환처럼 공간과 파수 사이에도 비슷한 푸리에 변환이 존재한다. 위에서 설명한 첫 번째 단계는 바로 초기에 주어진 파동을 파수별로 분해하는 푸리에 변환인 것이다. 그렇다면 두 번째 단계는 파수별로 분해된 평면파에 각각 자기 고유의 주파수를 붙여주고 진동하게 하는 것이다. 마지막으로 세 번째 단계는 이렇게 각각 진동하는 평면파를 조합해서 시간이 흐른 후의 파동을 공간의 함수로 재구성하는 것이다. 즉 파수의 함수에서 공간의 함수로 가는 역 푸리에 변환이다.
참고로 역 푸리에 변환은 평면파에서 파수의 부호를 바꾼 후에 더하면 된다. 즉 초기에 주어진 파동에 대해서 역 푸리에 변환을 적용하면, 각각 평면파의 계수 \(c_k\)를 다음과 같이 구할 수 있다.
\[
c_k =\int^{\infty}_{-\infty} d x^\prime \psi_0(x^\prime) e^{-ikx^\prime}
\]여기서 공간 적분에 쓰이는 가변수dummy variable는 이전의 \(x\)와 구분하기 위해서 \(x^\prime\)을 썼다.
지금까지 포기하지 읽고 있는 독자들에게 희망을 주자면, 알게 모르게 우리는 우리의 첫 번째 목표에 반 이상 다다랐다. 기억을 되살리기 위해서, 우리의 첫 번째 목표는 양자 삼위일체 중에서 파동 함수의 관점과 경로 적분의 관점이 왜 같은지 이해하는 것이다. 포기하지 말고 조금만 더 가 보자.
다시 본 논의로 돌아가 보자. 앞선 세 번째 단계에서 얻은 파동 함수에 바로 위에서 구한 평면파의 계수를 구하는 역 푸리에 변환 공식을 집어넣어 보자.
\[
\psi(x,t)=\sum_k e^{i (kx-\omega_k t)} \int^{\infty}_{-\infty} d x^\prime \psi_0(x^\prime) e^{-i k x\prime}
=\int^{\infty}_{-\infty} d x^\prime U(x,x^\prime;t) \psi_0(x^\prime)
\]여기서 \(U(x,x^\prime;t)\)는 다음과 같이 주어진다.
\[
U(x,x^\prime;t)=\sum_k e^{-i \frac{\hbar t}{2m}k^2}e^{i k(x-x^\prime)}
\]\(U(x,x^\prime;t)\)는 영어로 “프로파게이터propagator”라고 불리며 우리 말로는 “전파 인자”라고 불린다. 프로파게이터가 전파 인자로 불리는 이유는 “propagator”의 다른 이름으로 “transition amplitude”가 있는데, 이것을 직역하면 전파 인자가 되기 때문이다. 어쨌든 이제 전파 인자를 구체적으로 계산하기 위해서 위 공식에 나타난 합을 모든 가능한 파수 \(k\)에 대해서 취하면 된다. 하지만 구체적으로 계산하기 전에 앞선 식의 의미를 먼저 생각해보자.
앞선 식의 의미는 시간이 흐른 후의 파동 함수는 초기에 주어진 파동 함수(즉, 초기 조건)에 전파 인자를 곱한 후 초기 파동 함수의 공간 변수에 대해서 모두 적분하면 나온다는 것이다. 다시 말해서, 필자가 미리 언급했듯이, 슈뢰딩거 방정식이라는 미분 방정식을 푸는 대신에 초기 조건에 적절한 적분을 하면 된다는 것이다.
이제 구체적으로 전파 인자를 계산하는 문제로 돌아가 보자. 그런데 이때 조금 기술적인 질문 하나가 발생한다. 파수는 연속적인 변수인데 어떻게 정수와 같이 띄엄띄엄 떨어진 변수처럼 하나하나 더할 수 있을까? 다시 말해서, 평면파를 하나하나 따로 셀 수 있는가? 이 질문에 대한 답은 “평면파가 유한한 크기의 공간 안에 존재하면 하나하나 셀 수 있다”이다. 그 이유는 유한한 공간에 존재하는 평면파의 파수는 얇은 관에서 공명을 일으키는 주파수와 정확히 같은 공식으로 양자화되기 때문이다. 구체적으로 공간의 크기를 \(L\)이라고 할 때, 파수는 \(k=2\pi n/L\)로 양자화된다. 여기서 \(n\)은 정수이다. 이제 공간을 점점 키우면, 서로 인접한 평면파들의 파수 차이는 점점 줄어들어서 파수 자체가 거의 연속적인 변수가 된다. 따라서 공간의 크기를 무한으로 보내는 극한을 취하면 평면파에 대한 합은 적분으로 바뀐다.
\[
\sum_k f(k) \rightarrow \int^{\infty}_{-\infty} \frac{dk}{2\pi} f(k)
\]여기서 적분 변수를 \(2\pi\)로 나눈 것은 파수가 양자화되는 값에 들어있는 \(2\pi\)때문이다. 이제 전파 인자를 구하는 공식을 적분 형태로 다시 써 보자.
\[
U(x,x^\prime;t)=\int^{\infty}_{-\infty} \frac{dk}{2\pi} e^{-ak^2+bk}
\]여기서 \(a=i\hbar t/2m\)이고 \(b=i(x-x^\prime)\)이다. 이렇게 이상하게 생긴 적분을 도대체 어떻게 계산할 수 있을까?
사실 위에 쓰인 적분은 물리학자들과 수학자들(특히 통계학자들)에게 가장 중요한 적분 중의 하나이다. 이 적분은 일반적으로 “가우시안 적분Gaussian integral”이라고 불린다. 가우시안 적분의 결과를 가장 표준적인 형태로 쓰면 다음과 같다.
\[
\int^{\infty}_{-\infty} dx e^{-x^2} =\sqrt{\pi}
\]여기서 이 적분 결과가 어떻게 얻어지는지에 대해서 길게 얘기하지는 않을 것이다. 다만 여러 방법 중에서 프랑스 수학자 푸아송Poisson이 개발한 방법이 있는데, 그 방법에는 상상을 초월하는 천재성이 깃들여져 있다. 이 적분을 직접 계산하는 것은 쉽지 않은데, 이 문제를 돌파하기 위해서 푸아송은 원래 1차원 변수에 관한 적분을 제곱해서 2차원 변수에 관한 적분으로 바꾸는 방법을 고안한다. 이 2차원 적분은 생각보다 쉽게 계산된다. 잘 풀리지 않는 문제를 더 높은 차원에서 바라보니 쉽게 풀 수 있게 된 것이다. 인생의 좌우명으로 삼을 만큼 심오하지 않은가? 자세한 유도 과정은 Wikipedia에 “Gaussian integral”이라고 치면 찾을 수 있다.
위 표준 형태를 약간의 변수 변환을 통해 다시 쓰면 다음과 같이 쓸모가 굉장히 많은 일반적인 형태로 바꿀 수 있다.
\[
\int^{\infty}_{-\infty} dx e^{-ax^2+bx} =\sqrt{\frac{\pi}{a}} e^{\frac{b^2}{4a}}
\]이 형태는 위에서 우리가 전파 인자를 계산하기 위해서 필요한 바로 그 적분이다. 이 적분 결과를 이용해서 전파 인자를 계산하면 다음과 같다.
\[
U(x,x^\prime;t)=\sqrt{\frac{m}{2\pi i \hbar t}} e^{\frac{im}{2\hbar t}(x-x^\prime)^2}
\]이것이 의미하는 바는 무엇인가?
전파 인자의 의미를 알기 위해서 위 공식을 아래와 같이 다듬어 보자.
\[
U(x,x^\prime;t)=\sqrt{\frac{m}{2\pi i \hbar t}} e^{\frac{i}{\hbar}S(x,x^\prime;t)}
\]여기서 \(S(x,x’;t)\)는 다음과 같이 정의된다.
\[
S(x,x’;t)=\frac{1}{2}m\left(\frac{x-x^\prime}{t}\right)^2 t
\]여기서 \(S(x,x’;t)\)는 사실 단순히 운동 에너지와 시간의 곱에 불과한데 그 이유는 \((x-x^\prime)/t\)가 속도이기 때문이다. 하지만 지금 이 순간 왜 이렇게 하는지 아직 독자들은 모르겠지만 \(S(x,x’;t)\)에는 특별한 이름이 붙어있다. 그 이름은 바로 “작용action”이다.
\(S(x,x’;t)\)에 왜 작용이라는 특별한 이름이 붙어 있는지 알기 위해서, 공간에 (스칼라) 퍼텐셜 에너지가 \(V\)라는 상수 값으로 걸려 있는 경우를 생각해 보자. 이제까지 전파 인자를 구하는 과정을 복기해 보면, 상수인 퍼텐셜 에너지가 걸려 있을 때 생기는 유일한 차이는 평면파의 주파수가 다음과 같이 바뀌는 것이다.
\[
\omega_k=\frac{1}{\hbar}\left(\frac{\hbar^2 k^2}{2m}+V\right)
\]이제 가우시안 적분을 비롯한 이전 과정을 정확히 반복하면 다음과 같은 작용이 얻어진다.
\[
S(x,x’;t)=\left[\frac{1}{2}m\left(\frac{x-x^\prime}{t}\right)^2-V\right] t
\]퍼텐셜 에너지의 앞에 있는 부호가 바뀐 것을 눈치챈 독자가 있는가? 처음 보면 별 것 아닌 것처럼 보일 수 있다. 하지만 이것은 작용이 단순히 전체 에너지, 즉, 운동 에너지와 퍼텐셜 에너지의 합에 시간이 곱해진 것이 아님을 의미한다. 대괄호 안에 있는 양은 운동 에너지와 퍼텐셜 에너지의 차이이다. 사실 이 양도 물리적으로 매우 중요한 개념이어서 특별한 이름이 붙어 있다. 그 이름은 바로 “라그랑지안Lagrangian”이다. 결론적으로 작용은 전체 에너지와 시간의 곱이 아니라 라그랑지안과 시간의 곱(바로 아래 자세히 나오지만, 일반적으로는 라그랑지안의 시간에 관한 적분)으로 주어진다.
이제 퍼텐셜 에너지가 공간에 따라 임의로 변하는 일반적인 상황을 생각해 보자. 예상했겠지만 이 경우에는 전파 인자를 깔끔하게 계산할 수 없다. 하지만 굉장히 짧은 시간 동안에는 퍼텐셜 에너지가 거의 변하지 않을 테니, 이 짧은 시간 구간에서는 위에서 구한 전파 인자를 그대로 쓸 수 있을 것이다. 그렇다면 이 짧은 시간이 지난 이후에 얻어지는 파동 함수는 초기 시각 \(t_0\)의 파동 함수에 위에서 구한 전파 인자를 곱해서 초기 공간 변수 \(x_0\)에 대해서 적분하면 될 것이다.
\[
\psi(x_1,t_1)= \int^{\infty}_{-\infty} dx_0 U(x_1,x_0;\delta t) \psi(x_0,t_0)
\]여기서 시간 차이 \(\delta t\)는 물론 \(t_1-t_0\)이고, \(U(x_1,x_0;\delta t)\)는 다음과 같이 쓰인다.
\[
U(x_1,x_0;\delta t)= \sqrt{\frac{m}{2\pi i \hbar \delta t}} e^{\frac{i}{\hbar}\left[\frac{1}{2}m\left(\frac{x_1-x_0}{\delta t}\right)^2-\frac{1}{2}\left(V(x_1)+V(x_0)\right)\right] \delta t }
\]위에서 굉장히 짧은 시간 구간 동안에 느껴지는 퍼텐셜 에너지는 그 기간 동안의 퍼텐셜 에너지의 평균값으로 정했다. 아주 복잡하게 보이지만 자세히 보면 위 전파 인자는 오일러의 공식에 의해 주어지는 “가장 순수한 형태의 파동”과 같은 형태를 지니고 있다. 즉, 다음과 같이 다시 정리해 볼 수 있다.
\[
U(x_1,x_0;\delta t)= A(\delta t) e^{\frac{i }{\hbar} S(x_1,x_0;\delta t)}
\]어찌 보면 전파 인자는 작용 \(S(x_1,x_0;\delta t)\)라는 양이 위상각의 역할을 하는 평면파라는 것이다. 참고로 앞에 붙는 계수 \(A(\delta t)\)는 주된 논의에 있어서 크게 중요하지 않다.
비슷하게, 다시 굉장히 짧은 시간이 흐른 후의 다음 시각 \(t_2\)의 파동 함수는 \(t_1\)의 파동 함수에 다시 전파 인자를 곱하고 \(x_1\)에 대해서 적분하면 된다.
\[
\psi(x_2,t_2)= \int^{\infty}_{-\infty} dx_1 U(x_2,x_1;\delta t) \psi(x_1,t_1)
\]그런데 여기서 생각나는 아이디어 하나. 우리는 \(\psi(x_1,t_1)\)을 초기 시간 \(t_0\)의 파동 함수 \(\psi(x_0,t_0)\)에 전파 인자를 곱해서 적분하는 형식으로 표현할 수 있지 않은가? 다시 말해서 전파 인자를 2번 연거푸 써서 위 공식을 다음과 같이 다시 쓸 수 있다.
\[
\psi(x_2,t_2)= \int^{\infty}_{-\infty} dx_1 \int^{\infty}_{-\infty} dx_0 U(x_2,x_1;\delta t) U(x_1,x_0;\delta t) \psi(x_0,t_0)
\]그렇다면 이런 과정을 계속 반복하면 최종 시각 \(t_N\)의 파동 함수를 다음과 같이 얻을 수 있다.\[\psi (x_{ N },t_{ N })=\int _{ -\infty }^{ \infty } dx_{ N-1 }\cdots \int _{ -\infty }^{ \infty } dx_{ 1 }\int _{ -\infty }^{ \infty } dx_{ 0 }\\ \times U(x_{ N },x_{ N-1 };\delta t)\cdots U(x_{ 2 },x_{ 1 };\delta t)U(x_{ 1 },x_{ 0 };\delta t)\psi (x_{ 0 },t_{ 0 })\]이제 위 수식에서 적분 순서를 약간 정리를 하면 다음과 같은 최종 형식에 도달하게 된다.
\[
\psi(x_N,t_N)= \int^{\infty}_{-\infty} dx_0 U(x_N,x_0;t_N-t_0) \psi(x_0,t_0)
\]여기서 최종적인 전파 인자 \(U(x_N,x_0;t_N-t_0)\)는 다음과 같이 주어진다(편의상 중요하지 않은 비례 계수는 생략하였다).
\[
U(x_N,x_0;t_N-t_0)= \int^{\infty}_{-\infty} dx_{N-1} \cdots \int^{\infty}_{-\infty} dx_1 e^{\frac{i }{\hbar} S(x_N,x_0;t_N-t_0)}
\]위 수식에서 지수 함수에 들어가는 작용 \(S(x_N,x_0;t_N-t_0)\)는 다음과 같다.\[S(x_{ N },x_{ 0 };t_{ N }-t_{ 0 })=S(x_{ N },x_{ N-1 };\delta t)+\cdots +S(x_{ 2 },x_{ 1 };\delta t)+S(x_{ 1 },x_{ 0 };\delta t)\\ =\int _{ t_{ 0 } }^{ t_{ N } } dt\left[ \frac { 1 }{ 2 } m\left( \frac { dx }{ dt } \right) ^{ 2 }-V(x) \right]\]작용이 위와 같이 정리되는 이유는 각각의 짧은 시간 동안의 전파 인자를 다 곱하는 것은 결국 그것들의 작용을 다 더하는 것과 같기 때문이다. 결론적으로 작용은 주어진 경로, 즉 위치 \(x\)가 시간 \(t\)에 대해서 어떤 주어진 함수로 주어질 때, 그 함수의 형태에 따라 결정되는 라그랑지안을 시간에 대해서 적분해서 얻어진다. 여기서 라그랑지안은 다음과 같이 정의된다.
\[L\left(x,\frac{dx}{dt}\right)=\frac{1}{2}m\left( \frac{dx}{dt} \right)^2 -V(x)\]다시 한 번, 라그랑지안에서는 퍼텐셜 에너지 앞의 부호가 음수임을 명심하라!
이제 우리는 최종 결론에 도달했다. 이전 글 “믿기 힘든 양자 Incredible Quantum [2]: 가장 순수한 형태의 파동”에서 오일러의 공식은 다음과 같이 주어진다고 했다.
\[
e^{i \theta}= \cos{\theta} +i \sin{\theta}
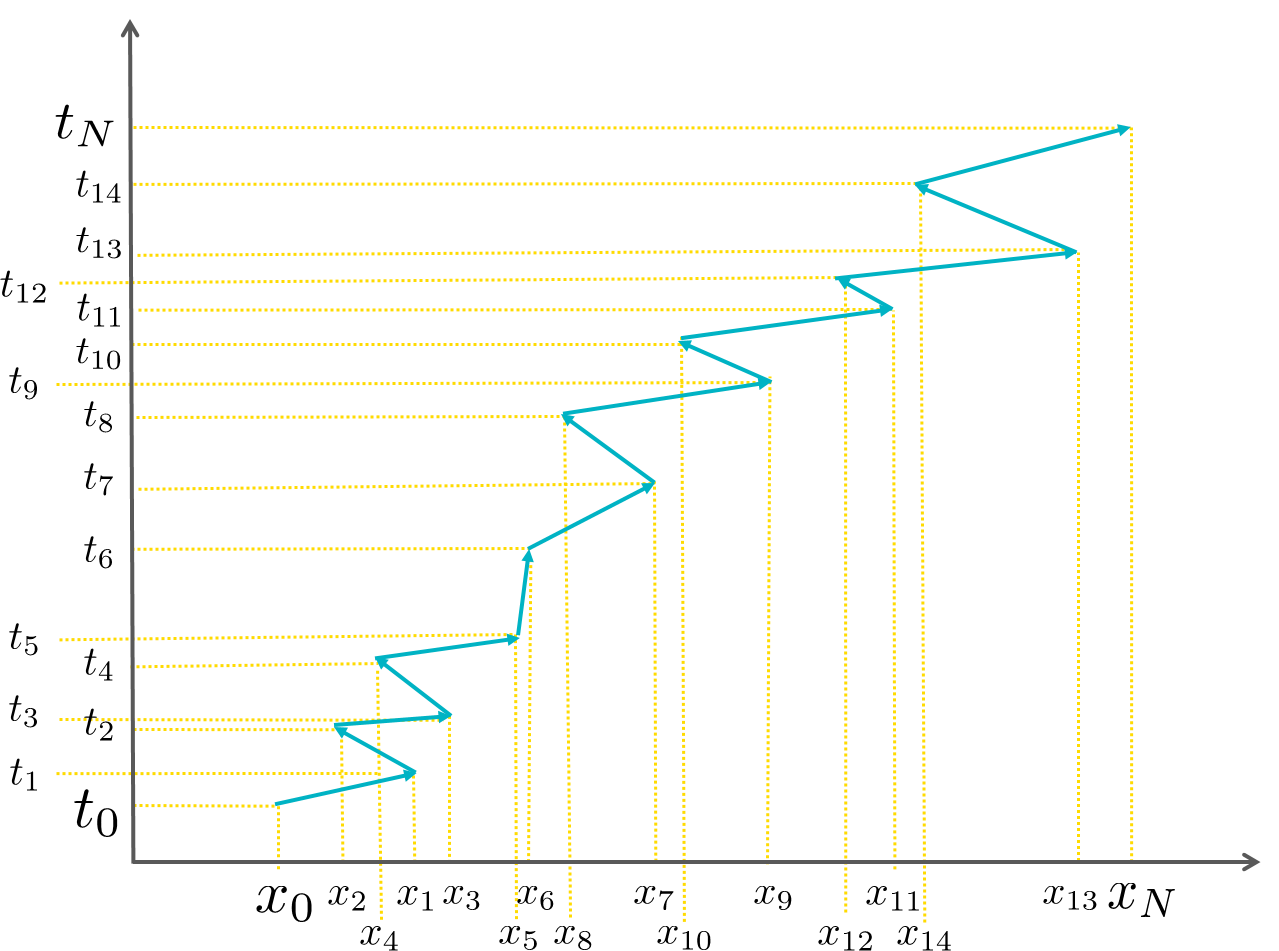
\]편의상 오일러의 공식이 주는 양을 앞으로 위상 인자phase factor라고 부르도록 하자. 앞에서 설명했듯이 전파 인자를 위한 공식을 살펴 보면, 위상 인자의 위상각의 자리에 작용이 들어간다는 것을 알 수 있다. 따라서 전파 인자는 작용이 위상각의 역할을 하는 위상 인자를 모든 가능한 경로에 대해서 적분을 해서 얻어지는 것이다. 여기서 모든 가능한 경로에 대해서 적분을 한다는 것은 중간 시점에서 발생하는 모든 공간 변수, 즉 \(x_1\), \(x_2\), …, \(x_{N-1}\)에 대해서 적분을 한다는 의미이다. 이를 시각적으로 표현하면 [그림8]과 같다.
구체적으로 [그림8]은 어떤 입자가 초기 시각 \(t_0\)에 위치 \(x_0\)로부터 출발해서 다양한 중간 지점을 거쳐서 최종 시각 \(t_N\)에 위치 \(x_N\)에 도달하는 임의의 한 경로를 표현한 것이다. 경로 적분은 이 경로를 포함한 모든 경로에 할당된 작용 값을 위상 인자의 위상각 자리에 집어 넣은 후 모두 다 더하면 얻어진다. 약간 우화적으로 말해서, 각 경로마다 나침반이 있는데 나침반의 바늘이 가리키는 방향이 위상각을 의미한다고 하자. 이 나침반의 바늘은 주어진 경로에 따라서 돌아가는 정도가 다 다르다. 경로 적분은 모든 주어진 경로에 따라서 나침반 바늘이 돌아간 정도를 다 더해서 “평균”을 내는 것이다. 다시 말해서 전파 인자는 초기 시각 \(t_0\)에 위치 \(x_0\)로부터 출발해서 최종 시각 \(t_N\)에 위치 \(x_N\)에 도달하는 사이에 나침반 바늘이 평균적으로 얼마나 돌아간 것인가를 재는 것이다.
드디어 우리는 “믿기 힘든 양자 Incredible Quantum [1]: 들어가며”에서 소개된 영화 <컨택트 Arrival>(2016)에서 외계인들이 세상의 모든 가능한 사건들을 동시에 본다는 것이 수학적으로 어떤 의미인지 알게 되었다. 약간 시적으로 말해서, 입자는 모든 가능한 경로를 다 거쳐서 이동하며, 입자의 확률을 주는 파동 함수는 모든 가능한 방식으로 출렁거린다. 여기서 중요한 점은 전혀 인과성이 없는 출렁거림을 포함해서 그야말로 모든 가능성이 더해져야 한다는 사실이다.
다만 모든 출렁거림이 똑같이 중요한 것은 아니다. 위에서 든 우화를 통해서 설명하면, 여러 경로 중에서 나침반 바늘이 돌아가는 정도가 평균값에 가까우면 가까울수록 중요한 경로인 것이다. 그렇다면 나침반의 바늘이 돌아가는 정도가 가장 평균값에 가까운 경로는 무엇일까?
위 질문에 대한 답은, 작용이 위상각(나침반 바늘이 돌아가는 정도)의 역할을 하고 있으므로 자신의 작용값이 그 “주변”에 있는 다른 경로들의 작용값과 거의 같은 경로이다. 다시 말해서 주변의 경로와 서로 보강 간섭constructive interference을 하는 경로이다. 수학적으로 말해서 우리는 작용값이 경로를 바꿈에 따라서 거의 변하지 않는 경로를 찾아야 한다. 여기서 잠깐…
우리는 어떤 함수가 변수를 바꿈에 따라서 그 값이 거의 변하지 않는 점을 찾는 방법을 알고 있다. 그 방법은 다름이 아니라, 미적분calculus이다. 구체적으로 함수의 미분값이 0인 점을 찾는 것이다. 미분값이 0이라는 것은 기울기가 0이라는 의미이고, 기울기가 0이라는 것은 함수값이 국소적으로 최고점이나 최저점에 있다는 의미이다. 그런데 위에서 우리에게 주어진 임무는 작용값이 거의 변하지 않는 경로를 찾아야 한다는 것이다. 그런데 경로는 그 자체로 시간에 따라서 공간 상의 위치가 결정되는 함수이다. 따라서 작용값은 어떤 경로 함수가 주어지면 계산되는 하나의 숫자이다. 이렇게 함수 하나가 주어지면 숫자 하나를 만들어내는 수학적 작업을 범함수functional라고 부른다. 물론 보통 함수는 숫자 하나가 주어지면 다른 숫자 하나를 만들어내는 수학적 작업이다. 우리의 임무는 경로 함수를 바꾸어 가면서 작용값의 변화가 0인 경로 함수를 찾아야 하는 것이다. 전문적으로 주어지는 함수에 대해서 범함수 값의 변화량이 0이 되는 함수를 계산하는 방법을 변분법calculus of variations이라고 한다.
여기서 자세하게 유도할 수는 없지만, 작용값에 변분법의 원리를 적용하면 라그랑지안이 다음과 같은 미분방정식을 만족해야 한다는 사실을 보일 수 있다.\[\frac{\partial L}{\partial x}-\frac{d}{dt} \frac{\partial L}{\partial(dx/dt)}=0\]여기서 우리에게 중요한 사실은 위 미분방정식에 앞서 구한 라그랑지안의 형태를 집어 넣고 계산하면 다음과 같은 결론을 얻어진다는 사실이다.\[m\frac{d^2 x}{d t^2}=-\frac{\partial V}{\partial x}\]이 공식이 의미하는 바는 무엇인가? 그것은 바로 고전역학적인 뉴턴의 운동 방정식, \(F=ma\)이다!
무슨 일이 일어났는가 생각해 보자. 파동 함수의 관점이 경로 적분의 관점과 정확히 같다는 것을 증명하는 과정에서 예기치 않은 부산물을 얻었다. 그것은 양자역학과 고전역학의 연결고리이다. 다시 말해서 전파 인자를 잘 분석하면 입자의 운동을 뉴턴의 운동방정식을 따르는 고전적인 궤도에 어느 정도의 양자역학적인 출렁거림, 전문적으로는 양자 요동quantum fluctuation이 덧붙여진 형태로 이해할 수 있다는 것이다(양자 요동이 얼마나 큰가 작은가는 시스템에 따라서 다르다). 이렇게 보면 경로 적분은 고전역학과 양자역학을 자연스럽게 연결시킬 수 있는 관점인 것이다.
그런데 가만히 생각해 보면 경로 적분의 관점에서는 파동 함수가 굳이 필요 없다. 어떤 의미로 파동 함수는 단지 초기 조건을 주는 것이다. 파동 함수이야말로 고전역학적으로 이해하기 힘든 개념인데, 경로 적분의 관점에서는 그것이 굳이 필요 없다는 것이다. 물론 파동 함수가 없어진 대신 다른 큰 단점이 있다. 정상파는 당연히 파동 함수 중의 하나이므로 경로 적분의 관점에서는 정상파를 이해하는 것이 자연스럽지 않다. 예를 들어 경로 적분의 관점에서는 원자의 전자 구조를 이해하는 것이 쉽지 않다. 원자의 전자 구조를 정확히 예측한 것이 초기에 양자역학을 정립하는 데에 지대한 역할을 했다는 역사적 사실을 생각할 때, 이것은 꽤 큰 단점이다. 세상은 공평하다고 했던가?
지금까지 파동 함수의 관점이 왜 경로 적분의 관점과 같은지 설명하였다. 다음에 이어질 2부에서는 파동 함수의 관점이 왜 연산자의 관점과 같은지 이해해 보자. 연산자의 관점에 붙은 다른 이름은 하이젠베르크의 “행렬역학matrix mechanics”이다.
[후록]
요즈음 필자는 “믿기 힘든 양자 Incredible Quantum” 시리즈를 읽고 있는 독자들로부터 이따금씩 이메일을 받을 때가 있다. 재미있게 읽고 있다는 얘기를 들을 때면 “아, 이런 보람으로 글을 쓰는구나”라는 느낌이 든다. 특히 몇몇 독자들이 평소 양자역학에 대해서 무척 궁금해 하던 질문들에 대해서 답을 못 찾고 있었는데, “믿기 힘든 양자”가 많은 도움이 되었다는 이메일을 보내 왔다. 참으로 고맙고 반가운 반응이다.
이러한 질문 중의 하나로 “양자역학은 왜 꼭 허수를 필요로 하는 것일까?”라는 질문이 있었다. 지금까지 “믿기 힘든 양자 Incredible Quantum”를 꾸준히 읽고 있는 독자들은 알겠지만, 사실 이 질문은 필자가 이번 연재를 통해서 설명하고 싶은 가장 중요한 메시지 중의 하나이다. 이 질문을 한 독자는 “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”을 읽고 대강의 느낌을 얻을 수 있었지만 조금 더 자세한 설명이 있으면 좋겠다고 했다. 필자가 최대한 쉽고 자세하게 설명하려고 노력했지만, 아직도 미진한 면이 많구나 절실하게 느끼게 되었다.
그래서 필자에게 직접 이메일을 보낸 독자를 비롯해서 혹시 아직도 이 질문에 대해서 궁금증을 가지고 있는 독자들을 위해서, “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”의 일부분을 보강해서 HORIZON에 새로 실어 놓았다. 이것으로 궁금증이 완벽히 해소되지는 않겠지만, 보강된 글이 조금 더 나은 설명을 제공하기를 기대해 본다.
사실 이렇게 독자의 피드백을 받아서 글을 그때그때 고칠 수 있다는 것이 웹진의 가장 큰 장점 중의 하나가 아닌가 싶다. 앞으로도 독자들의 많은 관심을 부탁드린다.