Less is more.
-Ludwig Mies van der Rohe
루트비히 미스 반 데어 로에Ludwig Mies van der Rohe라는 다소 긴 이름을 가진 건축가가 있다. 미스 반 데어 로에는 현대 건축가 중에서 가장 영향력 있는 건축가 중의 한 사람으로 평가된다. 그는 1919년 독일 바이마르에 세워져1933년 나치에 의해서 강제 폐교되기까지 단지 14년 동안만 지속되었지만 현대 디자인에 큰 획을 그은 예술 학교인 바우하우스Bauhaus의 교장을 역임했다. 하지만 그것에 못지 않게 그는 다음과 같은 유명한 말을 남긴 사람으로 역사에 길이 남아 있다.
“Less is more.”
위 문장은 미니멀리즘minimalism의 철학을 가장 잘 압축해서 표현한 말로 유명하다. 너무나 유명해서 부연 설명하는 것이 불필요할 수도 있지만, 이번 글에서 얘기하고 싶은 주제와 깊은 연관이 있으므로 짧게 의미를 설명하고자 한다. 어떤 물체나 아이디어에는 가장 중요한 핵심이 있는데 보통 그 핵심은 다양한 “장식decoration”들에 의해 둘러싸여 있다. 이러한 장식들을 없애면 핵심에 집중할 수 있고, 그렇게 될 때 우리는 장식에 가려 미처 놓치고 있던 더 많은 것을 볼 수 있다.
미스 반 데어 로에의 철학을 가장 잘 담아낸 건축물 중의 하나로 손 꼽히는 건축물로 판스워스 하우스Farnsworth house가 있다. ([그림 1]) 미국 시카고의 다운타운에서 남서쪽으로 약 90km 정도 떨어진 일리노이Illinois주 플라노Plano시에 자리 잡고 있는 판스워스 하우스는 평평한 지붕 아래에 360도 사방이 유리로 둘러싸인 방 하나로 이루어진 지극히 간단한 구조의 건축물이다. 이 건축물은 시카고의 유명한 신장 전문의였던 에디트 판스워스Edith Farnsworth의 별장으로 지어졌는데, 그녀의 취미 중의 하나는 자연을 관찰하는 것이었다.
미스 반 데어 로에는 판스워스 하우스의 사방을 유리로 만들어서 집 밖의 자연을 관찰할 수 있는 기능을 최대화하였다. 하지만 판스워스 하우스는 단순히 집 밖의 자연을 가장 효과적으로 관찰하는 건축물에 머물지 않았다. 모든 장식적 요소를 배제하고 집이라는 건축물의 가장 핵심적인 요소만 남겨 둠으로써 자연을 가장 최소한으로 침해하였고, 결과적으로 자연의 조화로운 일부가 되었다.
하지만 판스워스 하우스는 많은 예술적인 건축물들이 그렇듯이 실제로 살기에는 다소 불편한 점이 많았다고 한다. [그림 1]에서 볼 수 있 듯이 판스워스 하우스는 사방이 유리로 둘러싸였기 때문에 사생활 보호와 보안에 취약했으며, 특히 에너지 효율이 너무 낮았다고 한다. 딱 보기에도 하루나 이틀 머물기에는 환상적이겠지만 매일 살라고 하면 상당히 불편했을 것이다.
여기서 집이란 무엇인가에 대해서 다시 한번 생각해 보지 않을 수 없다. 바꿔 말해서 집의 궁극적인 목표는 무엇일까? 그것이 사람이 살기에 편안한 것이라면 판스워스 하우스는 제대로 된 집이 아닐지 모른다. 그럼에도 불구하고 판스워스 하우스가 모든 장식적인 요소를 배제하고 집의 핵심만 남겨 놓은 것은 분명하다. 어떤 이는 판스워스 하우스야말로 집의 핵심을 잡아 낸 걸작으로 느낄 것이고, 다른 이는 그 안에서 살아갈 사람을 배려하지 않았으므로 집으로서 자격이 미흡하다고 느낄 것이다.
그렇다면 최소한으로 절제된 핵심과 궁극적인 목표 사이의 적절한 균형은 무엇일까? 이 즈음에서 앨버트 아인슈타인Albert Einstein의 다음과 같은 유명한 말을 곱씹어 볼 필요가 있다.
“Everything should be made as simple as possible, but not simpler.”
아인슈타인이 실제로 이 말을 했는지 안 했는지에 대해서는 약간의 논쟁의 여지가 있다고 한다. 하지만 이 말은 우리가 핵심에 다가서기 위해서 모든 것을 모조리 잘라내는 것이 아니라 적당한 순간에 멈추어 한다는 것을 알려 준다. 사실 이 말은 흔히 “오컴의 면도날Occam’s razor”라고 불리는 원칙을 설명하기 위해서 자주 인용되는 말이다. 오컴의 면도날은 한가지 현상을 설명하는 여러 이론이 있을 때에는 가장 단순한 이론을 선택해야 한다는 원칙이다. 아인슈타인이 강조하고 싶었던 사실은 이론을 최대한 단순화하되 중요한 핵심마저 잘라내서는 안 된다는 것이다.
오컴의 면도날은 논리적으로 엄밀한 원칙은 아니지만 과학 전반에 걸쳐서 새 이론을 세우거나 이전 이론을 검증할 때 중요한 지침이 된다. 조금 더 구체적으로 말해서, 과학자들이 하는 일은 자연의 모든 미세 행동을 그대로 모사하는 것이 아니라 자연 현상 중에서 설명하고 싶은 핵심만을 담은 모형model을 구축하고 그것을 풀어서 자연 현상과 비교하는 일이다. 오컴의 면도날이 말해 주는 바는 모형은 가장 단순할수록 좋다는 것이다.
오컴의 면도날을 생각할 때 필자의 머릿속에 떠오르는 이미지가 하나 있다. 20세기 가장 유명한 화가 중의 한 사람으로 손꼽히는 파블로 피카소Pablo Picasso는 다양한 현대 미술 화풍을 만들어 낸 것으로 유명하다. 피카소의 여러 유명한 그림 중에서 <황소The bull>라 불리는 판화가 있다([그림2]). <황소>는 총 11개의 작은 판화로 이루어진 연작인데, 각각의 판화는 하나의 황소를 다양한 수준의 추상화 단계에서 표현한다. 구체적으로, 황소는 맨 왼쪽 세로줄의 위에서 첫번째 판화에서 가볍게 스케치되어 있다. 이 황소는 바로 밑에 있는 판화에서 살이 붙어 크고 건장한 황소로 변한다. 그리고는 다시 그 밑에 있는 판화에서 황소는 몸 위에 몇 개의 미세한 선이 그어지며 면과 면이 서서히 구획되기 시작한다. 황소의 몸이 다면체로 변형된다는 사실은 왼쪽 두번째 세로줄의 맨 위에 있는 황소에서 두드러지게 되고 그 밑의 황소에서 절정을 맞는다. 이후의 판화에서 황소는 몸의 다면체 성질이 점점 없어지며 3차원에서 2차원으로, 급기야는 단지 선 몇 개로 이루어진 황소로 귀착된다.
자, 독자들에게는 어떤 황소가 가장 황소답게 보이는가? 실제의 황소에 가장 가까운 황소를 고르자면 당연히 가장 자세하게 그려진 맨 왼쪽 세로줄의 위에서 첫번째 혹은 두번째 황소일 것이다. 반면에 질문을 조금 바꾸어서 맨 오른쪽 세로줄의 가장 끝에 있는 황소도 황소처럼 보이느냐고 물어 본다면 아마도 그렇다고 답을 할 수 있을 것이다. 단지 선 몇 개만으로 황소를 나타낼 수 있다는 사실이 놀랍다. (물론 피카소가 그렸다고 하니까 그렇게 보이지 그냥 보통 아이가 그렸다고 하면 이게 무슨 황소이냐고 조금 더 자세하게 그리라고 핀잔을 줄 수도 있을 것이다.) 필자 개인적으로는 황소의 몸이 다면체로 변한 효과가 가장 극적으로 표현된 왼쪽 두번째 세로줄의 위에서 첫번째 혹은 두번째 황소가 가장 아름다워 보인다. 물론 이 즈음에서 “아름답다”의 기준은 무엇인가라는 또 다른 질문이 제기되지만…
지금까지 “믿기 힘든 양자 Incredible Quantum” 시리즈를 꾸준히 읽고 있는 독자들은 아직 필자가 양자역학의 전체적인 구조만 얘기하고 어떤 구체적인 문제도 풀지 않았다는 것을 알고 있을 것이다. 이제 구체적인 문제를 풀어 볼 때가 되었다. 자, 그렇다면 오컴의 면도날에 의해서 불필요한 장식을 모두 덜어낸 가장 핵심적인 양자역학 문제는 무엇일까? 다시 말해서, 어떤 이가 이 문제를 푼다면 양자역학의 핵심을 완벽하게 이해하고 있다고 인정할 수 밖에 없는 그런 문제가 있을까?
위 질문에 대해서 다양한 답이 나올 수 있다. 양자역학은 근본적으로 수소 원자hydrogen atom의 스펙트럼을 이해하는 과정에서 발견되었다. 따라서 수소 원자 문제는 가장 핵심적인 양자역학 문제로서 자격이 충분하다. 하지만 수소 원자 문제보다 조금 더 간결한 문제를 찾는다면, 고전역학의 진자pendulum나 용수철 문제의 양자역학 버전에 해당하는 포물선parabola 모양의 퍼텐셜 우물potential well에 갇힌 입자의 문제, 즉 조화 진동자harmonic oscillator 문제를 생각해 볼 수 있다. 필자 개인적으로는 조화 진동자 문제가 수소 원자 문제보다 조금 더 오컴의 면도날 원칙에 가깝다고 느껴진다. 만약 그것도 아니라면 입자를 1차원 에너지 장벽에 충돌시켜서 반사되거나 투과되는 입자의 확률을 계산하는 문제, 다른 말로 해서 산란scattering 문제가 가장 단순하고 중요하다고 주장할 수도 있다. 혹은 더 나아가서 본격적으로 슈뢰딩거 방정식을 쓸 필요조차 없는 영의 이중 슬릿 실험Young’s double-slit experiment만 알고 있어도 양자역학의 핵심을 알고 있는 것이라고 주장할 수도 있다. 물론 이 모두 다 중요한 문제들로 양자역학 강의에서 반드시 다루어져야 할 문제들이다.
하지만 필자가 생각하기에 가장 핵심적인 양자역학 문제는 두 상태 문제two-state problem이다. 이 문제는 문자 그대로 두 개의 상태만으로 이루어진 시스템의 동역학에 관한 문제이다. 양자역학에 대해서 전혀 알지 못 한다고 하더라도, 순수하게 논리적인 추론을 따라서 상태가 단 하나뿐인 시스템의 동역학은 명백하게 너무 단순할 것이다. 그 다음 후보자는 두 상태 문제이다. 처음 듣기에는 두 상태 문제도 지나치게 단순하다고 생각할 수 있다. 하지만 두 상태 문제는 단순함에도 불구하고 양자역학의 핵심을 놀라울 정도로 정확하게 담고 있다.
두 상태 문제
두 상태 문제의 구체적인 예를 하나 들어보자. 상당히 특별한 상황이기는 하지만 입자가 단지 두 점에만 위치할 수 있다고 하자. 예를 들면 입자가 W모양의 퍼텐셜 우물에 갇혀 있는 상황을 상상해 보자. 편의상 두 점 중에서 왼쪽 점을 \(L\)로 표시하고 오른쪽 점을 \(R\)로 표시하자. 이제 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 배운 브라-켓 표기법을 사용해서 입자가 왼쪽 점에 있는 상태를 \(|L\rangle\)이라고 하고, 오른쪽 점에 있는 상태를 \(|R\rangle\)이라고 하자. 참고로 [그림3]을 보라.
그렇다면 임의의 파동 함수는 다음과 같이 \(|L\rangle\)과 \(|R\rangle\)의 합으로 표시할 수 있다. \[|\psi\rangle=a|L\rangle+b|R\rangle\]여기서 \(|a|^2\)와 \(|b|^2\)는 각각 입자가 왼쪽 점과 오른쪽 점에 있을 확률이며, 모든 가능성의 확률을 다 더하면 1이어야 하므로 \(|a|^2+|b|^2=1\)이다. 이 조건과 파동 함수 전체의 위상각phase angle은 임의로 정할 수 있다는 성질을 쓰면 임의의 파동 함수는 다음과 같이 다시 쓸 수 있다.
\(|\psi\rangle=\cos{\alpha}|L\rangle+\sin{\alpha}e^{i\beta}|R\rangle\)
여기서 임의의 파동 함수는 두 개의 각도 변수 \(\alpha\), \(\beta\)에 의해서 결정된다는 것을 알 수 있다. 구체적으로 \(\alpha\)는 입자가 왼쪽과 오른쪽 점에 있을 상대적인 확률을 결정하고, \(\beta\)는 두 상태 사이의 위상각 차이를 나타낸다. 이제 다시 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 배운 바와 같이 파동 함수를 숫자의 사슬, 즉 벡터로 쓰면 다음과 같다.
\(|\psi\rangle=\left(\begin{array}{c}\cos{\alpha} \\\sin{\alpha}e^{i\beta}\end{array}\right)\)
여기서 편의상 \(|L\rangle\)을 첫번째, \(|R\rangle\)을 두번째 기저로 잡았다. 즉, 벡터 형식으로 쓰면 다음과 같다.
\(|L\rangle=\left(\begin{array}{c}
1 \\ 0 \end{array}\right),
\;\;\;
|R\rangle=\left(\begin{array}{c}
0 \\ 1 \end{array}\right)\)
그렇다면 이제 \(\alpha\)와 \(\beta\)는 어떻게 정할 수 있을까? 물론 일반적인 파동 함수는 임의의 \(\alpha\)와 \(\beta\) 값을 가질 수 있다. 여기서 \(\alpha\)와 \(\beta\)를 정한다는 것은 어떤 특정한 동역학을 기술하는 해밀토니안Hamiltonian을 상정하고 그것에 해당하는 슈뢰딩거 방정식을 풀어서 정상파standing wave가 무엇인지를 알아 낸다는 것이다. 따라서 앞선 질문은 정상파의 경우에 \(\alpha\)와 \(\beta\)의 값이 무엇이 되는가라는 질문이 된다.
이 질문에 답을 하기 위해서 이제 두 상태 시스템을 기술하는 적절한 해밀토니안을 하나 생각해 보기로 하자. 입자가 어느 한 점에 영원히 머무르는 것이 아니라면 입자는 일반적으로 왼쪽과 오른쪽 두 점 사이를 왔다 갔다 뛰어다닐 것이다. 다시 말해서 \(|L\rangle\)이 \(|R\rangle\)로 바뀔 수 있고, 그 반대로 \(|R\rangle\)이 \(|L\rangle\)로 바뀔 수 있다. 이러한 작업을 할 수 있는 해밀토니안을 행렬 형식으로 쓰면 다음과 같다.
\(\hat{H}=\left(\begin{array}{cc}0 & 1 \\1 & 0\end{array}\right)\)
쉽게 확인할 수 있듯이 위 행렬에 벡터 형식으로 쓰인 \(|L\rangle\)을 작용하면 \(|R\rangle\)이 되고, 그 반대로 \(|R\rangle\)을 작용하면 \(|L\rangle\)이 된다. 지금까지는 좋다. 그런데 위 해밀토니안에는 아직 한가지 빠진 부분이 있다. 해밀토니안은 에너지의 차원dimension을 가지고 있으므로 위 행렬 앞에 에너지의 차원을 가지는 어떤 비례 계수를 붙여야 한다. 물리적으로 말하면 왼쪽과 오른쪽 점 사이를 뛰어다니는 정도의 세기를 나타내는 계수가 필요하다. 이 계수는 영어로 “hopping parameter”라고 불리는데, 일반적으로 쓰이는 국문 명칭이 없으므로 이제부터 “뜀 계수”라고 부르기로 하자. 이제 뜀 계수를 \(\Delta\)라고 표기하여 해밀토니안을 쓰면 다음과 같다.
\(\hat{H}=\left(\begin{array}{cc}0 & -\Delta \\-\Delta & 0\end{array}\right)\)
뜀 계수 앞에 음의 부호를 붙인 이유는 입자가 잘 뛰어 다닐수록 에너지가 낮아진다는 것을 반영한 것이다.
최종적으로 해밀토니안이 완성되기까지 아직 한가지 단계가 더 남아 있다. 일반적으로 입자가 왼쪽 점에 있을 때와 오른쪽 점에 있을 때에 서로 다른 에너지를 가질 수 있다. 구체적으로 입자가 왼쪽 점에 있을 때의 에너지를 \(E_L\)이라고 하고 오른쪽 점에 있을 때의 에너지를 \(E_R\)이라고 하면 최종적인 해밀토니안은 다음과 같이 쓰인다.
\(\hat{H}=\left(\begin{array}{cc}E_L & -\Delta \\-\Delta & E_R\end{array}\right)\)
대각화
이제 정상파를 얻기 위해서 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 배운 바와 같이 위 해밀토니안의 고유함수eigenfunction을 찾아야 한다. 수학적으로 말해서 다음의 방정식을 만족하는 파동 함수를 찾아야 한다.
\(\hat{H}|\psi\rangle=E|\psi\rangle\)
위 방정식은 다름 아니라 “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 언급한 “시간 독립적인 슈뢰딩거 방정식time-independent Schrödinger equation”이다. 참고로 파동 함수는 항상 벡터 형식으로 쓰일 수 있으므로 고유함수를 다른 말로 고유벡터eigenvector라고도 부른다.
위 방정식에서 중요한 사실은 고유벡터 \(|\psi\rangle\)를 찾기 위해서 고유값eigenvalue \(E\)도 동시에 찾아야 한다는 것이다. 사실 행렬의 고유값과 고유벡터를 찾는 문제는 수학, 특히 선형 대수linear algebra에서 매우 중요한 문제이다. 이 문제에는 특별한 이름이 붙어있는데, 그 이름은 바로 행렬의 대각화diagonalization이다.
행렬의 대각화는 문자 그대로 행렬을 “잘 정리해서” 대각선에 있는 원소를 제외하고 모든 원소가 0이 되게 만드는 것이다. 이렇게 대각선 원소를 제외하고 모든 원소가 0인행렬을 대각 행렬diagonal matrix이라고 부른다. 그렇다면 구체적으로 행렬을 잘 정리한다는 말은 무엇인가? “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 어떤 주어진 파동 함수를 벡터 형식으로 쓸 때에는 특정한 기저를 정해야 한다고 했다. 파동 함수를 벡터 형식으로 표현하기 위해서 기저를 정해야 하는 것처럼 해밀토니안을 포함한 모든 연산자들을 행렬 형식으로 표현하기 위해서도 기저를 정해야 한다. 물론 기저를 한번 정하면 파동 함수와 연산자에 동일하게 적용해야 한다. 이때 중요한 사실은 여러 가능한 기저들 중에서 잘 고르면 해밀토니안을 대각 행렬로 표현하는 기저를 항상 찾을 수 있다는 것이다. 이 기저가 다름 아닌 정상파들이다.
다른 말로 하면, “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 배웠듯이 다른 기저를 선택한다는 것은 힐버트 공간을 구획하는 축axis을 다른 축으로 회전한다는 것을 의미한다. 비유적으로 3차원 공간의 예를 들면, \(x\), \(y\), \(z\) 축 대신에 회전된 축인 \(x^\prime\), \(y^\prime\), \(z^\prime\) 축을 기저로 사용한다는 것이다. 결론적으로 해밀토니안을 대각화하는 것은 힐버트 공간을 구획하는 축을 잘 회전해서 정상파들이 기본 축들이 되게 좌표계coordinate system를 설정하는 것과 같다.
아직 행렬을 대각화하는 것이 도대체 물리적으로 무엇을 의미하는지 감이 잘 오지 않을 것이다. 당연하다. 처음 들었을 때 이해하기 쉬운 개념은 아니다. 행렬의 대각화에 대해서 물리적인 직관을 얻기 위해서 고전역학의 예를 하나 들어 보면 조금 도움이 될 것이다.
럭비공과 같이 완벽하게 구형이 아닌 공을 생각해 보자. 이러한 공을 던지면 보통 날아가면서 회전을 한다. 하지만 대개의 경우에는 공의 회전축이 잘 고정되지 않아서 회전축 자체가 흔들거리면서 날아간다. 그런데 경험상 공의 회전축이 잘 고정되면 공이 훨씬 더 멀리 잘 날아가는 것을 알 수 있다. 그래서 어떻게 하면 공의 회전축이 잘 고정되게 던질 수 있을까 고민하게 된다. 이 고민의 해결책이 바로 대각화이다. 참고로 여기서 자세하게 설명할 수는 없지만 이 고전역학의 예에서 대각화하는 행렬은 관성 모멘트moment of inertia, 혹은 관성 행렬inertia matrix이다. 비유적으로 말해서 흔들거리지 않는 좋은 회전축을 찾는 것이 대각화이고, 이 회전축이 바로 정상파인 것이다.
이제 양자역학의 세계로 돌아가자. 해밀토니안을 대각화하는 축은 어떻게 찾을 수 있을까? 이 질문에 답을 하기 위해서 앞선 대각화 방정식을 아래와 같이 다시 써보자.
\((\hat{H}-E\mathbb{I})|\psi\rangle=0\)
위 방정식은 앞선 해밀토니안을 대각화하는 방정식의 우변을 좌변으로 옮긴 것에 불과하다. 여기서 \(\mathbb{I}\)는 대각선의 원소는 모두 1이고 그 외의 원소는 모두 0인 행렬이다. \(\mathbb{I}\)는 보통의 숫자로 치면 1과 같은 역할을 하는 가장 기본이 되는 행렬이며, 항등 행렬identity matrix, 혹은 단위 행렬unit matrix이라고 불린다. 자, 이제 위 방정식을 가만히 음미해 보자. 너무나 당연한 것 같지만 위 방정식의 가장 중요한 성질은 선형 방정식이고 우변이 0이라는 사실이다. 무슨 의미인가?
이 사실의 의미를 이해하기 위해서 위 방정식의 좌변에 있는 행렬을 \(\hat{M}=\hat{H}-E\mathbb{I}\)이라고 하자. 이때 만약에 \(\hat{M}\)의 역행렬inverse matrix, 즉 \(\hat{M}\)과 곱했을 때 항등 행렬을 만들어내는 행렬을 찾을 수 있다면, 위 방정식을 만족하는 고유 벡터는 애초에 존재할 수 없다. 그 이유는 위 방정식의 양변에 \(\hat{M}\)의 역행렬인 \(\hat{M}^{-1}\)을 곱하면 다음과 같은 결론이 얻어지기 때문이다.
\(\hat{M}^{-1} \hat{M} |\psi\rangle = |\psi\rangle\) (좌변)
\(\hat{M}^{-1} \cdot 0 = 0\) (우변)
즉, \(|\psi\rangle = 0\). 다시 말해서 그러한 파동 함수는 존재할 수 없다. 이것이 의미하는 바는 해밀토니안 행렬 \(\hat{H}\)가 대각화되기 위해서 \(\hat{M}\)의 역행렬이 존재하지 않아야 한다는 것이다.
어떤 행렬의 역행렬이 존재하지 않아야 한다는 조건은 선형 대수에서 가장 중요한 정리theorem 중의 하나가 말해준다. 이 정리의 자세한 증명은 여기에서 하기에 너무 복잡하므로 결론만 기술하기로 하자.
“행과 열의 숫자가 같은 정사각행렬square matrix은 행렬식determinant이 0이 되지 않는 이상 항상 그것의 역행렬을 찾을 수 있다.”
(참고로 양자역학에서 다루는 모든 연산자는 정사각행렬로 표현된다.) 위 문장이 말이 되려면 우리는 물론 행렬식이 무엇인지 알아야 한다.
행렬식은 그것의 영어 이름인 “determinant”가 말해 주듯이 어떤 정사각행렬이 주어지면 그것의 가장 중요한 성질을 “결정determine”하는 숫자이다. 바로 위에서 언급했기 때문에 예상했겠지만 정사각행렬의 가장 중요한 성질은 그것의 역행렬의 존재 여부이다. 그렇다면 행렬식의 구체적인 정의는 무엇인가?
불행히도 행렬식의 정의는 매우 기술적이어서 자세하게 설명하기에 매우 복잡하고 지루하다. 이 문제를 최대한 극복하기 위해서 우화를 하나 생각해 보자. 구체적으로, 정사각행렬을 지하 주차장이라고 상상해 보자. 지하 주차장에는 여러 층이 있고 각 층마다 여러 주차공간이 있다. 특히 우리가 관심있는 지하 주차장은 층 수와 각 층에 있는 주차공간의 수가 정확히 같다고 하자. 이러한 상황에서 각 주차공간마다 어떤 숫자가 하나씩 할당되어 있다고 상상해 보자. 예를 들면, 그 숫자는 각 주차공간에 세워진 자동차의 차량 번호가 될 수 있다. 편의상 이 숫자를 원소element라고 부르자. 예를 들어서, 지하 3층 2호 주차공간에 세워진 자동차의 차량 번호를 “3층 2호 원소”라고 부르자. 이제 우리가 상상 속 지하 주차장의 행렬식은 다음과 같이 주어진다.
우선 지하 주차장의 각 층마다 하나의 주차공간을 선택하되 모든 주차공간들은 서로 번호가 다르게 되도록 선택한다. 이렇게 선택된 주차공간들의 원소, 즉 차량 번호를 모두 곱한다. 이제 이와는 별개로 주차공간의 번호를 재배열해서 층의 순서대로 나열하는 방법을 생각해 본다. 예를 들어서, 지하 1층에서는 3호, 지하 2층에서는 1호, 지하 3층에서는 2호 주차공간을 선택했다면 (3,1,2)을 (1,2,3)으로 재배열하는 방법을 생각해 본다. 재배열하는 방법은 한 번에 한 쌍씩 2개의 번호를 서로 치환permute하여 층의 순서대로 재배열될 때까지 계속 반복하는 것이다. 즉, 앞선 예에서는 (3,1,2)에서 3과 1을 치환해서 (1,3,2)로 바꾸고, (1,3,2)에서 3과 2를 치환해서 (1,2,3)으로 바꾼다. 이때 몇 번의 치환 단계를 거쳐서 재배열이 마무리되는지 기록한다. 앞선 예에서는 2번의 치환 단계가 필요하다. 이 치환 단계의 횟수가 홀수라면 “치환 부호”를 음, 짝수라면 양으로 정한다. 정리하면, 주어진 주차공간의 선택에 대해서 차량 번호들의 곱과 치환 부호가 얻어진다. 편의상 차량 번호들의 곱에 치환 부호를 붙인 수를 “선택 계수”라고 부르자.
이제 처음으로 돌아가 주차공간들을 다르게 선택하고 위 과정을 반복한다. 그뿐만 아니라 다르게 선택할 수 있는 모든 가능한 경우를 고려하여 위 과정을 반복한다. 이렇게 해서 얻어지는 선택 계수들을 모든 선택 가능한 경우에 대해서 다 더한다. 이 숫자가 바로 행렬식이다.
안다. 무엇인가 굉장히 복잡하다…
구체적인 예를 들면 조금 쉬워질 것이다. 우리가 현재 관심을 두고 있는 해밀토니안은 행과 열의 수가 모두 2인 \(2 \times 2\) 행렬이다. 이 경우의 행렬식은 매우 간단하다. 구체적으로, 임의의 \(2 \times 2\) 행렬이 다음과 같이 주어진다고 하자.
\(\hat{M}=\left(\begin{array}{cc}a & b \\c & d\end{array}\right)\)
앞선 우화를 이용하면, 지하 1층의 1호와 2호 주차공간에 각각 원소 \(a\)와 \(b\)가 들어있고, 지하 2층의 1호와 2호 주차공간에 각각 원소 \(c\)와 \(d\)가 들어있다. 우선, 첫번째 선택으로 지하 1층에서 1호 주차공간을 선택하면 2층에서는 2호 주차공간을 선택할 수밖에 없다. 이때의 선택 계수는 \(ad\)이다. 비슷하게 두번째 선택으로 지하 1층에서 2호 주차공간을 선택하면 지하 2층에서 1호 주차공간을 선택해야 한다. 이때의 선택 계수는 \(-bc\)이다. 조금만 생각해 보면 알 수 있듯이 \(2 \times 2\) 행렬에 대해서는 이 두가지 선택만 가능하다. 결론적으로 의 행렬식은 이 두가지 선택 계수를 더해서 \(ad-bc\)이 된다.
이제 위 공식을 이용해서 실제로 우리의 두 상태 문제를 위한 해밀토니안을 대각화해 보자. 우리가 구체적으로 행렬식을 계산해야 하는 행렬은 다음과 같다.
\(\hat{M}=\hat{H}-E\mathbb{I}=\left(\begin{array}{cc}E_L – E & -\Delta \\-\Delta & E_R – E\end{array}\right)\)
수학적 전통에 따라서 주어진 행렬 \(\hat{M}\)의 행렬식은 \(|\hat{M}|\) 혹은 \({\rm det}(\hat{M})\)이라고 표시된다. 구체적으로 \(|\hat{M}|\)은 앞선 설명에 따라서 다음과 같이 주어진다.
\(|\hat{M}|= \left|\begin{array}{cc}E_L – E & -\Delta \\-\Delta & E_R – E\end{array}\right| = (E_L -E)(E_R -E) -\Delta^2\)
위에서 설명했듯이 이 상황에서 해밀토니안이 대각화되는 조건은 \(|\hat{M}|=0\)이다.
\(E^2 –(E_L +E_R) E +(E_L E_R -\Delta^2)=0\)
위 방정식은 2차 방정식이므로 고등학교 때에 배운 2차 방정식의 근의 공식을 써서 쉽게 풀 수 있다. 즉, 해밀토니안의 고유값은 다음과 같다.
\(E=\frac{1}{2}(E_L +E_R \pm \sqrt{(E_L -E_R)^2 +4\Delta^2})\)
위 공식에 따르면 해밀토니안의 고유값으로 각각 양과 음의 부호를 가지는 서로 다른 2개의 해가 존재할 수 있다. 이제부터 구분의 편의를 위해서 양의 부호를 가지는 고유값을 \(E_+\), 음의 부호를 가지는 \(E_-\)라고 표시하자.
기억을 되살려 보면 이 고유값들은 다름 아닌 정상파들의 에너지이다. 위 두 에너지 중에서 \(E_+\)보다 \(E_-\)가 낮으므로 \(E_-\)를 바닥 상태ground state 에너지라고 부르고 \(E_+\)를 들뜸 상태excited state 에너지라고 부른다. 물론 우리 문제가 두 상태 문제가 아니라 \(N\) 상태 문제라면 \(N\) 개의 정상파가 있을 것이고 에너지가 가장 낮은 정상파로부터 에너지가 커지는 순서대로 바닥 상태, 1번째 들뜸 상태, 2번째 들뜸 상태 등등으로 불릴 것이다.
내친 김에 이제 고유벡터, 즉 정상파의 파동 함수를 구해 보자. 고유벡터가 만족하는 방정식은 다음과 같다.
\(\hat{M}|\psi\rangle=\left(\begin{array}{cc}E_L – E & -\Delta \\-\Delta & E_R – E\end{array}\right)\left(\begin{array}{c}u \\ v\end{array}\right)=0\)
여기서 \(u\)와 \(v\)는 고유벡터를 각각 첫번째와 두번째 기저로 분해했을 때의 계수이다. 이 계수는 흔히 진폭amplitude이라고 불린다. 우리가 익히 알고 있듯이 진폭의 절대값의 제곱은 입자가 해당하는 기저에 존재할 확률이다.
위에서 우리가 이미 \(E\)를 구했기 때문에 위 방정식은 단순한 1차 연립 방정식이 된다.
\((E_L -E)u-\Delta v=0\)
\(-\Delta u +(E_R -E)v=0\)
다만, 위 방정식은 겉으로는 2개의 1차 방정식으로 보이지만, 실제로 독립적인 방정식의 개수는 단 1개이어야 한다. 왜 그럴까? 그 이유는 \(u\)와 \(v\)를 결정하는 조건이 또 하나 있기 때문이다. 그것은 \(u^2+v^2=1\)이다. 이 조건은 물론 모든 경우에 대한 확률의 합이 1이라는 조건이다. (참고로 여기서 \(u\)와 \(v\)는 모두 실수로 잡을 수 있다.) 우리가 모르는 변수가 2개인데 방정식이 3개가 되면 안 되기 때문에 3개 중의 1개는 없어져야 한다. 사실 1개의 방정식이 사라지는 조건이 바로 행렬식이 0이 되는 조건이다!
이것을 이해하기 위해서 위 2개의 방정식 중에서 두번째 방정식을 풀어서 \(v\)를 \(u\)로 표현해 보자.
\(v=\frac{\Delta}{E_R -E} u\)
이제 이 식을 다시 첫번째 식에 넣어 보자.
\((E_R -E)u-\frac{\Delta^2}{E_R -E}u=0\)
다시 쓰면 다음과 같다.
\([(E_L -E)(E_R -E)-\Delta^2]u=0\)
자, 이 방정식은 대괄호로 묶인 양이 0이 되지 않는 이상 \(u\)가 0이 된다. 그렇다면 \(v\)도 0이 된다. 결론적으로 그러한 파동 함수는 존재하지 않는다. 따라서 파동 함수가 존재하기 위해서는 대괄호로 묶인 양이 0이 되어야 한다. 그런데 자세히 보면 그 양은 정확히 행렬식이다! 여기서 자세하게 증명할 수는 없지만 \(N\)개의 행과 열을 가지는 일반적인 정사각행렬을 대각화하는 조건도 다름 아니라 고유 벡터를 주는 \(N\)개의 연립 방정식 중에서 1개의 방정식이 사라지는 조건이다.
어쨌든 이러한 상황에서 고유벡터를 주는 2개의 방정식은 다음과 같다.
\(v=\frac{\Delta}{E_R -E}u\)
\(u^2+v^2=1\)
위 방정식은 다음과 같이 풀린다.
\(|\psi\rangle={\cal C}\left(\begin{array}{c}1 \\ \Delta/(E_R -E)\end{array}\right)\)
여기서 \({\cal C}\)는 파동 함수의 길이를 1로 만드는 상수라는 의미에서 “규격화 상수normalization constant”라고 불린다. 구체적으로 \({\cal C}\)는 다음과 같이 쓰인다.
\({\cal C}=\frac{1}{\sqrt{1+[\Delta/(E_R -E)]^2}}\)
위 공식에서 알 수 있는 중요한 사실 하나가 있다. 입자가 왼쪽 혹은 오른쪽 점에 가만히 멈추어 있지 않고 둘 사이를 뛰어 다님으로 해서 두 상태가 서로 얽히게 된다는 것이다. 이렇게 되면 바닥 상태 에너지는 각 점에 정지해 있을 때의 에너지보다 더 낮아지고 들뜸 상태 에너지는 반대로 더 높아진다.
이 사실을 명확하게 보기 위해서 왼쪽과 오른쪽 점의 에너지가 서로 같은 상황을 생각해 보자. 즉, \(E_L=E_R=E_0\)인 상황이다. 앞에 주어진 공식을 잘 정리하면 이 경우에 고유값은 \(E=E_0 \pm \Delta\)이 된다는 것을 보일 수 있다. 필자가 말한 바와 같이 바닥 상태 에너지는 \(E_0\)보다 내려가고 들뜸 상태 에너지는 올라간다. 이 경우에 고유 벡터는 다음과 같다.
\(|\psi\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1 \\ \mp 1\end{array}\right)\)
특히 두 상태 중에서 에너지가 낮은 바닥 상태에 집중하면, 바닥 상태 에너지는 \(E_g=E_0-\Delta\)가 되고, 바닥 상태 파동 함수는 다음과 같이 된다.
\(|\psi_g\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1 \\ 1\end{array}\right)\)
브라-켓 표기법으로 표시하면 다음과 같다.
\(|\psi_g\rangle=\frac{1}{\sqrt{2}}(|L\rangle+|R\rangle)\)
이것이 의미하는 바는 바닥 상태가 입자가 왼쪽 점에 있는 상태와 오른쪽 점에 있는 상태의 중첩으로 존재하게 된다는 사실이다. (공식을 자세하게 들여다 보면 바닥 상태와 들뜸 상태의 차이는 단지 \(|L\rangle\)과 \(|R\rangle\) 사이의 위상각의 차이가 0인지 아니면 \(\pi\)인지라는 것을 알 수 있다.) 이 양자역학적인 중첩 상태가 바로 그 유명한 슈뢰딩거의 고양이이다.
슈뢰딩거의 고양이
양자역학이 이상하다는 얘기를 할 때마다 가장 자주 드는 예로 슈뢰딩거의 고양이가 있다. 슈뢰딩거의 고양이는 너무 많이 회자되는 내용이라 어찌 보면 식상하기까지 하다. 하지만 슈뢰딩거의 고양이는 깊게 생각하면 할수록 우리로 하여금 물리적 직관을 심각하게 의심하게 만든다. 단도직입적으로 말해서 “슈뢰딩거의 고양이”는 고양이가 살아있는alive 상태와 죽은dead 상태의 중첩으로 존재할 수 있다는 것을 의미한다. 수학적으로 표현하면 다음과 같다.
Schrödinger’s cat \( = \frac{1}{\sqrt{2}}(|alive\rangle +|dead\rangle)\)
물론 고양이가 실제로 이렇게 양자역학적인 파동 함수에 의해서 기술되기는 불가능하다. 슈뢰딩거가 생각한 “사고 실험thought experiment”에서 고양이는 양자역학적인 파동 함수와 훨씬 더 미묘하게 연결된다. 필자는 아래에서 슈뢰딩거가 원래 생각했던 사고 실험 장치를 약간 현대적으로 변형해서 설명하고자 한다.
고양이 한 마리가 밀폐된 방 안에 갇혀 있다고 하자. 이 방 안에는 고양이 외에 작은 유리 상자가 하나 더 있는데, 그 안에는 원자가 하나 들어있다. 편의상 이 원자는 2개의 상태만을 가질 수 있다고 하자. 이 2 상태 중에서 에너지가 낮은 상태를 “원자 바닥 상태atomic ground state,” 높은 상태를 “원자 들뜸 상태atomic excited state”라고 하자. 만약에 원자가 원자 들뜸 상태에 있다면 원자 바닥 상태로 떨어지면서 광자photon를 하나 방출할 수 있다. 반면에 이 여분의 광자는 원자에 다시 흡수되어서 원자 바닥 상태를 원자 들뜸 상태로 올려놓을 수 있다. 이 경우에 원자와 광자를 모두 포함한 전체 시스템의 상태는 다음과 같은 2가지 상태로 구성된다.
\(|1\rangle=|atomic \;\; ground, \;\; one \;\; photon \rangle\) (원자 바닥 상태, 광자 있음)
\(|0\rangle=|atomic \;\; excited, \;\; zero \;\; photon \rangle\) (원자 들뜸 상태, 광자 없음)
위에서 1과 0은 광자의 숫자를 표현한다. 이 상황에서 앞서 설명한 광자의 방출과 흡수 과정을 통해서 \(|1\rangle\)과 \(|0\rangle\)은 서로 “뛰어다니며” 중첩될 수 있다. 결론적으로 원자-광자 전체 시스템의 바닥 상태는 다음과 같이 된다.
\(|\psi_g\rangle=\frac{1}{\sqrt{2}}(|1\rangle+|0\rangle)\)
이때 유리 상자 안에 광검출기photodetector가 하나 설치되어 있다고 하자. 이 광검출기는 광자가 검출되면 망치를 작동시켜 독가스가 든 병을 깨뜨린다. 즉, 고양이는 파동 함수가 \(|1\rangle\)에 있으면 죽고 \(|0\rangle\)에 있으면 산다. 그런데 원자-광자 전체 시스템의 바닥 상태는 \(|1\rangle\)과 \(|0\rangle\)의 중첩 상태이다. 따라서 고양이도 살아있는 상태와 죽은 상태의 중첩으로 존재한다! 이보다 더 이상한 결론이 있을 수 있을까?
물론 방문을 열어 보았을 때 고양이가 실제로 살아 있는 상태와 죽은 상태의 중첩으로 존재할 리는 없다. “코펜하겐 해석Copenhagen interpretation”이라고 불리는 양자역학의 정통적인 해석에 따르면, 방문을 열어서 고양이를 관찰하는 순간 고양이는 양자역학적인 중첩 상태에서 벗어나 살아 있는 상태나 죽은 상태 중의 하나로 “붕괴collapse”된다. 여기서 변환transform이나 변화change라는 용어를 쓰지 않고 붕괴라는 특별한 표현을 쓰는 이유는 “관찰observation”이라는 작업이 양자역학적인 중첩 상태를 순식간에 무너뜨려서 관찰의 결과로 나올 수 있는 여러 가능한 상태 중의 하나로 떨어뜨리기 때문이다. 각각의 관찰 가능한 상태로 떨어질 확률은 파동 함수를 그 상태로 분해했을 때의 진폭의 절대값의 제곱이다. 고양이가 삶과 죽음의 중첩 상태로 존재할 수 있는 것도 이상하지만, 이 해석도 매우 이상하기는 마찬가지이다. 하지만 어쩌겠는가? 이 해석은 지금까지 수많은 실험적 테스트를 굳건히 견디어 확고한 과학적 사실로 자리를 잡았다.
사실 슈뢰딩거 자신이 위 사고 실험을 생각한 이유는 코펜하겐 해석이 매우 비합리적이라는 사실을 명확하게 보이고 싶었기 때문이다. 오죽하면 슈뢰딩거 자신이 다음과 같은 말을 했다고 하지 않은가?
“I don’t like it, and I’m sorry I ever had anything to do with it.”
여기서 “it”은 양자역학의 확률론적 해석, 즉 코펜하겐 해석이다!
이러한 코펜하겐 해석에 대해서 불만을 가진 또 다른 사람은 아인슈타인이었다. 아인슈타인은 슈뢰딩거의 사고 실험을 조금 더 정교하게 바꾸어서 양자역학의 확률론적인 해석이 자신이 발견한 상대론적인 원리에 어긋난다는 것을 보이고 싶어했다. 이 어긋남이 바로 그 유명한 아인슈타인-포돌스키-로젠 역설Einstein-Podolski-Rosen paradox, 짧게 줄여서EPR 역설이다. EPR 역설에 대해서는 “믿기 힘든 양자 Incredible Quantum [9]: 양자 얽힘”에서 자세하게 얘기할 예정이니 궁금한 독자들은 약간 더 기다려 주기를 부탁한다. 다만 나중에 EPR 역설을 이해하기 위해서는 여기서 중요한 정지 작업을 하나 해 놓을 필요가 있다. 사실 이 정지 작업은 단순히 EPR 역설을 이해하기 위해서만 필요한 것이 아니라 양자역학에서 가장 중요한 개념 중의 하나를 이해할 수 있게 해 준다. 그것은 바로 스핀spin이다.
스핀
모든 입자들이 스핀을 가지고 있지만 여기서는 특히 전자의 스핀에 대해서 얘기를 하게 될 것이다. 일반적으로 물리학자들이 전자의 스핀에 관심을 두는 이유는 그것이 원자 및 물질의 구조를 이해하는 데에 중요하기 때문이다. 하지만 여기서 필자가 전자의 스핀에 관심을 두는 직접적인 이유는 전자의 스핀이 바로 이번 글의 주제인 두 상태 문제이기 때문이다.
스핀은 문자 그대로 해석하면 입자가 회전하는 것을 의미한다. 전자는 실제로 회전하는가? 이 질문은 일견 쉬운 질문인 것 같아도 실제로는 무척 어려운 질문이다. 사실 “배타 원리exclusion principle”의 창시자인 볼프강 파울리Wolfgang Pauli는 스핀을 전자의 회전으로 해석하는 것을 매우 싫어 했다. 나중에 자세히 설명하겠지만 파울리의 배타 원리는 근본적으로 전자의 스핀 상태가 2개라는 사실에 기인한다. 전자는 파울리 생전에도 그랬지만 현재까지 알려진 바로도 크기가 거의 없는 정말 점과 같이 작은 입자이다. 이렇게 작은 전자가 실험적으로 측정되는 각운동량을 가지고 회전하려면 무지막지하게 빠른 속도로 회전해야 한다. 전자의 크기가 거의 없다는 사실을 감안하면 전자의 표면은 빛의 속도보다 더 빨리 움직여야 한다! 불가능하지 않은가?
파울리는 스핀을 전자의 회전으로 보지 말고 고전역학적으로는 기술될 수 없는 그야말로 진정한 양자역학적인 개념으로 받아들여야 한다고 주장했다. 이에 파울리는 회전 대신에 전자의 스핀 상태를 기술할 수 있는 모종의 내부 자유도internal degree of freedom가 있을 것이라고 생각했다. 하지만 천하의 파울리도 그러한 내부 자유도를 주는 적절한 물리량을 찾을 수 없었고, 결국 스핀 자유도에 의한 두 상태를 “고전역학적으로는 기술할 수 없는 2가성classically non-describable two-valuedness”라고 부를 수밖에 없었다. 하지만 파울리의 저항에도 불구하고 스핀이 전자의 회전이라는 해석은 일반적으로 받아들여졌다.
사실 물리학자들에게는 전자가 진짜로 회전하는지 아닌지가 그리 중요하지 않다. 왜 그럴까? “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 배우기를 양자역학에서 모든 관찰 가능한 물리량은 반드시 연산자로 표현되어야 한다고 했다. 스핀을 기술하는 연산자는 “스핀 각운동량spin angular momentum”이다. 스핀 각운동량은 입자가 실공간real space에서 회전하는 운동을 기술하는 보통의 각운동량과 정확히 같은 교환 관계commutation relation를 만족한다. “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 필자는 기저를 무엇으로 잡든지 간에 바뀌지 않는 연산자 본연의 성질이 바로 교환 관계라고 했다. 따라서 스핀 각운동량이 실공간 회전 운동에 관한 보통의 각운동량, 즉 “궤도 각운동량orbital angular momentum”과 정확히 같은 교환 관계를 만족한다면, 스핀 각운동량은 모종의 회전 운동에 관한 각운동량인 것이다. 양자역학에 따르면 그 이상 알 필요도 없고 알 수도 없다.
스핀 각운동량의 교환 관계에 대해서는 아래에서 더 자세하게 얘기하게 될 것이다. 하지만 그보다 먼저 짚고 넘어 가야할 절박한 질문이 있다. 전자의 스핀은 왜 두 상태 문제일까?
각운동량의 양자화
가만히 생각해 보면 양자역학의 역사는 각운동량과 아주 밀접하게 연결되어 있다. 각운동량은 입자가 주어진 한 점을 중심으로 얼마나 강하게 운동을 하고 있느냐를 재는 물리량이다. 수학적으로는 다음과 같이 정의된다.
\({\bf L}={\bf r}\times{\bf p}\)
여기서 \({\bf r}\)은 위치 벡터이고 \({\bf p}\)는 운동량 벡터이다. 위 공식에서 볼 수 있듯이 각운동량은 위치 벡터와 운동량 벡터의 외적external product이다.
양자역학의 발견을 촉발시킨 닐스 보어Niels Bohr의 원자 모형의 핵심은 각운동량의 크기가 플랑크 상수Planck constant의 정수 배로 양자화된다는 것이다.
\(L=n\hbar\)
여기서 \(n\)은 정수이고 \(\hbar=h/2\pi\)는 환원된 플랑크 상수reduced Planck constant라고 불린다. 보어가 이러한 가정을 한 이유는 당시 실험적으로 밝혀진 수소 원자의 스펙트럼을 설명하기 위함이었는데, 그때까지는 아직 이론적으로 특별한 근거가 없었다. 이론적으로 보았을 때 굳이 하나의 이유를 들자면 각운동량의 물리적인 차원이 플랑크 상수의 그것과 같다는 것뿐이었다.
이제 보어의 가정을 써서 수소 원자의 에너지 준위energy level를 구해 보자. 수소 원자 내에서 전자가 안정적인 궤도를 유지하기 위해서는 원자핵이 전자를 당기는 전기력electric force이 전자의 운동을 인한 원심력centrifugal force과 균형을 맞추어야 한다.
\(\frac{e^2}{r^2}=\frac{mv^2}{r}\)
엄밀하게 말해서 위 공식에서 \(m\)은 전자의 질량 \(m_e\)와 수소의 원자핵인 양성자의 질량 \(M\) 사이의 환원된 질량reduced mass, 즉 \(m=m_e M/(m_e +M)\)이다. 하지만 양성자의 질량이 전자의 질량보다 훨씬 크므로 은 기본적으로 전자의 질량으로 보아도 무방하다. 위 공식을 잘 정리하면 다음과 같게 쓸 수 있다.
\(mrv^2=e^2\)
각운동량의 크기인 \(L=mrv\)를 써서 위 공식을 다시 쓰면 다음과 같다.
\(Lv=e^2\)
이제 각운동량의 양자화 조건을 쓰면 전자의 속도는 다음과 같이 얻어진다.
\(v=\frac{e^2}{n\hbar}\)
이제 다시 이 결과를 이용하면 전자 궤도의 반경을 알 수 있다.
\(r=\frac{\hbar^2}{me^2}n^2\)
최종적으로 위 두 결과를 이용해서 수소 원자 내에서 전자의 전체 에너지, 즉 운동 에너지와 퍼텐셜 에너지의 합을 구하면 다음과 같다.
\(E=\frac{1}{2}mv^2-\frac{e^2}{r}=-\frac{Ry}{n^2}\)
여기서 \(Ry=me^4/2\hbar^2\)는 뤼드베리 에너지 단위Rydberg unit of energy라고 부른다. 보어는 이 결과를 이용해서 수소 원자의 여기 상태에서 방출되는 빛의 에너지를 기술하는 공식, 즉 뤼드베리 공식Rydberg formula을 구할 수 있었다.
\(\Delta E = E_i – E_f= Ry\left( \frac{1}{n^2_f}-\frac{1}{n^2_i} \right)\)
여기서 \(E_i\)와 \(E_f\)는 각각 처음와 마지막 상태의 에너지이다. 이 공식의 유도는 과학사에 길이 남을 역사적인 사건이었다. 비록 완벽한 모습은 아니었지만 양자역학이 처음 인류에게 그 모습을 드러낸 순간이었기 때문이다.
앞선 성공에도 불구하고 보어의 원자 모형은 다양한 의문점을 제기한다. 가장 큰 의문점은 물론 각운동량이 양자화되는 이유이다. 각운동량이 양자화되는 이유는 사실 아인슈타인Einstein에 의해서 처음 이해되었다. 아인슈타인은 그 당시 드브로이de Broglie가 제안한 파동-입자 이중성wave-particle duality에 대해서 알고 있었다. 아인슈타인은 보어의 각운동량 양자화 조건이 원형 궤도 위에서 파동이 출렁거릴 때 정상파를 만들 조건과 정확히 같다는 사실을 깨달았다. 다시 말해서, 원의 둘레 길이가 파장의 정수배가 되어야 한다.
\(2\pi r = n\lambda\)
드브로이의 파동-입자 이중성은 수학적으로 다음과 같이 표현된다.
\(\lambda=\frac{2\pi\hbar}{p}\)
위 두 식을 결합하면 보어의 각운동량 양자화 공식이 나온다. 아름답지 않은가? [그림 4]를 참조하라.
이러한 아름다움에도 불구하고 보어의 각운동량 양자화 조건을 정상파 조건으로 해석하게 되면 또 다른 의문이 꼬리를 문다. 각운동량이 하나의 숫자로 확정된다는 사실은 전자의 운동이 각운동량 벡터에 수직인 2차원 평면에 제한된다는 의미이다. 직관을 얻기 위해서 태양 주위를 도는 지구를 생각해 보자. 지구의 공전 운동은 각운동량이 보존되어 2차원 평면에 제한된다. 전자도 양성자 주위를 돌 때 2차원 평면에 제한되어 있을까? 그렇다면 수소 원자가 납작할 텐데 명백하게 그렇지 않다. 전자의 움직임은 어떤 식으로든 3차원적으로 출렁거리는 파동이어야 한다. 물론 이러한 3차원적인 출렁거림을 기술하는 방정식은 슈뢰딩거 방정식이다.
나중에 이어질 연재글에서 보겠지만, 수소의 에너지 준위 공식에 나오는 정수 \(n\)은 그 자체로 각운동량이 양자화되는 조건에 직접적으로 필요한 정수가 아니다. 실제로 슈뢰딩거 방정식을 풀어서 얻어지는 양자화는 조금 더 복잡한 조건에서 나온다. 참고로 정수 \(n\)은 “주양자수principle quantum number”라고 불리는데, 주양자수는 파동 함수가 3차원적으로 출렁거릴 때 방사 방향radial direction으로의 양자화와 깊은 관계가 있다. 각운동량의 양자화에 관계된 정수는 2가지가 있는데, 각운동량의 전체 크기에 관계된 “각운동량 양자수angular momentum quantum number”와 각운동량의 특정한 방향 성분에 관계된 “자기 양자수magnetic quantum number”가 바로 그것이다. 보어의 각운동량 양자화 조건에 가장 직접적으로 연관된 양자수는 자기 양자수이다.
슈테른-게를라흐 실험
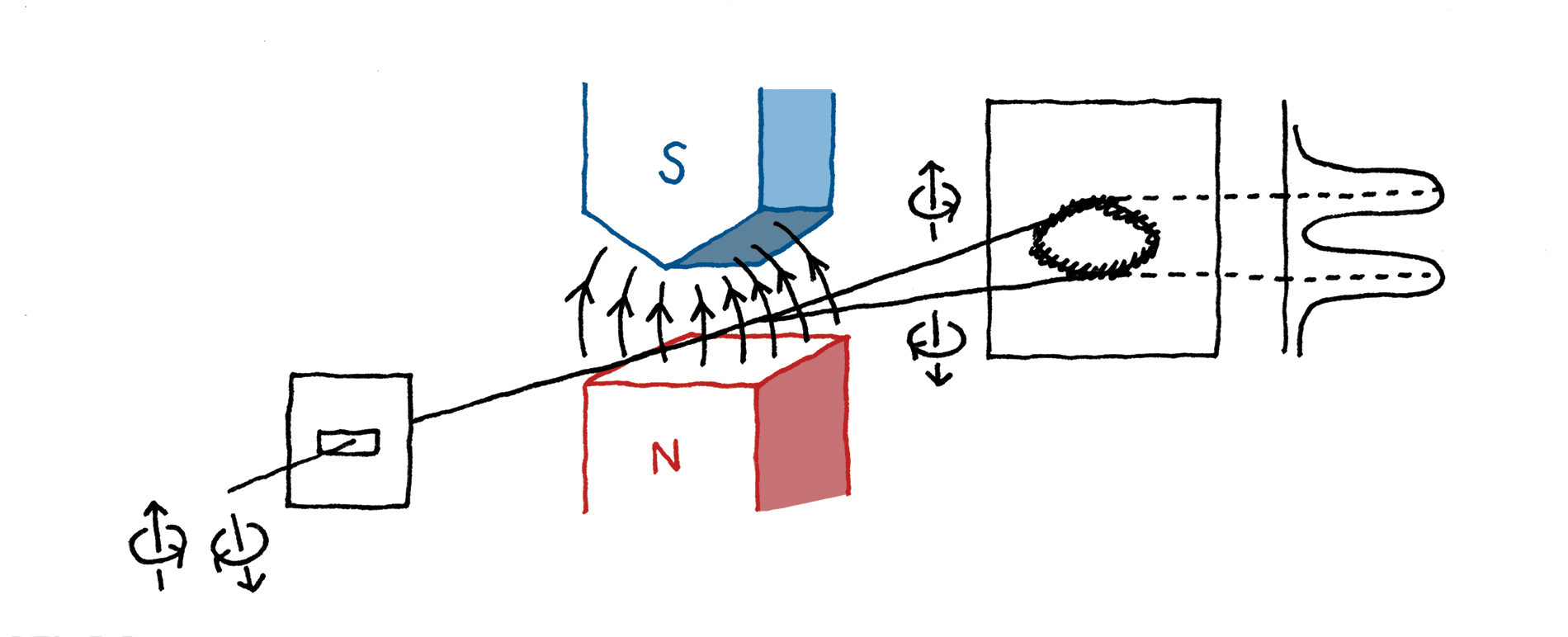
슈테른-게를라흐 실험은 보어의 원자 모형에서 나오는 각운동량의 양자화, 즉 자기 양자수의 존재를 직접 관측하려는 목적으로 계획되었다. 전자가 원자핵 주위를 회전하게 되면 마치 전류가 흐르는 도선이 자기장을 발생시키듯이 작은 자석이 된다. 다시 말해서 원자 자체가 작은 전자석이 되는 것이다. 조금 더 구체적으로 말해서, 전류가 위에서 보았을 때 시계 방향을 회전한다면 자기력선이 아래로 나가는 전자석이 되고, 반시계 방향으로 회전한다면 자기력선이 위로 나가는 전자석이 된다. 즉, 원자는 전자의 회전 방향에 따라서 내부 자기력선이 위 혹은 아래로 나가게 된다.
이제 이 작은 전자석이 외부 자기장이 걸려있는 공간을 날아간다고 상상해 보자. 특히 외부 자기장이 균일하지 않고 공간적으로 센 부분에서 약한 부분으로 변하는 상황을 상상해 보자. [그림 5]를 참조하라. 그림에서 볼 수 있듯이 두 개의 큰 자석은 서로 마주보고 있는데, S극이 밑으로 향하고 있는 위 자석은 끝이 뾰족하고 N극이 위로 향하고 있는 아래 자석은 끝이 평평하다. 자기력선은 물론 아래 N극에서 나와서 위 S극으로 들어간다. 하지만 자석 끝부분의 모양이 다르기 때문에 윗부분은 자기력선의 밀도가 높아서 자기장이 세고, 아랫부분은 자기력선의 밀도가 낮아 자기장이 약하다. 이때 작은 전자석, 즉 원자가 이 두 자석 사이의 공간을 날아가면 자기장의 공간적 변화에 비례하는 힘을 받게 된다. 즉, 내부 자기력선 방향이 위로 향하고 있는 원자는 외부 자기장의 밀도가 높은 윗쪽으로 힘을 받아서 움직이고, 아래로 향하고 있는 원자는 밀도가 낮은 아랫쪽으로 힘을 받아서 움직이게 된다. 결론적으로 원자가 받는 힘의 방향이 전자의 각운동량에 의해서 결정된다.
이제 원자 하나가 날아가는 것이 아니라 빛줄기, 영어로 빔beam의 형태로 수많은 원자들이 계속 쏘아 진다고 하자. 고전역학적으로 보면 원자의 각운동량은 연속적으로 분포되어 있을 것이다. 그렇다면 원자들은 앞서 설명한 이유에 의해서 서로 다른 힘을 받아서 휠 것이고, 결국 원자빔 자체가 연속적으로 퍼지게 될 것이다. 반면에 원자의 각운동량이 양자화되어 있다면 원자빔은 불연속적인 몇 개의 갈래로 갈라지게 될 것이다. 이것이 기본적으로 슈테른-게를라흐 실험의 아이디어이다.
오토 슈테른Otto Stern은 박사 학위를 받은 후에 프라하 카를 대학Charles University과 스위스 취리히 연방 공과대학ETH에서 아인슈타인의 조수로 일하면서 주로 양자역학과 통계역학에 대해서 이론적인 연구를 수행했다. 이후 그는 독일 프랑크푸르트 대학교로 옮겨서 강사로 일하게 되었는데, 이때부터 각운동량의 양자화를 실험적으로 증명하는 문제에 관심을 갖게 된다. 당시 막스 보른Max Born이 이끌고 있던 프랑크푸르트 물리학 연구소의 분위기는 매우 좋았는데, 특히 이론 물리학자와 실험 물리학자들이 활발하게 함께 논의했다고 한다. 이런 좋은 분위기 속에서 슈테른은 1921년 발터 게를라흐Walther Gerlach라는 유능한 실험 물리학자를 만나서 위에서 설명한 각운동량의 양자화를 검증하는 자신의 아이디어를 논의하게 된다.
역사에 민감한 독자들은 이미 눈치를 챘을지도 모르지만 이 당시는 아직 양자역학이 완벽하게 정립된 시기가 아니었다. 참고로 하이젠베르크의 행렬역학은 1925년, 슈뢰딩거의 슈뢰딩거 방정식은 1926년에 발견되었다. 물론 이때는 스핀이라는 개념도 아직 없을 때였다. 슈테른과 게를라흐는 약간은 잘못된 추측을 통해서 은silver 원자를 가지고 실험을 하면 은 원자빔이 두 갈래로 갈라질 것으로 예상했다. 현대적인 관점에서 보면 이 잘못된 추측은 정말 운이 좋은 것이었다. 원자 구조에 대해서는 나중에 자세하게 얘기할 기회가 있을 것이다. 여기서 결과만 말하면, 은 원자는 총 47개의 전자를 가지고 있는데, 46개의 전자는 2, 8, 18, 18개의 순서로 에너지가 낮은 오비탈부터 차근차근 채운다. 우연히도 맨 마지막 47번째 전자가 채우는 최외각 오비탈의 궤도 각운동량은 0이다. 거칠게 말하면 이 마지막 전자는 돌지 않는다. 따라서 궤도 각운동량만 존재한다면 은 원자빔은 전혀 갈라지면 안 되는 것이었다. 하지만 슈테른과 게를라흐는 은 원자빔이 갈라질 것이라고 굳게 믿었고 온갖 실험적인 난관을 뚫어 나갔다. 그리고 드디어 그들은 1922년 은 원자빔이 두 갈래로 갈라지는 것을 실험적으로 확인할 수 있었다! [그림 6]을 참조하라.
“They did not know it is impossible so they did it.”
-Mark Twain
위에 인용된 미국 작가 마크 트웨인Mark Twain의 유명한 말과 같이 그들은 원래 계획된 실험이 불가능한지 몰랐기 때문에 성공할 수 있었던 것이다. 슈테른-게를라흐 실험에 관련된 다양한 뒷이야기는 이강영 교수님의 “스핀: 파울리, 배타원리 그리고 진짜 양자역학”이라는 책에 자세하게 나와있다. 매우 흥미로운 책이다. 독자들에게 꼭 한번 읽어보기를 추천한다.
현대적인 관점에서 돌아보면 슈테른-게를라흐 실험은 각운동량이 양자화된다는 사실을 증명하기 위해서 계획되었지만 그것을 넘어 전자가 궤도 각운동량뿐만이 아니라 스핀 각운동량을 가지고 있다는 사실까지도 보여주었다. 구체적으로 말해서 은 원자빔이 두 갈래로 갈라진 것은 전자의 스핀이 2개의 상태로 이루어져 있다는 사실을 보여준 것이었다. 편의상 전자가 \(z\) 축을 기준으로 반시계 방향으로 회전하는 상태를 “스핀 업spin-up 상태,” 시계 방향으로 회전하는 상태를 “스핀 다운spin-down 상태”라고 부르자. 이 명칭을 사용하면, 전자의 스핀 상태는 스핀 업과 다운 상태라는 2개의 상태로 이루어져 있는 것이다.
그런데 잠깐! 왜 하필이면 \(z\) 축이 기준인가? 우리가 살고 있는 3차원 공간은 흔히 \(x\), \(y\), \(z\) 축이라고 표기되는 3개의 축을 가지고 있다. 전자는 물론 이 3개의 축, 일반적으로는 그것들의 결합으로 표시되는 임의의 축을 중심으로 회전할 수 있다. 그렇다면 이 3개의 축에 해당하는 스핀 각운동량이 각각 존재해야 할 것이다. 편의상 \(x\), \(y\), \(z\) 축에 해당하는 스핀 각운동량을 각각 스핀 각운동량의 \(x\), \(y\), \(z\) 성분이라고 부르자. 언뜻 생각하기에 각운동량의 3성분은 서로 독립적으로 스핀 업과 다운 상태를 가진다고 생각할 것이다. 하지만 놀랍게도 믿기 힘든 양자역학의 세계에서는 각운동량의 3개의 성분이 서로 독립적이지 않다. 마치 위치와 운동량이 불확정성 원리에 의해서 얽혀 있는 것과 비슷하게 3차원 공간에서 3개의 회전축은 서로 얽혀 있다.
파울리 행렬
3개의 회전축이 서로 얽혀 있다는 사실은 앞서 설명한 슈테른-게를라흐 실험을 약간 확장해서 보일 수 있다. 이제부터 논의의 편의를 위해서 앞서 설명한 슈테른-게를라흐 실험 장치를 “SG 장치SG apparatus”라고 부르자. 특히 \(z\)축 방향으로 정렬되어 원자빔을 \(z\) 축 방향으로 스핀 업과 다운 상태로 가르는 SG 장치를 “\(z\) 축 SG 장치z-axis SG apparatus”라고 부르자. 비슷하게 \(x\)와 \(y\) 축 방향으로 정렬된 SG 장치를 각각 “\(x\) 축 SG 장치”와 “\(y\) 축 SG 장치”라고 부르자.
이제 다음과 같은 상황을 생각해 보자. 우선 원자빔을 \(z\) 축 SG 장치에 통과시켜서 \(z\) 축 방향으로 스핀 업과 다운 상태를 갈라지게 만들자. 그 다음 \(z\) 축 방향으로 스핀 다운 상태에 있는 원자들을 모종의 장벽을 세워서 모두 제거하자. 그렇게 되면 원자빔 내에 있는 원자들은 모두 \(z\) 축 방향으로 스핀 업 상태에 있게 될 것이다. 이렇게 걸러진 원자빔을 다시 \(x\) 축 SG 장치에 통과시키자. 이제 원자빔은 \(x\) 축 방향으로 어떻게 갈라질까?
예상했겠지만 원자빔은 \(x\) 축 방향으로 스핀 업과 다운 상태의 두 갈래로 갈라진다. 이 사실은 별로 이상하지 않다. 왜냐하면 원래의 원자빔 내에 \(z\) 축 방향으로 스핀 업과 다운 상태가 반반의 확률로 존재하는 것처럼 \(x\) 축 방향으로도 스핀 업과 다운 상태가 반반의 확률로 존재할 수 있기 때문이다. 정말 재미있는 일은 \(x\) 축 방향으로 스핀 다운인 원자들을 모두 제거하고, 원자빔을 다시 \(z\) 축 SG 장치에 통과시키면 발생한다. 이렇게 두번째 걸러진 원자빔은 다시 \(z\) 축 방향으로 어떻게 갈라질까? 참고로 [그림 7]을 보라.
조금 헷갈릴 수 있으니 상황을 정리해 보자. 첫번째 거르는 단계에서는 \(z\) 축 방향으로 스핀 다운인 원자들이 모두 제거된다. 두번째 거르는 단계에서는 \(x\) 축 방향으로 스핀 다운인 원자들이 모두 제거된다. 만약에 \(x\) 축과 \(z\) 축이 서로 독립적이라면 이렇게 최종적으로 걸러진 원자빔 내에는 \(x\) 축과 \(z\) 축 방향으로 스핀 다운인 원자들이 모두 제거되어 있을 것이다. 하지만 놀랍게도 실제로 실험을 해 보면 최종적으로 걸러진 원자빔은 \(z\) 축 SG장치를 통과할 때 다시 두 갈래로 갈라진다. 다른 말로 하면, 첫번째 단계에서 제거되었던 \(z\) 축 방향으로 스핀 다운인 원자들이 다시 생긴 것이다!
이 놀라운 사실은 \(x\) 와 \(z\) 축 방향의 스핀 상태가 서로 얽혀 있다는 것을 의미한다. 구체적으로, \(x\) 축 방향으로 스핀 업 상태가 \(z\) 축 방향으로 스핀 업과 다운 상태를 모두 포함한다는 것을 의미한다. 양자역학적으로 표현하면, \(x\) 축 방향으로 스핀 업인 상태가 \(z\) 축 방향으로 스핀 업과 다운 상태의 중첩이 된다는 것을 의미한다.
편의상 \(z\) 축 방향으로 스핀 업과 다운 상태를 각각 브라-켓 표기법을 써서 \(|z,+\rangle\)와 \(|z,-\rangle\)로 표기하자. 비슷하게 \(x\) 축 방향으로 스핀 업과 다운 상태를 \(|x,+\rangle\)와 \(|x,-\rangle\)로 표기하자. 나중에 쓰겠지만 완결성을 위해서 미리 말하면 \(y\) 축 방향으로 스핀 업과 다운 상태는 \(|y,+\rangle\)와 \(|y,-\rangle\)로 표기하자. 그렇다면 \(x\) 축 방향으로 스핀 업인 상태가 \(z\) 축 방향으로 스핀 업과 다운 상태의 중첩 상태라는 결론은 브라-켓 표기법으로 아래와 같이 쓰인다.
\(|x,+\rangle=\frac{1}{\sqrt{2}}(|z,+\rangle+|z,-\rangle)\)
이 파동 함수는 앞에서 설명한 왼쪽과 오른쪽 점에 위치하는 상태의 중첩으로 존재하는 입자나 삶과 죽음의 중첩으로 존재하는 슈뢰딩거의 고양이를 기술하는 파동 함수와 정확히 동일하다!
사실 엄밀하게 말해서 위 파동 함수에서 \(|z,+\rangle\)와 \(|z,-\rangle\) 사이에는 임의의 위상각 차이가 존재할 수 있다. 다시 말해서, \(|z,-\rangle\)의 앞에 임의의 위상 인자phase factor \(e^{i\theta}\)를 붙일 수 있다. 이 위상 인자는 앞선 실험, 즉 원자빔이 최종적으로 다시 두 갈래로 갈라진다는 실험만으로는 유일하게 결정될 수 없다. 하지만 다행히도 이 위상 인자는 우리가 회전축을 정의하는 방법과 관련이 있으므로 편의상 위 공식에서 정한 것과 같이 \(|z,-\rangle\) 앞의 위상 인자를 그냥 1로 잡아도 무방하다. 다만 위 정의를 따르게 되면 \(|x,-\rangle\)는 \(|x,+\rangle\)와 수직이어야 한다는 조건으로 인해서 다음과 같이 유일하게 결정된다.
\(|x,-\rangle=\frac{1}{\sqrt{2}}(|z,+\rangle-|z,-\rangle)\)
이제 \(|x,+\rangle\)와 \(|x,-\rangle\)를 브라-켓 표기법 대신에 \(|z,+\rangle\)와 \(|z,-\rangle\)를 첫번째와 두번째 기저로 삼아서 벡터 형식으로 적으면 다음과 같다.
\(|x,+\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}
1 \\ 1 \end{array}\right)
\;\;\;\;\;\;
|x,-\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}
1 \\ -1 \end{array}\right)\)
앞서 설명한 상황을 \(x\) 축이 아니라 \(y\) 축 방향에도 적용할 수 있다. 그렇게 되면 거의 모든 것들이 상당히 유사하다는 것을 알 수 있다. 즉, \(y\) 축 방향으로 스핀 업과 다운 상태는 \(z\) 축 방향으로 스핀 업과 다운 상태의 중첩으로 표현된다. 이전과 유일한 차이는 \(|z,-\rangle\)의 앞에 붙는 위상 인자이다. 앞서 \(|x,+\rangle\)와 \(|x,-\rangle\)를 위한 위상 인자로 각각 1과 -1로 잡은 것을 고려할 때, \(|y,+\rangle\)와 \(|y,-\rangle\)를 위한 자연스러운 위상 인자는 각각 \(i\)와 \(-i\)라고 추정해 볼 수 있다. 그 이유는 이렇게 하면 위상 인자 속의 위상각이 360도를 정확히 4등분하기 때문이다. 이러한 추정 하에 \(|y,+\rangle\)와 \(|y,-\rangle\)를 벡터 형식으로 적으면 다음과 같다.
\(|y,+\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1 \\ i \end{array}\right)\;\;\;\;\;\;|y,-\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1 \\ -i \end{array}\right)\)
완결성을 위해서 \(|z,+\rangle\)와 \(|z,-\rangle\)도 벡터 형식으로 적으면 다음과 같다.
\(|z,+\rangle= \left(\begin{array}{c}1 \\ 0 \end{array}\right)\;\;\;\;\;\;|z,-\rangle=\left(\begin{array}{c}0 \\ 1 \end{array}\right)\)
이제 각 방향에 대해서 스핀 업과 다운 상태를 고유벡터로 가지는 행렬들을 생각해 보자. 슈테른-게를라흐 실험의 의미를 가만히 잘 생각해 보면, 어떤 특정한 방향에 대해서 스핀 업과 다운 상태가 된다는 것은 그것들이 그 특정한 방향에 해당하는 스핀 각운동량 연산자의 고유벡터가 된다는 의미이다. 다시 말해서…\(|x,\pm\rangle\), \(|y,\pm\rangle\), \(|z,\pm\rangle\)를 각각 고유벡터로 가지는 어떠한 행렬들이 존재해야 한다. 우선 \(|z,\pm\rangle\)를 고유벡터로 가지는 행렬은 매우 간단하다.
\(\sigma_z=\left(\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right)\)
여기서 \(|z,\pm\rangle\)의 고유값은 각각 \(\pm 1\)이다. 약간 시간을 들이면 \(|x,\pm\rangle\)를 고유벡터로 가지는 행렬도 그렇게 어렵지 않게 찾을 수 있다.
\(\sigma_x=\left(\begin{array}{cc}0 & 1 \\ 1 & 0\end{array}\right)\)
여기서도 \(|x,\pm\rangle\)의 고유값은 각각 \(\pm 1\)이다. 비슷하게 \(|y,\pm\rangle\)를 고유벡터로 가지는 행렬도 찾을 수 있다.
\(\sigma_y=\left(\begin{array}{cc}0 & -i \\ i & 0\end{array}\right)\)
여기서도 \(|y,\pm\rangle\)의 고유값은 각각 \(\pm 1\)이다. 이 3개의 행렬들이 바로 그 유명한 파울리 행렬Pauli matrices이다. 파울리 행렬은 거의 우리가 원하는 전자의 스핀 각운동량 연산자이다. 아직 완벽하지 않은 부분은 파울리 행렬의 앞에 붙는 계수이다.
이제 파울리 행렬들 사이의 교환 관계에 관심을 가져 보자. 구체적으로 파울리 행렬들 사이의 교환자commutator를 계산해 보면 다음과 같은 재미있는 관계가 존재한다는 것을 알 수 있다.
\([\sigma_x, \sigma_y]=2i\sigma_z\)
\([\sigma_y, \sigma_z]=2i\sigma_x\)
\([\sigma_z, \sigma_x]=2i\sigma_y\)
보는 바와 같이 \(x, y, z\) 축에 해당하는 파울리 행렬들은 서로서로 물고 물리는 교환 관계를 가지고 있다. 파울리 행렬이 기본적으로 각운동량을 기술하는 연산자라는 사실은 그것이 궤도 각운동량 연산자와 매우 유사한 교환 관계를 만족한다는 사실에 기인한다.
이 사실을 알기 위해서 궤도 각운동량이 어떤 교환 관계를 만족하는지 알아보자. 앞에서 궤도 각운동량은 다음과 같이 정의된다고 했다.
\({\bf L}={\bf r}\times{\bf p}\)
“믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 배웠듯이, 양자역학적으로 운동량 \({\bf p}\)는 공간에 대한 미분 연산자 \(\nabla\)에 \(-i\hbar\)를 곱한 양이다. 이로 인해서 위치와 운동량 연산자는 다음과 같은 교환 관계를 만족한다.
\([x,p_x]=i\hbar\)
\([y,p_y]=i\hbar\)
\([z,p_z]=i\hbar\)
물론 서로 다른 축에 해당하는 위치와 운동량 연산자 사이에는 아무런 관계가 없다. 따라서 그들 사이의 교환자는 0이다. 위 교환 관계는 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 이미 언급된 교환 관계로서 위치와 운동량 사이의 불확정성 원리를 나타낸다.
이제 위치와 운동량 연산자 사이에 존재하는 위 교환 관계를 잘 이용하면 궤도 각운동량 사이의 교환 관계를 구할 수 있다. 여기서는 자세한 유도 과정 없이 결과만 쓰기로 한다.
\([L_x, L_y]=i\hbar L_z\)
\([L_y, L_z]=i\hbar L_x\)
\([L_z, L_x]=i\hbar L_y\)
궤도 각운동량 사이의 교환 관계를 앞선 파울리 행렬들 사이의 교환 관계와 비교하면 그 둘이 매우 유사하다는 것을 알 수 있다. 실제로 스핀 각운동량 연산자를 다음과 같이 정의하면, 스핀 각운동량이 궤도 각운동량과 정확하게 동일한 교환 관계를 만족하도록 만들 수 있다.
\(S_i=\frac{\hbar}{2}\sigma_i\)
여기서 \(i\)는 \(x, y, z\)를 의미한다. 다시 말해서, 파울리 행렬에 \(\hbar/2\)를 곱하면 스핀 각운동량 연산자가 된다. 결론적으로 스핀 각운동량의 고유값은 \(\pm \hbar/2\)이 된다.
지금까지의 결과를 정리해 보자. 각각 \(x, y, z\)축 방향에 해당하는 스핀 상태는 서로서로 물고 물리는 중첩 상태이다. 이러한 스핀 상태가 고유벡터가 되는 행렬이 바로 파울리 행렬이다. 스핀 각운동량 연산자는 파울리 행렬에 \(\hbar/2\)를 곱한 것이다. 스핀 각운동량 연산자는 궤도 각운동량 연산자와 동일한 교환 관계를 만족한다. 따라서 스핀은 전자의 회전 운동에 관여하는 물리량이다. 앞서 언급했듯이 양자역학에서는 그 이상 알 필요도 없고 알 수도 없다.
두 상태 문제의 진가
이번 연재글은 양자역학의 핵심을 담고 있는 가장 단순한 문제가 무엇일까라는 질문으로부터 시작하였다. 필자는 그 답으로 두 상태 문제를 제시하였다. 두 상태 문제의 힐버트 공간은 2개의 기저로 구성되어 있다. \(2 \times 2\) 행렬로 표현되는 두 상태 해밀토니안은 2차 방정식의 근의 공식을 이용해서 쉽게 대각화할 수 있다. 대각화를 통해서 얻어진 정상파는 슈뢰딩거의 고양이가 어떻게 삶과 죽음의 중첩 상태로 존재할 수 있는지를 알려 준다. 이것만으로도 두 상태 문제는 우리에게 양자역학에 대해서 충분히 많은 것을 알려준다.
하지만 두 상태 문제의 진가는 전자의 스핀을 고려할 때 발휘된다. 전자의 스핀 문제는 글 초반에 언급한 양자역학을 완벽하게 이해했다고 인정할 수밖에 없는 그런 종류의 문제이다. 각운동량은 양자역학의 역사에서 줄곧 매우 중요한 역할을 했다. 각운동량은 공간의 회전 대칭성rotational symmetry과 깊은 연관이 있다. 공간의 회전 대칭성은 각운동량의 각 성분 사이에 특정한 교환 관계를 요구하는데, 앞서 보았듯이 전자의 스핀 각운동량을 나타내는 파울리 행렬은 정확하게 이 교환 관계를 만족한다.
사실 전자의 스핀 문제가 우리에게 정말로 중요한 이유는 따로 있다. 그것은 스핀이 위상각의 물리적인 중요성을 겉으로 드러낼 수 있기 때문이다. “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 배웠듯이 파동 함수의 위상각은 마음대로 변환될 수 있다. 다시 말해서, 위상각을 임의로 변환하더라도 전자의 동역학을 기술하는 슈뢰딩거 방정식의 수학적 구조는 변하지 않는다. 결과적으로 물리적으로 측정할 수 있는 전자기장electromagnetic field도 변하지 않는다. 이렇게 위상각의 변환에도 불구하고 측정할 수 있는 물리량이 변하지 않는다는 성질을 게이지 대칭성이라고 한다. 약간 시적으로 말하면 위상각은 존재하되 겉으로는 드러나지 않아야 한다. 그런데 놀랍게도 위상각은 스핀을 통해서 그 숨겨진 모습을 겉으로 드러낼 수 있다. 다음 글에서 필자는 스핀의 동역학이 어떻게 이러한 마법을 부릴 수 있는지에 대해서 이야기할 것이다. 다음 글의 제목은 “위상의 귀환Return of the Phase”이다.