Can quantum-mechanical description of physical reality be considered complete?
-A. Einstein, B. Podolsky, and N. Rosen
로빈 윌리암스Robin Williams라는 배우가 있다. 그는 살아생전에 세상에서 가장 웃긴 사람 중 한 명으로 꼽히고는 했다. 그가 출연한 많은 영화들은 대부분 평론가와 관객들로부터 동시에 좋은 평가를 받았는데, 이러한 영화들의 비평 및 상업적인 성공에는 그의 연기가 결정적인 역할을 했다. 그는 아카데미 상의 후보로 네 번 추천되었다. 특히, 1997년 개봉된 <굿 윌 헌팅Good Will Hunting>이라는 영화에서 그는 션 맥과이어Sean Maquire라는 심리학자의 역할을 한 공로로 ‘최우수 남우 조연상Best Supporting Actor’을 받았다.
여기서 <굿 윌 헌팅>의 전체 내용에 대해서 자세하게 이야기하지는 않을 것이다. 다만, 필자에게 잊지 못할 깊은 인상을 남긴 한 장면에 대해서 약간 자세하게 이야기하고자 한다. 주인공 윌 헌팅Will Hunting은 천재적인 수학 재능을 지녔지만 불우한 가정사로 인해서 제대로 된 교육을 받지 못했다. 매사추세츠 공대MIT에서 청소부로 일하고 있던 윌은 우연히 수학과 복도의 칠판에 적혀있던 수학 문제를 풀게 된다. 이 문제는 제랄드 램보Gerald Lambeau 교수가 수학과 대학원 학생들을 위해서 냈던 문제였다.
그러던 중에 윌은 어렸을 때 자신을 괴롭혔던 갱과의 싸움에 휘말리게 되고, 정신없는 틈에 경찰까지 폭행하게 된다. 윌이 폭행 혐의로 재판에 넘겨졌다는 사실을 알게 된 램보 교수는 판사에게 윌의 사정을 설명하여 윌이 징역형을 받는 대신에 자신의 밑에서 수학을 배우고 심리 상담을 받는 조건으로 석방되게 한다. 로빈 윌리암스가 연기한 션이 윌을 만나게 되는 계기이다.
어렸을 때 받은 학대로부터 마음에 깊은 상처를 입은 윌은 모든 일에 대해서 냉소적인 태도를 취하였다. 션도 마음에 깊은 상처를 안고 살아가는 것은 마찬가지였다. 사랑하는 아내를 잃었기 때문이다. 필자에게 깊은 인상을 준 영화의 한 장면은 이렇게 깊은 마음의 상처를 지닌 두 남자가 만나면서 발생한다.
윌은 우연히 바에서 스카일러Skyler라는 여자를 만나게 되는데, 그녀는 하버드Harvard 대학교를 졸업하고 스탠퍼드Stanford 의대로 진학을 앞두고 있었다. 그녀의 아름답고 지적인 모습에 반한 윌은 션과의 상담 시간에 그녀에 대해서 얘기를 한다. 아래는 영화 속 윌과 션의 대화이다. (비속어는 최대한 순화해서 표현했다.)
윌: 내 걱정은 하지 말아요. 내 앞가림을 내가 할 수 있으니까요. 그녀는, 그러니까, 아름다워요. 똑똑하고요. 그리고 웃겨요. 그녀는 내가 지금까지 사귀었던 다른 여자들하고는 달라요.
션: 그래, 그럼 전화 걸어, 로미오.
윌: 왜요? 그렇게 해서 그녀가 사실은 그렇게 똑똑하지 않다는 것을 알게 되라고요? 아주 지루하다는 것도요? 지금 이 순간 그녀는 아주 완벽해요. 망치고 싶지 않아요.
션: 아마 지금 이 순간 완벽한 것은 너겠지. 아마 네가 망치고 싶지 않은 것은 그걸 거야. 내 생각에 이건 초강력 철학super philosophy이야. 윌, 그 방식대로 하면 아무도 진짜 알 필요 없이 평생을 살 수 있게 되지… 내 아내는 긴장을 하면 방귀를 끼고는 했어. 그녀는 다양한 종류의 멋진 특이성idiosyncrasy들을 가지고 있었지. 그거 알아? 그녀는 자면서도 방귀를 끼고는 했어. [웃음] 그런 것들까지 네가 알게 돼서 미안하네. 어느 날 밤에는 소리가 너무 커서 개를 깨웠지. 그녀가 깨서 “당신이 그런 거예요?”라고 물어봤어. 그래서 그렇다고 했어. 진실을 말할 용기가 없었거든… [웃음] 오, 신이시여…
윌: [기절할 정도로 웃으며] 그녀가 자기자신을 깨웠다고요?
션: [역시 기절할 정도로 웃으며] 맞아! … 오, 신이시여… 하지만, 윌, 그녀는 2년 전에 죽었어. 그런데 그런 자질구레한 것shit이 내가 기억하는 거야. [윌은 웃음을 멈춘다.] 멋진 것은, 그러니까, 그런 작은 것들이야. 아, 그런 것들이야말로 내가 가장 그리워하는 것들이지. 나만이 알고 있는 작은 특이성들. 그런 것들이 그녀를 내 아내로 만들었던 것이지. 오, 그녀도 나에 관한 것들을 알고 있었지. 사소한 잘못들도 모두 알고 있었고. 사람들은 이런 것들을 결점imperfection이라고 부를 거야. 하지만 아니지. 그런 것들이야말로 진짜 좋은 것good stuff이야. 우리는 우리의 작고 이상한 세계에 누구를 들일지 선택할 수 있어. 너는 완벽하지 않아, 친구sport. 긴장감을 덜어주지. 네가 만난 그녀 있잖아, 그녀도 완벽하지 않아. 하지만, 질문은 너희가 서로에게 완벽하냐는 거야. 그게 중요한 거야. 그게 친밀함intimacy이라는 것이지. 너는 이 세계에 있는 모든 것을 알 수 있어. 하지만 친밀함에 관해서 알 수 있는 유일한 방법은 시도해 보는 것뿐이야. 확실히 나같은 늙은이로부터는 배울 수 없지. 설사 내가 알아도 너같이 하찮은 녀석에게는 말해주지 않을 거고.
윌: 왜 안 말해줘요? 젠장, 다른 것들은 모두 말해 주었잖아요. 내 인생에서 만난 그 어떤 심리상담사보다 말이 많으면서.
션: 내가 심리학을 가르치기는 하지만, 내가 어떻게 하는지 안다고는 말 안 했어.
윌: 그래요… 재혼에 대해서 생각해 본 적 있어요?
션: 내 아내는 죽었어.
윌: 그러니까 “재혼”이라고 했잖아요.
션: 그녀는 죽었어.
윌: 그렇군요… 내 생각에 이건 초강력 철학인 것 같아요. 션, 그 방식대로 하면 당신은 아무도 진짜 알 필요 없이 남은 평생을 살 수 있을 것 같아요.
션: [불편한 미소를 지으며] 상담 시간이 끝났군.
필자가 생각하기에, 위 장면에서만큼 친밀함 그리고 그리움이 무엇인가라는 질문에 대해서 절절하게 답을 준 영화는 그동안 없었던 것 같다.
필자의 외할머니는 2018년 6월 10일 일요일 아침에 돌아가셨다. 한국 나이로 99세까지 사셨다. 많은 사람들이 자신들의 외할머니에 대해서 특별한 감정을 지니겠지만, 필자도 필자의 외할머니와 무척 친했다.
외할머니는 나름 최근까지도 파마 머리를 하지 않으셨는데, 그전에는 머리를 말아서 비녀를 꽂고 다니셨다. 물론 외할머니도 언젠가부터 파마 머리를 하셨다. 본인은 무척 편하다고 좋아하셨지만, 그래도 손자인 필자의 눈에는 곱게 머리를 말아 비녀를 꽂으신 외할머니의 모습을 더 이상 볼 수 없다는 사실이 내내 아쉬웠다.
사실 외할머니는 지금 시각에서 보면 매우 안 좋은 습관을 하나 가지고 계셨다. 바로 담배를 피우시는 것이었다. 필자가 아주 어렸을 때 외할머니는 담배를 담뱃대에 꽂아 피우셨다. 나중에는 담뱃대 없이 그냥 피우셨는데, 외할머니가 담배를 피우시던 모습에는 매우 인상적인 점이 하나 있었다.
외할머니는 주로 다른 어떤 일을 하시면서 담배를 피우셨는데, 일에 집중하신 나머지 담뱃재를 터는 일을 자주 잊으시곤 하셨다. 아직도 정확히 어떻게 그렇게 하실 수 있었는지 모르겠지만, 외할머니는 담배를 입에 물으신 채로 담배가 그대로 타들어 가도록 놔두실 수 있는 특별한 재능(?)을 지니고 계셨다. 담뱃재에는 재미있는 사실이 하나 있는데 생각보다 구조적으로 안정적이라는 것이다. 다시 말해서, 불이 담배의 앞부분에서 뒷부분으로 옮아가면서 생기는 담뱃재는 밑으로 떨어지려고 하지만 생각보다 강한 접착력이 있어서 놀랍게도 잘 떨어지지는 않는다. 결과적으로 담뱃재는 활처럼 휠 수 있게 된다. 단순히 약간 휘는 정도가 아니라 담배의 거의 2/3 이상이 다 타들어 가도 담뱃재는 활처럼 휜 상태를 계속 유지할 수 있었다.
지금 시각에서 보면 외할머니는 어린 손자 앞에서 담배를 피우셨던 것이다. 그런데 그 당시 필자에게 곱게 머리를 말아 비녀를 꽂으신 외할머니가 일에 집중하시면서 담뱃재가 활처럼 휜 담배를 고요히 입에 물고 계신 모습은 너무나 멋지게 보였다. 이후로 외할머니는 파마 머리를 하시고 담배도 끊으셨다. 나중에 외할머니는 노환으로 쇠약해지시고 살도 많이 빠지셨다. 외할머니가 돌아가시기 얼마 전부터는 예전에 건강하셨던 모습을 전혀 찾아볼 수 없게 되었다. 하지만 지금 필자가 외할머니를 생각할 때면 외할머니가 쇠약해진 모습은 전혀 생각나지 않는다. 필자에게 가장 먼저 생각나는 이미지는 언제나 외할머니가 바로 그때처럼 담뱃재가 활처럼 휜 담배를 피우시던 모습이다.
션이 기억하는 아내의 방귀와 필자가 기억하는 외할머니의 담배는 이상한 이야기 같지만 둘 다 그리움이다.
죽는다는 것은 정말 완전히 사라진다는 것일까? 혹시 누군가의 마음속에 살아남아 있다면, 정말 완전히 사라지는 것이 아니라 적어도 존재의 일부는 살아남게 되는 것은 아닐까? 물리학자는 기본적으로 유물론자materialist이다. 그래서 그런지 필자의 마음속 깊숙이 그러한 헛된 희망을 가지면 안 된다는 소리가 울려 나온다. 그래도 어쩌겠는가? 외할머니는 물질적으로 돌아가셨지만 필자의 마음속에는 계속 살아 계신다. 배운 게 도둑질이라고, 필자는 외할머니가 완전히 사라지신 것이 아니라 혹시 삶과 죽음의 중첩 상태로 존재하시는 것은 아닐까라고 자신을 속여 본다. 마치 슈뢰딩거의 고양이처럼.
삶과 죽음의 중첩 상태라는 개념은 유물론자인 물리학자들이 받아들이기 결코 쉬운 개념이 아니다. 슈뢰딩거가 슈뢰딩거의 고양이라는 사고 실험을 고안한 이유도 다름 아니라 양자역학의 확률론적인 해석이 정말 말도 안 된다고 증명하고 싶었기 때문이다.
아인슈타인도 마찬가지였다. 아인슈타인은 슈뢰딩거의 고양이가 가지는 삶과 죽음이라는 철학적인 문제를 피하면서 양자역학의 확률론적인 해석을 논리적으로 공격하고 싶어 했다. 그래서 조금 더 강력한 사고 실험을 생각하게 된다. 이 사고 실험의 목적은 양자역학이 상대성 원리와 양립가능하지 않다는 것을 보이는 것이었다. 이 사고 실험의 이름은 아인슈타인-포돌스키-로젠Einstein-Podolski-Rosen, 줄여서 EPR 역설paradox이다.
양자역학적인 기술 방식은 완전한가?
1935년 알버트 아인슈타인Albert Einstein, 보리스 포돌스키Boris Podolsky, 네이선 로젠Nathan Rosen은 <피지컬 리뷰Physical Review>라는 미국 물리학회American Physical Society에서 발행하는 저명한 물리 저널에 다음과 같은 제목을 가진 논문을 출간한다.
“물리적인 실체에 관한 양자역학적인 기술 방식은 완전한 것으로 여겨질 수 있는가?”
“Can quantum-mechanical description of physical reality be considered complete?”
이 논문은 1933년 아인슈타인이 나치에 의해 지배당하고 있던 독일을 떠나 미국 프린스턴에 있는 고등과학원Institute for Advanced Study에 정착한 후에 1년여에 걸쳐서 완성되었다. 편의상 이 논문을 EPR 논문이라고 부르자. EPR 논문에서 3명의 저자들은 측정이 결과에 영향을 미친다는 양자역학의 기술 방식이 완전할 수 없다는 결론을 내린다. 이 당시 EPR 논문의 출간은 일반 대중의 관심을 끌어서 <뉴욕 타임즈New York Times>에 소개되기까지 한다. ([그림2] 참조)
조금 길지만 EPR 논문의 초록abstract을 자세히 살펴보기로 하자.
“완전한 이론에는 실체의 각 요소에 대응하는 요소가 있다. 물리량의 실체를 위한 충분 조건은 시스템을 어지럽히지 않으면서 확실하게 그것을 예측할 수 있는 가능성이다. 양자역학에서 교환가능하지 않는 연산자에 의해서 기술되는 두 물리량이 있는 경우에 어느 하나에 대한 지식은 다른 하나의 지식을 방해한다. 그렇다면 (1) 양자역학에서 파동 함수에 의해서 주어지는 실체에 대한 기술 방식은 완전하지 않거나 (2) 이러한 두 물리량은 동시적인 실체를 가지지 않는다. 이전에 서로 상호작용한 다른 시스템에서 수행된 측정에 기반하여 어느 시스템에 대해서 예측을 하는 문제를 고려할 때, (1)이 거짓이라면 (2)도 거짓이다. (필자의 부연 설명: 즉, 파동 함수에 의해서 주어지는 실체에 대한 기술 방식이 완전하다면, 두 물리량은 동시적인 실체를 가져야 한다.) 따라서 우리는 파동 함수에 의해서 주어지는 실체에 대한 기술 방식이 완전하지 않다는 결론에 도달하게 된다.”
(In a complete theory there is an element corresponding to each element of reality. A sufficient condition for the reality of a physical quantity is the possibility of predicting it with certainty, without disturbing the system. In quantum mechanics in the case of two physical quantities described by non-commuting operators, the knowledge of one precludes the knowledge of the other. Then either (1) the description of reality given by the wave function in quantum mechanics is not complete or (2) these two quantities cannot have simultaneous reality. Consideration of the problem of making predictions concerning a system on the basis of measurements made on another system that had previously interacted with it leads to the result that if (1) is false then (2) is also false. One is thus led to conclude that the description of reality as given by the wave function is not complete.)
전문적인 학술 논문이기 때문에 초록이 쉽지 않다. 최대한 쉽게 풀어서 설명하면 다음과 같다. 양자역학의 가장 핵심적인 성질 중의 하나는 교환가능하지 않는 연산자들이 있다는 사실이다. “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 설명했듯이 위치와 운동량 연산자는 교환가능하지 않다. 즉, 두 연산자 사이의 교환자는 0이 아니다.
\([x,p_x]=i\hbar\)
여기서 \(x\)와 \(p_x\)는 각각 \(x\)축 상에서의 위치와 운동량을 나타내는 연산자이다. 이 교환자 관계는 다름 아니라 하이젠베르크의 불확정성 원리이다. EPR 논문에서 주장하는 바는, 교환가능하지 않는 두 연산자가 나타내는 물리량 중에서 하나를 측정하면 다른 물리량을 정확히 잴 수 없다는 사실은 물리적인 실체를 부정하는 것과 마찬가지라는 것이다.
구체적으로, EPR 논문에서는 사고 실험 하나가 제시된다. 이 사고 실험은 초록에서 언급한 “이전에 상호작용한 다른 시스템에서 수행된 측정에 기반하여 어느 시스템에 대해서 예측을 할 수 있다는 문제점”을 보여준다. 이어지는 섹션에서는 이 사고 실험을 약간 현대적인 언어로 변형하여 설명하고자 한다. 그런데 그러기 위해서는 사전 지식이 하나 필요하다. 이 사전 지식의 이름은 스핀 단일항 상태 혹은 영어 명칭 그대로 스핀 싱글렛 상태spin singlet state이다.
스핀 싱글렛 상태
2개의 전자로 이루어진 전자 쌍electron pair을 하나 생각해 보자. 일반적으로 전자 쌍을 구성하는 개별 전자는 위치나 운동량과 같은 궤도 자유도orbital degree of freedom를 가진다. 하지만 여기서는 이러한 궤도 자유도를 무시하고 스핀 자유도에만 집중하도록 하자.
이제 어떤 물리적인 메커니즘에 의해서 전자 쌍이 원점에서 생성되었다고 하자. 모든 방향이 동등하다면 생성된 전자 쌍의 스핀 상태는 회전에 대해서 대칭성을 지녀야 한다. 무슨 말인가?
전자 쌍의 스핀 상태가 회전에 대해서 대칭성을 지닌다는 것은 우리가 이리저리 돌려 보아도 스핀 상태를 기술하는 파동 함수가 변하지 않는다는 것을 의미한다. 수학적으로는 전자 쌍의 전체 스핀 각운동량이 0이라는 것을 의미한다. 즉, 스핀이 전혀 회전하지 않는다는 의미이다. 그런데 알고 있듯이, 양자역학에서 어떤 주어진 물리량이 특정 값이 된다고 하는 것은 말처럼 단순하지 않다. “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 설명했듯이 양자역학에서 물리량은 단순히 숫자가 아니라 연산자이기 때문이다. 스핀 각운동량도 물론 연산자이다.
우선, 당연한 말 같지만, 2개의 전자로 이루어진 시스템의 전체 스핀 각운동량은 다음과 같이 주어진다.
\({\bf S}_{\rm tot}= {\bf S}_1 +{\bf S}_2\)
위 공식은 정말 당연하게 보인다. 즉, 전자 쌍의 스핀 각운동량은 개별 전자의 스핀 각운동량의 합이다. 우리가 관심을 두는 상태는 \({\bf S}_{\rm tot}\)의 제곱에 대한 고유상태eigenstate이다. 그중에서 특히 그것의 고유값eigenvalue이 0인 상태이다.
이제 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 배운 파울리 행렬을 사용해서 전체 스핀 각운동량을 다시 표현하면 다음과 같다.
\({\bf S}_{\rm tot}= \frac{\hbar}{2} (\boldsymbol{\sigma}_1 +\boldsymbol{\sigma}_2)\)
여기서 파울리 행렬로 이루어진 벡터 \(\boldsymbol{\sigma}\)는 다음과 같이 정의된다.
\(\boldsymbol{\sigma}=(\sigma_x,\sigma_y,\sigma_z)\)
여기서 혹시 독자 중에 왜 하필이면 \({\bf S}_{\rm tot}\), 즉 스핀 각운동량 자체가 아니라 스핀 각운동량의 제곱에 대한 고유상태에 관심을 두는지 궁금한 독자가 있는지 모르겠다. 매우 훌륭한 독자이다. 그 이유는 스핀 각운동량 자체에 대한 고유상태가 근본적으로 존재할 수 없기 때문이다. 왜 그럴까? “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명하기를 스핀 각운동량의 각 방향 성분은 서로 교환가능하지 않다. 따라서 마치 위치와 운동량에 대해서 동시에 고유상태가 되는 상태를 찾을 수 없듯이 스핀 각운동량의 모든 방향 성분에 대해서 동시에 고유상태가 되는 상태를 찾을 수 없다.
다행히 스핀 각운동량의 제곱에 대해서는 고유상태가 되는 상태를 찾을 수 있다. 하지만 고유상태를 구체적으로 찾는 문제는 그리 쉽지 않다. 참고로 스핀과 궤도 각운동량은 양자역학적으로 보면 동등한 연산 구조를 지니고 있으므로, 이 문제는 궤도 각운동량의 고유상태를 찾을 때에도 마찬가지로 발생한다. 앞으로 보겠지만 각운동량 연산자와 그것의 고유상태는 물리적으로 굉장히 중요하다. 따라서 각운동량 연산자의 고유상태를 찾는 문제는 충분한 시간을 가지고 자세하게 설명을 해야 한다. 하지만 지금 그러기에는 본론에서 너무 많이 벗어나야 하므로 여기서는 논의를 최대한 단순하게 하기로 한다.
우선, 개별 전자는 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명했듯이 스핀 업과 다운이라는 2가지 스핀 상태를 가질 수 있다. 이러한 2개의 전자가 가지는 스핀 상태들을 조합해서 만들 수 있는 전체 스핀 상태는 총 4개이다.
\(|\uparrow\uparrow\;\rangle, \; |\uparrow\downarrow\;\rangle, \; |\downarrow\uparrow\;\rangle, \; |\downarrow\downarrow\;\rangle\)
여기서 위와 아래 방향을 가리키는 화살표는 각각 스핀 업과 다운 상태를 나타내고, 두 화살표 중에서 왼쪽과 오른쪽에 있는 화살표는 각각 1번과 2번 전자의 스핀 상태를 나타낸다. 위 4개의 스핀 상태를 스핀 기저 상태spin basis state라고 부르자. 스핀 기저 상태들은 보통의 벡터 형식으로 바꾸면 다음과 같이 표현될 수 있다.
\(|\uparrow\uparrow\;\rangle=\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\right), \; |\uparrow\downarrow\;\rangle=\left(\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\right), \; |\downarrow\uparrow\;\rangle=\left(\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right), \; |\downarrow\downarrow\;\rangle=\left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}\right)\)
위 스핀 기저 상태들을 적절하게 잘 조합하여 선형 중첩linear superposition을 시키면 \({\bf S}_{\rm tot}\)의 제곱에 대한 고유 상태를 찾을 수 있다.
“믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명하기를 어떤 연산자의 고유 상태를 찾기 위해서는 그 연산자를 행렬로 표현한 다음에 그 행렬을 대각화diagonalization하면 된다고 했다. 따라서 이제 우리는 \({\bf S}_{\rm tot}\)의 제곱에 해당하는 연산자를 스핀 기저 상태를 기저로 사용해서 행렬로 표현하면 된다. 원칙은 좋지만 구체적으로 어떻게 해야 할까?
구체적으로는, 전체 스핀 각운동량의 제곱에 해당하는 연산자를 각각의 스핀 기저 상태에 작용하여 어떤 일이 생기는지 차근차근 알아보면 된다. 그렇게 하기 위한 첫 번째 단계로, 1번이든지 2번이든지 주어진 전자의 스핀에 파울리 행렬이 어떻게 작용하는지 알아보자.
우선, \(\sigma_x\)는 스핀을 뒤집는다.
\(\sigma_x|\uparrow\;\rangle=|\downarrow\;\rangle,\; \sigma_x|\downarrow\;\rangle=|\uparrow\;\rangle\)
비슷하게 \(\sigma_y\)도 스핀을 뒤집지만 다음과 같은 계수를 붙인다.
\(\sigma_y|\uparrow\;\rangle=i|\downarrow\;\rangle,\; \sigma_y|\downarrow\;\rangle=-i|\uparrow\;\rangle\)
마지막으로 \(\sigma_z\)는 스핀을 뒤집지 않지만, 계수로 스핀이 업이면 \(+1\)을, 다운이면 \(-1\)을 붙인다.
\(\sigma_z|\uparrow\;\rangle=|\uparrow\;\rangle,\; \sigma_z|\downarrow\;\rangle=-|\downarrow\;\rangle\)
두 번째 단계로, 전체 스핀 각운동량의 제곱 연산자가 개별 전자의 스핀 각운동량의 연산자로 어떻게 표현되는지 알아보자.
\({\bf S}_{\rm tot}^2= \left(\frac{\hbar}{2}\right)^2 (\boldsymbol{\sigma}_1 +\boldsymbol{\sigma}_2)^2\)
위 공식에서 1, 2번 파울리 행렬의 합의 제곱은 다음과 같이 다시 쓰인다.
\((\boldsymbol{\sigma}_1+\boldsymbol{\sigma}_2)^2 =\sum_{i=1}^2(\sigma_{xi}^2+\sigma_{yi}^2+\sigma_{zi}^2)+2(\sigma_{x1}\sigma_{x2}+\sigma_{y1}\sigma_{y2}+\sigma_{z1}\sigma_{z2})\)
이제, 예를 들어서 \(\sigma_{x1}\sigma_{x2}\)가 각각의 스핀 기저 상태에 작용하면 어떤 일이 일어나는지 알아보자.
\(\sigma_{x1}\sigma_{x2}|\uparrow\uparrow\;\rangle= |\downarrow\downarrow\;\rangle \\\sigma_{x1}\sigma_{x2}|\uparrow\downarrow\;\rangle= |\downarrow\uparrow\;\rangle \\\sigma_{x1}\sigma_{x2}|\downarrow\uparrow\;\rangle= |\uparrow\downarrow\;\rangle \\\sigma_{x1}\sigma_{x2}|\downarrow\downarrow\;\rangle= |\uparrow\uparrow\;\rangle\)
여기서 자세한 유도 과정을 보여 줄 수는 없지만 위와 같은 계산을 모든 상황에 대해서 빠짐 없이 수행해 보면 \({\bf S}_{\rm tot}\) 제곱 연산자를 다음과 같은 행렬로 표현할 수 있다는 것을 알 수 있다.
\({\bf S}_{\rm tot}^2= \hbar^2 \left(
\begin{array}{cccc}
2 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 2
\end{array}
\right)\)
이제 위 행렬을 대각화하면 다음과 같은 고유 상태들을 얻을 수 있다.
\(\chi_{1,1}=|\uparrow\uparrow\;\rangle=\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\right)\)
\(\chi_{1,0}=\frac{1}{\sqrt{2}}\left(|\uparrow\downarrow\;\rangle+|\downarrow\uparrow\;\rangle\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c} 0 \\ 1 \\ 1 \\ 0 \end{array}\right)\)
\(\chi_{1,-1}=|\downarrow\downarrow\;\rangle=\left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}\right)\)
\(\chi_{0,0}=\frac{1}{\sqrt{2}}\left(|\uparrow\downarrow\;\rangle-|\downarrow\uparrow\;\rangle\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c} 0 \\ 1 \\ -1 \\ 0 \end{array}\right)\)
대각화가 잘 수행되었는지 확인하기 위해서 \({\bf S}_{\rm tot}\) 제곱 연산자를, 예를 들어, \(\chi_{0,0}\)에 작용해 보자.
\({\bf S}_{\rm tot}^2 \chi_{0,0} = \hbar^2 \left(\begin{array}{cccc}2 & 0 & 0 & 0 \\0 & 1 & 1 & 0 \\0 & 1 & 1 & 0 \\0 & 0 & 0 & 2\end{array}\right)\cdot\frac{1}{\sqrt{2}}\left(\begin{array}{c}0 \\ 1 \\ -1 \\ 0\end{array}\right)=0\)
위 공식이 의미하는 바는 \(\chi_{0,0}\)가 우리가 원하는 전체 스핀 각운동량이 0인 고유 상태, 즉 스핀 싱글렛 상태라는 것이다.
참고로, \({\bf S}_{\rm tot}\) 제곱 연산자를 나머지 3개의 고유 상태에 작용하면 다음과 같은 결론에 이른다.
\({\bf S}_{\rm tot}^2 \chi_{1,m} = 2\hbar^2 \chi_{1,m}\)
위에서 \(m=1,0,-1\)이다. 이 3개의 고유 상태를 스핀 삼중자 상태 혹은 영어 명칭 그대로 스핀 트리플렛 상태spin triplet state라고 부른다.
스핀 싱글렛 상태의 물리적인 의미를 이해하기 위해서 그것의 파동 함수를 다시 써 보자.
\(\chi_{0,0}=\frac{1}{\sqrt{2}}\left(|\uparrow\downarrow\;\rangle-|\downarrow\uparrow\;\rangle\right)\)
위 공식에서 알 수 있듯이, 스핀 싱글렛 상태는 1, 2번 전자의 스핀이 각각 스핀 업과 다운인 상태, 즉 \(|\uparrow\downarrow\;\rangle\)와 그 반대로 스핀 다운과 업인 상태, 즉 \(|\downarrow\uparrow\;\rangle\)의 선형 중첩으로 주어진다. 이 상태는 마치 슈뢰딩거의 고양이가 삶과 죽음의 중첩인 것처럼 (업, 다운)과 (다운, 업) 상태의 중첩인 것이다. 이렇게 1, 2번 전자의 스핀 상태가 서로 양자역학적으로 얽히는 것을 “양자 얽힘quantum entanglement”이라고 부른다.
이제 스핀 싱글렛 상태를 바탕으로 EPR 역설을 이해해 보도록 하자.
EPR 역설
다시 한번, 어떤 물리적인 메커니즘에 의해서 전자 쌍 하나가 원점에서 생성된다고 하자. 그리고 앞선 섹션에서 설명한 회전 대칭성으로 인해서 이렇게 생성된 전자 쌍은 스핀 싱글렛 상태를 형성한다고 하자.
특히, 생성 메커니즘이 일종의 폭발이어서 전자 쌍을 구성하고 있는 두 전자, 즉 1, 2번 전자가 서로 반대 방향으로 발사되어 시간이 지날수록 서로 멀어진다고 하자. 이 상황에서 회전 대칭성이 지속적으로 유지된다면 원칙적으로 스핀 싱글렛 상태는 그것을 구성하고 있는 두 전자들이 아무리 멀어지더라도 계속 그 상태를 유지할 수 있다. 원리적으로 두 전자는 지구와 달 사이의 거리만큼까지도 멀리 떨어질 수 있다.
이제 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명한 “코펜하겐 해석Copenhagen interpretation”을 스핀 싱글렛 상태에 적용하면 어떤 일이 일어나는지 생각해 보자.
우선, 모종의 실험을 통해서 지구에 있는 1번 전자의 스핀 상태를 결정할 수 있다고 하자. 그렇게 되면 스핀 싱글렛 상태는 그것을 구성하고 있는 두 중첩 상태 중의 하나로 붕괴collapse될 것이다. 즉, 만약 지구에 있는 1번 전자가 스핀 업이라면 달에 있는 2번 전자는 스핀 다운이 되어야 한다. 반대로 지구에 있는 1번 전자가 스핀 다운이라면 달에 있는 2번 전자는 스핀 업이 되어야 한다.
결론적으로 지구에서 벌어지는 측정 결과가 달에서 얻어지는 물리 상태를 결정하는 것이다. 게다가 코펜하겐 해석에 따르면 이러한 결정은 순간적으로 일어난다. 파동 함수의 붕괴는 순간적으로 일어나기 때문이다. 빛보다 빠르게! 아인슈타인은 이렇게 빛보다 빠르게 원거리에 미치는 작용을 “유령과 같이 으스스한 원거리 작용spooky action at a distance”라고 불렀다.
혹시 위에서 설명한 내용이 뭐 그리 대단하냐고 반문하는 독자가 있을지 모르겠다. 왜냐하면 전자 쌍이 생성될 때 그저 확률적으로 스핀 업과 다운이 반반씩 생길 수 있기 때문이다. 비유적으로 말해서 이는 마치 주머니에 빨간 공과 파란 공이 한 개씩 들어 있는 상황과 같다. 주머니 속에 있는 두 공 중에 어떤 것이 빨간색이고 파란색인지 모를 뿐이지 결과는 이미 정해져 있는 것이다. 이런 상황에서 주머니 속에서 빨간 공을 꺼내면 다른 공은 파란 공일 수 밖에 없다. 물론 그 반대로 파란 공을 꺼내면 다른 공은 빨간 공일 수밖에 없다. 비슷하게 스핀 싱글렛 상태라는 주머니에서 스핀 업인 전자를 꺼내면 다른 전자는 스핀 다운일 수밖에 없다. 물론 그 반대로 스핀 다운을 꺼내면 다른 전자는 스핀 업이다. 그저 우리가 미리 알지 못했을 뿐이다.
그런데 상황이 이렇게 쉬웠으면 이 연재글의 제목이 “믿기 힘든 양자”가 아니었을 것이다. 아래에서 보겠지만 양자역학이 믿기 힘들 만큼 이상하다는 사실은 EPR 역설에서 적나라하게 드러난다.
EPR 역설을 이해하기 위해서, 앞서 쓰인 스핀 싱글렛 상태는 \(z\) 축 방향으로 스핀 방향이 설정된 스핀 업과 다운 상태로 구성되었다는 사실을 기억하자. “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 도입된 표기법을 이용해서 스핀 싱글렛 상태를 다시 쓰면 다음과 같다.
\(\chi_{0,0}=\frac{1}{\sqrt{2}}\left(|z,+;z,-\rangle-|z,-;z,+\rangle\right)\)
위에서 \(|z,+;z,-\rangle = |z,+\rangle |z,-\rangle\)는 1번 전자는 \(z\) 축 방향으로 스핀이 업이고, 2번 전자는 \(z\) 축 방향으로 스핀이 다운이라는 것을 의미한다. 물론 \(|z,-;z,+\rangle\)는 그 반대의 경우를 의미한다.
그런데 우리는 꼭 \(z\) 축 방향으로만 스핀 방향을 정할 필요가 없다. 예를 들어서 \(x\) 축 방향으로 스핀 방향을 정할 수 있다. 그리고 \(x\) 축 방향으로 스핀 방향을 설정하여 스핀 싱글렛 상태를 다시 쓸 수 있다.
\(\chi_{0,0}=\frac{1}{\sqrt{2}}\left(|x,+;x,-\rangle-|x,-;x,+\rangle\right)\)
위 공식은 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 배운 바 있는 다음 두 관계식을 통해서 유도할 수 있다.
\(|x,+\rangle = \frac{1}{\sqrt{2}}\left(|z,+\rangle +|z,-\rangle\right) \\|x,-\rangle = \frac{1}{\sqrt{2}}\left(|z,+\rangle -|z,-\rangle\right)\)
구체적으로, \(x\) 축 방향으로 스핀 방향을 정한 스핀 싱글렛 상태에 위 두 관계식을 집어넣으면 \(z\) 축 방향으로 스핀 방향을 정한 스핀 싱글렛 상태를 유도할 수 있다. 거꾸로 해도 마찬가지이다. 이렇게 스핀 싱글렛 상태는 스핀 방향을 임의로 정해도 항상 (업, 다운)과 (다운, 업) 상태의 중첩으로 표현된다. 이것은 스핀 싱글렛 상태가 회전에 대해서 대칭성이 있다는 사실을 생각해 보면 매우 자연스러운 결과이다.
자, 이제 우리는 지구에 있는 1번 전자의 스핀을 이전과 같이 \(z\) 축 방향을 기준으로 잴 수도 있고, 아니면 축을 돌려서 \(x\) 축 방향을 기준으로 잴 수도 있다. 만약 우리가 지구에 있는 1번 전자의 스핀을 \(x\) 축 방향을 기준으로 쟀을 때 업이 나온다면, 달에 있는 2번 전자의 스핀은 \(x\) 축 방향을 기준으로 쟀을 때 다운이 나올 것이다. 물론 그 반대로 지구에서 다운이면 달에서 업이다.
여기서 중요한 사실은 우리가 지구에서 어떤 축을 기준으로 전자의 스핀 방향을 재는가에 따라서 달에 있는 전자의 스핀 방향을 결정하는 기준 축도 같이 결정된다는 것이다. 이는 마치 스핀 싱글렛 상태라는 주머니 속에 빨간 공과 파란 공이 들어있을지, 아니면 매끈한 공과 거친 공이 들어있을지 모르는 상황과 유사하다. 빨간 공과 파란 공은 각각 \(z\)축 방향으로 스핀 업과 다운 상태를 의미하고, 매끈한 공과 거친 공은 각각 \(x\)축 방향으로 스핀 업과 다운 상태를 의미한다.
이러한 상황에서 우리는 주머니에서 공 하나를 꺼내어 그것의 성질을 색깔로 잴지, 아니면 촉감으로 잴지 결정할 수 있다. 그런데 이 결정에 따라서 나머지 공의 성질이 결정된다는 것이다. 다시 말해서, 꺼낸 공의 색깔이 빨간색이면 나머지 공의 색깔은 파란색이여야 하지만, 그것의 촉감은 알 수가 없다. 반대로 꺼낸 공의 촉감이 매끈하면 나머지 공의 촉감은 거칠어야 하지만, 그것의 색깔은 알 수 없다. 이는 마치 주머니 속에 남겨진 공이 이미 밖으로 꺼내진 공에 어떤 일이 벌어지는지에 따라서 자신의 정체성을 결정하는 것과 같다. 어찌 보면 정말로 관찰자의 의도가 측정 결과에 영향을 미치는 것이다!
아인슈타인과 그의 동료들이 느끼기에 이러한 결론은 얼토당토아니한 것이었다. 지구에서 모종의 측정이 수행되어 그것의 정보가 빛의 속도보다 빨리 전달되어 달에서의 실험 결과에 영향을 미친다는 것이었다. 이것은 명백하게 상대성 원리에 위배되는 것이었다. 양자역학 전체는 아니더라도 적어도 양자역학의 확률론적인 해석에는 문제가 있는 것이었다. 다시 말해서, 파동 함수에 의해서 주어지는 양자역학적인 기술 방식은 완전할 수 없는 것이다.
이러한 논쟁은 상당히 철학적으로 느껴진다. 곰곰이 생각해 보자. 어떤 이론이든지 그것이 완전한지 아닌지 증명할 수 있을까? 모든 이론은 항상 불완전한 것이 아닌가? 순수한 논리 구조 위에 구축된다고 믿어지는 수학 이론도 불완전하다. 쿠르트 괴델Kurt Gödel의 불완전성 정리incompleteness theorem에 따르면 모든 수학 이론에는 진리임에도 불구하고 증명할 수 없는 명제가 항상 담겨 있다. 하물며 양자역학과 같이 실험에 기반을 둔 물리 이론은 불완전할 수밖에 없을 것이다.
이렇듯 양자역학의 해석에 관한 문제는 상당히 오랫동안 실험적으로 검증 불가능한 철학적인 영역으로 치부되었다. 하지만 양자역학이 예측하는 실험 결과는 명확하다. 지구에서 수행된 측정은 달에서의 실험 결과에 영향을 주어야 한다. 다만 실제로 그런지 검증하기 위해서는 지구와 달에 있는 관찰자들이 서로 통신을 할 수 있어야 한다. 물론 이 통신의 속도는 빛보다 빠를 수 없다. 그렇다면 양자역학적으로 원거리에 영향을 줄 수 있다는 것은 실제로는 아무런 의미가 없다는 말인가? 어차피 실제로 통신하기 전까지 양자역학이 맞는지 아닌지 알 수 없으니 이 문제를 고민하는 것은 불필요하다는 말인가?
그런데 놀랍게도 양자역학적인 원거리 작용은 실제로 실험적으로 검증 가능하다! 이 실험의 기반은 “벨의 부등식Bell’s inequality”이라고 불리는 공식이다.
벨의 부등식
1964년 존 스튜어트 벨John Stewart Bell은 “아인슈타인-포돌스키-로젠 역설에 관하여On the Einstein Podolsky Rosen paradox”라는 기념비적인 논문을 쓴다. 이 논문에서 벨은 EPR 역설을 실제로 실험적으로 검증할 수 있는 방법을 제시하게 된다.
우선, 앞선 섹션에서 설명한 EPR 역설은 원칙적으로는 양자역학을 쓰지 않고 설명할 수 있다. 즉, 파동 함수를 쓰는 대신에 적절하게 잘 고안된 고전적인 확률 분포를 가정하면 EPR 역설을 설명할 수 있다. 물론 이렇게 하면 역설이라는 의미는 사라지게 된다.
고전적인 확률 분포 이론의 핵심은 다음과 같다. 우리의 측정 기술이 아직 충분히 좋지 않아서 정밀하게 잴 수는 없지만 양자역학을 넘어선 어떤 숨겨진 변수hidden variable가 있다. 그리고 이 변수는 모든 물리적인 상태를 정확히 인과적으로 결정할 수 있다. 다만 이 변수의 정확한 성질을 규정할 수 있는 방법이 아직 없으므로 현재로서는 각각의 물리적인 상태는 특정한 확률 분포를 가지고 발생하는 것처럼 보인다. 이러한 고전적인 확률 분포를 가지는 이론을 통칭해서 “숨겨진 변수” 이론이라고 부른다.
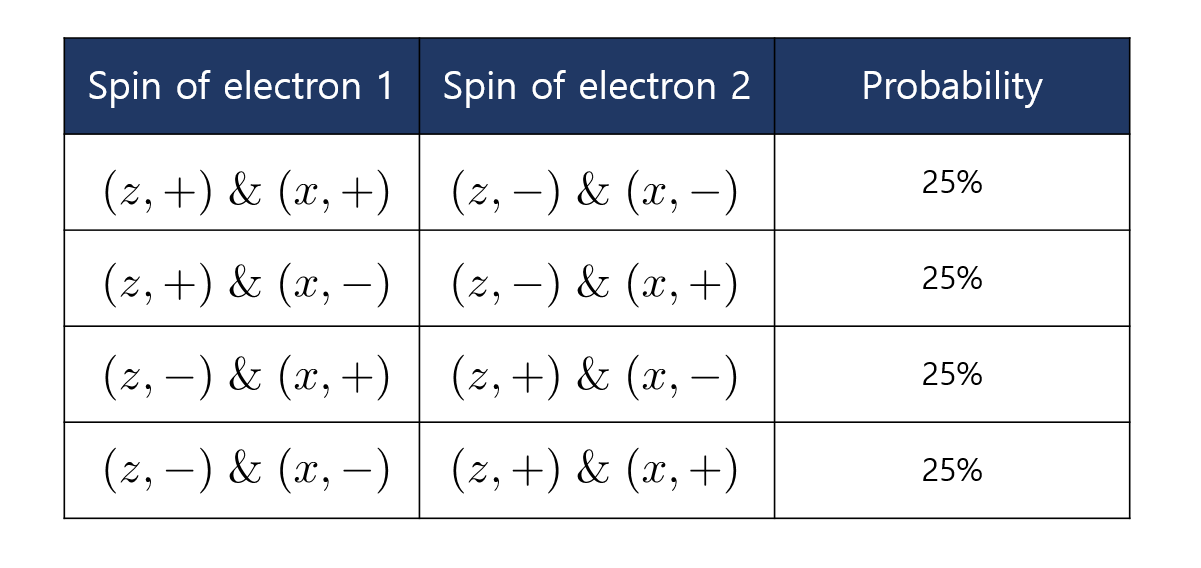
이제 구체적으로 앞선 섹션에서 설명한 EPR 역설을 모사하기 위해서 어떠한 확률 분포를 가정해야 하는지 생각해 보자. 우선, 전자의 스핀이 \(z\) 축과 \(x\) 축 방향으로 업이거나 다운일 확률은 서로 완전히 독립적이라고 가정하자. 즉, \(z\) 축 방향으로 특정한 스핀 상태를 가질 확률은 \(x\) 축 방향으로 특정한 스핀 상태를 가질 확률에 전혀 영향을 끼치지 않는다. 그다음 중요한 가정은 양자역학적인 스핀 싱글렛 상태를 고전적인 확률 분포로 모사하기 위해서 1번 전자의 스핀과 2번 전자의 스핀이 언제나 정반대가 되어야 한다는 것이다. 이러한 두 가지 가정하에 우리는 다음과 같은 고전적인 확률 분포를 구축할 수 있다.
위에서 \((z,+) \; \& \; (x,+)\)는 주어진 스핀이 \(z\) 축과 \(x\) 축 방향으로 동시에 업인 상황을 의미한다. 다른 기호들도 비슷하게 정의된다.
위 확률 분포는 앞선 섹션에서 설명한 EPR 역설의 결과를 완벽하게 재현할 수 있다. 비유적으로 말해서, 스핀 싱글렛 상태는 그 안에 들어 있는 2개의 공이 빨간색/파란색이라는 성질과 매끈함/거침이라는 성질을 각각 정확히 반반씩 가지고 있는 주머니와 같다. 물론 2 개의 공은 서로 반대의 성질을 가지고 있다. 이제 주머니를 딱 한 번만 열어보는 것이 아니라 위 확률 분포를 가지는 무수히 많은 주머니를 가져다 놓고 반복해서 실험을 한다면 양자역학이 주는 예측과 고전적인 확률 이론이 주는 예측은 정확히 같을 것이다. 아직까지 우리는 양자역학과 고전적인 확률 이론을 구분할 수 없다.
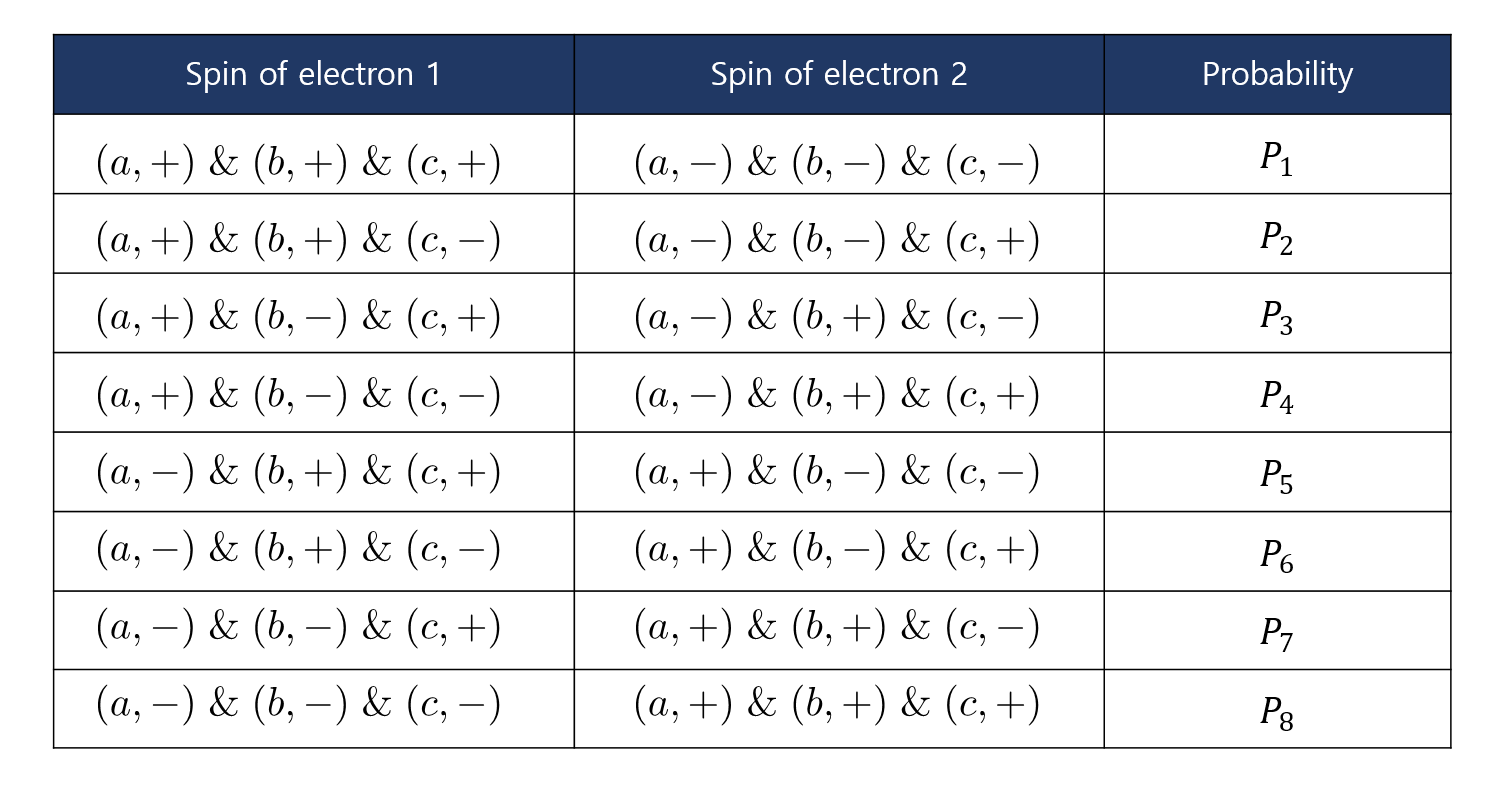
양자역학과 고전적인 확률 이론을 구분하기 위해서 우리는 조금 더 나아가야 한다. 구체적으로, 우리는 3개의 스핀 방향을 고려해야 한다. 이 3개의 방향을 \(a,b,c\)라고 하자. \(a,b,c\) 방향으로 스핀 업과 다운 상태를 가지는 모든 가능한 상황을 고려하면 다음과 같은 확률 분포를 구축할 수 있다.
여기서 중요한 것은 확률 분포가 어떤 구체적인 형태를 가진다고 가정하지 않았다는 사실이다. 즉, 각각의 \(P_n\) \((n=1,\cdots,8)\)이 어떤 특정한 값을 가지도록 규정하지 않았다. 아래 보겠지만 벨의 부등식은 이렇게 일반적인 상황에서도 항상 만족되어야 하는 부등식이다.
이제 1번 전자가 \(a\) 방향으로 스핀 업이고 2번 전자가 \(b\) 방향으로 스핀 업인 확률을 생각해 보자. 위에서 구축된 확률 분포를 이용하면 이 확률은 다음과 같이 주어진다.
\(P(a,+;b,+)= P_3 +P_4\)
비슷하게 1번 전자가 \(a\) 방향으로 스핀 업이고 2번 전자가 \(c\) 방향으로 스핀 업인 확률은 다음과 같이 주어진다.
\(P(a,+;c,+)= P_2 +P_4\)
마지막으로 1번 전자가 \(c\) 방향으로 스핀 업이고 2번 전자가 \(b\) 방향으로 스핀 업인 확률은 다음과 같이 주어진다.
\(P(c,+;b,+)= P_3 +P_7\)
이제, 모든 확률 분포 값은 언제나 0이거나 양수이어야 하므로 다음과 같은 부등식이 만족한다.
\(P(a,+;b,+) \leq P(a,+;c+) +P(c,+;b,+)\)
이것이 바로 벨의 부등식이다!
여기서 잠깐 벨의 부등식의 물리적인 의미를 생각해 보자. 벨의 부등식은 파동 함수 없이 개별 전자의 스핀에 대한 측정 결과가 고전적인 확률 분포로서 주어진다면 만족되어야 하는 근본적인 부등식이다. 확률 분포가 어떤 특정한 형태를 가진다고 가정할 필요가 없는 아주 일반적인 조건이다. 따라서 만약에 양자역학이 이 부등식을 위배한다면, “숨겨진 변수” 이론은 제아무리 어떤 확률 분포를 가정해도 양자역학과 양립할 수 없는 것이다.
이제 과연 양자역학이 실제로 벨의 부등식을 위배할 수 있는지 알아보자. 그러기 위해서는, 예를 들어서, 1번 전자가 \(a\) 방향으로 스핀 업이고 2번 전자가 \(b\) 방향으로 스핀 업인 확률, 즉 \(P(a,+;b,+)\)를 양자역학적으로 계산할 수 있어야 한다. 그런데 스핀 싱글렛 상태의 경우에, 2번 전자가 \(b\) 방향으로 스핀 업인 확률은 1번 전자가 \(b\) 방향으로 스핀 다운인 확률과 같다. 따라서 \(P(a,+;b,+)\)은 1번 전자가 \(a\) 방향으로 스핀 업이고 동시에 \(b\) 방향으로 스핀 다운인 확률과 같다. 물론 이 확률은 2번 전자가 \(a\) 방향으로 스핀 다운이고 동시에 \(b\) 방향으로 스핀 업인 확률과 같다.
모든 방향이 동등하고 각도의 기준은 언제나 원하는 축을 중심으로 정할 수 있으므로 편의상 \(a\) 방향을 \(z\) 축으로 정하도록 하자. 그리고 이 상황에서 \(b\) 방향은 \(a\) 방향을 \(y\) 축을 중심으로 \(\theta_{ab}\)만큼 회전시킨 방향이라고 정할 수 있다. 이해를 돕기 위해서 [그림2]를 보라. 참고로 [그림3]에서 \(b\) 방향은 \(x\) 축으로 정했다. 이 경우에 \(\theta_{ab}\)는 90도, 라디안으로 \(\pi/2\)이다. (왜 이 경우에 관심을 두는지는 아래에서 명확해질 것이다.)
이제, 1번 전자가 \(a\) 방향으로 스핀 업이고 동시에 \(b\) 방향으로 스핀 다운인 확률은 \(a\) 방향, 즉 \(z\) 축 방향으로 스핀 업인 상태와 \(b\) 방향, 즉 \(z\) 축을 \(\theta_{ab}\)만큼 회전한 방향으로 스핀 다운인 상태 사이의 오버랩overlap의 제곱으로 주어진다. 그런데 곰곰이 생각해 보면, \(z\) 축을 \(\theta_{ab}\)만큼 회전한 방향으로 스핀 다운인 상태는 원래 \(z\) 축으로 스핀 다운이었던 상태를 \(\theta_{ab}\)만큼 회전시킨 상태와 같다. 따라서 이제 우리가 해야 할 일은 \(z\) 축으로 스핀 다운인 상태를 \(y\) 축을 중심으로 \(\theta_{ab}\)만큼 회전시키는 것이다.
다행히 우리는 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 스핀을 회전시키는 연산자에 대해서 배웠다. 이 스핀 회전 연산자를 사용하면 우리는 \(b\) 방향으로 스핀 다운인 상태를 다음과 같이 얻을 수 있다.
\(|b,-\rangle =U_y(\theta_{ab})|z,-\rangle=\left(\begin{array}{cc}\cos{(\theta_{ab}/2)} & -\sin{(\theta_{ab}/2)}\\\sin{(\theta_{ab}/2)} & \cos{(\theta_{ab}/2)}\end{array}\right)\left(\begin{array}{c}0 \\ 1\end{array}\right)=\left(\begin{array}{c}-\sin{(\theta_{ab}/2)} \\\cos{(\theta_{ab}/2)}\end{array}\right)\)
여기서 \(U_y(\theta_{ab})\)는 \(y\) 축을 중심으로 \(\theta_{ab}\)만큼 스핀을 회전시키는 연산자이다. \(U_y(\theta_{ab})\)의 자세한 유도 과정은 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”를 참고하기를 바란다.
물론, \(a\) 방향, 즉 \(z\) 축 방향으로 스핀 업이 되는 상태는 보통의 스핀 업 상태인 \(|\uparrow\;\rangle\)이다.
\(|a,+\rangle = |\uparrow\;\rangle = \left(\begin{array}{c} 1 \\ 0 \end{array}\right)\)
결론적으로 1번 전자가 \(a\) 방향으로 스핀 업이고 2번 전자가 \(b\) 방향으로 스핀 업인 확률은 다음과 같이 주어진다.
\(P(a,+;b +)=|\langle a,+|b,-\rangle|^2=\sin^2{(\theta_{ab}/2)}\)
다른 방향에 대한 확률도 비슷하게 계산되므로, 벨의 부등식은 이제 다음과 같은 부등식으로 표현된다.
\(\sin^2{(\theta_{ab}/2)} \leq \sin^2{(\theta_{ac}/2)}+\sin^2{(\theta_{cb}/2)}\)
결론적으로 양자역학이 벨의 부등식을 위배하는 것을 증명하기 위해서는 위 부등식이 성립하지 않는 반례를 하나 찾으면 된다. 다시 말해서, 위 부등식이 성립하지 않는 3개의 각도 \(\theta_{ab}, \theta_{ac}, \theta_{cb}\)를 찾으면 된다.
이러한 반례는 [그림3]에 나타나 있다. [그림3]에서 보듯이, \(a\) 방향은 \(z\) 축 방향, \(b\) 방향은 \(x\) 축 방향, 그리고 \(c\) 방향은 \(z\) 축과 \(x\) 축 사이를 정중앙으로 가로지르는 방향이다. 이 경우에 \(\theta_{ab}, \theta_{ac}, \theta_{cb}\)는 각각 \(\pi/2, \pi/4, \pi/4\)이다. 그렇다면 우리는 다음과 같은 결론에 이른다.
\(\sin^2{(\theta_{ab}/2)} = \sin^2{(\pi/4)} = 0.5\)
\(\sin^2{(\theta_{ac}/2)} = \sin^2{(\theta_{cb}/2)} = \sin^2{(\pi/8)} \simeq 0.146447\)
이 경우에 벨의 부등식은 명백하게 위배된다!
앞서 말했듯이, 벨의 부등식은 고전적인 확률 이론이라면 반드시 만족해야 하는 부등식이다. 양자역학이 이 부등식을 위배한다는 사실은 양자역학과 숨겨진 변수에 의존하는 고전적인 확률 이론이 양립할 수 없다는 의미이다.
이제 양자역학과 고전적인 확률 이론 중에서 무엇이 맞는가에 대한 결정은 실험의 영역으로 넘어가게 된다. 여기서 자세하게 다양한 실험들을 소개할 수는 없지만 결론만 말하면 지금까지 수행된 실험들은 모두 양자역학의 손을 들어 주었다. 양자역학이 이긴 것이다. 단순히 확률이 아니라 파동 함수가 존재해야 하는 것이다!
양자 텔레포테이션
앞서 설명했듯이, EPR 역설은 양자역학이 불완전하다는 것을 증명하기 위해서 고안되었다. 그런데 이 EPR 역설이라는 양자역학의 믿기 힘들 만큼 이상한 예측은 실험 결과와 정확히 들어맞았다. 역설적이게도 EPR 역설은 양자역학의 공고함을 다시 한번 우리에게 각인시켜 주었다. 잘못된 것은 오히려 우리의 물리적인 직관이었다. 리처드 파인만Richard Feynman의 명언이 기막히게 적용되는 순간이다.
“역설은 현실과 현실은 어떠해야 한다는 당신의 느낌 사이의 충돌에 불과하다.”
“The ‘paradox’ is only a conflict between reality and your feeling of what reality ‘ought to be.’”
그런데 놀라운 일은 여기서 끝나지 않는다. ERP 역설은 단순히 양자역학의 원리를 증명하는 것을 넘어서 믿기 힘들 만큼 경이로운 응용 가능성을 제시한다. 그것은 바로 양자 원거리 전송, 다른 말로 양자 텔레포테이션quantum teleportation이다.
혼동을 피하기 위해서 양자 텔레포테이션에 대한 잘못된 환상부터 깨고 시작하자. EPR 역설은 양자역학이 예측하는 방식으로 해결되었다. 하지만 그렇다고 그것이 빛보다 빠르게 물질이 전송된다는 것을 의미하지는 않는다. 양자 텔레포테이션은 파동 함수의 붕괴가 원거리에서 순간적으로 작동한다는 EPR 역설에 기반을 두고 있다. 하지만 전송의 최종 단계에서 원래의 양자 상태를 재구성하기 위해서는 여전히 모종의 정보가 전송을 주고받는 지점 사이에 전달되어야 한다.
아무리 양자역학이라고 해도 실제로 “의미 있는” 정보가 빛보다 빨리 전달될 수는 없다. 따라서 양자 텔레포테이션은 순간 이동이 아니다. 그래도 물질의 전송이 빛의 속도로, 혹은 빛의 속도에 가깝게 이루어질 수 있다는 것은 정말 놀라운 일이 아닐 수 없다. 이 마법은 어디서 나오는가? 답은 바로 양자 얽힘이다.
자세하게 들어가기 전에 양자 텔레포테이션의 큰 줄거리를 설명하고 시작하자. 우선, 전송을 주고받는 지점 사이에 양자역학적으로 얽힌 상태가 존재한다고 하자. 이 양자 얽힘 상태는 앞선 섹션에서 언급한 스핀 싱글렛 상태일 수도 있고 스핀 트리플렛 상태일 수도 있다. 이 양자 얽힘 상태는 멀리 떨어진 두 지점을 연결하는 전송 채널의 역할을 한다.
이제, 전송하고 싶은 어떤 양자 상태가 있다고 하자. 여기서 이 양자 상태의 구체적인 형태를 알 필요는 없다. 중요한 점은 이 양자 상태와 전송 채널의 역할을 하는 양자 얽힘 상태의 한 부분이 전송하는 지점에서 공존하고 있다는 사실이다. 이때 전송하는 지점에서 모종의 측정을 하면 전체 파동 함수가 붕괴하고, 그 결과로 전송받는 지점에 있는 양자 얽힘 상태의 나머지 한 부분도 어떤 특정한 양자 상태로 붕괴한다. 이 특정한 양자 상태는 원래 전송하고 싶었던 양자 상태의 정보를 가지고 있다. 최종적으로 우리는 모종의 정보를 이용하여 이 특정한 양자 상태를 원래 전송하고 싶었던 양자 상태로 변환시킬 수 있다. 이 변환에 필요한 정보는 바로 전송하는 지점에서 수행된 측정의 결과이다.
이제 약간의 수학을 써서 양자 텔레포테이션의 원리를 조금 더 구체적으로 설명해 보자. 예를 들어서, 지구에 사는 앨리스Alice가 슈뢰딩거의 고양이 상태 \(\psi_C\)를 달에 사는 밥Bob에 전송하고 싶다고 하자. (참고로 앨리스와 밥이라는 이름은 이니셜이 A와 B이기 때문에 선정되었다.) 이제 앨리스와 밥이 각각 전자를 하나씩 가지고 있다고 하자. 이 2개의 전자는 스핀 쌍을 이루어 전송 채널의 역할을 하는 양자 얽힘 상태를 구성할 수 있다. 앞서 언급했듯이, 양자 얽힘 상태는 스핀 싱글렛 상태가 될 수도 있고 스핀 트리플렛 상태가 될 수도 있다. 편의상, 앨리스와 밥의 스핀 사이에 생성될 수 있는 스핀 싱글렛 상태와 트리플렛 상태를 다시 써 보자.
\(|s\rangle_{AB}=\frac{1}{\sqrt{2}}\left(|0\rangle_A |1\rangle_B -|1\rangle_A |0\rangle_B \right)\)
\(|t^0\rangle_{AB}=\frac{1}{\sqrt{2}}\left(|0\rangle_A |1\rangle_B +|1\rangle_A |0\rangle_B \right)\)
\(|t^+\rangle_{AB}=\frac{1}{\sqrt{2}}\left(|0\rangle_A |0\rangle_B +|1\rangle_A |1\rangle_B \right)\)
\(|t^-\rangle_{AB}=\frac{1}{\sqrt{2}}\left(|0\rangle_A |0\rangle_B -|1\rangle_A |1\rangle_B \right)\)
여기서 아랫첨자 A와 B는 앨리스와 밥을 의미한다. 그리고 위에서는 편의를 위해서 화살표 대신에 \(|0\rangle\)과 \(|1\rangle\)로 스핀 업과 다운 상태를 표시하였다. 참고로 \(|s\rangle\)와 \(|t^{0,+,-}\rangle\)는 각각 스핀 싱글렛과 트리플렛 상태를 의미한다. 위에서 스핀 트리플렛 상태 \(|t^+\rangle\)와 \(|t^-\rangle\)는 앞서 언급된 \(\chi_{1,1}\)과 \(\chi_{1,-1}\)을 선형 중첩시켜서 얻었다. 우리의 현재 예에서는 스핀 싱글렛 상태 \(|s\rangle_{AB}\)를 전송 채널로 쓰기로 하자.
우리의 목표는 지구에 있는 슈뢰딩거의 고양이의 양자 상태를 달로 전송하는 것이다. 엄밀하게 말해서, 슈뢰딩거의 고양이를 기술하는 파동 함수를 달에서 재구성하고자 한다. 구체적으로, 슈뢰딩거의 고양이가 다음과 같은 파동 함수로 주어진다고 하자.
\(|\psi\rangle_C = \alpha|0\rangle_C +\beta|1\rangle_C\)
여기서 \(|0\rangle_C\)와 \(|1\rangle_C\)는 각각 슈뢰딩거의 고양이가 살아있는 상태와 죽은 상태를 의미한다.
최종적으로 슈뢰딩거의 고양이와 스핀 싱글렛 전송 채널을 포함한 전체 파동 함수는 다음과 같이 쓰인다.
\(|\Psi\rangle_{\rm tot}=|\psi\rangle_C |s\rangle_{AB}= \frac{1}{\sqrt{2}}\left(\alpha|0\rangle_C +\beta|1\rangle_C\right)\left(|0\rangle_A |1\rangle_B -|1\rangle_A |0\rangle_B \right)\)
자, 이제 다음은 양자 텔레포테이션에서 매우 중요한 단계이다. 이 단계에서는 앨리스와 밥의 스핀 사이에 형성된 양자 얽힘 상태를 풀고, 대신 슈뢰딩거의 고양이와 앨리스의 스핀을 얽히게 만든다. 이 작업을 수행하기 위해서는 개별 스핀 상태를 스핀 싱글렛과 트리플렛 상태로 거꾸로 표현할 수 있음을 알아야 한다.
\(|0\rangle_C|0\rangle_A = \frac{1}{\sqrt{2}} \left( |t^+\rangle_{CA}+|t^-\rangle_{CA} \right)\)
\(|1\rangle_C|1\rangle_A = \frac{1}{\sqrt{2}} \left( |t^+\rangle_{CA}-|t^-\rangle_{CA} \right)\)
\(|0\rangle_C|1\rangle_A = \frac{1}{\sqrt{2}} \left( |t^0\rangle_{CA}+|s\rangle_{CA} \right)\)
\(|1\rangle_C|0\rangle_A = \frac{1}{\sqrt{2}} \left( |t^0\rangle_{CA}-|s\rangle_{CA} \right)\)
위에서 주목할 사실은 이제 슈뢰딩거의 고양이(C)와 앨리스(A)의 스핀이 양자 얽힘 상태를 구성한다는 것이다.
위 결과를 이용해서 전체 파동 함수를 다시 정리해서 쓰면 다음과 같다.
\(|\Psi\rangle_{\rm tot} = -\frac{1}{2} \Big\{|s\rangle_{CA}\Big(\alpha|0\rangle_B+\beta|1\rangle_B \Big)+|t^0\rangle_{CA}\Big(\alpha|0\rangle_B-\beta|1\rangle_B \Big) \\+|t^+\rangle_{CA}\Big(\beta|0\rangle_B-\alpha|1\rangle_B \Big)-|t^-\rangle_{CA}\Big(\beta|0\rangle_B+\alpha|1\rangle_B \Big)\Big\}\)
이제 지구에서 모종의 측정을 한다고 하자. 이 측정의 목적은 슈뢰딩거의 고양이와 앨리스의 스핀이 4가지 양자 얽힘 상태들, 즉 \(|s\rangle_{CA}, |t^0\rangle_{CA}, |t^+\rangle_{CA}, |t^-\rangle_{CA}\) 중에 무엇에 속하는지 알아내는 것이다. 이러한 측정을 전문적으로 “벨 측정Bell measurement”이라고 부른다. 다시 말해서, 지구에서 벨 측정을 통해서 전체 파동 함수를 4가지 양자 얽힘 상태 중의 하나로 붕괴시킬 수 있다. 재미있는 것은 이러한 붕괴의 결과로 달에서의 파동 함수도 따라서 결정된다는 것이다.
다음 표는 지구에서의 측정 결과와 그것에 따라서 결정되는 달에서의 파동 함수를 나타낸다.
예를 들어서, 지구에서의 벨 측정의 결과가 스핀 싱글렛 상태 \(|s\rangle_{CA}\)라면 달에서의 파동 함수는 원래 전송하고 싶었던 파동 함수 \(\alpha|0\rangle_B +\beta|1\rangle_B\)와 정확히 같다. 따라서 이 경우에는 여분의 작업을 할 필요 없이 지구에서의 파동 함수가 달에서 그대로 재구성된 것이다.
반면에, 지구에서의 벨 측정의 결과가 스핀 트리플렛 상태 \(|t^0\rangle_{CA}\)라면 달에서의 파동 함수는 \(\alpha|0\rangle_B -\beta|1\rangle_B\)이다. 이 상태는 원래 전송하고 싶었던 파동 함수는 아니지만 거의 비슷하다. 다시 말해서, \(|1\rangle_B\)앞에 붙는 계수의 부호만 바꾸면 원래 전송하고 싶었던 파동 함수를 재구성할 수 있다. 구체적으로, \(z\) 방향의 파울리 행렬인 \(\sigma_z\)를 달에서의 파동 함수에 작용하면 지구에서의 파동 함수를 얻을 수 있다.
\(\left(\begin{array}{cc}1 & 0 \\0 & -1\end{array}\right)\left(\begin{array}{c}\alpha \\ -\beta\end{array}\right)=\left(\begin{array}{c}\alpha \\ \beta\end{array}\right)\)
나머지 두 경우에도 측정 결과를 안다면 달에서의 파동 함수를 변환해서 원래 전송하고 싶었던 파동 함수를 재구성할 수 있다.
정리해 보자. 양자 텔레포테이션은 양자 얽힘 상태를 전송 채널로 이용하여 멀리 떨어진 지점 사이에 양자 상태를 전송하는 것이다. 엄밀하게 말해서 실제로 전송되는 것은 물질 자체가 아니라 정보이다. 아니, 조금 더 엄밀하게 말해서, 전송되는 것은 단순히 정보가 아니라 선형 중첩되어 전송되는 여러 양자 상태들을 이용해서 원래 양자 상태를 재구성할 수 있는 정보이다. 어떤 의미로 양자 상태들은 이미 도착해 있다. 다만, 우리는 붕괴된 파동 함수를 가지고 어떻게 할지 몰랐던 것이다. 전송하는 지점에서 수행된 측정 결과가 도착하면 우리는 원래 양자 상태를 재구성할 수 있다.
마지막으로, 혹시 지금까지 양자 텔레포테이션이 상상에 불과한 것이 아닌가 궁금해 한 독자가 있었는지 모르겠다. 놀랍게도 양자 텔레포테이션은 실제 실험적으로 구현되었다. 아직 고양이와 같이 큰 물체를 전송하는 것은 불가능하지만, 양자 텔레포테이션은 광자, 전자, 원자, 그리고 초전도 회로와 같은 다양한 시스템에서 이미 구현되었다. 공상 과학 소설에서나 나오는 이야기 같지만 우리는 이미 양자역학의 믿기 힘든 세계에 들어와 있다.
양자 컴퓨터
양자 텔레포테이션의 핵심 원리는 양자 얽힘이다. 그런데 크게 보면 양자 얽힘은 파동 함수의 선형 중첩이라는 양자역학의 근본적인 성질의 한 면이다. 양자 얽힘을 포함한 파동 함수의 선형 중첩이라는 성질은 양자 텔레포테이션보다 훨씬 더 중요한 다른 응용 가능성을 품고 있다. 이 가능성은 바로 양자 컴퓨터quantum computer이다.
양자 컴퓨터의 가능성을 처음 제안한 사람으로 꼽히는 사람은 놀랍게도 리처드 파인만이다. 그는 1981년 “컴퓨터로 물리 모의 실험하기Simulating Physics with Computers”라는 강연에서 다음과 같은 말을 했다.
“나는 고전적인 이론만을 가지고 하는 모든 분석에 만족할 수 없습니다. 왜냐하면 자연은, 젠장, 고전적이지 않기 때문이죠. 당신이 자연에 대해서 모의 실험을 하고 싶다면 양자역학적으로 해야 할 것입니다. 이건 정말 놀라운 문제입니다. 그리 쉬어 보이지 않기 때문이죠.”
“I’m not happy about all the analyses that go with just the classical theory, because nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy.”
위에서 파인만이 얘기하고 싶은 말은 자연을 근본적으로 모사하기 위해서는 양자역학을 사용해야 한다는 것이다. 다시 말해서, 양자 소자로 만들어진 컴퓨터를 사용하여 물리 문제를 풀 수 있다면, 우리는 자연을 간접적으로 흉내 내는 것이 아니라 아예 직접적으로 구현하게 되는 것이다.
그렇다면 양자 소자란 무엇인가? 원리적으로는 아주 간단하다. “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명한 두 가지 상태를 가지는 그 어떤 양자 시스템이라도 양자 소자가 될 수 있다. 스핀 업과 다운이 연산의 기본 단위인 비트bit를 나타내는 것이다. 전문적으로 양자 소자를 큐비트qubit이라고 부른다. 마치 보통 컴퓨터가 비트를 사용해서 연산을 수행하듯이 양자 컴퓨터는 큐비트를 사용해서 연산을 수행할 수 있다.
여기서는 지면 관계상 큐비트를 실제로 구현하는 시스템에 대해서 자세하게 이야기를 할 수는 없다. 다만, 결론부터 말하면 현재 최대 50개 정도의 큐비트까지는 만들 수 있지만 아직 실제로 의미 있는 양자 컴퓨터는 만들어지지 않았다. 현재는 여러 시스템들이 서로 경쟁하고 있는 단계이다. 여러 시스템들 중에서 중요한 몇 가지만 언급하고자 한다.
우선, 초전도체를 이용하는 다양한 시스템들이 있다. 이들은 구체적으로 초전도체의 어떤 성질을 이용하는지에 따라서 서로 차이점을 지닌다. 예를 들어서, 초전도 회로 자체가 큐비트가 될 수 있다. 특히, 이 경우에는 두 개의 초전도체를 접합할 때 발생하는 조셉슨 효과Josephson effect가 자주 이용된다. 다른 예로는 작은 초전도체 조각, 소위 쿠퍼쌍 상자Cooper pair box가 큐비트가 되기도 한다. 초전도체를 이용하는 시스템은 전체적으로 회로 제작에 있어서 앞선 기술을 가지고 있는 산업계에서 가장 집중하고 있는 시스템이다.
다른 시스템으로 “덫에 갇힌 이온trapped ions”이 있다. 이 시스템의 기본 아이디어는 레이저로 퍼텐셜 우물potential well을 만들고 그 안에 이온들을 가두는 것이다. 여기서는 개별 이온의 양자 상태가 큐비트를 구성한다. 이 시스템은 현재 실험적으로 가장 안정적인 큐비트를 제공할 수 있다고 알려져 있다. 참고로, 이 시스템은 원자 물리학에 관한 기술이 축적되어 있는 대학교 연구실이나 국립 연구소에서 선호하는 시스템이다.
또 다른 시스템으로 양자 점quantum dot에 갇힌 전자가 있다. 이 시스템은 개념적으로 매우 중요한 강점을 가지고 있는데, 그것은 전자의 스핀이 실제로 두 상태를 구성하기 때문이다. 지금까지 본 연재글에서 자세히 설명한 전자의 스핀이 정말로 큐비트를 구현하는 것이다. 이 시스템의 또 다른 강점은 양자 점이 반도체 기술에 기반을 두고 있다는 것이다. 현재 눈부실 정도로 발전된 반도체 기술을 곧바로 쓸 수 있다는 것은 매우 중요한 강점이다. 다만, 반도체 속의 전자는 스핀 상태의 결맞음coherence을 오래 유지할 수 없다는 것이 큰 약점이다.
또 다른 시스템으로는 다이아몬드 속에 형성되는 질소-공석 센터nitrogen-vacancy center, NV center가 있다. 알다시피 다이아몬드는 탄소로 이루어져 있다. 그런데 다이아몬드 속에 있는 탄소는 가끔씩 질소로 치환되어 결점이 발생한다. 그리고 그렇게 되면 그 주변의 탄소 하나도 같이 빠져버려 “공석vacancy”이 생긴다. 이렇게 형성된 질소-공석 결합체는 스핀 자유도를 가지게 되는데, 바로 이 스핀 자유도가 큐비트의 역할을 할 수 있다. 나름의 장점에도 불구하고 여러 개의 큐비트를 하나의 양자 얽힘 상태로 묶는 것이 어렵다고 알려져 있다.
마지막 시스템으로 소위 위상학적인 큐비트topological qubit가 있다. 필자가 전공하고 있는 주제인 양자 홀 효과quantum Hall effect와 깊은 관련이 있어서, 나름 대로 애착을 가지고 있는 시스템이다. 다만 현재까지 실험적으로 가장 진보가 느린 시스템이다. 이 시스템은 응집물질물리 학계에서 큰 관심을 끌고 있는데, 그 이유는 마치 위상학적인 구조를 지니는 소용돌이나 태풍이 오랫동안 그 형체를 유지할 수 있듯이 위상학적인 큐비트는 원칙적으로 각종 계산 오류로부터 보호될 수 있기 때문이다. 이론적인 관점에서 보아도 “비가환군 통계non-Abelian statistics”라고 불리는 재미있는 아이디어가 숨어 있어서 이 시스템에 대한 관심은 나름 계속 유지되고 있다. 참고로, 미국 IT 기업인 마이크로소프트Microsoft가 이 시스템에 많은 투자를 하고 있다.
이 단계에서 짚고 넘어갈 중요한 사실이 하나 있다. 양자 컴퓨터에 이토록 많은 연구실과 기업체에서 관심을 두는 이유는 단순히 파인만이 이야기한 자연을 근본적으로 모사하기 위함이 아니다. 진짜 이유는 양자 암호화 기술quantum cryptography에 있다.
양자 컴퓨터는 고전적인 컴퓨터에 비해서 모든 면에서 다 좋은 것이 아니다. 일반적인 문제를 푸는 소위 범용 컴퓨터의 입장에서 보면 양자 컴퓨터는 고전적인 컴퓨터를 아마 영원히 대체하지 못할 것이다. 다만, 특정한 작업에 관하여 양자 컴퓨터는 고전적인 컴퓨터에 비해서 지수함수적으로 빠른 성능을 발휘할 수 있다. 이 특정한 작업 중의 하나가 바로 양자 암호화 기술이다.
조금 더 구체적으로 말해서, 현재 우리가 인터넷에서 쓰고 있는 암호화 기술은 소위 RSARivest-Shamir-Adleman 알고리즘이다. 이 알고리즘은 어떤 굉장히 큰 자연수가 두 개의 큰 소수prime number의 곱으로 표현될 때, 답을 미리 가르쳐 주지 않으면 실제로 이러한 두 소수를 찾는 것이 매우 어렵다는 원리에 기반을 두고 있다. 다시 말해서, 굉장히 큰 자연수를 소인수 분해prime factorization하는 것이 매우 어렵다는 원리이다. 참고로 RSA 알고리즘에 쓰이는 소수는 보통 140자리 이상의 큰 수이다.
그런데 양자 컴퓨터는 이러한 소인수 분해를 매우 빠르게 수행할 수 있다. 이것이 가능한 이유는 쇼어의 알고리즘Shor’s algorithm 덕분이다. 만약에 충분히 많은 수의 큐비트를 가지는 양자 컴퓨터가 개발된다면, 쇼어의 알고리즘을 통해서 인터넷의 보완이 순식간에 무력화될 수 있다. 독자들은 이제 왜 많은 연구실과 기업체, 심지어는 국가 차원에서 양자 컴퓨터에 관심을 가지는지 알 수 있을 것이다.
쇼어의 알고리즘
쇼어의 알고리즘은 크게 두 개의 부분으로 나누어서 이해할 수 있다. 첫 번째 부분은 소인수 분해에 필요한 수학적인 기반을 제공하는 정수론 부분이고, 두 번째 부분은 이 정수론 이론을 이용하여 실제로 소인수 분해를 실행하는 양자역학 부분이다.
우선, 정수론 부분부터 시작하자. 고전적으로 소인수 분해를 하는 방법은 답이 될듯한 되는 소수를 그야말로 하나하나 시도해 보는 것이다. 예상할 수 있겠지만 몇백 개 이상의 자릿수를 가지는 자연수를 이런 방법으로 소인수 분해한다는 것은 매우 비효율적이다. 더 나은 방법이 필요하다.
페르마의 마지막 정리Fermat’s last theorem로 유명한 페르마Fermat는 약간 덜 유명하지만 그의 이름이 붙은 다른 정리를 하나 가지고 있다. 재미있게도 이 정리의 이름은 페르마의 작은 정리Fermat’s little theorem이다. 내용은 다음과 같다.
“어떤 소수 \(p\)가 있다고 하자. 그렇다면 임의의 정수 \(a\)에 대해서 \(a^p\)을 \(p\)로 나눈 나머지는 항상 \(a\)와 같다.”
이 정리는 나중에 오일러Euler에 의해서 일반화되어 다음과 같은 오일러-페르마 정리Euler-Fermat theorem이 되었다.
“서로 공약수가 없는 어떤 2개의 양의 정수 \(N\)과 \(a\)가 있다고 하자. 그렇다면 \(a^p\)을 \(N\)으로 나눈 나머지가 항상 1이 되게 하는 정수 \(p\)가 있다.”
조금 어려우니 약간 쉽게 풀어 쓰면 다음과 같다. 서로 공약수가 없는 어떤 2개의 양의 정수 \(N\)과 \(a\)가 있다고 하자. 그렇다면 \(a\)를 충분히 많이 곱하면 \(N\)으로 나눌 때 나머지가 항상 1이 되게 할 수 있다.
\(a\cdot a \cdots a = ({\rm some\;integer})\times N +1\)
수학적인 형식을 빌어 쓰면 다음과 같다.
\(a^p=mN+1\)
여기서 \(p\)는 \(a\)를 몇 번 곱하는지를 말해주는 양의 정수이고, \(m\)은 \(N\) 앞에 붙는 어떤 정수some integer이다.
이제 위 공식을 변형하면 재미있는 일이 벌어진다. 우선 우변의 1을 좌변으로 옮긴다.
\(a^p-1=mN\)
그 다음에 좌변을 아래와 같이 두 인수의 곱으로 표현한다.
\((a^{p/2}+1)(a^{p/2}-1)=mN\)
위 공식이 말해주는 바는 \(a^{p/2}+1\)과 \(a^{p/2}-1\)의 곱이 \(N\)의 배수multiple라는 것이다. 그런데 그렇다면 \(a^{p/2}+1\)과 \(a^{p/2}-1\)이 각각 \(N\)과 공약수를 가질 확률이 있다는 이야기가 된다. 물론 아닐 수도 있다. 예를 들어서, \(a^{p/2}+1\)과 \(a^{p/2}-1\), 둘 중의 하나가 \(N\)의 배수가 될 수 있다. 혹은 \(p\)가 홀수라면 두 숫자는 아예 정수가 되지 않는다. 하지만 \(a\)를 잘 고르면 위 두 문제가 생기지 않을 수 있다.
정리하면 다음과 같다. 어떤 큰 자연수 \(N\)를 소인수 분해하고 싶다고 하자. 우리의 방법은 기본적으로 답을 추측하는 것이다. 문제는 “어떻게 하면 답을 잘 추측할 수 있는가”이다. 위에서 설명한 오일러-페르마 정리가 말해주는 바는 어떤 \(a\)를 잘 고르면 \(a^{p/2}+1\)과 \(a^{p/2}-1\)이 각각 \(N\)과 공약수를 가질 확률이 크다는 것이다. 여기서 \(p\)는 \(a^p=mN+1\)를 만족하는 정수 \(p\)이다. 만약 \(p\)가 짝수이고, \(a^{p/2}+1\)과 \(a^{p/2}-1\) 중의 하나가 \(N\)의 배수가 아니라면 우리는 추측을 잘 한 것이다. 결론적으로, \(N\)은 \(a^{p/2}+1\)과 \(a^{p/2}-1\)이 각각 \(N\)과 가지는 공약수로 소인수 분해된다. (참고로 어떤 두 자연수의 공약수를 찾는 문제는 유클리드Euclid의 알고리즘이라고 불리는 방법에 의해서 매우 효율적으로 풀린다.)
조금 어려우니 구체적인 예를 하나 들어 보자. 예를 들어서, \(N=314191\)을 소인수 분해하고 싶다고 하자. 참고로, 이 예는 <minutephysics>라고 불리는 사람의 YouTube동영상에서 빌려 왔다. 위에서 설명한 방법에 따라서 우리는 \(a\)를 고르는 것부터 시작한다. 예를 들어서 \(a\)를 \(101\)로 골라보자. \(101\)을 몇 번 곱하면 \(314191\)로 나누었을 때 나머지가 \(1\)이 될까? 즉, \(a^p=mN+1\)을 만족하는 정수 \(p\)는 무엇인가? 쉽지 않지만 잘 해 보면 \(p=4347\)임을 알 수 있다. \(m\)은 너무나도 큰 숫자이어서 여기서는 쓰지 않기로 한다.
앗, 그런데 이 경우에 \(p\)는 홀수이다. 우리는 좋지 못 한 추측을 한 것이다. 다시 시작하자. 이제 \(a\)를 \(127\)로 골라보자. 이 경우에 위에서와 같이 잘 해 보면 \(p=17388\)임을 알 수 있다. 이제 우리의 추측은 \(a^{p/2}\pm 1=127^{17388/2}\pm 1\)이 \(314191\)과 가지는 공약수가 \(314191\)을 소인수 분해할 확률이 있다는 것이다. 실제로 해 보면, \(127^{17388/2}+ 1\)은 \(314191\)과 \(829\)라는 공약수를 가지고, \(127^{17388/2}- 1\)은 \(314191\)과 \(379\)라는 공약수를 가진다. 확인해 보면 정말로 \(829\times379 = 314191\)이다!
이제 우리에게 남겨진 어려운 문제는 시행착오로 선택되는 어떤 정수 \(a\)에 대해서 \(a^p=mN+1\)을 만족하는 정수 \(p\)를 찾는 것이다. 바로 이곳이 양자역학이 우리를 도와주는 부분이다. 조금 복잡하니까 자세하게 들어가기 전에 큰 줄거리를 설명하고 시작하고자 한다. 가장 근본적인 수준에서 양자 컴퓨팅이 강력한 이유는 많은 변수 값을 한꺼번에 함수에 집어넣어 병렬 계산parallel computation을 수행할 수 있다는 사실에 있다.
그런데 양자 컴퓨팅은 보통의 병렬 계산 방식과는 매우 다른 점이 있다. 그것은 각각의 변수 값에 대한 결과가 한꺼번에 계산되기는 하지만 그 결과들이 선형 결합의 상태로 얻어진다는 것이다. 다르게 말해서 우리는 답을 확률적으로만 알 수 있다. 그렇다면 양자역학은 도움이 안 된다는 말인가? 놀랍게도, 이 문제를 피하면서 양자역학의 병렬 계산의 효과를 오롯이 누릴 수 있는 좋은 방법이 있다. 아래에서 자세히 살펴보자.
앞서 설명했듯이, 우리는 어떤 주어진 \(N\)과 시행착오로 선택되는 \(a\)에 대해서 \(a^p=mN+1\)을 만족하는 정수 \(p\)를 찾고 싶다. 고전적으로는 \(a\)를 계속 곱해가면서 답이 맞는지 하나하나 체크해 보는 방법밖에 없다. 반면에 양자역학적으로는 모든 가능성을 한꺼번에 체크해 볼 수 있다. 구체적으로, 다음과 같은 선형 중첩 상태를 만들어 보자.
\(\sum_x |x\rangle = |1\rangle+|2\rangle+\cdots+|n\rangle+\cdots\)
위에서 \(|x\rangle\)은 \(a\)를 \(x\)번 곱하는 상태를 의미한다. 원칙적으로 \(|x\rangle\)는 여러 개의 큐비트를 가지고 구현할 수 있다. 예를 들어서, 3개의 큐비트가 있으면 우리는 \(2^3=8\) 개의 숫자를 표현할 수 있다.
\(|000\rangle=|1\rangle \\|001\rangle=|2\rangle \\|010\rangle=|3\rangle \\|011\rangle=|4\rangle \\|100\rangle=|5\rangle \\|101\rangle=|6\rangle \\|110\rangle=|7\rangle \\|111\rangle=|8\rangle\)
이것은 별게 아니라 2진수를 10진수로 변환하는 것이다. 참고로, 위에서는 2진수를 보통의 방식대로 10진수로 변환한 다음에 1을 더했다.
이제 모종의 방법을 써서 각각의 \(|x\rangle\) 상태에 그것에 해당하는 \(|a^x\rangle\) 상태를 만들어 다음과 같은 양자 얽힘 상태를 만들자.
\(\sum_x |x\rangle|a^x\rangle = |1\rangle|a\rangle+|2\rangle|a^2\rangle+\cdots+|n\rangle|a^n\rangle+\cdots\)
위에서 \(|a^x\rangle\) 상태는 \(|x\rangle\) 상태를 만들 때 썼던 큐비트들과는 다른 새로운 큐비트들로 구현한다. EPR 역설을 설명할 때 썼던 예를 비유로 들면, \(|x\rangle\) 상태는 지구에서의 양자 상태이고, \(|a^x\rangle\) 상태는 달에서의 양자 상태이다.
다음 단계에서는 \(a^x\)를 \(N\)으로 나누어 생기는 나머지 값 \(r_x\)을 계산한다. 이제 나머지 값을 이용해서 위 양자 얽힘 상태를 다음과 같이 다시 표현한다.
\(\sum_x |x\rangle|r_x\rangle = |1\rangle|r_1\rangle+|2\rangle|r_2\rangle+\cdots+|n\rangle|r_n\rangle+\cdots\)
그 다음은 나머지 값을 재는 측정을 통해서 파동 함수를 붕괴시키는 단계이다. 예를 들어서 나머지 값의 측정 결과가 \(r=r^*\)라고 하자. 그렇다면 위 파동 함수에서 \(r_x=r^*\)이 되는 성분만 살아 남고 나머지는 모두 없어진다.
\(\sum_l |x_0+lp\rangle|r^*\rangle = |x_0\rangle|r^*\rangle+|x_0+p\rangle|r^*\rangle+|x_0+2p\rangle|r^*\rangle+\cdots+|x_0+np\rangle|r^*\rangle+\cdots\)
위에서 왜 \(x=x_0+lp\)인지 궁금할 것이다. 다시 말해서, 왜 같은 나머지 값을 가지는 \(x\)는 \(p\)의 주기로 반복되는지 궁금할 것이다. 그 이유는 생각보다 간단하다.
우선 \(p\)는 다음을 만족한다.
\(a^p=mN+1\)
반면에 임의의 \(x\)는 다음을 만족한다.
\(a^x=m^\prime N+r_x\)
위 두 식을 곱하면 다음과 같은 결과를 얻을 수 있다.
\(a^{x+p}=m^{\prime\prime} N+r_x\)
여기서 \(m^{\prime\prime}\)은 또 다른 정수이다. 결론적으로, 만약 어떤 \(x\)가 \(r_x\)라는 나머지 값을 가진다면, \(x+p\)도 정확히 같은 나머지 값을 가진다. 다시 말해서, 같은 나머지 값을 가지는 \(x\)는 \(p\)의 주기로 반복된다.
지금까지의 상황을 정리해 보자. 나머지 값을 측정함으로서 우리는 파동 함수를 붕괴시켰다. 그런데 붕괴 후에 살아 남는 파동 함수는 특별한 주기를 지니게 된다. 우리가 원하는 \(p\)는 바로 이 주기이다.
마지막 단계로 소위 양자 푸리에 변환quantum Fourier transform, QFT을 수행하면 이 주기를 찾을 수 있다. 여기서는 지면 관계 상 자세하게 들어갈 수 없지만, 양자 푸리에 변환은 굉장히 효율적으로 수행될 수 있다는 것이 알려져 있다. 약간 기술적으로 말하면 양자 푸리에 변환 이후에 얻어지는 파동 함수는 다음과 같다.
\(\sum_l \left| \frac{l}{p} \right\rangle|r^*\rangle=\left(\left|\frac{1}{p}\right\rangle+\left|\frac{2}{p}\right\rangle +\cdots+\left|\frac{n}{p}\right\rangle+\cdots\right)|r^*\rangle\)
위에서 \(|l/p\rangle\)는 \(k=2\pi l/p\)의 파수를 가지는 평면파를 기술하는 상태이다. 참고로, 위에서 \(|r^*\rangle\)는 선형 중첩된 모든 파동 함수의 성분에 대해서 변하지 않으므로 양자 푸리에 변환에는 아무런 영향을 주지 않는다. 여기서 주목할 사실은 푸리에 변환 후에 얻어지는 평면파는 단순히 \(2\pi /p\)의 파수만 가지는 것이 아니라 일반적으로 \(2\pi /p\)의 정수배의 파수를 모두 가진다는 것이다. 전문적으로 말하기를, 소위 주기 \(p\)를 가지는 “디랙 빗 함수Dirac comb function”의 푸리에 변환은 주기 \(2\pi /p\)를 가지는 디랙 빗 함수이다. 디랙 빗 함수는 디랙 델타 함수가 마치 빗comb의 살과 같이 주기적으로 반복되는 함수이다.
[그림6]은 지금까지 설명한 쇼어의 알고리즘을 총정리해서 설명하는 그림이다.
양자 테크놀로지
과학의 성과는 기술의 진보로 이어진다. 개별적인 차이가 있을 수 있지만 수많은 과학의 성과는 결국 기술의 진보로 이어져 왔다. 아니, 엄밀하게 말해서 과학과 기술은 누가 먼저가 아니라 서로 긴밀하게 영향을 주고받으면서 진보해 왔다.
예를 들어서, 18세기 후반에서 19 세기 전반까지 진행된 산업 혁명industrial revolution은 증기 기관steam engine이라는 새로운 기계의 발명을 통해서 그 이전과는 차원이 기술의 진보와 그로 인한 사회문화적인 변혁을 가져왔다. 이에 자연스럽게 증기 기관의 효율을 증가시키는 문제는 당대 가장 중요한 기술적인 문제 중의 하나로 대두되게 된다. 그런데 이 문제는 단순히 구먹구구식의 요령을 찾는 것을 넘어서 열heat에 대한 근본적인 이해를 필요로 했다. 이후 열에 대한 근본적인 고찰은 열역학thermodynamics이라는 학문으로 발전하게 된다. 열역학은 더 나아가 볼츠만Boltzmann, 기브스Gibbs와 같은 선각자들에 의해서 통계역학statistical mechanics으로 발전하게 된다. 그리고 아래 보겠지만 재미있게도 통계역학은 양자역학의 발전에 중요한 역할을 하게 된다.
이보다 약간 늦은 19세기 후반에는 전자기학electromagnetism이 물리학 연구의 중심을 차지하게 된다. 맥스웰Maxwell은 1873년 출간된 “전기와 자기에 관한 논문A treatise on Electricity and Magnetism”을 통해서 맥스웰의 방정식을 정립한다. 이 방정식은 전기와 자기적인 현상이 실제로는 같은 현상의 서로 다른 모습에 불과하다는 사실을 보여 주었다. 맥스웰의 방정식은 그 이전에 쿨롱Coulomb, 옴Ohm, 줄Joule, 앙페르Ampere, 패러데이Faraday와 같은 물리학자들이 얻은 업적에 기반을 두고 만들어졌다. 이렇게 발전한 전자기학을 실생활로 응용하려는 노력은 동시대에 첨예하게 경주되었다. 전구를 발명한 에디슨Edison은 물론이거니와 테슬라Tesla와 같은 동시대의 훌륭한 발명가들은 전자기 현상을 응용한 다양한 발명품을 발명함으로써 소위 두 번째 산업 혁명에 큰 공헌을 하게 된다.
양자역학의 발견은 묘하게도 이렇게 발전한 전기 산업에 큰 영향을 받는다. 이전 연재글에서 양자역학은 수소 원자의 스펙트럼을 설명하는 과정에서 탄생했다고 했다. 즉, 양자역학은 전자가 입자이면서 동시에 파동이라는 원리에서 탄생했다. 그런데 잘 생각해 보면 양자역학의 탄생에는 두 개의 축이 있었다. 하나는 물론 앞서 언급한 수소 원자의 스펙트럼을 설명하기 위한 전자의 파동성이다. 다른 하나는 흑체 복사blackbody radiation를 설명하기 위한 빛의 입자성이다. 즉, 빛은 파동이지만 동시에 입자, 즉 광자이다.
1900년 빛의 광자 이론을 처음 제시한 사람은 독일의 물리학자 막스 플랑크Max Planck이다. 20세기 초 독일은 에디슨의 전구 발명에 의해서 시발된 조명 산업에서 뒤처지 않기 위해서 에너지 효율이 높은 필라멘트 재료를 찾고 그것들의 성질을 자세하게 연구할 필요가 있었다. 이 노력의 일환으로 독일의 과학자들은 완벽하게 열평형thermal equilibrium에 있는 광원, 즉 흑체blackbody의 복사 성질에 대해서 연구하게 된다.
흑체의 가장 직관적인 예로는 작은 구멍이 뚫려 있는 거울 상자를 생각할 수 있다. 여기서 거울 상자의 내부 벽면은 반사 시 빛의 손실이 거의 없는 매우 좋은 거울로 꼼꼼히 둘러싸여 있다고 하자. 구멍을 통해서 이러한 거울 상자의 안으로 들어간 모든 파장의 빛은 그 안에 갇히게 되고 결국 열평형에 도달하게 된다. 이후 이 거울 상자의 구멍을 통해서 다시 새어 나오는 빛이 바로 흑체 복사인 것이다. 그런데 플랑크는 이 흑사 복사를 통계역학적인 방법을 써서 연구하다가 빛이 입자성을 지녀야 한다는 사실을 발견하게 된다. 전기 산업과 통계역학이 양자역학의 발견에 결정적인 역할을 했던 것이다. 알다시피 그 이후 양자역학은 역사가 된다.
정확하게 언제를 시작과 끝으로 잡는가에 따라 다르겠지만(플랑크의 광자는 1900년, 보어의 원자 모형은 1913년, 하이젠베르크의 행렬 역학은 1925년, 슈뢰딩거의 파동 방정식은 1926년) 이제 양자역학이 발견된 지도 어느덧 100년이 되어간다. 그동안 양자역학은 우주 생성의 가장 근본적인 원리로부터 우리가 매일 접하는 다양한 물질의 성질까지 믿을 수 없을 정도로 많은 현상을 설명하는 데에 큰 성공을 거두었다. 우리의 현재 실험 기술이 허용하는 범위에서 양자역학은 완벽하게 정확하다. 적어도 아직까지 반례는 한 번도 없었다.
반도체semiconductor는 양자역학이 기술적으로 응용된 매우 중요한 예이다. 초전도체superconductor나 레이저laser와 같이 다른 중요한 예들도 있다. 하지만 이런 예들은 엄밀하게 말해서 양자역학에 의해서 형성된 물질의 성질을 이용하는 것이다. 양자 얽힘을 포함한 파동 함수의 선형 중첩이라는 양자역학의 가장 근본적인 원리를 직접 응용하는 것은 아니다.
그런 의미에서 이번 글에서 설명한 양자 텔레포테이션이나 양자 컴퓨터는 본격적인 양자역학의 기술적인 응용, 즉 양자 테크놀로지quantum technology의 중요한 출발점이 될 수 있을 것이다. 앞으로 실제로 이런 가능성들이 실현되는 날이 올지, 그리고 온다면 언제 올지 모르겠지만, 이러한 상상을 하는 것은 물리학자의 가슴을 뛰게 만든다.