양자 알고리즘의 세계

피터 쇼어^{Peter Shor}의 소인수 분해 알고리즘은 사람들이 양자 컴퓨터에 많은 관심을 갖게 된 시발점이었다. 양자 컴퓨터를 이용해 현실적으로 중요한 문제를 해결하는 데 필요한 연산량을 혁신적으로 줄일 수 있다는 사실은 많은 과학자들 사이에서 상당한 반향을 일으켰다. 만약 양자 컴퓨터가 소인수 분해를 더 빠르게 할 수 있다면, 다른 문제들도 빠르게 풀 수 있지 않을까? 양자 컴퓨터가 빠르게 풀 수 있는 문제에는 어떤 것들이 있을까? 이러한 종류의 질문들은 지난 20여 년간 양자 컴퓨터라는 분야를 이끌어 온 중요한 연구 화두였다. 이번 글에서는 양자 컴퓨터를 이용해서 할 수 있는 여러 유용한 일들에 대해 살펴보고자 한다.

신물질 개발

인류의 역사를 돌이켜 보면, 새로운 시대의 도래에는 거의 빠짐없이 신물질의 발견이 수반되었다. 먼 과거로 시간을 되돌려보면 인류의 역사는 사람들이 사용하는 도구의 종류로 구분되곤 했었다. 석기 시대의 인류는 자연에 존재하는 돌을 이용해 도구를 만들었지만, 시간이 지나면서 인간은 차츰 제련을 통해 더 강하고 유용한 도구를 만들어냈다. 이것이 청동기 시대의 도래이고, 이후 철기 시대는 우리에게 알려진 수많은 문명들의 시발점이 되었다.¹ 비교적 최근의 역사를 짚어봐도 마찬가지다. 우리 주변에서 항상 볼 수 있는 플라스틱, 전지, 유리 등의 물질이 없는 삶은 상상하기 힘들다. 이처럼 신물질의 발견은 인류의 삶이 직접적으로 크게 바뀌는 중요한 계기가 되곤 한다.

20세기에 들어선 뒤 물리학자들은 자연에 존재할 수 있는 모든 물질의 특성을 설명할 수 있는 이론을 만들어낸다. 바로 양자 역학이다. 우리에게 무한한 연산 능력만 있다면, 양자역학을 기술하는 공식을 이용해서 자연에 존재할 수 있는 모든 물질의 특성을 정확하게 계산해서 예측할 수 있다. 하지만 근사 없이 이러한 계산을 하기 위해 필요한 전체 연산량은 현재 지구상에 존재하는 컴퓨터를 전부 동원해도 턱없이 부족할 만큼 크다. 기존의 컴퓨터로 양자역학적인 효과를 다루기 위해서는 엄청나게 많은 연산이 필요하기 때문이다. 미국 에너지부에서 몇 년에 걸쳐 책정한 슈퍼컴퓨팅 관련 예산만 해도 2조 원이 넘는데[1], 이러한 엄청난 예산에도 불구하고 양자역학적인 효과가 강하게 나타나는 물질의 특성을 이론적으로 예측하기에는 아직도 많은 어려움이 많다.

그렇기 때문에, 많은 경우 물질의 특성을 파악하기 위해서는 직접 물질을 만들어 보는 수고를 할 수밖에 없다. 예를 들어 새로운 태양 전지를 만드는 것이 목표라고 가정해 보자. 두 가지의 물질을 혼합해서 태양 전지를 만들고자 한다면, 분명 최대의 효율을 낼 수 있는 혼합 비율이 존재할 것이다. 그렇다면 최대 효율의 혼합 비율은 어떻게 찾을 수 있을까?

각각의 혼합 비율에 대한 전지의 효율을 하룻밤 만에 직접 계산할 수 있다면, 최대의 효율이 얼마인지와 이를 위한 혼합 비율을 모두 알 수 있을 것이다. 이는 실로 중요한 정보다. 최대 효율의 계산을 통해 기존의 전지에 비해 새로운 전지가 얼마나 뛰어난지 알 수 있고, 최적화된 혼합 비율의 구체적인 정보를 통해 새로운 전지를 직접 만들어내는 공정 과정으로 바로 넘어갈 수 있기 때문이다. 그에 반해 이러한 연산을 할 수 없다면, 직접 각각의 혼합 비율 샘플을 여러 개 만들어서 매번 효율을 시험해보는 수밖에 없다. 이를 위해 필요한 인적, 물적 자원이 적지 않다는 것은 독자들도 쉽게 이해할 수 있으리라 생각한다. 일단 이러한 실험을 하기 위해서는 물질을 혼합하는 실험실 자체가 만들어져야 하고, 또 효율을 테스트하는 데 시간이 필요하기 때문이다. 일련의 실험을 직접 수행할 사람들이 필요하다는 사실은 두말할 나위 없다.

물질들의 특성을 예측하기 위해 만들어진 계산 방식이 있긴 하지만, 문제는 물질 속에 존재하는 수많은 전자들 사이의 강한 전기적 상호 작용의 효과를 정확히 계산하기에는 많은 어려움이 있다는 점이다. 결과적으로 전자 간의 상호작용 때문에 일어나는 현상을 이해하는 데에도 어려움이 생기게 된다. 양자 컴퓨터는 전자 간의 상호 작용이 강한 물질이 작동하는 원리를 이해하는 데 큰 도움을 줄 것으로 예상된다.

이론으로 설명되는 초전도 물질과 비교했을 때, 고온 초전도 현상을 나타내는 물질은 훨씬 높은 온도에서도 전기를 에너지 손실 없이 보낼 수 있다. 하지만 안타깝게도 고온 초전도체가 어떤 방식으로 작동하는지에 대한 미시적인 이해는 아직도 크게 부족하다. 만약 상온에서도 이런 초전도 현상을  나타내는 물질을 만들어 낼 수 있다면, 이는 인류의 에너지 소모를 크게 줄일 수 있는 중요한 일이 될 것이다. 양자 컴퓨터를 이용하면 고온 초전도체 물성의 미시적인 이해를 돕는 데 필요한 시간을 크게 줄일 수 있을 것으로 기대된다.[3]

또 다른 중요한 예로 질소 고정 과정을 들 수 있다. 질소 고정 과정은 공기 중에 있는 질소를 암모니아로 바꾸는 일을 말하는데, 현대 사회에서 비료를 만들 때 가장 중요한 화학 작용 중 하나이다. 이렇게 암모니아를 만드는 방식은, 1900년대 초반 하버^{Fritz Haber}라는 화학자가 만든 공정 방식을 아직까지도 이용한다.² 이 공정 과정에는 400도에 달하는 고온과 200기압에 달하는 고압 환경이 필요하고 이러한 환경을 유지하기 위해서는 상당한 에너지 소모가 수반된다. 실제로 현재 전 인류가 쓰는 에너지의 1% 내지 2% 정도가 해당 공정에 쓰인다고 알려져 있다.[2] 하지만 자연에서는 평범한 환경에서도 박테리아가 아무런 문제 없이 질소를 암모니아로 바꿀 수 있다. 만약 박테리아가 어떠한 방식으로 암모니아를 생성하는지 이해하면 에너지 효율이 훨씬 높은 공정 과정을 만들 수 있을지도 모른다. 최근 연구자들은 양자 컴퓨터를 이용해서 이러한 화학 반응이 어떻게 일어날 수 있는지 효율적으로 예측할 수 있다는 사실을 발견했다.³[4]

비록 필자가 제시한 예는 두 개에 불과하지만, 이처럼 우리는 아직도 인류에게 큰 영향을 미칠 수 있는 물질이 어떠한 원리로 작동하는지 정확하게 알지 못하는 경우가 많다. 물질의 특성을 예측할 수 있는 공식은 이미 우리에게 알려져 있지만, 공식을 통해서 특성을 계산하는 데에는 많은 어려움이 있기 때문이다. 양자 컴퓨터를 이용하면 물질의 특성을 파악하기 위한 계산량을 크게 줄일 수 있을 것으로 예상된다.

이러한 계산을 수행하기 위해서는 최소한 수만 내지 수십만 개의 큐빗을 갖고 있는 양자 컴퓨터가 필요할 것이라는 것이 학계의 정설이다. 현재 나와 있는 양자 컴퓨터의 큐빗이 100개도 안 되는 것을 생각하면, 아직도 갈 길이 멀어 보이는 것이 사실이다. 하지만 필자는 이러한 실험과 이론 사이의 간극이 계속해서 좁혀져 왔다는 사실을 강조하고 싶다. 큐빗의 숫자는 계속해서 늘어나고 있고, 대규모의 양자 컴퓨터를 만들기 위해서 쏟아붓는 자원과 노력은 시간이 지날수록 계속해서 더 많아지고 있다. 뿐만 아니라, 물성 계산에 필요한 연산량도 연구자들의 노력으로 계속 줄어들고 있다. 이러한 발전이 계속되면 생각보다 머지않은 시일 내에 큰 규모의 양자 컴퓨터를 이용해서 유용한 계산을 할 수 있게 될지도 모른다. 물론 그 시기가 정확히 언제일지는 예측하기 힘들지만 말이다.

필자는 간혹 이런 생각을 한다. 이렇게 물질들의 특성을 손쉽게 계산할 수 있는 때가 오면, 인류의 발전 양상은 이전과는 전혀 다른 모습을 보일 수도 있지 않을까? 여태껏 인류가 신물질을 발견해온 방법은 실험을 바탕으로 한 예측이었다. 만약 실험을 하는데 필요한 자원과 시간을 줄일 수 있다면 새로운 물질을 발견하고 공정 과정을 만들어내는 시간을 크게 단축할 수 있을지도 모른다. 인류의 거대한 발전의 이면에 항상 신물질의 발견이 있었다는 사실을 기억해 보면, 어쩌면 양자 컴퓨터의 도래는 인류의 발전 속도가 비약적으로 증가하는 중요한 역사의 한순간이 될지도 모르겠다는 생각이 든다.

빠른 최적화

수많은 산업체나 금용, 정부기관에서 결정을 내릴 때 어느 것이 최적의 선택인지 알아내는 데 많은 시간과 자원이 들어간다. 특히 요즘처럼 수많은 데이터가 산재하고 처리해야 할 결정의 수가 많아진 시대에는 어떠한 결정을 내려야 하는지 선택하기 쉽지 않은 경우가 많다. 이렇게 많은 경우의 수 중에서 최대의 효율이나 이득을 내는 방법을 찾는 문제를 최적화 문제라고 부른다. 최적화 문제와 관련해, 양자 컴퓨터는 기존의 컴퓨터들보다 적은 연산량으로도 같은 최적화 값을 찾아낼 수 있다.

양자 컴퓨터가 최적화 문제 해결의 속도를 향상시킬 수 있는 비결의 이면에는 놀라운 사실이 하나 있다. 만약에 독자들이 필자에게 1000개의 닫힌 상자를 가져왔다고 생각해 보자. 이 중 하나의 상자에는 100만 원짜리 상품권이 들어있고 나머지 상자들은 전부 꽝이다. 상품권이 들어있는 상자를 찾기 위해서는 상자를 총 몇 번 열어봐야 할까? 최악의 경우에는 1000번을 열어봐야 할 테고, 평균적으로는 수백 번은 열어봐야 높은 확률로 상품권을 찾을 수 있을 것이다. 하지만 양자역학적인 효과를 이용하면 상자를 단 25번만 열어서 100%에 가까운 확률로 상품권을 찾는 것이 가능하다.⁴

이 놀라운 사실은 그로버^{Lov Grover}의 알고리즘으로 알려져 있다.[6] 1990년대 벨 연구소에서 일하고 있던 그로버는 쇼어의 소인수 분해 알고리즘에 자극을 받아 양자 알고리즘에 대한 연구를 시작했다. 그는 다음과 같은 사실을 발견했다. 두 개의 값을 갖는 함수 \(f(x)\)를 생각해 보자. 이 함수가 단 하나의 \(x\)에 대해서는 \(f(x)=1\)의 값을 지니고 나머지 \(x\)에 대해서는 \(f(x)=0\)의 값을 지닌다고 가정해보자. 만약 가능한 \(x\)의 범위가 \(1\)부터 \(N\)이라면 \(f(x)\)를 대략 \(\frac{\pi}{4}\sqrt{N}\)번 계산해서 \(f(x)=1\)인 \(x\)를 찾을 수 있다. 여기에 \(N=1000\)의 값을 대입해 보면 대략 \(f(x)\)를 \(25\)번 정도 계산해서 답을 찾아낼 수 있다는 것을 알 수 있다. 위의 예에서 상자의 내용물을 확인하는 행위를, 함수를 계산하는 것으로 해석할 수 있다. 즉 상자를 열어 상품권이 나오는 경우를 \(1\)로, 꽝이 나오는 경우를 \(0\)으로 생각하면 된다.

그로버의 알고리즘은 이처럼 함수의 값을 계산하는 것 자체는 쉽지만, 특정한 조건을 만족하는 \(x\)의 값을 찾기는 어려운 경우에 유용하게 쓰일 수 있다. 그로버의 알고리즘을 이용하면 다양한 최적화 문제를 기존 컴퓨터에서 사용하는 알고리즘보다 빠르게 풀 수 있다. 최적화 값을 구하기 위해 기존 컴퓨터를 이용하는 알고리즘으로 \(N\)번의 계산이 필요하다면, 이 알고리즘을 그로버의 접근 방식을 이용한 양자 컴퓨터상에서는 대략 \(\sim \sqrt{N}\)번의 연산으로 계산할 수 있다는 식이다.

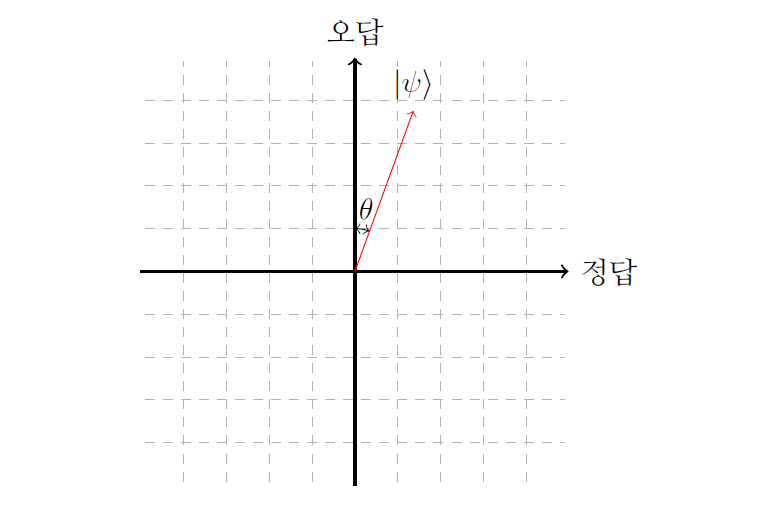
이 알고리즘의 작동 원리는 중고등학교 때 배우는 평면기하학을 통해 이해해 볼 수 있다. 알고리즘은 모든 상태가 같은 확률로 동시에 존재하는 중첩상태로부터 출발한다. 총 가능한 상태의 수가 \(N\)개이고 \(f(x)=1\)을 만족하는 \(x\)가 단 한 개 있다면, 이 중첩상태 \(|\psi\rangle\)는 다음과 같이 나타낼 수 있을 것이다.
\begin{equation}
|\psi\rangle = \frac{\sqrt{N-1} |\text{오답}\rangle + |\text{정답}\rangle}{\sqrt{N}}.
\quad \cdots \quad (1)
\end{equation}
이 상태는 정답, 즉 \(f(x)=1\)을 만족하는 \(x\)일 확률이 정확히 \(1/N\)이기 때문이다. 이 상태 \(|\psi\rangle\)를 그림으로 나타내보면 [그림1]과 같은 결과를 얻게 된다. 좀 더 풀어서 설명해 보자면 \(|\psi\rangle\)는 “오답”인 상태와 “정답”인 상태의 중첩상태이고, 우리는 이 상태를 2차원 평면에 존재하는 벡터로 이해할 수 있다.

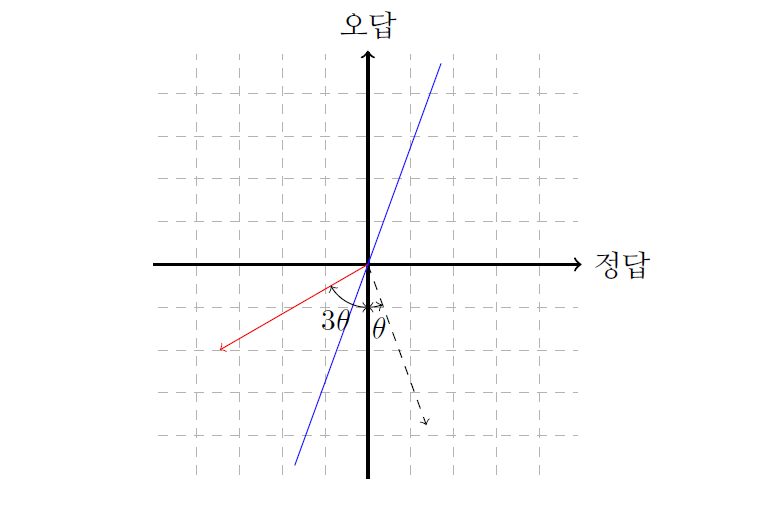
그로버의 알고리즘은 [그림1]에 그려져 있는 벡터 \(|\psi\rangle\)를 두 가지의 간단한 연산을 이용해서 “정답”이라고 쓰여 있는 \(x\)축으로 옮기는 것이 목표이다. 이 상태에서 측정을 하게 되면 높은 확률로 정답을 얻을 수 있다. 첫 번째 연산은 양자 역학적으로 \(f(x)\)를 계산해서 \(f(x)=1\)인 양자 상태의 위상을 180도 바꾸는 일이고, 두 번째 연산은 상태가 \(|\psi\rangle\)에 있으면 위상을 180도 바꾸는 연산이다. 이 연산들은 이전 글 “양자 컴퓨터의 기원”에서 말했듯이, 양자 컴퓨터가 손쉽게 할 수 있는 계산들이다. 양자 컴퓨터에서 첫 번째 연산을 하기 위해서는 고전 컴퓨터에서 \(f(x)\)를 계산하는데 필요한 정도의 연산량으로 충분하고, 두 번째 연산을 위해서는 \(n\)개의 큐빗이 있을 경우 \(n\)에 비례하는 연산량으로 충분하다. 이 연산 과정들이 어떠한 일을 하는지는 그림으로 쉽게 이해할 수 있다. 첫 번째 연산은 “정답” 축에 대하여 대칭 이동을 하는 것이고 두 번째 연산은 \(|\psi\rangle\)에 대해서 대칭 이동을 하는 것이다. 때문에, 이러한 대칭 이동을 통해서 어떻게 \(|\psi\rangle\)을 “정답”축으로 이동시킬 수 있는지 이해하면 그로버의 알고리즘이 어떠한 원리로 작동하는지 쉽게 이해할 수 있다.

이제 이 두 연산을 어떻게 이용할 수 있는지 알아보자. 우선 “정답”축에 대한 대칭 이동을 하게 되면 우리는 [그림2]와 같은 결과를 얻게 된다.

그다음 \(|\psi\rangle\)에 대한 대칭 이동을 하게 되면 우리는 [그림3]과 같은 결과를 얻게 된다.

두 번의 연산을 통해서 “오답”축에 대한 각도인 \(\theta\)가 \(\theta + 2\theta = 3\theta\)로 바뀌게 된다. 이를 \(n\)번 반복하면 각도는 \((2n+1)\theta\)로 바뀐다.

정답상태에 가까워지기 위해서는 \((2n+1)\theta\)가 \(90\)도, 즉 \(\frac{\pi}{2}\)에 가까워져야 한다. 이를 위해서는 \(n\)이 다음과 같은 식을 만족해야 한다:
\begin{equation}
\begin{aligned}
n= \frac{\pi}{4}(\arcsin(N^{-\frac{1}{2}}))^{-1}-1.
\end{aligned}\quad \cdots \quad (2)
\end{equation}\(N\)이 충분히 커지게 되면 이 식은 \(n\approx \frac{\pi \sqrt{N}}{4}\)로 단순화된다. 이는 정확히 앞에서 필자가 말했던 식이다. 이를 통해 평균적으로 \(\sim N\)번 \(f(x)\)를 계산해 보아야 하는 고전적인 방법보다 훨씬 적은 시도로도 \(f(x)=1\)을 만족하는 \(x\)를 찾아낼 수 있다. 이것이 가능한 이유는 양자역학적인 간섭 및 보강효과 때문이다. 고전적인 방식으로는 직접 \(f(x)\)를 계산해서 그 결과를 확인해야 하지만, 양자 역학적인 방식을 이용하면 상쇄간섭을 통해 오답이 나올 확률을 줄일 수 있다.

그로버의 알고리즘이 중요한 이유는 범용성에 있다. 실제로 위에서도 보았듯 우리는 함수 \(f(x)\)에 대해서 그다지 특별한 가정을 하지 않았다.⁵ 이는 쇼어의 소인수 분해에서 함수가 주기적인 특성을 보였다는 점과는 매우 다르다. 이 때문에 그로버의 접근 방식을 이용하면 훨씬 더 다양한 연산문제들에 대해서 속도 향상을 가져올 수 있다.

그로버의 접근 방식을 이용해서 기존 컴퓨터보다 문제를 빠르게 풀 수 있는 예로 최근에 나온 논문 하나를 소개해 보겠다.[7] 다음과 같은 상황을 생각해 보자. 독자 중 한 명이 새로 카페를 연다고 생각해 보자. 커피 메뉴로 두 가지 종류의 커피를 생각 중이다. 첫 번째 종류는 에스프레소 기계를 이용한 아메리카노, 라떼 같은 커피들이고, 두 번째 종류의 커피는 비교적 손쉽게 만들 수 있는 드립 커피다. 에스프레소 기계를 이용하면 더 비싼 값을 받고 다양한 손님을 모을 수 있지만, 대신에 더 많은 투자 비용이 필요하고 기계가 카페의 자리도 많이 차지한다. 드립 커피를 만들면 아메리카노나 라떼를 사려는 손님들을 받을 수는 없겠지만 대신에 투자 비용도 적고 자리도 적게 차지한다. 더 많은 투자를 해서 더 비싼 값을 받아야 할까, 아니면 더 적은 투자를 해서 박리다매를 해야 할까?

만약 카페 주인의 투자금이 천만 원이라고 가정해 보자. 그리고 에스프레소 기계 하나를 사는 데에는 75만 원, 드립 커피 기구에는 10만 원이 든다고 생각해 보자. 주인이 생각해 봤을 때, 에스프레소 기계 하나를 사면 대략 기계 하나로 시간당 15만 원을 벌어들일 수 있고, 드립 커피를 이용하면 시간당 만원을 벌어들일 수 있다. 또한 카페에는 대략 20평 정도만큼의 공간밖에 없다고 하자. 에스프레소 기계 하나를 설치하려면 3평 정도의 공간이 필요하지만 드립 커피를 만드는 데는 1평 정도의 공간이면 충분하다. 그렇다면 주인은 에스프레소 기계와 드립 커피 기구를 각각 몇 개씩 사야 할까? 이는 다음과 같은 문제로 나타낼 수 있다. \(x\)와 \(y\)를 에스프레소 기계와 드립 커피 기계의 숫자라고 하자. 우리는 다음과 같은 조건을 만족하는 \(x\)와 \(y\)중에서 최대한의 이득을 얻을 수 있는 \(x\)와 \(y\)를 찾아야 한다.

\begin{equation}
\begin{aligned}
75x + 15y &\leq 1000 \\
3x+ y &\leq 20
\end{aligned}\quad \cdots \quad (3)
\end{equation}여기서 총 이득은 \(15x+y\)이다. 어떻게 하면 최대한의 수익을 낼 수 있을까?

이는 혼합 정수 선형 계획법^{Mixed Integer Programming}이라고 불리는 문제의 한 종류이고, 변수의 숫자가 많아질수록 최적값을 찾아내는데 필요한 연산량이 변수의 숫자에 대해 지수함수적으로 증가한다. 비록 그로버의 알고리즘이 푸는 문제는 위에서 제시한 문제와는 완전히 달라 보이지만, 그 밑바탕에 있는 아이디어를 이용해서 비슷한 속도 향상을 가져올 수 있다. 기존의 컴퓨터에서 최대한의 이득을 얻는 조건을 구하는데 필요한 연산량이 \(N\)이라고 하면 양자 알고리즘을 이용하면 대략 \(\sim \sqrt{N}\) 정도의 연산량만 필요하다.[7]

이처럼 일상생활에서 쉽게 생각할 수 있는 일반적인 최적화 문제에 대해서도 양자 컴퓨터는 기존 컴퓨터보다 훨씬 적은 연산량으로 같은 계산을 할 수 있다. 최적화 문제는 사회 전반에 걸쳐 다양한 곳에 쓰이기 때문에, 양자 컴퓨터가 기존 컴퓨터보다 최적화 문제를 빠르게 풀기 시작하는 날이 오면, 신물질 발견보다 더 큰 영향을 인류에 미칠지도 모른다.

아쉽게도 이러한 문제들로부터 얻을 수 있는 속도 향상은 양자 시뮬레이션으로부터 얻을 수 있는 속도 향상에 비해서는 작은 편이다. 양자 시뮬레이션 같은 경우에는 기존 컴퓨터에서 지수함수적으로 늘어나는 연산량을 대수적으로 늘어나는 연산량으로 줄일 수 있지만, 이러한 최적화 문제들은 그렇지가 않다. 필요 연산량이 고전 컴퓨터에서 지수함수적으로 늘어나면 양자 컴퓨터에서도 지수함수적으로 늘어나게 된다. 단지, 지수함수적으로 늘어나는 속도가 다를 뿐이다. 예를 들어서, 고전 컴퓨터에서 필요한 연산량이 \(2^n\)이라고 하면 양자 컴퓨터에서는 필요한 연산량이 \(2^{n/2}\)인 식이다. 이 때문에 양자 컴퓨터를 이용한 속도 향상을 가져오기 위해서는 상당히 큰 규모의 양자 컴퓨터가 필요할 것으로 예상된다.

이렇게 속도 향상이 제한적인 이유는 위에서 다루었던 그로버 알고리즘의 작동 원리를 통해서 유추해 볼 수 있다. 그로버의 알고리즘을 액면 그대로 사용하면 우리는 함수를 \(\sim \sqrt{N}\)번 계산하는 것을 피할 수가 없다. 이는 “오답”축과 떨어져 있는 각도 \(\theta\)가 단조적으로 증가하기 때문이다. 이 때문에 그로버의 알고리즘에서 사용하는 대칭이동을 \(\sim\sqrt{N}\)번보다 적게 사용하면 정답 확률은 \(\sim\sqrt{N}\)번 했을 때보다 작을 수밖에 없다. 특히 \(N=2^n\)이라고 가정했을 때 대칭 이동을 \(n\)에 대해서 대수적으로 증가하는 횟수만큼만 적용하면 정답 확률은 여전히 \(n\)에 대해서 지수함수적으로 작을 수밖에 없다.

실제로 그로버의 알고리즘처럼 모든 함수에 대해서 답을 찾아낼 수 있는 알고리즘은 함수를 최소한 \(\sim \sqrt{N}\)번 계산해야 한다는 사실이 알려져 있다.[8] 물론 주기함수처럼 좀 더 특별한 특성을 지니는 함수들의 경우에는 그 특성을 이용해서 더 빠르게 답을 찾아낼 수 있을지도 모른다. 하지만 그러한 함수들의 특성을 이용하기 위해서는 그로버의 알고리즘과는 다른 알고리즘을 사용해야 할 것이다. 어떠한 특성을 이용하면 그로버의 알고리즘보다 더 많은 속도 향상을 가져올 수 있는지에 관한 연구는, 현대 양자 알고리즘 연구에서 중요한 화두이다.

마치며

대규모의 양자 컴퓨터가 만들어지면 인류 사회는 지금과 비교했을 때 상당한 변화가 있을 것으로 예상한다. 양자 컴퓨터를 이용하면 정확한 계산을 통해서 물질들의 작동 원리와 특성을 손쉽게 파악할 수 있고, 다양한 산업체에서 쓰이는 최적화 문제들에 대해서도 많은 속도 향상을 가져올 수 있기 때문이다.

하지만 그런 미래에 도달하기 위해서는 아직도 많은 노력이 필요하다는 점을 강조하고 싶다. 이러한 문제들을 푸는데 쓰이는 알고리즘을 사용하기 위해 필요한 양자 컴퓨터의 크기는 현재 나와 있는 양자 컴퓨터의 크기에 비해 너무나도 크다. 이 때문에 알고리즘들을 수행하기 위해 필요한 양자 컴퓨터의 크기와 연산량을 줄이는 연구는 앞으로도 계속되어야 할 중요한 연구 방향이다.

더불어 이러한 알고리즘을 직접 수행할 수 있는 대규모 양자 컴퓨터의 개발이 중요한 것은 두말할 나위도 없다. 다음 글에는 그러한 컴퓨터를 만들기 위해서 반드시 수반되어야 하는 양자 오류 보정이라는 분야에 대해서 이야기해보도록 하겠다.