월장의 추억

월^越은 넘는다 장^墻은 담이니 월장¹은 담을 넘는다, 즉 담넘기^{wall-crossing}를 말한다. 제목에 나온 월장을 보고 학문의 경계를 뛰어넘는 학제간^{interdisciplinary} 연구의 경험을 공유하려는 것인가 보구나 생각하셨다면 그런 고상한 글이 아님을 금방 아시게 될 것이므로 실망시켜 드리게 된 것을 유감스럽게 생각한다. 이 글은 문자 그대로 월장에 관한 필자의 기억을 좇기 위한 것이기 때문이다.

대학 시절 필자의 고결한 성품에 환경이 모반하여 일상적인 월장이 불가피하였다. 숙소에 통금이 시행되던 시절 삼경부터 문을 걸어 잠그는지라 공사다망한 대학 시절을 보내던 필자는 부득불 상층 창문을 통한 월장의 경험이 쌓일 수밖에 없었는데 경험상 장진주^將進酒2 후에는 삼가는 것이 옳다. 월장의 기법에 대한 관심이 커진 것은 환경의 모반 때문이었지만, 월장의 효과에 대해서 각성하게 된 것은 현대사의 질곡 때문이다. 독일의 베를린 장벽이 무너진 후 세계의 질서는 바뀌어 냉전이 해체된 새로운 시대를 맞게 되었으며 한반도가 유일한 분단국가로 남게 되었다. 또한 한국 현대사를 절절히 묘사한 드라마 <여명의 눈동자>에서 대치와 여옥의 철책을 넘는 애틋한 사랑을 통해 월장 이전과 이후 위상변화를 통찰하게 되었다.

이쯤에서 언어의 유희는 그만두고 수학 얘기를 시작하자. 대수기하학에서 최근 새 (웹진 HORIZON의 이름 그대로) 지평을 열고 있는 담넘기에 대한 연구의 흐름을 잡아보고자 한다. 전문적인 내용이 대부분이 될 것이므로 일반 독자들은 이런 일들이 벌어지고 있구나 정도로 이해하시기를 권한다.

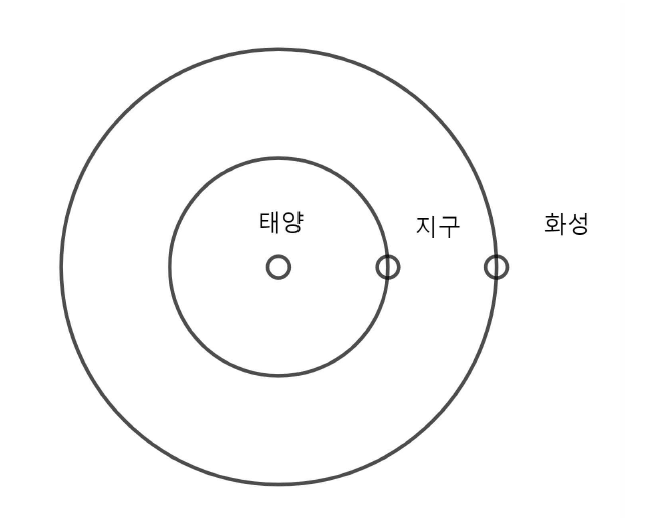
기하학에서 담넘기 현상이란 매개변수 \(t\)에 의존하는 대상 \(X(t)\)와 이로부터 얻는 값 \(I(t)\)가 있을 때, 매개변수 \(t\)가 속하는 공간 \(T\)가 부분집합들 \(T_i\)(이들을 방^chamber이라고 부른다)로 \(T= \sqcup _{i} T_{i}\)와 같이 분할되고 각 방 \(t \in T_{i}\)에서는 \(X(t)\)나 \(I(t)\)가 불변이고 다른 방으로 담을 넘어갈 때 변하는 경우를 말하며, 담넘기 공식이란 그 차이를 기술한 공식을 말한다. 예를 들어 [그림1]과 같은 곡면의 단면을 생각하면 각 구간의 내부에서는 모양이 바뀌지 않다가 다른 구간으로 넘어갈 때 모양이 바뀐다.³ 구간 또는 방이 바뀌는 경계점을 담^wall이라고 부른다.

^그림1 성분의 수가 담을 넘을 때마다 0, 1, 2, 1, 2, 1, 0과 같이 바뀐다. / 유랑

어떤 집합 \(X\)에 작용하는 대칭군 \(G\)란 집합 \(X\)에서 자신으로 가는 일대일 대응들의 집합인데 (1) 두 원소를 합성하면 다시 \(G\)의 원소가 되고, (2) \(G\)의 원소들의 역함수들이 모두 \(G\)에 포함되고, (3) 항등함수가 \(G\)에 포함되는 것을 말한다. 예를 들어 평면 \(R^2\)에서 원점을 중심으로 하는 회전변환들의 모임 \(U(1)\)은 평면의 대칭군이다. \(X\)에 작용하는 대칭군 \(G\)가 있을 때 \(X\)에서 정의된 함수 \(\mu :X \rightarrow T\)가 불변이라 함은

\(\mu (g \cdot x)=\mu (x), \forall g \in G, \forall x \in X\)

가 성립함을 말한다. 여기서 \(g \cdot x = g(x)\)로 썼다. 주어진 한 점 \(x\)의 궤도란 \(g \cdot x\)들의 집합

\(G \cdot x= \big\{g \cdot x:g \in G \}\)

를 말한다. 예를 들어 \(U(1)\)의 궤도는 원점을 중심으로 하는 원들이다.

집합 \(X\)에 포함되는 궤도들의 집합을 \(X/G\)라고 쓰고 궤도공간^{orbit space}이라고 부른다. 사교기하나 수리물리에서는 대칭성을 활용해 차원을 줄이는 기술³이 있는데 불변인 함수⁴ \(\mu :X \rightarrow T\)를 찾으면 훨씬 낮은 차원의 사교삭감^{symplectic reduction}

\(X// _{t} G= \mu ^{-1} (t)/G\)

을 생각할 수 있고 한 점 \(x \in \mu ^{-1} (t) \subset X\)의 운동에 대한 탐구는 \(X// _{t} G\)에서 탐구하는 것으로 환원된다. 필자가 월장신공을 한참 연마 중일 때 빅터 길멩^{Victor Guillemin}과 슬로모 스턴버그^{Shlomo Sternberg}는 \(G=U(1)\)의 경우 사교다양체 \(X\)의 사교삭감 \(X// _{t} G\)가 담넘기 현상을 보임을 관찰하고 이를 정확히 분석했다.[1] 비슷한 시기에 박사학위 논문에서 스티븐 브래들로^{Steven Bradlow}는 Vortex 방정식의 해집합들에서 담넘기 현상을 관측했다.[2] 담넘기가 유용한 이유는 우리가 분석하고자 하는 복잡한 공간에서 출발하여 매개변수를 변화시켜 점점 간단한 공간으로 나아가고 그 차이를 분석함을 통해 원래 공간의 성질을 알아낼 수 있게 해주기 때문이다.

사교삭감은 대수기하학적으로 기하학적 불변량 이론^{Geometric invariant theory, GIT}에 의한 궤도공간과 동일함이 마이클 아티야^{Michael Atiyah}, 라울 보트^{Raoul Bott}, 프랜시스 키르완^{Frances Kirwan}에 의해 1980년대 초 밝혀졌는데[3] 마이클 타데우스^{Michael Thaddeus}는 1994년 브래들로^Bradlow의 문제를 대수기하학적으로 해결하여 담넘기 현상을 flip/flop이라 불리는 대수적 수술을 통해 정확히 기술할 수 있음을 보였고 또 교차수의 담넘기를 분석하여 베를린데^Verlinde 추측을 증명해냈다.[4] 사실 베를린데^Verlinde의 추측은 대수적 곡선^{algebraic curve, Riemann surface}상의 벡터번들의 모듈라이 공간의 코호몰로지 환을 결정하게 해주는데 이는 60년대부터 대수기하학자들이 연구해왔으나 해결하지 못했던 문제였다. 타데우스^Thaddeus의 쾌거를 계기로 수학자들이 담넘기를 진지하게 연구하기 시작했고 GIT를 통한 안정성^stability 조건에 따른 궤도공간의 담넘기를 정밀하게 분석해내었다.[5]

한편 에드워드 위튼^{Edward Witten}의 제안에 기반하여 리사 제프리^{Lisa Jeffrey}와 프랜시스 키르완^{Frances Kirwan}은 등변 코호몰로지^{equivariant cohomology, BRST cohomology}류를 GIT 궤도공간에서 적분한 값을 구하는 비가환 국지화^{nonabelian localization} 공식을 발견했는데[6] 빅터 길멩^{Victor Guillemin}과 제이콥 칼크만^{Jacob Kalkman}은 이 복잡한 공식을 분석하여 \(G=U(1)\)인 경우 담넘기 공식이 유수^residue에 의해 주어짐을 발견하였다.[7]

제프리^Jeffrey와 키르완^Kirwan의 성과로 곡선상의 쉬프나 벡터번들을 세는 불변량에 대한 연구는 일단락되었다. 다음으로 곡면상의 불변량에 대해 생각하는 것이 자연스러운데 그것이 바로 도널드슨^Donaldson 불변량이다. 곡면부터는 모듈라이 공간이 심각한 특이점을 가질 수 있으므로 1990년대 중반까지는 특수한 경우(예를 들어 \(c_2 \gg 0\))에 대해서만 연구가 이루어졌다. 1995년 그로모프-위튼^{Gromov-Witten} 불변량의 대수기하학적 이론을 위해 가상교차이론^{virtual intersection theory}이 개발되었는데[8] 타쿠로 모치즈키^{Takuro Mochizuki}는 이를 도널드슨^Donaldson 불변량에 적용하고 담넘기를 분석하였고 도널드슨^Donaldson 불변량을 자이베르그-위튼^{Seiberg-Witten} 불변량을 통해 표현하는 공식을 발견하였으며 이를 통해 두 불변량이 동등함을 증명하였다.[9]

한편 그로모프-위튼^{Gromov-Witten} 불변량은 주어진 다양체에 포함되는 대수적 곡선의 수를 세는 방법인데, 안정성 조건에 매개변수가 없어서 담넘기를 통한 분석이 이루어지지 않았다. 2010년 이후 양자 특이점 이론^{quantum singularity theory} 덕분에 의사사상^quasimap에 대한 연구가 활발해지면서 이들을 통한 불변량이 정의되었고 (그로모프-위튼^{Gromov-Witten} 불변량이 특수한 경우이다) 그 담넘기 공식까지 최근 알려졌다.⁵

대수적 곡선의 수를 세는 또 다른 불변량으로 도널드슨-토마스^{Donaldson-Thomas} 불변량⁶이 있는데 풍부한 안정성 조건들을 갖는다. 3차원 칼라비-야우^Calabi-Yau 다양체의 도널드슨-토마스^{Donaldson-Thomas} 불변량은 가중치를 부여한 오일러 특성수와 같으므로, 조각내어 각각의 오일러 특성수를 구하고 합하면 원래의 값을 얻을 수 있다. 이를 사용하여 도미닉 조이스^{Dominic Joyce}와 이난 송^{Yinan Song}은 담넘기를 체계적으로 분석할 수 있게 해주는 조합론적 도구인 Hall 대수를 건설하였다.[10] 비슷한 시기 막심 콘체비치^{Maxim Kontsevich}와 야코프 소이 벨 만^{Yan Soibelman}은 도널드슨-토마스^{Donaldson-Thomas} 불변량의 담넘기를 motivic 이론으로 확장하고 곱셈 형태의 담넘기 공식을 발견했다.

자연스러운 관심은 4차원으로 올라가는데 2014년 야롱 카오^{Yalong Cao}와 코난 레응^{Conan Leung}은 사이먼 도널드슨^{Simon Donaldson}과 리처드 토마스^{Richard Thomas}의 1998년 논문의 제안에 기반하여 특수한 가정하에 4차원 도널드슨-토마스^{Donaldson-Thomas} 불변량을 정의하였고, 2017년 데니스 보리소프^{Dennis Borisov}와 도미닉 조이스^{Dominic Joyce}는 새롭게 만들어지고 있는 유도 미분기하학^{derived differential geometry}에 기반하여 일반적인 4차원 칼라비-야우^Calabi-Yau 다양체의 도널드슨-토마스^{Donaldson-Thomas} 불변량 이론을 확립하였다.[11] 2020년 오정석과 리처드 토마스^{Richard Thomas}는 유도 미분기하학 없이 순수히 대수기하학적으로 4차원 도널드슨-토마스^{Donalson-Thomas} 불변량을 건설하고 보리소프-조이스^{Borisov-Joyce}의 불변량과 동일함을 보였다.

3차원 칼라비-야우^Calabi-Yau 다양체의 도널드슨-토마스^{Donalson-Thomas} 불변량은 범주화를 통해 물리적으로 BPS 상태를 세는 것으로 정확히 해석되지만, 4차원 도널드슨-토마스^{Donalson-Thomas} 불변량은 물리적 의미가 정확히 알려져 있지는 않다. 하지만 큰 관심을 끌고 있으므로 조만간 자연스러운 해석과 이를 통한 다양한 응용이 기대된다.

정말 흥미로운 것은 이제부터인데 2018년 도미닉 조이스^{Dominic Joyce}는 아직 미완성인 논문을 통해 굉장히 일반적인 담넘기 공식을 설명하는 틀을 제공했다. 놀랍게도 주어진 (임의의 차원의) 칼라비-야우^Calabi-Yau 다양체⁷상의 쉬프들(더 일반적으로 유도 범주의 대상들)의 공간^{moduli stack}의 호몰로지들은 꼭지점 대수^{vertex algebra}의 구조를 가진다는 것이다.⁸

꼭지점 대수는 1986년 리처드 보처즈^{Richard Borcherds}가 정의한 대수적 구조로서 2차원 등각장 이론^{conformal field theory}을 설명하는 것이다. 카츠-무디^Kac-Moody 대수, 비라소로^Virasoro 대수, 하이젠베르크^Heisenberg 대수 등 수많은 흥미로운 대상들을 포함하는 것이 꼭지점 대수이다. 조이스^Joyce의 꼭지점 대수는 4차원 도널드슨-토마스^{Donaldson-Thomas} 불변량의 담넘기 공식을 위해 고안되었으나⁹, 꼭지점 대수의 풍부한 구조 덕분에 큰 파급효과가 예상된다.

예를 들어 1990년대 말 파란을 일으켰던 히라쿠 나카지마^{Hiraku Nakajima}와 이안 그로즈노스키^{Ian Grojnowski}의 대수적 곡면상의 힐버트 스킴의 호몰로지를 통한 하이젠베르크^Heisenberg 대수의 표현과 같이 무한차원 리 대수의 기하학적 구현이 여러 상황에서 쏟아져 나올 수도 있겠다. 점차 심오한 무언가에 다가가는 짜릿하고 오싹한 느낌이 든다. 듬성듬성 발견된 섬들을 모두 연결하는 거대한 해저 대륙이 실체를 조금씩 드러내는 것일까?