시간 단위 측정 [1] – 시간 측정의 역사와 원자시계

1.시간 눈금과 시계

측정이란 무엇일까? 한마디로 표현한다면 “비교”라고 할 수 있을 것 같다. 즉 측정하려는 어떤 양이 있고, 이를 기준이 되는 다른 양과 비교하는 것이라고 할 수 있다. 그리고 이 기준이 되는 양이 곧 “단위”이다. “단위”를 이용하면 자의 눈금과 같은 “눈금”을 만들 수 있고 이 눈금을 통해 원하는 양을 측정할 수 있다. 이러한 단위가 만족해야 할 조건은 (1) 단위 정의 당시 가능한 과학 기술로 “정확”하게 구현할 수 있어야 하고 (2) 변하지 않는 일정한 양이어야 한다. “시간”도 의 필요에 따라 사용자에 따라 그리고 과학 기술의 발전에 따라 다양한 눈금으로 측정되어 왔다.

 시간을 정확하게 측정하고 기록하는 일은 농사나 목축, 사냥 등의 생존을 위해 꼭 필요한 일이었기 때문에, 아주 오래전부터 많은 나라에서 시간을 측정하고, 정확한 눈금을 정의하고, 관리해 왔다. 가장 자연스럽게 생각하고 구현할 수 있는 시간 눈금은 자연의 주기적인 현상일 것이다. 가장 쉽게 발견할 수 있는 하루의 간격인 “일^day”은 하루에 해가 가장 높이 뜨는 정오와 다음에 다시 해가 머리 위로 뜰 때까지의 시간 간격으로 정할 수 있다. 그리고 밤에 보이는 달의 모양이 원래대로 돌아오는 시간 간격을 “달^Month”로 표시했다. 그리고 가장 긴 눈금은 계절의 변화와 함께 지구가 태양(해) 주위를 한 바퀴 돌아가는 데 걸리는 시간인 “해(년^year)”이다.

이 세 가지 눈금을 만들고 나서, 자연스럽게 “달”과 “해”를 가장 작은 단위인 “일”의 단위로 나타내려고 하였다. 고대 이집트에서는 한 해가 약 365일이라는 사실을 알아냈을 뿐 아니라, 실제 이보다 약 1/4일 정도가 더 길기 때문에, 4년에 한 번씩 “윤년”을 도입할 필요성을 알고 있었다고 한다. 하지만 당시의 지도자들을 설득하지 못해. 실제 윤년이 도입된 것은 기원전 약 46년 율리우스 카이사르에 의해 시작된 “율리우스력^{Julius Calendar}이 반포되면서부터였다. 하지만 이러한 윤년의 도입도 완벽하지 않아 약 천 년이 지나자, 실제 1년과 달력의 1년이 일주일가량 차이가 나기 시작했고, 당시 가장 중요한 절기 중 하나인 부활절이 점점 빨라지기 시작했다. 급기야 1582년 교황 그레고리 13세가 이를 보정하는 새로운 윤년 체계를 도입하여 “그레고리력^{Gregorian calendar}”을 만들게 되었고, 현재 우리가 사용하는 달력의 체계가 성립되었다. 4년에 한 번씩 윤년을 만들되 100의 배수에 해당하는 해에는 윤년을 도입하지 않고, 대신 400의 배수가 되는 해에만 윤년을 도입한다. 즉 2000년은 400의 배수이기 때문에 윤년이지만, 2100년은 100의 배수이면서, 400의 배수는 아니기 때문에 윤년이 아니게 된다. 이렇게 완성된 그레고리력의 1년은 평균 365.2425일로서 율리우스력보다는 실제 1년의 길이에 훨씬 근접했다. 이 숫자도 사실 정확하지 않기 때문에 그레고리력이 도입되고 난 뒤 약 3230년 후에는 다시 하루 이상 차이가 나기 시작할 것이라고 한다.

여러 가지의 자연의 주기 운동을 이용한 시간 눈금을 사용하면서 생겨나는 불일치 문제는 앞서 설명한 “윤년”을 적절히 잘 도입해서 해결할 수 있었다. 하지만 “달”과 “해”를 이용해서 지금이 몇 시인지 아는 것보다는 지금 눈에 보이는 하늘의 “태양”을 보고 지금 시각을 알아내는 방법이 가장 손쉽기 때문에, 가장 많이 사용되는 눈금은 “일” 혹은 “태양일^{solar day}”이었고, 이를 통해 구현한 시간 눈금을 “태양시^{solar time}“라 하였다. 여기서 만들어진 1″초”는 태양일을 86400으로 나눈 값이 되었다. 하지만 이 “태양일”에도 문제가 있었다. 지구의 운동이 실제로 여러 요인에 의해 그 주기가 변하기 때문이다. “태양일”을 이용하여 만든 시계로 일식이나 월식, 별의 운동 등을 예측했을 때 조금씩 어긋나기 시작했다. 이러한 천체들의 운동이 모두 불규칙적이라고 말하기는 힘들기 때문에, 원인은 지구의 자전 주기가 바뀌고 있다고 밖에 볼 수 없었다. 결국 태양시는 구현은 비교적 쉽게 가능하지만, 당시에 필요한 정확도로 천체의 운동을 예측할 수 있을 만큼 일정하지 않아 좋은 시간의 눈금이 되지 못했다. 이러한 불규칙한 지구의 자전은 달의 궤도운동, 조석 현상, 자구의 타원형 공전궤도, 지구 적도 면과 황도면의 불일치 등으로 생긴다고 알려져 있다.

그러면 어떻게 태양시를 좀 더 일정한 주기의 시간눈금으로 만들 수 있을까?  불규칙한 잡음이 섞여 있는 양의 잡음을 줄이는 쉬운 방법은 여러 번 측정해서 평균하는 방법이다. 백색잡음으로만 구성된 데이터는 평균하면 할수록 평균에 사용된 데이터의 개수만큼 그 분산이 줄어들기 때문이다. (하지만 평균이 항상 도움이 되지는 않는다. 이는 3장에서 살펴본다.) 그래서 일 년 동안의 “태양시”의 평균값인 “평균태양시^{mean solar day}“를 이용하기로 하였다. 즉 일 년 동안 일정하게 움직이는 “가상의 태양”을 가정하고, 이 태양을 기준으로 하루를 24시간,혹은 1440분, 혹은 86400초로 정의하여 만든 시간이 “평균태양시”이다. 그리고 이렇게 만들어진 시간을 UT0로 명명하였다. 여기서 “UT”는 Universal Time의 줄임말로, 어디서나 사용할 수 있는 시간이라는 뜻이며, 경도 0도를 그리니치 천문대를 지나는 자오선으로 정한 1884년 국제자오선 회의에서 처음 제안되었다. 그리고 여러 해에 걸쳐 일어나는 지구의 극운동과 계절에 따른 변화를 추가하면서 UT1, UT2 등으로 발전하였다. (여기서 독자는 “가상의 태양”을 어떻게 만들 수 있을지 궁금할 것이다. 이 부분은 2장에서 설명하기로 한다.)

지속해서 더 균일한 시간 눈금을 만들려는 노력이 계속되었고, 최종적으로는 지구의 자전이 아니라, 태양을 비롯한 천체의 운동을 고려하여 균일성을 향상한 “역표시^{Ephemeris Time}“가 탄생하였다. 여기서 “역표”란 태양을 비롯한 각종 천체의 시간에 따른 위치를 나타내는 일종의 표이다. 지구의 자전에 비해, 지구의 공전이나, 달이나 행성의 공전은 더 규칙적이기 때문에, 태양이나 달의 천구상의 위치를 정확하게 측정하면, 그때의 정확한 시간을 유추할 수 있는 것이다. 원자 내부의 주기적인 현상으로 시간 눈금이 옮겨가기 전, 천체의 운동에서 얻을 수 있는 시간 눈금의 “정점”이었다. 이로써 각각의 행성들은 일종의 시곗바늘과 같은 역할을 하게 되었고, 여러 개의 바늘의 위치와 움직임을 통해 시각을 유추할 수 있었다. 그런데 이러한 “역표시”는 여러 근본적인 한계가 있었다. 먼저는 “역표”가 천문 관측 기술과 천문학의 발전에 따라 바뀌면, 그에 따른 “역표시”도 바뀌어야 한다는 것이다. 무엇보다 중력장 하의 천체 움직임을 기술하는 상대성 이론이 전혀 고려되지 않았기 때문에 이미 정확한 눈금이라 볼 수 없었다. 그리고 더 큰 문제점은 “지금은 몇 시인가”라는 물음에 대답하기 어렵다는 것이었다. 먼저 천체의 위치를 높은 정확도로 측정하려면 충분히 오래 측정해야 하고, 이를 역표와 비교하는 과정을 거쳐야만 했다. 우리가 현재 필요로 하는 시간 정확도를 얻으려면 적어도 몇 년은 기다려야 한다. 예를 들어 0.05초 정확도를 얻기 위해 필요한 시간이 약 9년이나 되었다고 한다!

2.하늘에서 땅으로: 원자시계의 등장

 앞에서 우리는 하루, 달, 해의 주기를 이용한 시간 눈금을 살펴보았다. 여기서 두 가지 의문이 든다. 하나는, 천체의 운동으로부터 더 작은 단위인 시, 분, 초의 눈금은 어떻게 만들 수 있는가이다 해시계나 물시계와 같이 시간을 길이나 부피로 환산한 뒤, 등분하는 방법이 있다. 하지만 해시계의 경우, 앞서 설명한 바와 같이 하루의 길이는 계속 변하기 때문에 좋은 눈금이라고 할 수 없다. 그리고 또 하나는 일정한 시간 눈금을 위해 고안한 평균태양시의 “가상의 태양”을 어떻게 구현할 수 있을까이다. 이 두 문제를 해결하기 위해서는 더 빠르면서 일정하게 진동하는 장치가 필요했고, 일정한 주파수로 진동하는 조화진동자^{harmonic oscillator}가 그 대안이 되었다. 좋은 진동자의 요건은 진동수(1초에 진동하는 횟수, 주파수라고도 함)가 높으면서 그 진동이 줄어드는 정도가 작아야 하며 이를 흔히 진동자의 Q 인자^{quality factor}라고 한다. Q 값이 클수록 좋은 진동자에 해당한다. 조화 진동자의 대표적인 예가 “진자”와 “스프링”이다. 특히 진자의 주기는 달려있는 물체의 질량이나, 진폭(너무 크지 않으면)에 의존하지 않고, 진자의 “길이”에만 의존하기 때문에, 시간 눈금으로 사용하기에 매우 좋은 특성을 가지고 있었다. 이러한 사실을 처음 발견한 것을 갈릴레오였지만 이를 실제 시계로 구현한 사람은 네덜란드 과학자 호이겐스였다. 그가 만든 시계는 하루에 10초 정도밖에 틀리지 않았다고 한다. 이러한 진자의 도입의 시간눈금의 역사에 있어 획기적인 진보의 시작이었고, 하늘을 보지 않고 시간을 알 수 있는 시대의 서막이었다. 그리고 1920년대에 수정결정에 전기장을 가했을 때 생기는 주기적인 운동을 이용한 수정진동자^{quartz-crystal oscillator}가 처음 등장하였고 Q 값은 진자에 비해 100배 이상 높았다. 정밀도가 높아지면서 이를 이용해 지구의 자전 주기의 변화가 명확하게 보이기 시작했다.

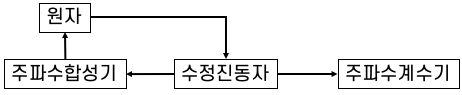
이렇게 일정한 진동자를 이용하여 시간 눈금을 만드는 장치를 통칭하여 “시계”라고 할 수 있다. 일반적으로 사용되는 시계는 내부에 일정하면서 높은 진동수로 진동하는 진동자, 그리고 이로부터 시, 분, 초를 만들어 내는 기계적 혹은 전자적 장치로 구성되어 있다. 현재 시계에 사용되는 진동자의 대표적인 예가 앞에서 언급한 수정진동자이며 1초에 보통 수만 번 이상 진동한다. 하지만 이러한 수정진동자의 진동수는 온도나 습도와 같은 주변 환경에 따라 값이 바뀌게 된다. 따라서 수정진동자의 진동수가 바뀌었는지를 알 수 있는 “주파수 기준”이 필요하다. 예를 들어 “태양시”를 사용한다면, 해가 자오선을 통과할 때 시각과 다음 날 다시 자오선을 통과할 때 시각차가 24시간 혹은 86400초가 되도록 진동자의 진동수를 조절하면 된다. 하지만 앞에서도 언급했듯이 지구의 자전은 불규칙적이기 때문에 적절한 “주파수 기준”이라고 하기 어렵다. “역표”에 따라 변할 수 있는 “역표시”도 마찬가지이고, 게다가 역표시로부터 원하는 정확도의 주파수 표준을 만들려면 충분히 오랫동안 관측을 해야 한다. 그렇다면 언제 어디서나 변하지 않는 진동수(혹은 주파수)를 갖는 “주파수 기준”은 어디서 찾을 수 있을까? 일단 사람이 만든 것은 항상 같을 수 없고 자연계에서 찾아야 한다. 이러한 생각이 발전하면서 1879년 영국의 윌리엄 톰슨(켈빈 경)은 “Elements of Natural Philosophy“라는 잡지에 처음으로 “원자”를 이용하면 우주 어디서나 완벽하게 똑같은 성질을 지닌 표준을 만들 수 있을 것이라는 아이디어를 내었다. 그로부터 60여 년이 지난 후, 2차세계대전과 함께 마이크로파 전자공학 기술이 비약적으로 발전하고, 양자역학의 성숙과 함께 원자에 대한 이해가 깊어지면서, “원자시계”가 처음으로 실험적으로 구현되기 시작하였다. [그림1]은 원자시계의 기본적인 원리를 나타낸다. 수정진동자로부터 시, 분, 초를 생성하는 주파수 계수기까지가 일반적인 시계가 가지고 있는 구조이다. 하지만 이 수정진동자의 주파수가 환경에 따라 변할 수 있기 때문에 그 기준이 필요하고, “원자”를 주파수 기준으로 삼아 수정진동자가 이를 따르도록 하는 시계를 원자시계라고 한다. 조금 더 세부적으로는 수정진동자의 주파수와 원자의 공진주파수가 다르기 때문에, 원자의 주파수에 맞도록 주파수를 합성하는 주파수 합성기를 거치게 된다. 그리고 이렇게 합성된 주파수로 원자를 조사하여, 주파수의 변화를 측정한 뒤, 수정진동자의 주파수를 적절히 조절하는 ‘되먹임^feedback‘회로를 구성하면 비로소 원자시계가 된다. 1948년 미국에서 처음 선을 보인 암모니아를 사용한 시계로부터, 원자시계 초기 형태가 개발되기 시작하였고, 1955년 마침내 영국 NPL의 Essen과 Parry가 세슘원자를 이용한 원자시계를 개발하는 데 성공하였다 [그림2].

 Essen은 성공적으로 3개월여간 원자시계를 동작하고, 1956년 “초”의 재정의를 위해 모인 국제천문연맹 회의에 참석하여, 그때까지 지구의 자전을 이용한 “초”의 정의에서 벗어나, 원자를 이용한 시간 정의의 필요성을 역설하였다. 하지만 아쉽게도 결국 당시 천체를 이용한 가장 정확한 시간 눈금인 역표시^ET를 기준으로 “초”를 정의하기로 합의하면서 이 회의는 끝이 났다. (결국 10년여 후 1967년 세슘원자를 기반으로 한 “초”의 정의가 다시 논의된 후 채택된다.) ET가 시간의 단위로 채택되었기 때문에 Essen은 세슘의 주파수를 ET를 이용하여 새롭게 정의된 “초”를 눈금으로 사용하여 측정해야 했다. 마침 회의장에서 만난 미국 해군 천문대^USNO의 Markowitz와 함께 세슘의 주파수 측정을 하기로 했다.

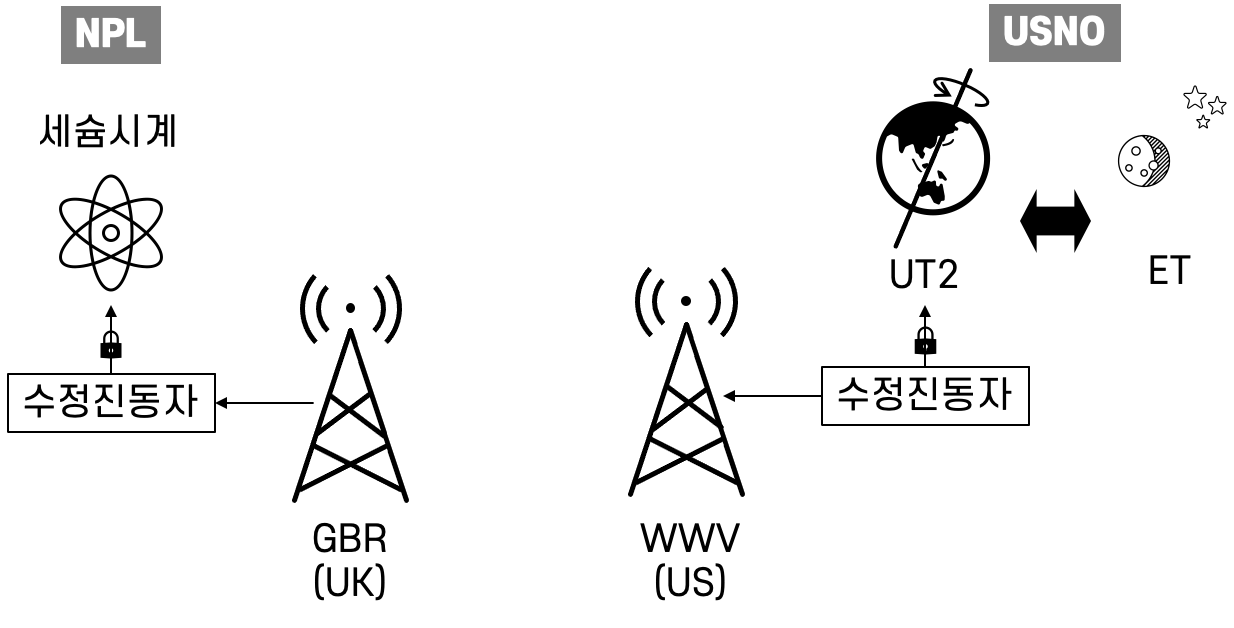
Essen은 원자시계를 가졌지만, ET를 측정할 방법이 없었고, Markowitz는 반대로 UT2와 ET를 정확하게 측정할 수 있지만, 원자시계를 가지고 있지 않았기 때문에, 둘은 서로 협력하여 주파수 측정을 하기로 하였다. 여기서 ET가 아닌 UT2를 사용한 이유는, UT2를 구현하는 것이 더 빠르고 간단하기 때문이다. 멀리 떨어져 있는 두 기관은 어떻게 세슘의 주파수를 정확하게 측정할 수 있었을까? 아래 [그림3]에 표현된 바와 같이, 먼저 영국의 NPL에서는 보유하고 있었던 수정진동자의 주파수를 세슘원자의 공진주파수에 일치(혹은 ‘잠금’)시켰다. 그리고 미국의 USNO에서는 평균태양시인 UT2에 주파수를 맞춘(잠근) 진동자를 가지고 있었다. 또한 Markowitz에 의해 특별히 고안된 달 카메라로 ET와 UT2의 차이를 알 수 있었다. 원래 ET는 태양의 천구상의 위치를 기준으로 만든 시간 눈금이지만, 태양의 움직임이 너무 늦기 때문에, 천구 상에서 가장 빠르게 움직이는 달의 움직임을 관측하여 얻는 방법이 주로 사용되었고, Markowitz는 이러한 달의 천구 상의 위치를 매우 정확하게 측정할 수 있는 특수한 달 카메라를 고안하였다. 이제 남은 것은 두 기관이 독립적으로 운용하고 있는 수정 진동자의 주파수를 비교하기만 하면 된다. 당시 시간을 가장 멀리 전송하는 수단은 장파 혹은 단파를 이용한 방송국이었다. 영국에는 GBR과 MSF이라는 이름의 방송국이 있었고, 미국에도 WWV라는 이름의 단파 방송국에서 시각 신호를 전송하였다. 거의 3년여에 걸친 동시 관측을 통해 마침내 세슘의 주파수 값이 UT2 기준으로 9,192,631,882 Hz라는 것을 알게 되었고, UT2를 ET로 변환하여 9,192,631,770(20) Hz 로 세슘의 주파수를 결정하였다. 여기서 괄호는 위아래로 20 Hz만큼의 불확도가 있을 수 있다는 뜻이다. (불확도에 대해서는 다음 장에서 다루기로 한다.)

ET가 시간의 공식적인 기본 단위가 되었던 1960년대 초에도 이미 몇몇 표준기관에서 만든 원자시계들이 천체 관측으로 얻을 수 있는 시간 눈금보다 훨씬 정확한 시간 눈금을 만들고 있었다. 그리고 앞의 두 나라의 동시 관측을 통해 세슘의 주파수가 결정되면서, 그동안 1년 넘게 달을 관측해야 비로소 얻을 수 있는 정확한 “초”를, 원자시계를 이용하면 수 분 만에 만들어 낼 수 있다는 것을 증명하였다. 결국 1967년 “초”는 세슘의 공진 주기의 9 192 631 770 배로 재정의되었다. 다시 말해 세슘의 주파수는 9 192 631 770 Hz로 고정된 것이다. 여기 숫자에서 주목할 점은 앞의 측정값과 달리 더 이상 괄호가 없다는 것이다. 마치 빛의 속도가 299 792 458 m/s로서 정해진 상수가 되었던 것처럼, 세슘의 주파수도 그 당시 측정한 가장 정확한 값을 이용하여 상수로 정의되었다. 이제 더 이상 시간은 천체의 움직임에 따라 좌우되지 않게 되었고, 천문학적인 시간은 그 역사적인 소명을 다하게 되었다.

3.시계의 정확도와 안정도(정밀도)

 앞서 지구의 자전이나 공전 등에서 생기는 불규칙적인 현상들이 시간 눈금의 구현에 있어 문제가 되었다고 언급하였다. 그렇다면 시간 눈금을 만드는 시계의 성능을 어떻게 정량적으로 측정할 수 있을까? 시계의 성능은 크게 “정확도^accuracy“와 “정밀도”로 구분할 수 있다. 특별히 시계의 경우 주파수가 시간에 따라 얼마나 안정적으로 나오는지가 정밀도를 결정하기 때문에, “정밀도”라는 표현보다는 “안정도^stability“라는 표현을 즐겨 쓰게 된다.

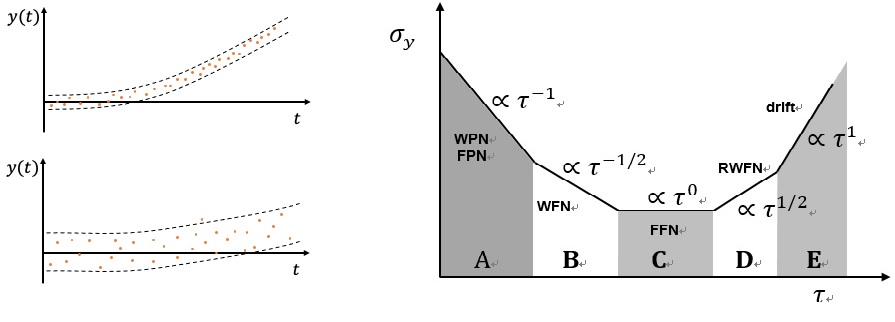
 그러면 주파수의 안정도를 나타내는 척도는 무엇이 있을까? “측정이란 무엇인가 2” 기고문에서 소개가 되었듯이, 안정도 혹은 정밀도는 데이터의 흩어진 정도를 알면 되기 때문에 통계적인 방법을 주로 사용하게 된다. 다만 시계의 경우는 통계적인 잡음 외에도, 시간에 의존하는 체계적 오차가 더해질 경우, 기존의 통계적인 방법으로 분석하기 어려운 경우가 생기게 된다. [그림4]의 경우를 살펴보자, 주파수를 y축, 시간을 x 축으로 하여, 시간에 따라 두 가지의 진동자의 주파수를 측정한 결과이다. 먼저 단순히 통계적인 방법을 사용하면, 값이 한 방향으로 늘어나기 때문에, 전체 데이터의 표준편차는 시간에 따라 계속 증가하게 될 것이다. 따라서 두 진동자의 특성을 표준편차만을 가지고 말하기 어렵다. [그림4]에서 위의 진동자의 경우는 시간에 따라 한 방향으로 흘러가는 경향이 아래의 진동자보다는 강하기 때문에 좋지 않은 진동자라고 생각할 수 있다. 하지만 짧은 시간 간격에서 데이터가 흩어진 정도를 살펴보면, 위의 진동자가 아래의 진동자보다 작기 때문에, 위의 진동자가 더 좋은 진동자라고도 말할 수도 있다. 사람마다 잠깐 보았을 때 좋은 사람이 있고, 오래 보아야 그 진가를 알 수 있는 사람이 있는 것처럼, 관측 시간에 따라 진동자의 특성이 달리 보이게 된다. 따라서 관측 시간에 따른 데이터의 특성을 반영한 지표가 필요하며, 이때 가장 많이 사용하는 지표가 알란분산^{Allan variance} 혹은 그 제곱근인 알란편차^{Allan deviation}이다. 이러한 분석 방법을 처음 개발한 미국 NIST의 David Allan 박사의 이름을 따서 지어진 명칭이다.

알란분산 혹은 알란편차를 간단하게 표현하면 인접한 두 평균 데이터 사이의 차이 값들만을 가지고 얻은 분산 또는 표준 편차라고 할 수 있다. 구하는 방법을 구체적으로 기술하면 다음과 같다. 먼저 알란편차를 구하고자 하는 관측시간간격을 \(\tau\)라고 하자. 그러면 데이터를 이 시간 간격으로 순서대로 묶는다. 예를 들어 1초마다 얻은 데이터가 있을 경우, 10초 관측시간의 알란편차를 구하고 싶으면, 1초~10초, 11~20초 등 각 구간별 평균을 구한다. 이를 시간의 순서대로 다음과 같이 나타내 보자.

 \(y_1, y_2, y_3, …. y_{N-1}, y_N\)

그러면 알란분산 \(\sigma_y^2\)(\(\tau)\)은 다음과 같이 쓸 수 있다.

\(\sigma_y^2\)(\(\tau)\)=\(\frac{1}{2}\)\(\langle (y_{i+1}-y_{i})^2\)\(\rangle\)=\(\frac{1}{2N}\)\(\sum_{i}^{N-1}(y_{i+1}-y_{i})^2\)

이렇게 구한 알란분산 혹은 알란편차의 좋은 점은 관측 시간 간격에 따른 값의 변화율을 보면 어떤 종류의 잡음이 있는지 매우 쉽게 알 수 있다는 점이다. [그림5]는 진동자 주파수의 알란편차의 예를 보여준다. 기울기가 -1인 A 구간의 관측시간동안은 백색위상잡음^{White phase noise, WPN}이나 플리커 위상잡음^{Flicker phase noise, FPN} 성분이 우세하고, 기울기가 -1/2인 B구간의 관측 시간 동안 측정하면 이제 백색 주파수 잡음^{White frequency noise, WFN}으로 잡음 성분이 바뀌게 되고, 기울기가 0인 C구간에서는 플리커 주파수 잡음^{Flicker frequency noise, FFN} 영역으로 들어간다. 이때부터는 아무리 오래 관측해도 더 이상 안정도가 좋아지지 않는다. 플리커 잡음의 흥미로운 특성이다. 오래 측정해서 평균을 한다고 항상 성능이 좋아지지 않는 경우가 여기서부터 생기기 시작한다. 그리고 더 길게 측정하면 기울기가 1/2인 D구간에 접어들면서, 임의 걸음 주파수 잡음^{Random walk frequency noise, RWFN}이 우세해지면, 안정도가 오히려 나빠지고 평균값이 시간에 따라 변하는 양상을 띠게 되며, 이보다 더 오래 측정하여 기울기가 1인 E구간에서는 평균 주파수 값이 시간에 따라 선형적으로 표류^drift하게 된다. 이러한 알란편차 관점에서 앞에서 살펴본 여러 가지 시간 눈금의 안정도를 비교한 그래프가 아래 [그림6]이다. 지구의 자전을 기준으로 한 UT의 경우 자전의 불규칙성으로 말미암아 표류하는 성질을 보인다. 역표시^ET의 경우는 UT보다 일정하기 때문에 오래 측정할수록 안정도가 좋아지는 것을 볼 수 있다. 하지만 시간을 결정하려면 많은 시간이 걸리는 것을 볼 수 있다. 이에 비해 원자시계를 기반으로 생성되는 “국제원자시”는 이러한 천체를 이용한 시간 눈금에 비해 월등한 성능을 보이는 것을 알 수 있다.

다음으로 원자시계의 정확도에 대해 살펴보자. 앞의 기고문 “측정이란 무엇인가 2” 기고문에서 설명했듯이, 이는 참값으로부터 떨어진 정도에 대한 예측을 얼마나 정확하게 알 수 있는지에 따라 결정된다. 즉 예측의 불확실한 정도, 곧 “불확^uncertainty”가 정확도를 결정하는 지표가 된다. 불확도가 작을수록 정확도는 높다. 다시 1967년 정의된 세슘 원자의 주파수로 돌아가면, 여기에는 몇 가지 가정이 더 있다. 주변 온도가 절대 온도 0 K이며, 어떤 주변의 환경에 의한 영향도 없는 가운데 결정된 공진주파수여야 한다. 하지만 우리가 사는 세상에 절대 온도가 0인 환경은 없으며, 전기장, 자기장 등 수 많은 환경 요인에 의해 원자의 공진주파수가 바뀔 수 있다. 이때 우리가 알아야 할 것은 원자의 주파수가 참값으로부터 얼마나 떨어져 있는지이며, 이를 완벽하게 알 수 없기 때문에, 확실하지 않은 정도, 즉 불확도가 존재하게 된다. 이 불확도를 얼마나 낮출 수 있느냐에 따라 원자시계의 성능이 좌우되며, 원자시계의 완성을 위해 가장 많은 시간과 노력이 필요한 부분이다. 다음 기고문에서 더 자세히 다룰 예정이지만, 예를 들어 온도에 의한 영향을 살펴보자. 세상 어느 곳도 완벽하게 온도가 절대온도 0 K인 곳은 없다. 그렇다면 어떻게 절대 온도 0 K에서의 주파수를 알 수 있을까? 일단은 온도에 따른 원자의 공진주파수 변화를 예측할 수 있는 물리적인 법칙을 찾는 것이 필요하다. 그 법칙에는 이론적으로만 계산이 가능한 변수와 실제 측정해야 하는 변수가 있을 것이다. 두 가지 모두 불확도를 가질 수 있다. 이론적인 계산의 경우 양자역학의 모든 효과를 포함하여 계산하는 것이 거의 불가능하기 때문에, 어느 정도 근사를 하면서 생기는 오차가 있을 수 있다. 또한 실제 측정의 경우도 완벽하게 불확도가 0인 측정은 있을 수 없기 때문에, 여기에서 생기는 불확도가 존재한다. 이러한 불확도 요인들을 종합하여, 주어진 온도와 절대온도 0 K에서의 주파수 차이를 추정할 때 생기는 오차의 불확도를 계산할 수 있다. 이러한 모든 요인을 고려하여, 현재 가장 정확하게 구현된 원자시계의 불확도는 주파수의 비율로 따지면 10^-18 수준이며, 우주가 시작하면서 시계가 동작하기 시작했다면, 지금까지 많아야 1초 정도 틀릴 것으로 예상되는 놀라운 수준이다. 이러한 불확도를 어떻게 달성하고, 산출하였는지 다음 편에서 자세히 살펴보도록 하자.